A dynamic cryptographic key assignment scheme in a tree structure

(1)

A D Y N A M I C C R Y P T O G R A P H I C

K E Y A S S I G N M E N T

S C H E M E I N A T R E E S T R U C T U R E

H. T. LIAW, S. J. W A N G A N D C. L. LEI Department of Electrical Engineering, National Talwan University

Taipei, Talwan 106, R.O.C.

(Received June 1995)

A b s t r a c t - - I n this paper, we propose a d y n a m i c cryptographic key assignment scheme based on Newton's i n t e r p o l a t i o n m e t h o d a n d a predefined one way function. All users are classified i n t o disjoint sets of security classes t h a t employ the relation o f p a r t i a l ordering, t h a t is, a security class at higher level can derive from his own cryptographic key the keys o f t h e o t h e r security class below him. C o m p a r e d with the existing assignment schemes, our scheme always produces economic cryptographic keys, which are smaller t h a n the keys generated by t h e previous work in a tree structure. Furthermore, whenever a new security class is inserted i n t o t h e user hierarchy system, the corresponding keys can b e d e t e r m i n e d without changing any existing keys. Therefore, our scheme is suitable for practical i m p l e m e n t a t i o n .

1. I N T R O D U C T I O N

Information security is a very important topic in the computer communication system. Up to the present, the popularity of computer networks and fast progress of computer technologies on a multi-user system make sharing of expensive resources a reality. However, sharing may cause some undesired phenomena such as unauthorized accesses and inconsistent status of shared resources. Therefore, an i m p o r t a n t issue in a multi-user computer environment is the question of how to control the access to computers. Besides, how to identify whether a user has enough privileges to retrieve the messages a n d / o r change the access rights of the other users is another i m p o r t a n t issue. To date, many papers [1-14] have addressed this problem. In this paper, we s t u d y this problem on a computer communication system organized in a tree structure. In order to broadcast information within a tree structured system, we need to have a m e t h o d to ensure the security of the system. A m e t h o d based on cryptography was proposed in [1] for controlling access to information among a group of users in a hierarchy. This m e t h o d employs the relation of partial ordering, t h a t is, a user at higher level can derive from his own cryptographic key the keys of the other users below him in the hierarchy organization, and then retrieve messages destined to the users at lower levels. In addition, this m e t h o d has another i m p o r t a n t p r o p e r t y of being able to provide security against two or more users at lower level of the system collaborating to derive a higher leveled key to which they are not entitled.

W h e n the n u m b e r of users becomes larger, the key generation algorithm in [1] becomes in- efficient and infeasible. Therefore, an improved m e t h o d was proposed in [12] for reducing the key values by using a canonical assignment method. Recently, Harn et ai. [8] presented another improved method. Instead of using the top-down key assignment approach as in [1,12], their scheme adopted a b o t t o m - u p approach.

Tree structure is a special case of the hierarchy structure, yet it is very popular in our daily life. For example, the personnel organization of a company or an army, the pedigree chart and the lineal chart [15] are typical tree structures. In this paper, we propose an efficient dynamic

This work was s u p p o r t e d in p a r t by the National Science Council of the Republic of C h i n a u n d e r the G r a n t NSC 81-0416-E-002-20.

Typeset by .AA~q-T ~ 109

(2)

cryptographic key assignment scheme in a tree structure for access control. The rest of this paper is organized as follows. In Section 2, we discuss the related research. Our efficient dynamic cryptographic key assignment scheme for assigning cryptographic keys in a tree structure is described in Section 3. The correctness of our security enforcing scheme is established in Section 4. Finally, concluding remarks are given in Section 5.

2 . R E L A T E D R E S E A R C H

A method for assigning cryptographic keys for access control in a hierarchy was first proposed in [1]. It assumes that all users in a computer communication system are distributed into m disjoint classes

Ci, i • S,

where S -- {1,2,... ,m}, and these classes receive messages from an authority Co. The set of classes is partially ordered by the partial ordering relation "<". If there exists a relation between Ci and

Cj,

i.e., Ci < Cj, it means that users in Cj can retrieve information destined for users in

Ci,

while the opposite is not allowed. Besides, every class

Ci,

i • S, must satisfy the relation

Ci <

Co, since no user in the system is allowed to retrieve messages of Co.

First, the authority Co generates a set of keys Ki's, and secretly sends each

Ki

to the class Ci, i = 1, 2 , . . . , m. In [1], the keys

Ki

can be generated as follows. A public integer

ti

is assigned to each class

Ci

with the condition

Ci <_ Cj

if and only if tj [ti.* (2.1)

In addition, the authority C0 chooses a random secret key K0 and a secret pair (p, q) of large prime numbers, and makes M = p • q public. Then Ki = K~ ~ (mod M) is sent to Ci. By condition (2.1),

ti/tj

is an integer if

Cj >_ Ci.

Thus, Cj can compute

Ki

by the following deduction

K, =

K~'

= (KtoJ) t'pj =

K~ 'l'i

(mod M).

However, if

Cj ~ C~,

then

ti/tj

is not an integer. Thus, Cj does not have the ability to retrieve the information destined to users in Ci in case the information is encrypted by

Ki.

Unfortunately, there exists a very serious problem: two or more users of the system can collaborate to derive a key to which they are not entitled. In order to avoid this drawback, a new scheme was proposed in [1]. This new scheme demands that each

ti,

1 < i < m, should be computed from t/ = 1-Ivj~gc~ PJ, where Pj, j • S, is a distinct prime assigned to Cj. These t~'s can ensure that condition (2.1) is not violated. Moreover, collaborative attacks are not possible.

Furthermore, a canonical assignment method [12] was proposed to reduce the value of ti. In this algorithm, the hierarchy structure is first decomposed into a set of disjoint chains. Each chain is a tOtally ordered subset and is assigned a distinct prime. For node i, they define the rule

ni = pe.,

where

ei

denotes the depth of the node from the top of the chain whose associated

prime is P. After all ni's are assigned,

ti's

are computed from the formula

ti -

lcmvjl~c~n j. Recently, Harn et

al.

[8] presented another improved method. Instead of using the top-down key assignment approach as in [1,12], their scheme adopts a bottom-up approach. It first assigns each security class

Ci

a distinct prime

Pi,

and makes these primes public. Then it calculates the multiplication inverse

di

for each class C/. It means that

di = p~-I

mod ¢(M), where ~ ( M ) denotes the Euler's number of M. This new scheme demands that each tj, 1 < j < m, should be computed from tj = l-I

Pi,

for all i such that

Ci

is the successor of

Cj.

Then Kj =

KorId,

rood ¢(M)(mo d M) is sent to Cj. Once the secret keys and the corresponding public keys

are generated, Cj can compute

Ki

by the following deduction

Ki = Kj j/t'

mod M.

The common drawback of the previous work is the size of storage for storing public keys grows dramatically. In the following section, we present a dynamic cryptographic key assignment scheme based on Newton's interpolation method and a predefined one way function. Comparing with the existing assignment schemes, our scheme always produces economic cryptographic keys, which are smaller than the keys generated by the previous work in a tree structure.

(3)

Cryptographic key assignment scheme

3. A D Y N A M I C K E Y A S S I G N M E N T S C H E M E F O R A C C E S S C O N T R O L IN A T R E E S T R U C T U R E

111

Since our proposed scheme is based on a predefined one way function and Newton's interpolation polynomials (NIP for short) [16-18] in this section, we first introduce their ideas and methods. Intuitively, a one way function is a function that is easy to apply but hard to reverse. Formally, if a function F : A -~ B is a one way function, it is a one-to-one function and implies that

(1) for every x in A, F(x) can be computed easily, and (2) for every y = F(x) in B, it is infeasible to compute z.

On the other hand, suppose there exist n + 1 points denoted as ( x l , y i ) , 0 < i < n. Then the NIP with degree n passing through these n + 1 points can be derived as

NP(x)

= •

j---O "--

(3.1)

Each coefficient f [ z 0 , x x , . . . , z j ] in equation (3.1) can be computed by the divided differences [16,17]. Without loss of generality, let each coefficient be represented in some residue class of prime P and P > yl, 0 < i < n. Then a NIP can be expressed as equation (3.2),

NP(~e) = (c~n(z - Xn-1)(x - x , - 2 ) . . . (x - z0) + " " + c~2(z - zx)(x - z0) + oq(z - x0)

+ c~0) rood P. (3.2) In equation (3.2), let N P ( z i ) = Yi rood P, 1 < i < n, and all c~i's are constant coefficients.

In our scheme, let P be a large prime number and F be a predefined one way function. Besides, both P and F are public. Furthermore, let Cil, Ci2,..., Ci~ be the immediate successors of Ci with the public key pairs ( t l q , t2q), ( t l i 2 , t 2 i 2 ) , . . . , (tli~,t2i~), respectively. In the following, an efficient algorithm for assigning the secret key and the corresponding public key pairs for each security class is presented. Our algorithm essentially consists of two phases.

(1) In the first phase, we assign public key pair (tll,t2i) for each security class Ci, starting from the root and going down to leaves.

(2) In the second phase, we generate secret key K~ for each security class Ci, starting from the root and going down to leaves.

The first phase of our algorithm assigns each security class Ci of the tree T a key pair (tl~,t2i), which is equal to the pair (c~i, zi) in NIP. After all ( t l l , t 2 i ) ' s are assigned, all Ki's are computed in phase 2.

ALGORITHM ASSIGNMENT INPUT: A tree T.

OUTPUT: A set of (tli, t2i)'s and Ki's being assigned to the nodes of T, respectively.

Phase 1: Assign public key pair (tli, t2i) for each node Ci, starting from the root and going down to leaves.

STEP 1.1: Assign distinct key pairs ( t l l , t 2 i ) ' s for all the non-root nodes Ci's, 1 < i < n. Phase 2: Generate a secret key Ki for each node Ci, starting from the root and going down to

leaves.

STEP 2.1: For root node Co, do

(2.1.1) randomly select an integer K0 among 1 and P - 1.

(2.1.2) let C1, C 2 , . . . , Ck be immediate successors of Co, then generate a NIP of degree k over the Galois field G F ( P ) , denoted as N P ( x ) = ( a k ( z - Z~-l)(X - z k - 2 ) . . . ( X - X 0 ) + ' ' " "~ a l ( X - X0)+ a0) mod P, where (ao,zo) = (0, Ko), and ( a i , z i ) = (tli,t2i), 1 < i < k.

(4)

STEP 2.2: For each non-root and non-leaf node (7/, do

(2.2.1) let

Cil, C i 2 , . . . , Cik

be immediate successors of

Ci,

then generate a NIP of degree k over the Galois field

GF(P),

denoted as

N P ( x )

= (ak(z - Zk_l)(Z - z k - 2 ) . . .

( X - X 0 ) . ~ t . . . . + O~1( x __ X0 ) + O~0) m o d P , where ( a 0 , z 0 ) =

(o, gl),

and ( a j , z j ) =

(tlb,t2ij), 1 < j <_ k.

(2.2.2) compute the secret key

Kij

of

Cij as Kij =

F(NP(t2ij))

mod P, 1 < j < k. The following example illustrates how

Ki's

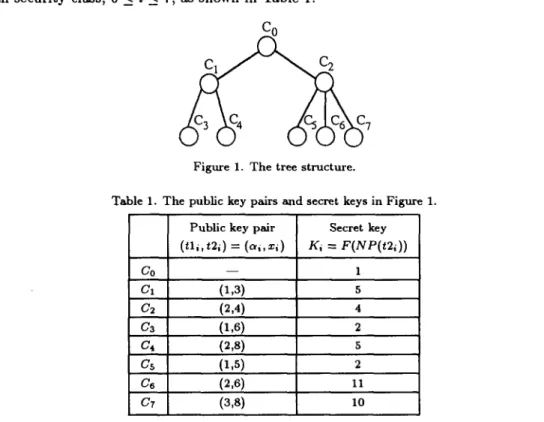
are assigned by the algorithm proposed above. EXAMPLE 1. Consider the tree structure as depicted in Figure 1. Without loss of generality, let the prime number P = 13 and the pseudo one way function F(x) = z 2 + 1 (mod P). By employing the algorithm Assignment, C0 can assign public key pairs

(tli,t2i)

and generate

Ki

for each security class, 0 < i < 7, as shown in Table 1.

C o

Figure 1. The tree structure.

Table I. T h e public key pairs and secret keys in Figure I.

Co

C1

C4

CZ

Public key pair Secret key ( t l i , t 2 i ) = ( a i , x i ) K i = F ( N P ( t 2 1 ) ) - - 1 (x,3) 5 (2,4) 4 (1,6) 2 (2,s) s (1

,s)

2 (2,6) 11 (3,8) I0

Note that the security class Ci can compute the keys of the security classes below him, which is not an immediate successor, by repeatedly employing algorithm Derivation below.

A L G O R I T H M DERIVATION

INPUT: Secret key Ki.

O U T P U T : Secret key

Kij.

STEP 1: Using Newton's interpolation method, reconstruct interpolating polynomial

N P ( z ) =

( ~ k ( x - - ~ _ , ) ( z - - x k _ 2 ) . . . ( z - - x 0 ) + . . . - h a l (z--x0)q-a0) mod P, where (so, z0) - (0, g , ) , and

( a j , x j ) = (tlij,t21~), 1 < j < k.

STEP 2: Compute the secret key

Ki, as Ki i = F(NP(t2ij))

rood P, where

t2ij

is the public key

of

Cij.

Now, a new node is inserted to the tree structure, say Cs. Figure 2 shows this condition.

C o

(5)

Cryptographic key assignment scheme 113 In our scheme, whenever a new node is inserted into the user hierarchy system, the corresponding secret key will be determined i m m e d i a t e l y without changing any previously defined secret keys and public key pairs. T h a t is, by employing the algorithm Assignment, a new public key pair ( t l s , t 2 s ) = (4, 7) is given and a secret key K s is c o m p u t e d as

N P ( z ) = 4 ( x - S ) ( x - 6 ) ( x - 5 ) ( z - 4 ) + 3 ( x - 6 ) ( x - 5 ) ( x - 4 ) + 2 ( x - 5 ) ( z - 4 ) T l ( x - 4 ) + O ) m o d 13. Thus, N P ( 7 ) - ( - 2 4 + 18 + 12 + 3) m o d 13 = 9 and K e = F ( N P ( 7 ) ) "- (92 + 1) m o d 13 = 4.

4. T H E S E C U R I T Y A N D C O M P U T A T I O N A L C O M P L E X I T Y

In our scheme, each security class Ci can derive the secret keys of his i m m e d i a t e successors by using N I P and the predefined one way function F. However, it is impossible to reconstruct N I P by only knowing the public key pairs of Ci's i m m e d i a t e successors, because all the public key pairs of C i ' s i m m e d i a t e successors can only construct an N I P ' , which has one less degree t h a n t h a t of the original NIP. Therefore, our scheme can provide security against two or more users at lower level of the s y s t e m collaborating to derive a higher leveled key to which they are not entitled. In addition, each i m m e d i a t e successor Ci~ of Ci cannot reveal the root of N I P by using his secret key K i j , because the secret key is c o m p u t e d f r o m the predefined one way function F . Hence, a user at lower level cannot derive f r o m his own c r y p t o g r a p h i c key the keys of the other users above h i m in a tree structure. Hence, the correctness of our security enforcing scheme is established. Furthermore, it is easily seen t h a t the c o m p u t a t i o n a l complexity of our scheme heavily relies on the construction of NIP. However, K n u t h [18] has proposed an efficient 0(k log s k) time algorithm for NIP, where k is the n u m b e r of i m m e d i a t e successors of the current security class. Therefore, our scheme only needs O ( n log s n) time for practical i m p l e m e n t a t i o n .

5. C O N C L U D I N G R E M A R K S

In this paper, we have proposed a d y n a m i c scheme to assign c r y p t o g r a p h i c keys in a tree s t r u c t u r e for access control. It is ensured to prevent the cooperative attacks and effectively reduce the values of ti's. Besides, no modification of the secret keys and public key pairs is needed when a new security class is inserted into the s y s t e m or an old security class is deleted f r o m the s y s t e m , while almost all past access control schemes need. Hence, this scheme is feasible for assigning c r y p t o g r a p h i c keys in a tree structure.

REFERENCES

1. S.G. Aid and P.D. Taylor, Cryptographic solution to a problem of access control in a hierarchy, A CM Transactions on Computer System 1 (3), 239-247 (August 1983).

2. C.C. Chang, On the design of a key-lock*pair mechanism in information protection systems, B I T 26,410--417

(1986).

3. C.C. Chang, An information protection system scheme based upon number theory, The Computer Journal 30 (3), 249-253 (1987).

4. C.C. Chang, On the implementation of user hierarchy structure in information system, In Proceedings of International Conference on Computer Software and Applications, IEEE, Tokyo, Japan, 412-415, (October

1987).

5. R.W. Conway, W.L. Maxwell and H.L. Morgan, On the implementation of security measures in information systems, Communication of A C M 1 5 (4), 211-220 (1972).

6. G.S. Graham and P.L. Denning, Protection-principles and practices, In Proe. Spring Jr. Computer Confer- ence, Vol. 40, AFIPS Press, Montvale, N.J., 417-429, (1972).

7. E. Gudes, The design of a cryptography-based secure file system, IEEE Transactions on Software Engi- neering (5), 411-419 (September 1980).

8. L. Ham and H.Y. Lin, A cryptographic key generation scheme for multilevel data security, Computers Security 9,539-546 (1990).

9. J.K. Jan, A single-key access control scheme in information protection systems, Information Sciences 51, 1-11 (1990).

10. J.K. Jan, C.C. Chang and S.J. Wang, A dynamic key-lock-pair access control scheme, Computers ~ Security 10 (2), 129-139 (1991).

11. C.H. Lin, Ft.C.T. Lee and C.C. Chang, A dynamic access control mechanism in information protection systems, Journal of Information Science and Engineering 6, 25-35 (1990).

(6)

12. S.T. Mackinon, P.D. Taylor, H. Meijer and S.G. Akl, An optimal algorithm for assigning cryptographic keys to control access in a hierarchy, IEEE TransactionJ on Computere C-34 (9), 797-802 (September 1985). 13. J.H. Seltzer and M.D. Schroeder, The protection of information in computer systems, In Working papers

presented at the Proc. IEEE, 1278-1308, (September 1975).

14. M.L. Wu and T.Y. Hwang, Access control with single-key-lock, IEEE Transactions On Software Engineering SE-10 (2), 185--191 (March 1984).

15. E. Horowitz and S. Smmi, F*tndamentab o / D a t , Structures, Computer Science Press, Rockvile, MD. 16. R.L. Burden, J.D. Falres and A.C. Reynolds, N~merical AnalyJis, 2 nd ed., Prindle, Weber & Schmidt,

Reading, MA, (1981).

17. M.K. Jaln, S.R.K. Lyengar and R.K. J&in, Numerical Methods for Scientific and Engineering Computation, Wiley Eastern, New Delhi, (1985).

18. D.E. Knuth, The Art of Computer Programming, Vol. 2 (Seminumerical Algorithm), 2 nd ed., Addi- son-Wesley, Reading, MA, (1980).