遞迴圖上泛迴圈相關性質之研究
Pancyclic Properties of the WK-Recursive Networks
方覺非1,* Jywe-Fei Fang 馮士丞1 Shr-Cheng Feng 黃玉潔2 Yu-Chieh Huang 1國立台中教育大學 數位內容科技系
Department of Digital Content and Technology
National Taichung University * jffang@mail.sju.edu.tw
2國立台中教育大學
資訊科學系
Department of Computer and
Information Science
National Taichung University
Abstract
In this paper, we study the pancyclic properties of the WK-Recursive networks. We show that a WK-Recursive network with amplitude W and level L is vertex-pancyclic for W ≥ 6. That is, each vertex on them resides in cycles of all lengths ranging from 3 to
N, where N is the size of the interconnection network.
On the other hand, we also investigate the
m-edge-pancyclicity of the WK-Recursive network.
We show that the WK-Recursive network is strictly 3×2L-1-edge-pancyclic for W ≥ 7 and L ≥ 1. That is,
each edge on them resides in cycles of all lengths ranging from 3×2L-1 to N; and the value 3×2L-1
reaches the lower bound of the problem.
Keyword: Pancyclicity, Interconnection networks,
WK-Recursive networks.
1. Introduction
In massively parallel MIMD systems, the topology plays a crucial role in issues such as communication performance, hardware cost, potentialities for efficient applications and fault tolerant capabilities [9, 16]. A topology named
WK-Recursive network has been proposed [24]. The
topology has many attractive properties, such as high degree of regularity, symmetry and efficient communication. Particularly, for any specified number of degree, it can be expanded to an arbitrary size level without reconfiguring the edges. Because it demonstrates many attractive properties, researchers have devoted themselves to various issues of the WK-Recursive networks, such as broadcasting
algorithms [12], topological properties [18, 14] and communication [8].
Paths and cycles are popular interconnection
networks owing to their simple structures and low degree. Moreover, many parallel algorithms have been devised on them [16, 17, 19]. Many literatures have discussed how to embed cycles and paths into various topologies [3, 5, 16]. A cycle with length s is denoted by Cs, where s ≥ 3. A graph is Hamiltonian if
it embeds a Hamiltonian cycle that contains each vertex exactly once [7]. In other words, that a graph is Hamiltonian implies that it embeds the maximal cycle. However, in the resource-allocated systems, each vertex may be allocated with or without a resource [4, 10]. Thus, it makes sense to discuss how to join a specific pair of vertices with a Hamiltonian
path in such systems. For example, let X and Y be
two vertices in a resource-allocated system, where the former and the latter are assigned with an input device and an output device, respectively. If we find a Hamiltonian path joining the pair of vertices, we can utilize the whole system to perform the systolic algorithm on a linear array [19]. A graph is Hamiltonian-connected if there is a Hamiltonian path joining each pair of vertices. No wonder that there are many researchers discussing the
Hamiltonian-connectivity of various interconnection
networks [6, 20].
On the other hand, to execute a parallel program efficiently, the size of the allocated cycle must accord with the problem size of the program. Thus, many researchers study the problem of how to embed cycles of different sizes into an interconnection network. A graph is pancyclic if it embeds cycles of every length ranging from 3 to N, where N is the size of the graph [2]. A graph is
m-pancyclic if it embeds cycles of every length
ranging from m to N, where 3 ≤ m ≤ N. Clearly, an
heterogeneous computing system, each vertex and
each edge may be assigned with distinct computing power and distinct bandwidth, respectively [22]. Thus, it is meaningful to extend the pancyclicity to the
vertex-pancyclicity and the edge-pancyclicity [1, 11,
15]. A graph is vertex-pancyclic (edge-pancyclic) if each vertex (edge) lies on cycles of every length ranging from 3 to N. Clearly, each edge-pancyclic graph must be vertex-pancyclic.
The concepts of the vertex-pancyclicity and the edge-pancyclicity are generalized to the
m-vertex-pancyclicity and the m-edge-pancyclicity
[21]. A graph is said to be m-vertex-pancyclic (m-edge-pancyclic) if each vertex (edge) lies on cycles of all lengths ranging from m to N. Obviously, every m1-vertex-pancyclic (m1-edge-pancyclic) graph
must be m2-vertex-pancyclic (m2-edge-pancyclic),
where N ≥ m2 ≥ m1. A graph is strictly
m-vertex-pancyclic (m-edge-pancyclic) if it is not
(m-1)-vertex-pancyclic ((m-1)-edge-pancyclic) but
m-vertex-pancyclic (m-edge-pancyclic); that is, the
value m reaches the lower bound of the problem. Clearly, every m-edge-pancyclic graph is
m-vertex-pancyclic. A graph G with N vertices is panconnected if for each pair of distinct vertices X, Y
and for any integer d(X, Y) ≤ l ≤ N-1, there exists a path of length l in G connecting X and Y, where d(X,
Y) is the distance between X and Y in G [6].
A WK-Recursive network with amplitude W and level L is denoted by a WK(W, L). Vecchia and Sanges have shown that a WK(W, L) is Hamiltonian for W ≥ 3 [24]. Fernandes et al. have shown that a WK(W, L) is pancyclic for W ≥ 5 [13]. However, to the best of our knowledge, there exists no article addressing the m-vertex-pancyclicity and the
m-edge-pancyclicity of the WK(W, L). In this paper,
we show that a WK(W, L) is vertex-pancyclic for W ≥ 6. The WK(W, L) network is strictly
7-vertex-pancyclic, for 5 ≥ W ≥ 4 and L ≥ 2. On the other hand, we also prove that the WK(W, L) is strictly 3×2L-1-edge-pancyclic for W ≥ 7 and L ≥ 1.
The rest of this paper is organized as follows. In Section 2, we present some notations and background that will be used throughout this paper. In Section 3, we study the pancyclicity and the
m-vertex-pancyclicity of the WK-Recursive network.
In Section 4, we investigate the m-edge-pancyclicity of the WK-Recursive network. Conclusions are given in Section 5.
2. Notations and background
A WK(W, L) can be recursively constructed. A WK(W, 0) is a vertex with W free edges. A WK(W, 1) is a W-vertex complete graph that is denoted by a KW.Each vertex has one free edge and W-1 edges that are used for connecting to the other vertices. Clearly, a
WK(W, 1) has W vertices and W free edges. A WK(W,
H) consists of W copies of WK(W, H-1) as
supervertices and the W supervertices are connected as a KW, where 2 ≤ H ≤ L. By induction, it is easy to
see that a WK(W, L) has WL vertices and W free
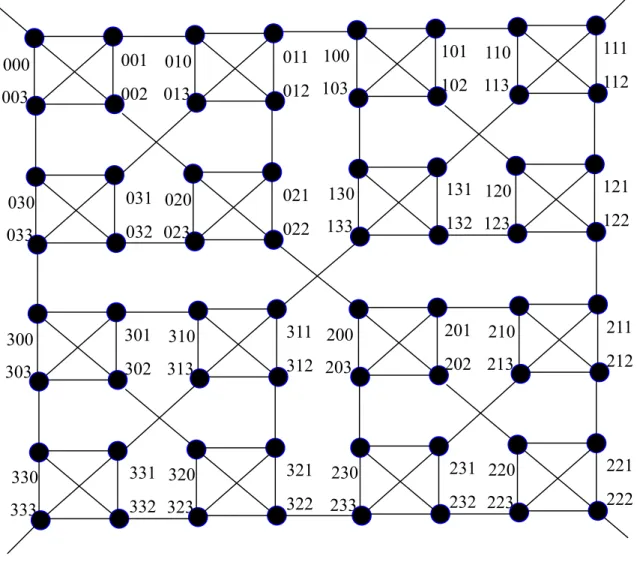
edges. Consequently, for any given amplitude W, WK-Recursive networks can be expanded to any arbitrary level L without reconfiguring the edges. In Figure 1, the structures of a WK(4, 0), a WK(4, 1), a WK(4, 2) and a WK(4, 3) are illustrated.
The following addressing scheme for a WK(W,
L) is described in [23]. After fixing an origin and an
orientation (clockwise or counterclockwise), for each WK(W, 1) subnetwork, every vertex is labeled with an index digit d1 ∈ {0, 1, …, W-1}. Likewise, for
each WK(W, H) subnetwork, every WK(W, H-1) subnetwork is labeled with an index dH ∈ {0, 1, …,
W-1}, where 2 ≤ H ≤ L. Hence, each vertex of a WK(W, L) is labeled with an unique address
dLdL-1…d2d1 as illustrated in Figure 1. Likewise, a
subnetwork of a WK(W, L) can be represented by a string of L symbols over set {0, 1, …, W-1} ∪ {*}, where * is a “don't care” symbol. That is, each WK(W, H) subnetwork of a WK(W, L) can be denoted by dLdL-1…dH+1(*)H, where (*)H represents H
consecutive *’s. For example, in a WK(4, 3), 0** is the subnetwork {0d2d1 | 0 ≤ d2 ≤ 3 and 0 ≤ d1 ≤ 3 }.
For a subnetwork dLdL-1…dH+1(*)H in a WK(W,
L), a vertex with address dLdL-1…dH+1(dH)H is called a
corner vertex of dLdL-1…dH+1(*)H. For example, in a
WK(4, 3), 000, 011, 022 and 033 are corner vertices of 0**. Specifically, the vertex dLdL-1…dH+1(dH)H is
called the dH-corner of dLdL-1…dH+1(*)H. For example,
in a WK(4, 3), 033 is called 3-corner of 0**. In this paper, an edge within a WK(W, 1) subnetwork is called an inner-cluster edge.
Definition 1. The inner-cluster edges of vertex
dLdL-1…d2d1 are defined as (dLdL-1…d2d1,
dLdL-1…d2h), where 0 ≤ h ≤ W-1 and d1≠ h.
For example, in a WK(5, 3), (002, 000), (002, 001), (002, 003) and (002, 004) are inner-cluster edges of the vertex 002. Clearly, each vertex has W-1 inner-cluster edges in a WK(W, L). An edge connecting two WK(W, H) subnetworks, where 1 ≤ H ≤ L-1, is called an inter-cluster edge and specifically a level-H edge.
Definition 2. The level-H inter-cluster edge of vertex
dLdL-1…dH+1(dH)H, where dH+1≠ dH, is defined as
(dLdL-1…dH+1(dH)H, dLdL-1…dH(dH+1)H ).
For example, in a WK(4, 3), (022, 200) is a level-2 edge. Observe that each vertex except the corner vertices (dL)L has exactly one inter-cluster
edge in a WK(W, L). Each corner vertex (dL)L of a
WK(W, L) has no inter-cluster edge but a free edge. In this paper, the outline graph of a WK(W, L), denoted by an OG(WK(W, L)), is to take each WK(W, 1) subnetwork as a supervertex. As stated before, a
WK(W, L) can be constructed recursively. If each WK(W, 1) subnetwork of a WK(W, L) is taken as a supervertex, the WK(W, L) will be transformed to a WK(W, L-1). Moreover, each original level-1 inter-cluster edge will be an inner-cluster edge in the WK(W, L-1); and each original level-J inter-cluster edge will be a level-(J-1) inter-cluster edge in the WK(W, L-1), where L-1 ≥ J ≥ 2. We have the following proposition.
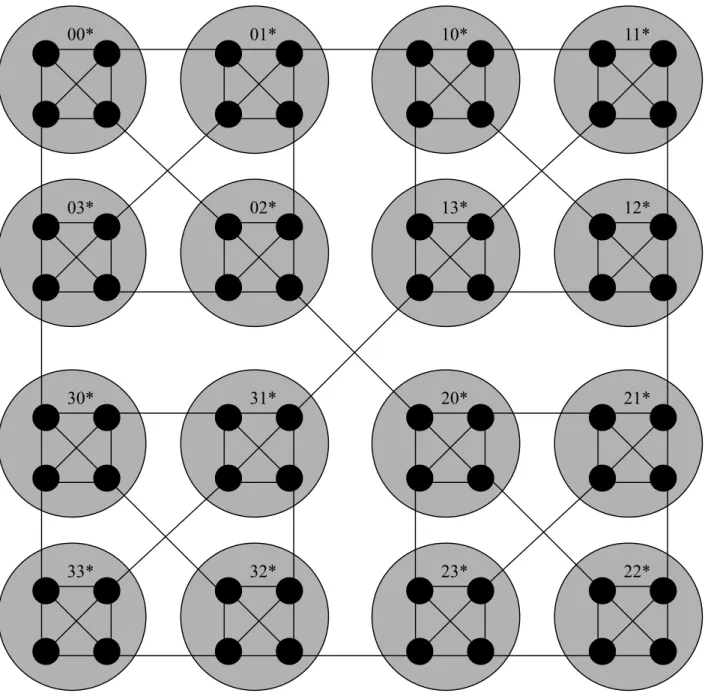
Proposition 1. An OG(WK(W, L)) is a WK(W, L-1).
As illustrated in Figure 2, the OG(WK(4, 3)) is a WK(4, 2). Because an OG(WK(W, L)) is a WK(W,
L-1); and each vertex of the WK(W, L-1) has W-1
inner-cluster edges, thus we have
Proposition 2. In each WK(W, 1) subnetwork of a
WK(W, L), there exist W-1 level-1 edges and at most one higher level edge.
3. The Pancyclicity and the
Vertex-Pancyclicity of a
WK-Recursive Network
In this section, we will discuss the pancyclicity and the vertex-pancyclicity of the WK-Recursive network. Suppose that vertices U1, U2, …, UW locate
in a common WK(W, 1) subnetwork. Because a WK(W, 1) subnetwork is a KW, (U1, UW) forms a path
of length 1. The vertex Uj is called an appending
vertex, where 2 ≤ j ≤ W-1.Clearly, appending vertices can be appended one by one to the path. That is, (U1,
U2, …,Ui , UW) forms a path of length i, where 1 ≤ i
≤ W-1. Recall that OG(WK(W, L)) is obtained from
WK(W, L) by taking each WK(W, 1) subnetwork as a
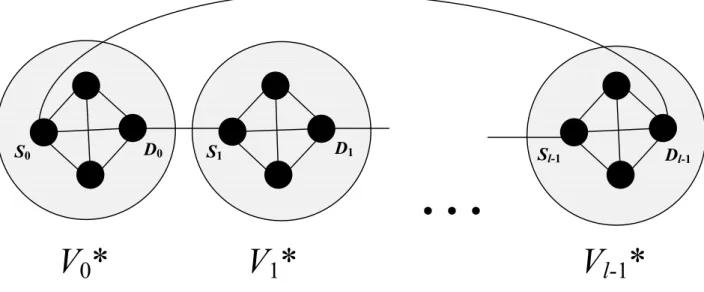
supervertex. Suppose that there is a cycle of length l, denoted by (V0*, V1*, V2*, …,Vl-1*), in the
OG(WK(W, L)) as illustrated in Figure 3. Clearly,
there exists an inter-cluster edge connecting consecutive two WK(W, 1) supervertices in the cycle.
Since each vertex has one inter-cluster edge at most, we can find two vertices Si and Di in each
supervertex Vi*, where 0 ≤ i ≤ l-1, such that they
are incident to the inter-cluster edges connecting to
V(i-1) mod l* and V(i+1) mod l*, respectively. Obviously, (S0,
D0, S1, D1,… , Sl-1, Dl-1) forms a cycle of length 2l. In
each supervertex Vi*, there are W-2 appending
vertices. Totally, there exist (W-2)l appending vertices. Thus, we have the following lemma.
Lemma 1. If there exists a cycle of length l in the
OG(WK(W, L)), a WK(W, L) embeds cycles of all
lengths ranging from 2l to Wl.
Theorem 2. A WK(W, L) is pancyclic for W ≥ 5.
Proof. We will prove the theorem by induction on L.
For L = 1, a WK(W, 1) is a KW. Clearly, it embeds
cycles of all lengths ranging from 3 to W, where W ≥ 5.
Hypothesis: Suppose that a WK(W, k) is pancyclic. Induction Step: Recall that OG(WK(W, k+1)) is a
WK(W, k) network. By the hypothesis, we know that a WK(W, k) embeds cycles of all lengths ranging from 3 to Wk. Thus, by Lemma 1, a WK(W, k+1)
can embed {Cs| 6 ≤ s ≤ 3 W } (for 3 WK(W, 1) supervertices) ∪ {Cs| 8 ≤ s ≤ 4 W } (for 4 WK(W, 1) supervertices) …, ∪ {Cs| 2n ≤ s ≤ n W } (for n WK(W, 1) supervertices) ∪ {Cs| 2(n+1) ≤ s ≤ (n+1) W } (for n+1 WK(W, 1) supervertices) …, ∪ {Cs| 2Wk ≤ s ≤ WkW =Wk+1} (for Wk WK(W, 1) supervertices).
Clearly, nW is always greater than 2(n+1) for W ≥ 5 and n ≥ 3. Thus, a WK(W, k+1) can embed {Cs| 6
≤ s ≤ W k+1}. By the recursive structure of the
WK-Recursive Network, the WK(W, 1) is a subgraph of a WK(W, k+1) for k ≥ 1. Thus, we know that a WK(W, k+1) can embed {Cs| 3 ≤ s ≤ W} ∪ {Cs|
6 ≤ s ≤ W k+1} = {C
s| 3 ≤ s ≤ W k+1}, where W ≥ 5.
This extends the induction and completes the proof. Q. E. D.
Although, in fact, the above theorem has been shown by Fernandes et al. [13], our proof is much easier and clearer. Moreover, we will discuss the
m-vertex-pancyclicity and the m-edge-pancyclicity of
a WK(W, L) upon the above discussion.
In the following, we investigate the
m-pancyclicity of a WK(4, L). Obviously, a WK(4, 1)
embeds C3 and C4. By Lemma 1, a WK(4, 2) can
embed {Cs| 6 ≤ s ≤ 12 }∪{Cs| 8 ≤ s ≤ 16 } = {Cs| 6 ≤
s ≤ 16 }. Suppose that a WK(4, k) can embed {Cs| 6 ≤
s ≤ 4k } for k ≥ 3. Likewise, a WK(4, k+1) can embed
{Cs| 12 ≤ s ≤ 24 } ∪ {Cs| 14 ≤ s ≤ 28 } ∪…∪ {Cs|
2(4k-1) ≤ s ≤ 4(4k-1) } ∪ {C
s| 2×4k ≤ s ≤ 4×4k = 4k+1 }
= {Cs| 12 ≤ s ≤ 4k+1}. By the recursive structure of a
WK(W, L), the WK(4, 2) is a subgraph of a WK(4, L) for L > 2. Thus, a WK(4, k+1) can embed {Cs| 6 ≤ s ≤
16} ∪ {Cs| 12 ≤ s ≤ 4k+1} = {Cs| 6 ≤ s ≤ 4k+1}. Thus,
we have
Lemma 3. A WK(4, L) is 6-pancyclic, where L ≥ 2. Then, the m-pancyclicity of a WK(3, L) is studied. Because a WK(3, 1) is nothing but a C3, a
WK(3, 2) can embed {Cs| 6 ≤ s ≤ 9} by Lemma 1.
We have
Corollary 4. A WK(3, 2) is 6-pancyclic.
A WK(3, 3) can embed {Cs| 12 ≤ s ≤ 27}.
Similarly, if a WK(3, k) can embed {Cs| 12 ≤ s ≤ 3k},
where k ≥ 3, a WK(3, k+1) can embed {Cs| 12 ≤ s ≤
27} ∪ {Cs| 24 ≤ s ≤ 3k+1 } = {Cs| 12 ≤ s ≤ 3k+1 }. Thus,
we have
In the following, we investigate the vertex-pancyclicity and the m-vertex-pancyclicity of a WK(W, L).
Lemma 6. If each WK(W, 1) supervertex resides in a
cycle of length l in the OG(WK(W, L)), each vertex of a WK(W, L) resides in cycles of all lengths ranging from 2l+1 to Wl.
Proof. Suppose that an arbitrary vertex X of a WK(W, L) reside in the supervertex V0* of the OG(WK(W,
L)). By the hypothesis, there exists a cycle, denoted
by (V0*, V1*, V2*, …, Vl-1*), of length l containing
V0* in the OG(WK(W, L)). As illustrated in Figure 3,
there exists an inter-cluster edge connecting consecutive two WK(W, 1) supervertices in the cycle.
Since each vertex has one inter-cluster edge at most, we can find two vertices Si and Di in each
supervertex Vi*, where 0 ≤ i ≤ l-1, such that they are
incident to the inter-cluster edges connecting to
V(i-1) mod l* and V(i+1) mod l*, respectively. Obviously, (S0,
D0, S1, D1, …, Sl-1, Dl-1) forms a cycle of length 2l.
Case 1: X is not S0 and X is not D0. Clearly, (S0, X,
D0, S1, D1, …, Sl-1, Dl-1) forms a cycle of length 2l+1.
Totally, there are (W-2)l-1 appending vertices. Thus,
X resides in cycles of all lengths ranging from 2l+1 to Wl.
Case 2: Xis S0 or X is D0. Clearly, X resides in cycles
of all lengths ranging from 2l to Wl. Q. E. D
Theorem 7. A WK(W, L) is vertex-pancyclic for W ≥ 6.
Proof. We will prove the theorem by induction on L.
For L =1, a WK(W, 1) is a KW. Clearly, it’s
vertex-pancyclic.
Hypothesis: Suppose that a WK(W, k) is
vertex-pancyclic, where W ≥ 6.
Induction Step: Because the OG(WK(W, k+1)) is a
WK(W, k). By the hypothesis, we know that each supervertex of the OG(WK(W, k+1)) resides in cycles of all lengths ranging from 3 to Wk. From the Lemma
6, we know that each vertex of a WK(W, k+1) resides in {Cs| 7 ≤ s ≤ 3 W } (for 3 WK(W, 1) supervertices) ∪ {Cs| 9 ≤ s ≤ 4 W } (for 4 WK(W, 1) supervertices) …, ∪ {Cs| 2n+1 ≤ s ≤ n W } (for n WK(W, 1) supervertices) ∪ {Cs| 2n+3 ≤ s ≤ (n+1) W } (for n+1 WK(W, 1) supervertices) …, ∪ {Cs| 2Wk+1 ≤ s ≤ WkW =Wk+1} (for Wk WK(W, 1) supervertices).
For W ≥ 6 and n ≥ 3, nW is always greater than 2n+3. Thus, each vertex of a WK(W, k+1) resides in cycles of all lengths ranging from 7 to Wk+1. By the
recursive structure of the WK-Recursive Network, each vertex of a WK(W, k+1) must reside in a WK(W,
1) subnetwork. Thus, each vertex of a WK(W, k+1) resides in {Cs| 3 ≤ s ≤ W} ∪ {Cs| 7 ≤ s ≤ Wk+1} =
{Cs| 3 ≤ s ≤ Wk+1} for W ≥ 6. Q. E. D.
Then, we investigate the vertex-pancyclicity of a WK(4, L) and a WK(5, L). Clearly, a WK(4, 1) and a WK(5, 1) are vertex-pancyclic for L = 1. That is, each vertex of a WK(4, 1) (WK(5, 1)) resides in {Cs|
3 ≤ s ≤ 4} ({Cs| 3 ≤ s ≤ 5}). From Lemma 6, we know
that each vertex of a WK(4, 2) (WK(5, 2)) resides in {Cs| 7 ≤ s ≤ 16} ({Cs| 7 ≤ s ≤ 25}). Thus, a WK(4, 2)
and a WK(5, 2) are 7-vertex-pancyclic. Suppose that a WK(4, k) and a WK(5, k) are 7-vertex-pancyclic for
k ≥ 2. By the recursive structure of the WK(W, L), each vertex of a WK(W, k+1) must reside in a WK(W, 2) subnetwork for k > 2. According to Lemma 6, each vertex of a WK(4, k+1) (WK(5, k+1)) resides in {Cs|
7 ≤ s ≤ 16} ∪ {Cs| 15 ≤ s ≤ 4 k+1} = {Cs| 7 ≤ s ≤ 4 k+1}
({Cs| 7 ≤ s ≤ 25} ∪ {Cs| 15 ≤ s ≤ 5 k+1}= {Cs| 7 ≤ s ≤ 5 k+1}). Thus, we have
Lemma 8. A WK(4, L) and a WK(5, L) are
7-vertex-pancyclic, where L ≥ 2.
In a WK(4, L) (WK(5, L)), a corner vertex (dL)L
has no inter-cluster edge, where 0 ≤ dL ≤ 3 (0 ≤ dL ≤ 4)
and L ≥ 2. Thus, the corner vertex cannot reside in a
C6.
Corollary 9. A WK(4, L) and a WK(5, L) are strictly
7-vertex-pancyclic, where L ≥ 2.
A WK(3, 1) is nothing but a C3. From Lemma 6,
each vertex of a WK(3, 2) resides in {Cs| 7 ≤ s ≤
9}. Each vertex of a WK(3, 3) resides in {Cs| 15 ≤ s ≤
27}. Each vertex of a WK(3, 4) resides in {Cs| 31 ≤
s ≤ 81}. If each vertex of a WK(3, k) resides in {Cs|
31 ≤ s ≤ 3k} for k ≥ 4, each vertex of a WK(3, k+1)
resides in {Cs| 63 ≤ s ≤ 3k+1}. By the recursive
structure of the WK-Recursive Network, each vertex of a WK(W, k+1) must reside in a WK(W, k) subnetwork. Clearly, 3k is always greater than 63 for
k ≥ 4. Thus, each vertex of a WK(3, k+1) resides in {Cs| 31 ≤ s ≤ 3k} ∪ {Cs| 63 ≤ s ≤ 3k+1} = {Cs| 31 ≤ s ≤
3k+1 } for k ≥ 4. Thus we have
Lemma 10. A WK(3, L) is 31-vertex-pancyclic for L
≥ 4.
4. The Edge-Pancyclicity of a
WK-Recursive Network
In this section, we investigate the edge-pancyclicity of the WK-Recursive network. To study the edge-pancyclicity of a WK-Recursive network, the following lemmas are required.
Lemma 11. If each inner-cluster edge of the
OG(WK(W, L)) resides in a cycle of length l, each
inner-cluster edge of a WK(W, L) resides in cycles of all lengths ranging from 2l+2 to Wl, where W ≥ 4.
Proof. In a WK(W, L), let (X, Y) be an arbitrary
inner-cluster edge residing in an arbitrary WK(W, 1) supervertex V1*. By Proposition 2, because W ≥ 4,
there exists a vertex S1 residing in the V1* such that S1
≠ X and S1 ≠ Y; and S1 is incident to a level-1 edge
(V0*, V1*) of the WK(W, L). By the hypothesis, we
know that the inner-cluster edge (V0*, V1*) of the
OG(WK(W, L)) resides in a cycle (V0*, V1*, …, Vl-1*)
of length l, where 3 ≤ l ≤ WL-1, as illustrated in Figure
3. Let D1 be the vertex that resides in V1* and is
incident to the next edge (V1*, V2*) of the cycle.
Case 1: X ≠ D1 and Y ≠ D1. Clearly, (S0, D0, S1, X, Y,
D1, S2, D2, …, Sl-1, Dl-1) forms a cycle of length 2l+2.
Totally, there are (W-2)l-2 appending vertices. Thus, (X, Y) resides in cycles of all lengths ranging from 2l+2 to Wl.
Case 2: X = D1 or Y = D1. Without loss of generality,
let Y = D1. Clearly, (S0, D0, S1, X, Y (i.e., D1), S2,
D2, …, Sl-1, Dl-1) forms a cycle of length 2l+1. Totally,
there are (W-2)l-1 appending vertices. Thus, (X, Y) resides in cycles of all lengths ranging from 2l+1 to
Wl. Q. E. D.
Lemma 12. Each inner-cluster edge of a WK(W, L),
where W ≥ 7, resides in cycles of all lengths ranging from 3 to WL.
Proof. We will prove the lemma by induction on L.
For L =1, a WK(W, 1) is a KW. Clearly, the lemma is
true.
Hypothesis: Suppose that each inner-cluster edge of
a WK(W, k), where W ≥ 7, resides in cycles of all lengths ranging from 3 to Wk.
Induction Step: The OG(WK(W, k+1)) is a WK(W, k).
By the hypothesis and Lemma 11, we know that each inner-cluster edge of a WK(W, k+1) resides in
{Cs| 8 ≤ s ≤ 3 W } (for 3 WK(W, 1) supervertices) ∪ {Cs| 10 ≤ s ≤ 4 W } (for 4 WK(W, 1) supervertices) …, ∪ {Cs| 2n+2 ≤ s ≤ n W } (for n WK(W, 1) supervertices) ∪ {Cs| 2n+4 ≤ s ≤ (n+1) W } (for n+1 WK(W, 1) supervertices) …, ∪ {Cs| 2Wk+2 ≤ s ≤ WkW =Wk+1} (for Wk WK(W, 1) supervertices).
For W ≥ 7 and n ≥ 3, nW is always greater than 2n+4. Thus, each inner-cluster edge of a WK(W, k+1) resides in cycles of all lengths ranging from 8 to Wk+1.
By the recursive structure of the WK-Recursive Network, each inner-cluster edge of a WK(W, k+1) must reside in a WK(W, 1) subnetwork for k ≥ 1. Thus, each inner-cluster edge of a WK(W, k+1) resides in {Cs| 3 ≤ s ≤ 7} ∪ {Cs| 8 ≤ s ≤ Wk+1} =
{Cs| 3 ≤ s ≤ Wk+1}, where W ≥ 7. This extends the
induction and completes the proof. Q. E. D. Clearly, each inner-cluster edge of a WK(W, 1),
where 5 ≤ W ≤ 6, resides in cycles of all lengths ranging from 3 to W. By Lemma 11, each inner-cluster edge of a WK(W, 2), where 5 ≤ W ≤ 6, resides in {Cs| 3 ≤ s ≤ W or 8 ≤ s ≤ W2}. Suppose
that each inner-cluster edge of a WK(W, k), where 5 ≤
W ≤ 6, resides in {Cs| 3 ≤ s ≤ W or 8 ≤ s ≤ Wk}. By
Lemma 11, we know that each inner-cluster edge of a WK(W, k+1), where 5 ≤ W ≤ 6, resides in {Cs| 3 ≤ s ≤
W or 8 ≤ s ≤ W2 or 18 ≤ s ≤ Wk+1}. For 5 ≤ W ≤ 6,
W2 is always greater than 18. Thus, we have
Corollary 13. Each inner-cluster edge of a WK(W, L),
where 5 ≤ W ≤ 6, resides in {Cs| 3 ≤ s ≤ W or 8 ≤ s ≤ WL}.
Likewise, we have the following corollary.
Corollary 14. Each inner-cluster edge of a WK(4, 2)
resides in {Cs| 3 ≤ s ≤ 4 or 8 ≤ s ≤ 16}.
Each inner-cluster edge of a WK(4, 3) resides in {Cs| 3 ≤ s ≤ 4 or 8 ≤ s ≤ 16 or 18 ≤ s ≤ 64}.
Suppose that each inner-cluster edge of a WK(4, k) resides in {Cs| 3 ≤ s ≤ 4 or 8 ≤ s ≤ 16 or 18 ≤ s ≤ 4k}
for k ≥ 3. By Lemma 11, each inner-cluster edge of a WK(4, k+1) resides in {Cs| 3 ≤ s ≤ 4 or 8 ≤ s ≤ 16 or
18 ≤ s ≤ 4k or 38 ≤ s ≤ 4k+1 }. Clearly, for k ≥ 3, 4k is
always greater than 38. Thus, we have
Corollary 15. Each inner-cluster edge of a WK(4, L)
resides in {Cs| 3 ≤ s ≤ 4 or 8 ≤ s ≤ 16 or 18 ≤ s ≤ 4L }
for L ≥ 3.
Lemma 16. There exist paths of all lengths ranging
from 2L-1 to WL-1, between each pair of corner
vertices of a WK(W, L), where W ≥ 4.
Proof. We will prove the lemma by induction on L.
For L = 1, a WK(W, 1) is a KW. Clearly, there exist
paths of all lengths ranging from 2L-1(i.e., 1) to WL-1
(i.e., W-1), between each pair of corner vertices of a WK(W, 1).
Hypothesis: Suppose that there exist paths of all
lengths ranging from 2k-1 to Wk-1, between each pair
of corner vertices of a WK(W, k), where W ≥ 4.
Induction Step: The OG(WK(W, k+1)) is a WK(W, k).
Let (P, Q) be a pair of corner vertices of a WK(W,
k+1). The WK(W, 1) supervertex that P(Q) resides in
is denoted by VP* (VQ*). By the hypothesis, we know
that there exist a path (V0*, V1*, …, Vl-1*) of length
l-1, where 2k ≤ l ≤ Wk, V
0* = VP* and Vl-1* = VQ*.
There exist paths of all lengths ranging from 2×2k-1 =
2k+1-1 to W×Wk-1 = Wk+1-1, between P and Q. This
extends the induction and completes the proof. Q. E. D.
If each WK(W, 1) subnetwork of a WK(W, L) is taken as a supervertex, the WK(W, L) will be transformed to a WK(W, L-1). Moreover, each original level-1 inter-cluster edge will be an inner-cluster edge in the WK(W, L-1); and each original level-J inter-cluster edge will be a level-(J-1)
inter-cluster edge in the WK(W, L-1), where L-1 ≥ J ≥ 2. As stated before, a WK(W, L) can be constructed recursively. By induction, it is easy to see that if each WK(W, H) subnetwork of a WK(W, L) is taken as a supervertex, the WK(W, L) will be transformed to a WK(W, L-H); the original level-H inter-cluster edge of the WK(W, L) will be transformed as an inner-cluster edge of the WK(W, L-H); and the original level-J inter-cluster edge of the WK(W, L) will be transformed as a level-(J-H) inter-cluster edge of the WK(W, L-H), where L-1 ≥ J > H.
Lemma 17. If each inner-cluster edge of a WK(W,
L-H) resides in a cycle of length l, each level-H
inter-cluster edge of a WK(W, L) resides in cycles of all lengths ranging from 2H×l to WH×l. Q. E. D
Proof: By hypothesis, we know that each
inner-cluster edge of a WK(W, L-H) resides in a cycle of length l. Thus, in the corresponding WK(W, L), each level-H inter-cluster edge resides in the cycles through l WK(W, H) subnetworks and l level-H inter-cluster edges. From Lemma 16, we know that each level-H inter-cluster edge of a WK(W, L) resides in cycles of all lengths ranging from (2H-1)×l + l =
2H×l to (WH-1)×l + l = WH×l. Q. E. D.
Lemma 18. A level-H inter-cluster edge of a WK(W,
L), where W ≥ 7 and H ≥ 1, resides in cycles of all lengths ranging from 3×2H to WL.
Proof. By Lemma 12, each inner-cluster edge of the
WK(W, L-H) resides in cycles of all lengths ranging from 3 to WL-H, where W ≥ 7. From Lemma 17, we
know that each level-H inter-cluster edge of a WK(W,
L) resides in {Cs| 3×2H ≤ s ≤ 3×WH } ∪ {Cs| 4×2H ≤ s ≤ 4×WH } ∪…∪ {C s| (WL-H –1)×2H ≤ s ≤ (WL-H –1)×WH } ∪ {C s| WL-H ×2H ≤ s ≤ WL-H ×WH = WL} = {C
s| 3×2H ≤ s ≤ WL}. That is, each level-H
inter-cluster edge of a WK(W, L) resides in cycles of all lengths ranging from 3×2H to WL, where W ≥ 7
and H ≥ 1. Q. E. D. In this paper, the shortest path between X and Y is denoted by X ⇒S Y; and an edge connecting U and
V is denoted by U → V. The highest level of the inter-cluster edges of a WK(W, L) is L-1. Consider an level-(L-1) inter-cluster edge (da(db)L-1, db(da)L-1) of a
WK(W, L), where da ≠ db. By the structure of a
WK(W, L), da(*)L-1 and db(*)L-1 are connected by only
one edge (da(db)L-1, db(da)L-1). Thus, the shortest cycle
embedding (da(db)L-1, db(da)L-1) is (da(db)L-1→ db(da)L-1
⇒S d
b(dc)L-1→ dc(db)L-1 ⇒S dc(da)L-1 → da(dc)L-1 ⇒S
da(db)L-1) where da, db and dc are distinct digits. The
distance between db(da)L-1 and db(dc)L-1 (dc(db)L-1 and
dc(da)L-1, da(dc)L-1 and da(db)L-1) is 2L-1-1 [8]. The total
length of the cycle is 3(2L-1-1)+3 = 3×2L-1. Thus, we
have
Lemma 19. The length of the shortest cycle
containing a level-(L-1) inter-cluster edge of a WK(W,
L) is 3×2L-1.
Combining Lemma 12, Lemma 18 and Lemma 19, we have
Theorem 20. A WK(W, L) is strictly
3×2L-1-edge-pancyclic, where W ≥ 7 and L ≥ 1.
Then, we investigate the m-edge-pancyclicity of a WK(5, L) and a WK(6, L). According to Corollary 13 and Lemma 17, we can derive that each level-H inter-cluster edge of a WK(5, L) resides in {Cs| 3×2H ≤ s ≤ 5L} for L ≥ 3. Clearly, the highest
level of the inter-cluster edges of a WK(5, L) is L-1. From Corollary 13 and Lemma 19, we have the following lemmas:
Lemma 21. A WK(5, 2) is 8-edge-pancyclic. Lemma 22. A WK(5, L) is strictly
3×2L-1-edge-pancyclic for L ≥ 3.
Like the above discussion, we can derive the following lemmas:
Lemma 23. A WK(6, 2) is 8-edge-pancyclic. Lemma 24. A WK(6, L) is strictly
3×2L-1-edge-pancyclic for L ≥ 3.
Then, we investigate the m-edge-pancyclicity of a WK(4, L). By Corollary 15 and Lemma 17, we can derive that each level-H inter-cluster edge of a WK(4, L) resides in {Cs| 3×2H ≤ s ≤ 4L} for L ≥ 4.
Clearly, the highest level of the inter-cluster edges of a WK(4, L) is L-1. From Corollary 14, Corollary 15 and Lemma 19, we have the following lemmas:
Lemma 25. A WK(4, 2) is 8-edge-pancyclic. Lemma 26. A WK(4, 3) is 18-edge-pancyclic. Lemma 27. A WK(4, L) is strictly 3×2L-1-edge-
pancyclic for L ≥ 4.
Consider the edge ((0)L-11, (0)L-12) of a WK(3,
L), where L ≥ 2. Clearly, the edge cannot be contained in a Hamiltonian cycle. As illustrated in Figure 4, edge (01, 02) cannot reside in a Hamiltonian cycle of a WK(3, 2). Thus, a WK(3, L) is not m-edge-pancyclic for L ≥ 2.
5. Conclusions
In this paper, we have shown that a WK-Recursive network with amplitude W and level L is vertex-pancyclic for W ≥ 6. The WK-Recursive network is proved to be strictly 7-vertex-pancyclic, where 5 ≤ W ≤ 6 and L ≥ 2. On the other hand, we also investigate the m-edge-pancyclicity of the WK-Recursive network. We show that the WK-Recursive network is strictly 3×2L-1-edge-pancyclic for W ≥ 7 and L ≥ 1. However,
the panconnected problem of the WK-Recursive network is still open.
Acknowledgments
This work was supported in part by the National Science Council of the Republic of China under the contract number: NSC95-2221-E-142-003.
REFERENCE
[1] B. Alspach and D. Hare, “Edge-pancyclic
block-intersection graphs”, Discrete Math, 97 (1–3), pp.17–24, 1991.
[2] T. Araki and Y. Shibata, “Pancyclicity of
recursive circulant graphs”, Information Processing Letters, 81(4), pp.187-190, 2002.
[3] A. Auletta, A. Rescigno, and V. Scarano,
“Embedding graphs onto the supercube”, IEEE Trans. Comput, 44 (4), pp.593-597, 1995.
[4] M.M. Bae, “Resource placement in torus-based
networks”, IEEE Transactions on Comput, 46(10), 1083-1092, 1997.
[5] H.Y. Chang and R.J. Chen, “Embedding cycles
in IEH graphs”, Inform. Process. Lett, 64, pp.23-27, 1997.
[6] J. M. Chang, J. S.Yang, J. S. Yang, Y. L. Wang
and Y. Cheng, “Panconnectivity, Fault-Tolerant Hamiltonicity and Hamiltonian-Connectivity in Alternating Group Graphs”, Networks, 44(4), pp.302-310, 2004.
[7] G. Chartrand and O. R. Oellermann, “Applied
and Algorithmic Graph Theory”, McGraw-Hill, New York, 1993.
[8] G.H. Chen and D.R. Duh, “Topological
properties, communication, and computation on WK-recursive networks”, Networks, 24(6), pp.303-317, 1994.
[9] G.H. Chen, J.S. Fu and J.F. Fang,
“Hypercomplete: A pancyclic recursive topology for large-scale distributed multicomputer systems”, Network, 35(1), pp.56-69, 2000.
[10] H.L. Chen and N.F. Tzeng, “Efficient resource
placement in hypercubes using multiple-adjacency codes”, IEEE Trans. Comput. 43(1), pp.23-33, 1994.
[11] J. Fan, X. Lin and X. Jia, “Node-pancyclicity
and edge-pancyclicity of crossed cubes”, Information Processing Letters, 93(3), pp.133-138, 2005.
[12] J.F. Fang, G.J. Lai, Y.C. Liu and S.T. Fang, “A
novel broadcasting scheme for WK-recursive networks”, in Proceedings of 2003 IEEE Pacific Rim Conference on Communications, Computers and signal Processing, 2, pp.1028-1031, 2003.
[13] R. Fernandes, D.K. Friesen and A. Kanevsky,
“Embedding rings in recursive networks”, Proceedings of the International Parallel Processing Symposium, pp.273-280, 1994.
[14] J.S. Fu, “Hamiltonicity of the WK-recursive
network with and without faulty nodes”, IEEE Transactions on Parallel and Distributed Systems, 16(9), pp.853-865, 2005.
[15] A. Hobbs, “The square of a block is vertex
pancyclic”, J. Combin. Theory Ser. B, 20(1), pp.1-4, 1976.
[16] F.T. Leighton, “Introduction to Parallel
Algorithms and Architectures: Arrays, Trees, Hypercubes, Mogran Kaufmann”, California, 1992.
[17] Y.C. Lin, “On balancing sorting on a linear
array”, IEEE Transactions on Parallel and Distributed Systems, 4(5), pp.566-571, 1993.
[18] A.I. Mahdaly, H.T. Mouftah and N.N. Hanna,
“Topological properties of WK-recursive networks”, Proceed. Second IEEE Workshop on Future Trends of Distributed Computing Systems, pp.374-380, 1990.
[19] D.R. O'Hallaron, “Uniform approach for solving
some classical problems on a linear array”, IEEE Transactions on Parallel and Distributed Systems, 2(2), pp.236-241, 1991.
[20] C.D. Park and K.Y. Chwa, “Hamiltonian
properties on the class of hypercube-like networks”, Information Processing Letters, 91(1), pp.11-17, 2004.
[21] C. Peters and L. Volkmann, “Vertex 6-pancyclic
in-tournaments”, Discrete Math, 285(1–3), pp.227–238, 2004.
[22] B. Ucar, C. Aykanat, K. Kaya and M. Ikinci,
“Task assignment in heterogeneous computing systems”, Journal of Parallel and Distributed Computing, 66(1) , pp.32-46, 2006.
[23] G.D. Vecchia and C. Sanges, “Recursively
scalable network for message passing architecture”, Proceed. Int. Conf. Parallel Processing and Applications, 1, pp.33-40, 1987.
[24] G.D. Vecchia and C. Sanges, “A recursively
scalable network VLSI implementation”, Future Generat. Comput. Syst, 4(3), pp.235-243, 1988.