國 立 交 通 大 學
土 木 工 程 學 系
博 士 論 文
整合時間尺度之隨機降雨序列模擬機制之發展與應用
Development and Application of Stochastic Generation Model
for Rainfall Series with Time Scale
研 究 生:吳祥禎
指 導 教 授:楊錦釧 博士
湯有光 博士
整合時間尺度之隨機降雨序列模擬機制之發展與應用
Development and Application of Stochastic Generation Model
for Rainfall Series with Time Scale
研 究 生 : 吳祥禎 Student : Shiang-Jen Wu 指 導 教 授 : 楊錦釧 Advisors : Jinn-Chuang Yang
湯有光 Yeou-Koung Tung
國 立 交 通 大 學
土 木 工 程 學系
博 士 論 文
A Dissertation
Submitted to Institute of Civil Engineering College of Engineering
National Chiao Tung University in Partial Fulfillment of the Requirements
for the Degree of Doctor of Philosophy
in
Civil Engineering 2006
Hsinchu, Taiwan, Republic of China.
誌謝
在交通大學就博士班期間,承蒙恩師楊教授錦釧及香港科技大學土木 湯教授有光在研究上悉心的指導與生活上用的的照顧,使我在研究生涯中 獲益匪淺,更使我的拙作能得以完成,在此致上最誠摯的謝枕與敬意。另 要感謝口試委員鄭教授克聲、葉教授克家、李教授天浩及黃教授文政的悉 心指正與寶貴意見,使本論文更趨完善。此外,系上老師多年來在課業上 的發與教導,亦是學生受用不盡的寶藏,在此謹致由衷的感謝 在求學的期間,我很幸運地能夠有機會前往香港科技大學,跟隨湯有 光教授作論文相關研究,在香港科大期間除了讓我有機會接觸不同於台灣 學習環境,同時也讓我了解到本身學識之不足,尤其是湯老師嚴謹的研究 觀念及態度深深地影響我往後求學作研究的態度,唯有紮實地下苦心作研 究,才會有成功的一天。另要特別感謝香港研究資助局(Hong Kong Research Grant Council, HKSAR)提供計畫研究經費(計畫名稱及編號 HKUST6016/01E: Investigating Issues in Rainfall Intensity-Duration and Time-Scale Relations in Hong Kong),使我能夠在香港科大完成論文中的相關研究成果。 在學期間所有伴我成長的朋友、交大楊老師研究團隊,及香港科技大 學土木系的 Joanne 小姐、杏元、Seba、志華、王穎、Eddy、水利實駭室其 他成員、及室友朱宇與張暉,謝謝你們在此期間,對我的幫助及鼓勵。 最後謹將本論文獻給爸爸、媽媽、老婆佳玉、大姐昭寬、大哥祥銘、 大嫂桂英、侄子哲瑋、侄女怡宣及小兒彥廷。摘要
大多數水利相關工程例如洪水預報、防洪工程,應用於邊坡穩定評估之 排水及入滲分析等,降雨資料為必需已知之基本資料。然而常因發生雨量 資料不足或其時間尺度不符合要求,而使水利相關工程在分析設計上產生 了不確定性進而造成了失敗的風險。由於降雨資料主要由降雨事件年發生 次數(Annual Occurrence Number of Rainstorm Events)、降雨延時(Storm Duration)、總降雨量(Rainfall Depth),事件間隔時間(Inter-event Time)及降 雨時間分布(Time Distribution of Rainfall) (即降雨雨型, Storm Pattern) ,等 五種特性所組成 (Marien 及 Vandewiele, 1986),故本文將以由實測雨量資 料所得降雨特性之統計性質為基礎,發展一套隨機降雨序列模擬機制 (Stochastic rainfall series generation model, SRSG model),期使能解決因雨量 資料不足所衍生的相關水利工程問題。為了驗證此模式,本文分別比較由 模式所得之合成降雨序列與不同紀錄年限的實測雨量資料所推得年最大 降雨量-延時-頻率曲線(Rainfall depth-duration-frequency, DDF, Curve),藉 以測試模式在延伸降雨序列之成效。 另為了克服在設計水利相關工程常遇到另一問題,即因自計雨量站不足 而造成短時間尺度( )雨量資料短缺,但卻有相當多的普通雨量站 可提供長時間尺度雨量(例如日雨量),故本文亦發展一套可藉由日雨量來 推估不同延時(小時)之降雨 DDF 曲線之時雨量頻率分析模式。依據所採 用 雨 量 資 料 型 式 , 模 式 可 區 分 為 二 類 型 : (1) 年 最 大 值 事 件 模 式 (Annual-maximum-events, AME, Model):即不同連續日降雨事件總雨量年 最大值及其所對應的不同延時最大降雨量;及(2)所有事件模式(All-events, AE, Model):即採用所有降雨事件之模式。在發展模式過程中,降雨事件 依連續降雨天數被區分為不同連續日降雨事件類型,擷取其總雨量及其所 對應於不同延時之最大降雨量,建立其分位數之關係,並將其應用於由日 雨量機率分布函數所組成之時雨量頻率分析模式之建置。如同驗證隨機降 雨序列模擬機制,為了驗證 AME 及 AE 模式的正確性,本文亦分別由 AME hrs 24 t≤
及 AE 模式推得的降雨 DDF 曲線與一般常用之年最大降雨序列(Annual Maximum Rainfall Series)配合頻率分析法(本文定義為 AMS 模式)之推估結 果來相互比較,以評估模式可藉由日雨量資訊推估不同延時之降雨 DDF 曲線之準確性及可靠度。 本文採用香港天文台站 1884 至 1990 年之 100 年時雨量資料 (其中 1940 至 1946 因第二次世界大戰而中斷記錄),驗證所發展之隨機降雨序列模擬 機制(SRSG 模式)及採用日雨量之時雨量頻率分析模式(AME 及 AE 模式)。 由驗證結果可知,SRSG 模式確實有能力能製造保存原有統計性質之降雨 事件,且可將所有模擬事件等性成降雨序列,藉以延伸降雨資料紀錄,進 而改善降雨 DDF 曲線之準確性,特別是在推估重現期距大於實測時雨量 紀錄之年最大降雨量分位數時,其改善程度最為明顯。另對於 AME 及 AE 模式而言,在相同現有時雨量紀錄年限下, AME 及 AE 模式因採用不同 類型的連續日降雨事件之雨量資料,相對於採用年最大降雨序列之 AMS 模式而言,AME 及 AE 模式因可採用較多的雨量資訊,而可推得較具有可 靠及準確性之降雨 DDF 曲線。此外由 AME 及 AE 模式比較結果可知,AE 模式較適用於短實測時雨量資料之不同延時降雨 DDF 曲線之推估,相對 地,AME 模式則適用於當具有較長的日雨量資料紀錄年限之降雨 DDF 曲 線之推估。 最後本文將 SRSG 模式與 AME 及 AE 模式整合成一可考量不同時間尺 度之隨機降雨序列模擬機制,此整合模式不僅可藉由 SRSG 模式模擬合成 降雨序列,用以增加日雨量及時雨量資料紀錄年限,改善總雨量及其所對 應的不同延時最大降雨量分位數關係,藉以提高時雨量頻率分析模式之可 靠度,更可由將 SRSG 模式所衍生大量的降雨序列應用於 AME 及 AE 模 式所推得降雨 DDF 曲線之不確定性分析,藉以提供需要降雨 DDF 曲線之 水利相關工程例如洪水預報、防洪工程,及水資源規劃等進行風險分析。 關鍵詞:降雨特性、雨型、年最大降雨量序列、多變量蒙地卡羅法、頻率 分析;降雨量-延時-頻率曲線;隨機模擬
Abstract
Rainfall data are often required in many water-related engineering studies, such as flood forecast, prevention and mitigation, seepage and infiltration analysis for slope stability assessment. However, engineers frequently face the problem of not having insufficient rainfall data to conduct good the quality and reliable water-related engineering. In general, the occurrence of the rainstorm events can be characterized by the annual occurrence number of events, storm duration, rainfall depth, inter-event time and temporal variation of rainfall (Marien 及 Vandewiele, 1986). To solve the problem associated with insufficient rainfall data, this thesis presents a stochastic rainfall series generation (SRSG) model based on the statistical properties of correlated rainstorm characteristics calculated from observed rainfall data. To verify the proposed SRSG model, comparisons are made on the derived rainfall depth-duration-frequency (DDF) relationships of the annual maximum rainfall from the simulated rainfall sequences with those solely obtained from observed annual maximum rainfall.
Furthermore, due to the fact that short-duration rainfall data (e.g., hour) are insufficiently long compared with relatively long and widely available rainfall data, this thesis also proposed hourly rainfall frequency models that incorporate daily rainfall information to estimate hourly rainfall depth-duration-frequency (DDF) relationships. According to the type of rainfall data used, the proposed hourly rainfall frequency models can be classified two models. One is annual-maximum-events (AME) model incorporated with the annual maximum series of consecutive-rainy-daily events and the other is all-event (AE) model based on all consecutive-rainy-daily events. In the process of deriving the proposed AME and AE
models, the rainstorm events are classified according to the number of consecutive-rainy days and their total rainfall amount are extracted. And then, the relationship of quantiles between total rainfall and associated t-hr maximum rainfall are derived for the AME and AE models. Similar to the SRSG model, to verify the proposed the AME and AE models, comparison are made on the rainfall depth-duration-frequency relations of the annual maximum rainfall estimated by the proposed the AME and AE models with those by the conventional frequency analysis by directly using annual maximum series. The frequency analysis based on annual maximum rainfall series is denoted herein as the AMS model.
Hourly rainfall data at the Hong Kong Observatory over the period of 1884-1990 are used to demonstrate the development and application of the proposed stochastic rainstorm series generation (SRSG) model and daily-based hourly rainfall frequency model that incorporate daily rainfall information (AME and AE models). From the numerical experiments, the proposed SRSG model is found to be capable of capturing the essential statistical features of rainstorm characteristics and annual extreme rainstorm events calculated from the available data. Since the rainfall series can be synthesized by the proposed SRSG model, it is obvious that the model can be applied to extend the record length of the rainfall data for improving the reliability and accuracy of rainfall quantiles, especially for return period larger than the record length of available rainfall data. For the verification of the AME and AE models, the numerical experiments indicate that AME and AE model are found to produce more accurate and reliable frequency quantiles of annual maximum rainfall than those derived by the AMS model based on the same available hourly rainfall data. Furthermore, the AME and AE models show a promising potential to improve accuracy of rainfall DDF relationships by incorporating extended daily-based rainfall
record. It is also found that the AME model is suitable for estimating rainfall DDF curves of various storm durations incorporated with the low record length of hourly rainfall data whereas AE is adequate for the estimation of rainfall DDF curves based on the long-record daily rainfall data.
Eventually, in this thesis, the SRSG model, AME and AE models are integrated to be a stochastic rainfall generation model associated with varying time-scale rainfall data. This model can add hourly rainfall data composed of rainstorm characteristics simulated by the SRSG model to modify the quantiles relationship between total daily rainfall and the associated t-hr maximum rainfall. Using the modified quantiles relationship, the AME and AE models can estimate more reliable rainfall DDF relationships of storm durations of interest. Furthermore, the simulated rainfall series by the SRSG model can be applied to risk reliability analysis for the design of hydrosystem infrastructures and water resource planning requiring rainfall DDF relationships.
Keywords: Rainstorm characteristics; rainfall pattern; annual maximum rainfall series; multivariate Monte Carlo simulation method; frequency analysis; rainfall depth-duration-frequency, DDF, curve; stochastic modeling.
目錄
謝誌...I 摘要... II Abstract ...IV 目錄... VII 表目錄...IX 圖目錄... X 符號表... XV 第一章 緖論...1-1 1.1 研究背景...1-1 1.2 文獻回顧...1-1 1.3 研究內容及目的...1-4 1.4 論文架構...1-5 第二章 隨機降雨序列模擬機制之建置...2-1 2.1 降雨特性之定義...2-1 2.2 降雨事件發生次數之模擬...2-2 2.3 降雨延時、雨量及事件間隔時間之模擬 ...2-3 2.3.1 非常態多變量蒙地卡羅模擬 ...2-3 2.3.2 邊際機率分布函數之檢定...2-4 2.3.3 模擬程序...2-5 2.4 降雨雨型之模擬...2-5 2.4.1 雨型特性之分析與歸納...2-6 2.4.2 雨型之分群及判識...2-7 2.4.3 具有約制條件之非常態多變量隨機變數之模擬 ...2-8 2.4.3.1 對數比率轉換...2-9 2.4.3.2 多變量 Johnson 分布函數之模擬 ...2-10 2.4.4 模擬流程...2-11 2.5 隨雨序列模擬流程...2-12 第三章 採用日雨量之時雨量頻率分析之建置 ...3-1 3.1 降雨事件之分類...3-1 3.2 時雨量與日雨量分位數關係之建立 ...3-2 3.2.1 降雨量分位數之推求...3-2 3.2.2 線性動差法之簡介...3-2 3.2.3 權重頻率曲線法之簡介...3-5 3.2.4 分位數闔係之建立...3-6 3.3 時雨量頻率分析模式之建置...3-73.3.1 年最大降雨事件為基礎之模式 ...3-7 3.3.1.1 模式推導...3-7 3.3.1.2 k 日連續降雨事件具有零值雨量資料之處理 ...3-8 3.3.2 所有降雨事件為基礎之模式 ...3-9 3.3.2.1 模式推導...3-9 3.3.2.2 k 連續降雨事件發生頻率分布之推導 ...3-10 3.4 重現期距 T 年 t 小時降雨頻率關係推導過程 ...3-11 第四章 模式應用與驗證...4-1 4.1 研究區域及資料說明...4-1 4.2 隨機降雨模擬機制之建置...4-1 4.2.1 降雨特性統計分析...4-1 4.2.1.1 降雨事件發生次數...4-2 4.2.1.2 降雨延時、雨量及事件間隔時間 ...4-2 4.2.1.3 降雨雨型...4-3 4.2.2 模式驗證...4-6 4.2.2.1 驗證方法及步驟...4-6 4.2.2.2 降雨特性統計特性之比較 ...4-8 4.2.2.3 年最大降雨量統計特性之比較 ...4-8 4.2.2.4 不同重現期距降雨量之比較 ...4-9 4.3 採用日雨量之時雨量頻率分析 ...4-11 4.3.1 降雨事件之分類 ...4-11 4.3.2 k 日連續降雨事件總雨量及所對應 t 小時最大降雨量分位關係 式之建立 ...4-12 4.3.3 模式驗證 ...4-12 4.3.3.1 驗證方法及步驟 ...4-13 4.3.3.2 與時雨量為基礎之頻率分析之比較 ...4-14 4.3.3.3 增加日雨量紀錄年限對 AME 及 AE 模式之影響評估 ... ...4-16 4.3.3.4 AME 及 AE 模式之比較 ...4-17 4.4 隨機降雨模擬機制與採用日雨量礎之時雨量頻率分析之整合運用 ...4-17 第五章 結論與建議...5-1 5.1 結論...5-1 5.2 建議...5-3 參考文獻...R-1 附錄...A-1
表目錄
表 2.1 不同機率分布函數之轉換因子(Transformation factor)表... 2-13 表 3.1 不同機率分布函數參數及各階動差之關係(乘積動差) ... 3-13 表 3.2 不同機率分布函數參數及各階動差之關係(L-動差) ... 3-14 表 4.1 香港雨量站及其相關資訊表... 4-19 表 4.2 香港天文自計雨量站 100 年時雨量資料中降雨事件年發生次數表4-19 表 4.3 100 年 1690 場降雨事件年發生次數之統計特性及其離散指數表. 4-20 表 4.4 100 年 1690 場降雨事件之延時、降雨量及間隔時間之統計特性 .4-20 表 4.5 100 年 1690 場降雨事件之延時、降雨量及間隔時間 K-S 檢定表.4-21 表 4.6 無因次降雨量(Pτ)之統計特性(六群雨型)...4-22 表 4.7 無因次降雨量對數比率 之 Johnson 分布類型及其參數值(六群雨 型) ...4-28 ) R ( τ 表 4.8 六群雨型之列聯表分析結果...4-29 表 4.9 不同現有時雨量資料中降雨事件年發生次數離散指數表 ...4-32 表 4.10 不同現有時雨量資料中降雨事件之延時、降雨量及間隔事件之合適 機率分布函數 K-S 檢定表 ...4-32 表 4.11 不同現有時雨量資料(m=20、50r 及 80 年)降雨事件之延時、降雨量 及事件間隔時間之合適機率分佈函數 K-S 檢定表 ...4-35 表 4.12 不同現有時雨量資料與依其模擬所得合成降雨序列中降雨特性平 均值之相對誤差...4-36 表 4.13 由不同現有時雨量資料與依其模擬所得合成降雨序列所得不同延 時年最大降雨量之統計特性比較...4-37 表 4.14 不同連績日降雨事件之 K-S 檢定結果表 ...4-40 表 4.15 100 年時雨量資料中不同連續日降雨事件總雨量及其不同延時最大 降雨量分位數表...4-41圖目錄
圖 2.1 降雨特性之定義...2-14 圖 2.2 模式發展過程...2-15 圖 2.3 多變量蒙地卡羅 MMCS 方法之模擬程序 ...2-16 圖 2.4 降雨事件之無因次化過程...2-17 圖 2.5 降雨序列之模擬過程...2-17 圖 3.1 完整降雨事件與部份降雨事件之定義 ...3-15 圖 3.2 k 日連續降雨事件之定義...3-15 圖 3.3 k 日連續降雨事件總雨量及其延時 t 小時最大降雨量分位數之關係示 意圖...3-16 圖 3.4 AME 模式推導過程...3-16 圖 3.5 AE 模式推導過程 ...3-17 圖 4.1 香港雨量站相關位置圖...4-42 圖 4.2 平均無因次累積降雨量 (五群雨型)...4-43 Fτ 圖 4.3 平均無因次累積降雨量 (六群雨型)...4-44 Fτ 圖 4.4 平均無因次累積降雨量 (七群雨型)...4-45 Fτ 圖 4.5 六群雨型之平均無因次降雨量 ...4-46 Pτ 圖 4.6 模式驗證過程...4.47 圖 4.7(a) 由 100 年雨量資料所得 t 小時頻率曲線與 20 年現有時雨量及依其 模擬所得合成頻率曲線統計特性之比較(t=1-hr) ...4-48 圖 4.7(b) (t=2-hr) ...4-48 圖 4.7(c) (t=6-hr)...4-49 圖 4.7(d) (t=12-hr) ...4-49 圖 4.7(e) (t=24-hr) ...4-50 圖 4.8(a) 由 100 年時雨量資料所得 t 小時頻率曲線分別與 50 年現有時雨量 及依其模擬所得合成頻率曲線統計特性之比較(t=1-hr) ...4-51 圖 4.8(b) (降雨延時 t=2-hr) ...4-51 圖 4.8(c) (降雨延時 t=6-hr) ...4-52 圖 4.8(h) (降雨延時 t=12-hr) ...4-52圖 4.8(e) (降雨延時 t=24-hr) ...4-53 圖 4.9(a) 由 100 年時雨量資料所得 t 小時頻率曲線分別與 80 年現有時雨量 及依其模擬所得合成頻率曲線統計特性之比較(t=1-hr) ...4-54 圖 4.9(b) (降雨延時 t=2-hr) ...4-54 圖 4.9(c) (降雨延時 t=6-hr) ...4-55 圖 4.9(d) (降雨延時 t=12-hr) ...4-55 圖 4.9(e) (降雨延時 t=24-hr) ...4-56 圖 4.10(a) 20-yrs 降雨 DDF 曲線(Observed)與合成降雨 DDF 曲線平均值
(Mean)及中位數(Median)之相對誤差比較(降雨延時 t=1-hr) ....4-57 圖 4.10(b) (降雨延時 t=2-hr) ...4-57 圖 4.10(c) (降雨延時 t=6-hr) ...4-58 圖 4.10(d) (降雨延時 t=12-hr) ...4-58 圖 4.10(e) (降雨延時 t=24-hr) ...4-59 圖 4.11(a) 50-yrs 降雨 DDF 曲線(Observed)與成降雨 DDF 曲線平均值(Mean)
及中位數(Median)之相對誤差比較(降雨延時 t=1-hr) ...4-60 圖 4.11(b) (降雨延時 t=2-hr) ...4-60 圖 4.11(c) (降雨延時 t=6-hr)...4-61 圖 4.11(d) (降雨延時 t=12-hr) ...4-61 圖 4.11(e) (降雨延時 t=24-hr)...4-62 圖 4.12(a) 80-yrs 降雨 DDF 曲線(Observed)與合成降雨 DDF 曲線平均值
(Mean)及中位數(Median)之相對誤差比較(降雨延時 t=1-hr)..4-63 圖 4.12(b) (降雨延時 t=2-hr) ...4-63 圖 4.12(c) 降雨延時 t=6-hr)...4-64 圖 4.12(d) 降雨延時 t=12-hr)...4-64 圖 4.12(e) (降雨延時 t=24-hr) ...4-65 圖 4.13 100 年時雨量資料中 2 日連續降雨事件之 1 小時最大降雨量分位數 ( t )與經由(4.3)所求得之分位數 之比較 ...4-66 p , k h t k hˆ
圖 4.14 不同連續日降雨事件之 1 小時降雨 DDF 曲線之比較 ...4-66 圖 4.15(a) AME 模式採用 10 年現有時雨量資料所得降雨 DDF 曲線平均值 與 95%信賴區間 (降雨延時 t=1-hr)...4-67 圖 4.15(b) (降雨延時 t=2 小時)...4-67 圖 4.15(c) (降雨延時 t=6 小時) ...4-68 圖 4.15(c) (降雨延時 t=12 小時) ...4-68 圖 4.15(e) (降雨延時 t=24 小時) ...4-69 圖 4.16(a) AE 模式採用 20 年現有時雨量資料所得降雨頻率曲線平均值與 95%信賴區間 (降雨延時 t=1-hr) ...4-70 圖 4.16(b) (降雨延時 t=2-hr) ...4-70 圖 4.16(b) (降雨延時 t=6-hr) ...4-71 圖 4.16(b) (降雨延時 t=12-hr) ...4-71 圖 4.16(b) (降雨延時 t=24-hr) ...4-72 圖 4.17(a) AME 及 AE 模式所得降雨 DDF 曲線與 AMS 模式所得降雨 DDF
曲線之相對誤差平均值比率(降雨延時 t=1-hr) ...4-73 圖 4.17(b) (降雨延時 t=2-hr) ...4-73 圖 4.17(c) (降雨延時 t=6-hr) ...4-74 圖 4.17(d) (降雨延時 t=12-hr) ...4-74 圖 4.17(e) (降雨延時 t=24-hr) ...4-75 圖 4.18(1a) AME 及 AE 模式採用 10 年現有時雨量資料及不同日雨量增加 年限(l=10、20、30 及 40 年)所得相對誤差平均值(現有雨量年限 m=10 年及降雨延時 t=1-hr) ...4-76 圖 4.18(1b) (降雨延時 t=2-hr) ...4-76 圖 4.18(1c) (降雨延時 t=6-hr) ...4-77 圖 4.18(1d) (降雨延時 t=12-hr) ...4-77 圖 4.18(1e) (降雨延時 t=24-hr) ...4-78 圖 4.18(2a) AE 模式採用 10 年現有時雨量資料及不同日雨量增加年限 (l=10、20、30 及 40 年)所得降雨 DDF 曲線之相對誤差平均值(現 有雨量年限 m=10 年及降雨延時 t=1-hr) ...4-79 圖 4.18(2b) (降雨延時 t=2-hr) ...4-79 圖 4.18(2c) (降雨延時 t=6-hr) ...4-80 圖 4.18(2d) (降雨延時 t=12-hr) ...4-80 圖 4.18(2e) (降雨延時 t=24-hr) ...4-81
圖 4.19(1a) AME 模式採用 20 年現有時雨量資料及不同日雨量增加年限 (l=10、20 及 30 年) 所得降雨 DDF 曲線之相對誤差平均值 el mod , m l+ ε (降雨延時 t=1-hr) ...4-82 圖 4.19(1b) (降雨延時 t=2-hr) ...4-82 圖 4.19(1c) (降雨延時 t=6-hr) ...4-83 圖 4.19(1d) (降雨延時 t=12-hr) ...4-83 圖 4.19(1e) (降雨延時 t=24-hr) ...4-84 圖 4.19(2a) AE 模式採用採用 20 年現有時雨量資料及不同日雨量增加年限 (l=10、20 及 30 年)所得降雨 DDF 曲線之相對誤差平均值(現有 雨量年限 m=20yrs 年及降雨延時 t=1-hr) ...4-85 圖 4.19(2b) (現有雨量年限 m=20yrs 年及降雨延時 t=2-hr)...4-85 圖 4.19(2c) (現有雨量年限 m=20yrs 年及降雨延時 t=6-hr) ...4-86 圖 4.19(2d) (現有雨量年限 m=20yrs 年及降雨延時 t=12-hr)...4-86 圖 4.19(2e) (現有雨量年限 m=20yrs 年及降雨延時 t=24-hr) ...4-87 圖 4.20(1a) AME 模式採用 30 年現有時雨量資料及不同日雨量增加年限 (l=10 及 20 年)所得降雨 DDF 曲線之相對誤差平均值(現有雨量 年限 m=30 年及降雨延時 t=1-hr) ...4-88 圖 4.20(1b) (降雨延時 t=2-hr) ...4-88 圖 4.20(1c) (降雨延時 t=6-hr) ...4-89 圖 4.20(1d) (降雨延時 t=12-hr) ...4-89 圖 4.20(1e) (降雨延時 t=24-hr) ...4-90 圖 4.20(2a) AE 模式採用 30 年現有時雨量資料及不同日雨量增加年限(l=10 及 20 年)所得降雨 DDF 曲線之相對誤差平均值(降雨延時 t=1-hr) ...4-91 圖 4.20(2b) (降雨延時 t=2-hr) ...4-91 圖 4.20(2c) (降雨延時 t=6-hr) ...4-92 圖 4.20(2d) (降雨延時 t=12-hr) ...4-92 圖 4.20(2e) (降雨延時 t=24-hr) ...4-93 圖 4.21(a) AME 及 AE 模式採用 10 年現有時雨量資料所得降雨 DDF 曲線
之 相 對 誤 差 εm l+,model 小 於 AMS 之 εm,AMS 之 機 率
(
m ,model m,AMS)
Pr ε +l ≤ε (重現期距 T=50-yr) ...4-94 圖 4.21(b) (重現期距 T=100-yr)...4-94 圖 4.21(c) (重現期距 T=200-yr) ...4-95 圖 4.21(d) (重現期距 T=1000-yr)...4-95 圖 4.22(a) AME 及 AE 模式採用 20 年現有時雨量資料所得降雨 DDF 曲線之 相 對 誤 差 εm l+,model 小 於 AMS 之 εm,AMS 之 機 率
(
m ,model m,AMS)
Pr ε +l ≤ε (重現期距 T=50-yr)...4-96 圖 4.22(b) (重現期距 T=100-yr)...4-96 圖 4.22(c) (重現期距 T=200-yr) ...4-97 圖 4.22(d) (重現期距 T=1000-yr)...4-97 圖 4.23(a) AME 及 AE 模式採用 30 年現有時雨量資料所得降雨 DDF 曲線之 相 對 誤 差 εm l+,model 小 於 AMS 之 εm,AMS 之 機 率
(
m ,model m,AMS)
Prε +l ≤ε (重現期距 T=50-yr) ...4-98 圖 4.23(b) (重現期距 T=100-yr)...4-98 圖 4.23(c) (重現期距 T=200-yr) ...4-99 圖 4.23(d) (重現期距 T=1000-yr)...4-99 圖 4.24 採用隨機降雨模擬機制所得 1000 年模擬合成降雨序列所推得不同 延時之降雨 DDF 曲線 ...4-100 圖 4.25(a) AME、AE 及 AMS 模式所推得降雨 DDF 曲線(降雨延時 t=1-hr)...4-100 圖 4.25(b) (降雨延時 t=2-hr) ...4-101 圖 4.25(c) (降雨延時 t=6-hr) ...4-101 圖 4.25(d) (降雨延時 t=12-hr) ...4-102 圖 4.25(e) (降雨延時 t=24-hr) ...4-101 圖 4.26(a) AME 及 AE 模式所得降雨 DDF 曲線之相對誤差(降雨延時 t=1-hr) ...4-102 圖 4.26(a) (降雨延時 t=2-hr) ...4-103 圖 4.26(c) (降雨延時 t=6-hr) ...4-104 圖 4.26(d) (降雨延時 t=12-hr) ...4-104 圖 4.26(e) (降雨延時 t=24-hr) ...4-105
符號表
I
D :Fisher 離散指數(Dispersion index)
α:統計顯著水準 ij ρ :隨機變數 Xi及 Xj之相關係數 i μ 及μj:隨機變數 Xi及 Xj之平均值 i σ 及σj:隨機變數 Xi及 Xj之標準偏差 * ij ρ :標準常態變數 Zi及 Zj之相關係數 ij T :標準常態轉換因子(Transformation factor) τ:無因次時間 ∗ τ :無因次時間指標 τ F :無因次累積雨量 τ P :無因次降雨量 τ R :無因次降雨量對數比率 λ ξ δ γ, , , :Johnson 機率函數參數
SL: Johnson 機率函數之對數常態系(Lognormal system)
SU: Johnson 機率函數之無界限系(Unbounded system)
SB: Johnson 機率函數之有界限系(Bounded system)
r λ :第 r 階 L-動差(L-moments) r τ :第 rL-動差比率 r l :第 r 階 L-動差樣本估計值 r t :第 r 階 L-動差比率樣本估計值 s , r , p M :權重機率動差 w , p X :權重分位數
MSE:均方誤差(Mean Square error) wi:第 i 分佈權重係數
DDF:降雨量-延時-頻率曲線(Depth-duration-frequency, DDF, curve) (h) F t max H :t 小時之年最大降雨量機率分佈函數 p , k d 及 :分別為在某一發生機率 P 下 k 日連續降雨事件總雨量與相對應 t 小時之雨量 t p , k h k max, D 與 :為 k 日連續降雨事件之年最大總雨量與其對應之事件的最 大 t-小時雨量的分位數 t k max, H nk:k 日連續降雨事件之場次 i k, D 與 t :k 日連續降雨事件總雨量與所相對應之最大 t 小時雨量 i k, H
( )
h ε :推求重現期距 T 年 t 小時降雨量之目標函數 AMS , m θ :在現有 m 年實測時雨量資料下,應用 AMS 模式所推得降雨 DDF 曲 線 el mod , m θ : 在現有 m 年實測時雨量資料下,應用模式(AME 模式或 AE 模式) 所推得降雨 DDF 曲線 ,AMS m+l θ :在現有 m 年實測時雨量及 l 年延伸日雨量資料下,應用 AME 模式 或 AE 模式所推得降雨 DDF 曲線 AMS , m ε :在現有 m 年實測時雨量資料下,由 AMS 模式所得降雨 DDF 曲線與 由 100 年降雨資料配合 AMS 模式所得 DDF 曲線之相對誤差 el mod , m ε :在現有 m 年實測時雨量資料下,由 AME 及 AE 模式所得降雨 DDF 曲線與由 100 年降雨資料配合 AMS 模式所得 DDF 曲線之相對誤 差 el mod , m l+ ε :在現有 m 年實測時雨量及 l 年延伸日雨量資料下,由 AME 模式或 AE 模式所得降雨 DDF 曲線與由 100 年降雨資料配合 AMS 模式所 得 DDF 曲線之相對誤差(
m,model m,AMS)
Prε ≤ε :在現有 m 年實測時雨量資料下,AME 模式或 AE 模式 所得降雨 DDF 曲線之相對誤差小於或等於 AMS 模式 所得結果之機率(
m ,model m,AMS)
Prε +l ≤ε :在現有 m 年實測時雨量及 l 年延伸日雨量資料下,AME 模式或 AE 模式所得降雨 DDF 曲線之相對誤差小於或 等於 AMS 模式所得結果之機率
第一章 緒論
1.1 研究背景
大多數水利相關工程例如洪水預報、防洪工程,應用於邊坡穩定評估 之排水及入滲分析等,降雨資料為必需已知之基本資料。降雨資料主要由 降雨事件發生次數(number of rainstorm events)、降雨延時(storm duraiton)、 總降雨量(rainfall depth),降雨時間分佈(time distribution of rainfall) (即降雨 雨型, storm pattern)及事件間隔時間(inter-event time)等五種特性所組成 (Marien 及 Vandewiele, 1986)。 上述各降雨特性不僅代表降雨事件之規模及在時間上分佈的性質外, 其組合而成之降雨序列(即雨量記錄)長短及其品質,更會影響水利系統相 關工程設計之可靠度。一般而言,在進行水文相關分析時,若具有足夠的 降雨特性資料,則可得到可靠之推估及設計結果,例如防洪水工結構物設 計、或乾旱預防及水資源開發規劃及分配水量等。然而,實際上水利工程 師常面臨降雨資料短缺,或雖有足夠的雨量資料但符合分析所需的資料型 態卻不足之情況,例如需時雨量進行頻率分析卻只有日雨量資料等情形。 而在台灣雖約有 1250 雨量站(大多分屬於各地水利會、中央氣象局、水利 署及台電公司),但其中部份站因缺乏管理、人為疏失或儀器故障等原因, 造成紀錄中斷或過短,或者雖具有足夠的資料,但卻係為長時間尺度之降 雨量(例如日雨量),而無法提供於需時雨量資料之不同延時(小時)雨量頻率 分析或需要降雨時間歷線也就是降雨組體圖之降雨-逕流演算等水文分析。 因此,如何由過去降雨資料來衍生符合水文水理分析所需的合適時間 尺度之降雨量,藉以有效地增加原有實測降雨資料之可用性,並提高相關 分析結果之準確性及可靠度,實為目前水文分析之重要課題之一。
1.2 文獻回顧
降雨事件之模擬已有相當多有關於降雨模擬的模式已被發展,而這些模式基本上依其採 用的理論可區分定率模式也就是氣候模式(Meteorological model)(Mason, 1986)、統計模式(Statistical model)及序率模式(Stochastic model)。氣候模式 主要採用大尺度且複雜的方程式來描述控制降雨甚致於其他氣候因子的 物 理 過 程 (Mason, 1986) ; 統 計 模 式 主 要 考 量 降 雨 在 空 間 的 非 定 常 性 (Non-stationarity)及時間上的趨勢(Temporal Trend),例如單站或多站時間模 式(Single or Multisites Temporal Model) (Stern 及 Coe, 1984)。而序率模式可 分 為 將 變 數 假 設 為 獨 立 的 多 尺 度 模 式 (Multi-scaling Models) , 例 如 Multifractal Cascades 模式(Lovejoy 及 Schertzer, 1990; Gupta 及 Waymire, 1994),或是依據實際雨量紀錄分析其降雨特性,並作一簡易的假設來隨機 模擬降雨在時間及空間之情形的模式(Onof 等 2000)。上述模式除了氣侯模 式外,其他模式皆採用不同統計分析方法來模擬降雨,其中序率模式依模 擬對象可分為降雨核胞模式(Rain Cell Model) (Cowpertwait, 1991, 1994, 1996, 1998, 2004,與其他合作者, 1996a, b; Glasbey 等, 1995; Verhoest 等, 1997; Oncf 等, 2000; Koutsoyiannis 及 Onof, 2001) ,例如 Waymire 及 Gupta(1981a,b,c)發表 一 系 列 之 文 章 來 採 討 模 擬 降 雨 核 胞 之 Bartlett-Lewis (BL) 模 式 及 Nyman-Scott (NS)模式,在很多研究中 BL 及 NS 模式皆被應用於衍生單站 之點降雨(Point-rianfall)事件(Glasbey et al., 1995; Verhoest et al., 1997; Koutsoyiannis 及 Onof, 2001);另一模式主要模擬降雨事件之特性來衍生降 雨序列,例如 Raudkivine1Lawgun(1970)發展了一階馬可夫過程模式( The first-order Markov process model)來模擬都市中的降雨序列,此模式採用降 雨延時及降雨量之聯合機率分佈函數模擬其值,且假設事件相隔時間符合 Weibull 分佈並由此分佈衍生其值。Eagleson(1977)發現降雨延時及降雨量 及事件相隔時間皆符合 Exponential 分佈,稱之為指數模式(Exponential model)(Cameron et. al., 2000)。Acreman(1990)發展一隨機模式來製造單站之 時雨量序列。此模式有能力分別採用 Exponential、Conditional Gamma 分 佈、及 Generalized Pareto 分佈來重新製造降雨延時、降雨量及乾時期時間
(Dry-spell),此外亦採用 Beta 分佈來模擬不同延時之平均降雨事件剖面 (Average event profiles),也就是降雨在時間的分佈即雨型。Cernesson 等 (1996)發表一具有 7 個參數之模式來模擬降雨過程不連續之自然現象及及 尖峰值結構。Lambert 及 Kuczera(1996)發表了一簡單點降雨模式能夠代表 延時、平均事件降雨強度、間隔時間及雨型。此模式使用可在無因次降雨 及時間空間上之約制隨機移動(Constrained random walk)來代表每一降雨 事件在降雨量上隨機分佈特性。Harrold 等(2003)發展了一套適用於雨季的 無參數降雨量模擬模式,此模式以 Kernel density estimation 法取代需先決 定雨量之合適機率分佈函數之假設,並且以移動視窗方式(Moving window) 分析雨量在不同季節之變異程度。
上述文獻回顧可歸納出,降雨序率模式基本上採用機率分佈函數配合蒙 地卡羅方法(Monte Carlo simulation method)方式來衍生降雨特性,而其中 主要的差異在於雨型之模擬也就是將雨量拆解(Disaggregation)成較小時間 尺度的降雨量(例如時雨量)方式之不同。如 Acreman 模式採用 Beta 分佈描 述 平 均 累 積 降 雨 剖 面 , Englson 模 式 假 設 降 雨 型 態 矩 型 (Rectangular Pattern),其他模式如 Bartlett-Lewis (BL)式及 Nyman-Scott (NS)模式則假設 每一雨胞為為矩型雨型,但各雨胞當組合成事件時,則形成非矩型的降雨 型態,亦有模式以 Johnson 機率分佈函數描述雨型以考慮其在時間上的變 異性例如 Wu 等(2005)。由於有甚多方法可模擬降雨,故 Cameron 等(2000) 應用英國的雨量站資料之統計特性來評估三種較常用的模式,分別為修正 Eaglesion 指數模式(Modified Eagleson’s exponential model, MEEM)、由 Camerson 等(1999)所發展之累積機率函數及 Generalized Pareto 分佈函數 (Cumulative density function and generalized Pareto distribution model, CDFGPDM) 及 隨 機 參 數 Bartlett-Lewis Gamma 模 式 (Random parameter Bartlett-Lewis Gamma model, RPBLGM)。其研究發現 MEEM 與 RPBLGM 模式可有效重複製造與實測資料之統計特性相近之降雨量,但在年最大降 雨量之模擬效果則較差。CDFGPDM 之模擬成效在文中所列的驗證指標下
皆顯示良好。 不同時間尺度降雨量之轉換 在不同時間尺度雨量間轉換方面,亦有相當多模式被發展成能由長時間 尺度雨量資料推得短時間尺度雨量。例如 Hershenhom 及 Woolhiser(1987) 發展一有效參數(Parameter-efficient)模式將日雨量拆解(disaggregate)成數 個獨立暴雨事件(Showers),並根據日雨量模擬各暴雨事件之延時與雨量。
Nguyen 與其工作團隊(Nguyen 及 Chaleeraktrakoon, 1990; Nguyen 及 Pandcy, 1994;Nguyen et al., 1998)發展不同時間尺度雨量間(主要是日雨量及時雨 量)統計分位數(statistical quantiles)關係之方法。將所有日雨量及時雨量應 用於頻率分析,藉以推得與日雨量分位數具有相關性之時雨量分位數。此 一方法可提供在只具有日雨量的區域藉以推得時雨量之統計特性,因而可 提高日雨量在工程上之應用性。Glasbey 等(1995)利用 Rodriguez-Iturbe 模 式(由 Rodriguez-Iturbe 於 1987 年所發展)衍生時雨量資料,並由模擬時雨 量中計算 3 日雨量與實測值相互比較藉以驗證模式推估成效。Connolly 等 (1998)發展了一將日雨量分解時雨量之模式,並以澳洲四雨量站降雨資料 來驗證明模式,其結果顯示此模式同樣地可以衍生降雨特性。Koutosyiannis 及 Onof(2001)建置了一機制應用 Barlett-Lewis 模式將日雨量分解成時雨 量,且此機制更被推廣應用於降雨量在時間及空間之相關性之研究,以建 立可由日雨量站推求時雨量資料之區域化模式。Onof 等(2005)發展一套以 Log-Poisson 分佈為基礙,可將時雨量拆解成 5 分鐘降雨量之二參數模式。 作者採用 London 各季的時雨量資料分別來率定模式參數。由模式驗證結 果可知,模式在由時雨量推求 5 分鐘雨量之成效良好,應可適用需要較小 時間尺度降雨量的都市水文分析。
1.3 研究內容及目的
本文主要目的為發展一套可考量不同時間尺度之隨機降雨序列模擬機制,來解決降雨資料短缺的問題。其研究內容為蒐集具有足夠時雨量資料 之雨量站,且根據所設定的條件選取降雨事件,並擷取各事件之降雨特性 並計算其統計量,其中除了考量各降雨特性彼此間的相關性,更特別著重 於雨型之變異性,作為建置隨機降雨序列模擬機制之基礎,期使所發展的 模式能合理地製造符合過去降雨特性之事件並將其組合成降雨序列,進而 達到增加降雨紀錄年限之目的。 另從降雨序列中推導日雨量與不同延時(小時)之降雨量分位數關係,作 為推導採用日雨量資料之時雨量頻率分析模式,其模式發展之目的為可藉 由具有較多的日雨量資訊來推得時雨量分位數,也就是降雨量-延時-頻率 曲線(Rainfall Depth-duration-frequency, DDF, Curve)。
最後將上述之隨機降雨模式機制與日雨量為基礎之時雨量頻率分析模 式,整合成為一可考量不同時間尺度之降雨模式機制,用以衍生不同時間 尺度的降雨序列而應用於水文及水理分析。
1.4 論文架構
本論文架構主要可分為三部份:第一部份為為介紹降雨特性及隨機降 雨模擬機制發展過程(如第二章所示);第二部份為詳細說明採用日雨量之 時雨量頻率分析模式之發展架構(第三章);第三部份為模式建立與驗證, 包括隨機降雨模擬機制及時雨量頻率分析模式之個別驗證與評估,並與上 述二模式整合運用範例(第四章)。最後本論文針對第四章之驗證成果提出 結論,並建議未來研究方向(如第五章)。第二章 隨機降雨序列模擬機制之建置
降雨序列主要由不同場次之降雨事件所組合而成,而各降雨事件又由 不同之降雨延時、雨量、雨型及事件間隔時間所組成(如圖 2.1 所示),故 降雨事件發生次數(Number of Rainstorm)、降雨延時(Storm Duration)、雨量 (Rainfall Depth)、雨型(Storm Pattern)及事件間隔時間(Inter-event Time)為組 成降雨序列之基本元素,稱之為降雨特性。本文將針對各降雨事件之統計 特 性 來 發 展 一 套 隨 機 降 雨 序 列 模 擬 機 制 (Stochastic Rainfall Series Generation, SRSG, Model)並依降雨特性將模式區分成三部份:(1)降雨事件 發生次數之模擬;(2)降雨延時、雨量及事件間隔時間之模擬;及(3)雨型之 模擬,本文將依據上述降雨特性發展模式,其發展過程如圖 2.2。 2.1 降雨事件之定義 在發展隨機降雨模擬機制前,首先需先將降雨序列分成數個獨立的降 雨事件,以利於分析及歸納其降雨特性之統計特性。若從氣象觀點來看, 降雨事件之形成與當時的氣候條件(例如溫度及濕度等)有關,故不同降雨 事件存在於不同的氣候環境,也就是說各事件因發生條件並不相同而使彼 此間可能不具有相關性,因此各降雨事件間可視為一獨立的事件。在水文 學上可用來定義互為獨立之不同降雨事件的統計方法有:(1) 自相關法 (Autocorrelation Method) (Morris, 1978);(2)級序相關法(Rank Correlation Method (Bonta 及 Rao, 1988); 及(3)指數法(Exponential Method) (Eagleson, 1977; Bonta and Rao, 1988; Restrepo and Eagleson, 1982)。
許多降雨-逕流研究(特別是在排水系統工程方面)較著重於颱洪期間所 發生的所有降雨量是否會造成洪災,並不需將降雨區分為不同的事件。相 反地,若要進行雨型分析則需將降雨區分成不同事件。故根據水文分析目 的,降雨事件可分為二種:(1) 設定一段無降雨時間(Dry Time),以求得延 時內每一時刻皆有降雨量之連續降雨事件(Yen and Chow, 1980);及(2)設定
一降雨標準(例如降雨延時或降雨強度需大於某一標準)來選取事件,而此 類事件之每一時刻並非皆有降雨量,即允許短暫無降雨時刻存在。 由於降雨序列模擬機制之建置係以實測降雨資料為基礎,故降雨事件 之選取標準會直接影響模式模擬結果,需慎選降雨事件選取標準。由於本 文主要著重於會形成顯著逕流狀況之降雨事件,故降雨事件研選標準設定 為總降雨量及平均降雨強度需達某一特定標準之事件。 2.2 降雨事件發生次數之模擬 在模擬 N 年內所發生的降雨序列時,每一年的事件發生次數之機率分 佈函數需先予以決定。一般而言,可應用於水文事件發生次數之機率分佈 主要有 Binomial 分佈、Negative Binomial 分佈及 Poisson 分佈。將上述三 機率分佈介紹如下, a. Poisson 分佈函數 0,1,2,... n , n e n) P(N n n = μ = = − (2.1) 式中 N 為事件次數;及μ為在特定之單位時段內發生次數之平均值。 b. Binomial 分佈函數 2,... 1, 0, n , a) (1 a n r n) P(N ⎟⎟ n − r n = ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = − (2.2) 式中 r 為所有降雨事件;及 a 為降雨事件之發生機率。 c. Negative binomial 分佈函數 2,... 1, 0, n , r a) (1 a n 1 n r n) P(N ⎟⎟ n − = ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − = = (2.3)
Cunnane(1979)提出以 Fisher 離散指數(Dispersion Index, )來檢定降 雨事件發生次數之合適分佈 I D
∑
= − = − = N 1 i 2 i I ) m ( E ) m ( Var ) 1 N ( m ) m m ( D (2.4) 式中 mi為第 i 年降雨事件發生次數;m為年平均發生次數。其中 DI屬於χ2分佈且具有(N-1)個自由度。其判斷準則如下, a. 若 2 2 1 I 2 2 D −α α ≤ ≤χ χ ,則事件發生次數(m)為 Poisson 分佈。 b. 若 2 2 I D ≤χα ,則事件發生次數(m)為 Binomial 分佈。 c. 若 2 2 1 I D ≥χ−α ,則事件發生次數(m)為 Negative binomial 分佈 其中統計顯著水準α通常為 1%或 5%。
在過去文獻(Eagleson, 1977; Alexandersson, 1985; Marien and Vandewiele, 1986; Waymire and Gupta, 1981a,b,c), Poisson 分佈廣泛用於水文事件發生 次數之模擬。因此本文將沿用前人研究成果採用 Poisson 分佈於事件發生 次數之模擬。
2.3 降雨延時、雨量及間隔時間之模擬
2.3.1 非常態多變量蒙地卡羅模擬(Non-normal Multivariate Monte Carlo Simulation) 在實際水文系統中,降雨量通常隨著延時增加而增加,且在雨季時降 雨事件多且密集,相對地各事件間隔時間縮短。相反地,在旱季時,降雨 事件少連帶著間隔時間增長。由這些水文現象可知,降雨延時、總雨量及 事件間隔時間彼此之間存在著某種程度上的相關性,且具有不同的統計特 性(包括機率分佈函數種類),更詳細來說降雨延時、雨量及事件間隔時間 為非常態(Non-normal)且具有相關性之變數。由於此類隨機變數不易建立 聯合機率分佈函數,使得模擬其值相當困難。Chang 等(1994)發表了一套 應用多變量的邊際機率分佈函數(Marginal Probability Distribution)及變量 之 相 關 係 數 配 合 蒙 地 卡 羅 方 法 之 模 擬 方 法 (Multivariate Monte Carlo Simulation, MMCS, Method)。MMCS 法除了傳統蒙地卡羅法模擬變量外, 包含以下三個步驟(如圖 2.3 所示):
(1) 標準常態轉換(Normal Transformation)
第一步驟先利用 Nataf 二變量分佈(如 2.5 式)將相關性變量由原先空間 轉換至標準常態空間,也就是將非常態相關變量轉換成常態相關變量。
(
)
i j * ij j i j j j i i i ij z ,z dz dz x x ρ φ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ σ μ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ σ μ − = ρ∫ ∫
∞ ∞ − ∞ ∞ − (2.5) 式中 Xi及 Xj 為具有相關係數ρij之隨機變數;μi及μj分別為隨機變數 Xi 及 Xj之平均值; 及 分別為隨機變數 Xi及 Xj之標準偏差;Zi及 Zj為具 有相關係數 標準常態變數; i σ σj * ij ρ φ( )
z 為標準常態分佈。其中將已知變量 Xi 及 Xj之邊際機率分佈函數及相關係數ρij代入解(2.5)式,可求得所對應在常 態變量空間之相關係數 ,若(2.5)式無解析解則以數值方法求其解。Liu 及 Der Kiureghian (1986)將(2.5)式簡化為下式, * ij ρ ij ij * ij =T ×ρ ρ]
(2.6) 式中 為轉換因子(Transformation Factor),其型式隨著不同邊際機率分佈 函數種類與隨機變數特性而異(如表 2.1),。 ij T (2) 正交轉換(Orthogonal transform)常態多變量分析(Multivariate normal analysis)中處理具有相關性的隨機 變量時,正交轉換為一相當重要的步驟。此步驟主要係將由步驟(1)所得相 關性多變量經過常態轉換成具有相關性的標準常態變量後,再利用正交轉 換成獨立的常態變量。最後再藉由蒙地卡羅法模擬獨立常態變量,並將獨 立常態變量模擬值再經由正交轉換成具有相關性的標準常態變量。 (3) 逆轉換(Inverse Transform) 由步驟(2)模擬標準常態變數後,可藉由下式將具有相關性之常態變數 模擬值各別轉換成原空間變量。
[
(z ) F x i 1 i i = Φ − (2.7) 式中Fi( )
• 為變量 Xi之邊際機率分佈函數。 上述模擬過程可參見圖 2.4。 2.3.2 邊際機率分佈函數之檢定 在水文頻率分析中,一般常用 Kolmogorov-Smirnov (K-S)檢定水文量之 合適機率分佈。雖 K-S 檢定可決定合適分佈,但卻易於發生二種以上的分佈之通過檢定,也就是其 p-value 值皆大於某一特定顯著水準,而成為最 佳分佈。為了解決這問題,本文將採用具有最大 p-value 之分佈為可被接 受之機率分佈,並將其應用在於降雨延時、雨量及事件間隔時間之 MMSC 模擬。 2.3.3 模擬程序 根據上述理論將模擬降雨延時、雨量及間隔時間之步驟整理如下: Step[1]: 由蒐集的降雨事件計算其延時、雨量及事件間隔時間之各階統計 動差。 Step[2]: 應用 K-S 檢定決定降雨延時、雨量及事件間隔時間之合適機率分 佈函數。 Step[3]: 應用非常態多變量蒙地卡模擬法衍生各事件之降雨延時、雨量及 事件間隔時間。 2.4 降雨雨型之模擬 降雨組體圖基本上為降雨量或降雨強度在時間上的分佈,也就是降雨 雨型(Rainstorm Pattern),換言之,雨型決定了降雨在時間上的分佈情形, 進而影響了集水區之水文反應(Hydrologic Response),例如暴雨所形成的逕 流。已有許多學者進行相關研究如 Huff(1967)提出平均法設計雨型,此方 法主要針對 3 至 48 小時降雨事件,依其嚴重程度分成四組(Quartile),對 較嚴重之降雨事件組,推求各場降雨無因次累積曲線,最後計算所有無因 次累積曲線之平均值,作為該組之設計雨型; Pilgrim 及 Cordery(1975)發 展一級序平均雨型法,此方法係將每場降雨事件分為數個時段,將每一時 段之降雨量百分比給予級序,總級序最小者給予最小降雨量百分比,反之 總級序最大則給予平均降雨量百分比最大值;Yen 與 Chow(1980)提出三角 形設計雨型法,此法主要求得各場降雨之重心時間,加以無因次化並平均 之,以此計算尖峰前後之直線公式,即得三角形法設計雨型;國內則有張 守陽(1983)利用序率水文學原理,以馬可夫一階歷程(Markovian First-order
Process) 觀 念 , 求 取 逐 時 雨 量 之 轉 移 機 率 矩 陣 (Transitional probability matrix),依此矩陣推求序率法設計雨型;余濬(1988)應用中央氣象局台北 測站 1968 年至 1987 年之逐時降雨資料,以極端值選用法,選出 18 場降 雨延時為 22 小時至 26 小時之最大降雨量,以 K-S 檢定法求得台北市最佳 一日設計雨型;顏清連等(1989)發展無因次移動平均法 (Dimensionless Moving average Method)設計雨型,以移動平均法計算每三小時平均雨量並 予以無因次化,將各場降雨累加平均之,以求取設計雨型;林國峰及張守 陽(1992)分別針對長延時降雨(18 小時~30 小時)及較短延時降雨(3 小 時~9 小時)之降雨事件,對降雨量進行統計特性分析、持續性檢定,建立 不同設計方法,並開發合適的雨型評估方法。鄭克聲等(1999)視每一場降 雨事件為一隨機歷程,考慮每個時刻之序列符合常態分佈,以一階高斯馬 可夫歷程模擬臨前水文條件的遺傳效應,以序率方法得到具最大概似度之 雨型。 由於不同的降雨事件會有不同的雨型,因此在模擬降雨事件時,除了 需衍生降雨延時、雨量及事件間隔時間外,亦需製造雨型。因此,本文將 發展一模擬降雨雨型之機制,包括(1)雨型特性之歸納(Characterization of Rainstorm Patterns);(2)雨型之分群及判識(Classification and Identification of Rainstorm Patterns);及(3)雨型之模擬(Simulation of Rainstorm Patterns)。茲 將各部份之詳細內容說明如下: 2.4.1 雨型特性之分析與歸納 由於各降雨事件之延時及雨量彼此間具有差異性,連帶造成降雨型態 間亦有所不同,故宜先將各降雨事件予以無因次化,以利於雨型的分群。 降雨事件之無因次化可藉由調整累積降雨曲線之時間(橫軸)及雨量(縱軸) 之尺度(如圖 2.5)求得,如下式 1 d d ; P F F D D F ; d t − τ τ τ × τ τ = = − = τ (2.8) 式中 為無因次時間,其值介於 0 跟 1 之間(t∗τ τ∈(0,1
]
);d 為降雨延時;Fτ為[ ]
0,1 ∈ τ 無因次累積雨量(F ); 無因次降雨量。其中需注意的是在無因次 時間第一點 ( )之 。降雨事件在進行因次化時,須先決定無因次時 間點數目,以便將降雨延時分成數段後求取每一時間點相對應的無因次雨 量。但須注意的是若取的時間點數目太少則可能無法完整地描述降雨型 態,反之太多點將因太詳細描述雨型之細部變化,複雜了雨型並且掩蓋了 雨型主要之變化。在考量以上的原因後,在本文中降雨延時將被區分成 11 段也就是無因次時間點數目 M 為 12(M=12),並求得各時間點之相對無因 次累積雨量 或無因次降雨量 。 τ P 1 τ 1 1 P Fτ = τ τ F Pτ =Fτ−Ft−1 ,τ=i/M (i=1, 2, K, M) 藉由上述無因次化方法,所有降雨事件的時間及雨量全被調整成同一 尺度,也就是每一場降雨事件之降雨延時及雨量均被調整為 1。故降雨事 件之無因次化不僅可使雨型去除了降雨延時及雨量多寡的影響而僅存在 時間上的變異,更可以使原本具有不同雨量及延時之事件予以彙集、測試 並分群而得到不同之降雨型態(雨型)。 2.4.2 雨型之分群及判識 常用於水文事件之分群的方法主要有主成分(Principle Component Analysis, PCA)及群集分析(Cluster analysis, CA)( Zurich, 1971; Fang 及 Tung, 1996; Hannah et al., 2000; Lin et al., 2004)。其中群集分析的基本原理為依照 各獨立個體的相關屬性(Attribute)予以分類(Collins, 1980),也就是按自然類 別(Natural Grouping)將分佈於某一計量空間(Metric Space)的點予以分類, 使得同一群集內的個體具有相似屬性,而各群集彼此間卻具有不同屬性。 在分群過程中為了將不同變量之尺度效予以消除,故在計算之前先將不同 屬性變量標準化成為平均值為零而標準偏差為一的變量。 在進行集群分析前,需先訂定衡量變數間的相似程度尺標,最常被使 用 的 相 似 度 尺 標 係 計 算 各 屬 性 變 量 在 計 量 空 間 的 距 離 (Distance Measurement),主要有以下三種型式:(
)
12 m 1 2 , j l , i j , i x x DE ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − =∑
= l l (2.9) (2) 皮爾生距離(Pearson distance, DP)(
)
[
}
{
]
∑
= ν − = m 1 2 1 2 , j , i j , i x x DP l l l l (2.10) (3) 曼哈頓距離(Manhattan distance, DM)∑
= − = m 1 l , j l , i x x DM l (2.11) 式中 m 為變量數目; 及 為在計量空間中第 i 點跟 j 點對第 l 點之距離 (k=1, 2, …, m);及 為 l 群之樣本標準偏差。將各變量間的相似程度加以 衡量後,接著應用集群方法將各樣本歸入不同集群中。在集群分析中一般 採用層次分析法(Hierarchical Method),例如平均連鎖法(Average Linkage Method) 與 華 德 法 (Ward’s Method) , 另 一 方 法 為 非 層 次 分 析 法 (Nonhierarchical Method),例如 K-平均值法(K-means Method)。 根據 Fang 及 Tung(1996)與 Ramos(2001)等人研究指出不同集群方法所得最後的分群 結果並不會有明顯的差別,但以 K 平均值法具有較佳的分群效益也就是在 分群的過程耗費較少的計算時間並具有較簡單的分析步驟(Ramos, 2001)。 因此本文將採用以歐基里得距離為基礎的 K-平均法(MacQueen, 1967),並應 用統計軟體 Minitab(Minitab, 1999),進行雨型之分群。茲將 K-平均值法分群 步驟說明如下, l , i x xj,l l ν Step[1]: 將各變量分割成 K 個原始集群,並求出各集群之重心; Step[2]: 將每一樣本點分配到重心最接近的群集中; Step[3]: 重新計算每一個群集的重心; Step[4]: 將群集中每一個樣本點距重心之歐基理得距離加以平均; Step[5]: 找出新群集,每一樣本點再次被分配到重心最接近的群集中; Step[6]: 重複進行直到群集邊界不再變動為止。 2.4.3 具有約制條件之非常態多變量隨機變數之模擬在模擬降雨事件過程中,當模擬降雨延時、降雨量及事件間隔時間後, 接著需模擬降雨在時間的分佈(即雨型)。但在模擬雨型前,必需了解雨型 的二種重要性質:(1)無因次降雨量 為非負變量且局限於 0 跟 1 之間 ( );及(2)不同的無因次時間 τ P 1 P 0≤ τ ≤ τ的 彼此間存在著相關性,也就是 屬於具有相關性之非常態多變量。根據上述雨型的性質可知在模擬雨型需 考量以下限制式, τ P Pτ (1) 總合為 1: P 1 (2.12a) M / M M / 1 =
∑
= τ τ (2)非負變量:Pτ ≥0, τ=1/M,2/M,K,M/M (2.12b) 式中 M 為無因次降雨時間點之數目,在本文中 M 定為 12。 由於無因次降雨量 屬於多變量非常態隨機變數,理論上可使用 MMCS 蒙地卡羅法模擬雨型,但因具有(2.12)限制式存在,使得 MMCS 在 模擬無因次降雨量 時,除了 2.4 節中所述的非常態多變量模擬步驟外, 仍需以下二種程序將具有約制條件之多變量轉變無限制式之多變量。 τ P τ P2.4.3.1 對數比率轉換(Log-ratio Transformation method)
目前已有相當多方法被提出以解決具有約制條件之多數量相關問題。 例如 Aitchison(1986)曾針對具有約制條件的模擬技術詳細的探討,其研究 成果建議可採用 Log-ratio 處理方法。Borgman 及 Faucette(1993)發展一實 用的方法可將具有線性限 制之多變量高斯模擬轉換成一條件多變量高斯 模擬(Conditional multivariate Gaussian simulation)。Zhao(1992)提出一方法 來模擬同樣具有總合需為 1 限制的單位歷線,且用在評估水工結構物因單 位歷線不確定性所承受設計失敗的風險。其中亦有文獻針對雨型提出解決 方法,例如 Lambert 及 Kuczera(1996)認為可將無因次降雨量 轉換成一對 數常態隨機變數(Log-normal Random Variables),藉以消除(2.12)式之限 制。Fang 及 Tung(1996)採用接受-拒絕方法(Acceptance-rejection Method)、 累積機率曲線法(Cumulated Probability Curve Method)及 log-ratio 法去模擬
τ
無因次降雨量 ,發現 log-ratio 法具有較佳的適用性及較穩定的計算結果 (Computational Robust),因此本文將延用 Fang 及 Tung 之研究,採用 log-ratio 法應用於無因次降雨量 之模擬。 τ P τ P Log-ratio 轉換法應用於雨型之模擬主要採用下式,
(
)
* ; M / M , , M / 2 , M / 1 , P P log Rτ = τ τ* τ= K τ≠τ (2.13) 式中為 為無因次時間指標。無因次降雨量 介於 0 跟 1 之間,所以其對 數比率 則介於 及∞。在模擬過程中,須注意的是 及 皆不可為 0 以避免在取對數之計算上的錯誤。 ∗ τ Pτ τ R −∞ Pτ Pτ* 當無因次降雨量 經由 log-ratio 法轉換成 ,則原本屬於具有約制條 件之非常態多變量模擬轉變成如同模擬降雨延時、雨量及間隔時間一樣的 非常態多變量,可直接用 MMCS 蒙地卡羅法模擬對數比率 ,當求得對 數比率模擬值 後,可由(2.13)式求得 τ P Rτ τ R τ R Pτ =Pτ* exp( )
Rτ ,將其代回(2.12)式 求得Pτ*(如下式),( )
∑
τ ≠ τ= τ τ τ + = M/M M / 1 * * R exp 1 1 P (2.14) 再將(2.14)式代回(2.12)式,則可求得 Pτ( )
( )
* M / M M / 1 ; 1 0 , R exp 1 R exp P * τ ≠ τ ≤ τ < + =∑
τ ≠ τ= τ τ τ τ (2.15) 2.4.3.2 多變量 Johnson 分布函數之模擬 由上節所述經由 log-ratio 轉換分法,可將具有約制條件之非常態多數量 模擬問題將轉變為無約制條件非常態多數量模擬,也就是說可應用 MMCS 法模擬對數比率 值。然而,由 2.3.1 節可知,若需使用 MMCS 法,則先 要檢定變量之合適機率分佈,由於雨型具有 M(M=12)個 變量需檢定其 τ R τ R合適分佈,無形中增加了檢定上的因難及模擬之繁雜度,為此具有較廣泛 適用性的 Johnson 分佈函數組群可適用於描述Rτ之統計性質。 Johnson( 1949)提出一個四參數之機率分佈函數
(
)
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ λ ξ − × δ + γ = λ ξ δ γ =g X , , , f X Z (2.16) 式中 Z 為標準常態變量;X 為原隨機空間之非常態變量; 為機率 函 數 參 數 其 中 λ ξ δ γ, , ,ξ 為 位 置 因 子 (Location Parameter)及λ為 尺 度 因 子 (Scale parameter)。 Johnson 分佈主要有以下三種型式 (1) 對數常態系(Lognormal System, SL)
(
−ξ)
<ξ δ + γ = ln X , X Z : SL (2.17) (2) 無界限系(Unbounded System, SU)(
)
[
−ξ λ δ + γ = − / X sinh Z : SU 1]
(2.18) (3) 有界限系(Bounded System, SB) λ + ξ < < ξ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − λ + ξ ξ − δ + γ = , X X X ln Z : SB (2.19) Hill 等(1976)發展了一套演算法,利用變量 X 的前四階動差來率定數γ,δ,ξ,λ 值並決定 Johnson 分佈之型式。 2.4.4 模擬程序 根據上述的雨型分群及模擬理論方法,其模擬過程可整理如下, Step[1]: 應 用 (2.8) 式 將 降 雨 事 件 無 因 次 化 , 則 可 得 無 因 次 降 雨 量 ,其中本文將無因次時間點數目 M 定為 12(M=12)。 M , , 2 , 1 i , M / i , F F Pτ= τ − t−1 τ= = K Step[2]: 應用集群分析將雨型分為數群並定義各類型。 Step[3] 應用 Log-ratio 轉換法,即(2.13)式。將有約制條件之 轉換成不具 約制條件之非常態多變量數 τ P(
)
* ; 12 / 12 , , 12 / 2 , 12 / 1 , P P log Rτ = τ τ* τ= K τ≠τ,其中本文將無因次 時間指標 定義為τ* 。 3 * = τ Step[4] 決定 M(M=12)個對數比率值 之 Johnson 分佈類型並率定其參數 值 τ R λ ξ δ γ, , , 。 Step[5]: 經由 Johnson 分佈函數求得對數比率值Rτ之相對標準常態值(
γ δ ξ λ)
= τ τ τ g R , , , Z 。 Step[6]: 採用多變量蒙地卡羅模擬(MMCS)法衍生Zˆτ。 Step[7]: 再利用 Johnson 分佈函數將對Zˆτ模擬數轉換成對數比率模擬值(
γ δ ξ λ)
= − τ τ τ g Zˆ , , , Rˆ 1 Step[8]: 最後藉由(2.14)及(2.15)式將Rˆτ摸擬值轉換成無因次降雨 。 Pˆτ 2.5 降雨序列模擬過程 綜合 2.1 至 2.5 各節所說明降雨特性之模擬理論,隨機降雨序列模擬過 程整理如下: Step[1]: 決定降雨事件選取標準並整理各事件之降雨特性。 Step[2]: 計算降雨特性之統計特性。 Step[3]: 模擬降雨延時、雨量及事件間隔時間。 Step[4]: 模擬降雨型態(雨型)。 Step[5]: 由模擬所得之降雨延時及降雨量配合雨型則可產生降雨組體圖, 並依各事件之間隔時間模擬值,將各事件之模擬組體圖串連成一 降雨序列(如圖 2.5)。表 2.1 不同機率分布函數之轉換因子(Transformation Factor)表 (Liu and Kiureghian, 1986)
圖 2.1 降雨特性之定義
圖 2.3 多變量蒙地卡羅 MMCS 方法之模擬程序(參數 12 t t
x ,V ,
D− Λ 之推
圖 2.4 降雨事件之無因次化
第三章 採用日雨量之時雨量頻率分析模式之建置
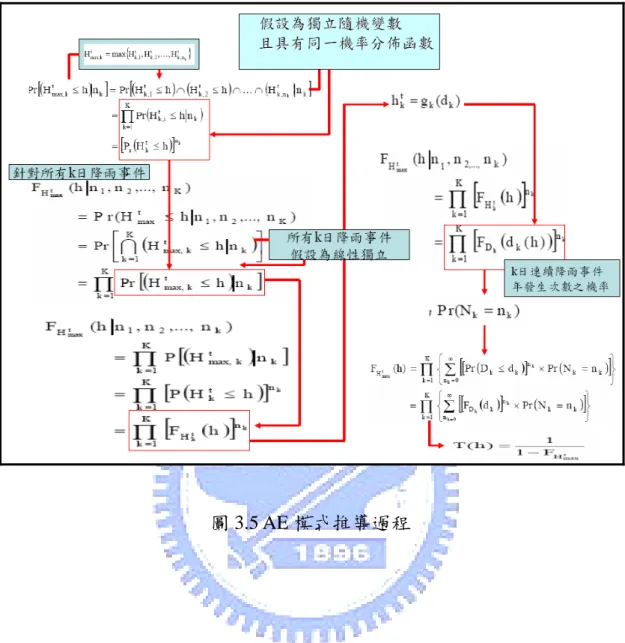
本章主要發展一套藉由日雨量資料推估不同延時(小時)之年最大降雨 量分位數,也就是推求不同重現期距之降雨量之模式,此模式之基本概念 為建立日雨量及時雨量分位數(Quantile)之轉換機制,此機制主要包含三部 份:(1)降雨事件之分類;(2)日雨量與時雨量分位數關係式之建立;及(3) 以日雨量為基礎之時雨量機率分佈函數之推導。 3.1 降雨事件之分類 根據降雨發生時間,可將降雨事件區分成完整降雨事件(Complete Storm Event)與部份降雨事件(Partial Storm Event)二類(如圖 3.1)。所謂完整降雨事 件為降雨發生與結束時間皆在同一天;而部份降雨事件發生與結束時間並 不在同一日。一般而言,若將所有降雨事件視為完整事件,也就是只從單 日的降雨紀錄中選取短延時(2hr≤t <24hr)最大降雨量,則可能發生因忽略 跨日的部份降雨事件導,致沒選取真正的年最大降雨量,而影響了水文分 析之結果,例如低估降雨量-頻率關係。為了減少此類誤差。本研究將根據 完整事件及部份事件之定義,配合降雨發生時間及降雨延時,將降雨事件 區分為以下類型: (1) 單日降雨事件(Single-rainy-day Events):所有降雨事件之開始與結 束時間皆在同一日,且前後二日並其他無降雨事件發生。 (2) 二日連續降雨事件(Two-consecutive-rainy-day Event):所有降雨事 件之開始與結束時間皆在連續二日內,且前後二日並無降雨事件 發生。 (3) k 日連續降雨事件(k-consecutive-rainy-day Event):所有降雨事件 皆發生在連續 k 日內(k≥3)。 上述各類降雨事件可參見圖 3.2。3.2 時雨量與日雨量分位數關係之建立 3.2.1 降雨量分位數之推求 在建立日雨量與時雨量分位數相關式前,需先由合適的機率分佈函數 推求日雨量與不同延時之時雨量分位數。其中最適合的機率分佈函數一般 可由合適度準則(Goodness-of-fit Criteria)決定,但如同 2.2 中所提及不同合 適度可能得到不一致的檢定結果。為避免此一問題,本文應用楊錦釧等 (1997)所發展以八種常用的機率分佈函數(如下所示)為基礎之權重頻率曲 線(Weighted frequency curve)法。
(1) 常態分佈(Normal distribution)
(2) 對數常態分佈(Log-normal distribution) (3) 皮爾遜分佈(Pearson distribution)
(4) 對數皮爾遜分佈(Log-Pearson distribution) (5) 伽瑪分佈(Gamma distribution)
(6) 極端值第 I 型分佈(Generalized Extreme value distribution) (7) 帕爾多分佈(Generalized Pareto distribution)
(8) 邏輯分佈(Generalized logistic distribution)
各分佈函數之定義及其參數與各階乘積動差之關係請參見表 3.1。雖使用 權重頻率曲線可解決因檢定合適分佈所產生的不確定性,但仍存在因推估 分佈函數參數所產生的不確定性。造成此不確定性之原因主要為過去在推 估各分佈函數之參數時大多使用乘積動差 (Product Moments),但因乘積動 差之誤差會隨階數增加而提高,為此 Hosking(1987)提出 L-動差(L-moments) 來解決此類偏差可獲得得相當不錯的結果。基於上述原因,本文將採用權 重頻率曲線法及 L-動差法推求 k 日連續降雨事件總雨量及其所對應的 t 小 時最大降雨量之分位數。現將 L-動差法及頻率曲線法之理論說明如下, 3.2.2 L-動差法(L-moments method)之簡介
性組合。相關文獻(Hosking, 1986, 1990, 1992 及 1997; Vogel 及 Neil, 1993; 張斐章等, 1995; 王如意等, 1999)顯示 L-動差不僅應用在估計離散資料之 分位數時比傳統乘積動差為優,且其計算結果較無偏差(Unbiased)。此外 Hosking 亦更進一步證明在樣本數少時,線性動差估計參數比最大概似 (Maximum likelihood)法較為準確。 第 r 階 L-動差λr定義如下
(
X)
, r 1,2,K E k 1 r ) 1 ( r 1r 1 1 k r : k r r ⎥ = ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = λ∑
− = − (3.1) 式中 表示每次由母體中抽出 r 個樣本,按小至大排序中第(r-k)個樣 本之期望值。L-動差與乘積動差相似,不同階動差比率可定義為(
Xr k:r E −)
L- CV : 1 2 2 λ λ = τ (3.2a) L-Skewness : 2 3 2 λ λ = τ (3.2b) L-Kurtosis : 2 4 2 λ λ = τ (3.2c) 雖使用(3.1)式推估機率分佈函數參數相當複雜且困難,但可透過 L-動差跟 權重機率動差(Weighted Probability Moments)之關係式,來簡化推導過程。 權重機率動差係由 Greewood 等(1979)推導,其定義為( )
[
]
[
( )
]
{
p r s}
s , r , p EX F X 1 FX M = − (3.3) 式中 p,r,s 為實數若令 s=0,則 即為傳統的乘積動差。若令 p=1 則(3.3) 式可形成一線性型式,若另令 0 , r , p M s , 0 , 1 s =M α 及βr =M1,r,0,則可得( )
[
]
{
X1 F X}
, s 0,1,2,K E M1,0,s s s = = − = α (3.4a)( )
[
]
{
XFX}
, r 0,1,2,K E M1,r,0 r r = = = β (3.4b) Hosking 用 來建立 L-動差跟權重機率動差之關係式,即將 n 個獨立樣本 按小至大排序,即 r β ( )n X(n 1) X( )2 X( )1 X ≤ − ≤K≤ ≤ ,則小於或等於第 j 個順序統 計量的機率F[ ]
X( )j 可由點繪公式(如 3.5 式)求得,( )
[ ]
, a 0, b 0 b n a j 1 X F j ≥ ≥ + − − = (3.5)當 a=0 且 b=1 時,(3.12)式為常用的 Weibull 公式,而 a=0.35 及 b=0 時具 有較小的誤差(Hosking, 1986)。L-動差可用權重機率動差表示,
( )
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = = α − = β = λ − ∗ = ∗ = ∗ +∑
∑
k k r k r 1 P , 2 , 1 , 0 r , P ) 1 ( P k r k , r r 0 k k k , r r r 0 k k k . r 1 r K (3.6) 則前四階之 L-動差(λi,i=1, 2, 3, 4)可表示為 0 1 2 3 4 0 1 2 3 0 1 2 0 1 12 30 20 6 6 2 β − β + β − β = λ β + β − β = λ β − β = λ β = λ (3.7) 因 之樣本估計量βr br可表為 ( ){
[ ]
( )∑
= r j j r X FX n 1 b}
(3.8) 則前四階之 L-動差樣本估計值(li,i=1, 2, 3, 4)為 0 1 2 3 4 0 1 2 3 0 1 2 0 1 b b 12 b 30 b 20 l b b 6 b 6 l b b 2 l b l − + − = + − = − = = (3.9) 且 L-動差比率樣本估計值為 2 4 4 2 3 3 1 2 2 t t t l l l l l l = = = (3.10) Hosking(1986)與 Stedinger 等(1993)已推導各機率分佈參數與各階 L-動 差之關係式(如表 3.1),因此本文將採用由(3.16)及(3.17)式所推導各階L-動差與 3.2.3 節所列八種機率分佈函數參數之關係式來(如表 3.2)推估雨量 分位數。
3.2.3 權重頻率曲線法(Weighted frequency curve method)之簡介
權重頻率曲線法基本理論為先假設每一分佈皆為合適分佈,應用機率 點繪法,推估各資料樣本點之相對發生機率 p,並將此機率 p 代入假設的 分佈中推得分位數,最後將此分位數與樣本代入不同合適度準則,將其所 得計算結果作為權重係數,最後加權總合各分佈之分位數,則可得權重分 位數Xp,w,其公式如下
(
)
∑
= × = M 1 i i , p i w , p w X X (3.11) 式中 為第 i 分佈所得發生機率為 p 之分位數;及 wi為第 i 分佈之權重 係數,將不同發生機率之權重分位數組合起來則可得權重頻率曲線。權重 係數之訂定取決於合適度型式。在本文中主要採用表示分位數與樣本的差 異程度之均方誤差(Mean Square error, MSE)為合適度準則 (如下式),i , p X ( ) ( )