1
行政院國家科學委員會專題研究計畫成果報告
邊界頻譜法在聲學問題的研究與開發
Boundar y spectr al method for acoustic scatter ing
and r adiation pr oblems
計畫編號:NSC 87-2611-E-002-011
執行期限:86 年 8 月 1 日至 87 年 7 月 31 日
主持人:黃維信 國立台灣大學造船及海洋工程學系
一、中文摘要 本文應用邊界頻譜法求解邊界積分方 程式。利用某些數學恆等式,將 Helmholtz 積分方程的其異性解除,所以頻譜法所用 的基礎函數與非奇異核函數乘積積分能有 效且精確完成。與傳統方法作比較,本方 法並不直接求解節點之物理量,而是求解 廣義 Fourier 係數,這對未知數數目和儲存 矩陣大小的降低都有很大的幫助。本文中 以圓球的散射及輻射問題為例作為本方法 的驗證。 關鍵詞:邊界頻譜法、Helmholtz 積分方 程、聲波 Abstr actThe spectral method is considered in solving boundary integral equations. By sub-tracting known solutions from the Helmholtz integral equation, the singularities of the Helmholtz integral equation are removed. Therefore, any order of basis functions, used in spectral methods, that times non-singular kernels in the modified Helmholtz integral equation can be integrated easily and effi-ciently. Instead of solving the variables at collocation points in the conventional meth-ods, the generalized Fourier coefficients are solved in the spectral method which reduces the number of unknowns and the storage of matrix elements in computation. Scattering and radiation problems from a sphere are used to illustrate the technique in the present
paper.
Keywor ds: Boundary Spectral Methods,
Helmholtz Integral equation, Acoustics
二、緣由與目的
The prediction of acoustic fields from radiation or scattering is a problem of practi-cal importance in many applications of engi-neering and science. Analytical solutions for such problems are generally limited to very special cases. Therefore, the boundary inte-gral equation has gained popularity for solv-ing the arbitrary shape of body in the past few decades. The boundary integral equations contain both known and unknown boundary variables in the formulation. The unknown variables are obtained numerically by solving a system of algebraic equations which are discretized from the boundary integral equa-tions. The discretization technique which is developed in finite element methods is com-monly used and this approach is sometimes called the boundary element method. The boundary element method is one of the most important computational schemes in practice.
There is an essential discrepancy be-tween the integral formulation and finite element methods. In finite element methods, the interpolation functions, in general, are low-order polynomials and affect only on the adjacent local elements. The resultant system of algebraic equations is banded or sparse, which means the local variables can affect nearby elements only. It is consistent
be-2
tween the usual finite element formulation and its effect of interpolation functions. In the other hand, boundary integral equations have completely different properties which any local variables will affect the global be-havior directly. That is why the algebraic equations formed from boundary integral equations are always full matrices. Therefore, the local discretization technique in finite element methods does not really match the global influence very well in the boundary integral formulation. A global approximation technique should be more suitable for the boundary integral formulation.
In the literature, spectral methods have been developed for solving partial differenti-al equations since early 1970s, especidifferenti-ally in computationally intensive applications in meteorology and fluid dynamics.1,2 Spectral methods generate algebraic equations with full matrices, in which is consistent with the integral formulation, and the high order of the basis functions gives high accuracy for a given number of basis functions for compen-sation to solve full matrices. However, the boundary integral equation involves another difficulty in handling singular integrals, and special kinds of treatment are needed for the numerical implementation. Usually, the accu-racy of numerical quadrature depends on not only the number of integration points but also the order of interpolation function. The high order interpolation function usually gives high accuracy also. Again, this property is close to spectral methods. Although spectral methods have those advantages and are suc-cessfully used in solving partial differential equations, they does not be applied in the boundary integral equations until the re-cent.3,4 In acoustics, only a special geometry, circular cylinder, is formulated by spectral method for boundary integral equation.5 In the present paper, we apply this global ap-proximation technique to solve boundary integral equations for arbitrary body geome-try instead of the local discretization schemes from finite element methods. We believe the spectral method is more suitable for boundary integral equations than the local
shape functions developed in finite element methods.
In the integral formulation of acoustic problems, the non-uniqueness problem has frequently been discussed in the literature for a long time. The combined Helmholtz inte-gral equation formulation (CHIEF) proposed by Schenck.6 In the present proposal, CHIEF was adopted in the first year(86-87) because it was simple and easy to be programmed.
三、結果與討論
A. Application to scatter ing fr om a spher e
For simplicity, a sphere is chosen for the demonstration, since its analytic solution of the scattering problem of a plane incident wave is well known and easy to compute. By utilizing the axisymmetric shape of sphere, the velocity potential can be treated as a one-dimensional case, and the Chebyshev poly-nomials are chosen to be the basis functions, though the analytic solution is known to be Legendre functions in the present case. The incoming unit plane wave travels to the right along x axis and is described as Φin =
exp(ikx). For the scattering wave from a sphere of radius a, the scattered velocity po-tential at a distance r from the center of sphere and an angle θ from the x axis is de-noted by ΦS( , )r θ .
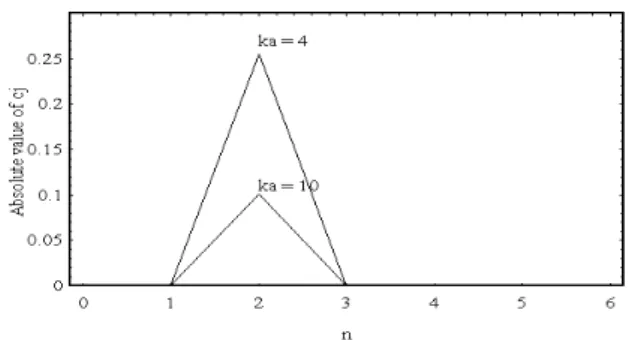
Figure 1 shows the distribution of the absolute values of generalized Fourier coeffi-cients for nondimensional wave numbers ka=4 and 10. A 24-point Gaussian formula is applied for the numerical integration in both cases. The variation of coefficients indicates the speed of convergence and one can deter-mine the number of orthogonal functions for the required accuracy. Figures 2 and 3 show the comparison of analytical and numerical results for real and imaginary parts of scat-tered velocity potentials on the sphere surface for ka=4, respectively. As Fig. 1 shows, 8 terms of Chebyshev polynomials for ka= 4 are enough to approximate the analytic result.
3
The analytical solution of the velocity potential for an oscillating sphere of radius a with a radial velocity cosθ is given by
Φ( ) ( ) cos ( )( ) ( ) P e a r a ikr k a ika k a ik r a = − − − + − 2 2 2 4 4 1 2 2 4 θ (1)
Eq. (1) shows that the solution is a one-term polynomial when the velocity potential is on the sphere surface, r = a. Figure 4 indicates this fact that the coefficient is at a peak when n=2 and almost zero when n≠2. In Figs. 5 and 6, a 24-point Gaussian formula is applied for the numerical integration and six terms of Chebyshev polynomials are selected. The comparison between analytical and numerical results is presented for real and imaginary parts of radiating velocity potentials on the sphere surface for ka=4, respectively.
C. Conclusion
The spectral method is developed in solving boundary integral equations. The new scheme presents orthogonal functions as ba-sis functions for acoustic variables instead of low-order shape functions. The spectral method shows several advantages over con-ventional boundary element methods. The accuracy of spectral methods is high and can be estimated directly from the variation of generalized Fourier coefficients. If extremely high accuracy is required, spectral methods are even better than conventional boundary element methods. In general, the number of unknowns in the present method can be much less than that of conventional boundary ele-ment methods. Therefore, the present method saves a large amount of matrix storage and time when the matrix is solved.
四、參考文獻
[1] C. Canuto, M. Y. Hussaini, A. Quarteroni, and T. A. Zang, Spectral Methods in Fluid Dynamics (Springer-Verlag, Berlin, 1987).
[2] J. P. Boyd, Chebyshev & Fourier Spectral Meth-ods (Springer-Verlag, Berlin, 1989).
[3] J. M. Occhialini, G. P. Muldowney, and J. J. L. Higdon, "Boundary Integral/Spectral Element
Approaches to the Navier-Stokes Equations," Int. J. Numer. Methods Fluids, 15, 1361-1381 (1992).
[4] L. R. Hill and T. N. Farris, "Fast Fourier Trans-form of Spectral Boundary Elements for Tran-sient Heat Conduction," Int. J. Num. Meth. Heat Fluid Flow, 5, 813-827 (1995)
[5] Fang Q. Hu, "A fast numerical solution of scat-tering by a cylinder: Spectral method for the boundary integral equations," J. Acoust. Soc. Am. 96, 3693-3703 (1994).
[6] H. A. Schenck, "Improved Integral Formulation for Acoustic Radiation Problems," J. Acoust. Soc. Am. 44, 41-58 (1968).
[7] O. D. Kellogg, Foundations of Potential Theory (Dover Publications Inc., New York, 1954). [8] M. A. Jaswon and G. T. Symm, Integral
Equa-tion Methods in Potential Theory and Elas-tostatics (Academic Press Inc., London, 1977). [9] W. S. Hwang "A Boundary Integral Method for
Acoustic Radiation and Scattering," accepted by J. Acoust. Soc. Am. (1997).
[10] K. E. Atkinson, An Introduction to Numerical Analysis (John Wiley and Sons, Inc., New York, 1988). 五、成果自評 本研究內容與原計畫相符、並達成預期 目標、研究成果兼具學術及應用價值、適 合在學術期刊發表。
4 Fig. 1 Absolute values of generalized Fourier
coeffi-cients when scattering from a sphere for ka = 4 and 10.
Fig. 2 Real parts of scattered velocity potentials on the surface of a sphere when ka = 4.
Fig. 3 Imaginary parts of scattered velocity poten-tials on the surface of a sphere when ka = 4.
Fig. 4 Absolute values of generalized Fourier coeffi-cients on the surface of an oscillating sphere for ka = 4 and 10.
Fig. 5 Real part of the velocity potential on the sur-face of an oscillating sphere when ka = 4.
Fig. 6 Imaginary part of the velocity potential on the surface of an oscillating sphere when ka = 4.