JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 105, NO. C12, PAGES 28,785-28,804, DECEMBER 15, 2000
Fourier and wavelet analyses of TOPEX/Poseidon-derived
sea
level anomaly
over the South China Sea: A contribution
to the South China Sea Monsoon Experiment
Cheinway
Hwang and Sung-An
Chen
Department
of Civil Engineering,
National
Chiao
Tung
University,
Hsinchu,
Taiwan
Abstract.
We processed
5.6 years
of TOPEX/Poseidon
altimeter
data
and
obtained
time
series
of
sea
level anomaly
(SLA) over
the South
China
Sea
(SCS).
Fourier
analysis
shows
that sea
level
variability
of the SCS contains
major
components
with periods
larger
than 180 days
and is
dominated
by the annual
and semiannual
components.
Tidal aliasing
creates
30-180 day
components
that can
be misinterpreted
as wind-induced
variabilities.
Continuous
and
multiresolution
wavelet
analyses
show
that the SLA of the SCS has
monthly
to interannual
components
of time-varying
amplitudes,
and
the
regional
slope
of SLA
is 8.9
mm
yr
'1,
which
may
be caused
by the decadal
climate
change.
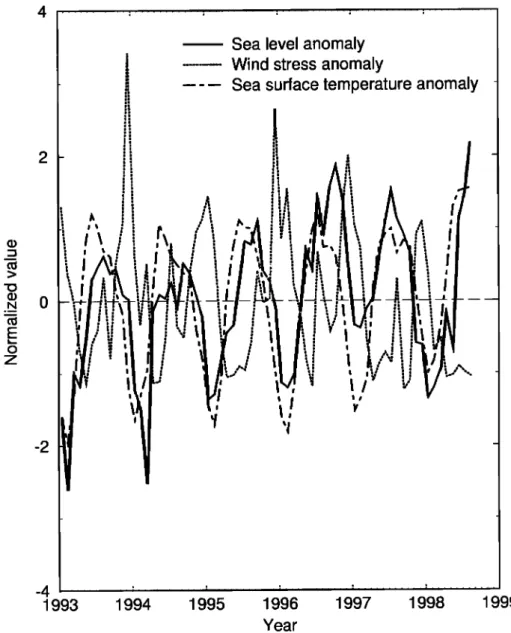
Coherences
of SLA with wind stress
anomalies
(WSA)
and sea
surface
temperature
anomalies
(STA) are significant
at the annual
and semi-annual
components.
At periods
of 2-5 years
the wavelet
coefficients
of SLA, WSA, and STA have
the
same
pattern,
but WSA leads
SLA, and STA follows
SLA. The zero
crossing
of SLA in spring
is
highly
correlated
with the onset
of the summer
monsoon.
The interannual
variability
of SLA is
correlated with E1Nifio-Southern Oscillation, and most important is that when the El Nifio-like wavelet coefficients of SLA over the warm pool northeast of Australia or the SCS changecurvature
from negative
to positive,
an E1 Nifio is likely
to develop.
This is a contribution
to the
South China Sea Monsoon Experiment (SCSMEX).
1. Introduction
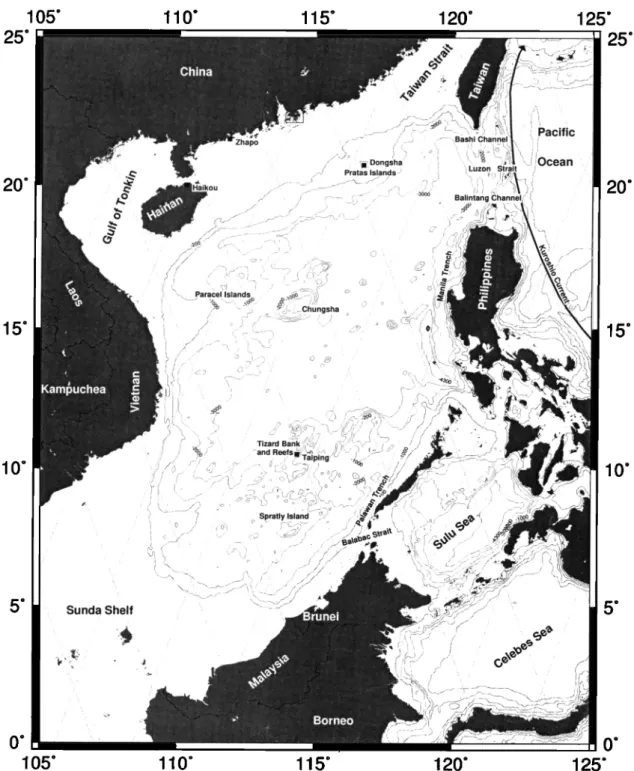
The South China Sea (SCS) is the largest marginal sea in the
western Pacific with a total area of 2,590,000 km 2. Figure 1 shows
the countries, waters, major islands and bottom features, and major
depth contours around the SCS. The South China Sea Monsoon Experiment (SCSMEX) is an international project to study the
monsoons over the SCS. The participating countries include most
countries in east Asia and southeast Asia, Australia, and the United
States. Its purpose is to "better understand the key physical processes in the onset, maintenance, and variability of the
the summer and winter monsoons over the SCS and to E1 Nifio-Southem Oscillation (ENSO) will also be studied.
2. Sea Level Anomaly From TOPEX/Poseidon
T/P is a satellite altimeter mission specifically designed tomeasure the height of the sea level with a repeat period of 9.9156
days. We used the T/P Version
C Geophysical
Data Records
(GDRs) from Archiving,
Validation,
Interpretation
of Satellite
Oceanographic Data (AVISO) [1996] to generate corrected sea surface heights (SSHs) from cycle 10 (December 26, 1992) to
monsoon
over
southeast
Asia
and
southern
China"
[Lau,
1997,
p. cycle
219 (August
29, 1998).
The
first
nine
cycles
were
not
used
599].
We have
joined
SCSMEX
to investigate
the
characteristics
of because
of a pointing
problem
[Fu et al., 1994].
The
orbit
we used
sea level variability over the SCS derived from the in the T/P GDRs is based on the Joint Gravity Model 3 (JGM3)
TOPEX/Poseidon
(T/P) altimeter.
We will perform
Fourier
and gravity
field [Tapley
et al., 1996]
and
has
an accuracy
of about
4
wavelet
analyses
of the T/P-derived
sea level time series. cm. The dry tropospheric
and
inverse
barometric
corrections
were
Compared
to Fourier
analysis,
wavelet
analysis
is a recently based on the European
Centre for Medium Range Weather
developed
tool that
is best
suited
for analyzing
phenomena
with Forecasts
(ECMWF)model.
The
wet
tropospheric
corrections
were
time-varying
frequencies
and amplitudes.
An extensive
body
of directly
taken
from
the TOPEX
Microwave
Radiometer
(TMR)
literature
associated
with
wavelet
analysis
has
been
developed
over measurements.
For the ionospheric
correction,
TOPEX uses
its
the past decade.
The lectures
by Daubechies
[1992]
provide dual
frequency
measurements
and
Poseidon
is based
on the
model
readers
with
both
an introductory
and
an in-depth
understanding
of of Doppler
orbitography
and radiopositioning
integrated
by
wavelets.
A practical
guide
to wavelet
analysis
is given
by in satellite
(DORIS). The CSR3.0
ocean
tide model
[Eanes
and
Totfence
and Compo
[1998].
A collection
of applications
of Bettadpur,
1995]
was used
to detide
the data.
In particular,
an
wavelets in geophysics and oceanography is given by in oscillator drift correction has been applied to the TOPEX range Foufoula-Georgiou and Kumar [1994]. Moreover, we will measurements [AVISO, 1996]. To produce SLAs for the
compute
the frequency
response
functions
and
coherence
functions
subsequent
analyses,
we first formed
stacked
along-track
SSHs
by
[Bendat
and Piersol,
1993] between
sea level, wind, and sea averaging
the point SSHs from the 210 T/P cycles.
When
surface
temperature
over
the SCS
to see
the degrees
of interaction
averaging,
the gradient
of a geoid computed
from the Earth
among these signals. The relationships of sea level variability to Gravitational Model 1996 (EGM96) to harmonic degree 360 [Lemoine et al., 1998] was used to reduce point SSHs to the nominal ground tracks selected to correspond with the tracks of
Copyright
2000
by
the
American
Geophysical
Union.
cycle
92 for
this
study.
A point
SLA
was
computed
as
Paper number 2000JC900109.
0148-0227/00/2000JC900109509.00 zlh = h- h , (1)
28,786 HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA 105 ø 25 ø ß 20' 110 ø 115 ø 120 ø 125 ø ß 25 ø 20'
15 ø -
15'
::'Kam•Uchea.
•.
" / • 'x•
•./'•
Tizard
Bank
ß ") J •b,• o ? •and Reefs / : ) . Spratly Island'. ••. . ,- •.--. ... • ... ..5 ø
Sunda
Shelf
.,
./•/ :o
5 ø
',
...
: I
•' /
- '::."• ' . (-"-', • -i . • .... :...:.•. • • • •...
-, :,h•-' ,,-'•. •'
... •. .: ', ..'
-, '-•' • ' ,' I , .... •.. •% • . • ... ß .... •.q, /.?p,• . .,•.•-:.•• • •>_•, • .,?? ... , .. ,/•0 ø .
... ' ' '."'/
...
/•, , •zp•-•,•-•••:• ß
• 0 o105 ø
11 O'
1150
120 ø
125 ø
Figure 1. The South China Sea and its surrounding countries and waters. Also given are selected depth contours (solid lines), the ground tracks of TOPEX/Poseidon (dots), major bottom features, and islands. Squares indicate tide gauge stations.
where h and h are point and averaged SSH, respectively. An
area-averaged SLA over a given area is the simple mean of all
point SLAs in the area, and the associated time is the central time
of the T/P cycle. In computing the simple mean we rejected outlier
SLAs using Pope's [ 1976] • - test. An outlier point SLA satisfies
=
.
(2)
where v i and • are the residual of a SLA (observation minus
area mean) and the residual's a posterior standard error,
respectively, a is the confidence level, which is 95% in this
paper,
n is the number
of point
SLAs,
and *a;•,,-2 is the critical
, value with degrees of freedom of 1 and n -2. Outlier rejection
was performed iteratively until no outlier was found, and the final
area-averaged SLA was computed from the "clean" set of point SLAs. On the basis of Figure 1, SCS depths range from less than 200 m over the continental shelf to 6000 m at the center of the
basin
and
at the Manila
Trench.
From
numerical
models
[Shaw
and
Chao, 1994] and dritter data [Hu, 1998] the SCS has two distinct
HWANG
AND CHEN:
FOURIER
AND WAVELET
ANALYSES
OF SOUTH
CHINA
SEA
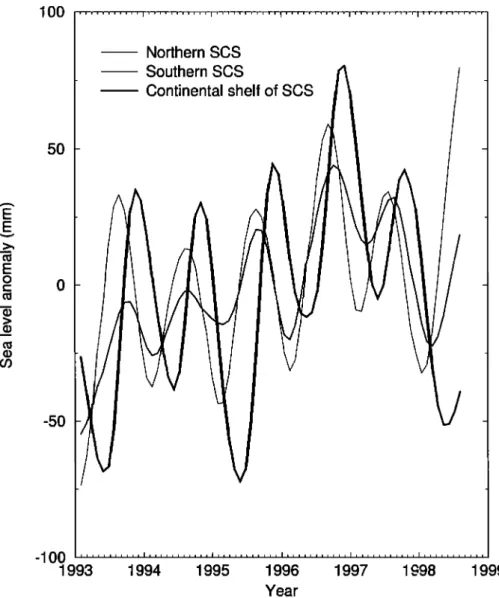
3OO 250 -250 -300 1993 SLA1 (Northern SCS) -- SLA2 (Southern SCS) ---- SLA3 (all SCS)... SLA4 (continental shelf of SCS)
I i i I J i i , i i i i i i , , I
1994
1995
1996
1997
1998
1999
Year
Figure
2. Time
series
of SLA
in four
areas
of the
SCS.
28,787
altimeter-observed
SSHs
over
shallow
water
will
have
larger
errors
Table
1 shows
the
statistics
in generating
the
four
SLA
time
series.
than
those
over
the
deep
ocean.
To
see
the
spatial
characteristics
of The
large
percentage
of rejected
SLAs
in SLA4
is due
to the
large
the
SCS
sea
level,
we
computed
SLA
time
series
in four
subareas
ocean
tide
model
error,
distortions
of altimeter
footprints,
and
of the SCS:
The first one
(SLA1)
is over
the deep
ocean
(depths
>
200 m) between
14.5
ø and 22øN,
the
second
(SLA2)
is over
the
deep
ocean
between
5 ø and 14.5øN,
the
third
(SLA3)
is over
the deep
ocean
between
5 ø and 22øN
(this
area
combines
the
first and the second areas), and the last (SLA4) is over thecontinental
shelf
(defined
as the area
with depths
<200
m) and
between
14.5
ø and 22øN. Figure
2 shows
the four SLA time
series.
Note
that
the time
series
in Figure
2 and
other
figures
in this
paper
have
the beginning
of each
year
(January
1) labeled.
In
general,
SLA1,
SLA2,
and
SLA3,
which
are
over
the
deep
ocean,
agree
very
well
with
each
other
but
are
significantly
different
from
SLA4.
SLA3
behaves
basically
as the average
of SLA1
and
SLA2.
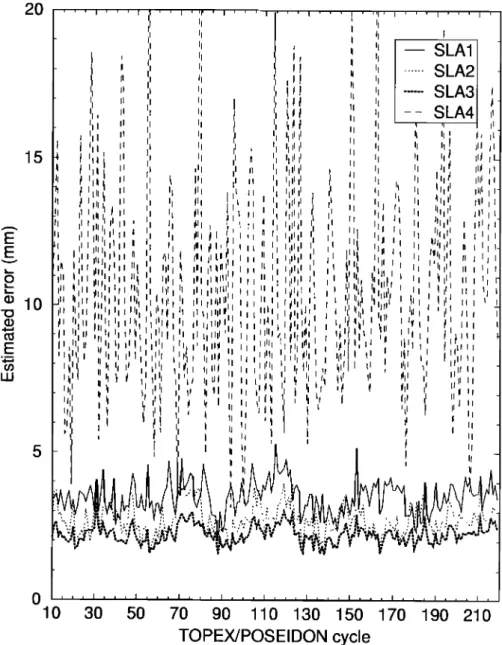
wind-driven events. Figure 3 shows the standard errors of the area
means in the four SLA time series. The standard error of an area
mean, tyro, is computed by
O'm
=
I(
• V,
t=l2
)/n(n
--
1)
,
(3)
where v t and n are defined
in (2). By this definition
a SLA
standard error will be affected by the variability of the sea surface under study. It appears that the SLA4 error is not random and has
periodic
components
arising
from ocean
tide model
errors.
A
Table 1. Statistics of Area-Averaged SLA over the SCS
Number of selected points
Percentage of rejected points, % Mean standard error, mm
North 727 0.76 3.49 South 997 1.66 2.75
All Continental Shelf
1726 132
1.15 3.73
28,788 HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA 2O
"
• ,,
SLA1
I I,
i
, I
', ', ...
SLA2 1
', " ', '' ', ... SLA3',, "
" t
, t t
', ,, -- SLA4 ,,1
11 ' II I I I ] I' I, I ½ i • ', I ' I t • ,• i I J II I I1 I I I I I i • I II It II I I1• i t •15
•" "
'•
" " "'•"
"
" "I ,'•,d
I Ill •l
• Ill
I II I I iI
i'• I I
tl Illll Ill
I
illl
•, II
I l
IlI
i.• rl I I I,illl . I '
I I
II •II II Illl
'Ill
?l I
I I Illl • !'I I • Ill I Ill I! I I' ii '
I, , Ill
' I Ill I I I
"•
III I II
I I III1•!
i I iii
Ii1
III !
II 1
I I I1•11
I1 1
Illl I IIIII
•
• II I I 1 I
III I III I II
i •I I I •11111
Illl
• i I II I' I , I II
I II I. i ifl
II ' • I . •, ,I •
, ,I' iii'
I I II IIII
• ii Iiii,
' ii i i I Iit
II
I II I
•Ii ' ' ' • ,"1 ,, ,' '1'1' •' ', ' ,•',', •, ,,,1', ,I,,,d
II I1 '.i' I
I !•l I • II I Ill
III I I I ' i I
II • 11 'Ii:'11Ii'
I I •t II I Ij Ii
1
• 10 ,, '. ',:I',
.
,• ,•,....,'.'
..,,
,';,,I,
,
Illl'" •.. ,,, ..
• I I I I IIß
•
,i ,, !"
i
", ,',
•,l,•',
!',,'
,•
,i, ,
,
,,:I1 ",,
',, ,I,,," ,l',,'
',i!' '•
I t' ,
:,,I, /
.• r..,,.
I•1• ,, II ', I II, , I .,..,, ,,',
Iit I il• 1 • I ' 1 I I I II.i ,•' •, . t•, t ,,,,,
I 1 • ' • I . Ir II II ..I /Ii, l/ •.• I I ,I •, ,. Ui II I llll • I, II • II I1,1 I•.
,,.' ',',,,
.',, I,i ! I..,.!ii..., ,,,
.'l ', .,,,ll .
,,,. !•
,.,, • I. "'•" •'
"I I 'i'l.
,,,' II ',' i !l '• f t , ',' : t ',' i " I 1 t • 'I
' I
II • I
I
II
""::,',ii'
"'" ..., ""?'
',",..
"'
',
'
',¾"::' '"'"'
10
30
50
70
90
110 130 150 170 190 210
TOPEX/POSEIDON
cycle
Figure 3. Estimated errors (1 standard deviation) of the area-averaged SLA in four areas of the SCS.
spectral
analysis
shows
that
the spectrum
of the SLA4
error
is SLA1
is much
larger
than
that
of SLA2
because
of the higher
almost
"flat,"
except
at two distinct,
large
components:
the largest latitude
of the northern
SCS, which is more sensitive
to the
component
has
a period
of 59 days
and
an amplitude
of 1.2 mm, seasonal
variation
in solar
insulation
than
the
southern
SCS.
Figure
and
the
next
one
has
a period
of 27 days
and
an amplitude
of 0.8 5 shows
the filtered
SLA
time
series
that
were
computed
using
a
mm.
These
two components
have
to do with
the T/P tidal
aliasing
Gaussian
filter
with
a wavelength
of 1 year;
see
Wessel
and
Smith
discussed
below.
In addition,
the SLA2
error
is smaller
than
the [1995]
for the
definition
of the
Gaussian
filter
and
its
wavelength.
SLA1
error
because
SLA2
uses
more
data
points
than
SLA1,
and Clearly,
the annual
components
over
the northern,
southern,
and
the
northern
SCS
has
a much
larger
sea
surface
variability
than
the continental
shelf
parts
of the
SCS
have
summer
peaks
at different
southern
SCS
[Hwang
and
Chen,
2000].
times
of the
year.
Comparing
the
phases
of the
annual
components,
3. Fourier Spectra
of Sea Level Anomaly
3.1. Periodograms
To see the overall characteristics of the sea level variability over the SCS in the frequency domain, we performed Fourier transforms to obtain periodograms of SLA1, SLA2, SLA3, and SLA4 (Figure 4). Table 2 shows the amplitudes and periods of the
first 10 largest components of the four SLA series. All four SLA
we find that summer peaks for SLA1 lead those of SLA2 by 21
days and SLA4 by 76 days. In the four SLA time series, there are
two strong interannual components with periods of 1036 and 2072
days, which will be investigated in connection to ENSO. Again, in
all aspects, SLA3 behaves essentially as the average of SLA1 and
SLA2.
3,2. Tidal Aliasing in TOPEX/Poseidon
SLA4, being over the continental shelf, has a distinct Fourier
series
have
strong
components
with
a period
of 345
days,
which spectrum
compared
to those
of SLA1-SLA3.
SLA4
has
strong
HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA 28,789 50 40 .-. 30 E E E
<t: 20
SLA1 SLA2 SLA3 ... SLA410 ':i
.
?.,
::
i !iii!i .;',.,.. • !0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Frequency
(cycle/year)
Figure
4. Periodograms
of SLA
time
series
in four
areas
of the SCS.
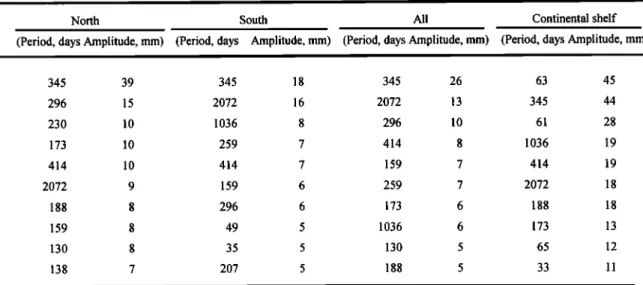
Table 2. Periods and Amplitudes of the 10 Leading Components of the Four SLA Time Series Over the SCS
North South All Continental shelf
(Period, days Amplitude, mm) (Period, days Amplitude, mm) (Period, days Amplitude, mm) (Period, days Amplitude, mm)
345 39 345 18 345 26 63 45 296 15 2072 16 2072 13 345 44 230 10 1036 8 296 10 61 28 173 10 259 7 414 8 1036 19 414 10 414 7 159 7 414 19 2072 9 159 6 259 7 2072 18 188 8 296 6 173 6 188 18 159 8 49 5 1036 6 173 13 130 8 35 5 130 5 65 12 oo • 1 1 138 7 •" 5 Ioo 5
28,790 HWANG AND CHEN' FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA
1993 1994 1995 1996 1997 1998
60 .... • --] ,- 14½ I- $-• +-•..1. • ... 4- • 4.- •.-i- i ' ' ',-4 .•- •--: ... l--L.-•-.•..,•'•k • ... ,.;•Z•' "•LL-.L..I-I-•.:.•...L .;-.. [.¾', ' ' ' .'
- F -• • ' / ' • • t ' ß , i • ß ' • ß : • • - • ' ' i -•-• • •-•- ;- • •' • ß I : t ' :• t • i • ' ' • • , • ß
,-' ... [ '. .... i ... ;.-4 .: ... i--i ... -]• -.•. 4--r.- --. •--• q -, •--,-,--- .-,.-•.i ... i...• ... •d.-i --I ...
a tt*. ,,:,,:- ,,, , .... ... ß r,,::,- ,, .... l
54 ( ) ....
...
... ...
...
, ...
, ...
...
, ...
...
48 1-4 -•--P .[-•4-14--i-PJ-L4•-• z. ! ::-!-.-i--:r--•.- :•--[. 4- !..-•-. i--•q.•-P.i-P..L_•-'• -•%•. -••.4•-.P.k.L..L.-p+ ' ..;....i....:....i..4...!...
•[, •-4- •--*--• &.•._.•.• ._•..- ...,;;_& .[_•_ • ... • ... &..[..•..,•.,•,-[ ... ; •....• ... : . • .... [.-•.•,...•_• ... • ... • ... &..L_•
- -• " • •- • "•'• ß -•'-'•* •--'*• " s •.' '? ' • -- ' ,. -- .r .... . '•.'•' •'*•'-:-• -"r- ;-'• ... • ... • .... • • ....
O 24 / • • F • •'*-•"• I'=½ •-• •'-'F• •'• , •'"r-•-•-•'-F"ir'-•- .... • '--i-' *"T"•-•"r ' r •-•-• •-• •W'F'• ... ... •- •---•' -•--:--•-+---•-.r-•-- %'•r"F-'c' r-'i • •'"Fz"'F 'r i- =- -r-F • "T"i". • •- • 'i' •-'7" i -i--• + -- i•-f.-•--, ... i.--f- .• -i-- wr.-,--
ß i i ! ß . : • . • : : ! ! : • • • i 1 : : i ß : i - • - i • • . i : : . : . ! ! • i i I
" • ... [' 'F'I .-q--r.---,--.• ... '"'+-"-•-T '+ ... * ... •-"-,'--½ -1-•-• .... i ... •----r--q--.f .-.I -• -i ... i ... i ... i ... i' '-•"! ... '""*""i ....
•,, z_i j_, X_•.J._L LL Li.. • i..%.i._L • ..'__Li., '•._L i' i._L LJ '[ J ... •...: ==...•._i j. i_i_L' _L.L..t%.L_' _[.•_.t ..• •..
3 • ß ' ,-- :• i = r -'• -[ ' •.-. ' ß •-•-- r-•"i ,'- i-"=T'•?'-w'•F ', •", T-mr -,-{-L • i .... L..-.:•-I-..½ ... •-, • -'r-F'r" 4•.4.•- • r c' r"t r .... 7r' %-r' !--•-•.-=-+-O-.!.- =-.-•4. -::- !.-.H-..• .... '. -•-4--+-: --.- t-? 'rw-rm-r'? r ... rw T •-r'
6O 54 48 42 36 3O 24 18 12 60 ß : : . , ß : * : ß : : : : ß - : : : • : ..: • • r t':- , • i ß • , - : i : : : : ß : : : : i : • .. ß t • • : 60 . _ •.---i --t.-~4.--i----,- -i - i---•-~ t---I--..i-. i--- ,-- -i -4. -i--.- i- , ---i-- -, --; --{-.-{.--,--.-4.-.-•.. ,---,---•4---,•-...I.•-.,.,-,.-..I.,,,4,r -. ,.•,.-,--..I-...,,..-..i....i,.- ..i. -i---.i-.-i-- ..i-.-i---.4.--i----.•--.-,,---•,..-4.--} .-.•-..-•--[--.:-i ,.4. (•. I --,-,--,- ,--•..---+-!-?-,-,-'t ... ,-'--,'-' .--',' ': -, ... ,-',--?'-,'---," -,-""+-•-'", "' .-'=','"".'-' ,-:"'i' -,--,--,---,--4-.,----.,---,----:----,--: ... !--..-!-,--, .--t ',' 54
54 v ' ! I i ! ": : i i i "' : I "i : ! • * : ' ': } I-•-: : ' t*"i I ! • ' • i%"I - : : : •.-,- : : : : • .*-,-! : z t ß : : : : : : I : • • : . : ;.- ß . . 3 ' i ! i ! ! ! i t : * i '• i ! *• ß i I : : : . : ; ! ! . : : ß ß
• /' •- *•'-"--q-'"•'---• "--'--•-'-" ... -" ... •-'" ... •' +---'- -'--*'"1'--'--- '- L.•-• ... ,--,-- r ... , ... +-~•---, ... •-F•i•.
,__, _. : ' LL LI.2... L..•LL •-_LU •.J-%J-L..L-L-L ',. .-L •....L L_L .[ _.L .L..i..j.i_ L4._.L_LL_Li...[". i-...L..L.J _L ..L.. t_.L .L_:..4 ..•._i...L2-.-"-L.L.2.. •.L. .... 48
48 ...,,: . -,---•-.•-i- F ' -•-q.-.•.-.•-'!--.•-4-•-i--.•-F•.--i--•:-.•--.• ,.:: ,:,:::,:,,:..,,,,::,:,:,,,, ' !--'--•---F---.•-!---i---.:-•--.•-!---!--.•-• , -'-.-.P--'.- , ,,,,.:,.:,-.,,,,:. 4. _•'-+.•_q_.F-,....•..•_•-:_..• , ß
42 _:•.L • .i__•_•__i._.;_4.• _• ß _•.•.•_•4•-,__t•.• ... ,•:_.•_;•.,.•:_: • ß • ... ... • '••.'-.:•.4•4-k•. s • • • • .... -i ,•_ !--•-•-..L. P-i- i._•L_-;•....i....• ß t ß ß . • - . .... i._.•_ i....• ! -k .... 4. --'.•-•-i-'.•-.L-i-:•k ... •. •-•- • .l..-.•.•,-.•-•.[,..• .... •-.i..-•i • • , r ß ß ß t ß •-..:--P.½4--.L•--i--i--:.•--P ß , • ß ß • • ß ß • • •_4._•_, ... '• •.4 --•: ..4 i ß , --• • ,_ • 42
36 ... :- ... ',---'• ... • ... ' ... .•'-'• ... ' ... : ... • ... '*• .... r ... ,--.' ... :-.'- ... 36
ß ß : : - : :.. : ; * : : i : : • : : • : . . : m. : , : : i : : • : .• : • : : : : r ß T 't: t•l !---? .--:'--? ":"":--T-r--. : . •
• , : - - ß -. - _ .... :_ .• .... •...•_._ ... ... , :•...:. • :_.-_. ß ... .._ ._....:...;•.•u ..: .... : .- ...:. --...-.._.: .•-....:..._,.• ... L ...- ...
-,-, 30 '.---• • _,._:-..3._ ... .... •_i...LJ_2_ •-+.-•-•-+-. !--L--:..-: -i .... •--':- !--,4-: .•L. L_L.-_.i...L_L..L....• ... i .-•.--; ... .Z...:..._2._:-...!...:;..•.._L.J...L. ';--k..:--:--:---;---+-i--. :--e--'•-4----:.--:.--."----•+-i-. :,._LJ_.L...'.'._L...LL.L_': 4- ... ..i_.[.4_LJ_.•....LL_•_;...i....L.i...•....L_L '--...[.~•--: ... .t.-:.4-.:-...I...•4.-:•..4-.•-,..-+ 4_ • 30
f t =-T- -- '[- -- u -• ----'-:- ß •.--.-r .--r--: ... :---•---: -•- :--'-r ... •._ ,- ,•..._:..._= ._..:.. ... .•-•...a. ... .•.
O 24 •..L• _!.. ... L• • -', L•_•-._L___i_L_L_L;_•_ !. ... L..-_::_.:._,i....L_:' .:..J-"•-`-.•--•:•...:-&..L...L-.:--..L-.`-...•`-L•.-.•.:-.L.L.-...-.L.:..--L-L.! ;...,•...,.'_,'..._i_.i_..i....•_._•_• , . 24
: . ; . :
l:::: 18 __Z_T-'.. ß ::_:..'-:_Z_--::_E • • i •- ;7.'7.Z.•.-7•_T.F'.-_UC-' -L-•']'œE-r7.-F-•,'.]Z-E:•.-.:- ' '• .... : F-r::...•ZZ•27;Z!•'4L-.F•;.r-:..-'"E;]E:.•E'L4- 18
-o 12 ...
i . : i i ' ' ! i i ii:ii' ...
' t i { i [ { ; i :: i.: ...
: J :: ; iiiiiß i : ' ' ': ...
12
': ... t ... '- "t• ... • ... '•'"' ' - --"' ... :- ... T ... :' "-' -•" ...
O i -•'-: i" i :"t. -::-'•-i-i ! • • !-'•-'.r!'T-½"::.-'1-i .-,TT'.:.-". '--i F-h-i, .'--: ; i'"'t-• ?r-h!-h:. :--;"½-i'"t
ß • 9 .• +-4.-: -f .... f-": -'+---=-f-i--: ... -.:---? .+-:-?+.-..-.•-•--.:..--+..½-,:--:.-. ;-..r-: ... P•:-'-r-'•--'•-,-'-•-":--:'•- *--•.--•-•-•-t'-* ... :- ... •-?-:.-• -' ß v- 9 --*-'T'w -"r-,"'r-r-:"-..-:---r.-r----r"•-'-, '• "-:~?---.'-? , r'"•"r'-,-'T-w r-".:'"'r-.:-'"r'-:-r•.--r-.:'"'r--: ... c-r-?", ':'-:--'??'-r"'?-7. ':"T"JF-r"T • ß
(1)
t
, , • : -: -:..!
....
,. ,_• , * : L -• :' •. : : .,i_,L_L
:. _:
'-'
•. :-.J
i..
L.:_
i..
:...i
2 ...:....•_.•
•..•.
L-"...,..i_:._
i .s • i_i_:..L.~L
,' • ..:..:...•.,
! 1: f
•, i : T-• -,'?Ti':.. ;-• i'-'F '-'!-i'"•-i ,W'T. i: !'• '!-f-iT !-i 'i 'i "• •' '".-- iii f¾.'!'-:: t ['i FTf"FF !' ;"i ',-'!-;•'i"• T':• ],: F
13_ 6 ...
6
: ' : : : i ,; [ : : } ' ß : : i • ' i i i '• ; : i * : r: : : •""•:
; .... i-? ..: •.T ? -7?-? - :' • , ,- , i .: --IT..- .... .-'• i•. !-"?-: ... .'--7 '•:--:--*'--• , .: -.- .... ... !'--?'~!'""T : • , ... : . .-' :: - "-':'-' i'- ?•T"i-•?'"F""i .. • • ß •* : : • • : ß
' '"•-'-- I""T--:'"?': : • . • •-: • , • : .'. , : ß '... , : ..' -: !.•'•
-?-!"i
'"l-"-'""'T'"F""i'•"'"'T'"r-'"'"~?"T"'="'-'"l--t""'i: : : i i = : i : --
: .
-~,..•.1- .•,..:f':,,,..,
,•:,,i,.•,...,..i•.,!:,:•,T•
...
øF_L,:..,•:.•..,,:,•,,:....,,
•
'q ' F.'F'r
!'.-'F'f
i'-:--7'-•
: 'T":7'qT'•
....
FT'•
• i'--:-fW'.-
f-•-'--.'.--:
F'T.T-i
C-iTTF'=
;-i-.?'i
i"'i
i"¾':.7-i'"i
':-
?'•'-[T'-f-i-FTT
3 -• .... : . : . .- • .... 'r•--• ',"-""'?-'-'-, ... "-'---'.- ß ß ; ,• : : . - - . . • . s ,- ß : ... r-:-',- ... . : . . - . : . ?--.- ... : . . . • . :--,-,--,-,-? ; : : I, : . ... . •---.--,--.-- . : : ß : : ... :---,- : . . • 3
-I'..--'"-e--":,-'-"'.•--+• ,L.'? :--'"'--i--- .-'--:--"•-' '."'."!-- .... e"-i:."-•:' "•-. -'-' .: .-'--:'W---"--- •'"= "'•;-'•-: '. '•' '• •---:--'--:' .-I•:-:.--'•-.:--':-'• .... F-"I- ..• - ß . - - - . . : : : : - : - I : : . : : - : - ß ß : I I : o ß . : : - : - . : : t : : ß . : t : : ' L I I
1993 1994 1995 1996 1997 1998
Time (year)
I
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100105110115120125130
Plate 1. Wavelet coefficients of (a) SLA, (b) wind stress anomaly, and (c) sea surface temperature anomaly over the $CS. The period of a wavelet coefficient is in the sense of Fourier analysis. The unit of coefficients is arbitrary. A coefficient of 130 means that the corresponding wavelet has the maximum similarity with the signal,f(t); a coefficient of 0 means that the wavelet has the maximum similarity with -fit); a coefficient of 65 implies the least similarity
HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA 28,791 1980 1982 1984 1986 1988 1990 1992 80 ' ' ' [ ' :
(a) , i
i
'.
i :,
: ' ' • '" j ... :i ... j ... -_! L ... 70 4 ... 1 i ... ! ! ... i : i ... t ! • ... ! i .... i t • : :t
• I ! I i '
i ß ' "
!
ß
60 ...
l ...
i ... , ...
7
...
.T-
...
r
...
T'
t ...
t • ! _c: 1 i , I ! i o 50 ... •.-x- œ ... .:.- ... * E .t ... -X,'- ... • ... 1994 1996 I i2O
I
o 50 E .o 40 i 1998 ' 80 I I .... 40 E - 30,i !
,..
,
•
•
,: x i
ix i
,'
.x {
30 ...
• ...
,.-
...
z ...
,;
...
.t
...
.•
...
i ...
• ...
] ...
i ...
• ...
,t
...
i -"' ?-' •
}
...
I -! • i i i ; , i i • i { i' i { i I ' : 20 ... ½ ... ,4 ... .• ... i ... p ... '.-... • .... ...,- -! ... ..'.- ... • ... : ... -:' ... •I---- -'- ... .'-. ... I t ! ! '!l 'l , i,i. ., { • i •.-'-. •, . . !i-/
"
-f
' ' '1
'
'1 '" '
I - -'
i
"' '"!' ' 'F --i' '• =:1
I '-
10 ß •' • ..-" l " r ! ... : .... •, .,.--, ... 1980 1982 1984 1986 1988 1990 1992 1994 1996 1998Time (year)
lO 8o - 70 60 - 5o - 4o - 30 20 10 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100105110115120125130Plate 2. Wavelet coefficients of (a) NINO3 SST and (b) extended SLA over the SCS. Period and interpretation of wavelet coefficients are the same as those given in Plate 1. The centers of "E" and "L" mark the locations of the peaks of E1Nifio and La Nina, and the center of "X" marks the location where the E1 Nifio-like wavelet coefficients of SLA
28,792 HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA 100 ... , ... , ... , ... , ... , ... 5O -5O Northern SCS Southern SCS Continental shelf of SCS -100 ... ' ... ' ... ' ... ' ... ' ... 1993 1994 1995 1996 1997 1998 1999 Year
Figure 5. Time series of smoothed SLA showing the annual variation of sea level in the northern, southern, and continental shelf of SCS.
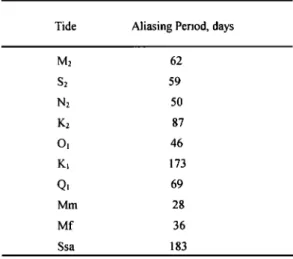
relatively weak in the other SLA series. The amplitudes of the length we used is 1 year. Then the phases and the amplitudes of the components with periods of 173 and 188 days in SLA4 reach 1-2 errors at given tidal frequencies were computed by a least squares
cm and are considered large compared to the same components in harmonic analysis. In general, CSR3.0 has the least error at
the others. These components may well be aliased tidal signals Dongsha, which is surrounded by deep waters. At Haikuo the
arising
from the error of the CSR3.0
tide model
we used
in largest
error
occurs
at K•, while
at Taiping
and
Dongsha
the largest
generating SLAs. Table 3 lists the tidal aliasing periods of 11 errors occur at M 2. Although Haikuo is located on the continentalmajor ocean tides for T/P, which were computed using [Parke et shelf and has the largest error at K•, the strongest components in al., 1987; Schlax and Chelton, 1994] SLA4 are those with periods of 60-62 days, which we believe are
T(f) =
P
fp- [fp
+ 0.5]
'
(4)
where f is the tidal frequency, p = 9.9156 days is the T/P repeat
period, and [fp + 0.5] is the integer part of OCp +0.5). For T/P the
due to aliased M 2 and S2. Moreover, SLA1 has a relatively strong
173 day component, which becomes smaller in SLA3. SLA3,
being the average of SLA1 and SLA2, contains less tidal aliasing effect because it has no significant components with periods close to the tidal aliasing periods. In practice, if the phase of an aliased tide is spatially smooth, then the tidal aliasing effect may be reduced by averaging SLAs over an area larger than the aliasing periods of the major ocean tides range from 28 to 183 days
and
can
be
mistakenly
associated
with
monthly,
intraseasonal,
and wavelength
of this
aliased
tide.
Formulae
for computing
the
semiannual
sea
level
variability
generated
by wind
and
other
wavelengths
of aliased
tides
are
given
by Schlax
and
Chelton
forcings.
Table
4 shows
the
amplitudes
and
phases
of the
CSR3.0
[1994].
For
example,
the
wavelength
of the
aliased
M2
for
T/P
is
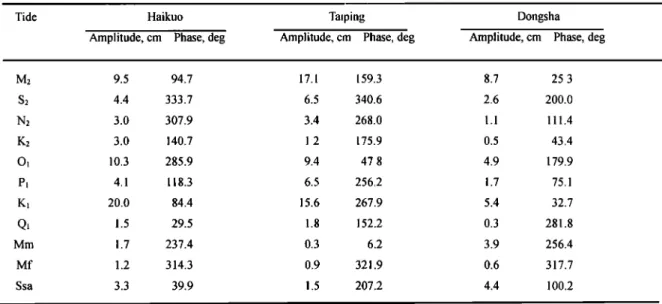
9 ø The widths of the northern SCS and the southern SCS are just tide model errors at Haikuo, Dongsha, and Taiping tide gauge ß
stations,
whose
locations
are given
in Figure
1. To determine
the about
the wavelength
of the aliased
M2, and hence
SLA1
and
CSR3.0
model
error
at a tide
gauge
station,
we first
subtracted
the SLA2
may
marginally
escape
the contamination
of the aliased
M 2
CSR3.0 modeled values from the measured values to get the errors. tide. Because the whole SCS extends more than 9 ø , SLA3 is less
HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA 28,793
Table 3. Tidal Aliasing Periods of TOPEX/Poseidon for
11 Major Ocean Tides
Tide Aliasing Period, days
M2 62 S2 59 N2 50 K2 87 O2 46 K• 173 Q• 69 Mm 28 Mf 36 Ssa 183
the continental shelf of the SCS is < 9 ø , hence, along with the fact that the M2 error and its phase variation are large, SLA4 contains a
strong component with period equal to the aliasing period of M2.
For comparison, in Figure 6 we show the periodograms of SLA4,
as well as SLA series over the Taiwan Strait, the East China Sea,
and the Yellow Sea, which are all located on the continental shelf
of east Asia. All the SLA series in Figure 6 contain strong
components with periods of about 60 days, which are due to the
aliased M2 and S2 tides. Comparing the periods of the dominant
cmnponents in Figure 6 and the aliasing periods in Table 3, we
believe that the T/P-derived SLAs over the Taiwan Strait and the East China Sea are affected by almost all aliased major ocean tides.
As an example, we find that the Rms difference between CSR3.0
modeled and observed tidal values over 1993-1994 at the Taichung
tide gauge station is 50 cm. The Taichung station is located on the central west coast of Taiwan, and there the tidal amplitude is 3 m.
This explains why SLAs over the Taiwan Strait are so seriously
affected by the aliased tides.
Wind has components with periods of 30-60 days [Philander, 1990], and in particular, the wind over the SCS has a component
lOO
II
- Continental
shelf
of SCS
II - Taiwan Strait
III
,. East
China
Sea
. ]
I .Yellow
Sea
so 'i
,-
0 2 4 6 8 10 12 14 16 18 20
Frequency (cycle/year)
Figure 6. Comparison of periodograms of TOPEX/Poseidon-derived SLA in four areas of the continental shelf of
28,794 HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA
with
a period
of 180
days
due
to the
summer
and
winter
monsoons
be easily
used
to identify
the
scale
of the
signal
and
its location
on
(here
we consider
only
the
magnitude
of wind;
see
below).
All the
t axis.
The
constant
1/•a in (5) is to ensure
that
the
norm
of
these wind components may give rise to sea level variability of the
same
frequencies.
Because
of
the
closeness
between
the
periods
of •((t- b)/a) is equal
to the norm
of •(t), i.e.,
the
wind
components
and
the
aliased
periods
of tides,
there
is
The
wavelet
function
•(t) must
have
a
considerable
uncertainty
as to whether
certain
components
in the compact
support
and satisfy
the admissibility
condition,
which
four SLA time series
are due
to aliased
tides
or are due
to wind. demands
that the mean
of •(t) up to a certain
order
of moment
However,
if a component
is due
to an aliased
tide,
then
this be zero.
Furthermore,
small
scale
corresponds
to high
frequency
component
should
show
consistent
amplitude
throughout
the
entire
and large
scale
corresponds
to low frequency.
Thus
C(a,b)
time
span
of a time
series.
To detect
the
time-variation
of the represents
the
time-scale
structure
of a signal.
amplitude of a component will rely on wavelet analysis discussed Since data are always given in a discrete form, the continuous
below. Moreover, to have less tidal aliasing effect and to have a
wavelet transform is approximated as
time series that represents the overall behavior of the SCS sea level,
only
SLA3
will
be
used
in
the
following
analysis.
1 2v-•
nat-
b•,
= • 5• f(nzlt)•( )zlt , (6)
Cj'k
•j .=0
aj
4. Wavelet Analysis of Sea Level Anomaly
In the Fourier
analysis
performed
in Section
3.1, a time
series where
N is the number
of records
and zlt is the sampling
interval.
is regarded as a stationary signal, so that in theory the spectral Equation (6) can be evaluated by algorithms such as fast Fourier content of a segment of the series should be equivalent to that of transform [Totfence and Compo, 1998]. The discrete scales and any other segment. However, many signals, including SLA, are translations are selected as
nonstationary and have time-varying frequencies and amplitudes.
For
example,
sea
level
variabilities
can
be due
to wind,
sea
surface
a• = jAt, j = 2,---,d
max
temperature
(SST),
ENSO,
and
other
forcings
that
have
different bk
= kAt,
k = 0,---,N-1 ,
(7)
magnitudes and frequencies at different times. To see the
time-varying
components
of a signal,
a better
tool
than
Fourier
where
dmax
is a number
<N.
The
indexj
starts
from
2 because
2zlt
analysis
is wavelet
analysis.
In this
study
we employ
both
the is the
smallest
resolvable
scale.
The
choice
of dmax
depends
on
the
continuous
wavelet
transform
and
the
wavelet
multiresolution
spectral
content
of the
analyzed
signal,
[see
also
Torrenee
and
transform
to analyze
SLA and
other
data.
The continuous
Compo,
1998;
Kumar
and
Foufoula-Georgiou,
1994].
Note
that
one-dimensional
wavelet
transform
of a signal,
f(t), is defined
as Torrenee
and
Compo
[1998]
and
Kumar
and
Foufoula-Georgiou
[Daubeehies,
1992]
[1994]
present
two
different
criteria
for
choosing
dmax.
1 Plate l a shows the wavelet coefficients of SLA3 computed
C(a,b)=•aalf(t)•(t-b)dt
a
,
(5)
with
1992]
the
real
part
of
the
Morlet
wavelet,
defined
as
[Daubechies,
where
a and
b are
scale
and
translation,
respectively,
•(t) is the
•(t) ----II•-l/4e-t2/2
COS(5t)
,
(8)
wavelet function, and C(a,b) is the wavelet coefficient. If • is a
comr•lex
function,
then
we must
use
the conjugate
of • in (5). The
Morlet
wavelet
is widely
used
in geophysical
research
such
as
Mathematically,
C(a,b)
is
the
projection
off(t)
on
•((t - b)
/ a) or seismic
and frequency domains are given bydata
analysis.
Properties
of
the
Morlet
wavelet
Kumarin
the
time
and the inner product of fit) and •((t-b)/a). The greater the Foufoula-Georgiou [1994]. It is easy to show that the Morletsimilarity
between
f(O and •((t - b) / a), the larger
the coefficient
wavelet
in (8) has
a compact
support
and
satisfies
the
admissibility
C(a,b).
Thus
large
absolute
values
of the wavelet
coefficients
can condition
up to any order
of moment,
see, for example,
the
Table 4. Amplitudes and Phases of CSR3.0 Tide Model Errors :•t Three Tide Gauge Stations of the SCS
Tide Haikuo Taiping Dongsha
Amplitude, cm Phase, deg Amplitude, crn Phase, deg Amplitude, cm Phase, deg
M2 9.5 94.7 17.1 159.3 8.7 25.3 S2 4.4 333.7 6.5 340.6 2.6 200.0 N2 3.0 307.9 3.4 268.0 1.1 111.4 K2 3.0 140.7 1.2 175.9 0.5 43.4 O• 10.3 285.9 9.4 47.8 4.9 179.9 P• 4.1 118.3 6.5 256.2 1.7 75.1 K• 20.0 84.4 15.6 267.9 5.4 32.7 Q• 1.5 29.5 1.8 152.2 0.3 281.8 Mm 1.7 237.4 0.3 6.2 3.9 256.4 Mf 1.2 314.3 0.9 321.9 0.6 317.7 Ssa 3.3 39.9 1.5 207.2 4.4 100.2
HWANG AND CHEN: FOURIER AND WAVELET ANALYSES OF SOUTH CHINA SEA 28,795
Signal
al
a2
a3
a4 a5a6
a7dl
d2
d3
d4
d5
d6
d7
Figure 7. Wavelet decomposition tree of a seven level multi-
resolution wavelet transform.
integration result by Gradshteyn and Ryzhik [1994, p. 531].
According to Torrerice and Compo [ 1998, Table 1 ] the relationship
between the period p (or wavelength) of a Fourier component and
the scale a of the Morlet wavelet given in (8) is
4/ra
p = = 1.232a , (9)
5+42+52
which
helps
to interpret
the wavelet
coefficients
in the Fourier
sense. Furthermore, to reduce the edge effect in the waveleta zone called "cone of influence (COI)" [Torrence and Compo, 1998] where the coefficients are less reliable than those in other parts of the plot. However, according to Totfence and Compo [1998, p. 67], if the time series is cyclic, there will be no COI. Since the SLA time series (also the time series in Plates lb and lc) is dominated by the annual cycle (see Figure 5) and is almost cyclic, the COI of the wavelet coefficients in Plate 1 should be negligible. Below is a summary of the SLA components identified in Plate 1 a.
1. The 30-120 day components are strong from January 1993 to January 1995 and weak after January 1995. The fact that these components have different amplitudes at different times suggests that SLA3 is not affected by the aliased M2 and S2 tides.
2. The semiannual component is identified as a local high in spring and a local high in winter in each year at period of 6 months. This component is due to the summer and winter monsoons of the SCS. The peaks always occur in May to June (for the spring high) and in November to December (for the winter high). In the springs of 1995 and in the winter of 1997-1998, such semiannual highs
almost disappear. The time-varying amplitude of this component
shows no contamination of aliased K• and Ssa tides in SLA3.
3. The annual component creates the almost periodic wavelet
coefficients that can be easily identified in Plate 1 a. It has a peak in summer, and the time span between two consecutive summer
peaks is about 12 months. The amplitude varies from one year to
another with the largest in 1996 and the smallest in 1994.
4. The wavelet coefficients corresponding to the interannual
components are rather smooth. At periods of 2-3 years, two bands
of highs occur between late 1993 and the summer of 1994 and
between the summer of 1996 and the spring of 1997. Notice that
the two bands of highs occur about 1 year before both the
1994-1995 and the 1997-1998 E1 Nifios. At periods > 3 years, a
band of highs begins in late 1995 and ends in the spring of 1997. In fact, the spring of 1997 is the time when the 1997-1998 E1 Nifio
starts to develop.
Next we perform wavelet multiresolution transform on SLA3.
The multiresolution transform applies a wavelet matrix, consisting
of scaling coefficients, to a data vector hierarchically to obtain a sequence of vectors containing approximations and details at
different levels; see, for example, Press et al. [1993, p. 594] and Chui [1992, p. 20] for the computational algorithm. Thus, with the
wavelet multiresolution transform, a signal is decomposed into
components of different resolutions. For example, Figure 7 shows
the wavelet decomposition tree of a seven-level decomposition of a signal. In Figure 7 we have the relationships a, = a,+•+d,+•, and
signal = a7+d7+do+ds+dg+ds+d2+d•. The higher the degree of
approximation, the lower the resolution. For example, a2 is coarser than a•. This is also true of the details. In this study we used the
scaling coefficients of the Daubechies number 3 (db3) wavelet
[Daubechies, 1992] to form the wavelet matrix for the
multiresolution transform. The db3 wavelet has a compact support
length of five, and up to the third order derivative of its Fourier
transform at the origin (frequency = zero) is zero. Figure 8 shows a
seven-level decomposition of SLA3, which is summarized as
follows.
1. Detail d• detects five anomalously negative SLA values between January 1993 and January 1995. The responsible T/P cycles are 31, 41, 55, 65 and 79, when the Poseidon altimeter was
on. It also shows that between January 1993 and January 1995, the
monthly variability is much stronger than at any other time. 2. Approximations a2 and a3 show the seasonal variations of SLA. Detail d3 shows the almost semiannual variation of sea level
related to the summer and winter monsoons.


![Figure 8. Approximations (a]-a7) and details (d•-d7) of sea level anomaly over the SCS from a seven-level](https://thumb-ap.123doks.com/thumbv2/9libinfo/7630962.135065/12.898.195.705.98.798/figure-approximations-details-level-anomaly-scs-seven-level.webp)