A Theorem on Permutation Graphs with Applications
CHANG-WU YU and
GEN-HUEY CHEN*
Department of Computer Science and Information Engineering, National Taiwan Uniuersity, Taipei, Taiwan
Communicated by Tosiyasu L. Kunii
ABSTRACT
In this paper, a theorem that characterizes a relation between cographs and permutation graphs is introduced. This theorem has an application to the recognition of a cograph. By the aid of this theorem, sequential and parallel algorithms to determine if a given permutation graph is a cograph can be derived.
1. INTRODUCTION
An undirected graph G with vertices (IQ, u2,. . . , u,J is called a permutu- tion graph [lo] if there exists a permutation m on N = (1,2,. . . , n} such that for all i, j EN,
(i-j)(Wl(i) -W’(j)) <0
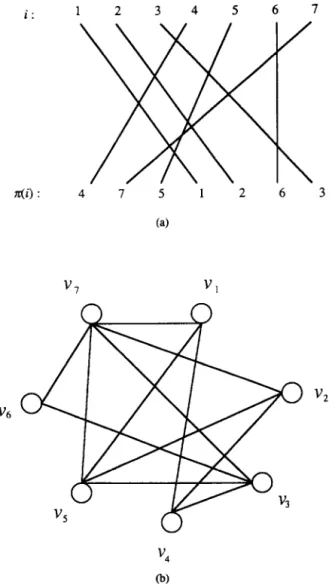
if and only if V, and 15 are joined by an edge in G. Pictorially, draw the vertices u1,u2,...,un in order on a line, and u~(~),u,,(~) ,..., qn) on a parallel line such that for each i E N, ui is directly above uqci). Next, for each i EN, draw a line segment from vi on the upper line to ui on the lower line. Then, there is an edge (LJ,,v,) in G if and only if the line segment for ui intersects the line segment for 9. As an illustrative
*Corresponding author. 0 Elsevier Science Inc. 1994
example, Figure 1 shows a permutation T= (4, 7, 5, 1, 2, 6, 3) and its corresponding permutation graph.
Much research [3], [4], 181, [lo], [18], [21]-[26] has been devoted to the study of permutation graphs. In [18], Pnueli, Lempel, and Even proposed an 0(n3) time algorithm that recognizes a permutation graph of n vertices by applying the transitively orientable graph test. Later, Spinrad [211
i: 1 2 3 4 5 6 7 n(i) : 4 7 5 1 2 6 3 (a) v6
V4
OJ)improved their result by presenting an U(n2) time recognition algorithm. Besides, Spinrad also gave an algorithm that determines if two permuta- tion graphs are isomorphic in the same time complexity. In 1221, Spinrad, Brandstadt, and Stewart showed that a bipartite permutation graph can be recognized in linear time by some algorithmic properties. In [121 and (151, the problem of recognizing a permutation graph was shown to be in the NC class. In [23], Supowit solved the coloring problem, the maximum clique problem, the cliques cover problem, and the maximum independent set problem, all in O(n log n) time. In 181, using dynamic programming, Farber and Keil solved the weighted domination problem and the weighted independent domination problem in 0(n3> time. In [41, Brandstadt and Kratsch presented an 0(n2) time algorithm for the weighted independent domination problem. In [3], Atallah, Manacher, and Urrutia solved the independent domination set problem in O(n log2 n> time. In [24], Tsai and Hsu solved the domination problem and the weighted domination problem in O(n loglog n) time and 0(n2 log2 n) time, respectively. In [25] and 1261, Yu and Chen presented various NC algorithms for permutation graphs.
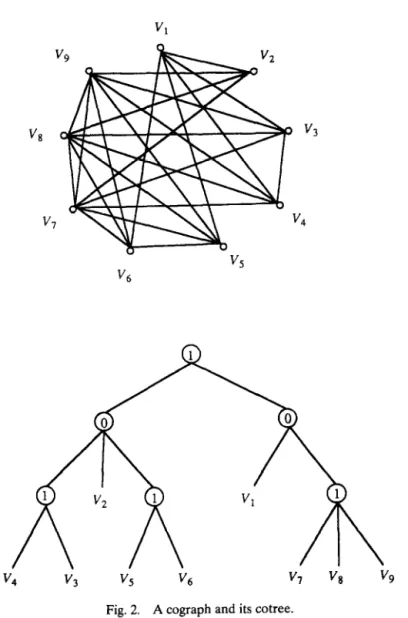
Cographs (or complement reducible graphs) 161 are defined as the class of graphs formed from a single vertex under the closure of the operations of union and complement. More detailed description about cographs can be found in [6]. Cographs were independently discovered under various names and were shown by Corneil, Lerchs, and Burlingham [6] to have the following two remarkable properties. First, they are P,-restricted graphs [6]. In a P,-restricted graph, there exists no path of length 3 (four nodes in this path) such that no edge exists between two nodes that are not adjacent in this path. Second, a cograph has a unique tree representation called cotree. The leaves of a cotree represent the vertices of its corresponding cograph, and its internal nodes are labeled alternately with 0 and 1 along every path starting from the root. The root is labeled with 1 if the cograph is connected, and 0 otherwise. Two vertices x and y in a cograph are adjacent if and only if the lowest common ancestor of their corresponding nodes in the cotree is a l-node. An example of a cograph and its cotree is shown in Figure 2. The cotree forms the basis of many fast polynomial time algorithms for cographs. In [13], it was shown that a cograph must be a permutation graph, but the reverse is not always true. In this paper, like [7], we consider the cotree unordered. If the cotree is considered ordered, then a cograph may have many cotrees.
In this paper, we first introduce a theorem about permutation graphs, in which three equivalent statements are shown. This theorem characterizes a relation between cographs and permutation graphs. More concretely, it states that a permutation graph is a cograph if and only if either of two predefined conditions is satisfied. Then, we show an application of this
v8 v3
V5 v6
v4 v3 v6 v7 v8 v9
Fig. 2. A cograph and its cotree.
theorem to the recognition of a cograph. By the aid of this theorem, sequential and parallel algorithms to determine if a given permutation graph is a cograph can be derived.
The rest of this paper is organized as follows. In the next section, we introduce some necessary definitions. In Section 3, we give a theorem on permutation graphs. Then, based on this theorem, we present sequential and parallel algorithms for recognizing a cograph in Section 4. In Section 5, we conclude this paper with some final remarks.
2. DEFINITIONS
Given a set S of plane points, a = (x1, yl> E S is said to be dominated by b =(x~,~~)ES (or B dominates a> if x1 <x2 and y, <y2. Further, a is said to be directly dominated by b (or b direct& dominates a) if a is dominated by b and there exists no other point c in S such that a is dominated by c and c is dominated by b. The minimal set of S is defined as the set of points in S that dominate no point in S.
Let U and I/ be two sequences of integers. We define U* V as the concatenation of U and V, and U < V if each integer in U is smaller than each integer in I’. For example, if U=(l,3,2,4) and V=(5,6,9,8,7), then U< V and U*V= (1,3,2,4,5,6,9,8,7). In the following, we define parenthesizable sequences.
DEFINITION 1. A sequence is parenthesizuble if it can be constructed according to the following two rules.
(1) An integer is parenthesizable.
(2) If V,,V*,... , V, are parenthesizable sequences satisfying Vi < V, < *I- <Vk or V1>V..> .a. > V,, and C = V,*V,. **a .Vk contains consecutive integers, then C is also parenthesizable.
For example, by rule 1, each integer in the sequence w= (6,5,7,9, 8,1,4,3,2) is parenthesizable. Then, by rule 2, (6,5), (9, B), and (4,3,2) are all parenthesizable. Again, by rule 2, (6,5,7,9,8) and (1,4,3,2) are paren- thesizable. Finally, we have (6,5,7,9,8,1,4,3,2) parenthesizable. Conve- niently, we can express the above construction as ((((6XSlX7X(9XS))X(l> ((4X3X2)))). Note that it is possible that a parenthesizable sequence may be parenthesized in more than one way. For example, ((((6X5)X7)((9)(8))) ((1X(4X(3X2))))) and ((((6XS)X(7X(9XS>))X(lX((4X3)X2)))) are another two parenthesizations of r. In the rest of this paper, we use (~1 to denote the parenthesization of 7~ with the least number of pairs of parentheses, which is unique. In our example, (7~) denotes ((((6X5)X7X(9XB))X(lX(4X3X2)))). Note that no two pairs of parentheses intersect in a parenthesization; that is, for only two pairs of parentheses, one appears inside or outside the other.
The size of a pair of parentheses is defined as the number of integers it contains. For example, the size of the pair of parentheses that consists of the second left parenthesis and the eighth right parenthesis from the left in ((((6X5)X7X(9XB))X(lX(4X3X2)))) is 5.
Given a graph G =(V, E), where V denotes the vertex set and E denotes the edge set, the induced subgruph of G by V’ c V is the subgraph of G whose vertex set is V and whose edge set contains those edges in E having both end vertices in V’. We denote the subgraph by G,,.
3. A THEOREM
In this section, we introduce a theorem that characterizes a relation between cographs and permutation graphs. It will be seen in the next section that this theorem has an application to the recognition of a cograph.
LEMMA 1. Let r be a permutation on N = { 1,2,. . . , n}. Zf IT is parenthesiz- able and there exist a, b, c EN satisjjkg a <b <c and r-l(c) < ~‘(a) < I’, then there exists a pair of parentheses in (T) that contains a, b, but does not contain c.
Proof. Because + l(c) < ~‘(a) < 6’(b), we assume r = ( . . . , C,..., a,. . . , b,. . .>. There are three possible ways to include c, a, b in a pair of parentheses. The first way is to include c,a, b directly by a pair of parentheses, i.e., . . . ( . . . , c, . . . , a,. . . , b, . . . ). . . , which is impossible by rule 2. The second way is to include c, a first by a pair of parentheses, and then include b by another pair of parentheses, i.e., . . . ( . . . ( . . . , c, . . . , a,. . .I.. . b, . . . 1 . . . ) which is again impossible by rule 2. Therefore, the only one way to include c,a, b in a pair of parentheses is like the form . . .(. ..c. . .
( . . . ) ) . . . ) a b ,... )...)... . This completes the proof. q
The following lemmas can be proved similarly.
LEMMA 2. Let 7~ be a permutation on N = {1,2,. . . , n). Zf 7~ is parenthesiz- able and there exist a, b, c E N satisfying a <b CC and ~-l(b) < ~‘(a) < W’(C), then there exists a pair of parentheses in (n) that contains b, a, but does not contain c.
LEMMA 3. Let z- be a permutation on N = (1,2,. . . , n}. Zf r is parenthesiz- able and there exist a, b,c E N satisfying a <b <c and r-l(a) < r-l(c) < n-‘(b), then there exists a pair of parentheses in (r) that contains c, b, but does not contain a.
LEMMA 4. Let rr be a permutation on N = { 1,2,. . . , n}. Zf rr is parenthesiz- able and there exist a, b,c EN satisfying a <b <c and r-‘(b) < r-l(c) < ~‘(a), then there exists a pair of parentheses in (r) that contains b,c, but does not contain a.
LEMMA 5 [61. G is a cograph if and only if G does not contain a P4 as an induced subgraph, where P4 denotes a path of length 3 (P4 contains four vertices and three edges).
Now we show the main result of this section.
THEOREM 1. Let G be a permutation graph with r= (r(l), 1r(2), . . . , r(n)) (a permutation of { 1,2,. . . , n)). The following statements are equivalent.
(2) r is a parenthesizable sequence.
(3) There do not exist a, b, c, d E (1,2,. . . , n) satisfying a < b < c < d and (K’(C) <r-‘(a) <r-‘(d) <n-‘(b) or
v-‘(b) <r-‘(d) <~‘(a) <W’(C)).
Proof. We prove this theorem by showing that (1) implies (21, (2) implies (31, and (3) implies (1).
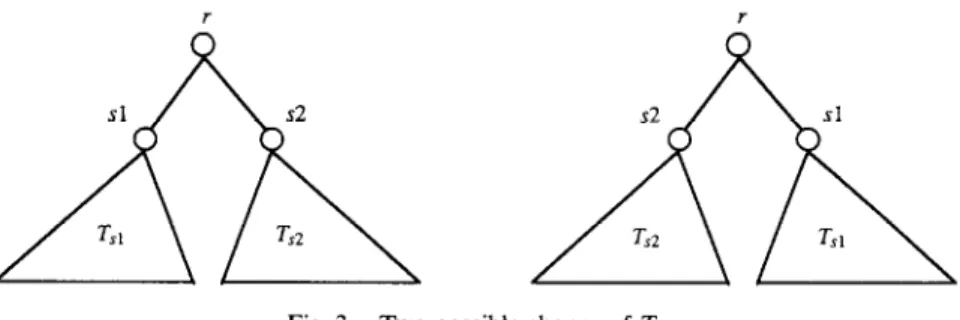
(1) + (2): Let T denote the cotree of G, and T, the subtree of T whose root is r. First, we show that all permutations rr that can represent G can be obtained from T. For the convenience of discussion, we suppose that the root node of T has two children sl, ~2, and qS1 = k, qs2 =n -k, where q,, is the number of leaf nodes in TSi, i = 1,2. The tree T may be of either of two shapes shown in Figure 3. The extension to three or more children is rather straightforward. If the root node of T is a l-node, then every leaf node in T,, is adjacent to every leaf node in TS2. Thus, the correspond- ing permutation 7~ of G is in either of the two forms: r=(r(l), 7429,. . . , r(k), r(k + 11, 7r(k + 21,. . . , 7r(n)), where (r(l), 7421,. . . , m(k)) is a permutation of (n -k + 1, k + 2,. . . , n) and {n(k + l),T(k + 21,. . . , r(n)) is a permutation of {1,2,. .., n -k), and 7r=(7r(l), r(2),.. ., n(n -k), rr(n -k + 1),7r(k + 21,. . . , r(n)), where (rr(l), 77(2), . . . , m(n -k)) is a per- mutation of (k + 1, k + 2,. . . , n) and (&n -k + 11, r(k + 2), . . . , m(n)) is a permutation of {1,2,. . . , k).
Similarly, if the root node of T is a O-node, then every leaf node in T,, is not adjacent to any leaf node in T,,. Thus, the corresponding permuta- tion rr of G is in either of the two forms: r= (n(l), 7421,. . . , r(k), r(k + 11,4k+2),..., r(n)), where (rr(l), r(2), . .., r(k)) is a permutation of Il,2,..., k) and (r(k+l),v(k+2),..., r(n)) is a permutation of (k+ 1, k + 2, . . . , n), and 7~ = (r(l), 421,. . . , 7r(n - k), 7r(n - k + 11, r(k +
(:” 2’ . ’
4n)), where (r(l), 421,. . . , 4n -k)) is a permutation of 9 ,‘..7 n -k) and (r(n -k + l), 7r(n -k + 21,. . . , r(n)) is a permutation of (n-k+l,n-k+2 ,..., n).
If we repeat the above analysis for nodes sl,s2 and all other internal nodes of T, we can generate all corresponding permutations T of G. More concretely, we have the following generation method for each possible shape of T.
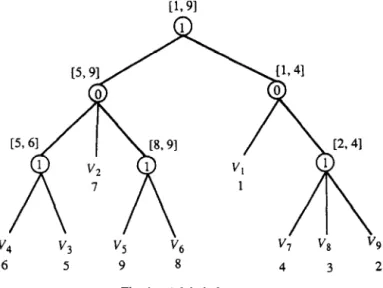
What we have to do is to label leaf nodes of T with integers 1,2,. . . , n. First, we associate each internal node r of T with an interval, which represents the set of integers that are used to label leaf nodes of T,. The root node of T is assigned with the interval [l, nl, and the other nodes are assigned with intervals as follows. Let ~1, ~2,. ..,sk denote the children from left to right of r. If r is a l-node and has been assigned with an interval [b,c], then s&s2 ,..., sk are assigned with intervals [c - qsl +
17cl,[c-((q~~ +~~~~+1~C~4~~l~~~~~~C~~~~~~~~~~+1~C~~~~~~~-~~~~l~
respectively, where qsi is the number of leaves in TSi. On the other hand, if r is a O-node, then sl,s2 ,..., sk are assigned with intervals [b, b + qsl -
11,
[b + qsl, b +
(q,l + q,,) -11,. . . , Lb+ C1<iCk-l qsiyb+ Cl<i<k qsi-11,
respectively. In this way, each leaf node will be assigned with an interval that contains only one integer. An example is shown in Figure 4.Let u,,uz )...) v,, denote the leaf nodes from left to right of T, and f(y) the integer assigned to q. Now, T,, = (l(q), I(v,), . . . , l(v,J) is the permuta- tion obtained from T by the above labeling procedure.
As a result of the labeling procedure, we claim that for i <j, the lowest common ancestor of ui and r+ in T is a l-node if and only if l(u,)>l($. The proof is easy and therefore left as an exercise. By the claim and the
6 5 9 8 4 3 2
fact that G is both a permutation graph and a cograph, it is easy to see that nodes ui and Uj in G are adjacent if and only if (l(u$ - l(t+)Xrr; ‘(l(y)) - 7r; l(l(r+))) = (l(ui) - I(y)Xi -i> < 0. So, no can represent G exactly. Besides, m. is parenthesizable as a result of the labeling procedure.
Because all corresponding permutations of G can be generated by executing the labeling procedure for all possible shapes of T, 7~, like 7ro, is parenthesizable.
(2) + (3): Suppose there exist a, 6, c, d E {1,2,. . . , FZ) satisfying a < 6 < c<d and ~7T-1(c)<~-1(u)<~-1(d)<~TT-1(6). Because b<c<d and V-‘(C) < r-‘(d) < p-‘(6), by Lemma 4 there is a pair of parentheses in (~1 that contains c, d, but does not contain 6. On the other hand, because a <6 <c and n-‘(c) < IT-‘< a-‘(b), by Lemma 1 there is a pair of parentheses in (?T) that contains a, 6, but does not contain c. So, these two pairs of parentheses intersect, which is a contradiction.
Similarly, by Lemmas 2 and 3, we can prove that there do not exist u,b,c,d~{1,2 ,..., n} satisfying a<b<c<d and r-‘(b)<r-‘Cd)< 7r-Yu) < r-‘(c).
(3) -t (1): Suppose G is not a cograph. Then, by Lemma 5, G contains a P4 as an induced subgraph. Let W denote the set of four vertices in P4 (that is, G,= P,), and a, b,c, d denote the four integers in 7~ that repre- sent the four vertices in P4. Without loss of generality, we assume a < 6 <c cd. Then, 7r-l (a> (~-l(d)) is not the minimal (maximal) value of {7r- ‘(a), 7r- 1 (b), r-l (c), r-‘(d)), because otherwise G, is not connected. On the other hand, 7r-‘(u) (n-‘(d)) is not the maximal (minimal) value of {r-‘(a), 7~-’ (6) , T-‘(C), r-‘(d)}, because otherwise the maximal degree of G, is equal to 3. Hence, the maximal value and the minimal value of (7r-‘(a), rr-l(6>, m-l(c), r-‘(d)) are in (n-‘(b), T-~(C)).
If r-‘(c)< r-‘(b), then rr-‘(a) < r-‘(d), because otherwise ~-l(c) < v-‘(d)< r-l(u) < r-‘(b) and Gw forms a cycle. If 7r-l(6)< r-l(c), then n-‘(d) < n-‘(a), because otherwise 7r-‘(6) < 7~-l(u) < r-‘(d) < r- ‘Cc> and G, is not connected.
Therefore, we have r-‘(c) < rr-‘(a> < r-‘(d) < p-‘(b) or r-‘(b) < n-‘(d) < w’(u) < wl(c). This completes the proof. 0
4. APPLICATIONS
In this section, we show an application of Theorem 1 to the problem of recognizing a cograph. First, we survey previous work on this problem. Throughout this section, we let it and m denote the numbers of vertices and edges, respectively.
The fastest sequential algorithm, which was proposed by Corneil, Perl, and Stewart [7], takes O(n +m> time. As for parallel algorithms, various results have been proposed on different computation models. In [l], Adhar and Peng presented an U(log’ n) time algorithm on CRCW PRAM (concurrent read, concurrent write parallel random access machine), which requires O(nm) processors. In [14], Kirkpatrick and Przytycka presented an 000g2 n> time algorithm on CREW (concurrent read, exclusive write) PRAM, using O(n3/log2 n> processors. In [171 and [201, an O(log n) time algorithm, which uses 0(n3) processors on CRCW PRAM, is obtained by Novick and Shyu, independently. In [161, Lin and Olariu gave an O(log n) time algorithm, which uses O((n’ +nm)/log n> processors on EREW (exclusive read, exclusive write) PRAM. In [ll], He presented an O(log2 n> time algorithm, which uses O(n +m> processors on CRCW PRAM.
All the algorithms above have arbitrary graphs as their input. In the remainder of this section, as an application of Theorem 1, we show that time complexity and/or processor complexity can be reduced, provided the input graph is restricted to a permutation graph.
First, we present a sequential algorithm to recognize a cograph, assum- ing the input is a permutation graph. It is known by Theorem 1 that given a permutation graph G with its corresponding permutation 7~, G is a cograph if and only if ~=(r(l), m(2),. . ., r(n)) is a parenthesizable sequence. So, the problem of recognizing a cograph is transformed into the problem of recognizing a parenthesizable sequence r. In the following, an algorithm for the latter is presented.
In the algorithm, a stack is used to store parenthesizable subsequences that are identified during the execution of the algorithm. The algorithm scans the input VT from left to right and tries to merge each n(i), i=1,2 , . . . , n, with previously found parenthesizable subsequences (stored in the stack). The resulting subsequence is parenthesizable and is again pushed into the stack. After finishing the scanning of QT, we can easily determine whether 7r is parenthesizable or not. If only one subsequence remains in the stack, then rr is parenthesizable. Otherwise, r is not parenthesizable.
ALGORITHM 1.
Step 1. Scan the input 7r= (n(l), 7r(2), . . . , r(n)> from left to right and perform the following for each r(i), i = 1,2,. . . , n.
1.1. Push 4) into the stack.
1.2. If the top two subsequences in the stack can be merged into a longer parenthesizable subsequence (by rule 2 of Definition 11, then
merge them into a new parenthesizable subsequence, push the resulting subsequence into the stack, and go to Step 1.2.
Step 2.If there is only one parenthesizable subsequence in the stack, then rr is a parenthesizable sequence. Otherwise r is not a parenthesizable sequence.
The time complexity of Algorithm 1 is dominated by Step 1.2, which is executed n times. Each of the pop, merge, and push operations takes constant time, and they occur whenever the top two subsequences in the stack satisfy rule 2 of Definition 1. Because each merge operation will result in a longer subsequence, the merge operation is executed at most IZ times. So, the time complexity of Algorithm 1 is proportional to n. Also, the space complexity of Algorithm 1 is proportional to n.
It is easy to construct (7~) by modifying Algorithm 1 at two places. First, before a new parenthesizable subsequence is pushed into the stack, we add a pair of parentheses to enclose the subsequence. Second, while merging two smaller parenthesizable subsequences into a longer one, the two pairs of parentheses that enclose the two smaller subsequences may become redundant, and therefore need to be eliminated. The redundant pairs of parentheses can be identified by rule 2 of Definition 1.
The cotree T can be constructed from (rr) as follows. We simply let each integer in (7) be a leaf node of T and all the pairs of parentheses that contain two or more integers be the internal nodes of T. The parent of a pair of parentheses is the pair of parentheses that encloses it and has the smallest size. It is not difficult to check that the time complexity and space complexity of constructing the cotree are still O(n).
Next, we present a parallel algorithm, as a consequence of statement (3) of Theorem 1. The following algorithm determines if there exist a, b, c, d E I1,2,..., nlsatisfying a<b<c<dand(~~‘(c)<~-‘(a)<~-‘(d)<~-’(b)
or m-‘(b) < r-‘(d) < r-‘(a) < 7f1(c)).
ALGORITHM 2.
Step 1. Determine if there exist a, b, c, d E (1,2,. . . , n} satisfying a <b < c<d and ~~‘(c)<~~‘(u)<~-‘(d)<~~‘(b).
1.1. Generate all pairs (7r(i>,r(j)) satisfying i <j and r(i) < rr( j).
1.2. For each pair (rr(i>, r(j)) created in Step 1.1, determine the maximal value in the set (rr(i + 1>,4i + 21,. . . , r(j - 1)). We denote the maximal value by ki,j.
ing k,,j > r(j), determine if there exists a value, denoted by Zi,j, in Ml), r(2), . . . , r(i - 1)) satisfying V(j) <Zi, j < ki,j. If Zi,j exists for at least
one pair (r(i), n(j)), then the answer is yes. Otherwise, the answer is no.
Step 2. Determine if there exist a, 6, c, d E (1,2,. . . , n) satisfying a <b <
c <d and rr-‘(b) < r-‘(d) < r-‘(a) < v-‘(c).
2.1. Generate all pairs (r(i), v(j)) satisfying i <j and r(i) >
4 j).
2.2. For each pair (r(i), m(j)) created in Step 1.1, determine the maximal value in the set {~(i + 0, n(i + 2), . . . , rT(j - 1)). We denote the maximal value by ki,j.
2.3. For each pair (&I, r(j)) created in Step 1.1 satisfying ki, j > r(i), determine if there exists a value, denoted by Zi,j, in (rr( j + 11, 4 j + 21,. . . , r(n)) satisfying r(i) <Zi,j <ki,j. If Zt,j exists for at least
one pair (a(i), r(j)), then the answer is yes. Otherwise, the answer is no.
Step 3. If the answers obtained in Steps 1 and 2 are all no, then the
input graph G is a cograph. Otherwise, G is not a cograph.
The correctness of Algorithm 2 can be assured by letting a = v(i),
b = r(j), c =z~,~, and d =ki, j in Step 1 and a = r(j), b = r(i), c =Zi,j) and
d = ki+ j in Step 2.
Algorithm 2 can be executed in O(log n) time using O(n*) processors on CREW PRAM. Clearly, Steps 1.1 and 2.1 take O(1) time if O(n’) processors are used. Steps 1.2 and 2.2 can be executed in O(log n> time using O(n2) processors if the well-known doubling technique [91 is applied. We simply assign n -i processors to set (r4i + 11, r(i + 2), . . . , r(n)} for computing kii+2,ki,i+3,...,ki,.,i=1,2,...,n-2.Step1.3canbeexecuted
in Ologn) time using 0(n2) processors if we first sort each set (n(l), 7r(2), , . . , di - 111, i = 2,3,. . . , n, using O(i) processors, and then perform a binary search on the sorted list for finding Zi, 1, zi,*, . . . , qn. The sorting can be completed in O(log n) time, if cost-optimal sorting algorithms, e.g., Cole’s sorting algorithm 151, are used. Similarly, Step 2.3 can be executed in O(log n> time using 0(n2) processors.
If the given permutation graph is a cograph, we can construct its cotree from rr by the following algorithm.
ALGORITHM 3.
Step 1. Construct (~1 from 7~.
1.1. For each pair (r(i), w(j)), where i <j, find the maximal integer (Y and minimal integer p in (w(i), T&’ + 0,. . . ,4 j)}. If (Y - /3 = i -j, then add a pair of parentheses, denoted by Pi,j, to enclose the integers 7r(i>, 7r(i + 11,. . . , rr(j). We let pi,j be of type 0 if r-‘(cu)> r-‘(p), and of type 1 otherwise.
1.2. Delete those pi,js that intersect with each other.
1.3. Set i as the weight of di), i = 1,. . . , n, and set i -(j - i)/n,
i + (j - i)/n as the weights of the left parenthesis and the right parenthesis
of pi, j, respectively.
1.4. Sort di), i = 1, ..,, II, and the left and right parentheses of remaining pi, js increasingly according to their weights. Suppose (7~) = c,c2 0.. ck is the sorted list.
Step 2. Transform (7~) into a set of plane points by the following rules. For each di> = cj, 1 G i G n, 1 <j Q k, generate a plane point c-j, j). For each pj,j whose left parenthesis and right parenthesis are c, and cs, respectively, generate a plane point ( -r, s).
Step 3. Construct the cotree as follows. A pair of parentheses is the parent of another pair of parentheses (or an integer) if and only if the corresponding point of the former directly dominates the corresponding point of the latter. Also, a pair of parentheses is assigned as a l-node of it is of type 1 and a O-node if it is of type 0.
The correctness of Algorithm 3 is discussed as follows. In Step 1, because v is parenthesizable, we have {di), di + 11,. . . ,n( j)} parenthe- sizable if (Y - p = i -j. Because the set of pairs of parentheses in (7~) is exactly the set of P~,~s that do not intersect with each other, all pi jS that
intersect with each other are redundant and need to be deleted. It is clear that after setting weights as stated in Step 1.3, (7~1 will be obtained after sorting. So, Step 1 constructs (7~) from rr.
On the other hand, with transforming (7r) into a set of plane points in Step 2, we have the fact that pi,j encloses p,,, and is of the smallest size (that is, pi,j is the parent of p,,$ in the cotree) if and only if the corresponding point of pi,j directly dominates the corresponding point of P I,S. Moreover, pi,j being of type 0 (type 1) means diMi + 1) *.* rr(j) =
V,.V,* *.* .V,, where V, <V, < ... < V, (V, > V, > -1. > V,>, according to rule 2 of Definition 1. So, pi,j represents a l-node if it is of type 1 and a O-node if it is of type 0.
Algorithm 3 can be implemented in O(log n) time using 06~‘) proces- sors on CREW PRAM. Using the doubling technique, Step 1.1 can be implemented, similar to Step 1.2 of Algorithm 2, in O(log n) time using O(n’> processors.
Because pi, j intersects with p,, s if andonlyif i<r<j<s or r<i<s<j,
we can complete Step 1.2 in O(log n> time using O(n’) processors as follows. Let us define wi = max{jl for all P~,~s created in Step 1.11, i =
12 , ,. . ., n, and mj = max{il for all P~,~s created in Step 1.11, j = 1,2,. . . , n. Using the doubling technique, all wis and m,s can be computed in O(log n) time using 0(n2) processors. Then, pi,, intersects with some
other pairs of parentheses if and only if max{wi+l,wi+2,.. .,wj_,l >j or min{mi+ i, mi+2,. . . , mj_ I} < i. Similar to Step 1.2 of Algorithm 2, mm(Wi+i,Wi+2,..., wj_i} and min{mi+,,mi+2,...,mj_11 can be deter- mined for all pi,js in O(log n) time using 0(n2> processors.
Steps 1.3 and 1.4 take O(1) and O(logn) time, respectively, if O(n) processors are used. Step 2 takes O(1) time using O(n) processors. Step 3 can be completed in O(log n) time using O(n2> processors, if for each point, we first find all points that dominate it, and then determine their minimal set (in our case, the minimal set contains only one point) [2].
5. CONCLUDING REMARKS
It is known that the class of cographs is a subclass of permutation graphs, which is again a subclass of circle graphs [131. In [191, Read, Rotem, and Urrutia found that a circle graph is a permutation graph if it satisfies a predefined condition. In this paper, we have shown in Theorem 1 that a permutation graph is a cograph if it satisfies either of two predefined conditions. Then, by the aid of Theorem 1, we designed sequential and parallel algorithms for recognizing a cograph. Also, the cotree is constructed if the input graph is recognized as a cograph. When the input graph is dense [i.e., m =O(n log n) or O(n2)], our algorithms require less time and/or fewer processors than all previous ones. The improvement made by our algorithm has a sacrifice that the input graph has to be a permutation graph.
REFERENCES
1. G. S. Adhar and S. Peng, Parallel algorithms for cographs and parity graphs with applications, J. Algor. 11:252-284 (1990).
2. M. Atallah, R. Cole, and M. Goodrich, Cascading divide-and-conquer: a technique for designing parallel algorithms, in Proceedings of the 28th Annual Symposium on Foundations of Computer Science, 1987, pp. 151-120.
3. M. J. Atallah, G. K. Manacher, and J. Urrutia, Finding a minimum independent dominating set in a permutation graph, Discrete Appl. Math. 21:177-183 (1988). 4. A. Brandstadt and D. Kratsch, On domination problems for permutation and other
graphs, Theor. Comput. Sci. 54:181-198 (1987).
5. R. Cole, Parallel merge sort, SLAM J. Comput. 17:770-785 (1988).
6. D. G. Comeil, H. Lerchs, and L. S. Burlingham, Complement reducible graphs, Discrete Appl. Math. 3:163-174 (1981).
7. D. G. Corneil, Y. Perl, and L. K. Stewart, A linear recognition algorithm for cographs, S.ktM J. Comput. 14:926-934 (1985).
8. M. Farber and J. M. Keil, Domination in permutation graphs, J. Algor. 6:309-321 (1985).
9. A. Gibbons and W. Rytter, Efficient Parallel Algorithms, Cambridge University Press, Cambridge, 1988.
10. M. C. Golumbic, Algonthmic Graph Theory and Perfect Graphs, Academic, New York, 1980.
11. X. He, Parallel algorithm for cograph recognition with applications, Report TR 91-16, Computer Science State Dept., State University of New York at Buffalo, 1991.
12. D. Helmbold and E. Mayr, Perfect graphs and parallel algorithms, in Proceedings of the International Conference on Parallel Processing, 1986, pp. 853-860.
13. D. S. Johnson, Ed., The NP-completeness column: an ongoing guide, J. Algor. 6:434-451 (1985).
14. D. G. Kirkpatrick and T. Przytycka, Parallel recognition of complement reducible graphs and cotree construction, Discrete Appl. Math. 29:79-96 (1990).
15. D. Kozen, U. V. Vazirani, and V. V. Vazirani, NC algorithms for comparability graphs, interval graphs, and testing for unique perfect matching, in Proceedings.of the Fifth Conference on Foundation of Software Technology and Theoretical Computer Science, New Dehli, 1985, pp. 498-503.
16. R. Lin and S. Olariu, An NC recognition algorithm for cographs, J. Parallel Distributed Comput. 13:76-90 (1991).
17. M. Novick, Fast parallel algorithms for modular decomposition, Report TR 89-1016, Computer Science Dept., Cornell University, 1989.
18. A. Pnueli, A. Lempel, and S. Even, Transitive orientation of graphs and identifica- tion of permutation graphs, Can. .I. Math. 23:160-175 (1971).
19. R. C. Read, D. Rotem, and J. Urrutia, Orientations of circle graphs, J. Graph Theory 6:325-341 (1982).
20. C. H. Shyu, A fast algorithm for cographs, French Israeli Conference on Combina- torics and Algorithms, Nov. 1988.
21. J. Spinrad, On comparability and permutation graphs, SD1MJ. Comput. 14:658-670 (1985).
22. J. Spinrad, A. Brandstadt, and L. Stewart, Bipartite permutation graphs, Discrete Appl. Math. 18:279-292 (1987).
23. K. J. Supowit, Decomposing a set of points into chains, with applications to permutation and circle graphs, Inform. Process. Lett. 21:249-252 (1985).
24. K. H. Tsai and W. L. Hsu, Fast algorithms for the dominating set problem on permutation graphs, Lecture Notes in Computer Science: Algorithms, vol. 450, Springer, Berlin, 1990, pp. 1099117.
25. C. W. Yu and G. H. Chen, Parallel algorithms for permutation graphs, Technical Report 91-11, Dept. of Computer Science & Information Engineering, National Taiwan Univ., July 1991.
26. C. W. Yu and G. H. Chen, The weighted maximum independent set problem in permutation graphs, Technical Report 91-12, Dept. of Computer Science & Infor- mation Engineering, National Taiwan Univ., July 1991.