國立交通大學
電子物理學系
碩 士 論 文
分子接面的電子傳輸與熱電效應
Molecular junction of Transport properties and Seebeck coefficients calculations
研 究 生:翁廷達
指導教授:陳煜璋 教授
分子接面的電子傳輸與熱電效應
Molecular junction of Transport properties and Seebeck coefficients calculations
研 究 生:翁廷達 Student:Ting-Da Weng 指導教授:陳煜璋 Advisor:Yu-Chang Chen 國 立 交 通 大 學 電 子 物 理 學 系 碩 士 論 文 A Thesis
Submitted to Department of Electrophysics College of Science
National Chiao Tung University in partial Fulfillment of the Requirements
for the Degree of Master
in
Electrophysics September 2009
Hsinchu, Taiwan, Republic of China
Acknowledgement
首先要感謝我的指導教授,陳煜璋老師,老師對學生總是極細心地指導,由 淺入深、循序漸進的栽培我們。每當我遭遇困難瓶頸,老師也總是不吝嗇的指教 我,教導我正面的研究態度,向我分享他的經驗與知識,在學短短兩年受益良多, 老師敦敦教誨,使我銘感五內。 第二要感謝曾經給予我協助的學長學姐們,包智傑、馬春蘭、Diu Nghiem、 劉玉申和盧書楷,因為他們豐富的經驗,讓我在學習的過程中不論是基本觀念或 是操作技巧,都給我相當大的幫助;另外也要感謝輔助我的學弟學妹,因著他們 的幫忙使得處理數據得以完備,再次感謝那些曾經幫忙過我的人。 第三要感謝我的家人,家人總是默默的支持我,在物質上心靈上都給我很大 的鼓勵,所以為了回饋家人的支持,我便有力量繼續前進,不叫他們失望。 最後要感謝 天父上帝,因為 上帝的指引使我有幸來到交通大學學習,同樣 也因著 上帝的保守,我才能有現今小小的成果,真是由衷地感謝 天父上帝的看 顧,願 主賜下平安喜樂予所有幫助過我的人,感謝 主。分子接面的電子傳輸與熱電效應
學生:翁廷達 指導教授:陳煜璋
國立交通大學電子物理學系碩士班
摘要
我們研究分子接面的傳輸性質與熱電效應。以第一原理計算的方式,研究苯 環胺基取代以及硝基取代兩種系統的電子輸運性質與熱電效應。我們藉著源漏電 壓與閘極偏壓去調控其狀態密度,進而影響電子的輸運性質與熱電效應。我們發 現有著不同官能基取代的苯環分子,其電子輸運性質與熱電效應的表現也不盡相 同。官能基的取代可增加或減少-orbital 的電子,導致導電性產生變化。胺基取 代後的苯環分子接面會使-orbital 的電子減少,導致導電率下降。反之,硝基取 代後的苯環分子接面會提供電子,在費米面附近產生新的能態,導致導電率上升。 當我們觀察電子輸運性質與熱電效應時,因為相同原因,硝基系統易受源漏電壓 與閘極偏壓的影響,其可調性較胺基系統為佳。Molecular Junction of Transport Properties
and Seebeck Coefficients Calculations
Student:Ting-Da Weng Professor:Yu-Chang Chen
Department of Electrophysics
National Chiao Tung University
Abstract
We investigate the electron transport and thermoelectric properties in amino-substituted (-NH2) and nitro-substituted (-NO) 1,4-benzenedithiolates
molecular junctions by using first-principles approaches. We compare the density of states (DOSs) in the above systems by applying the source-drain biases and the gate voltages, which provide a means to control the electron transport and the thermoelectric properties. We find that the functional substitutions of 1,4-benzenedithiolates may donate or retrieve electrons from the -orbital, and thus have influence on the conductance of molecular junctions. The amino-substituted 1,4-benzenedithiolates molecular junctions withdraw electrons from-orbital, and suppresses the conductance. The nitro-substituted 1,4-benzenedithiolates molecular junctions donate electrons to
-orbital and create states closer to the current-carrying window such that the conductance is enhanced. Consequently, the I-V characteristics and the Seebeck coefficients in NO-substituted 1,4-benzenedithiolates molecular junctions display richer features due to theses -donating states.
Contents
ACKNOWLEDGEMENT ... I ABSTRACT(CHINESE) ... II ABSTRACT(ENGILSH) ... III CONTENTS ... IV CHAPTER 1 INTRODUCTION ... 11-1THEORETICAL AND EXPERIMENTAL RESEARCHES ... 1
1-2OUR SYSTEMS ... 8
CHAPTER 2 THEORIES ... 10
2-1DENSITY FUNCTIONAL THEORY ... 10
2-1-1 Hohenberg and Kohn theorem ... 10
2-1-2 Kohn-Sham equation ... 12
(A) Pseudopotential Method...13
(B) Pseudopotential ...15
(C) Local Density Functional Approximation ... 17
2-2CURRENT OF ATOMIC WIRES24 ... 19
2-2-1 Bimetal junction ... 20
2-2-2 Metal-molecule-metal junction ... 21
2-1-3 Current in nanojunction ... 23
2-3SEEBECK COEFFICIENT ... 26
CHAPTER 3 RESULTS AND DISCUSSIONS... 29
3-1ELECTRONIC TRANSPORT OF SINGLE-MOLECULE JUNCTIONS ... 30
3-1-1 The effect of finite source-drain biases ... 30
3-1-2 The effect of gate voltages ... 32
3-2SEEBECK COEFFICIENT OF SINGLE-MOLECULE JUNCTIONS ... 35
3-2-1 The effect of finite source-drain biases ... 35
3-2-2 The effect of finite gate voltages ... 38
CHAPTER 4 CONCLUSIONS ... 41
List of Figures
FIG.1.THE RESULTS ARE THAT THE GROUPS OF M.DI VENTRA AND N.D.LANG VARIED THE SOURCE-DRAIN BIAS AND THE GATE VOLTAGE TO OBTAIN THE I-V CHARACTERISTICS.[PHYS.REV.LETT.84,5(2000)] ... 2 FIG.2.I-V CHARACTERISTICS FOR PLANAR MOLECULES OF I–III.[PHYS.REV.B67,121411(2003)] ... 2 FIG.3THE MOLECULAR JUNCTION OF 1,4-BENZENEDITHIOLATES SYSTEM AS THE FUNCTION OF BIAS (STEPS OF 0.1V).[C.M.
SCIENCE 27,151(2003)] ... 3 FIG.4.(COLOR ONLINE)GEOMETRY OF MONOLAYERS A–C CONNECTED WITH TWO AU (111) SURFACES.COLOR CODES:C
(DARK GRAY OR GREEN),H(WHITE),O(BLACK OR RED),N(BLACK OR BLUE),S(LIGHT GRAY OR YELLOW), AND AU
(LIGHT GRAY OR GOLD).AND I-VB CHARACTERISTICS FOR MONOLAYERS A,B, AND C.[PHYS.REV.B68,
121101(2003)] ... 3 FIG.5.SCHEMATICS OF THE JUNCTION WITH CORRESPONDING I-V CURVES (EXPERIMENTAL DATA):I-V AND GDIFF-V
CHARACTERISTICS OF BDT MEASURED AT (A)250K AND (B)50K.THE GRAY AREA IN (A) SHOWS THE ENVELOPE OF ALL CURVES MEASURED.[PHYS.REV.LETT.98,176807(2007)] ... 4 FIG.6.SCHEMATIC DESCRIPTION OF THE EXPERIMENTAL SET UP BASED ON AN STM BREAK JUNCTION.MOLECULES OF BDT,
DBDT, OR TBDT ARE TRAPPED BETWEEN THE AU STM TIP KEPT AT AMBIENT TEMPERATURE AND A HEATED AU SUBSTRATE KEPT AT TEMPERATURE ∆T ABOVE THE AMBIENT.WHEN THE TIP APPROACHES THE SUBSTRATE, A VOLTAGE BIAS IS APPLIED AND THE CURRENT IS MONITORED TO ESTIMATE THE CONDUCTANCE.WHEN THE CONDUCTANCE REACHES A THRESHOLD OF 0.1G0, THE VOLTAGE BIAS AND THE CURRENT AMPLIFIER ARE DISCONNECTED.A VOLTAGE
AMPLIFIER IS THEN USED TO MEASURE THE INDUCED THERMOELECTRIC VOLTAGE,∆V, AND THE TIP IS GRADUALLY PULLED AWAY FROM THE SUBSTRATE. ... 6 FIG.7.(A)A PLOT OF THE THERMOELECTRIC VOLTAGE MEASURED AS A FUNCTION OF THE TIP-SAMPLE DISTANCE WHEN A
TEMPERATURE DIFFERENTIAL ∆T=20K IS APPLIED (AU TIP AT AMBIENT AND SUBSTRATE AT AMBIENT +20K).THE BLUE CURVE IS OBTAINED WHEN A AU-BDT-AU JUNCTION IS BROKEN.THE RED CURVE SHOWS A CONTROL EXPERIMENT PERFORMED ON A CLEAN GOLD SUBSTRATE.(B)TYPICAL THERMOELECTRIC VOLTAGE TRACES FOR TIP-SUBSTRATE TEMPERATURE DIFFERENTIALS OF 0,10,20, AND 30K FOR AU-BDT-AU JUNCTIONS. ... 6 FIG.8.PLOT OF MEASURED JUNCTION SEEBECK COEFFICIENT AS A FUNCTION OF MOLECULAR LENGTH FOR BDT,DBDT, AND
TBDT. ... 7 FIG.9.RELATING THE MEASURED SEEBECK COEFFICIENT OF AU-BDT-AU JUNCTION TO THE POSITION OF FERMI LEVEL.(A)
THEORETICAL PREDICTION OF THE TRANSMISSION FUNCTION OF A AU-BDT-AU JUNCTION PLOTTED AS A FUNCTION OF THE RELATIVE POSITION OF THE FERMI LEVEL OF THE AU ELECTRODES WITH RESPECT TO THE HOMO AND LUMO
LEVELS.(B)THE PREDICTED SEEBECK COEFFICIENT OF A AU-BDT-AU JUNCTION AS A FUNCTION OF THE RELATIVE POSITION OF THE FERMI LEVEL WITH RESPECT TO THE HOMO AND LUMO LEVELS.WHEN THE MEASURED VALUE OF
SAU-BDT-AU =+8.7 2.1 ΜV/K(BLUE BAND) IS SHOWN, IT IS CLEAR THAT THE FERMI LEVEL IS 1.2 EV ABOVE THE
HOMO LEVEL.AT THIS ENERGY LEVEL, THE TRANSMISSION FUNCTION IS( )E 0.01... 7 FIG.10.THE SCHEMES OF THE THREE TERMINAL JUNCTIONS USED IN THE PRESENT STUDY.THE LEFT PANEL IS THE -NH2
SUBSTITUTED 1,4-BENZENEDITHIOLATES MOLECULAR JUNCTION AND THE RIGHT PANEL IS THE -NO
SUBSTITUTED 1,4-BENZENEDITHIOLATES MOLECULAR JUNCTION. ... 9 FIG.11.THE SCHEMATIC OF BIMETAL JUNCTION WITH EXTERNAL SOURCE-DRAIN BIAS. ... 20
FIG.12.THE INSTALLED SYSTEM ON THE SOURCE-DRAIN BIAS AND GATE VOLTAGE IN THE -NH2 AND –NO 1,4-BENZENEDITHIOLATES MOLECULAR JUNCTION: THE ATOMIC SIZE CONDUCTORS WHERE BOTH CHEMICAL POTENTIAL AND TEMPERATURE GRADIENTS ARE PRESENT. ... 22 FIG.13.THE CURRENT (LEFT AXIS) AND DIFFERENTIAL CONDUCTANCE (RIGHT) AS A FUNCTION OF VSD IN AMINO-SUBSTITUTED
(-NH2) AND NITRO-SUBSTITUTED (-NO)1,4-BENZENEDITHIOLATES JUNCTIONS. ... 31 FIG.14.THE DENSITY OF STATES FOR VARIOUS SOURCE-DRAIN BIASES (VSD=-1.0,-0.4,-0.1,0.01,0.1,0.4,0.7, AND 1.0) IN
AMINO-SUBSTITUTED AND NITRO-SUBSTITUTED JUNCTION.THE LEFT FERMI LEVEL ΜL(RED LINES) IS SET TO BE THE ZERO
OF ENERGY, AND THE RIGHT FERMI LEVEL ΜR(BLUE LINES) DEFINES VSD=(ΜR-ΜL)/E ... 32 FIG.15.THE SOURCE-DRAIN CONDUCTANCE AS A FUNCTION OF GATE VOLTAGE IN THREE-TERMINAL GEOMETRY FOR
NH2-SUBSTITUTED AND NO-SUBSTITUTED 1,4-BENZENEDITHIOLATES. ... 33 FIG.16.THE DENSITY OF STATES FOR NH2-SUBSTITUTED (LEFT) AND NO-SUBSTITUTED (RIGHT)1,4-BENZENEDITHIOLATES IN
DIFFERENT GATE-VOLTAGES. ... 34 FIG.17.THE SEEBECK COEFFICIENT AS A FUNCTION OF SOURCE-DRAIN BIASES FOR THE SYSTEM OF NH2-SUBSTITUTED
1,4-BENZENEDITHIOLATES.THE OTHER GRAPH EXPRESSES THE PROBABILITY OF TRANSMISSION UNDER THE DISTINCT BIASES. ... 36 FIG.18.THE SEEBECK COEFFICIENT AS A FUNCTION OF SOURCE-DRAIN BIASES FOR THE SYSTEM OF NO-SUBSTITUTED
1,4-BENZENEDITHIOLATES.THE OTHER GRAPHS EXPRESSES THE PROBABILITY OF TRANSMISSION UNDER THE DISTINCT BIASES. ... 37 FIG.19.THE SEEBECK COEFFICIENT IN A THREE TERMINAL GEOMETRY WITH VSD=0.01V FOR THE SYSTEM OF MOLECULAR
JUNCTION,NH2-SUBSTITUTED 1,4-BENZENEDITHIOLATES.THE GATE FIELD IS APPLIED IN A DIRECTION PERPENDICULAR
TO DIRECTION OF CHARGE TRANSPORT.THE OTHER GRAPH EXPRESSES THE PROBABILITY OF TRANSMISSION UNDER THE DISTINCT GATE VOLTAGES ... 39 FIG.20.THE SEEBECK COEFFICIENT IN A THREE TERMINAL GEOMETRY WITH VSD=0.01V FOR THE SYSTEM OF MOLECULAR
JUNCTION NO-SUBSTITUTED 1,4-BENZENEDITHIOLATES.THE OTHER GRAPH EXPRESSES THE PROBABILITY OF
Chapter 1 Introduction
Building electronic circuits from molecules is an inspiring idea1-4. The system of metal-molecule-metal tunnel junctions has drawn much attention from theoretical, experimental, and technological studies. Much attention has been devoted to investigate the various transport properties that might be applicable in developing new forms of electronic and energy-conversion devices, such as electron transfer5,6, shot noise7, heat transport8,9, negative differential resistance10, and gate controlled effects11. It is well-known that these electron transport and thermoelectric characteristics are influenced by the intrinsic properties of the molecules, including their lengths, conformations, and the density of states. In the followings, I will briefly introduce several recent investigations on this subject.
1-1 Theoretical and Experimental Researches
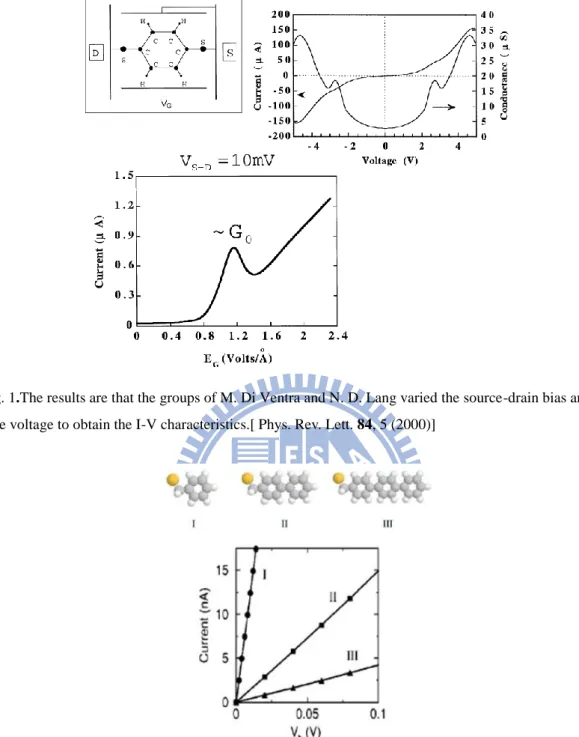
M. Di Ventra and N. D. Lang have reported the first-principles calculations of the current-voltage characteristics in a 1,4-benzenedithiolates molecular junction11,15. They find that the shape of the I-V curve is largely determined by the electronic structure of the molecule, while the presence of single atoms at the molecule-electrode interface play a key role in determining the absolute value of the current (Fig.1). The results show that such simulations would be useful for the design of future microelectronic devices for which the Boltzmann-equation approach is no longer applicable.
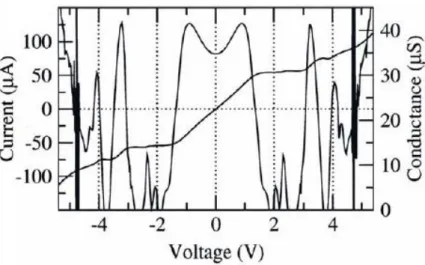
Moreover, Chao-Cheng Kaun, Brian Larade, and Hong Guo calculated charge transport properties of molecular wires from first principles16. The wires are made of oligophenylene molecules of three different lengths, in contact with atomic scale Au electrodes. (Fig. 2)Most surprising is the quantitative consistency between their theory and the experimental data on the exponential increase of resistance for longer wires.
Fig. 1.The results are that the groups of M. Di Ventra and N. D. Lang varied the source-drain bias and the gate voltage to obtain the I-V characteristics.[Phys. Rev. Lett. 84, 5 (2000)]
Fig. 2. I-V characteristics for planar molecules of I–III.[ Phys. Rev. B 67, 121411(2003)]
J. Taylor and M. Brandbyge have considered the 1,4-benzenedithiolates system. They presented state of the art calculations of the electron transport through 1,4-benzenedithiolates coupled to Au(1,1,1) surfaces using the code TRANSIESTA. The
method is based on density functional theory (DFT) and determines the self-consistent electronic structure of a nanostructure coupled to 3-dimensional electrodes with different electrochemical potentials, using a full atomistic description of both the electrodes and the nanostructure17. Their result is as shown in Fig.3.
Fig. 3The molecular junction of 1,4-benzenedithiolates system as the function of bias(steps of 0.1 V). [C. M. Science 27, 151(2003)]
Simultaneously, J. Taylor and M. Brandbyge also investigated the transport properties in the mono layers of Tour wires functionalized with different side groups18. (Fig. 4) They found that functionalization of TW’s has a stronger effect on the energetics of the monolayers than on the orbitals responsible for current transport, and a better understanding of the intermolecular interactions in such monolayers could hopefully be exploited in order to design molecular electronic devices with specific properties.
Fig. 4.(Color online) Geometry of monolayers A–C connected with two Au (111) surfaces. Color codes:
C (dark gray or green), H (white), O (black or red), N (black or blue), S (light gray or yellow), and Au
(light gray or gold). And I-Vb characteristics for monolayers A, B, and C. [Phys. Rev. B 68,
121101(2003)]
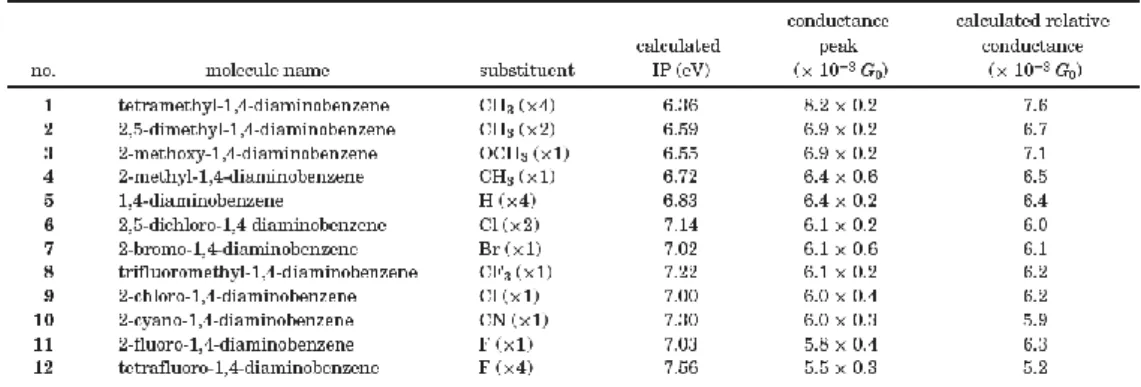
Lately, Mowbray, Jones, and Thygesen also have applied density functional theory (DFT) to analyze the influence of five classes of functional groups, as exemplified by NO2, OCH3, CH3, CCl3, and I, on the transport properties of a 1,4-benzenedithiolate
(BDT) and 1,4-benzenediamine (BDA) molecular junction sandwiched between gold electrodes19. They have found that functional substitutions have a weak influence on a molecule’s conductance (see Table I), and the reason for the weak influence is that charge neutrality pins the HOMO/LUMO molecular levels, making it difficult to shift them relative to EF.
Table I. Conductance G of BDT and BDA species between a gold (111) surface and tip.
[J. Chem. Phys. 128, 111103 (2008)]
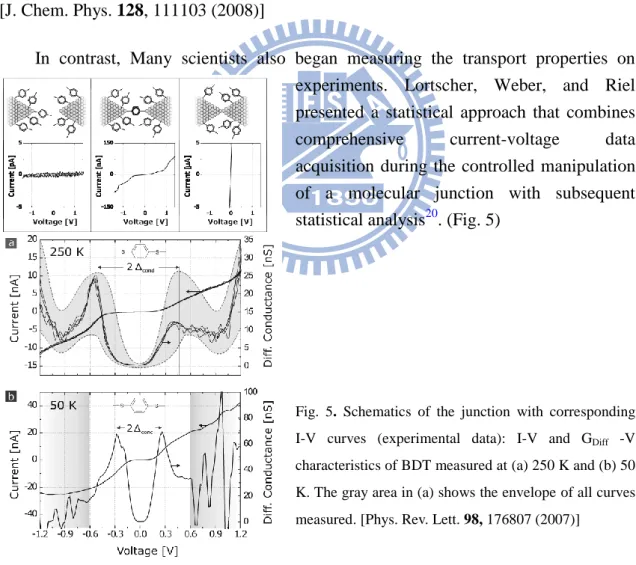
In contrast, Many scientists also began measuring the transport properties on experiments. Lortscher, Weber, and Riel presented a statistical approach that combines
comprehensive current-voltage data
acquisition during the controlled manipulation of a molecular junction with subsequent statistical analysis20. (Fig. 5)
Fig. 5. Schematics of the junction with corresponding I-V curves (experimental data): I-V and GDiff -V characteristics of BDT measured at (a) 250 K and (b) 50 K. The gray area in (a) shows the envelope of all curves measured. [Phys. Rev. Lett. 98, 176807 (2007)]
The groups of Venkataraman, they observed the electronics and chemistry by varying single-molecule Junction conductance using chemical substituents. They still measure the low bias conductance of a series of substituted benzene diamine molecules
while breaking a gold point contact in a solution of the molecules21. Table II is their result. They have observed that the nature of molecular junction can be changed by different functional substitutions in the bridging molecule.
Table II. List of the Molecules Studied Showing the Number and Type of Substituents,
Measured Conductance Histogram Peak Position, Calculated IP, and Calculated Relative Conductance a[Nano Lett. 7, 502(2007)].
In this study, we have investigated the effects of function substitutions in the 1,4-benzenedithiolates molecular junctions on the I-V characteristics and the Seebeck coefficients with external biases and gate voltages12,13,14.
Thermoelectric effects were observed long time ago. The macroscopic and microscopic models have been well developed and have been able to successfully explain the thermoelectric properties in the bulk materials. In the past few decades, thermoelectricity has gained renewal interests due to the progress in growing micro and nano structures, such as quantum well, super lattice, and quantum dot. Small structure can significantly alter the features of density of states by changing the dimensionality. Thus, it leads to novel thermoelectric properties beyond the bulk materials. The efficiency of energy conversion could be enhanced due to the enhancement of the Seebeck coefficient by small structures in materials.
Although extensive researches have been made on electron transport in the nanoscale junctions, the thermoelectricity in molecular junctions has never been measured until very recent. In 2007, Prof. Majumdar’s22 group at UC, Berkeley has measured the Seebeck coefficients in a single-molecule junction. These experiments open a new era to study the thermoelectric effects at atomic level and demonstrated the capability to fabricate the thermoelectric molecular devices.
Fig. 6. Schematic description of the experimental set up based on an STM break junction. Molecules of BDT, DBDT, or TBDT are trapped between the Au STM tip kept at ambient temperature and a heated Au substrate kept at temperature ∆T above the ambient. When the tip approaches the substrate, a voltage bias is applied and the current is monitored to estimate the conductance. When the conductance reaches a threshold of 0.1 G0, the voltage bias and the current amplifier are disconnected. A voltage amplifier is then used to measure the induced thermoelectric voltage, ∆V, and the tip is gradually pulled away from the substrate.
The results they have obtained are: (i) the Seebeck coefficients is independent of the number of molecules as shown in Fig. 7; (ii) the length dependence of molecular junction on the Seebeck coefficients is shown in Fig. 8; and (iii) the Seebeck coefficients can reveal more detailed information about the electronic structures of the molecule sandwiched between the nanojunctions beyond what the conductance measurements can provide as shown in Fig. 9.
Fig. 7.(A) A plot of the thermoelectric voltage measured as a function of the tip-sample distance when a temperature differential ∆T= 20 K is applied (Au tip at ambient and substrate at ambient + 20 K). The blue curve is obtained when a Au-BDT-Au junction is broken. The red curve shows a control experiment performed on a clean gold substrate. (B) Typical thermoelectric voltage traces for tip-substrate temperature differentials of 0, 10, 20, and 30 K for Au-BDT-Au junctions.
In Fig. 7, blue curve, we observed a constant thermoelectric voltage of about ∆V= -200 μV, which lasted until all of the molecules trapped in the junction broken away, suggesting that the Seebeck coefficient is independent of the number of molecules.
Fig. 8.Plot of measured junction Seebeck coefficient as a function of molecular length for BDT, DBDT, and TBDT.
Fig. 8 shows a weak linear dependence of the thermopower on the lengths of molecules sandwiched in the junctions. The Seebeck coefficients increase as the lengths of molecules increase. The Seebeck coefficient in Au-BDT-Au obtained from experiments is around +8.7 2.1 μV/K, which depends on the slope of DOSs as shown in Fig. 9(B).
The conductance in the Landauer formalism can be related to the transmission function at EF as 2 0 2 ( ) ( ) , F F molecule E E E E e G E E G h (1.1)
Fig. 9. Relating the measured Seebeck coefficient of Au-BDT-Au junction to the position of Fermi level. (A) theoretical prediction of the transmission function of a Au-BDT-Au junction plotted as a function of the relative position of the Fermi level of the Au electrodes with respect to the HOMO and LUMO levels. (B) The predicted Seebeck coefficient of a Au-BDT-Au junction as a function of the relative position of the Fermi level with respect to the HOMO and LUMO levels. When the measured value of SAu-BDT-Au = +8.7 2.1 μV/K (blue band) is shown, it is clear that the Fermi level is 1.2 eV above the HOMO level. At this energy level, the transmission function is( )E 0.01.
Measurements of the Seebeck coefficient in nanojunctions can provide insight into the electronic structure of the heterojunction, but the results also bear on an as-yet unexplored field of thermoelectric energy conversion based on molecules. The efficiency in thermoelectric device can be optimized if resonant tunneling occurs through an energy level between the left and right Fermi levels. Metal-molecule-metal heterojunctions are ideal in this regard because they (i) the overwhelming joule heating may be absent for the bias smaller than the threshold voltage, where no heating is possible; (ii) Diversified atomic-sized junctions may be achieved by manipulating the species of nano-structured objects and the contact region. Such manipulations may lead to a significant change in the density of states, consequently varying the the Seebeck coefficients of nanojunctions. A full exploration of all the possibilities in such an unknown system may lead to observations of practical thermoelectric devices at atomic level.
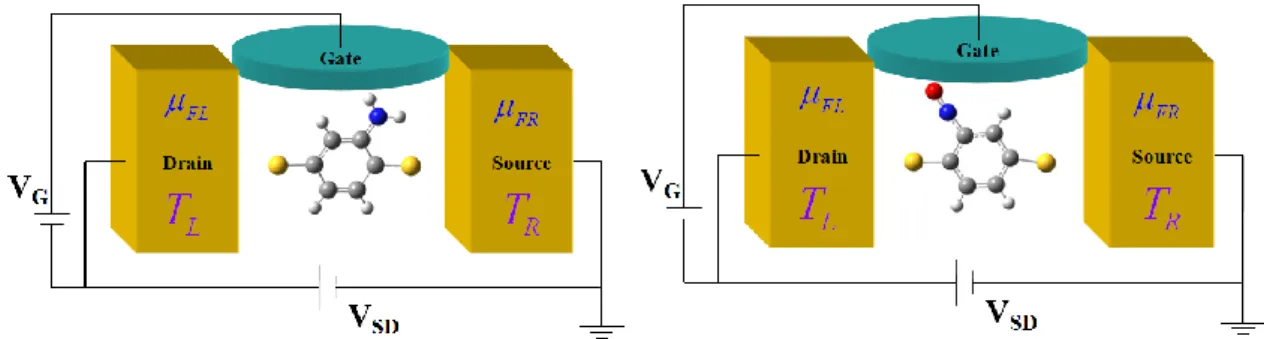
1-2 Our Systems
In this work, we model two systems of molecular junctions: the amino-substituted (-NH2) and nitro-substituted (-NO) 1,4-benzenedithiolates sandwich between two gold electrodes.
At first, we optimize a 1,4-benzenedithiolates molecule using the program, Gaussian, with the method of Hartree-Fock theory. We choose the basis set 3-21G. The optimized 1,4-benzenedithiolates molecule are taken out to reconstruct the amino-substituted (-NH2) and nitro-substituted (-NO) 1,4-benzenedithiolates molecule and optimize the structure of -NH2 and -NO 1,4-benzenedithiolates again. These relaxed molecules are put into the designed molecular junctions as shown in Fig. 10.
Fig. 10. The schemes of the three terminal junctions used in the present study. The left panel is the -NH2 substituted 1,4-benzenedithiolates molecular junction and the right panel is the -NO substituted 1,4-benzenedithiolates molecular junction.
The benzene is a stable and symmetrical molecule, and it is also a fundamental module in the chemistry. The interesting thing is that we can make the different chemical substituents, and the molecular feature can be changed easily. Charge distributions determining the electrostatic potential in monosubstituted benzenes are investigated23. So we can use the characteristic to look for some applicable materials.
We investigate the dependence of conductance on the external biases and gate field in the two nanoscale junction. In the two terminal systems, the Fermi level in the right/left electrodes is determined by filling the conduction band with the valence electrons in the bulk metal electrode described by jellium model (Rs=3). The stationary scattering wave functions of the whole system are calculated by solving the Lippmann–Schwinger equation iteratively until self-consistency is obtained. Finally, we calculate the density of stat and wave functions to simulate the I-V quality.
After studying the electronic transport properties, we also propose using the external biases and gate field as means to modulate the Seebeck coefficients in our molecular junctions. The Seebeck coefficients are relevant not only to the magnitude but also to the slope of electronic transmission functions near the Fermi levels in the metal electrodes. Therefore, observing the probability of transmission makes us understand the trend of Seebeck coefficients.
Chapter 2 Theories
We have investigated the electron transport properties and the thermoelectric efficiency in the amino-substituted (-NH2) and nitro-substituted (-NO) 1,4-benzenedithiolates molecular junctions. Our calculations are based on ab initio self-consistent density functional theory. We have computed the I-V characteristics by using the N. D. Lang’s methods24
. I will briefly introduce the density functional theory in section 2-1 and the method of appllying DFT to compute the electric current in section 2-2 and the Seebeck coefficient S in section 2-3.
2-1 Density Functional Theory
The fundamental physical quantities in the ground state can be uniquely described
from the electron density n r in many-particle system. All ground state properties of ( )
the many electron system are functional of n r . In 1964 Hohenberg and Kohn prove ( ) that the ground state electron density uniquely determines the external potential. Kohn and Sham extended the theorem by separating the total energy into the kinetic energy of electron, the potential energy of attraction between electrons and nuclei, the coulomb potential energy of repulsion, and the exchange-correlation energybetween electrons.
2-1-1 Hohenberg and Kohn theorem
The external potential is uniquely determined by the ground state electron density. The above theorem can be proved as follows: We assume that two different potential
1
V and V2 have the same n r . Suppose ( ) V1V2constant and 1 2 where 1
is the ground state wave function. The Schrodinger equation can be expressed as
1 1 1 1
H E
2 2 2 2,
where E1 and E2 are eigen-energies of H1 and H2, respectively. With different external potentials, the Hamiltonian can be expressed as
1 2 1 2.
H H V V
Because E1 1 H1 1 is the ground energy, we can obtain
1 H1 1 2 H1 2 3 1 2 2 2 2 1 2 2 2 ( 1 2) ( ), E H V V E
d r V V n r (2.1) and 3 2 1 1 1 1 2 1 1 1 ( 2 1) ( ). E H V V E
d r V V n r (2.2) Combine with Eq.(2.1) and Eq.(2.2), we obtain3
1 2 ( 1 2) ( ) 1 2,
E E
d r V V n r E E(2.3)
which leads to a contradiction and means that the assumptions are wrong. Thus, two different external potentials cannot correspond to the same non-degenerate ground state density. The total energy can be expressed as a functional of ground state charge density
( )
n r in many-electron system.
[ ].
tot T
E E n
If the charge density n r is determined, all the ground state properties of the ( ) many-electron system will be determined.
2-1-2 Kohn-Sham equation
From the Hohenberg and Kohn theorem, it is known that the ground state
properties of many-particle system can be determined by the electron density n r . The ( ) charge density in the ground state can be solved iteratively until the self-consistent is achieved.
The ground state energy of a homogeneous interacting electron gas can be written as ' 3 3 3 ' ' 1 ( ) ( ) [ ] [ ] ( ) ( ) [ ]. 2 T ext xc n r n r E n T n V r n r d r d rd r E n r r
(2.4)In the right-hand side, the first term is the kinetic energy as a functional of
non-interacting electrons with density n r ; the second term is external potential ( ) energy relative to electrons; the third term is Coulomb energy between electrons; and the fourth term is the exchange-correlation energy functional of an interacting system with density n r . By the variational principle with the total electron ( ) N
n r d r( ) 3 for the ground state, one has3 ' [ ] ( ) ( ) ( ) , ext xc T n n r V r d r V r n r r
(2.5) where [ ] xc[ ] xc E n V r n , H ( )' 3 n r V d r r r
, and is Lagrange parameter.In the absence of the exchange-correlation potential, it goes back to Hartree approximation. Comparing Eq.(2.5), it is regarded as an effective potential of the single-electron wave equation which is called Kohn-Sham Equation.
2 2 ( ) ( ) ( ) ( ) ( ), 2m Vext r VH r Vxc r i r i i r (2.6) [ ] xc
E n is the exchange and correlation energy of an interacting system with
density n r . ( )
(A) Pseudopotential Method
The early calculations of first-principles pseudopotential are made within the scheme of orthogonalized-plane-wave (OPW) atomic calculation. The wave functions in this way exhibit the correct shape outside the core region; however, they differ from the real wave functions by a normalization factor. Hamann, Schluter and Chiang (HSC) propose a model pseudopotential to solve the problems that have four properties:(1) real and pseudo valence eigenvalues agree for a chosen atomic configuration; (2) real and pseudo wave functions agree beyond a chosen core radius rc; (3) the integrals from 0 to r of the real and pseudo charge densities agree for rrc for each valence state, this is norm conservation condition; (4) The logarithmic derivatives of the real and pseudo wave function and their first energy derivates agree for rrc.
Because the lattice has the periodic characteristic, the wave functions must satisfy the Bloch theorem. It can be written as expansion of the following form:
( ) 1 ( ) nk i k G r. nk G G r e
(2.7)In the pseudopotential method, the pseudopotential V is constructed on the ps
valence electrons and the core electrons have been transformed away. The pseudo-Hamiltonian of the valence electrons can be expressed as
2 , 2 ps H xc p H V V V m (2.8) where
( ). ps ion j R V
V r r R ( ) ionV r is non-local potential and it is relation to the angular momentum l. The
angular momentums of the electron in the s, p and d orbitals are 0, 1 and 2, respectively. The potential can be expressed as
2 0 ( ) ( ) . ion l l i V r V r P
(2.9) lP is the projection operator of the angular momentum . The Hartree potential
satisfies the Poisson equation and it can be written as
2 ( ) 8 ( ). H V r n r (2.10) ( )
n r is the density of the pseudo valence electrons and the Vxc can be regarded
as functional of n r from LDA. We define the elements of the matrix ( ) Sthat
' ' ' , , . k G G G G S kG kG (2.11)
The pseudopotentials of the ion Vion can be separated into local and non-local
potential (Vion VionlocVionnl ). The VH and Vxc are functional of n r that are also ( ) local potential. The Hamiltonian can be rewritten as
loc nl H T V V 2 , 2 p T m (2.12) ' 2 ' , , G G kG T kG k G (2.13) ' ' ( ), loc loc kG V kG V G G (2.14)
' '
( , ).
nl nl
kG V kG V kG kG (2.15)
(B) Pseudopotential
Pseudopotentials are introduced to simplify electronic structure calculations by eliminating the need to atomic core states and the strong potentials responsible for binding them.
To construct atomic pseudopotential lm at a given energy which are identical to atomic eigenfunctions. The lm are continued inside rc with the condition that
l
lm r
for r0 and with the norm-conserving condition, one has
2 3 2 3 0 0 , c c r r lmd r lmd r
(2.16)The pseudopotentials are obtained by inverting the Schrodinger equation
2 2 ( 1) ( ) [ ] / . l r l l l l V r E r (2.17)
The complete pseudopotential is then written as
( ) ( ) ( ) ,
PS loc non loc lm l lm
lm
V V V V r
Y Y (2.18) where l 0 for rrc and Vloc is the local potential and is an arbitrary function for rrc. The semilocal form (i.e. nonlocal in angular coordinates but local in radial coordinate) of the Hamman-Schluter-Chiang (HSC) pseudopotential which used in an expansion of N plane waves requires the evaluation of ( 1)2
N N
integral for each l. The nonlocal form can be introduced,
1 ( ) ( ) ( ) ( ) , ps loc lm l l lm l lm V V
r r B r r (2.19) where.
l lm l lm
B
Vanderbilt generalized Eq.(2.19) with i( )r and i( )r where the i subsumes the l m and also includes two or more energies at which the , lm( )r are evaluated. This result in Bl becoming a matrix
,
ij i j j
B
which is not Hermitian and the generalized norm-conservation requirement,
3 * * 3 0 ( ) 0 ( ) ( ) ( ) ( ) 0, c c r r ij ij i j i j Q
Q r d r
r r r r d r (2.20) and Vanderbilt defines1 ( ) , i ji j j j B
(2.21)which is substituted into the Eq.(2.24) and one can obtain the pseudopotential
,
.
ps loc i ij j
i j
V V
B (2.22)In general, it is difficult to apply Eq.(2.20), results in lm whose plane-wave expansions are extremely slowly converging. To avoid applying Eq.(2.20), Chou constructed norm-conserving nlm at two energies En and inverted the Schrodinger equation to obtain their nl which she averaged to obtain l, yielding
1 ( ) rlm( ) l( ) rlm( ) l( ) , ps loc nl nlm V V r
r r A r r (2.23) where . n nlm nlm nl A The Anl is Hermitian and the nlm( )r are solutions of the pseudo Schrodinger equation at En with nl replaced by l.
(C) Local Density Functional Approximation
The exchange-correlation energy is relation to the electronic distribution in the system. It is difficult to give an exact expression for Exc because of its complexity. In order to simplify this complexity, Kohn and Sham suggested using the homogeneous electron gas system to approximate the energy contribution from Exc[ ]n in 1965. If the electronic density varies slowly, the exchange-correlation functional can be written as
3
[ ] [ ] ( ) ,
xc xc
E n
n n r d r(2.24)
where the exchange-correlation potential can be expressed as
[ ] ( ) xc { ( )}, xc xc E n d V r n n n dn (2.25)
where xc[ ]n is the exchange-correlation energy density of the homogeneous electron gas. Vxc( )n is the exchange and correlation contribution to the chemical potential of a homogeneous gas of density n.
The exchange-correlation energy density can be separated into x[( )]n and
[( )]
c n
. x[( )]n is the exchange energy of a homogeneous electron gas and c[( )]n is the correlation energy of a homogenous electron gas.
Within Hartree-Fock approximation the exchange energy density can be obtained by solving the Schrodinger equation of the non-interacting homogenous electron gas.
0.458 ( ) x s r r rs is Wigner-Seitz radius,
where 1 3 1 3 4 4 ( ) ( ) ( ) 0.458( ( )) . 3 s x 3 n r r r n r (2.26)
From the Eq.(2.26), we can know that the exchange energy density x( )r is proportion to the electron density n r to the power of one third. ( )
An approximation of the correlation energy is based on Quantum Monte Carlo calculations by Ceperley and Alder. The wave function for electrons in a finite volume subject to periodic boundary conditions and extrapolated the energy per electron to infinite volume. The Ceperley’s parameterization of the correlation energy for rs 1 is
1 2 0.1423 ( ) , 1 1 1.0529 0.3334 s c s s s s r r r r r r (2.27)
the high-density form of c (rs 1) is
( ) 0.0311ln 0.048 0.002 ln 0.0116
c r rs rs rs rs
Substituting Eq.(2.26) into Eq.(2.25), the relation between exchange-correlation potential and electronic density can be expressed as
[1 ] . 3 s xc xc s r d V dr (2.28)
In many-electron system, we give the initial data of the electronic density to calculate the potential each term, and get the effective potential V to solve the eff
solution of the Kohn-Sham equation. The wave function is obtained by Kohn-Sham equation and the new electronic density is calculated from the wave function. If the difference in value between the new electronic density and the initial electronic density is too big, they will be mixed to generate another electronic density, and repeat the above procedures until the difference in value between the new density and last density is very small. The above procedures are called self-consistent procedure.
The convergence of the flow chart:
2-2 Current of atomic wires
24We start with a brief introduction of how to calculate the electric current carried by the electron transport in the DFT framework. We picture a nanoscale junction as formed by two semi-infinite electrodes held a fixed distance apart, with a nano-structured object bridging the gap between them. The full Hamiltonian of the system is H = H0+V,
wherein H0 is the Hamiltonian due to the bare electrodes, and V is the scattering
potential of the nano-structured object. The nano-structured object could be a single atom, a chain of atoms, a molecule, or any system with nanoscale dimension. The effective single-particle wave functions of the whole system in the continuum states are calculated in scattering approach by solving the Lippmann-Schwinger equation with exchange and correlation energy included within the local density approximation. Two planar metallic electrodes, represented as a uniform-background (jellium) model.
The applied bias is given by FR FL
B
V
e
, where L(R)is the chemical potential
deep in the left (right) electrode. The single-particle wave functions and self-consistent density distribution are obtained by solving the coupled Poisson equation and Shrödinger equation for the pair of bare metallic electrodes in the presence of the bias voltage. Next, corresponding to each of these wave functions, a Lippmann-Schwinger equation involving a Green’s function for the biased bimetallic junction is solved to obtain an effective single-particle wave function for the total system, consisting of the two electrodes plus a group of atoms. From these wave functions, the charge density for the total system is obtained, and the problem is solved self-consistently using a modified iterative procedure. Atomic units are used here, withe m 1.
2-2-1 Bimetal junction
Fig. 11. The schematic of bimetal junction with external source-drain bias.
Two bulk electrodes are modeled as two semi-infinite bulk metals described by Jellium model. The wavefunction of the bare electrodes can be obtained by solving the Shrödinger equation and Poisson equation until the self consistency is achieved. Electrons incident from the left hand side can be partial transmitted and partially reflected. The unperturbed wavefunctions EKM ( )r of the electrons satisfy the boundary condition as shown in Eq. (2.30), i.e.,
( )
i K R( ),
M EKr
e
u
EKz
(2.29) where 1/2 3/2,
1
( )
,
(2 )
,
R R L ik z ik z EK R ik ze
Re
z
u
z
k
Te
z
(2.30)We first note that M( )r , the superscripts M refer to the pair of bare biased metal electrodes, has the formei K RuEK ( )z , where R is the coordinate parallel to the surfaces
will take henceforth to be the left electrode), uEK ( )z has the form of a linear
combination of left-moving and right-moving plane waves with wave vector
k
L. Here,the energies of electrons are conservative as described by
2 2 1 1 ( ) 2 2 M L eff
k E K U , where E is the energy eigenvalue in the single-particle
equations for the pair of biased electrodes and UeffM( )z is the total effective potential
(electrostatic plus exchange correlation).
Next we will specify the character of uEK ( )z by an additional subscript :
( )
EK
u z . For propagating states, we will replace either by “+,” which will correspond to a wave incident from the left (together with its reflected and transmitted parts) or by “,” which will correspond to a wave incident from the right and thus kR is as defined
as 1 2 1 2 ( )
2 2
M
R eff
k E K U . The coefficient has been chosen to accord with the continuum normalization which we impose on the wave functions M, specified by
* 3 ' '
( )
( )
(
') (
' )
M M E K EKd r
r
r
E
E
K
K
. (2.31)2-2-2 Metal-molecule-metal junction
We investigate the electron transport and thermoelectricity of molecules wire and atomic wires sandwiched between two bulk electrodes with finite external source-drain bias and finite temperature difference as shown in Fig. 11, where the bias is given by
FR FL SD V e .
system consisting of the metal electrodes and the group of atoms between them, are solved in scattering approaches. Thecontinuum wave functions MA are solved by the Lippmann-Schwinger equation, where M will have the same labeling ( ,E K , ) ,
even though K no longer refers to a conserved quantity. These solutions will also
have the same normalization as the M, a fact that facilitates the calculation of the electron density distribution and the current. For EFL E EFR, where EFL is the Fermi level in the left electrode and EFR EFLeVB is the Fermi level in the right electrode (bias VB taken positive), we occupy only states corresponding to a wave incident from the right, i.e., only EKMA and not EKMA.
Fig. 12. The installed system on the source-drain bias and gate voltage in the -NH2 and –NO 1,4-benzenedithiolates molecular junction: the atomic size conductors where both chemical potential and temperature gradients are present.
The Hamilton of complete system can be put into Lippmann-Schwinger form : 3 3 ( ) ( ) ' " ( , ') ( ', ") ( "), MA M M MA r r d r d r G r r V r r r
(2.32)this equation embodies the motion that electrons in states of the electrodes impinge on and are scattered elastically by the potential V r r( , '), which describes the difference in potential between the complete system and the bare electrodes. It can be written
3 ( ") ( , ') ( , ') ( ( )) ( ( )) " ( '), " MA M ps xc xc n r V r r U r r U n r U n r d r r r r r
(2.33)the term Ups( , ')r r is the sum of the (nonlocal) pseudopotentials representing the
atomic cores, Uxc( ( ))n r is the exchange-correlation potential, ( )
M
n r is the electron
number density for the pair of biased metal electrodes, nMA( )r is the density for the
complete system, andn r( )nMA( )r nM( )r . We will use the atomic pseudopotentials introduced by Hamann25.
2-1-3 Current in nanojunction
First, we calculate the current with left/right electrode temperature at 0 K, Fermi-Dirac distribution equal to 1. The electron number density is given by the sum of
squares of the occupied states EKMA, with a factor 2 included for spin degeneracy (we take the system to be unpolarized) the electric current density in the full system is given by
2 * ( ) 2 Im [ ( )] ( ) , FR FL E MA MA MA EK EK E j r
dE d K r r (2.34)where the integral over K is restricted by K 2E U effM( ) . Now let jM be the current density for the pair of biased electrodes in the absence of the group of atoms. Then the quantity of interest to us is
2
,
MA M
I
d R zj j (2.35)which is independent of z since our system has no current sources or sinks. Here z is the unit vector point to the right and perpendicular to the surfaces of the electrodes. If we write MAM , then 2 2 * * * 2 Im [ ( )] ( ) ( ) ( ) ( ) ( ) , FR FL E M EK EK E M EK EK EK EK d I dE d K d R r r dz d d r r r r dz dz
(2.36)where the integration range for is the same as in Eq. (2.34).
Next, we calculate the current trough the tunnel junction where the temperatures and chemical potentials in source and drain electrodes can be different, Fermi-Dirac distribution not equal to 1.
( EL EELL ER EERR), I i dE dR dK f I
f I (2.37) where * * ' ( , ) ( , ) ( , ) '( , ), ij i i i i EE E E E E I r K r K r K r K (2.38)where ,i jL R, . EL R( )( ,r K ) is the single-particle wave function incident from the
left (right) electrode with energy E and component of the momentum K parallel to the
electrode surface11,26, and dR represents an element of the electrode surface. We assume that the left/right electrode serves as the electron and thermal reservoir with the electron population described by the Fermi-Dirac distribution function
( ) ( ) ( ) ( ) ( ) 1 ( , ) , exp[( ) / ] 1 L R E L R L R L R B L R f T E k T (2.39)
where L R( ) and TL R( ) are the chemical potential and the temperature in the left (right) electrode, respectively, and kB is the Boltzmann constant. For simplicity, we define the transmission probability of electron with energy E incident from the left (right) electrode as ( ) ( , ) ( ) ( , ). L R LL R R EE E i dR dK I r K
(2.40)By using the relation ( )E R( )E L( )E , a direct consequence of the time-reversal symmetry, the current in Eq. (2.37) can be rewritten as
1
( L, L, R, R) ER( R, R) EL( L, L) R( ),
I T T dE f T f T E
(2.41)where the left and right electrode have different chemical potentials given by the bias
(the source-drain bias is FR FL
SD
V
e
) . We also assume that the left/right electrode can be connected to its own heat bath such that TL can be different fromTR.
2-3 Seebeck coefficient
Consider a tunnel junction that may have different temperatures in the source and drain electrodes, a small thermoelectric voltage (∆V) in the junctions can be induced by an additional temperature difference (∆T) applied in the electrodes. The ratio of the thermoelectric voltage to the temperature difference is defined as the Seebeck coefficient. . V S T (2.42)
When we calculate the self-consistently on density functional theory (DFT) by using the second-quantization field-operator method with the effective single-particle wave functions, we presented the form of current.
1
[ ER( R, R) R( ) EL( L, L) L( )].
I dE f T E f T E
(2.43)The current is described by the Fermi-Dirac distribution function Eq. (2.44) and the transmission function Eq. (2.45). Moreover, the parameters, μL(R) and TL(R), are the
chemical potential and the temperature in the left (right) electrode, respectively.
( ) ( ) ( ) 1 , exp[( ) / ] 1 L R E L R B L R f E k T (2.44) ( ) ( ) ( ) ( , ), L R LL RR EE E i dR dK I r K
(2.45)where IEEij '[Ei]*Ej'[ Ei]* Ej' and i j, L R, . EL R( )( ,r K ) is the single-particle wave function incident from the left(right) electrode with energy E and component of the momentum K∥ parallel to the electrode surface and dR represents an
element of the electrode surface. The stationary wave function ( )
( , )
L R E r K
can be
calculated by solving the Lippmann-Schwinger equation iteratively to self-consistency. The exchange-correlation potential is included in density-functional formalism by using
the local-density approximation. Once the single-particle wave functions are calculated self-consistently, the transmission function of electron with energy E can be calculated using Eq. (2.45). We had completely explained at the section 2-2.
When the system comes to equilibrium, the electric current generated by an additional infinitesimal temperature ∆T across the electrodes is compensated by an induced small voltage ∆V across the junction. For simplicity, we assume that the additional temperature and the induced voltage are distributed symmetrically in the left/right electrodes, that is,
2 ( , ; , ) ( , ; , ) ( , ; , ).
2 2 2 2
L L R R L L R R L L R R
T T e V e V
I T T I T T I T T (2.46)
We make the differences of extra current from the changed temperatures and voltages be zero to control the relation between T and V . The next step, we expand the Fermi-Dirac distribution function to the first order in Tand V . So we can obtain the Eq. (2.47) 1 1 0 0 1 ( , , , ) , L R L R L R L R L R K K T T S T T e K K (2.47) where ( ) ( ) ( ) ( ) ( ). L R L R n E n L R f K dE E E E
(2.48) And ( )E R( )E L( )E , a direct consequence of the time reversal symmetry.We can simplify the Eq.(2.47) by using the Sommerfeld expansion27.
2 2 ( ) ( ) . 3 ( ) ( ) L R L R E E B L R E E T T E E k S e (2.49)
From Eq. (2.49), the Seebeck coefficient relates closely to the transmission function in the vicinity of the left and right Fermi levels.
In the first step for our analysis, we study the Seebeck coefficient in a three-terminal geometry in the linear response regime(VSD 0.01V andL R EF), where both electrodes have the same temperatures (TL TR T). In this case, the Seebeck coefficient can be simplified as
( ) ( ) 1 . ( ) E F E f E E E dE E S f eT E dE E
(2.50) When we consider the case of low-temperature regime, the Seebeck coefficient can be also further simplified by using the Sommerfeld expansion as2 2 ln ( ) , 3 F B E E k T E S e E (2.51)
which implies that the Seebeck coefficient is closely related to the slope of the transmission probability at Fermi level. When S>0, the carriers are p type. In this case the direction of electric current is the same as the direction of thermal current. When S<0, the carriers are n type. In this case, the direction of electric current is opposite to the direction of thermal current. The final Eq. (2.51) has been applied to several atomic and molecular systems.27 The investigation explores the dependence of the Seebeck coefficient on the gate voltages, temperatures of the electrodes, and the source-drain biases in both the linear and nonlinear response regimes.
Chapter 3 Results and Discussions
We have performed first-principles calculations to investigate the electron transport and the thermoelectric properties in the amino-substituted (-NH2) and nitro-substituted (-NO) 1,4-benzenedithiolates based on the density functional theory (DFT) as described in the previous chapter. In this work, we have applied the source-drain biases and the gate voltages to explore I-V characteristics in the amino-substituted (-NH2) and the nitro-substituted (-NO) 1,4-benzenedithiolates
molecular junctions.
Following the study of electronic transport properties, we proceed a step further to investigate the thermoelectric properties in the amino-substituted (-NH2) and the nitro-substituted (-NO) 1,4-benzenedithiolates molecular junctions. We perform comparative study on the Seebeck coefficient as a function of source-drain biases and gate voltages for various temperatures in the amino-substituted and the nitro-substituted 1,4-benzenedithiolates molecular junctions.
We find that the functional substitution of 1,4-benzenedithiolates molecular junctions may donate or retrieve electrons from the -orbital, and thus it may have
influence on the conductance. For example, the amino-substituted
1,4-benzenedithiolates molecular junctions withdraw electrons from the -orbital and suppresses the conductance. In contrast to -NH2 substituted 1,4-benzenedithiolates
molecule which retrieve electrons, the nitro-substituted 1,4-benzenedithiolates molecular junctions donate electrons to -orbital and create states closer to the current-carrying window such that the conductance is enhanced. Consequently, the I-V characteristics and the Seebeck coefficients in -NO substituted 1,4-benzenedithiolates molecular junctions display richer features in the I-V characteristics and the Seebeck coefficients due to theses -donating states.
We will discuss the electron transport and the Seebeck coefficients in section 3-1 and 3-2, respectively.
3-1 Electronic transport of single-molecule junctions
3-1-1 The effect of finite source-drain biases
Firstly, we investigate the current (I) and the differential conductance (dI/dVSD) as a function of source-drain biases (VSD) for the amino-substituted (-NH2) and the
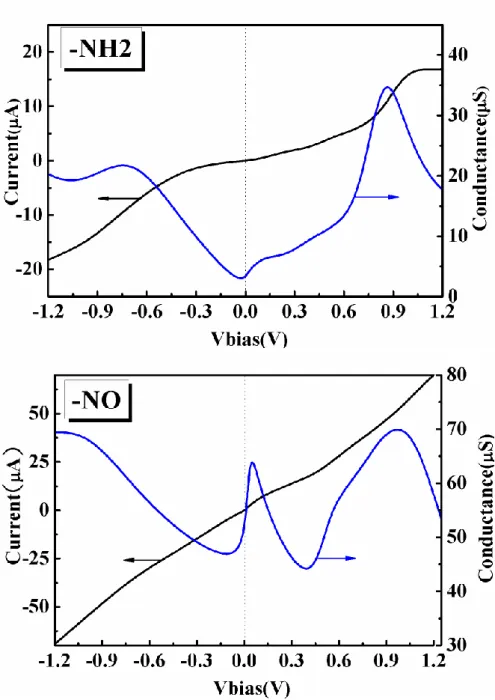
nitro-substituted (-NO) 1,4-benzenedithiolates junctions as shown in Fig.13. As shown in Fig.14, the density of states is very different according to the electron-retrieving and electron-donating natures of the amino-substituted and nitro-substituted systems.
In the -NH2 substituted system, the withdrawal of electrons does not contribute
new state around the Fermi levels as shown in the left panel of Fig. 14. The Fermi levels remain sitting between the HOMO-LUMO gap. As a result, the conductance is small in the small bias regime with a value around 0.07 G0 (1 G0 77 S), which is
comparable with the case without functional substitution (dI dV/ SD 0.12 G0). The functional substitution breaks the symmetry of the molecular junction and leads to asymmetric I-V curve. We find two peaks (34.7μS and 22.5μS) in the differential conductance at the biases 0.85V and -0.75V, respectively.
In contrast, the -NO substituted system donates electrons to the -orbital and create new states near the current-carrying energy window, formed between the left and the right Fermi levels. Consequently, the differential conductance in the small bias regime is greatly enhanced to 0.71 G0 due to more electrons with the energy within the
current-carrying energy window. As shown in the right panel of Fig. 14, there are more electron states created near the current-carrying energy window. As the bias increases, these states may gradually enter the current-carrying energy window and cause richer features in the I-V characteristics. We observe two peaks (63.8μS and 70.2μS) in the differential conductance at the bias 0.05V and 1.0V, respectively.
Fig. 13. The current (left axis) and differential conductance (right) as a function of VSD in amino-substituted (-NH2) and nitro-substituted (-NO) 1,4-benzenedithiolates junctions.
Fig. 14. The density of states for various source-drain biases (VSD=-1.0,-0.4,-0.1, 0.01, 0.1, 0.4, 0.7, and 1.0) in amino-substituted and nitro-substituted junction. The left Fermi level μL (red lines) is set to be the zero of energy, and the right Fermi level μR (blue lines) defines VSD=(μR -μL)/e
The above calculations provide evidence that the resonant tunneling may exist in the nitro-substituted benzenedithiolates junction, in contrast to the non-resonant tunneling in the amino-substituted system. Our calculations show that the substitutions of valence orbital have the influence on the molecular conductance and the I-V characteristics. The conductance ofwithdrawal (-NH2) is lower than the conductance
ofdonation (-NO) in the 1,4-benzenedithiolates molecular junctions.
3-1-2 The effect of gate voltages
As three-terminal field-effect transistor like devices are highly desirable, we also investigate source-drain conductance as a function of gate voltage when a small source-drain bias is applied. In Fig. 15, we compare the conductance of the -NH2
substituted and the -NO substituted 1,4-benzenedithiolates molecule junctions. In the -NH2 substituted system, the response of the conductance to the gate voltage is mild.
the Fermi levels lie between the HOMO and LUMO gap. However, in the -NO substituted system, as the gate voltage varies from -1.18 to 1.18 V, the conductance decreases from 1.18 to 0.73 G0.
To explain why gate voltage can significantly modulate the source-drain conductance, we examine the DOSs for the various gate voltages, as shown in the inset of Fig. 16. At zero gate voltage, the energies between two Fermi levels open a current-carrying window. The -NH2 substitution withdraws electrons from-orbital and
produces a large HOMO-LUMO gap. Conversely, the -NO substitution donates electrons to the -orbital and create new states around the Fermi levels. When we strengthen the resonant tunneling by shifting the position of the state peak toward the current-carrying window, we find that the change of donating system is obvious.
Considering the density of states for an -NH2 substituted 1,4-benzenedithiolates
molecule junctions as shown in Fig.16, we observe that Fermi levels lie between the HOMO-LUMO gap. Thus, the dependence of the conductance on the gate voltage is weak. In contrast, we observe new states introduced by the -NO substitution in the 1,4-benzenedithiolates molecule junction. These states significantly enhance the conductance and improve the ability to modulate the conductance by the gate voltage. At a gate voltage of −0.57 V, the central peak of state is between the left and right Fermi levels, and the conductance reaches a maximum. Conversely, a positive gate voltage shifts the position of the state peak away from the current-carrying window, and therefore, the source-drain conductance decreases.
Fig. 15. The source-drain conductance as a function of gate voltage in three-terminal geometry for NH2-substituted and NO-substituted 1,4-benzenedithiolates.
Fig. 16. The density of states for NH2-substituted (left) and NO-substituted (right) 1,4-benzenedithiolates in different gate-voltages.