科技部補助專題研究計畫成果報告
期末報告
開發一個以區塊特性為基礎的啟發式演算法求解流程式排程問
題
計 畫 類 別 : 個別型計畫 計 畫 編 號 : MOST 103-2221-E-004-002-執 行 期 間 : 103年08月01日至104年07月31日 執 行 單 位 : 國立政治大學資訊管理學系 計 畫 主 持 人 : 陳春龍 計畫參與人員: 博士班研究生-兼任助理人員:許皓然 博士班研究生-兼任助理人員:陳則匡 處 理 方 式 : 1.公開資訊:本計畫可公開查詢 2.「本研究」是否已有嚴重損及公共利益之發現:否 3.「本報告」是否建議提供政府單位施政參考:否中 華 民 國 104 年 10 月 30 日
中 文 摘 要 : 流程式排程問題(PFSP)是製造現場常見的問題。因為它在實務上 的價值以及計算的複雜度,流程式排程問題長久以來都是學術界和 產業界非常重視的問題。以總完成時間為目標的流程式排程問題 (PFSP- makespan)是研究者最有興趣的問題之一。我從1993就開 始該問題的研究,我的兩篇主要的論文分別刊登在EJOR (1995,在 WOS資料庫中被引用118次) 和 C&IE (1996,在WOS資料庫中被 引用66次)。2011年和2012年國科會計畫的研究成果也以分別刊登在 IJAMT (2012), Soft Computing和Applied Soft Computing。 2014年的國科會研究計畫則已開發一個比IGRIS 和 DDERLS(兩個到 目前為止最好的演算法)為佳的啟發式演算法(BBLS),因此求解 PFSP-makespan,研究的成果最近已經被Soft Computing所接受 (DOI10.1007/s00500-013-1199-z)。本研究計畫利用PFSP-makespan問題之解的區塊特性(Block)開發一個新的演算法 (block-based local search, BBLS)。BBLS先利用NEHT產生一個 起使解,設定其為起使期之週期最佳解(local best solution)。然 後在每一週期(iteration),利用週期最佳解的區塊特性,產生有 效的鄰近解(neighbor solutions),再應用一個新的篩選方法 (filtered local search)在這些鄰近解上,以產生新的週期最佳 解,再重複下一週期的搜尋;篩選機制的主要目的是希望將搜尋的 方向導引向尚未搜尋的區域。此外,如果搜尋陷入區域最佳解中 (local optimum),我們也計畫開發一個逃離策略(jump strategy),幫助搜尋跳出區域最佳解。最後,我們會利用IGRIS 和 DDERLS(兩個到目前為止最好的演算法)來評價BBLS的效能。 中 文 關 鍵 詞 : 區塊特性,流程式排程問題,總完成時間,啟發式演算法
英 文 摘 要 : Permutation flow shop scheduling problem (PFSP) is a common problem in the manufacturing shop floor. Due to its value in the real-world and its computational complexity, it has received considerable attention in academia and in
practitioners for years. PFSP with minimum makespan as the objective (PFSP-makespan) is one of the most studied NP-hard scheduling problems; more than 1000 technical papers for solving PFSP-makespan can be found in Web of Science (WOS). I started conducting research in this field in 1994, and two of my notable works were published in European Journal of Operational Research (1995, cited 109 times in WOS) and Computers and Industrial Engineering (1996, cited 66 times in WOS).
This proposal is a follow-up research of my NSC projects in 2011 and 2012 (100-2221-E-004-004 and 101-2221-E-004-004). The project in 2011 developed a novel metaheuristic
(EDAACS) to solve PFSP-makespan, and the result of the project was published in International Journal of Advanced Manufacturing Technology (2012). The project in 2012
developed another metaheuristic (RDPSO) to solve PFSP-makespan, and the result of the project has recently been accepted for publication by Soft Computing
(DOI10.1007/s00500-013-1199-z). This research utilizes the block property of the solution of PFSP-makespan to develop a new metaheuristic (block-based local search, BBLS) for solving PFSP-makespan. BBLS applies NEHT to generate an initial solution and set the solution be the local best solution. Then, in each iteration, BBLS utilizes the block property of the local best solution to efficiently generate promising neighbor solutions and applies a new filtered local search method to the generated neighbor solutions to update the local best solution. The purpose of the filtered local search is to filter the solution regions that have been reviewed and guides the search to new solution regions in order to keep the search from trapping into local
optima. In addition, a new jump strategy will be developed to help the search escape if the search does become trapped at a local optimum. Computational experiments on the well-known Taillard‘s benchmark data sets will be conducted to compare the performance of BBLS with that of IGRLS and DDERLS, the two most effective heuristics for PFSP-makespan up to now.
英 文 關 鍵 詞 : Block; Metaheuristic; Permutation Flow Shop Scheduling; Makespan
An Effective Block-based Algorithm for PFSP
1. Introduction
Permutation flow shop scheduling problem (PFSP) is a common problem in the manufacturing shop floor. Given a set of n jobs, a set of m machines, and requiring all the jobs to be processed in the same processing order on all the machines, PFSP determines the best sequence of all the n jobs on each one of the
m machines in order to optimize a predetermined objective. Due to its value in the real-world and its
computational complexity, PFSP has received considerable attention in academia and in practitioners for years. Over 1,300 technical papers can be found in Web of Science (WOS) in the past decade.
This research proposes to develop an effective metaheuristic for PFSP with minimum makespan as the objective (PFSP-makespan). The candidate problem is one of the most studied NP-hard scheduling problems [1] and more than 1000 technical papers for solving the problem have been published in SCI journals in the past decade. In addition, due to its computational burden, the development of metaheuristics that find near-optimal solutions in a reasonable computation time has held the attention of many researchers recently. These include genetic algorithm (GA) [2, 3, 4, 5], ant colony optimization (ACO) [6, 7, 8], particle swarm optimization (PSO) [9, 10, 11, 12], differential evolution (DE) [13, 14, 15], iterated greedy algorithm (IG) [16], iterated local search (ILS) [17], simulated annealing (SA) [18, 19, 20], tabu search (TS) [21, 22, 23, 24, 25] and hybrid metaheuristics [26, 27, 28, 29]. Several research papers reviewing heuristics for the candidate problem can be found in Framinan et al. [30], Hejazi & Saghafian [31], and Ruiz & Maroto [32].
This research proposes to utilize the block property of the solution of PFSP-makespan to develop a new metaheuristic (block-based local search, BBLS) for solving PFSP-makespan. BBLS applies NEHT to generate an initial solution and set the solution be the local best solution. Then, in each iteration, BBLS utilizes the block property of the local best solution to efficiently generate promising neighbor solutions and applies a modified filter local search method to the generated neighbor solutions to update the local best solution. The purpose of the filter local search is to filter the solution regions that have been reviewed and guides the search to new solution regions in order to keep the search from trapping into local optima. In addition, a new jump strategy will be developed to help the search escape if the search does become trapped at a local optimum. Computational experiments on the well-known Taillard's benchmark data sets [33] will be conducted to compare the performance of BBLS with that of IGRIS and DDERLS [15], the two most effective heuristics for
PFSP-makespan up to now.
2. The proposed algorithm: block-based local search (BBLS)
The basic process of BBLS is presented as follows:
1. Set t = 0. Generate an initial solution using NEHT and let it be the local best solution and the best-so-far
solution.
2. do {
3. Find a critical path of the local best solution for iteration t.
4. Generate m new solutions using the proposed job moving rule.
5. Apply the modified filter local search method to select a solution from the m solutions generated in Step
4 and update the local best solution
7. t = t + 1
8. } until (Terminate criteria are met )
9. Return best-so-far solution
The BBLS algorithm, different from general population-based metaheuristics, produces only a solution using the heuristic NEHT (Taillard 1990) in the initial iteration and sets the solution to be the local best solution and the best-so-far solution. The major loop in BBLS (step3~step7) finds a critical path for the local best solution, generates m new solutions using the job moving rule, and updates the local best solution with the solution produced by applying the modified filter local search to the m new solutions. Note that m is the number of machines considered in a problem. If the local best solution is not able to improve the best-so-far solution in a certain number of iterations, it is assumed that the search has trapped into a local optimum. Then the new jump strategy is launched to find a new initial solution as the local best solution and the same loop (step3~step7) is performed on the new initial solution. The major components of BBLS, job moving rule, modified filter local search and jump strategy will be discussed in detail in the following sections.
2.1 Job moving rule
The job moving rule is applied to generate neighbor solutions of the local best solution in every iteration. The purpose of the job moving rule is to generate only the neighbor solutions which may improve the local best solution so as to significantly reduce the number of neighbor solutions searched in every iteration. The job moving rule is proposed based on the research of Grabowski and Wodecki (2004) and Jin and Song (2007). Given an example with n jobs and m machines and setting π = (π(1), π(2), … , π(i), … , π(n)) as a
job-sequence of the n jobs, Grabowski and Wodecki showed that there would be at least a critical path u = (u1,
u2, … , um-1) such that the makespan of π:
Cmax(π) = + + … + .
Grabowski and Wodecki defined a block on each machine based on the critical path: Bk = ((π(uk-1), π(uk-1 +
1), … , π(uk)), k = 1, 2,..., m, where u0 = 1 and um = n. They also defined an internal block for each block as
follows: 𝐵1∗ = B1 – {π(u1)}, 𝐵𝑚∗ = Bm – {π(um-1)}, and 𝐵𝑘∗ = Bk – {π(uk-1), π(uk)} for the rest of the blocks. A
simple 7-job and 3-machine example given in Jin and Song (2007) can be used to illustrate the notion above. Figure 1 presents a schedule of the example; The job-sequence of the schedule is π = (1, 7, 3, 2, 4, 5, 6) and the critical path of the schedule is u = (u1 = 2, u2 = 6), which generates three blocks: B1 = (1, 7), B2= (7, 3, 2, 4,
5), and B3 = (5, 6), and three relevant internal blocks: 𝐵1∗ = (1), 𝐵2∗ = (3, 2, 4) and 𝐵3∗ = (6). It should be
noted that B1 is the block on machine 1, B2 is the block on machine 2, and so on.
1 1 7 3 2 4 5 6
2 1 7 3 2 4 5 6
3 1 7 3 2 4 5 6
1 5 10 15 20 25 30 35 38
Figure 1. A schedule of the 7-job and 3-machine example
In addition, Theorem 1 in Jin and Song (2007) proved that, given a schedule πa with blocks Bk, k = 1,
2,…, m, and job j is a job in 𝐵𝑝∗ and p
jp and pjq are the processing times of job j on machines p and q
the result of Cmax(πb) ≧ Cmax(πa) + (pjq - pjp) is produced. This theorem shows that schedule πa can only be
improved when (pjq - pjp) is negative; that is when pjp > pjq stands. The same 7-job and 3-machine example can
be used to illustrate the application of the theorem to the proposed moving rule. If πa = (1, 7, 3, 2, 4, 5, 6) is
currently the local best solution, the proposed moving rule will generate only the neighbor solutions that may improve πa. According to the internal blocks of the schedule, 𝐵1∗ = (1), 𝐵2∗ = (3, 2, 4) and 𝐵3∗ = (6), the
theorem will be applied to each job in the internal blocks to generate neighbor solutions. For instance, according to Figure 1, job 1 is in block 1 and the condition of p12 > p11 > p13 stands, so the neighbor solution
that may improve πa by moving job 1 is to insert job 1 into feasible positions in 𝐵3∗, which are the positions
before and after job 6. Thus, the neighbor solutions, which are generated by moving job 1, are (7, 3, 2, 4, 5, 1, 6) and (7, 3, 2, 4, 5, 6, 1). Compared with the commonly used insertion method, which inserts job 1 into the positions between every two consecutive jobs of (7, 3, 2, 4, 5, 6) and the position after job 6, the proposed moving rule obviously generates a smaller number of neighbor solutions.
Although the job moving rule is a very efficient approach, it is noticed that the equation Cmax(πb) ≧
Cmax(πa) + (pjq - pjp) provides only a lower bound of πb. Therefore, we are not able to justify which neighbor
solutions are better than the others. For instance, in the previous example, we cannot justify which of the two neighbor solutions generated by inserting job 1 in 𝐵3∗ is better. This problem will become critical when the
job moving rule is applied to large-scale problems. Since there will still be a large number of neighbor solutions generated by the job moving rule and only m solutions from them will be chosen for the following procedure of BBLS, an efficient approach needs to be developed for choosing better neighbor solutions.
In this research, we set a table recording the operation with the smallest processing time for each job and the machine processing the operation. In each iteration, starting from 𝐵1∗, we evaluate each job in 𝐵1∗ to
determine a neighbor solution generated by 𝐵1∗; a job is evaluated by finding the difference between the
processing of the job on machine 1 and the smallest processing time of the job. The job with the largest difference is chosen to be randomly inserted into a feasible position in 𝐵𝑞∗, where q is the machine with the smallest processing time of the job. If there are more than one job having equal ‘largest difference’, one of them is randomly chosen. The same process is applied to 𝐵2∗, 𝐵3∗, …and 𝐵𝑚∗, and the m neighbor solutions
will be efficiently generated.
2.2 Modified filter local search
Local search methods are crucial for improving the effectiveness of population-based metaheuristics. They usually are applied to the best solution in an iteration or the global best solution to improve the quality of the solution; however, this may cause a search trap into the local optima. Tzeng et al. [34] proposed a filter strategy to address this problem. The filter strategy is applied when the m neighbor solutions are generated by the job moving rule. Its purpose is to filter the solution regions that have been reviewed and guide the search to new solution regions in order to keep the search from trapping into local optima. A filter-list, defined as a first-in, first-out queue, is used to store the makespan of the chosen solution in each iteration and a parameter,
f-size, is defined as the size of the queue. The queue is set to be empty initially. When all the m solutions are
generated, the solutions are sorted according to their makespans in ascending order, and the filter strategy is applied from the top of the m solutions until the first solution, whose makespan is different from all the makespans in the filter-list, is found and store the makespan of the solution in the filter list. If none of the m solutions has a different makespan from the makespans in the filter-list, the last of the m solutions is chosen (but the makespan will not be stored in the filter-list). The purpose of comparing makespans instead of
job-sequences of solutions while using the filter strategy is two-fold. Firstly, it may guide the search to the solution regions which have not been examined. Secondly, it can significantly reduce computation time by comparing each of the m solutions and the solutions stored in the filter-list; this is especially critical when the number of jobs considered in a problem is large. In addition, the idea of choosing the solution with the largest makespan when none of the m solutions has a different makespan from the makespans in the filter-list is that it may prevent the search of BBLS from quick convergence.
Once a solution is chosen using the filter strategy, a local search method (denoted as NEHT_LS) is applied to improve the makespan of the solution. NEHT_LS integrates Taillard’s Modified-NEH method [35] with Ruiz and Stützle’s [16] iterative improvement method. Given that π is the job sequence of the chosen solution, NEHT_LS first randomly chooses a job k and removes it from π; then it inserts job k into the first position, the last position, and the positions between every two consecutive jobs in π to generate n different solutions, and lets π’’ be the best of the n generated solutions. If the makespan of π’’ is smaller than that of π, NEHT_LS will update π with π’’ and will repeat the same procedure until π cannot be further improved. If the makespan of π is smaller than that of the local best solution, it will update the local solution with π; if the makespan of πis smaller than that of the best-so-far solution, it will update the best-so-far solution with π. The procedure integrating the filter strategy and NEHT_LS is denoted as filter local search (FLS) in this research. The modified filter strategy first implements FLS, then determines if the makespan of the schedule generated by FLS dominates the best-so-far solution. If so, it will stop; otherwise, it will implement FLS one more time by using the filter strategy to find a solution different from the one found by the filter strategy in the first FLS.
2.3 Jump strategy
The main idea of the jump strategy is to guide the search to jump to another solution region when the search is trapped in a local optimum. We define the search trapped in a local optimum when the search is not able to improve the best-so-far solution in a number of iterations. The solution generated by the jump strategy is considered to be a new initial solution, and the search procedure is restarted.
The jump strategy proposed in this research first applies the Destruction and Construction Operation [16] to the detected local optimum m times to generate m new solutions. The solution with the minimum makespan, which satisfies the following conditions: (i) the makespan is less than or equal to a pre-determined
objective-value distance and (ii) the job sequence of the solution is different from the job sequence of the local optimum, will be chosen and used as the new initial solution. The objective-value distance is defined to be the distance of a jump from the objective value of the current local best solution and is calculated by multiplying the objective value of the current local best solution with a parameter, jump rate. If none of the m solutions satisfies the conditions, the same procedure will be implemented until a solution is produced. In order to apply the Destruction and Construction Operation to a schedule, S, first randomly choose n1 jobs from
S and let the job sequence of the n1 jobs be s1 and the job sequence of the rest of the jobs in S be s2.Then,
insert the first job in s1 into the first position, the last position and the positions between every two
consecutive jobs in s2 and choose the sequence with the smallest makespan; repeat the same process until all
the n1 jobs in s1 are inserted in s2. In this research, n1 is defined to be the second parameter, denoted as DC-n1,
of the jump strategy, and the jump strategy is implemented three times in order to generate a new initial solution.
3. Computational Results
The well-known Taillard's test problems for PFSP-makespan [33] are used to evaluate the performance of BBLS. The test problems are composed of 12 different problem sets with different numbers of jobs (n) and different numbers of machines (m) and 10 instances are included in each problem set. Twelve instances, selecting the last instance from each of the 12 problem sets, denoted as Test1, are used to investigate the effects of the major components of HLBS: the filter strategy and the jump strategy. Note that the parameters defined for these components are: f-strategy, f-size, jump-rate and DC-n1 respectively. Therefore, experiments
will be designed based on the parameters to investigate the effects of the components. Then, BBLS with the best combination of the parameters will be applied to solve all the test problems, and its performance will be compared to two of the best heuristics, IGRIS and DDERLS [15], for PFSP-makespan under limited
computation times. Furthermore, Note that all the algorithms in this paper are coded in C language and executed on the Linux operating system.
The levels considered for the four major parameters of BBLS are: two levels are set for f-strategy: fs1 and
fs2; three levels are set for f-size: none, 10 and 20, where none refers to no filter strategy is applied; three
levels are set for jump-rate: none, 1.01 and 1.11, where none refers to no jump strategy is applied; three levels are set for DC-n1: 4, 5 and 6. The remaining factors of BBLS are the number of the solutions (M) constructed
in each iteration, the number of iterations without improvement for defining trapping at a local optimum and the termination criterion. The first two parameters are determined by trial-and-error and set to be the number of machines (m) of the instances solved, and the execution time, like most of the other researches, is chosen to be the termination criterion. Therefore, there are a total of 54 different combinations of the four parameters.
The BBLS is applied with each of the 54 combinations to solve the 12 instances in Test1 with limited computation times, n×(m/2)×30 milliseconds [15], for three trials (executed on an Intel Xeon CPU X3220 2.4GHz PC). The Average Relative Performance (ARP) is used to measure the performance of the BBLS. The
formula of ARP is as follows:
3 1 3 / ) 100 ( i sol sol i Best Best solutionARP ; given an instance, solutioni is the
makespan obtained by trial i of the HLBS with a combination of the parameters for the instance, and Bestsol is
the best makespan that all the research has found for the instance provided by Zobolas et al. [28]
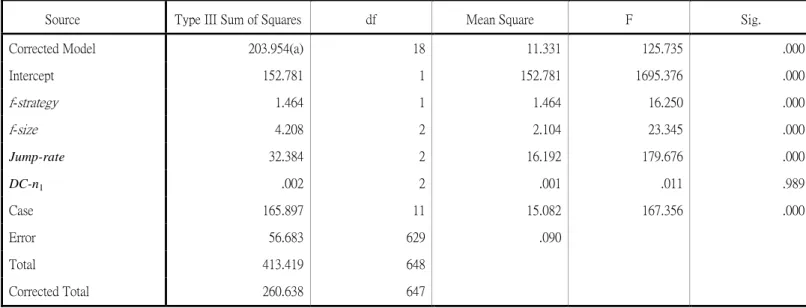
The analysis of variance (ANOVA) is applied to analyze the ARPs produced. Table 1 presents the results of the ANOVA table. The results show that all the parameters, except DC-n1, significantly affect the ARP of the
test problems. Therefore, the Duncan’s test is applied to test all the significant parameters. Table 2
summarizes the results of the Duncan tests: the minimum average ARP for each parameter is: f-strategy = fs1,
f-size = 20, jump-rate = 1.01 and DC-n1 = 5. This condition is same as the condition that generates the best
Table 1 ANOVA table for testing the significance of the four factors
Source Type III Sum of Squares df Mean Square F Sig.
Corrected Model 203.954(a) 18 11.331 125.735 .000
Intercept 152.781 1 152.781 1695.376 .000 f-strategy 1.464 1 1.464 16.250 .000 f-size 4.208 2 2.104 23.345 .000 Jump-rate 32.384 2 16.192 179.676 .000 DC-n1 .002 2 .001 .011 .989 Case 165.897 11 15.082 167.356 .000 Error 56.683 629 .090 Total 413.419 648 Corrected Total 260.638 647
(a): R Squared = .783 (Adjusted R Squared = .776)
Table 2 Results of Duncan’s test for the four major factors
f-strategy Average ARP
Subset
1 2 3
fs-1 .438 A
fs-2 .533 B
f-size Average ARP
Subset
1 2 3
20 .394 A
10 .395 A
none .612 B
Jump-rate Average ARP
Subset 1 2 3 1.01 .324 A 1.11 .329 A none .748 B DC-n1 Average ARP Subset 1 2 3 5 .457 A 4 .468 A 6 .476 A
BBLS with the best combination of the parameters is then applied to solve all the 120 test problems, and its performance is compared to that of IGRIS and DDERLS with n×(m/2)×30 milliseconds as the termination
criteria. All the heuristics were run on a PC with Intel Pentium IV at 2.8 GHz and same the number of replication runs (R=5) were executed for each heuristic on each test problem. Table 3 presents the average ARPs produced by IGRIS and DDERLS and BBLS for the twelve problem sets with each of the three
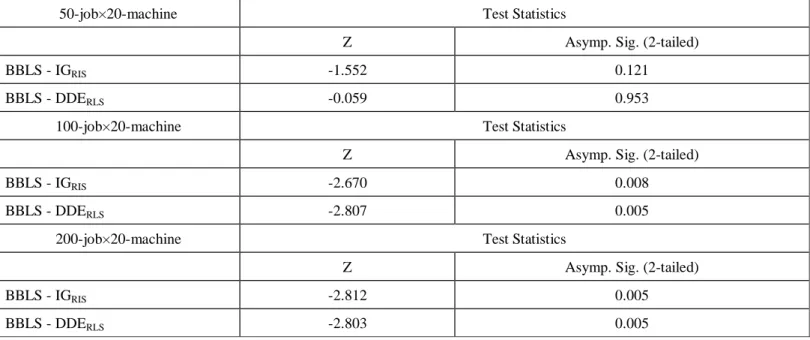
and DDERLS [9], BBLS was applied to solve the three hardest test sets in Taillard's test bank (ten
50-job×20-machine instances, ten 100-job×20-machine instances and ten 200-job×20-machine instances). Thirty trials were implemented for each instance, using n×(m/2)×150 milliseconds as the termination criteria, and the best solution was chosen to be the solution for the instance. A non-parametric test, Wilcoxon sum rank, is applied to compare the performance of DDERLS and BBLS on the hardest test sets. Table 4 summarizes the
results of the tests, and the results show that BBLS significantly dominates DDERLS on 100-job×20-machine
instances and 200-job×20-machine instances. This concludes that BBLS is the most effective heuristic for PFSP-makespan under limited computation times up to now. Several new ideas are studied to further improve the performance of BBLS.
Table 3 Computational Results of IGRIS, DDERLS and BBLS
Test Problems IGRIS DDERLS BBLS
20x5 0.04 0.04 0.02 20x10 0.01 0.01 0 20x20 0.01 0.02 0.03 50x5 0 0 0 50x10 0.46 0.45 0.47 50x20 0.63 0.66 0.77 100x5 0 0 0.01 100x10 0.17 0.15 0.12 100x20 1.04 0.98 0.97 200x10 0.09 0.07 0.04 200x20 0.96 0.99 0.96 500x20 0.47 0.49 0.47 Average 0.33 0.32 0.32
Table 4 Results of Wilcoxon Signed Ranks Test for IGRIS, DDERLS and BBLS
50-job×20-machine Test Statistics
Z Asymp. Sig. (2-tailed)
BBLS - IGRIS -1.552 0.121
BBLS - DDERLS -0.059 0.953
100-job×20-machine Test Statistics
Z Asymp. Sig. (2-tailed)
BBLS - IGRIS -2.670 0.008
BBLS - DDERLS -2.807 0.005
200-job×20-machine Test Statistics
Z Asymp. Sig. (2-tailed)
BBLS - IGRIS -2.812 0.005
Reference
1. Garey MR, Johnson DS, Sethi R (1976) The complexity of flowshop and jobshop scheduling. Mathematics of Operations Research 1(2):117-129
2. Chen CL, Vempati VS, Aljaber N (1995) An application of genetic algorithms for flow shop problems. European Journal of Operational Research 80(2):389-396
3. Chen, CL, Neppalli, VR, Aljaber, N (1996) Genetic Algorithms Applied to the Continuous Flow Shop Problem. Computers & Industrial Engineering, 30(4), 919-929
4. Ruiz R, Maroto C, Alcaraz J (2006) Two new robust genetic algorithms for the flowshop scheduling problem. Omega 34:461–47
5. Chen YM, Chen MC, Chang PC, Chen SH (2012) Extended artificial chromosomes genetic algorithm for permutation flowshop scheduling problems. Computers & Industrial Engineering 62(2):536–545
6. Stützle T (1998) An ant approach to the flow shop problem. In: Proceedings of the 6th European Congress on Intelligent Techniques & Soft Computing, Aachen, Germany 3:1560-1564
7. Rajendran C, Ziegler H (2004) Ant-colony algorithms for permutation flowshop scheduling to minimize makespan/total flowtime of jobs. European Journal of Operational Research 155(2):426–438
8. Ying KC, Liao CJ (2004) An ant colony system for permutation flow-shop sequencing. Computers & Operations Research 31(5):791-801
9. Lian Z, Gu X, Jiao B (2006) A similar particle swarm optimization algorithm for permutation flowshop scheduling to minimize makespan. Applied Mathematics and Computation 175(1):773–785
10. Liao CJ, Tseng CT, Luarn P (2007) A discrete version of particle swarm optimization for flowshop scheduling problems. Computers & Operations Research 34(10):3099-3111
11. Kuo IH, Horng SJ, Kao TW, Lin TL, Lee CL, Terano T, Pan Y (2009) An efficient flow-shop scheduling algorithm based on a hybrid particle swarm optimization model. Expert Systems with Applications 36(3):7027–7032
12. Zhang J, Zhang C, Liang S (2010) The circular discrete particle swarm optimization algorithm for flow shop scheduling problem. Expert Systems with Applications 37:5827–5834
13. Andreas N, Omirou S (2006) Differential evolution for sequencing and scheduling optimization. Journal of Heuristics 12(6):395-411
14. Onwubolu G, Davendra D (2006) Scheduling flow shops using differential evolution algorithm. European Journal of Operational Research 171(2):674-692
15. Pan QK, Tasgetiren MF, Liang YC (2008) A Discrete differential evolution algorithm for the permutation flowshop scheduling problem. Computers & Industrial Engineering 55(4):795-816
16. Ruiz R, Stützle T (2007) A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. European Journal of Operational Research 177(3):2033-2049
17. Stützle T (1998) Applying iterated local search to the permutation flowshop problem. Technical Report, AIDA-98-04, FG Intellektik, TU Darmstadt.
18. Osman I, Potts C (1989) Simulated annealing for permutation flow shop scheduling. Omega 17(6):551-557
19. Ogbu F, Smith D (1990) The application of the simulated annealing algorithm to the solution of the n/m/Cmax flowshop problem. Computers & Operations Research 17(3):243-253
20. Lin SW, Ying KC (2011) Minimizing makespan and total flowtime in permutation flowshops by a bi-objective multi-start simulated-annealing algorithm. Computers & Operations Research doi:10.1016/j.cor.2011.08.009.
21. Widmer M, Hertz A (1989) A new heuristic method for the flow shop sequencing problem. European Journal of Operational Research 41(2):186-193
22. Reeves CR (1993) Improving the efficiency of tabu search for machine sequencing problem. Journal of the Operational Research Society 44(4):375–382
23. Nowicki E, Smutnicki C (1996) A fast tabu search algorithm for the permutation flowshop problem. European Journal of Operational Research 91:160-175
24. Watson JP, Barbulescu L, Whitley LD, Howe AE (2002) Contrasting structured and random permutation flowshop scheduling problems: Search space topology and algorithm performance. ORSA J Comput 14(2):98-123
25. Grabowski J, Wodecki M (2004) A very fast tabu search algorithm for the permutation flowshop problem with makespan criterion. Computers & Operations Research 31(11):1891-1909
26. Qian B, Wang L, Hu R, Wang WL, Huang DX, Wang X (2008) A hybrid differential evolution method for permutation flow-shop scheduling. International Journal of Advanced Manufacturing Technology 38:757-777
27. Laha D, Chakraborty UK (2009) An efficient hybrid heuristic for makespan minimization in permutation flow shop scheduling. International Journal of Advanced Manufacturing Technology 44:559-569
28. Zobolas GI, Tarantilis CD, Ioannou G (2009) Minimizing makespan in permutation flow shop scheduling problems using a hybrid metaheuristic algorithm. Computers & Operations Research 36(4):1249-1267 29. Liu YF, Liu SY (2011) A hybrid discrete artificial bee colony algorithm for permutation flowshop
scheduling problem. Applied Soft Computing doi:10.1016/j.asoc.2011.10.024
30. Framinan J, Gupta JND, Leisten R (2004) A review and classification of heuristics for the permutation flowshop with makespan objective. Journal of the Operational Research Society 55:1243–1255
31. Hejazi SR, Saghafian S (2005) Flowshop scheduling problems with makespan criterion: a review. International Journal of Production Research 43(14):2895–2929
32. Ruiz R, Maroto C (2005) A comprehensive review and evaluation of permutation flowshop heuristics. European Journal of Operational Research 165:479–494.
33. Taillard E (1993) Benchmarks for basic scheduling problems. European Journal of Operational Research 64(2):278-285
34. Tzeng YR, Chen CL, Chen CL (2012) A hybrid EDA with ACS for solving permutation flow shop scheduling. International Journal of Advanced Manufacturing Technology 60:1139-114
35. Taillard E (1990) Some efficient heuristic methods for the flow shop sequencing problem. European Journal of Operational Research 47(1):65–74
36. Dorigo M, Gambardella LM (1997) Ant colony system: a cooperative learning approach to the travelling salesman problem. IEEE Transactions on Evolution Computing 1:53–66
37. Grabowski J, Pempera J (2001) New block properties for the permutation flow shop problem with application in tabu search. Journal of the Operational Research Society 52:210-220
38. Jin F, Song SJ, Wu C (2007) An improved version of the NEH algorithm and its application to large-scale flow-shop scheduling problems. IIE Transactions 39:229-234
39. Gao S, Zhang W (2007) An efficient approach to simplify the calculation of makespan in permutation flow shop scheduling problem. International Journal of Advanced Manufacturing Technology 35:325–332
科技部補助計畫衍生研發成果推廣資料表
日期:2015/10/30科技部補助計畫
計畫名稱: 開發一個以區塊特性為基礎的啟發式演算法求解流程式排程問題 計畫主持人: 陳春龍 計畫編號: 103-2221-E-004-002- 學門領域: 作業研究無研發成果推廣資料
103年度專題研究計畫研究成果彙整表
計畫主持人:陳春龍 計畫編號: 103-2221-E-004-002-計畫名稱:開發一個以區塊特性為基礎的啟發式演算法求解流程式排程問題 成果項目 量化 單位 備註(質化說明 :如數個計畫共 同成果、成果列 為該期刊之封面 故事...等) 實際已達成 數(被接受 或已發表) 預期總達成 數(含實際 已達成數) 本計畫實 際貢獻百 分比 國內 論文著作 期刊論文 0 0 100% 篇 研究報告/技術報告 0 0 100% 研討會論文 0 0 100% 專書 0 0 100% 章/本 專利 申請中件數 0 0 100% 件 已獲得件數 0 0 100% 技術移轉 件數 0 0 100% 件 權利金 0 0 100% 千元 參與計畫人力 (本國籍) 碩士生 0 0 100% 人次 博士生 0 0 100% 博士後研究員 0 0 100% 專任助理 0 0 100% 國外 論文著作 期刊論文 0 1 100% 篇 研究報告/技術報告 0 0 100% 研討會論文 0 0 100% 專書 0 0 100% 章/本 專利 申請中件數 0 0 100% 件 已獲得件數 0 0 100% 技術移轉 件數 0 0 100% 件 權利金 0 0 100% 千元 參與計畫人力 (外國籍) 碩士生 0 0 100% 人次 博士生 0 0 100% 博士後研究員 0 0 100% 專任助理 0 0 100% 其他成果 (無法以量化表達之 成果如辦理學術活動 、獲得獎項、重要國 際合作、研究成果國 際影響力及其他協助 產業技術發展之具體 效益事項等,請以文 字敘述填列。) 無成果項目 量化 名稱或內容性質簡述 科 教 處 計 畫 加 填 項 目 測驗工具(含質性與量性) 0 課程/模組 0 電腦及網路系統或工具 0 教材 0 舉辦之活動/競賽 0 研討會/工作坊 0 電子報、網站 0 計畫成果推廣之參與(閱聽)人數 0