Nonlinear responses of degenerate two-level systems to intense few-cycle pulses

(1)

Nonlinear responses of degenerate two-level systems to intense few-cycle pulses

Kuninobu Nagaya, Chaoyuan Zhu, and Sheng Hsien Lin

Citation: The Journal of Chemical Physics 127, 094304 (2007); doi: 10.1063/1.2767260 View online: http://dx.doi.org/10.1063/1.2767260

View Table of Contents: http://scitation.aip.org/content/aip/journal/jcp/127/9?ver=pdfcov Published by the AIP Publishing

Articles you may be interested in

A search for the sulphur hexafluoride cation with intense, few cycle laser pulses J. Chem. Phys. 139, 194302 (2013); 10.1063/1.4830222

Communication: Ionization and Coulomb explosion of xenon clusters by intense, few-cycle laser pulses J. Chem. Phys. 133, 061101 (2010); 10.1063/1.3469821

Field-free molecular orientation with terahertz few-cycle pulses J. Chem. Phys. 132, 244311 (2010); 10.1063/1.3458913

Experimental control of excitation flow produced by delayed pulses in a ladder of molecular levels J. Chem. Phys. 125, 014301 (2006); 10.1063/1.2203629

Analysis of adiabatic passage by light-induced potentials with chirped laser pulses in three- and four-level diatomic systems

J. Chem. Phys. 124, 024320 (2006); 10.1063/1.2150435

(2)

Nonlinear responses of degenerate two-level systems to intense

few-cycle pulses

Kuninobu Nagayaa兲

Institute of Atomic and Molecular Sciences, Academia Sinica, P.O. Box 23-166, Taipei 106, Taiwan Chaoyuan Zhub兲

Department of Applied Chemistry, National Chiao-Tung University, Hsinchu 300, Taiwan; Institute of Molecular Science, National Chiao-Tung University, Hsinchu 300, Taiwan; and Center for Interdisciplinary Molecular Science, National Chiao-Tung University, Hsinchu 300, Taiwan

Sheng Hsien Lin

Institute of Atomic and Molecular Sciences, Academia Sinica, P.O. Box 23-166, Taipei 106, Taiwan 共Received 30 April 2007; accepted 5 July 2007; published online 4 September 2007兲

Population transfers in degenerate 共or almost degenerate兲 two-level systems interacting with the few-cycle laser pulse are investigated. A simple and analytical formula of nonadiabatic transition probability is derived with completely degenerate condition, demonstrating the sensitive dependence of the transition probability on the phase of the few-cycle pulses. As one of the applications of this formula, a new way of controlling the nuclear wave packet dynamics at a potential curve crossing by 1 cycle laser pulse is proposed. © 2007 American Institute of Physics. 关DOI:10.1063/1.2767260兴

I. INTRODUCTION

Active control and manipulation of molecular processes and chemical dynamics by laser fields have been at the fore-front of research for both chemistry and physics over the last couple of decades. The recent remarkable progress in laser technology has led to new possibilities to control molecule transitions. Control algorithms involve in manipulation of the phase and intensity of laser pulses including Rice-Tannor pump-dump scheme,1 Brumer-Shapiro coherent control scheme,2optimal control scheme,3,4 adiabatic rapid passage scheme,5–7and periodic sweeping of laser parameters.8

Recent advances of laser technology have made it pos-sible to generate intense laser pulses shorter than 10 fs.9 Un-like the conventional laser pulses, these pulses contain only few optical cycles. Therefore, it is expected that the phenom-ena induced by such the few-cycle laser pulses are sensitive to its phase. For examples, Chelkowski et al. have reported that angular distributions of the photoelectrons created by an intense few-cycle laser pulses clearly depend on the phase.10 Recently, Kamta et al. have shown strong phase dependences of enhanced ionization in asymmetric diatomic molecules such as HeH2+_{interacting with the few-cycle laser pulses.}11 In this paper, we report the population dynamics in de-generate 共or almost degenerate兲 two-level systems exposed to an intense few-cycle laser pulses. For a two-level system interacting with the continuous-wave 共cw兲 laser field F cos共␻t +␾兲, the population dynamics is well known as

Rabi oscillation.12 Under the rotating wave approximation, the transition probability P12 is described by a simple

for-mula P12= ⍀2 ⍀2₊_⌬2 sin 2

冉

冑

⍀ 2₊_⌬2 2 t

冊

, 共1兲

where ⍀=␮12F /ប denotes the Rabi frequency, ␮12 is the

transition dipole moment between the two levels, ⌬=␻ −␻12 is the detuning, and ␻12 is the resonance frequency

between the two levels. In this case, P12does not depend on

the phase␾ at all. In the case of a conventional long pulse F共t兲cos共␻t +␾兲 where F共t兲 is the envelope function, the tran-sition probability is derived with use of the semiclassical theory of the Rosen-Zener 共RZ兲-type nonadiabatic transition13–15 and the Floquet 共or dressed兲 state representation,16,17and it is given as8

P₁₂= 4p共1 − p兲sin2_␺_, _共2兲

where p is the nonadiabatic transition probability at one complex crossing point, and␺ is the phase difference accu-mulated between the two adiabatic Floquet states. In this case, P₁₂does not depend on␾either. Since Eqs.共1兲and共2兲 are valid for the cw laser fields and slowly varying long pulses, they cannot be applied to the few-cycle laser pulses. As there is no simple and analytical formula of transition probability for the few-cycle laser pulses, especially for 1 cycle laser pulse, we derive a simple formula of transition probability for two-level systems interacting with an intense 1 cycle laser pulse in this paper for the sake of the simplicity. Fortunately, when two-level system is completely degenerate we can derive an exactly analytical solution. As we know for nondegenerate two-level systems, we must utilize the semi-classical matrix propagation method14,15to obtain an analyti-cal formula of nonadiabatic transition probabilities. These a兲_{Permanent address: Science & Technology Systems, Inc., 1-20-1 Shibuya,}

Shibuya-ku, Tokyo 150-0002, Japan. Electronic mail: kuninobu.nagaya@st-systems.co.jp

b兲_{Electronic mail: cyzhu@mail.nctu.edu.tw}

THE JOURNAL OF CHEMICAL PHYSICS 127, 094304共2007兲

(3)

schemes have successfully been applied to the conventional long pulses along with the Floquet state representation.

This paper is organized as follows. In Sec. II, we derive a simple and analytical formula of nonadiabatic transition probability for degenerate 共or almost degenerate兲 two-level systems interacting with 1 cycle laser pulse. This formula consists of sin2 _{function, including the field amplitude,}

fre-quency, and phase of the 1 cycle pulse as parameters. This analytical formula is compared with the numerical solution of the time-dependent Schrödinger equation in Sec. III. Fur-thermore, as one of the applications of this formula, we pro-pose a new laser control of nonadiabatic dissociation dynam-ics of a diatomic molecule at a potential curve crossing, and agreement and limit of the formula are extensively analyzed as well. Concluding remarks are provided in Sec. IV.

II. THEORETICAL FRAMEWORK

In this section, we consider the interaction of the degen-erate 共or almost degenerate兲 two-level system with linearly polarized few-cycle laser pulses E共t兲. Throughout this paper, it is assumed that E共t兲 is defined as

E共t兲 =

再

E0E共t兲 for 0艋 t 艋 2tc 0 for t⬍ 0, t ⬎ 2tc,

冎

共3兲 E共t兲 = ␧共t兲cos关␻共t − tc兲 +␾兴, 共4兲 ␧共t兲 = ␧0sin2

冉

␲ 2tc t

冊

, 共5兲 and tc= n␲ ␻ , 共6兲

where E₀is the polarization vector共unit vector, 兩E₀兩=1兲, ␧共t兲 is the pulse envelope,␻ is the laser frequency,␾is the ab-solute phase of the laser pulse 共0艋␾⬍2␲兲, ␧0 is the peak

amplitude, and n is the number of the optical cycle. Equation

共3兲represents the n-cycle laser pulses. It is also assumed that there is a dipole-allowed transition between the two levels兩1典 and兩2典. Therefore, the Hamiltonian Hˆ for this system under the dipole approximation is given by

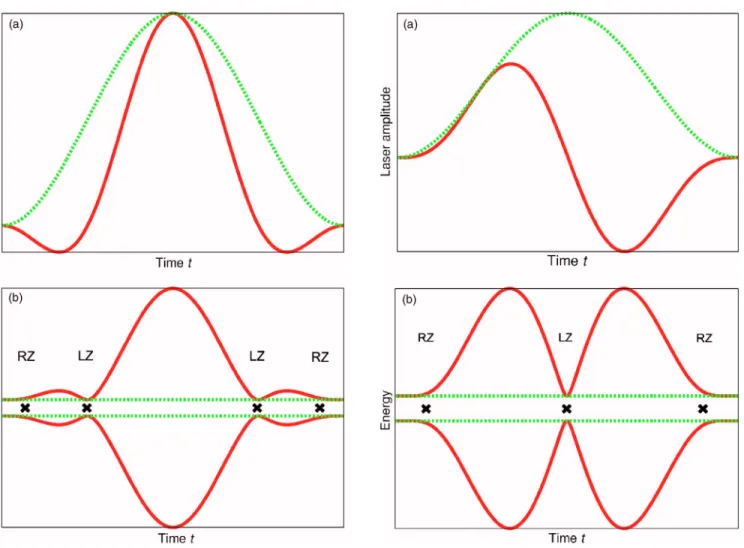
FIG. 1.共Color online兲共a兲 Time variation of the laser amplitude for 1 cycle pulse. The phase␾is fixed at 0.共b兲 Time variation of the energy levels for 1 cycle pulse shown in共a兲. Solid line, adiabatic energy levels; dotted line, energy levels ±ប␻12/ 2 of a field-free two-level system.⫻ denotes the times

when the LZ or RZ type nonadiabatic transitions are induced.

FIG. 2. 共Color online兲 The same as Fig.1but the phase␾is fixed at␲/ 2.

094304-2 Nagaya, Zhu, and Lin J. Chem. Phys. 127, 094304共2007兲

(4)

Hˆ =

冋

−ប␻12/2 −␮E共t兲 −␮E共t兲 ប␻12/2

册

, 共7兲

whereប␻₁₂denotes the energy spacing between兩1典 and 兩2典, and ␮=␮12· E0, where ␮12 is the transition dipole moment

between 兩1典 and 兩2典. Time-dependent Schrödinger equation for the two-level system in Eq.共7兲is given by18

iបd dt

冋

c₁共t兲 c2共t兲

册

= Hˆ

冋

c1共t兲 c2共t兲

册

. 共8兲

The scattering matrix is defined by

冋

c₁共+ ⬁兲 c2共+ ⬁兲

册

=

冋

S11 S12 S21 S22

册冋

c₁共− ⬁兲 c2共− ⬁兲

册

. 共9兲

The off-diagonal matrix element represents the overall nona-diabatic transition probability P₁₂=兩S₁₂兩2_{. In general, an}

ex-actly analytical solution cannot be obtained with Hamil-tonian in Eq.共7兲. However, if we take completely degenerate case in which␻12= 0, we can have

iបd

dt关c1共t兲 + c2共t兲兴 = ⌬共t兲关c1共t兲 + c2共t兲兴,

共10兲 iបd

dt关c1共t兲 − c2共t兲兴 = − ⌬共t兲关c1共t兲 − c2共t兲兴,

1 − 1 2共共␲/␻tc兲 + 1兲 + 1 2共共␲/␻tc兲 − 1兲

册

sin␻tccos␾. 共14兲

If cycles of laser pluses n艌2 in Eq. 共6兲, ⌿共n艌2兲=0. At 1 cycle laser pulse n→1, Eq. 共14兲turns to be

FIG. 3. 共Color online兲 Calculated population dynamics 共lower panel兲 of a degenerate two-level system 共␻12= 0 cm−1,␮= 1.0 a.u.兲 interacting with 1 cycle

pulse共upper panel: ␧0= 0.009 a.u.,␻= 2000 cm−1兲 against time t. 共a兲␾= 0 and共b兲␾=␲/ 2.

094304-3 Nonlinear responses of two-level systems J. Chem. Phys. 127, 094304共2007兲

(5)

⌿ =␲兩␮兩␧0

2ប␻ cos␾. 共15兲

The overall nonadiabatic transition probability is

P12= sin2

冉

␲兩␮兩␧0

2ប␻ cos␾

冊

. 共16兲

The condition for the population inversion reads

FIG. 4. 共Color兲 Transition probabilities P12for a degenerate two-level

sys-tem共␻12= 0 cm−1,␮= 1.0 a.u.兲 interacting with 1 cycle pulse as a function

of␻and␧0.关共a兲 and 共b兲兴 Numerical solutions and 关共c兲 and 共d兲兴 analytical

formula, Eq.共16兲.␾is set to 0.

FIG. 5. 共Color兲 Transition probabilities P12for a degenerate two-level

sys-tem共␻12= 0 cm−1,␮= 1.0 a.u.兲 interacting with 1 cycle pulse as a function

of␻and␾.关共a兲 and 共b兲兴 Numerical calculations and 关共c兲 and 共d兲兴 analytical formula, Eq.共16兲.␧₀is fixed at 0.01 a.u.

(6)

兩␮兩␧0

ប␻ cos␾= 1 + 2n共n = 0,1,2, ... 兲. 共17兲

Let us define the pulse area of 1 cycle pulse in the same way as the conventional long pulses:

pulse area =兩␮兩 ប

冕

0

2tc

␧共t兲dt = ␲兩␮兩␧0

ប␻ . 共18兲

From Eqs. 共17兲 and 共18兲, the minimum pulse area for the population inversion is␲/ cos␾, which is equal to or larger than␲. We note that it is impossible to make the pulse area smaller than ␲. This is the same as the conventional long pulse case.

It should be emphasized that for degenerate two-level system, only 1 cycle laser pulse gives nonzero transition for the two-level systems. For the nondegenerate system ␻12

⫽0, Eq.共8兲cannot be solved exactly in the analytical form, and the semiclassical propagation method has to be em-ployed to derive analytical nonadiabatic transition probabil-ity. We briefly discuss semiclassical procedure for two rep-resentative cases, as shown in Figs. 1 and 2. We show the pulse envelope ␧共t兲 and the electric field E共t兲 with␾= 0 in Eq.共4兲as a function of time for the 1 cycle pulse in Fig.1共a兲 and depict the adiabatic energy levels in Fig.1共b兲 in which there are four complex crossing points关see ⫻ in Fig. 1共b兲兴 where nonadiabatic transitions are taken place; the two out-ermost transitions are well described by RZ-type nonadia-batic transitions,13–15 and the two inner transitions are Landau-Zener 共LZ兲-type nonadiabatic transitions.14,15,19,20 Next we consider the case that electric field E共t兲 in Eq. 共4兲

with ␾=␲/ 2 shown in Fig. 2共a兲 and depict the adiabatic energy levels in Fig. 2共b兲 in which there are three complex crossing points关see ⫻ in Fig.2共b兲兴 where nonadiabatic tran-sitions are taken place; the outermost two are the RZ-type transitions and the central transition is the LZ-type transition. Based on those complex crossing points, we can derive over-all nonadiabatic transition probability semiclassicover-ally, and its results are the same as those obtained in Eq.共16兲for 1 cycle laser pulse with degenerate two-level system. We will dis-cuss more details for nondegenerate two-level systems in the future publication. Furthermore, the above formulation can also be extended to the general m-level systems共m⬎2兲.21In the next section, we demonstrate the validity of Eq.共16兲by comparing it with the numerical solution of the time-dependent Schrödinger equation 共8兲. Equation 共16兲 is also applied to a new laser control of the nuclear wave packet dynamics at a potential curve crossing.

III. RESULTS AND DISCUSSIONS

A. Numerical demonstrations of Equation_„16…

In this section, for the degenerate共or almost degenerate兲 two-level systems interacting with 1 cycle laser pulse, we compare the analytical formula in Eq.共16兲with the numeri-cal solutions of the time-dependent Schrödinger equation共8兲 in which ck共t兲 denotes the probability amplitude of the level

兩k典, and Eq.共8兲is solved in terms of the conventional fourth-order Runge-Kutta method.22 Throughout this section, we assume␮= 1ea0with initial condition c1共0兲=1 and c2共0兲=0.

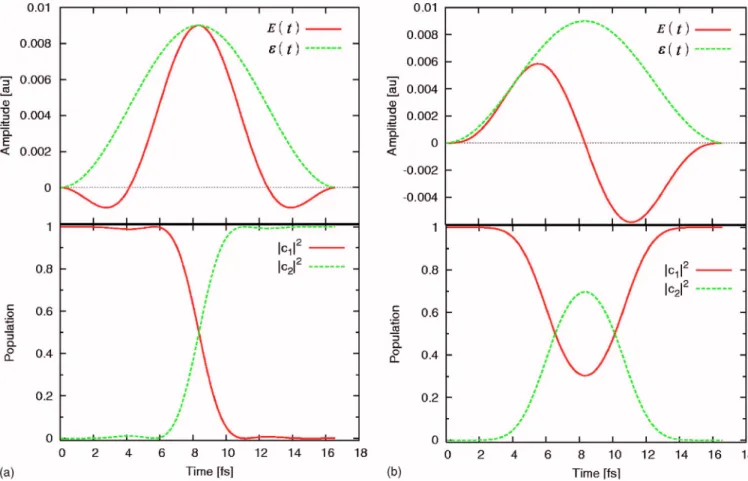
In Fig.3, the time evolution of the populations in a degen-erate two-level system共␻12= 0兲 under 1 cycle laser pulse is

plotted for共a兲␾= 0 and共b兲 ␾=␲/ 2. The peak amplitude␧0

and frequency␻of the 1 cycle pulse are fixed at 0.009 a.u. and 2000 cm−1_{. Since} _兩_␮_兩␧

0/共ប␻兲 is equal to 0.99, the

con-dition of P12= 1, i.e., Eq. 共17兲is almost satisfied in the case

of ␾= 0. As the analytical solution predicts, the calculation result for␾= 0 clearly indicates the population inversion. On the other hand, in the case of␾=␲/ 2, although some popu-lation is transferred into 兩2典 in the middle of the pulse, no population remains in 兩2典 at the end of the pulse, which is also the same as the analytical prediction.

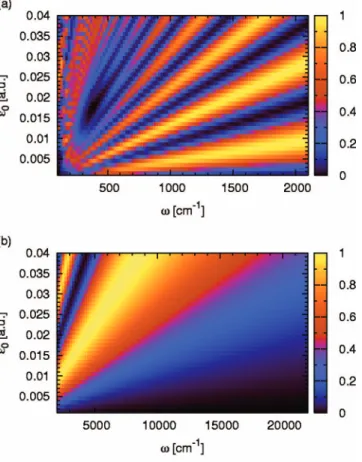
Two-dimensional plots of the transition probability are depicted against␻and␧0in Fig.4. The phase␾is fixed at 0.

As is easily found from Eq. 共17兲, the population inversion takes place when the linear relation ␧0=ប␻共1+2n兲/兩␮兩 is

satisfied. This is clearly seen in Fig. 4. The numerical solu-tions completely agree with the analytical solution in a very wide range of laser parameters. As the laser frequency be-comes larger, larger peak amplitudes are necessary for the population inversion. In Fig.5, two-dimensional plots of the transition probability are shown as a function of ␻ and␾. The peak amplitude ␧0 is set to 0.01 a.u.. In this case, we

also see that the numerical solutions are in perfect agreement with the analytical solution. It is noted that the transition probability is periodic as a function of ␾at the intervals of

␲/ 2 and the complete inversion takes place unless ␾=␲/ 2 共3␲/ 2兲. So far, we consider a degenerate two-level system. However, Eq. 共16兲 is also valid for an almost degenerate two-level system. In Fig.6, we show the population dynam-ics of a two-level system with ␻₁₂= 500 cm−1 _{as a function}

of t for共a兲␾= 0 and共b兲␾=␲/ 2. The other laser parameters are the same as those used in Fig.3. We note that the popu-lation in兩2典 at the end of the pulse slightly deviates from Eq.

共16兲because of the nondegeneracy of the system. In Fig.7共a兲

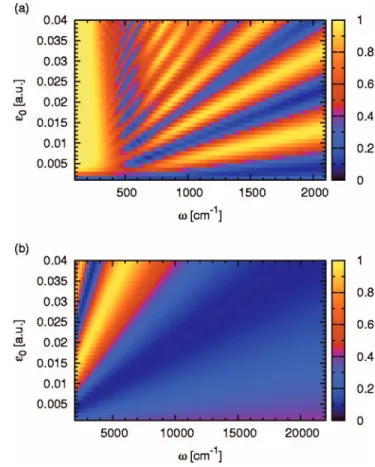
, two-dimensional plots of the calculated transition probabil-ity are depicted as a function of ␻ and␧0 共␻ and␾兲. The

laser parameters are the same as those used in Fig.4共a兲. The lower the laser frequency, the worse the agreement between the numerical and anlytical results becomes 关compare Figs.

7共a兲,7共b兲,8共a兲, and8共b兲with Figs.4共c兲,4共d兲,5共c兲, and5共d兲, respectively兴. At such low laser frequencies, we cannot re-gard the system as a degenerate two-level and thus it is nec-essary to derive semiclassical solution to model this situa-tion. It can be seen, however, that as the laser frequency becomes higher, the numerical solutions almost follow the analytical one in Eq. 共16兲. This is natural since the system can be regarded as degenerate two levels at the higher laser frequencies. In the next section, Eq. 共16兲 is applied to the wave packet dynamics at a potential curve crossing under a 1 cycle pulse. It is demonstrated that controlling molecular nonadiabatic dissociation by a 1 cycle pulse can be achieved.

B. Application to the control of the wave packet dynamics at a potential curve crossing by 1 cycle laser pulse

Here, 1 cycle laser pulse is shined to the propagating wave packet to control its dynamics at a potential curve

(7)

crossing. We treat a simple model of diatomic molecules which consist of two dissociative linear potential energy curves共PECs兲, V₁共R兲 and V₂共R兲, where

Vi共R兲 = Fi共R − RX兲 + EX 共i = 1,2兲, 共19兲

where R denotes the internuclear distance of diatomic mol-ecules, and F2⬍F1⬍0. At R=RX, these PECs cross, and we

have a LZ-type avoided crossing due to a diabatic potential coupling V12共R兲共see Fig.9兲. Let us consider a situation that

a Gaussian wave packet is placed at R = RI on V2共R兲 with its

initial momentum equal to zero. This wave packet propa-gates downward along V2共R兲 and bifurcates into two at RX

because of the diabatic potential coupling: one dissociates into channel 1 and the other into channel 2. The branching ratio depends on the coupling strength VX= V12共RX兲, ⌬F

=兩F1− F2兩, and the velocity␷X of the wave packet at RX

be-cause the dissociation probability into channel 2 is given by the LZ formula exp关−2␲VX2/共ប␷X⌬F兲兴. We propose a control

scheme to achieve selective dissociations into any one of the two channels with use of a 1 cycle laser pulse. The basic idea is as follows: when the wave packet reaches the crossing, the situation can be regarded as an almost degenerate two-level system. By applying 1 cycle laser pulse at the time when the

wave packet reaches the crossing, it may be possible to con-trol the wave packet transitions between the two states, lead-ing to selective dissociations. Under the Born-Oppenheimer and the dipole approximation, the Hamiltonian Hˆ of the sys-tem is given as18

Hˆ =

冋

Tˆ + V1共R兲 V12共R兲 −␮共R兲 · E共t兲 V₁₂共R兲 −␮共R兲 · E共t兲 _{Tˆ + V}₂_共R兲

册

,

共20兲 where Tˆ = −共ប2_{/ 2M兲共d}2_{/ dR}2_{兲 is the nuclear kinetic energy}

operator, M is the reduced mass of the system, ␮共R兲 is the transition dipole moment between V1共R兲 and V2共R兲, and E共t兲

is the electric field of 1 cycle laser pulse in Eq.共3兲. Through-out this paper, we assume the following: 共i兲 molecular rota-tions can be neglected, 共ii兲 molecules are aligned along the laser polarization 关␮共R兲//E0兴, and 共iii兲␮共R兲 is independent

of R. For the Hamiltonian Hˆ in Eq.共3兲, using the fast Fourier transformation and split operator method,18,23 we solve the time-dependent Schrödinger equation iប共⳵/⳵t兲⌿=Hˆ⌿, where ⌿=关␺1共R,t兲␺2共R,t兲兴t, ␺i共R,t兲 is the nuclear wave

function on Vi共R兲, and the superscript t denotes the matrix

transpose. The parameters of the system are given as follows: F1= −0.005 hartree/ a0, F2= −0.01 hartree/ a0, RX= 9.0a0,

EX= 0.15 hartree,␮= 1.0 e a0, and m = 20 amu. We assume a

Gaussian function for V12共R兲, i.e., V12共R兲=VXexp关−共R

− RX兲2兴, where VX= 0.001 hartree. The initial wave packet is FIG. 6.共Color online兲 Calculated population dynamics of an almost

degen-erate two-level system共␻12= 500 cm−1,␮= 1.0 a.u.兲 interacting with 1 cycle

pulse 共␧0= 0.009 a.u.,␻= 2000 cm−1兲 against time t. 共a兲 ␾= 0 and 共b兲 ␾

=␲/ 2.

FIG. 7. 共Color兲 Transition probabilities P12obtained by the numerical

cal-culations for an almost degenerate two-level system 共␻₁₂= 500 cm−1_, _␮

= 1.0 a.u.兲 interacting with a 1 cycle pulse as a function of␻and␧0.␾is set

to 0.

(8)

placed on V2共R兲, that is, ␺1共R,0兲=0 and ␺2共R,0兲

=共␲␴₀2兲−1/4_{exp关−共R−R}

I兲2/共2␴02兲兴. RI is set to 2a0 and ␴0

= 0.25a₀−1. Since this wave packet reaches the crossing around t = 173.4 fs, the center of 1 cycle pulse is set to tc

= 173.4 fs. The dissociation flux is integrated over time at R = 18a0to obtain the corresponding dissociation probability.

In order to prevent the unphysical reflection of the wave packet at the edge, the negative imaginary potential 共absorp-tion potential兲24

is set at R = 19a0. The grid sizes of t and

R are ␦t = 1.0 a.u. and ␦R = 0.0137a0, respectively. VX

= 0.001 hartree corresponds to an intermediate coupling strength, and thus the dissociation probability into the chan-nel 1 is close to one-half共P₁= 0.4206兲 in the field-free case. Figure 10 depicts P₁共wp兲共wave packet calculation results of the dissociation probability into channel 1兲 as a function of␻

and␧0of 1 cycle laser pulse.␾is fixed at 0. It is clearly seen

that P₁共wp兲drastically changes between 0 and 1. Thus, selec-tive dissociations into any one of the channel can be achieved by properly choosing␻and␧0. At the low

frequen-cies of␻艋400 cm−1_{, we note that P} 1

共wp兲_{is almost unity and}

does not depend on␻and␧₀. This is because 1 cycle pulse at such low frequencies does not change its amplitude during the passage of the wave packets around the crossing and the 1 cycle pulse acts as a strong static electric field, leading to the complete wave packet transfer from V₂共R兲 to V₁共R兲. On the other hand, at the higher frequencies of␻⬎400 cm−1, it can be seen that the population inversion takes place when some linear relation between ␧0 and␻is satisfied. We note

that the linear relation deviates a little from ␧0=ប␻

共1+2n兲/兩␮兩, which is found from the analytical solution in Eq.共16兲. This seems to be due to the fact that, in the case of wave packet dynamics, the transition induced by the nuclear motion also takes place. Equation 共16兲 does not take into account such transitions induced by the nuclear motion. Some scheme for treating both dependent and time-independent nonadiabatic transitions25 is necessary to fully understand the transition mechanism. In Fig. 11, P₁共wp兲 is shown as a function of␻and␾of 1 cycle laser pulse.␧0is

FIG. 8. 共Color兲 Transition probabilities P12obtained by the numerical

cal-culations for an almost degenerate two-level system 共␻12= 500 cm−1, ␮

= 1.0 a.u.兲 interacting with 1 cycle pulse as a function of ␻ and ␾. ␧₀ = 0.01 a.u.

FIG. 9.共Color online兲 A two-state model of diatomic molecules is depicted. The initial wavepacket is placed on V₂共R兲 at RI. When the wave packet

reaches the crossing of the potential energy curves at RX, 1 cycle laser pulse

is shined to control the branching ratio.

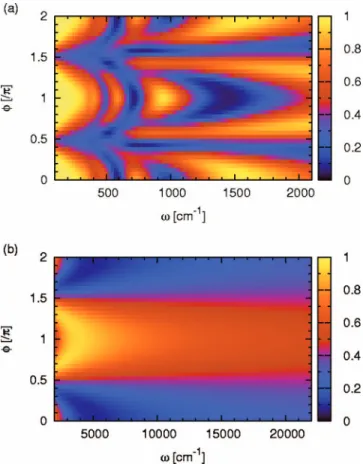
FIG. 10. 共Color兲 For the two-state system shown in Fig.9, the calculated dissociation probability into channel 1, P₁共wp兲, is plotted as a function of␻ and␧0of 1 cycle pulse.␾is set to 0.

(9)

set to 0.01 a.u.. At the low frequencies of␻⬍400 cm−1, as is mentioned above, P₁共wp兲 is almost unity except the case of

␾=␲/ 2 or 3␲/ 2 because 1 cycle pulse is regarded as a strong static electric field. At the higher frequencies, the be-havior of P₁共wp兲 is similar to but not the same as Eq. 共16兲关compare Figs.11共a兲and11共b兲with Figs.5共c兲and5共d兲兴. The discrepancies arise from the fact that Eq. 共16兲does not clude any transition induced by the nuclear motion. It is in-teresting to see that the behavior of P₁共wp兲 at ␾= 0 is com-pletely different from the one at ␾=␲. If we use 1 cycle pulse of ␻= 950 cm−1 _and_␧

0= 0.01 a.u., we can switch the

dissociation channel by changing only the phase␾. The dif-ferences between P₁共wp兲and Eq.共16兲in Figs.11may contain some information on the potential coupling at the crossing. For example, the coefficient k for the linear relation␧0= k␻

where the population inversion takes place strongly depends on the coupling strength. This might be useful for extracting such information.

IV. CONCLUDING REMARKS

A simple and analytical solution of nonadiabatic transi-tion probability for the degenerate 共or almost degenerate兲 two-level systems interacting with 1 cycle laser pulse has been derived. The probability depends on the peak ampli-tude, frequency, and phase of 1 cycle pulse. The population inversion is possible unless the phase is ␲/ 2 nor 3␲/ 2 by properly choosing both the amplitude and frequency. It has also been found that the minimum pulse area for the

popu-lation inversion never becomes smaller than␲. As one of the applications of this formula, the new way of controlling the nuclear motions of diatomic molecules at a potential curve crossing by 1 cycle laser pulse has been proposed. We have treated a simple two-state model, in which two dissociative PECs cross at a certain internuclear distance. In the field-free case, since the potential coupling strength at the crossing is intermediate, the dissociation probability into one channel is almost one-half. It has been demonstrated that selective nonadiabatic dissociations into any one of the two channels can be achieved by properly choosing the laser frequency, amplitude, and phase of the 1 cycle laser pulse. The applica-tion to the real system such as NaIwill be presented some-where. Although we have concentrated on 1 cycle laser pulse in this paper, the extensions of the present semiclassical scheme to the general n-cycle pulses 共n⬎1兲 and/or compli-cated systems with more than two levels are straightforward. Since the amplitude is larger and the pulse duration is longer than the 1 cycle pulse used in Fig.3, the population dynam-ics is much more complicated. However, the final transition probability is equal to unity. The general formula of the tran-sition probability for n-cycle pulses with nondegenerate two-level system will be reported in the near future.

ACKNOWLEDGMENTS

One of the authors共K. N.兲 would like to thank Academia Sinica for support and another author 共C.Z.兲 would like to thank National Chiao Tunng University for support. This work is partly supported by National Science Council of the Republic of China under Grant No. 95-2113-M-009-014.

1_{D. J. Tannor and S. A. Rice, J. Chem. Phys. 83, 5013}_共1985兲. 2_{P. Brumer and M. Shapiro, Annu. Rev. Phys. Chem. 43, 257}_共1992兲. 3_{R. Kosloff, S. A. Rice, P. Gaspard, S. Tersigni, and D. J. Tannor, Chem.}

Phys. 139, 201共1989兲.

4_{D. Neuhauser and H. Rabitz, Acc. Chem. Res. 26, 496}_共1993兲. 5_{J. S. Melinger, S. R. Gandhi, A. Haribaran, J. X. Tull, and W. S. Warren,}

Phys. Rev. Lett. 68, 2000共1992兲.

6_{S. Chelkowski and A. D. Bandrauk, J. Chem. Phys. 99, 4279}_共1993兲. 7_{Y. B. Band and P. S. Julienne, J. Chem. Phys. 97, 9017}_共1997兲. 8_{Y. Teranishi and H. Nakamura, J. Chem. Phys. 111, 1415}_共1999兲. 9_{T. Brabec and F. Krausz, Rev. Mod. Phys. 72, 545}_共2000兲.

10_{S. Chelkowski, A. D. Bandrauk, and A. Apolonski, Phys. Rev. A 70,}

013815共2004兲.

11_{G. L. Kamta and A. D. Bandrauk, Phys. Rev. Lett. 94, 203003}_共2005兲. 12_{R. W. Boyd, Nonlinear Optics}_{共Academic, New York, 1992兲.} 13_{N. Rosen and C. Zener, Phys. Rev. 40, 502}_共1932兲.

14_{C. Zhu, Y. Teranishi, and H. Nakamura, Adv. Chem. Phys. 117, 127}

共2001兲.

15_{H. Nakamura, Nonadiabatic Transition: Concepts, Basic Theories and}

Applications共World Scientific, Singapore, 2002兲.

16_{Molecules in Laser Fields, edited by A. D. Bandrauk}_{共Dekker, New York,}

1994兲.

17_{S. I. Chu, Advances in Multiphoton Processes and Spectroscopy}_共World

Scientific, Singapore, 1986兲, Vol. 2.

18_{B. M. Garraway and K. A. Suominen, Rep. Prog. Phys. 58, 365}_共1995兲. 19_{L. D. Landau, Phys. Z. Sowjetunion 2, 46}_共1932兲.

20_{C. Zener, Proc. R. Soc. London, Ser. A 137, 696}_共1932兲.

FIG. 11. 共Color兲 For the two-state system shown in Fig.9, the calculated dissociation probability into channel 1, P₁共wp兲, is plotted as a function of␻ and␾of 1 cycle pulse.␧0is set to 0.01 a.u.

(10)

21_{K. Nagaya, Y. Teranishi, and H. Nakamura, ACS Symp. Ser. 821, 98}

共2002兲.

22_{W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery,}

Nu-merical Recipes in Fortran: The Art of Scientific Computing, 2nd ed.

共Cambridge University Press, Cambridge, England, 1992兲.

23_{C. Leforestier, R. H. Besseling, C. Cerjan, M. D. Feit, R. Friesner, A.}

Guldberg, A. Hammerich, G. Jolicard, W. Karrlein, H. D. Meyer, N. Lipkin, O. Roncero, and R. Kosloff, J. Comput. Phys. 94, 59共1991兲.

24_{Á. Vibók, and G. G. Balint-Kurti, J. Chem. Phys. 96, 7615}_共1992兲. 25_{H. Nakamura, Chem. Phys. 295, 269}_共2003兲.