國
立
交
通
大
學
資訊科學與工程研究所
碩
士
論
文
在無線隨意網路上基於可自我驗證簽名系
統的安全的群組金鑰協議協定
A Secure Group Key Agreement Protocol with Self-Certified
Signature in Mobile Ad Hoc Networks
研 究 生:曾智暘
在無線隨意網路上基於可自我驗證簽名系統的安全的群組金鑰協議
協定
A Secure Group Key Agreement Protocol with Self-Certified Signature
in Mobile Ad Hoc Networks
研 究 生:曾智暘 Student:Chih-Yang Tseng
指導教授:曾文貴 Advisor:Wen-Guey Tzeng
國 立 交 通 大 學
資 訊 科 學 與 工 程 研 究 所
碩 士 論 文
A ThesisSubmitted to Institute of Computer Science and Engineering College of Computer Science
National Chiao Tung University in partial Fulfillment of the Requirements
for the Degree of Master
in
Computer Science June 2008
Abstract
A group key agreement protocol allows participants to cooperatively estab-lish a common session key which is used to encrypt or decrypt transmitted messages among them over an open network environment. In this paper we propose a secure group key agreement protocol based on the self-certified signature scheme which is suitable for the mobile ad hoc network environ-ment. Under the DDH assumption, the proposed protocol is demonstrated to be secure against passive adversaries. Under the random oracle model and DL assumption, the proposed protocol is demonstrated to be secure against active adversaries. Besides, our protocol provides forward secrecy and with-stands known-key attacks.
中文摘要
群組金鑰協議協定能讓一個群組中的參與者合作建立一個可在開放網路環境中加 密或解密訊息的對話金鑰。 在本論文中我們提出了一個基於可自我驗證簽名系統, 可適用於無線行動隨意網路上的安全的群組金鑰協議協定。 在DDH 假設下, 此協 定可抵抗被動的攻擊者。 而在 random oracle 模型與 DL 假設下, 此協定可抵抗 主動的攻擊者。 此外,我們設計的協定還提供了向前安全性以及能夠抵抗已知金鑰 的攻擊。誌 謝
在此感謝我的指導老師曾文貴教授, 在我碩士班的學習過程中帶領著我進入了密 碼學與資訊安全的領域。 老師不只在學業與研究上使我獲益良多,更在生活以及言 行舉止方面給予我許多鼓勵與指導。 另外, 我要感謝口試委員, 交大資工蔡錫鈞教 授、 謝續平教授,以及中研院資科所呂及人教授,給予我許多論文上的建議與指導, 使得內容更臻完善。 除此之外,我要感謝實驗室的成康學長、 煥宗學長以及孝盈學 姊給予我的建議與指導, 實驗室同學宣佐、 怡翔、 翎恩、 宏達、 慈潔與學弟們在這 段期間所給予的幫助以及精神上的支持與鼓勵。 最後, 我要感謝我的家人, 在我碩 士班的這段時間,無論是在精神上或物質上都給我最大的支持,讓我可以在無後顧 之憂的情況下完成學業。 在此,謹以此文獻給所有該感謝的。Table of Contents
1 Introduction 1
1.1 Related Work . . . 4
2 Preliminaries 11 2.1 (t, n)-threshold Secret Sharing Scheme . . . 11
2.2 Bilinear Map . . . 12
2.3 Proof of Equal Logarithm . . . 12
3 Background and Security Model 14 3.1 Definition of the Problem . . . 14
3.2 Assumption . . . 15 3.3 Adversary Model . . . 15 3.4 Security Requirement . . . 16 3.5 Notations . . . 17 4 Our Scheme 18 4.1 Overview . . . 18
4.2 Self-Certified Signature Scheme . . . 19
4.2.1 Key Generation Phase . . . 19
4.2.2 Registration Phase . . . 20
4.2.4 Verification Phase . . . 21
4.2.5 Join Phase . . . 22
4.2.6 Leave Phase . . . 23
4.3 Group Key Agreement . . . 24
4.3.1 Initialization Phase . . . 24
4.3.2 Join Phase . . . 25
4.3.3 Leave Phase . . . 26
5 Security Analysis 28 5.1 Security against Passive Adversary . . . 29
5.2 Security against Active adversary . . . 30
5.3 Other Security Properties . . . 33
6 Performance Analysis 35 6.1 Initialization . . . 35 6.2 Join . . . 36 6.3 Leave . . . 36 7 Conclusions 38 Bibliography 40
List of Figures
1.1 CKDS setup . . . 5 1.2 Message flow in GDH.2 . . . 6 1.3 Message flow in A-GDH.2 . . . 7
List of Tables
3.1 Notations . . . 17
Chapter 1
Introduction
Recently, mobile computing and wireless communication technology have significant advances. Mobile devices have gained more powerful com-munication and computation capability and sufficient memory resources. A mobile ad hoc network (MANET) is formed with some mobile devices and this kind of networks differentiate themselves from traditionally existing net-works by the fact that they rely on no fixed infrastructures [15]. Instead, nodes rely on each other to keep the network connected. Mobile nodes that are within each other’s transmission range can communicate directly via wire-less links, while those that are far apart rely on other nodes to relay messages as routers [24]. Because there is no fixed infrastructure in an ad hoc network, all network functions have to be performed by the nodes in it.
Each mobile node in a MANET can move unrestrictedly so that the topology of the network changes very rapidly. Node mobility and wireless connectivity allow nodes to spontaneously join and leave the network. This characteristic is called dynamic topology. Usually mobile nodes are small hand-held devices which cannot be locked up in a secure region and therefore they are easily compromised by either being lost or stolen. Due to this reason,
MANETs cannot rely on any form of central authority to avoid a single point failure. A MANET which does not rely on any form of offline trusted third party (TTP) is self-organized; however, a distributed online TTP can exist [15].
Authentication is an important issue in MANETs. Any nodes in the network have to be authenticated so that no others can impersonate them. Without a robust authentication mechanism in place, the remaining security objectives, for example confidentiality, data integrity, and non-repudiation, cannot be achieved. However, it is not easy to authenticate each node without the help of a trusted authority [15]. In the public key infrastructure (PKI), each user contains a certificate which binds the public key to the user identity. Each user can obtain the other’s public key by either querying its certificate or accessing to the certificate directory in the certification authority (CA). Then it checks the validity of the certificate and begins secure communication. In the identity-based (ID-based) infrastructure, the private key generation (PKG) authority is responsible for the generation of a user’s private key. After the private key is generated, PKG have to send it to the corresponding user via a secure channel. The identity of each user is the public key and can be used for encryption or signature verification.
In 1991, Girault introduced self-certified public keys (SCK) [12] which can be regarded as intermediate between the PKI and the ID-based infras-tructure. In SCK approach, a user chooses his private key, computes the corresponding public key, and sends the public key to the authority. The authority then computes certificate parameters for the user, which are com-putationally unforgeable given the public key and the identity of the user. A verifier can use the identity and the public keys to compute the certificate parameters. In SCK approach, the validity of a SCK is verified only after a
successful communication which is called implicit authentication. Compared to the PKI, it can provide an implicit validation of public keys. Compared to identity-based framework, there is no key escrow problems and secure channels problems in SCK approach.
As stated above, a trusted authority is still necessary in authentication and the authority should not suffer from single point failure. An intuitive and practical approach is to distribute the trust to each node in the network to form an online distributed authority. The most commonly used is threshold cryptography. An (t, n)-threshold cryptography scheme allows n parties to share the ability to perform a cryptographic operation, so that any t parties can perform this operation jointly, whereas it is infeasible for at most t − 1 parties to do so, even by collusion [24].
Due to the characteristic of no fixed infrastructure and it is easy to cap-ture any messages transmitted over a wireless network, it is usually necessary to establish a common group key in MANETs to secure group communica-tion. A common group key can be used to encrypt all the communication in a MANET so that only nodes in the MANET can use the corresponding decryption key to decrypt the messages they receive. Besides, due to the char-acteristic of dynamic topology, Join and Leave procedures are needed to cope with join or leave of nodes. The establishment of a group key in MANETs is similar to that of a so-called conference key in traditional networks with infrastructure, however, a proper and secure authentication scheme should be considered.
There are two types of group key establishment protocols which allow participants to establish a common session key for encrypting their commu-nication over an insecure network. The first type is group key distribution protocol in which a chairman selects a key and distributes it to the
partici-pants. The group key established in this type of protocols is pre-distributed and fixed, and compromise of the a priori secret of any participant breaches the security of all past group keys, thus failing to provide forward secrecy. The second type is group key agreement protocol in which a group key is computed by all participants without a chairman. The group key established in this type of protocols is dynamic and different for each session, and no one can predetermine the group key.
In this paper, we propose a secure group key agreement protocol in MANETs. In this protocol we use a self-certified signature scheme for entity authentication. Since the terms “group key” and “conference key” have the same purpose, we will use them alternately in the following sections.
1.1
Related Work
In 1976, Diffie and Hellman [10] proposed a key establishment protocol which enabled two participants to establish a common key using their own se-cret information and some other publicly exchanged information. After that, there have been efforts to extend two-party Diffie-Hellman key exchange to group setting [13, 8, 19]. Ingemaresson et al. [13] proposed the first confer-ence key establishment protocol which is denoted conferconfer-ence key distribution
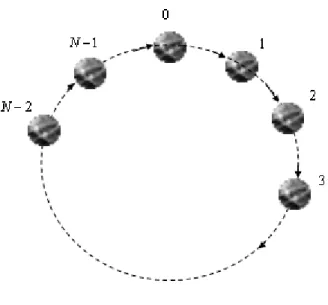
system, CKDS. In this system, the nodes who want to participate in the
conference are connected in a ring so that node i always sends messages to node i + 1 and node n − 1 sends messages to node 0. Figure 1.1 shows this CKDS setting. Based on this setting, the authors proposed a CKDS of order 2 in the beginning and then generalized it to order j, 2 < j ≤ n. In their CKDS of order 2, the session key is a symmetric function of degree two which has the form gP0≤i,j≤n−1,i6=jrirj, where r
Figure 1.1: CKDS setup
randomly by node i. However, this particular system is insecure because the information exchanged by the nodes makes it possible for a passive adver-sary to compute the key. Besides, their system needs n − 1 rounds for all participants to establish a group key and hence it is very inefficient for large scale participants.
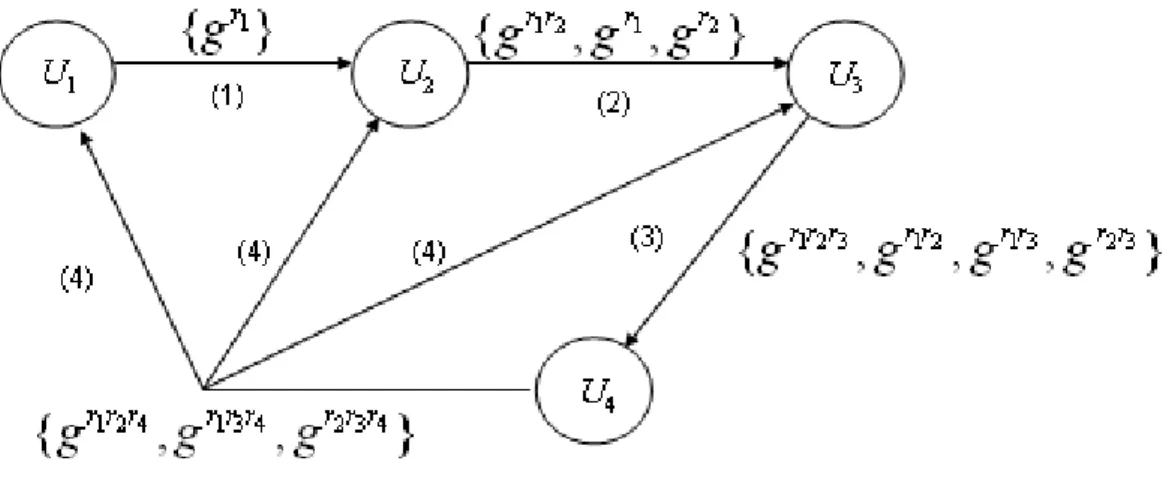
In [19], Steiner et al. extended the Diffie-Hellman key exchange to n-party case naturally. These key agreement protocols are GDH.1, GDH.2, and GDH.3. The main feature of these protocols is that they are all asyn-chronous protocols. This means that any participants can send messages whenever they like. The main drawback of GDH.1 is its relatively large number of rounds. It requires 2(n − 1) rounds for n participants. In order to reduce the number of rounds in GDH.1, the authors modified the protocol as GDH.2. An example of four participants is shown in Figure 1.2. The number marked on each edge stands for the order of the rounds. In GDH.2 it only requires n rounds to compute the common group key. However, in GDH.1
Figure 1.2: Message flow in GDH.2
and GDH.2 each participant Ui requires i + 1 exponentiations, and the
com-putational burden increases as the group size grows. In order to reduce the computational overhead of each participant, the authors proposed GDH.3. In GDH.3 it only requires constant exponentiations for all participants and has the same communicational efficiency as in GDH.2. The security of these three protocols is based on DH assumption.
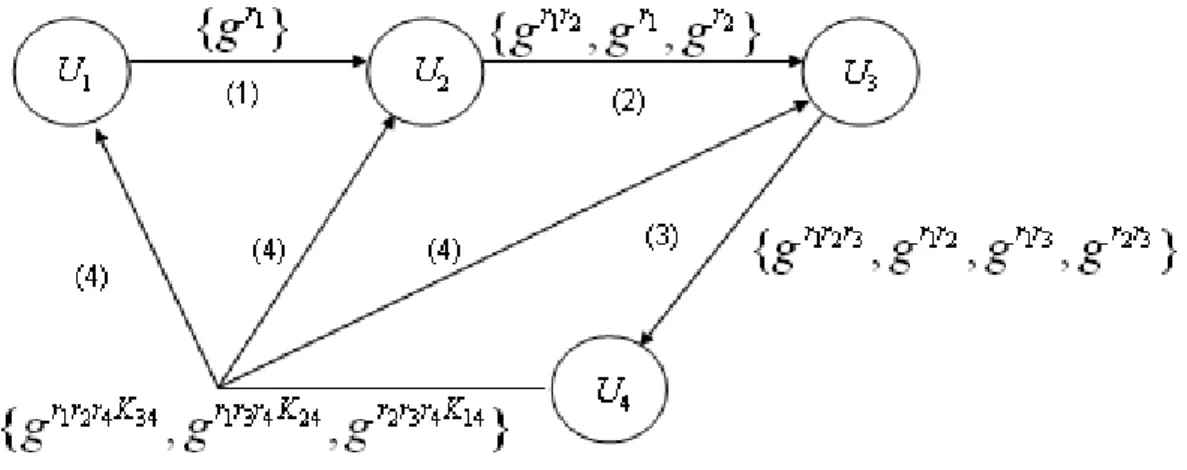
Although [19] deals with node join and node leave operations, it does not consider entity authentication. So it is not secure against active adversaries. In [1], Ateniese et al. modified GDH.2 in [19] and proposed authenticated GDH.2 (A-GDH.2) and strong authenticated GDH.2 (SA-GDH.2). In their schemes, before the protocol execution each pair of participants has to estab-lish a DH key which is used to provide entity authentication. In A-GDH.2, each participant Ui computes a DH key with Un, thus each pair of (Ui, Un)
can authenticate each other. However, if Un is not trusted, participants may
not agree on the same group key. An example of four participants is shown in Figure 1.3. The number marked on each edge stands for the order of the
Figure 1.3: Message flow in A-GDH.2
rounds. Essentially Figure 1.3 is the same as Figure 1.2 except that the last round messages contain long-term keys Kin in the exponents. SA-GDH.2
makes an arbitrary pair of (Ui, Uj), i 6= j, authenticate each other. Both
A-GDH.2 and SA-A-GDH.2 provide perfect forward secrecy (PFS) and resistance to passive known-key attacks. PFS is a property that ensures that compro-mise of a long-term key cannot result in the comprocompro-mise of past session keys and it is important in an authenticated group key agreement protocol. The member join and member leave procedures are also provided in A-GDH.2 and SA-GDH.2, and they are similar to those in GDH.2 except that each message in the broadcast flow contains long-term keys in the exponent.
In [6], Bresson et al. developed the first formal security model for an authenticated conference key agreement protocol. They model instances of players via oracles available to the adversary through queries. The queries are available to use at any time to allow modeling attacks involving mul-tiple instances of players activated concurrently and simultaneously by the adversary. The two modes of corruptions, which are weak-corruption model and strong-corruption model, are modeled. In the weak-corruption model, a
corruption only reveals the long-lived key (LL-key) of player U. However in the strong-corruption model, a corruption not only reveals the LL-key of U but also all internal data that his instances did not explicitly erase. In order to model these two modes of corruption, they consider the presence of two cryptographic devices, secure coprocessors and smart cards, which are made available to the adversary through queries. Before their work, there had been little formal security analysis [9, 18]. They modified the protocols in [7] and [5] to obtain a protocol which is referred to as AKE1+ secure against
strong corruptions. Their security theorem does not need a random oracle assumption [3] and thus holds in the standard model.
The above protocols mentioned are generalized from the Diffie-Hellman key exchange protocol. Burmester and Desmedt [8] presented a notable re-sult. They proposed several conference key agreement protocols based on var-ious types of network connections. In their broadcast channel based scheme, the session key is a cyclic function (of the indices of the users) of degree two which has the form gr1r2+r2r3+···+rnr1, where r
i ∈ [1, n] is a secret value chosen
randomly by node i. Their unauthenticated conference key agreement pro-tocol based on broadcast channel requires only two rounds and is very com-municational efficient. Based on the Diffie-Hellman (DH) assumption, their protocols are proven secure against a passive adversary. For data origin au-thentication they use an interactive public key auau-thentication scheme which is proven secure based on discrete logarithm (DL) assumption. Combining the interactive data origin authentication scheme with the unauthenticated conference key agreement protocol makes the conference key agreement pro-tocol provably secure against malicious active adversaries based on the DH assumption. However, [13] and [8] did not provide member join and member leave procedures.
In [2], Becker and Wille derived a lower bound of only one round for multi-party contributory key agreement protocols. However, no generalized Diffie-Hellman key exchange is able to meet this bound. They left as an open problem whether any contributory key agreement scheme can meet this bound. There are some group key agreement protocols [4, 23] proposed after Becker and Wille, and they only require constant rounds.
In [23], the authors proposed two group key agreement protocols which are proved to have fault-tolerance, correctness, fairness, authentication, and
no useful information leakage and require only one round. The main feature
of [23] is that non-interactive proof systems (NIPVS) and non-interactive proof systems with authentication (NIAPVS) are used. In their proposed protocols, fault-tolerance and authentication can be achieved by using either NIPVS and digital signature or NIAPVS. Their protocols are secure against passive and active adversaries under the random oracle model. They also modified Protocol 3 in [8] to obtain a protocol with fault-tolerance.
In [4], Boyd and Nieto pointed out that in [23] the session token (ST) is used to prevent replay attacks and unless the ST is agreed beforehand their protocols cannot be completed in one round. They proposed a protocol which requires only one round on the side. Their protocol is proved secure in Bellare and Rogaway’s model [3]. However, both [23] and [4] do not provide forward secrecy.
In [22] the author proposed a conference key agreement protocol with both forward secrecy and fault tolerance. Before this work, [14] proposed a protocol with forward secrecy and [21] proposed a protocol with fault toler-ance. However, [14] and [21] do not provide both forward secrecy and fault tolerance.
intro-duces some tools we use in our protocol. Chapter 3 describes the problem and the security requirements of a group key agreement protocol. Chapter 4 gives an overview and describes details of our secure group key agreement protocol. The security analysis and the performance analysis are discussed in Chapter 5 and Chapter 6. Finally, we give a conclusion and future works in Chapter 7.
Chapter 2
Preliminaries
In this chapter we introduce some tools used in our protocol.
2.1
(t, n)-threshold Secret Sharing Scheme
The goal of a secret sharing scheme is to share a secret s among n parties so that each one Pi keep a share si for 1 ≤ i ≤ n. A coalition of some of the
parties is able to recover s.
Shamir proposed a (t, n)-threshold secret sharing scheme in 1979 [16]. In their scheme a threshold t is set. Each t of the n shares are sufficient to recover s. It is impossible to do so from t − 1 or fewer shares. The scheme comprises two parts : secret sharing and secret recovery.
• Secret sharing :
Given a secret s ∈ Zq, a threshold t, and a number n, randomly select
a (t − 1)-degree polynomial f (x) = t−1 X i=1 aixi+ s (mod q)
and compute
si = f (i) (mod q)
as a share of Pi for 1 ≤ i ≤ n.
• Secret recovery :
Given t shares (i, si), s can be recovered by
s = t X i=1 (si· Y 1≤j≤t,j6=i j j − i) (mod q)
from the Lagrange’s interpolation formula.
2.2
Bilinear Map
Let G1 and G2 be two cyclic groups of order q for some large prime q.
Let ˆe be a mapping ˆe : G1 × G1 → G2. ˆe satisfies :
1. Bilinear: ˆ
e(aP, bQ) = ˆe(P, Q)ab for all P, Q ∈ G
1, a, b ∈ Zq.
2. Non-degenerate: ˆ
e does not map all pairs in G1× G1 to the identity in G2. Since G1, G2
are groups of prime order this implies that if P is a generator of G1
then ˆe(P, P ) is a generator of G2.
3. Computable:
There is an efficient algorithm to compute ˆe(P, Q) for all P, Q ∈ G1.
2.3
Proof of Equal Logarithm
In our group key agreement protocol we use non-interactive proof of knowledge of the common logarithm r of y = gr ∈ Z∗ and y = gr ∈ Z∗. It
is easy to convert an interactive proof into a non-interactive one. Thus, we first give the interactive version of the proof.
P roof LogEq(g1, y1, g2, y2) :
1. Prover chooses s ∈R Zq and computes a = (a1, a2) = (gs1, g2s). Prover
sends a to Verifier.
2. Verifier chooses c ∈RZq and sends c to Prover.
3. Prover computes b = s − cr and sends b to Verifier.
4. Verifier accepts if and only if a1 = g1by1c and a2 = gb2y2c.
• Completeness
If Prover knows r and both Prover and Verifier are honest, then a1 =
gb
1y1c and a2 = gb2y2c, and Verifier will accept.
• Soundness
If any cheating prover can convince Verifier with a probability greater than 1/q, it can find (a1, a2) such that two challenges c and c0 can be
answered. This results in computing r.
To obtain a non-interactive proof, we use the Fiat-Shamir heuristic [11]. Let h : {0, 1}∗ → Z
q be a collision-resistant hash function. We replace the
challenge c ∈ Zq from Verifier with c := h(g1||y1||g2||y2||a1||a2). So the
non-interactive proof P roof LogEq(g1, y1, g2, y2) = (c, b) is obtained. Verifier
Chapter 3
Background and Security
Model
In this chapter, we describe the group key agreement problem and the security requirement of a group key agreement protocol. We also consider the possible adversaries who want to obtain the information of the group key and the assumption in our protocol.
3.1
Definition of the Problem
The goal of a group key agreement protocol is to establish a group key securely. Each participant cannot obtain others’ secret values. Besides, each message transmitted has to be authenticated so that the participants can know who sends that message. Finally, each participant computes the same group key.
3.2
Assumption
Since we use (t, n)-threshold secret sharing scheme to share a master key s, any t participants can collude with each other to recover s. In this paper, we assume that at most t−1 participants can collude with each other.
3.3
Adversary Model
In this paper, we consider two types of adversaries : passive adversary and active adversary.
• Passive Adversary
A passive adversary can obtain information about the established group key by only eavesdropping on messages transmitted over the network. This kind of adversaries is also called eavesdropper.
• Active Adversary
Active adversaries can be classified into two kinds, one is impersonator and the other is malicious participant.
– The purpose of an impersonator is to impersonate a legitimate participant. If the impersonator successfully impersonate a le-gitimate participant, the others cannot distinguish a lele-gitimate message from a fake one.
– A malicious participant is a member of the group but he does not follow the protocol. He can send some error messages to disrupt the key establishment.
3.4
Security Requirement
• Correctness
Since the group key computed in a group key agreement protocol is de-termined by all of the participants, the protocol fails as long as anyone does not follow the protocol steps. So it is necessary to detect those who does not follow the protocol steps. After excluding those malicious participants, a common group key can be evaluated by each remaining honest participant.
• Privacy
Any eavesdroppers and malicious participants cannot obtain informa-tion about the group key by observing messages transmitted over the network. Besides, the information about the private values of each participant cannot leak out.
• Authentication
To defeat an impersonator, authentication mechanism is necessary. Al-though an impersonator can use messages transmitted by legitimate participants to produce new legitimate messages, he still cannot im-personate a legitimate participant if he cannot convince others.
• Robustness
To prevent a malicious participant, robustness is necessary. A mali-cious participant has to be excluded so that he cannot disrupt the key agreement protocol. After excluding those malicious participants, the common group key can be evaluated by each remaining honest partic-ipant.
3.5
Notations
We summarize the notations used in our protocol in Table 3.1.
Table 3.1: Notations Notation Description
Ui group participant with index i
q large prime number G1, G2 bilinear group of order q
ˆ
e bilinear map ˆe : G1× G1 → G2
P generator of G1 H hash function, H : G1 × {0, 1}∗× G1 → G1 F hash function, F : {0, 1}∗× G 2× G1 → Z∗q s master key of P KG, s ∈R Zq PP KG public key of P KG, PP KG = sP
P arams system parameters, P arams = {q, G1, G2, ˆe, P, H, F }
IDi identity of Ui, IDi ∈ {0, 1}∗
xi private key of Ui, xi ∈ Zq
Yi public key of Ui, Yi = xiP
di private key of Ui computed by P KG, di = sH(PP KG, IDi, Yi) = sHi
SigM signature of message M
Chapter 4
Our Scheme
In this chapter, we describe our group key agreement protocol in MANET. We first give an overview and then describe details of the protocol.
4.1
Overview
In this paper we propose a group key agreement protocol which is based on the self-certified signature scheme in [17]. We modify the scheme to be distributed and hence it is suitable to MANETs.
The purpose of the signature scheme is to provide authentication of par-ticipants. In the beginning, there is a private key generator (PKG). The PKG computes and sends the shares of the master key to the initial participants via secure channels and each one has to register a pair of public/private key which is used for signature. When a participant want to join the group for the first time, the participants in the group have to cooperatively compute a share of the master key and a pair of public/private key for him. When a participant want to leave the group, the others have to perform key evolving procedure to refresh their shares of the master key. We note that a share of
the master key has to be computed for a join participant every time.
The group key agreement scheme used in our protocol is modified from [22]. We combine the group key agreement scheme with the self-certified signature scheme to obtain our group key agreement protocol in MANETs.
4.2
Self-Certified Signature Scheme
The self-certified signature scheme is composed of six phases which are
Key Generation, Registration, Signature, Verification, Join, and Leave.
4.2.1
Key Generation Phase
In this phase the system parameters are generated. The P KG selects a private number as a master key and computes the corresponding public key. Each initial participant selects a private value and computes the correspond-ing public value. The phase is shown as follows:
Key Generation:
1. {q, G1, G2, ˆe, P } ← IG(1k).
2. Choose two hash functions H : G1 × {0, 1}∗ × G1 → G1 and
F : {0, 1}∗×G
2×G1 → Z∗q. The system parameters are P arams =
{q, G1, G2, ˆe, P, H, F }.
3. P KG selects a master key s ∈R Z∗q and sets PP KG = sP as its
public key.
4. Each initial participant Ui with identity IDi ∈ {0, 1}∗ selects
xi ∈R Z∗q as its private key and sets Yi = xiP as public. The
public key of the participant is
4.2.2
Registration Phase
In this phase each participant registers to the P KG for his private key and a share of the master key. Here we use verifiable threshold secret sharing scheme to share the master key. The public key of each participant can be used to establish a secret channel to send the share securely. When a message is encrypted by the public key of a particular participant, only those who know the corresponding private key can decrypt it. The phase is shown as follows:
Registration:
1. Each initial participant Uiauthenticates himself to P KG and then
sends (IDi, Yi) to P KG.
2. P KG randomly selects a degree-(t−1) polynomial f (x) = Pt−1k=1akxk+
s and computes the share si of s for the participant
si = f (i)
3. P KG computes Hi = H(PP KG, IDi, Yi) and sets the private value
di = sHi. Then P KG selects a number r ∈R Z∗q and computes
U = rP, V = di + rYi, W = si+ rYi, and a1P, a2P, . . . , at−1P .
Fi-nally P KG sends (U, V, W, a1P, a2P, . . . , at−1P ) to the participant
publicly.
4. The participant recovers di = V − xiU and si = W − xiU. Then
hold Hi = H(PP KG, IDi, Yi) ˆ e(di, P ) = ˆe(Hi, PP KG) si = P t−1 X k=1 (akP )ik+ PP KG.
If the checking passes, the participant obtains his private key
hxi, dii and the share si of the master key s.
4.2.3
Signature Phase
When a participant sends a message out, he has to compute the signa-ture of the message. The signasigna-ture is computed as follows:
Sign:
1. To sign a message M, the signer Ui selects a random number
k ∈ Z∗
q and computes
Hi = H(PP KG, IDi, Yi)
r = ˆe(kHi, P )
fi,M = F (M, r, Hi)
Vi,M = kHi+ fi,MxiHi+ fi,M2 di.
SigM = (fi,M, Vi,M) is a signature of M.
4.2.4
Verification Phase
When a participant receives a signature of a message, he has to verify the signature. The verification is as follows:
Verify:
1. The verifier computes
Hi = H(PP KG, IDi, Yi)
r0 = ˆe(V
i,M, P )ˆe(−Hi, fi,MYi+ fi,M2 PP KG).
then checks the equation
fi,M = F (M, r0, Hi).
4.2.5
Join Phase
When a new member wants to join, t participants are randomly chosen to compute jointly the share of the master key and a pair of public/private key for him. The process is as follows:
Join: Assume new member Un+1 wants to join.
1. Un+1 selects xn+1 ∈ Z∗q as its private value , then broadcasts
Yn+1 = xn+1P and IDn+1.
2. Randomly select t participants {U1, U2, . . . , Ut}. Each Ul
ran-domly selects a degree-(t − 1) polynomial hl(x) =
Pt−1 k=1al,kxk+ sl(n+1), where sl(n+1) = f (l)· Q 1≤k6=l≤t (n+1)−k l−k . Then Ulselects
a number rl ∈RZ∗q and sends Zlj = hl(j) + rlYj and rlP to Uj.
3. When Ul receives Zjland rjP from the other t − 1 participants, he
recovers hj(l) = Zjl− xl(rjP ) and computes F (l) =
Pt
k=1hk(l).
4. Un+1 computes f (n + 1) = t X k=1 F (k) · Y 1≤k6=j≤t j j − k PP KG = t X k=1 skP · Y 1≤k6=j≤t j j − k dn+1= t X k=1 skHn+1· Y 1≤k6=j≤t j j − k
In this process, each participant Ulin the list randomly selects a
degree-(t−1) polynomial with the constant sl(n+1) = f (l)·
Q
1≤k6=l≤t
(n+1)−k
l−k . Since
f (n+1) =Ptj=1f (j)·Q1≤k6=j≤t (n+1)−kj−k , we only need to recover the constant of F (l) which is Ptk=1F (k) ·Q1≤k6=j≤t j
j−k. So f (n + 1) can be computed
correctly.
4.2.6
Leave Phase
When a participant wants to leave, the others have to refresh their shares of the master key. The process is as follows:
Leave:
1. Each participant Ul who still in the network randomly selects a
degree-(t − 1) polynomial rl(x) with constant 0 and broadcasts
rl(j), 1 ≤ j ≤ n.
2. When Ul receives rj(l) from the other participants, he computes
f0(l) = f (l) +Pn
j=1rj(l) which is his new share of the master key
s.
In this process, each remaining participant Ulrandomly selects a
degree-(t − 1) polynomial rl(x) with constant 0. Since f0(x) = f (x) +
Pn
j=1rj(x),
4.3
Group Key Agreement
Now we describe the group key agreement protocol. The protocol con-sists of three phases which are Initialization, Join, and Leave. In these three phases, signatures are computed for broadcast messages each time. For sim-plicity, we do not write out signatures.
4.3.1
Initialization Phase
In this phase the initial group key is established. The phase is shown as follows:
Initialization:
1. Each Ui selects ri ∈RZ∗q and broadcasts wi = gri mod p.
2. When Ui receives wi−1, wi+1, it computes
bi =wi+1/wi−1 mod p
zi =brii mod p
ci =h(g||wi||bi||zi||gsi||bsii)
ai =si− ciri mod q
in which si ∈RZ∗q. Then broadcast zi, ai, bi, and ci.
3. When Ui receives zj, aj, bj, and cj from the others, it checks the
following equations bj =wj+1/wj−1 mod p cj =h(g||wj||bj||zj||gaj· wcjj||b aj j · z cj j ).
If the checking passes, Ui can use them to compute the group
session key
Ki =wi−1nrizn−1i zi+1n−2. . . zi−2 mod p
=gr1r2+r2r3+···+rnr1 mod p.
It is notable that we use the non-interactive proof system to prove that
Ui knows ri and the exponent of zi is exactly ri. This is necessary so that no
one can forge zi based on the Diffie-Hellman (DH) assumption.
4.3.2
Join Phase
When a new member wants to join, a new group key is established. However, the old group key cannot be known by the new member. The phase is shown as follows:
Join: Assume Un+1 wants to join.
1. Un+1 selects rn+1 ∈RZ∗q and broadcasts wn+1= grn+1 mod p.
2. • U1 selects r10 ∈R Z∗q and computes
w10 =gr01 mod p b =wn+1w2 K∗ =K · br0 1 · w−r1 n mod p c1 =h(g||w01||b||br 0 1||gs||bs) a1 =s − c1r01 mod q c2 =h(g||w1||wn−1||(w−1n )r1||gs||(w−1n )s) a2 =s − c2r1 mod q,
in which s ∈RZ∗q. Then broadcast w01, K∗, EK(br
0
1), EK(w−r1
n ),
• Ui, 2 ≤ i ≤ n, broadcast wi = gri mod p.
3. When each participant receives EK(br
0
1) and EK(w−r1
n ) from U1,
it decrypts and gets br0
1 and w−r1
n . Then it checks the following
equations c1 =h(g||w10||b||br 0 1||ga1 · (w0 1)c1||ba1 · (br 0 1)c1) c2 =h(g||w1||wn−1||(w−1n )r1||ga2 · w1c2||(wn−1)a2 · (w−rn 1)c2) K∗ =K · br10 1 · w−rn 1 mod p,
then checks whether wi, 2 ≤ i ≤ n, are the same as those received
previously. If the checking passes, then each node updates w1 by
gr1+r10 = w1w0
1 mod p.
4. Un computes k = wn+1rn mod p and broadcasts k.
5. When Un+1 receives k, it checks whether k = wnrn+1 mod p.
6. Each participant computes the new session key
K0 = K∗· k mod p.
It is notable that br0
1 and w−r1
n in step 2 are broadcast in encrypted form
so that Un+1cannot compute K from K∗by K = K∗·(br
0
1)−1·(w−r1
n )−1 mod p.
4.3.3
Leave Phase
Leave: Assume Ul wants to leave and the remaining participants form a
group G0 = G − {U
l} in which all participants are re-indexed from 1 to
n0 = n − 1.
1. Each participant in {Ui}, 1 ≤ i ≤ n and i mod 2 = 1, selects
2. Each participant in G0 computes
bi =wi+1/wi−1 mod p
zi =brii mod p
ci =h(g||wi||bi||zi||gsi||bsii)
ai =si− ciri mod q
in which si ∈RZ∗q. Then broadcast zi, ai, bi, and ci.
3. When Ui receives bj, zj, aj, and cj from the others, it checks the
following equations bj =wj+1/wj−1 mod p cj =h(g||wj||bj||zj||gaj· wcjj||b aj j · z cj j ).
If the checking passes, Ui can use them to compute the session key
Ki0 =wn0ri
i−1zn
0−1
i zn
0−2
i+1 . . . zi−2 mod p
Chapter 5
Security Analysis
In this chapter, we discuss the security of the proposed group key agree-ment protocol.
The signature scheme had been proved existential unforgeability against adaptive chosen message attacks (EUF-CMA) in the random oracle model under the difficulty of the computational Diffie-Hellman (CDH) problem by using the Forking Lemma [17]. It is proved secure against Type 1 and Type 2 adversaries. A Type 1 adversary is an uncertified user who wants to imper-sonate a victim by using public keys of its choice along with the identity of the victim. However, a Type 1 adversary cannot query the private key of the challenge public key from the PKG. A Type 2 adversary is a malicious PKG which wants to impersonate a victim with a given public key. However, a Type 2 adversary cannot access the corresponding private key chosen by the victim. Since in our scheme the PKG is distributed to the initial participants and we assume that at most (t − 1) participants can collude with each other, we do not consider Type 2 adversaries.
5.1
Security against Passive Adversary
We show that an eavesdropper cannot efficiently distinguish a group key constructed from our protocol and a random value under the decisional Diffie-Hellman (DDH) assumption.
Theorem 1. Under the decisional Diffie-Hellman assumption, (wi, zi, K =
gr1r2+r2r3+···+rnr1 mod p) and (w i, zi, Rn/(z1n Qn j=2z j−1 j )), for 1 ≤ i ≤ n, are
computationally indistinguishable, where R is a random value in Z∗ p.
Proof. We prove this theorem by contradiction. Assume that there exists an
algorithm A that can efficiently distinguish (wi, zi, K) and (wi, zi, Rn/(zn1
Qn
j=2z j−1 j )),
for 1 ≤ i ≤ n. We can use algorithm A to construct another algorithm
A0 that can efficiently distinguish (y
1, y2, gx1x2 mod p) and (y1, y2, R), where
y1 = gx1 mod p, y2 = gx2 mod p, and x1, x2 ∈ Z∗q. The values y1, y2, and
R are the input of algorithm A0. We let w
1 = y1, w2 = y2 without loss of
generality. Then algoritm A0 computes the following values :
w3 =w1· gs1 mod p w4 =w2· gs2 mod p . . . wn−1 =wn−3· gsn−3 mod p wn=wn−2· gsn−2 mod p
where si ∈ Z∗q is a random value, for 1 ≤ i ≤ n − 2. Let wi = gri mod p,
for 1 ≤ i ≤ n. A0 can compute z
2 = (w3/w1)r2 mod p = y2s1 mod p and
If n is even, then z1 =(w2/wn)r1 mod p = y−(t1 2+t4+···+tn−2) mod p zn =(w1/wn−1)rn mod p = wn−(t1+t3+···+tn−3) mod p. If n is odd, then z1 =(w2/wn)r1 mod p = (y2/y1)y1−(t1+t3+···+tn−2) mod p zn =(w1/wn−1)rn mod p = (y1/y2)wn−(t2+t4+···+tn−3) mod p.
So if algorithm A0 has constructed w
i, zi for 1 ≤ i ≤ n, and computes
Rn/(zn
1
Qn
j=2z j−1
j ), A0 can call A with these values. If A can efficiently
dis-tinguish (wi, zi, K) and (wi, zi, Rn/(z1n
Qn
j=2z j−1
j )) for 1 ≤ i ≤ n, then A0 can
use A to efficiently distinguish (y1, y2, gx1x2 mod p) and (y1, y2, R), which is
a contradiction for the DDH assumption.
In the Leave phase, Ul can still receive the broadcast messages from the
group G0 after it leaves. All it can do is to use the original group key K
and the broadcast messages from G0 to attempt to compute the new group
key K0 = gr0
1r2+r2r30+···+rnr10 mod p. However, Ul cannot know any information
about the new group key K0 under the CDH assumption. So the group key
agreement protocol is secure against a passive adversary.
5.2
Security against Active adversary
In the registration phase, the PKG computes the partial private key
di = sHi for Ui. We notice that Hi can be computed by any participants,
however, an adversary cannot recover s and obtain di under the DL
to collaboratively compute the share of the master key and a pair of pub-lic/private key for a new member. By our assumption that at most t − 1 participants can collude with each other, an adversary cannot obtain di from
these t participants as well.
A participant joins the group successfully means that his identity has been authenticated by the others. Since the adversary cannot obtain di, he
cannot impersonate Ui.
To demonstrate that the group key agreement protocol is secure against an active adversary, we have to argue two things :
1. wi is computed and broadcast by the legal participant Ui.
2. zi is the form of (wi+1/ww−1)ri and is computed by the participant who
knows the secret value ri.
Theorem 2. Under the random oracle model and the discrete logarithm (DL)
assumption, any malicious adversary A with di cannot compute the valid wi
of any participant Ui.
Proof. Assume that there exists a malicious adversary A which can
imper-sonate Ui to sign wi with a non-negligible probability ε. The hash
func-tion F is a truly random funcfunc-tion under the random oracle model, that is,
F (wi, r, Hi) is independent of wi, r, and Hi, where Hi = H(PP KG, IDi, Yi),
r = ˆe(kHi, P ), and k ∈ Z∗q is a random number selected by Ui. A can
compute two valid signatures (fi,wi, Vi,wi) and (fi,w0 i, V
0
i,wi) of wi with a
non-negligible probability, where fi,wi and f
0
i,wi are two hash values of F (wi, r, Hi)
under the random oracle model, Vi,wi = kHi+ fi,wixiHi+ fi,w2 idi, and V
0 i,wi = kHi+ fi,w0 ixiHi+ (f 0 i,wi) 2d
i. A can compute xi by solving the two equations
Vi,wi =kHi + fi,wixiHi+ f 2 i,widi V0 i,wi =kHi + f 0 i,wixiHi+ (f 0 i,wi) 2d i
and obtain xi = (V0 i,wi− Vi,wi) − ((f 0 i,wi) 2− f2 i,wi)di (f0 i,wi − fi,wi)Hi , which is a contradiction.
Theorem 3. Under the random oracle model and the discrete logarithm (DL)
assumption for elliptic curves, any malicious adversary A without knowing ri or with a fake ri cannot generate the right form of (wi+1/wi−1)ri.
Proof. Assume that there exists a malicious adversary A which can
imperson-ate Ui to generate c0iand a0i used to verify Xi with a non-negligible probability
ε. Under the random oracle model, A can generate two valid tuples (zi, ci, ai)
and (zi, c0i, a0i) such that
gai = gsi− wci i ga0 i = gsi− wc0i i and bai i = bsii/zici ba0i i = bsii/z c0 i i . Then ri = logPwi = logbizi = a0 i− ai ci− c0i , which is a contradiction.
By Theorem 2, only the legal participant Ui with the secret xi can
compute the valid wi. Since an impersonator does not know xi, it cannot
impersonator. Even the malicious impersonator can be detected in the veri-fication step of Initialization, Join, and Leave phase. By Theorem 3, zi is of
the form (wi+1/wi−1)ri and is computed by the legal participant who know ri.
Therefore, the key agreement protocol is secure against an active adversary.
5.3
Other Security Properties
Our proposed protocol also provides forward secrecy and withstand known-key attacks. We prove these two properties in the following theo-rems.
Theorem 4. Our protocol provides forward secrecy under the DL
assump-tion.
Proof. Let U = {Ui}Ni=1 be the set of participants who have established a
group key K at some past time τ . Suppose that the secret key (xi, di) of
some participant Ui ∈ U is compromised by an adversary A at time τ + 1.
Since (xi, di) is only used to signature of message and the computation of K
is only related to wi = gri and Sigwi = (fi,wi, Vi,wi), learning ri from (xi, di)
is impossible. Also, learning ri from wi and Sigwi is infeasible under the DL
assumption. Since ri is randomly chosen by Ui, it is obvious that A with
(xi, di) cannot learn K at time τ . Therefore, our protocol provides forward
secrecy under the DL assuption.
Theorem 5. Our protocol is secure against known-key attacks under the
random oracle model.
Proof. Suppose that an adversary knows the group key K and attempts to
learn other established group keys. We note that K = gr1r2+r2r3+···+rnr1 does
by Uiat each time τ , all established group key are independent of each other.
So the adversary cannot learn other group key and cannot impersonate any participant at time τ +1. Therefore, our protocol is secure against known-key attacks under the random oracle model.
Chapter 6
Performance Analysis
In this chapter we discuss the performance of each phase in our proposed protocol.
6.1
Initialization
In this phase we only need 2 rounds to establish a common group key when no malicious participants are detected. If any malicious participants
Uj are detected in step 3, Uj−1 and Uj+1 have to re-compute the broadcast
messages in step 2. So one additional round is required.
Each participant Ui requires 3 exponentiations in step 2. In step 3
each participant Ui requires 4 exponentiations to verify messages received,
and n exponentiations to compute the group key. So there are total 5n exponentiations.
wi is broadcast in step 1 and zi, ai, bi, and ci are broadcast in step 2.
6.2
Join
In this phase each participant including Un+1 have to use K∗ and k
which are broadcast by U1 and Un respectively to compute a new group key.
We notice that both K∗ and k are computed after receiving w
n+1. Since the
messages from U1and the messages from Uncan be broadcast simultaneously,
it requires at least 2 rounds to establish the new group key.
Each participant requires 8 exponentiations in step 3 to check whether
c1 = h(g||w10||b||br 0 1||ga1·(w0 1)c1||ba1·(br 0 1)c1) and c 2 = h(g||w1||w−1n ||(w−1n )r1||ga2· wc2
1 ||(wn−1)a2 · (wn−r1)c2). U1 requires 7 exponentions in step 2. Un requires 2
exponentions.
For each Ui, 1 ≤ i ≤ n+1, the commitment wi is broadcast. In addition,
U1 broadcasts K∗, EK(br
0
1), EK(w−r1
n ), c1, c2, a1, and a2, and Un broadcast
k.
6.3
Leave
The round number, computation overhead, and communication over-head are the same as in Initialization phase except that Ui,1≤i≤n,imod 2=0 need not broadcast wi again.
Despite message signature, we compare our protocol with [22] in Table 6.1.
Table 6.1: Performance comparison with [22]
Protocol Round Exponentiation Messages
Protocol[22] Join 2 4 4|p| + |q| Leave 2 4 4|p| + |q| Our Join 2 U1 : 6 Un, Un+1 : 2 others : 1 U1 : 4|p| + 4|q| Un : 2|p| others : |p|
Leave 2 Ui,i is even : 3
Ui,i is odd : 4
Ui,i is even : 2|p| + 2|q| Ui,i is odd : 3|p| + 2|q|
Chapter 7
Conclusions
We have proposed a secure group key agreement protocol based on self-certified public keys in this paper. We use the properties of self-self-certified public keys to adapt the group key agreement protocol to mobile ad hoc networks. The correctness is specified when we describe our protocol and the protocol has the following security properties :
• Secure against a passive adversary :
We have proved that an eavesdropper cannot efficiently distinguish a group key established and a random value under the DDH assumption in our protocol. Also, a participant Ul who has left the group cannot
know any information about the new established group key K0.
• Secure against an active adversary :
We provide two theorems for security against an active adversary. In the first theorem we prove that any malicious adversary A cannot im-personate another Ui to compute the valid commitment wi. In the
second theorem we prove that any malicious adversary A without se-cret ri or with a fake secret ri cannot generate the right form of the
other commitment (wi+1/wi−1)ri. Also the malicious impersonator can
be detected and be excluded from the group.
• Forward secrecy
Any adversary with private key (xi, di) at time τ + 1 cannot obtain any
information about the group key k at time τ .
• Secure against known-key attacks
Any adversary with the group key K at time τ cannot learn other group key and cannot impersonate any participant at time τ + 1.
For the future works, we have two goals to achieve. First, find a com-putationally symmetric Join phase. Second, reduce the computation cost in the Leave phase.
Bibliography
[1] Giuseppe Ateniese, Michael Steiner, and Gene Tsudik. New multiparty authentication services and key agreement protocols. IEEE Journal of Selected Areas in Communications, Vol. 18, No. 4, pp. 628-639, 2000.
[2] Klaus Becker and Uta Wille. Communication complexity of group key distribution. In Proceedings of the 5rd ACM Conference on Computer
and Communications Security (CCS’98), pp. 1-6, ACM Press, 1998.
[3] Mihir Bellare and Phillip Rogaway. Random oracles are practical: a paradigm for designing efficient protocols. In Proceedings of
Euro-crypt’00, LNCS 1807, pp. 139-155, 2000.
[4] Colin Boyd and Juan Manuel Gonzalez Nieto. Round-optimal contrib-utory conference key agreement. PKC 2003, LNCS 2567, pp. 161-174, Springer, 2003.
[5] Emmanuel Bresson, Olivier Chevassut, and David Pointcheval. Provably authenticated group Diffie-Hellman key exchange - the dynamic case. In
Proceedings of Asiacrypt’01, LNCS 2248, pp. 290-309, 2001.
[6] Emmanuel Bresson, Oliver Chevassut, and David Pointcheval. Dynamic group Diffie-Hellman key exchange under standard assumptions. In
[7] Emmanuel Bresson, Olivier Chevassut, David Pointcheval, and Jean-Jacques Quisquater. Provably authenticated group Diffie-Hellman key exchange. In ACM CCS’01, pp. 255-264, 2001.
[8] Mike Burmester and Yvo Desmedt. A secure and efficient conference key distribution system. In Advances in Cryptology - Eurocrypt’94, pp. 275-286, Springer, 1995.
[9] Giovanni Di Crescenzo, Niels Ferguson, Russell Impagliazzo, and Markus Jakobsson. How to forget a secret. In Proceedings of STACS’99, LNCS 1563, pp. 500-509, 1999.
[10] Whitfield Diffie and Martin E. Hellman. New directions in cryptography.
IEEE Transactions on Information Theory, Vol. IT-22, No. 6, pp.
644-654, 1976.
[11] Amos Fiat and Adi Shamir. How to prove yourself: Practical solutions to identification and signature problems. CRYPTO’86, 1987.
[12] Girault. Self-certified public keys. In Proceedings of the Eurocrypt’91, pp. 491-497, 1991.
[13] Ingemar Ingemarsson, Donald T. Tang, and C.K.Wong. A conference key distribution system. IEEE Transactions on Information Theory, Vol. IT-28, No. 5, pp. 714-720, 1982.
[14] Jonathan Katz and Moti Yung. Scalable protocols for authenticated group key exchange. In Advances in Cryptology - Crypto’03, pp. 110-125, 2003.
[15] Johann van der Merwe, Dawoud S. Dawoud, and Stephen McDonald. A survey on peer-to-peer key management for mobile ad hoc networks. ACM Computing Surveys (CSUR), Volume 39, Issue 1, 2007.
[16] Adi Shamir. How to share a secret. Communications of the ACM 22(11), pp. 612-613, 1979.
[17] Zuhua Shao. Self-certified signature scheme from pairings. Journal of Systems and Software (JSS), Vol. 80, Issue 3, pp. 388-395, 2007.
[18] Victor Shoup and Avi Rubin. Session key distribution using smart cards. In Proceedings of Eurocrypt’96, LNCS 1070, pp. 321-331, 1996.
[19] Michael Steiner, Gene Tsudik, and Michael Waidner. Diffie-Hellman key distribution extended to group communication. In Proceedings of the 3rd
ACM Conference on Computer and Communications Security (CCS’96),
pp. 31-37, ACM Press, 1996.
[20] Joseph Chee Ming TEO and Chik How TAN. Authenticated dynamic group key agreement for autoconfigurable mobile ad hoc netowrks. IE-ICE Transactions on Communications 2006 E89-B(9):2480-2492.
[21] W. G. Tzeng. A secure fault-tolerant conference-key agreement protocol.
IEEE Transactions on Computers, Volume 51, Issue 4, pp. 373-379,
2002.
[22] Y. M. Tseng. A communication-efficient and fault-tolerant conference-key agreement protocol with forward secrecy. Journal of Systems and Software (JSS), Volume 80, Issue 7, pp. 1091-1101, 2007.
[23] W. G. Tzeng and Z. J. Tzeng. Round-efficient conference key agreement protocols with provable security. ASIACRYPT2000, LNCS 1976, pp. 614-627, 2000.
[24] Lidong Zhou and Zygmunt J. Haas. Securing ad hoc networks. IEEE
![Table 6.1: Performance comparison with [22]](https://thumb-ap.123doks.com/thumbv2/9libinfo/8382577.178266/46.892.153.746.511.790/table-performance-comparison-with.webp)