Melting of the vortex lattice in high-T-c superconductors

Melting of the vortex lattice in high-T

superconductors

Dingping Li1,2,3 _{and Baruch Rosenstein}1,2

1_{Electrophysics Department, National Chiao Tung University, Hsinchu 30050, Taiwan, Republic of China} 2_{National Center for Theoretical Sciences, No. 101, Sec 2, Kuang Fu Road, Hsinchu 30043, Taiwan, Republic of China}

3_{Department of Physics, Nanjing University, Nanjing 210093, China} 共Received 12 April 2002; published 28 May 2002兲

The precise measurements of vortex melting point towards a need to develop a quantitative theoretical description of thermal fluctuations in vortex matter. To tackle the difficult problem of melting, the description of both the solid and the liquid phase should reach the precision level well below 1%. Such a theory in the framework of the Ginzburg-Landau approach is presented. The melting line location is determined, and mag-netization and specific-heat jumps along it are calculated. We find that the magmag-netization in the liquid is larger than that in the solid by 1.8% regardless of the melting temperature, while the specific-heat jump is about 6% and slowly decreases with temperature. The magnetization curves agree with experimental results on Y-Ba-Cu-O and Monte Carlo simulations.

DOI: 10.1103/PhysRevB.65.220504 PACS number共s兲: 74.60.⫺w, 74.25.Dw, 74.25.Ha

A magnetic field generates an array of vortices in type-II superconductors. The vortices strongly interact with each other forming highly correlated configurations such as the vortex lattice. In high-Tccuprates at relatively high tempera-tures, vortices move and vibrate due to thermal fluctuations to the extent that the lattice can melt becoming a ‘‘vortex liquid.’’1 Several recent remarkable experiments clearly de-termined that the vortex lattice melting in high-T_c supercon-ductors is a first-order phase transition with magnetization jumps2 and spikes in specific heat.3 The magnetization and entropy jumps were measured using diverse techniques such as local Hall probes, superconducting quantum interference device,4,5 torque magnetometry,6,7 and integration of the specific-heat spike.3 Related investigations indicate that, in addition to the spike, there is also a jump in specific heat.3,8 In spite of those precise measurements of vortex melting, a quantitative theoretical description of vortex melting is still lacking. We present such a theory in the framework of the Ginzburg-Landau approach in this work.

Thermal fluctuations in vortex matter have attracted great attention since the high-Tc superconductors were discovered over a decade ago. In highly anisotropic superconductors like Bi-Sr-Ca-Cu-O near the melting point vortices are quite well separated and the system can be approximated by an array of pointlike objects.1 In less anisotropic ones like Y-Ba-Cu-O, near the melting point the vortices overlap and one has to use the Ginzburg-Landau 共GL兲 model. The model is defined by the following free energy:

F⫽

冕

⬘

where A⫽(By,0) describes magnetic field 共considered con-stant and nonfluctuating, see below兲 in Landau gauge and covariant derivative is defined by D⬅“⫺i(2␲/⌽0)A,⌽0 ⬅(hc/e*)(e*⫽2e). When ␬⫽␭/␰ is large 共greater than 10), where ␭ magnetic penetration depth and ␰ coherence

length, the magnetic field can be considered constant and nonfluctuating 共an excellent approximation in the region studied兲. Statistical physics is described by the statistical sum

Z⫽兰D␺D␺¯ exp(⫺F/T). It accurately describes thermal

fluc-tuations in the range of relatively large magnetic fields (H Ⰷ Hc1⫽100 G in Y-Ba-Cu-O兲 and temperatures near Tc (70–110 K in Y-Ba-Cu-O兲. Near Tc, a(T) can be approxi-mated bt ␣T_c(1⫺t). In this paper, we will consider only high ␬ and temperatures near Tc. The model is, however, highly nontrivial even within the lowest Landau-level共LLL兲 approximation. In this approximation, which is valid when the magnetic field is high, only lowest Landau-level mode is retained and the free energy simplifies共after rescaling兲:9

f⫽ 1 4␲

冑

冕

冋

册

The simplified model has only one parameter, the dimension-less scaled temperature aT⫽⫺(b␻/4␲

冑

冑

2_␰T c␥/⌽0

2

)2, and the anisotropy parameter␥ is

冑

The LLL GL model was studied by a variety of different nonperturbative analytical methods. Among them are the density functional,10 1/N,11 elasticity theory,12 and others.13 The model was also studied numerically in both three-dimensional14共3D兲 and 2D.15,16However, we will not discuss those approaches in this paper.

While applying the renormalization group 共RG兲 on the one-loop level to this model, Brezin, Nelson, and Thiaville17 found no fixed points of the 共functional兲 RG equations and thus concluded that the transition to the solid phase is not continuous. The RG method therefore cannot provide a quantitative theory of the melting transition. Two perturba-tive approaches were developed and greatly improved re-cently to describe the solid phase and liquid phases, respec-tively. The perturbative approach on the liquid side was pioneered by Ruggeri and Thouless,18who developed an

ex-RAPID COMMUNICATIONS

PHYSICAL REVIEW B, VOLUME 65, 220504共R兲

pansion in which all the ‘‘bubble’’ diagrams are resummed. Unfortunately, they found that the series are asymptotic and, although first few terms provide accurate results at very high temperatures, the series become inapplicable for aTless than ⫺2 which is quite far above the melting line 共located around

aT⫽⫺10). We obtained recently an optimized Gaussian series9 that is convergent rather than asymptotic with radius of convergence of aT⬇⫺5, but still above the melting line. On the solid side, Eilenberger19calculated the fluctuations spectrum around Abrikosov’s mean-field solution. Maki and Takayama20noticed that the vortex lattice phonon modes are softer than those of the usual acoustic phonons in atomic crystals and this leads to infrared共IR兲 divergences in certain quantities. This was initially interpreted as the destruction of the vortex solid by thermal fluctuations and the perturbation theory was abandoned. However, the divergences resemble the ‘‘spurious’’ IR divergences in the critical phenomena theory. A recent analysis demonstrated that all these IR di-vergences cancel in physical quantities21and the series there-fore are reliable. The two-loop calculation was performed, so that the LLL GL theory on the solid side is now precise enough even for the description of melting.

However, on the liquid side, a theory for aT⭐⫺5 is re-quired. Moreover this theory should be extremely precise since the internal energies of the solid and the liquid near melting differ by a few percents only. Developing such a theory requires a better qualitative understanding of the metastable phases of the model. It is clear that the overheated solid becomes unstable at some finite temperature. It is not clear, however, whether the overcooled liquid becomes un-stable at some finite temperature共like water兲 or exists all the way down to T⫽0 as a metastable state. Despite its limited precision, the Gaussian 共Hartree-Fock兲 variational calcula-tion, is usually a very good guide to the qualitative features of the phase diagram. While such a calculation in the liquid was performed quite some time ago,18 on the solid side a more complicated one sampling inhomogeneous states was performed recently.9 The results are as follows. The solid state is the stable one below the melting temperature, be-comes metastable at somewhat higher temperatures and is destabilized at aT⬇⫺5. The liquid state becomes metastable below the melting temperature, however, in contrast to the solid, it does not loose metastability all the way down to T ⫽0 and the excitation energy approaches zero.

Meanwhile, similar qualitative results have been obtained in a different field of physics. A variety of analytical and numerical methods22have indicated that liquid共gas兲 phase of the classical one-component Coulomb plasma also exists as a metastable state down to T⫽0 with energy gradually ap-proaching that of the Madelung solid and the excitation en-ergy diminishing. We speculate that the same phenomenon would appear to happen in any system of particles interacting via long-range repulsive forces. In fact the vortices in the London approximation resemble repelling particles with the force even more long range than the Coulomb. In light of this impetus to consider the above scenario in the vortex matter, we provide both theoretical and phenomenological evidence that the above picture is a valid one.

Assuming the absence of singularities on the liquid branch allows to develop a sufficiently precise theory of the LLL GL model in a vortex liquid 共even including an over-cooled one兲 using the Borel-Pade23共BP兲 method at any tem-perature. After clarifying several issues that prevented its use and acceptance previously we then combine it with the re-cently developed LLL theory of solids21 to calculate the melting line and the magnetization and specific-heat jumps along it. Early on, Ruggeri and Thouless18 tried unsuccess-fully to calculate the specific heat by using BP because their series was too short. Subsequent attempts to calculate the melting point by using BP also ran into problems. Hikami, Fujita, and Larkin24 attempted to find the melting point by comparing the BP 共liquid兲 energy with the one-loop solid energy and, in doing so, obtained the melting temperature

a_Tm⫽⫺7. However, their one-loop solid energy was incorrect

and, in any case, the two-loop correction is necessary. As demonstrated in the following, the BP energy combined with the correct two-loop solid energy computed recently not only gives a_Tm⫽⫺9.5, but also allows to obtain a wide range of quantitative predictions within the model.

Now we present the solution of the LLL GL model. The liquid LLL 共scaled兲 effective free energy 关of the scaled model defined in Eq. 共2兲兴 is written as f_liq⫽4␧1/2_关1 ⫹g(x)兴 . The function g can be expanded as g(x) ⫽兺cnxn, where the high-temperature small parameter x ⫽1

2␧⫺3/2is defined as a solution of the Gaussian gap

equa-tion, ␧3/2⫺a_T␧1/2⫺4⫽0 for the excitation energy . The co-efficients can be found in Refs. 24 and 25. We will denote

gk(x) by the关k,k⫺1兴 BP transform of g(x) 共other BP ap-proximants clearly violate the correct low-temperature as-ymptotics兲. The BP transform is defined as 兰0⬁g_k

⬘

⬘

2k⫺1

(cnxn/n!). For k⫽4 the liquid energy already con-verges. We used in this work k⫽5 to achieve the required precision (⬃0.1%). The liquid energy completely agrees with the optimized Gaussian expansion results9above its ra-dius of convergence at aT⫽⫺5. In addition similar results we obtained in the 2D GL model agree with existing Monte Carlo simulations.15The solid effective energy to two-loops is:21 fsol⫽⫺ a_T2 2␤_A⫹2.848兩aT兩 1/2_⫹2.4 a_T. 共3兲

Comparing the solid energy to that of the liquid共inset in Fig. 1兲, reveals that a_Tm⫽⫺9.5. This is in accord with experimen-tal results. As an example, in Fig. 2 we present the fitting of the melting line of fully oxidized YBa2Cu3O7 共Ref. 7兲 that gives Tc⫽88.2, Hc2⫽175.9, Gi⫽7.0 10⫺5, ␬⫽50. Melting lines of optimally doped untwinned3 YBa2Cu3O7⫺␦ and DyBa₂Cu₃O₇ 共Ref. 26兲 are also fitted extremely well. For example, for YBa2Cu3O7⫺␦ in共Ref. 3兲, the melting line fit-ting gives T_c⫽93.07, H_c2⫽167.53, Gi ⫽ 1.9 10⫺4, ␬ ⫽48.5 共see also Ref. 27兲.

The 3D Monte Carlo simulations14are not precise enough to provide an accurate melting point since the LLL scaling is violated. One gets different values of a_Tm⫽⫺14.5, ⫺13.2,

RAPID COMMUNICATIONS

DINGPING LI AND BARUCH ROSENSTEIN PHYSICAL REVIEW B 65 220504共R兲

⫺10.9 at magnetic fields 1, 2, 5 T, respectively. This viola-tion is perhaps due to a small sample size 共of order 100 vortices兲. The situation in 2D is better since the sample size is much larger. We performed similar calculation in the 2D LLL GL model and found that the melting point is a_Tm ⫽⫺13.2. It is in good agreement with the MC simulations.15 Phenomenologically the melting line can be located using Lindemann criterion or its more refined version using Debye-Waller factor.28The more refined criterion is required in the case of Y-Ba-Cu-O since vortices are not pointlike. Numerical investigation of the Yukawa gas28 indicated that the Debye-Waller factor e⫺2W 共a ratio of the structure func-tion at the second Bragg peak at melting to its value at T ⫽0) is about 60%. We get using methods of Ref. 29 e⫺2W

⫽0.59 for aT

m_⫽⫺9.5.

The scaled magnetization is defined by m(aT) ⫽⫺(d/daT) fe f f(aT). At the melting point aT

m_{⫽⫺9.5 the}

magnetization jump ratio defined by ⌬M divided by the magnetization at the melting on the solid side is found to be equal to

⌬M

Ms ⫽ ⌬m

ms ⫽0.018. 共4兲

This prediction is compared on Fig. 2共the upper inset兲 with the experimental results on fully oxidized YBa2Cu3O7 共Ref. 7, rhombs兲 and optimally doped YBa2Cu3O7⫺␦ 共Ref. 5 stars兲.

These samples probably have the lowest amount of disor-der that is not included in the calculations. From the model, we caculate the specific-heat jump ratio at the melting

⌬c⫽0.0075

冉

冊

冉

冊

In addition to describing the melting, we present here an example of quantitative results that are obtained using the present approach—the magnetization curves. Our LLL mag-netization curve coincides with the LLL Monte Carlo共MC兲 result of Ref. 14共which is very accurate since the LLL scal-ing is obeyed兲 to the precision of MC. However in experi-ments away from the melting line higher Landau levels 共HLL兲 are no longer negligible. Naively in vortex solid when the distance from the mean-field transition line is smaller than the inter-Landau-level gap, 1⫺t⫺b⬍2b, one expects that the higher Landau modes can be neglected. More care-fully examining the mean-field solution reveals that a weaker condition 1⫺t⫺b⬍12b should be used for a validity test of the LLL approximation30 in vortex solids. In vortex liquid

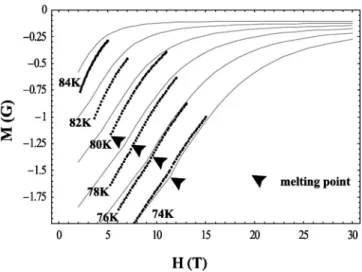
FIG. 3. Comparison of the theoretical magnetization curves 共lines兲 of fully oxidized YBa2Cu3O7 utilizing parameters obtained by fitting the melting line on Fig. 2 with torque magnetometry experimental results7共dots兲. Arrows indicate melting points while at low magnetic field the experimental data start from the point in which the magnetization is reversible indicating low disorder. FIG. 1. Free energy of solid共line兲 and liquid 共dashed line兲 as

function of the scaled temperature. The solid line ends at a point 共dot兲 indicating the loss of metastability. Inset shows a tiny differ-ence between liquid and solid near the melting point.

FIG. 2. Comparison of the experimental melting line for fully oxidized YBa2Cu3O7in Ref. 7 with our fitting. Inset on the right shows the relative universal magnetization jump of 1.8%共line兲 and experimental results for fully oxidized YBa2Cu3O7 in Ref. 7 共rhombs兲 and optimally doped untwinned YBa2Cu3O7⫺␦in Ref. 5 共stars兲. Inset on the left shows the relative nonuniversal specific-heat jump 共line兲 and experimental results for optimally doped un-twinned YBa2Cu3O7⫺␦in Ref. 3.

RAPID COMMUNICATIONS

MELTING OF THE VORTEX LATTICE IN HIGH-Tc. . . PHYSICAL REVIEW B 65 220504共R兲

one has to go beyond the mean field to estimate the HLL contribution.31 In 3D, Lawrie in Ref. 31, calculated the ex-citation energy in the framework of the Gaussian 共Hartree-Fock兲 approximation. The excitation gap is 10 times smaller than inter Landau gap for fields in a wide range around melt-ing line for fields larger than 0.1 T in Y-Ba-Cu-O. Therefore in the range of values of the interest in the present paper the LLL contribution should be dominant. Experimentally it is often claimed that one can establish the LLL scaling for fields above 3 T共see, for example, Ref. 32兲.

The theoretical expressions we use are the LLL contribu-tion to the magnetizacontribu-tion plus the correccontribu-tions due to HLL calculated in Gaussian approximation. The results are com-pared on Fig. 3 with the experimental magnetization curves of Ref. 7. We use the parameters from the fitting of the melting curve 共see Fig. 2兲 . The agreement is fair at higher

fields, while at low magnetic fields the higher Landau-levels theory beyond Gaussian approximation is required. The LLL scaling has a limited validity away from melting line.

To summarize, the problem of the quantitative description of melting of the vortex lattice in the framework of the LLL Ginzburg-Landau approach is solved. The results for melting line, magnetization jump, and specific-heat jump are in good agreement with experiments and MC simulations. This is the first quantitative theory of the first-order melting of any kind to our knowledge. We believe that similar methods can be applied to other systems undergoing the first-order melting transition.

We are grateful to T. Nishizaki and A. Junod for providing details of their experiments. The work was supported by NSC of Taiwan Grant No. NSC#90-2112-M-009-039.

1_{D.R. Nelson, Phys. Rev. Lett. 60, 1973共1988兲.}

2_{E. Zeldov, D. Majer, M. Konczykowski, V.B. Geshkenbein, V.M.} Vinokur, and H. Shtrikman, Nature共London兲 375, 373 共1995兲. 3_{A. Schilling, R.A. Fisher, N.E. Phillips, U. Welp, D. Dasgupta,}

W.K. Kwok, and G.W. Crabtree, Nature 共London兲 382, 791 共1996兲; A. Schilling, R.A. Fisher, N.E. Phillips, U. Welp, W.K. Kwok, and G.W. Crabtree, Phys. Rev. Lett. 78, 4833共1997兲. 4_{H. Pastoriza, M.F. Goffman, A. Arribere, and F. de la Cruz, Phys.}

Rev. Lett. 72, 2951共1994兲.

5_{U. Welp, J.A. Fendrich, W.K. Kwok, G.W. Crabtree, and B.W.} Veal, Phys. Rev. Lett. 76, 4809共1996兲.

6_{M. Willemin, A. Schilling, H. Keller, C. Rossel, J. Hofer, U.} Welp, W.K. Kwok, R.J. Olsson, and G.W. Crabtree, Phys. Rev. Lett. 81, 4236共1998兲.

7_{T. Nishizaki, K. Shibata, T. Sasaki, and N. Kobayashi, Physica C}

341, 957共2000兲.

8_{M. Roulin, A. Junod, and E. Walker, Science 273, 1210共1996兲.} 9_{D. Li and B. Rosenstein, Phys. Rev. Lett. 86, 3618共2001兲.} 10_{Z. Tesanovic and A.V. Andreev Phys. Rev. B 49, 4064共1994兲.} 11_{I. Affleck and E. Brezin, Nucl. Phys. B 257, 451共1985兲; A.}

Perez-Garrido and M.A. Moore, Phys. Rev. B 58, 9677 共1998兲; A. Lopatin and G. Kotliar, ibid. 59, 3879共1999兲.

12_{V. Zhuravlev and T. Maniv, Phys. Rev. B 60, 4277共1999兲.} 13_{Z. Tesanovic, L. Xing, L. Bulaevskii, Q. Li, and M. Suenaga,}

Phys. Rev. Lett. 69, 3563 共1992兲; Z. Tesanovic and A.V. An-dreev, Phys. Rev. B 49, 4064共1994兲.

14_{R. Sasik and D. Stroud, Phys. Rev. Lett. 75, 2582共1995兲.} 15_{Y. Kato and N. Nagaosa, Phys. Rev. B 48, 7383共1993兲.} 16_{Z. Tesanovic and L. Xing, Phys. Rev. Lett. 67, 2729共1991兲; J. Hu}

and A.H. MacDonald, ibid. 71, 432 共1993兲; Phys. Rev. B 56, 2788共1997兲.

17_{E. Brezin, D.R. Nelson, and A. Thiaville, Phys. Rev. B 31, 7124} 共1985兲.

18_{G.J. Ruggeri and D.J. Thouless, J. Phys. F: Met. Phys. 6, 2063} 共1976兲.

19_{G. Eilenberger, Phys. Rev. 164, 628共1967兲.}

20_{K. Maki and H. Takayama, Prog. Theor. Phys. 46, 1651共1971兲.} 21_{B. Rosenstein, Phys. Rev. B 60, 4268共1999兲; D. Li and B.}

Rosen-stein, ibid. 65, 024513共2002兲; 65, 024514 共2002兲.

22_{R. Leote de Carvalho, R. Evans, and Y. Rosenfeld, Phys. Rev. E}

59, 1435共1999兲.

23_{G.A. Baker, Quantitative Theory of Critical Phenomena} 共Aca-demic Press, Boston, 1990兲.

24_{S. Hikami, A. Fujita, and A.I. Larkin, Phys. Rev. B 44, R10400} 共1991兲.

25_{E. Brezin, A. Fujita, and S. Hikami, Phys. Rev. Lett. 65, 1949} 共1990兲.

26_{B. Revaz, A. Junod, and A. Erb, Phys. Rev. B 58, 11 153共1998兲.} 27_{S.W. Pierson and O.T. Walls, Phys. Rev. B 57, R8143共1998兲.} 28_{M. Stevens and M. Robbins, J. Chem. Phys. 98, 2319共1993兲.} 29

D. Li and B. Rosenstein, Phys. Rev. B 60, 10 460共1999兲. 30_{D. Li and B. Rosenstein, Phys. Rev. B 60, 9704共1999兲.} 31_{I.D. Lawrie, Phys. Rev. B 50, 9456共1994兲; A.E. Koshelev, ibid.}

50, 506共1994兲.

32_{J. Sok, Ming Xu, Wei Chen, B.J. Suh, J. Gohng, D.K. Finnemore,} M.J. Kramer, L.A. Schwartzkopf, and B. Dabrowski, Phys. Rev. B 51, 6035共1995兲.

RAPID COMMUNICATIONS

DINGPING LI AND BARUCH ROSENSTEIN PHYSICAL REVIEW B 65 220504共R兲