The minimum size of critical sets in latin squares

journalof

statisticalplanning

and inference

Inference 62 (1997) 333-337 E L S E V I E R

The minimum size of critical sets in latin squares

Chin-Mei Fu a'b, Hung-Lin Fu b'c, C.A. Rodger b'*

a Department o/" Mathematics. Tamkan 9 University, Tamsui, Taipei Shien, Taiwan, Republic of China b Department q[' Discrete and Statistical Sciences, Auburn University, 120 Math Annex, Auburn.

AL 36849-5307, USA

c Department of Applied Mathematics. National Chino Tum t University, Hsin Chu, Taiwan, Republic of China

Received 17 April 1995: revised 15 August 1996

Abstract

A critical set C of order n is a partial latin square of order n which is uniquely completable to a latin square, and omitting any entry of the partial latin square destroys this property. The size s(C) of a critical set C is the number of filled cells in the partial latin square. The

I size of a minimum critical set of order n is s(n). It is likely that s(n) is approximately ~n-, though to date the best-known lower bound is that s(n)>~n + 1. In this paper, we obtain some conditions on C which force s(C)>~ L ( n - l)/2J 2. For n > 20, this is used to show that in general s(n)>~ [(7n - 3 ) / 6 j , thus improving the best-known result. © 1997 Elsevier Science B.V. A M S class![ication: primary 62K05

Keywords: Latin squares; Critical sets; Design construction

1. Introduction

A ( p a r t i a l ) latin square o f order n is an n x n array with entries in S = {crl,a: . . . an} such that e a c h cell c o n t a i n s (at m o s t ) o n e s y m b o l , and e a c h e l e m e n t o f S occurs (at m o s t ) o n c e in e a c h r o w and (at m o s t ) o n c e in e a c h c o l u m n . A n incomplete latin square L o f order n on the s y m b o l s al . . . a~ is an n x n array in w h i c h each cell contains e x a c t l y one o f the s y m b o l s ( p o s s i b l y s o m e s y m b o l s o c c u r in no cells), and e a c h r o w and c o l u m n contains e a c h s y m b o l at m o s t o n c e ; so clearly n<~v, and it" n =: v then L is a latin square. I f L is a partial or i n c o m p l e t e latin square, t h e n let L ( i , j ) be the s y m b o l in cell ( i , j ) o f L ( i f o n e exists). A critical set C o f order n and size s ( C ) is a partial latin square o f o r d e r n, with e x a c t l y s ( C ) filled cells, w h i c h satisfies

(1) C is c o n t a i n e d in a u n i q u e latin square L ( C ) o f order n, and

* Corresponding author. Research supported by NSF grant DMS 9225046.

0378-3758/97/$17.00 @ 1997 Elsevier Science B.V. All rights reserved PII S 0 3 7 8 - 3 7 5 8 ( 9 6 ) 0 0 1 87-5

334

C-M. Fu et al./Journal of Statistical Plannin9 and Inference 62 (1997) 333~37

(2) if any entry o f C is removed then the resulting partial latin square is contained

in at least two latin squares o f order n.

A critical set o f order n with minimum size is called a m i n i m u m critical set, and

its size is denoted by s(n).

The problem o f determining s(n) turns out to be very interesting, and is probably a

difficult one (Colbourn, 1984). It is well known that every critical set must contain at

least one filled cell in each row except possibly for at most one (and in each column

except possibly for at most one, and must contain each symbol except possibly for at

most one); for if C contains no cells in two rows then in any completion L ( C ) these

two rows can be interchanged. So clearly s(n)>~n - 1. This lower bound for s(n) was

later improved (Donovan et al., to appear) to s(n)>~n for n~>4. More recently, it was

independently shown (Cooper et al., 1994; Fu et al., 1995) that s(n)>>-n + 1 for n~>5.

In this paper, we shall further improve the lower bound to s(n)>>-[~(7n- 3)J for

n > 20. Our result is a corollary o f a proposition we prove which gives conditions on

a critical set C o f order n that imply that C has size at least [ ½ ( n - 1)J 2.

2. The main results

To obtain our results, we will rely on the following theorem.

Theorem 2.1 (Rodger, 1984). L e t n > 2v and v>~ 10, so n > 20. A n incomplete latin

square A o f order v on symbols al, ~r2 .. . . . an can be embedded in a latin square L o f

order n with completely prescribed diagonal D outside A i f and only i f

(1) N A ( a j ) > ~ 2 v - n + ND(aj) f o r l <~j<~n,

(2) f o r 1 <~j<<,n, i f NA(aj) = v then NA(aj) + ND(aj) ~ n -- 1, and

(3) i f A is a latin square on v symbols, say al . . . av, and i f n = 2v + 1, then

~ j = l ND(aj) 7 ~ 1,

where NA( aj ) and ND(aj ) are the numbers o f times aj occurs in A and D, respectively.

(It is worth noting that a companion to Theorem 2.1 in which D has at least one

n N

empty cell (so ~ i = 1

o(cri) < n - v) has also been proved by Andersen et al. (1980);

see also Rodger, 1984, Theorem 4.)

Two partial latin squares are isotopic if one can be transformed into the other by

permuting rows, permuting columns and renaming the symbols. That is, two partial latin

squares L and U are isotopic if there exists an ordered triple (~, 13, 7) o f permutations

such that L ( i , j ) = ak if and only i f U ( i ~ , j f l ) = cry,; the ordered triple (~,/3,7) is called

an isotopism. Thus, the following result is clear.

L e m m a 2.2 (Donovan et al., to appear). L e t C be a critical set o f order n, and let L

be the unique latin square o f order n containing C. L e t (~,/3, 7) be an isotopism f r o m

the critical set C onto C t. Then C ~ is a critical set in the latin square U obtained

f r o m L by applying the isotopism (~,/3, 7)-

C.-M. Fu et al./Journal of Statistical Planning and lnJOren~e 62 (1997) 333 337 335

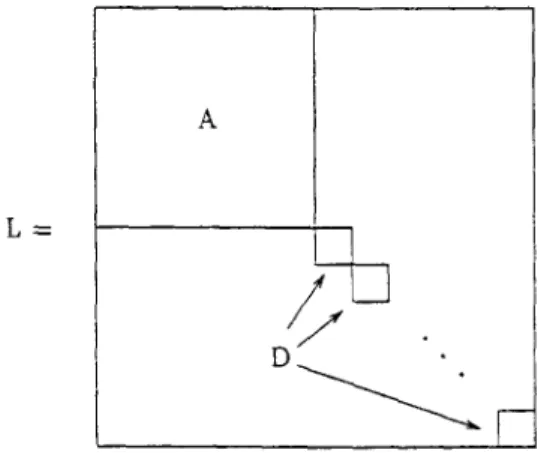
L -=

A

Fig. 1. D is the diagonal of L outside A.

In order to apply Theorem 2.1, we need to arrange for the entries of a critical set in a latin square L to occur inside A and D (see Fig. 1), which we can sometimes do using Lemma 2.2.

Proposition 2.3. L e t n > 20 and v = L½(n - 1)j. Suppose that C is a critical set q f order n, and suppose that C is isotopic to a partial latin square in which i f row (column) i contains at least two f i l l e d cells then i<~v and f o r such rows (columns), all filled cells occur in columns (rows) 1 . . . v. Then s(C)>~ v 2.

Proof. By L e m m a 2.2 and the assumption in this proposition, we can assume that rows and columns v + 1, v + 2 . . . . , n each contain at most one filled cell of C, and if these rows and columns contain a filled cell then it is a diagonal cell. Let L = L ( C ) be the unique latin square of order n that contains C. Let A be the incomplete latin square of order v consisting of the first v rows and columns of L, and let D be the diagonal of L outside A (see Fig. 1). Since A is embedded in L, it follows that ( I ) - ( 3 ) o f Theorem 2.1 all hold.

Suppose s ( C ) < v 2. Since C contains at least n - v - 1 filled cells of D (for any critical set C' there is at most one row containing no filled cells of C~), at mosl ~.2 __ 1 - (n - ~' - 1 ) cells o f A are filled cells in C. So A contains at least n - t cells that are not filled in C.

The n u m b e r of cells in A containing symbols that are needed to make sure tha~

n

condition (1) of Theorem 2.1 is satisfied is at most ~ j = l max{0, N D ( ~ ) - 1} ~< n - z : - I

n

(since ~ j = l N ~ ( a j - ) . . ~ n - v). So there exists a cell that is not filled in C, and such that if the symbol in this cell in A is replaced by any other symbol to form an incomplete latin square A ~, then A ~ also satisfies (1); let c be such a cell. By this choice of c, the symbol Crc in cell c of A cannot satisfy

NA(O'c)+

At most 2v - 2 symbols other than a¢ occur in the row or column of A containing c, ;and n >~ 2v + 1, so there is a choice o f at least two symbols that can be used to

336 C-M. Fu et al./Journal o f Statistical Plannin9 and Inference 62 (1997) 333-337

replace the s y m b o l in cell c o f A to p r o d u c e a n i n c o m p l e t e latin square A t o f order v. Therefore, since clearly at m o s t o n e s y m b o l ~ c a n satisfy N A ( ~ ) + N D ( a j ) = n - 2 (so i f o) is u s e d to replace trc in c to form A ' then N A , ( a j ) + N o ( a j ) = n - 1), since w h e n

v N

~-]i=1 D ( a i ) -- 1, at m o s t o n e s y m b o l ak c o u l d m a k e A t a latin square w h e n u s e d to replace ai in c, a n d since these two cases c a n n o t h a p p e n s i m u l t a n e o u s l y , it is easy to see that we c a n choose the s y m b o l to replace ac in cell c so that A t satisfies ( 1 ) - ( 3 ) o f T h e o r e m 2.1.

U s i n g T h e o r e m 2.1 we c a n e m b e d A t in a latin square U o f order n in w h i c h the d i a g o n a l o f L t outside A t is D. This is a contradiction, since L ~ U (they differ at cell c), y e t both c o n t a i n C w h i c h is a critical set. []

W i t h the a b o v e t h e o r e m for n > 20 it is clear that all the p r e v i o u s l y k n o w n results o n the l o w e r b o u n d o f the size o f critical sets are easy to obtain. W e c a n increase the lower b o u n d o n s(n) with the f o l l o w i n g result.

Theorem

P r o o f . Suppose C is a critical set o f size at most ~ = L - ~ ( 7 n - 9)J. Since C is a critical set, at least n - 1 rows a n d c o l u m n s in C m u s t c o n t a i n a filled cell. So at m o s t c~ - (n - 1) rows o f C c o n t a i n at least two filled cells, a n d each o f at least n - 1 - (~ - (n - 1)) = 2 n - 2 - c~ rows o f C c o n t a i n s exactly o n e symbol. Similarly, there are at m o s t 2(~ - (n - 1)) s y m b o l s that occur in c o l u m n s that c o n t a i n at least o n e other s y m b o l . Therefore, there is a set D o f at least 2n - 2 - ~ - 2(~ - (n - 1 )) = 4 n - 4 - 3L(7n - 9)/6J ~>4n - 4 - ( 7 n - 9 ) / 2 = (n + 1)/2 cells in C, each o f w h i c h is the o n l y filled cell in the r o w a n d c o l u m n c o n t a i n i n g it. So there exists an isotopic partial latin square C t in w h i c h the cells in D are p e r m u t e d to the cells ( n - i , n - i ) for 0~<i < IDI, where ID[/> Vl(n + 1)1. It follows that i f r o w or c o l u m n i o f C t c o n t a i n s m o r e t h a n o n e s y m b o l t h e n i < ~ n - [D[ ~< [ ½ ( n - 1)J = v. Therefore, we c a n apply P r o p o s i t i o n 2.3 to o b t a i n a contradiction, since clearly c~ < v 2. []

Acknowledgements

The authors w o u l d like to t h a n k the referees for their sterling efforts c o n c e r n i n g this paper.

References

Andersen, UD., R. Hfiggkvist, A.J.W. Hilton and W.B. Poucher (1980). Embedding incomplete latin squares whose diagonal is almost completely prescribed. European J. Combin. 1, 5-7.

Colbourn, C.J., M.J. Colbourn, and D.G. Stinson (1984). The computational complexity of recognizing critical sets. Lecture Notes in Mathematics, Vol. 1073, Springer, Berlin, 248-253.

C.-M. Fu et al./Journal of Statistical Planning and lnjerence 62 (1997) 333 337 337

Cooper, J.A., D. Donovan and J. Seberry (1991). Latin squares and critical sets of minimal size. Australas.

Z Combin. 4, 248 253.

Cooper, J.A., T.P. McDonough and V.C. Mauron (1994). Critical sets in nets and latin squares. J. Statist.

Plann. lnJer. 41, 241-256.

Curren, D and G.H.J. van Rees (1978). Critical sets in latin squares, Congr. Numer. 22, 165--168.

Donovan, D., J. Cooper, D.J. Nott and J. Seberry (1995). Latin squares: critical sets and their lower bounds. Ars. Combin. 39, 33-48.

Fu, C.M., Hung-Lin Fu and Wen-Bin Liao (1995). A new construction for a critical set in special latin

squares. Congr. Numer. 110, 161-166.

Rodger, C.A. (1984). Embedding an incomplete latin square in a latin square with a prescribed diagonal. Discrete Math. 51, 73-89.