Quantum Circuit Design and Analysis for Database
Search Applications
Yi-Lin Ju, I-Ming Tsai, and Sy-Yen Kuo, Fellow, IEEE
Abstract—In this paper, we show how quantum Boolean circuits can be used to implement the oracle and the inversion-about-av-erage function in Grover’s search algorithm. Before illustrating how this can be done, we present the circuit design principle using the satisfiability (SAT) problem as an example. Then, based on this principle, we show the quantum circuits for two different kinds of applications. The first one is searching a phone book. Although this is a typical example of Grover’s algorithm, we show that it is impractical as a real-world application. As the second tion, we give the quantum circuits for a more practical applica-tion—breaking a symmetric cryptosystem. Although these two ap-plications have quite different types of search criteria, they are both one-way functions and the proposed circuits can actually be gener-alized to any such problems. In this perspective, we conclude this paper by proposing a template of quantum circuits that is capable of searching the solution of a certain class of one-way functions.
Index Terms—Grover’s algorithm, nanoscale circuits, one-way function, quantum circuits.
I. INTRODUCTION
O
VER THE PAST years, the density of transistors on con-ventional integrated-circuit chips has been increased dra-matically. However, with the components continue to shrink, the conventional transistor technology will eventually reach its physical limit. Nanoelectronics is regarded as the most likely direction of developing computer technologies. It is believed that nanocomputer can be smaller, more densely integrated and more powerful. A promising way of achieving this is to take the advantage of quantum mechanics. Recent discoveries on se-cure key distribution [1], polynomial time prime factorization [2], and fast database search [3] are good examples. They take advantage of quantum mechanics to improve the efficiency of a computation process. As a result, quantum computing has be-come the most rapidly expanding fields of research.As an example, unordered database search is an important and widely discussed problem. Unordered database search is
impor-Manuscript received December 11, 2006; revised June 12, 2007. This work was supported by the National Science Council, Taiwan, R.O.C., under Grant NSC 95-2221-E-002-068. This paper was recommended by Guest Editor C. Lau.
Y.-L. Ju is with the Department of Electrical Engineering, National Taiwan University, Taipei 10617, Taiwan, R.O.C.
I.-M. Tsai is with the Department of Electrical Engineering, National Taiwan University, Taipei 10617, Taiwan, R.O.C., and also with Chunghwa Telecom-munication Laboratories, Yaoyuan 32601, Taiwan, R.O.C.,
S.-Y. Kuo is with the Department of Electrical Engineering, National Taiwan University, Taipei 10617, TaiwanR.O.C., and also with the Department of Com-puter Science and Information Engineering, National Taiwan University of Sci-ence and Technology, Taipei 10617, Taiwan, R.O.C. (e-mail: sykuo@cc.ee.ntu. edu.tw).
Digital Object Identifier 10.1109/TCSI.2007.907845
tant because, from an engineering point of view, many problems can be formulated as a database searching process. For instance, cracking a 1024-digit secret key in a key space is essen-tially an unordered database searching process. Classically, the only way to search such a database is to test the elements se-quentially against the condition until the target is found. For a database of size , this brute force search requires an average of comparisons. However, Grover’s algorithm can iden-tify the target in steps, which is more efficient.
The main idea of Grover’s algorithm is to amplify the prob-ability amplitude of the target state so it can be found with a high probability when the final measurement is performed. More specifically, given a Boolean expression , Grover’s al-gorithm allows the target state to be marked by an “oracle”, so the target with can be found with a com-plexity. It has also been shown that, when there are multiple targets, the problem can still be solved in even if is not known in advance [4]. The optimality of Grover’s algorithm [5] and several generalizations including searching multiple ob-jects [6], analyzing the initial state and optimal unitary operator [7], [8], and studying the stability and robustness of Grover’s algorithms [9]–[12] have also been studied. In addition, varia-tions of this algorithm have been applied to many other prob-lems such as state preparation [13], finding the minimum [14], element distinctness [15], and many others [16]–[18].
Implementation of Grover’s algorithm is also the focus of many researches. For example, Diao et al. showed how to use 1-bit unitary gates and 2-bit quantum phase gates to realize Grover’s algorithm in cavity QED systems [19]. Roland et
al. analysed the differences between continuous-time analog
Hamiltonian search algorithms and original discrete circuit based Grover’s algorithm [20]. Xiao et al. described how to robust single and two qubit logic gates based on nuclear magnetic resource (NMR) technologies and use the gates to implement counting algorithm [21], which is based on Grover’s algorithm. Most of the studies described above emphasized on either theoretical study or small-scale physical implementation. However, for large quantum circuits designed for a real-world application, some modifications should be made. For example, in a database query application, the demand should not only be finding the target (answering if there is a satisfying but also getting the related information (given , answering if there is a fulfilling ). Therefore, in this paper we aim to discuss the quantum circuit design issues in a realistic way. We discuss, from the circuit design perspective, what kind of applications are suitable for Grover’s algorithm and propose a circuit template for such applications. We begin by showing the main idea about how to design quantum Boolean
database search in a phone book. We show the quantum circuits for establishing an empty database, inserting data, and querying the database. In this process, we found that one has to traverse the entire phone book to build the database. As a result, we point out that it is not practical in a real-world scenario. In the second application, we give a detailed circuit design for breaking a symmetric cryptosystem. Our discussion is based on known plaintext attack. We show how the known plaintext, after encrypted by all possible keys, can be compared with its ciphertext.
Although the search criteria of the two applications we discussed above are quite different, both of them are actu-ally one-way functions. In this perspective, we conclude this paper by proposing a template of quantum circuits to solve well-formulated one-way functions. As a result, we believe that this paper makes the following contributions. First, we give a detailed quantum circuit design for implementing large scale Grover’s algorithm. Second, we extend our circuits to a template for solving any one-way functions.
II. BACKGROUND
A. States and Gates
In quantum mechanics, the state of a single two-level quantum bit (qubit) can be written as a linear combination in a two-dimensional complex vector space as
(1)
where and . The state shown above
ex-hibits a unique phenomenon in quantum mechanics called
su-perposition. When you measure such a particle, the system is
projected to one of its eigenstates (i.e., either or ). The probability for projecting to each state is given by the absolute square of its probability amplitude, i.e., and . Obvi-ously, the sum of and shall be 1 to satisfy the proba-bility rule. Multiple qubits can also form a quantum system. A multi-qubit system is spanned by the basis of the tensor product of each space. For example, the joint state of qubit and qubit
is spanned by , i.e.
(2)
where and .
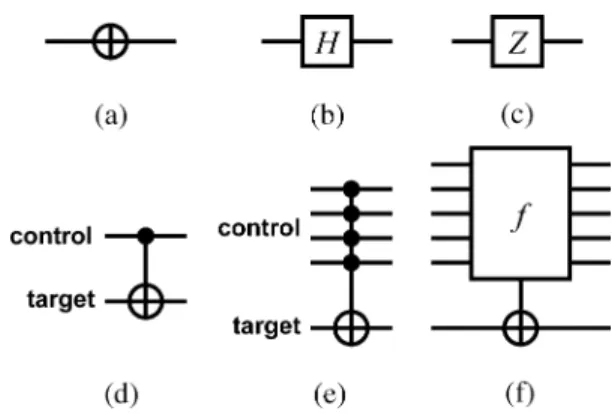
A quantum system can be manipulated in many different ways, called quantum gates. An example is the quantum Not
gate, which functions as
(3)
Fig. 1. Symbols for basic quantum gates.
As a result, when a qubit goes through a quantum gate, the state transforms into . The symbol of an gate is shown in Fig. 1(a). Note that the horizontal line con-necting the input and the output is not a physical wire, instead it represents a qubit under time evolution.
The Hadamard gate is an important gate. It changes the state as
(4) and its symbol is depicted in Fig. 1(b). Another useful quantum gate which shifts the relative phase by is called the gate. The operation can be described as
(5) and its symbol is depicted in Fig. 1(c).
Similarly, a two-bit quantum system can be manipulated using a two-bit gate. For example, a Control-Not gate performs the following transformation:
(6)
More specifically, a gate consists of one qubit, which does not change its value, and a qubit, which changes its value only if the control qubit is . The operation can be written as
, where “ ” denotes exclusive-or (XOR). The symbol of a gate is shown in Fig. 1(d). A generalization of the gate involves multiple control qubits. For example, a
gate is defined as
(7) This gate inverts the target qubit if all the control qubits are ’s. When this gate reduces to the gate described before. The symbol of a generalized gate is shown in Fig. 1(e).
Further generalization can be made if the inversion of the target is controlled by evaluating the control qubits using a given Boolean function. In other words, the target is inverted if the
control qubits satisfy a given Boolean expression, otherwise it is unchanged. The Boolean function can be as simple as evaluating whether the control qubits are all ’s (or ’s), or a compli-cated Boolean expression which is satisfied by more than one Boolean variable assignment. The symbol of such an
-Con-trol-Not gate is shown in Fig. 1(f). Note that, a special case of gates is to invert the target qubit when some of the control bits are ’s (indicated by black dots) and some are
’s (indicated by white circles).
It is interesting that if the target is initially set as
, applying an gate results in an eigenvalue kickback, which causes a phase shift on some components of the input state. This phenomenon is described as follows.
Without loss of generality, we assume the quantum state of the control qubits is
(8)
where is the set of satisfied assignments and S-A is the set of
un-satisfied assignments, i.e., and
.
Due to the linearity of quantum mechanics, we have
(9) which effectively inverts the phase of those satisfied assign-ments, i.e., . This mechanism is used as the basic function in our circuits.
B. Grover’s Algorithm
The main idea of Grover’s algorithm is to first prepare a register in a superposition state with the probability amplitudes uniformly distributed. Then, selectively invert the target and perform an inversion-about-average operation. The selec-tive-inversion followed by an inversion-about-average will cause amplification on the probability amplitude of the target. After such iterations, we have a high probability of getting the target upon a final measurement.
As we can see, the only request in Grover’s algorithm is the information regarding whether an item is the target. This is also known as an oracle. If we label the items in a database with the
integers and denote the label of the unknown marked record by , the oracle is an -bit binary function
(10) defined by
if
otherwise. (11)
Note that, as a standard oracle, we have no access to the internal structure of the function . It operates transparently in Grover’s algorithm as a black-box function, which we can query as many times as we like.
Using the oracle, the selective-inversion can be defined as the following unitary function:
if
otherwise. (12) This function does an inversion on the input if it is the target, while leaving all other cases unchanged. Due to the linearity of quantum mechanics, all items in the database can be processed simultaneously by applying to the superposition state of all items.
Obviously, the operation described above can be written as
(13) and it is actually an inversion in about the hyperplane perpen-dicular to . Following the same notation, if we define
(14) the inversion-about-average operation can be regarded as an in-version in about the hyperplane perpendicular to [23], and
(15) As a result, the operation of a selective-inversion followed by an inversion-about-average can be written as
(16) Based on this operator, Grover’s algorithm can find the target with a high probability (approaching 1) by applying the operator
to the superposition state
(17)
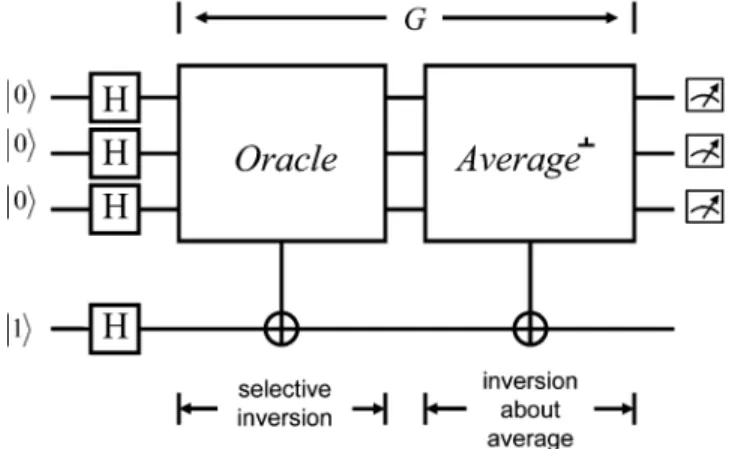
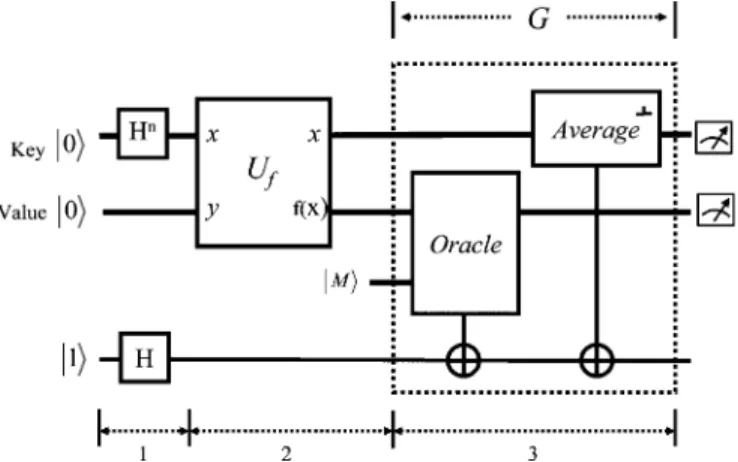
Fig. 2. Circuit block diagram of Grover’s search algorithm.
III. CIRCUITBLOCKDIAGRAM
As described before, the implementation of the operator consists of two parts: selective-inversion , and inversion-about-average . The eigenvalue kickback is used in the construction of these two parts, as shown in Fig. 2.
The initial qubits in Fig. 2 include qubits prepared in the ground state and one auxiliary qubit in the excited state . This can be written as
(18) After the Hadamard transform and , all possible states are superposed as , where
(19) (20)
A. Selective-Inversion
The first part of the circuits is the oracle-Control-Not , as shown in Fig. 2. Theoretically, the oracle is only a func-tion that checks whether a specific item is the target. However, due to the linearity of quantum mechanics, when the oracle is applied to the superposition state , all possible items are examined against the criteria. It follows from the fact that the eigenvalue of , i.e., 1, is kicked back to the target state, so the effectively inverts the target, as
(21) In other words, the circuits are computationally equiv-alent to the operator , which inverts the unknown target in one single operation. Since most practical engineering problems can be binary encoded, searching the target in a database is the same thing as finding a satisfiable solution for a binary Boolean expression. This means the oracle function can be represented by a Boolean logic.
There are two ways to implement such a Boolean logic. The straightforward method uses elementary gates to simulate clas-sical gates includingAND,OR, andNOT, as shown in Fig. 3. Note
Fig. 3. The straightforward implementation of classical (a)NOT, (b)AND, (c)
OR, (d)FANOUTgates.
Fig. 4. Minimum space implementation of a half adder.
that, unlike classical circuits, theFANOUTfunction must be done explicitly by a quantum gate, instead of a metallic contact.
An alternative way that achieves the minimum space con-sumption is based on the concept of permutation. Since an -bit quantum Boolean operation is a permutation on the set of all -bit binary patterns, the desired Boolean function can be achieved on a subset of the qubits [24]. For example, the circuits for a half adder are shown in Fig. 4. However, the construction of the permutation requires a full listing of the truth table, which is as hard as finding the target. As a result, the first method has to be used to construct the oracle circuits.
B. Inversion-About-Average
The second part of the operation is the circuit implementing the function of inversion-about-average. When the operation is applied to a superposition state, it actually keeps the component in the direction unchanged, while inverting the components in dimensions that are perpendicular to . This can be repre-sented as
(22) where
(23) represents the average. Using the same concept of eigenvalue kickback, the component in the dimension can be selec-tively inverted, as shown in Fig. 2. Note that this part of the circuits does not depend on the search criteria.
IV. SEARCHING ASAT SOLUTION
The SAT problem is a well-known problem in theoretical computer science. Given a Boolean expression in conjunctive normal form, the problem of deciding whether this expression has an assignment that satisfies the formula has been shown to be an NP-complete problem [25]. In this section, we will show
Fig. 5. Oracle circuits for a single-target search.
Fig. 6. The circuits of inversion-about-average.
how Grover’s algorithm can be used to find a satisfiable solu-tion for the SAT problem. Without loss of generality, we use the binary expression
(24) as an example. As described before, the circuits of the oracle can be implemented according to the Boolean expression itself, which is shown in Fig. 5. In Fig. 5, gate 1, 2, 3, and 4 copy the input , , and to , , , and , so subsequent operations do not affect the original input. Gate 5, 6, and 7 implement the function , gate 8 inverts , gate 9, 10, and 11 implement the function , and finally gate 12 performs theAND func-tion for these three clauses. The final result is in qubit , which is the control qubit for the selective inversion in Fig. 2. Note that although the three-inputANDfunction can be imple-mented by cascading two two-inputANDgates, it is shown as one gate for simplicity.
The second part of the circuits performs the function of in-version-about-average. To invert the component in the di-mension, Hadamard gates are used to transform to , then the state is selectively inverted. After the inversion, the state is transformed back by another set of Hadamard gates. The cir-cuits can be represented by
(25) as shown in Fig. 6.
Note that the function of is implemented by an eigenvalue kickback. It is shown in Fig. 6 as a generalized gate which
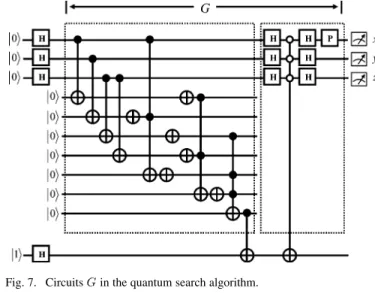
Fig. 7. CircuitsG in the quantum search algorithm.
Fig. 8. Template for recovering the auxiliary qubits.
inverts the target when all the control qubits are ’s. This is shown as white circles, instead of black dots, in Fig. 6. Although it does not affect the measurement, the minus sign in can be implemented by applying a phase of to any one of the qubits. This is shown as the transform in Fig. 6. Note that since this part of the circuits is completely independent of the search criterion, it can be used to do any single- or multi-target search. The complete circuit design for is shown in Fig. 7. After applying times of , a final measurement on qubit , , and will reveal the target with high probability.
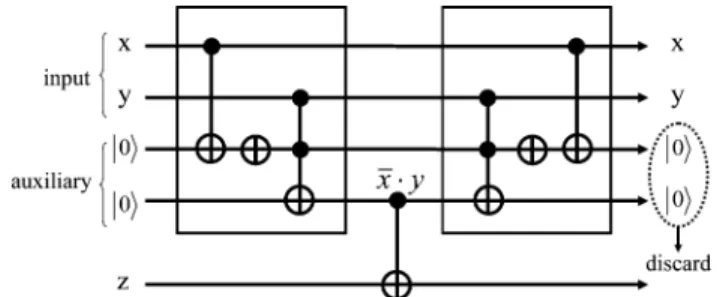
Although the circuits can be used to find the target, the auxil-iary qubits must be restored and discarded to avoid the accumu-lation of qubits and to reduce the extra efforts needed for pre-serving the auxiliary qubits from noise. A general circuit block diagram for removing auxiliary qubits is shown in Fig. 8.
The operation in the figure calculates the result with the help of some auxiliary qubits. Then the qubit representing the result is used as the control qubit of a gate to save the state in . Since quantum operations are reversible by nature, the auxiliary qubits can be restored back to their initial states by simply applying the reverse operation , then they can be discarded safely. In Fig. 9, we give a simple example showing how to implement with the help of auxiliary qubits and how to restore and discard the auxiliary qubits safely.
With the principle described above, auxiliary qubits in Fig. 7 can be removed by applying the gates shown in Fig. 10. Since this part does not affect the result, we will skip the recovering circuits for the rest of this paper in order to make our discussion clear.
The circuit design for a single-object search can be easily generalized to search multiple objects. The only difference is
Fig. 9. Example circuits for recovering the auxiliary qubits.
Fig. 10. Circuits in the reverse order to discard the auxiliary qubits.
Fig. 11. Circuits for searching the first target.
that, after each target is found, the oracle has to be modified to exclude this target. A typical scenario is shown in the following example.
Assuming the problem is binary encoded as
(26) the oracle for searching the first target is shown in Fig. 11. In these circuits, gate 1 copies the variable , gate 2, 3, and 4 im-plement the function , and finally gate 5 performs the
ANDfunction for these two clauses. Then, the circuits followed by the same circuits in Fig. 6 implement the operation for the first target. A final measurement after times of gives one of the targets with equal probability.
Fig. 12. Circuits for searching the second target.
Fig. 13. Circuits for searching the third target.
After the first measurement, the same process is repeated again, the only difference is that the oracle is modified to ex-clude the target that has been found. Assuming the first result is
, , , the oracle is now modified as
(27) The clause is used to exclude the target , , and . The new oracle is shown in Fig. 12. In these circuits, gate 7, 8, and 9 are used to implement . Then, gate 10 gives the oracle’s result. This new oracle and the same circuits of inversion-about-average are used to find the second target.
Similarly, assuming the result of the second measurement is , , and , the third oracle is then changed to be
(28) The new clause is added to exclude the second target. The oracle is shown in Fig. 13. Again, gates 10 and 11 are used to implement the new criterion , gate 12 gives the result
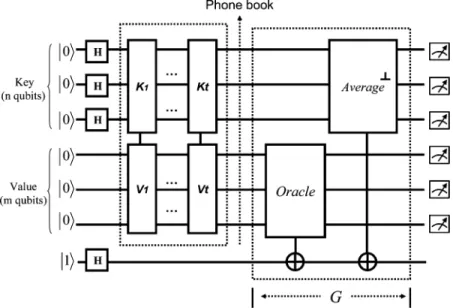
Fig. 14. Quantum circuits for searching a phone book.
of the new oracle. This new oracle, together with the circuits of inversion-about-average, is used to find the third target.
V. SEARCHING IN APHONEBOOK
In this section, we give the circuits for applying the Grover’s algorithm to a phone-book-like database searching problem. Al-though this is a well-known example of Grover’s algorithm, it is not so practical from a circuit point of view. We will give more discussions about the drawbacks at the end of this sec-tion. The scenario of the “phone book searching” problem is described as follows. Imagine that one day you miss a phone call, but fortunately you have caller ID and the phone number is recorded in the phone. Based on the number and a phone book, you decide to find who was calling you. Since a classical phone book is sorted by name, there is no easy way to iden-tify the caller except to browse through all the entries until you find the number. Assuming the size of the phone book is , the number of entries you have to search is on average , while in the worst case you would have to search all the entries (which could be thousands or millions of entries). In addition to finding the phone number, we also want to retrieve other asso-ciated information about the number (i.e., name and address). Although it is often cited that Grover’s algorithm can help iden-tify the phone number with only queries, they are usually mentioned without further explanation or implementa-tion. In fact, with a little more consideration, the problem inher-ently has some drawbacks in realizing the circuits and is actually not a good example. In the following we will show the detailed circuits about how a phone book is encoded and why such ap-plication is not practical.
The structure of each entry in a phone book is naturally a pair of (key, value). Classically, the key is the name while the value includes other associated information such as the number and/or address. Without loss of generality, we assume that there are no duplicate names in the phone book, and each name (the key) is encoded as an -bit binary string so they can be represented as . This means the number of entries in the phone book is . Similarly, the numbers (the value) are encoded
as -bit binary strings. As a result, in a quantum phone book, all the entries are superposed like
(29) which is equivalent to
The circuits for encoding a phone book are shown in Fig. 14. It consists of two parts. The first part is for establishing an empty phone book while the second part is for inserting data into the phone book.
The qubits in a quantum phone book are separated into two groups ( key-qubits and value-qubits). Initially all the key qubits and value qubits are in the state. This can be written as
(31) By applying the Hadamard gates, the state of the key-qubits are transformed into a uniform superposition of all possible states
. The resulting state is
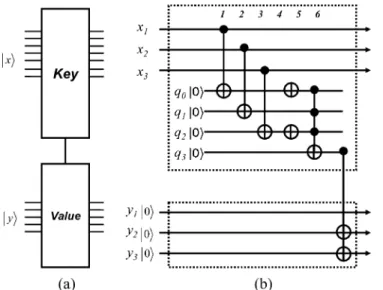
Note that an entry with its as indicates an in-valid entry. As a result, (32) is an empty phone book with keys (names) ranging from to . With an empty quantum phone book, the data can be inserted with a key-control-value gate, as shown in Fig. 15(a). The key-control-value gate includes a key gate and a value gate, each with input qubits and . If the key gate with input state evaluates true, the value gate will be applied on the qubits. Otherwise, it does nothing. A sample key-control-value gate is shown in Fig. 15(b). In this example, if the input state satisfies (which
Fig. 15. (a) Key-control-value gate. (b) Implementation example.
means , , ), then it changes
from to . Otherwise it does nothing. In other words, the key gate is a simple comparison gate, which outputs true if the input state equals to a specific value and otherwise it out-puts false. And if the key gate outout-puts true, the value gate is ap-plied on the values qubits, which functions as storing the value into the value qubits. Therefore, if we pass the empty quantum
phone book through
key-control-value gates, each gate will record one key(name) with the cor-responding value(number) into the phone book.
After inserting all the data, the quantum phone book becomes
(33)
with all entries in a uniform distribution. The description above only shows how a quantum phone book is encoded. It has nothing to do with the searching process. The searching process is described in the following paragraphs.
As illustrated, the effect of the gate is to apply a phase of if the input state is the target (i.e., the state satisfies the or-acle). It is noteworthy that, the oracle can be applied to selected groups of qubits according to a specific query condition. For example, assuming the query is to find a given phone number (which is much harder for a classical computer), the oracle cir-cuits can be applied on the “value-qubits” only, as illustrated in Fig. 14. For each entry state , it only checks if the “value-qubits” are equal to the query string and flips the sign of its amplitude accordingly. Note that the same mechanism can also be used to query the “key-qubits” with equal cost in com-plexity. As a matter of fact, the database can be designed as , in which case it can be queried either by name, number, or address (or any combination) and get all other information after applying times of . The only trick is to apply an appropriate oracle on appropriate qubits. This means, unlike in a classical phone book, searching a phone book by either name or number is equal in terms of computation complexity.
(34) to
(35)
where and , are key and value
respec-tively. The query process is applied times to enhance the probability of getting the target. A final measurement will reveal the target with a high probability. Thus, we can find the target information (number) and get other associated informa-tion such as name and address at the same time.
By applying the Grover’s algorithm, the query process can be speed-up without problem. However, the solution has sev-eral drawbacks. The first and the most obvious one is that the database has to be built before the search process, and it takes steps to build the database. Once the database is built, it means that the entire database has been traversed once, and any searching problem can be done in constant time. The second problem is that the database would have to be completely re-constructed after each query, because each query is ended with a measurement and that will destroy the whole quantum database due to the collapse of quantum state. Another problem is that, in our quantum circuit design methodology, we say that the query condition can be applied on any field of the data (name, number, or even a subset of a name), which is an improvement in com-parison to the classical way. The query condition can be decided until the query stage, with no influence on the query complexity. However, a classical database can also achieve this by making indexes on all combination of the fields before querying after database construction. (Though it would be a heavy loading for if the data is stored in bits, it would have to be make kinds of indexes.)
VI. BREAKINGSYMMETRICCRYPTOSYSTEMS
A classical phone book can be regarded as a function
(36) which takes a name as the input and a corresponding number as the output. This function is a one-way function since it is easy to find the number for a given name, but it is hard to find a name for a given number. However, the circuits we illustrated in the previous section can help find the corresponding name for a given number (which is the reverse function) more efficiently. Enlightened by this fact, we find this method can be used to break some cryptosystems that rely on one-way functions. In this section, we use a DES-like symmetric cryptosystem as an example to show how this can be done with quantum circuits.
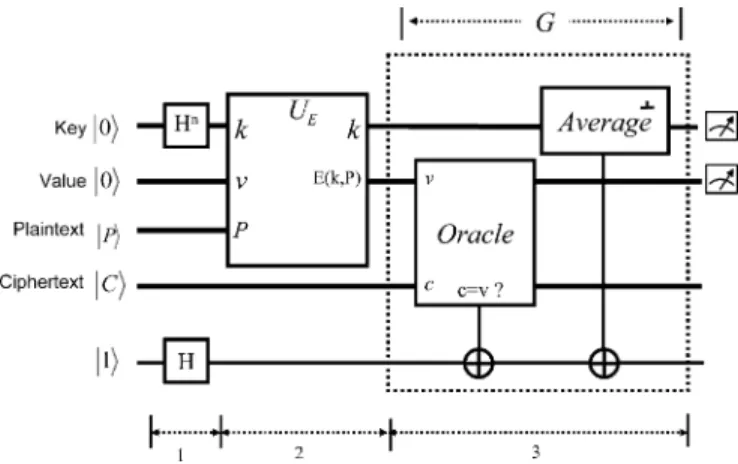
Fig. 16. Quantum circuits for attacking a symmetric encryption algorithm.
To attack a symmetric cryptosystem, the most straightforward way is to try all possible bit patterns with brute force until the correct key is identified. In order to identify the correct key, methods like “known plaintext attack” and “chosen plaintext at-tack” are used in case the attacker has access to some (plaintext, ciphertext) pairs. This is possible because some plaintext has special formats (like the header of an e-mail), or the attacker can feed plaintext of his choice to the encryption device and get the corresponding ciphertext. The only unknown part is the encryp-tion key. If brute force attack is used, the exponential key space is a problem for a classical computer. This is because commands are serially processed in a classical computer. With quantum parallelism, we will show how quantum circuits can help attack a symmetric cryptosystem more efficiently.
A general symmetric cryptosystem takes the key and a plain-text as the input and outputs one cipherplain-text as
(37) where and stands for plaintext and ciphertext respectively. Given encryption algorithm , one plaintext , and the corre-sponding ciphertext , the problem is to find the key such that (37) is met.
The quantum circuits for such an exhaustive search are illus-trated in Fig. 16. As shown in the figure, there are four input registers, key, value, plaintext and ciphertext. If the encryption algorithm uses a 56-bit encryption key, there would be 56 qubits in the key register . At the initializing stage, the key register is initialized to a superposition of all possible key states by Hadamard transformations, while the qubits in the value reg-ister are all initialized to ’s. The other two registers store the plaintext and the ciphertext .
In the second stage, the encryption algorithm is represented by a unitary gate , with the function
(38) The state of the qubits before the unitary gate is , which represents a superposition of all possible keys, each with a corresponding value as . After applying the operation, the state would then be transformed into .
In other words, with a single operation, we get all possible (key, ciphertext) pairs.
In the third stage, we use Grover’s operation to find the one that matches the real ciphertext from all possible cases . For these matches, the corresponding key is the answer. The oracle simply compares the two inputs. It outputs true when they are the same, otherwise it outputs false. Then the inversion-about-average follows as usual to amplify the probability amplitude of the target. Therefore, after
Grover’s iterations, a final measurement gives the key that
satisfies .
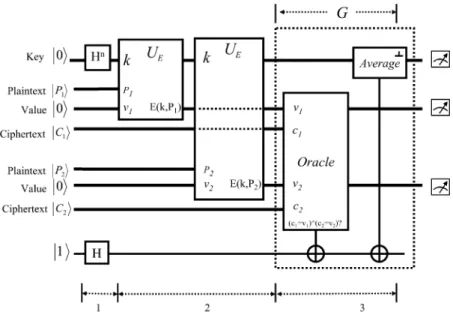
It is noteworthy that the probability of successfully finding the correct target does not increase with the number of itera-tions. Furthermore, as denoted in [4], the precise number of it-erations of Grover’s operation depends on the number of solu-tions. In other words, the precise number of iterations with mul-tiple solutions is different from that with only one solution. In Fig. 16 we assume that there is one and only one target, so we use one (plaintext, ciphertext) pair to check the validity of the target key. However, there might be another key that also sat-isfies (37). Therefore, the more (plaintext, ciphertext) pairs are used, the more precise we can determine the correct key. With this consideration, we illustrate the circuits for multiple known (plaintext, ciphertext) pairs in Fig. 17. In this example,
and are two known pairs, two unitary encryption op-erations are used and the oracle has to test whether both known pairs are satisfied, i.e.,
and (39)
This eliminates the ambiguity when multiple keys satisfying (37) and enhances the efficiency.
VII. IMPLEMENTATION ANDANALYSIS
Physical realization of a scalable quantum computer is a challenge [26]–[28]. One of the primary difficulties is how to keep the components of the computer in a coherent state, while still allowing initialization, control, and measurement. David DiVincenzo [27] has listed some criteria for building a practical quantum computer. Different technologies including silicon-based solutions [29]–[31], polarized photons [32], [33], and nuclear magnetic resonance (NMR) [34]–[36] have also been experimentally demonstrated recently. Taking NMR as an example, information is carried by nuclei in molecules and Radio Frequency (RF) pulses that manipulate nuclear spin orientations are used to implement a quantum operation. The effect of a RF pulse depends on three factors: the power level, the duration, and the direction. For example, a single-qubit gate which performs rotations about can be implemented with RF pulses along in the rotating frame for a specific time under a predefined power level. Besides, a CN gate can be implemented by a free evolution time of , where is the coupling constant [37]. Since the set of single-qubit rotation and CN gate is universal [38], [39], these two gates are sufficient to implement any quantum circuits. In the following paragraphs, we use the DES cracking problem as an example
Fig. 17. Attacking a symmetric cryptosystem with multiple known (P,C) pairs.
to compare the performance of quantum circuits with classical computers.
The DES algorithm [40] enciphers a 64-bit plaintext by a 64-bit key, of which 56 bits as effective key and 8 bits for parity checking. The enciphering consists of three stages: an initial permutation IP, 16 rounds of key-dependent computation, and finally a permutation , which is the inverse of the initial permutation. It is noteworthy that the permutation for classical bits and the key scheduling process correspond to nothing but changing the order of qubits and hence no quantum gate has to be applied. As a result, we have to deal with only the ciphering function. The ciphering function used in this algorithm has four stages: expansion, key mixing, substitution, and permu-tation.
1) Expansion: The input is expanded from 32 bits to 48 bits by linear permutation and duplicating some bits according to a predefined table. The permutation takes no quantum gate and the duplication process can be performed by
CN gates. Since the 16 CN gates can be done at the same time, expansion can be accomplished in one (quantum) gate delay.
2) Key mixing: PerformXORon the generated 48 bits and a
subkey. All theXORoperations can be done by gates at the same time and therefore be executed in one (quantum) gate delay.
3) Substitution: The output is then divided into 8 blocks of 6 bits each. Each block goes through its selection function, which uses a table to specify the mapping from the 6-bit value to its corresponding 4-bit value. In quantum circuits, each table can be performed using generalized
gates [like the key-value gate in Fig. 15(a)]. Since these operations are applied sequentially, it takes quantum gates to accomplish the substitution.
4) Permutation: A final permutation is applied. However, as before, no quantum gate is needed in this process. In summary, the total number of quantum gates in the ci-phering function is . The ciphering function is then used in the key-dependent part of the algorithm, which
includes 16 rounds of identical computation (under control of 16 subkeys). Assuming the 64-bit input of each round is rep-resented as [ is the left half block (32 bits) and is the right half block (32 bits)], each round passes and a subkey through the ciphering function , then performs anXORon
the output of and . TheXORresult becomes the new and
the original becomes the new . The new cascaded is the input to the next round. In this stage, the exchange of takes no quantum gate as discussed before and theXOR opera-tions can be performed by CN gates. Since theXORoperations are performed on each qubit in parallel, each round takes 66 (ci-phering function) plus 1 (XOR) quantum gates. As a result, this key-dependent part takes a total of quantum gates (delay).
Other quantum gates involved in searching the target include 1 level of Hadamard gates to prepare the initial superposition and some quantum gates for Grover’s iteration (oracle and inver-sion-about-average). The oracle in Grover’s operation simply compares the two registers by performingXORon each qubit and then uses a generalized gate to check if these two regis-ters are the same. Since theXORon each qubit can be performed
in parallel, this process totally costs 2 quantum gates (delay). As to the circuits for inversion-about-average, 4 quantum gates (delay) are needed, as illustrated in Fig. 6. Since the oracle and the inversion-about-average are iterated for times, there will be a total of gates delay. Overall,
it takes quantum gates in terms
of duration.
Taking one experiment we have performed on a Bruker Avance DMX-500-MHz NMR system [36] as an example. With a quantum computer which uses atom in carbon-13 labelled chloroform as the information carrier and sets the power of the pulses at 3.00 dB, the duration for a pulse is 9.5 s. In this scale, it takes about 3.3 h to crack a DES key. Compared with a classical technology record [41], in which a DES key is cracked in 22 h and 15 min (by Distributed.Net [42], Electronic Frontier Foundation’s DES Cracker [43], and nearly 100 000 computers on the Internet),
Fig. 18. Template quantum circuits for a general exhaustive search.
the proposed quantum circuits outperform the classical solution in a significant way. It is worth noting that this example is in a relatively small key space. Since the speed-up of Grover’s algorithm is quadratic, there will be a dramatic difference as the key space increases.
VIII. CONCLUSION
Due to its wide application in classical engineering prob-lems, Grover’s algorithm is an example application that can take advantage of quantum mechanics to perform nanoscale puting. This algorithm allows a quadratic improvement com-pared with classical brute force search. The algorithm is built on top of two key operations, namely: selective inversion and inversion-about-average. In this paper, we present how quantum Boolean circuits can be used to implement the selective inver-sion and inverinver-sion-about-average in the quantum search algo-rithm. We give detailed circuit designs for three applications. The first application is for solving problems that are expressed in Boolean function. The other two applications include searching in a phone book and attacking a symmetric cryptosystem. As previously discussed, though these two examples are usually referred in explanation of Grover’s algorithm, they are quite different when implemented with quantum circuits. The main reason is that each record in a database is different and cannot be formulated effectively. As a contrast, the key-value pair in a cryptosystem has a very specific formulation, which can be ap-plied to all the keys.
As a matter of fact, not any problem involving a brute-force search can be solved by the proposed quantum circuit design method. The problem can only be applied in the following situation: Given a one-way function
and a -bit integer , the purpose is to find an -bit integer such that . The template circuits for solving such a one-way function is shown in Fig. 18. The first step in Fig. 18
prepares a superposition of . Then the
second step applies a unitary gate implementing the function to get . The third step is the Grover’s iteration which consists of the oracle and inversion-about-av-erage as described before. Finally, the result can be obtained with a measurement.
REFERENCES
[1] C. Bennett and G. Brassard, “Quantum cryptography: Public key dis-tribution and coin tossing,” in Proc. Int. Conf. Comput. Syst. Signal
Process., 1984, pp. 175–179.
[2] P. Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” in Proc. 35th Annu. Symp. Foundations Comput. Sci., Santa Fe, NM, USA, 1994, pp. 124–134.
[3] L. Grover, “A fast quantum mechanical algorithm for database search,” in Proc. 28th Ann. ACM Symp. Theor. Comput., 1996, pp. 212–219. [4] M. Boyer, G. Brassard, P. Hoyer, and A. Tapp, “Tight bounds on
quantum searching,” Fortschritte Der Phys., vol. 46, pp. 493–506, 1998.
[5] C. Zalka, “Grover’s quantum searching algorithm is optimal,” Phys.
Rev. A, vol. 60, pp. 2746–2751, 1999.
[6] G. Chen, S. A. Fulling, and J. Chen, , R. K. Brylinski and G. Chen, Eds., “Generalization of grover’s algorithm to multiobject search in quantum computing, part i, continuous time and discrete time,” in Mathematics
of Quantum Computation. Boca Raton, FL: CRC, 2002, pp. 135–160. [7] B. Ofer, S. Daniel, and S. Yishai, “Analysis of grover’s quantum search algorithm as a dynamical system,” Phys. Rev. A, vol. 68, p. 022326, 2003.
[8] L. Accardi and R. Sabbadini, A Generalization of Grover’s Algorithm. ArXiv Quantum Physics e-Prints, Cornell Univ., Ithaca, NY, Dec. 2000 [Online]. Available: http://www.arxiv.org/abs/quant-ph/0012143 [9] G. Alber, M. Musinger, and A. Delgado, “Dynamical stabilization of
Grover’s algorithm with embedded quantum codes,” in Proc. SPIE, 2001, vol. 4429, pp. 37–51.
[10] A. Galindo and M. A. Martin-Delgado, “Family of Grover’s quantum-searching algorithms,” Phys. Rev. A, vol. 62, p. 62303, 2000. [11] S. Aaronson, “Lower bounds for local search by quantum arguments,”
in Proc. 36th. ACM Symp. Theor. Comput., 2004, pp. 465–474. [12] A. Ambainis, “Quantum search algorithms,” SIGACT News, vol. 35,
no. 2, pp. 22–35, 2004.
[13] A. N. Soklakov and R. Schack, Efficient State Preparation for a Reg-ister of Quantum Bit. ArXiv Quantum Physics e-Prints, Cornell Univ., Ithaca, NY, Nov. 2005 [Online]. Available: http://www.arxiv.org/abs/ quant-ph/0408045
[14] C. Durr and P. Hoyer, A Quantum Algorithm for Finding the Minimum. ArXiv Quantum Physics e-Prints, Cornell Univ., Ithaca, NY, Jan. 1999 [Online]. Available: http://xxx.lanl.gov/quant-ph/9607014
[15] H. Buhrman, C. Durr, M. Heiligman, P. H. Yer, F. Magniez, M. Santha, and R. de Wolf, “Quantum algorithms for element distinctness,” in
Proc. Computational Complexity. 16th Annu. IEEE Conf., Chicago, IL,
2001, pp. 131–137.
[16] S. Okubo, T. Nishino, K. Ohta, and N. Kunihiro, “A quantum algorithm for finding the minimum on nmr quantum computers,” in Proc. ERATO
Workshop Quantum Inf. Sci., 2004, pp. 152–153.
[17] G. Brassard, P. Hoyer, and A. Tapp, “Quantum cryptanalysis of hash and claw-free functions,” in Proc. LATIN’98, 1998, pp. 163–169. [18] G. Brassard, P. Hoyer, and A. Tapp, “Quantum counting,” in Proc. 25th
Int. Colloquium Autom., 1998, pp. 820–831.
[19] Z. Diao, Z. M. Suhail, and G. Chen, “A quantum circuit design for grover’s algorithm,” Phys. Rev. Lett., vol. 57, pp. 701–708, 2002. [20] J. Roland and N. J. Cerf, “Quantum-circuit model of Hamiltonian
search algorithms,” Phys. Rev. A, vol. 68, p. 62303, 2003.
[21] L. Xiao and J. A. Jones, “Robust logic gates and realistic quantum com-putation,” Phys. Rev., vol. 73, p. 032334, 2006.
[22] I. M. Tsai, S. Y. Kuo, and D. Wei, “Quantum boolean circuit approach for searching an unordered database,” in Proc. 2nd IEEE Conf.
Nan-otechnology, 2002, pp. 315–318.
[23] S. Lomonaco, Grover’s Quantum Search Algorithm. ArXiv Quantum Physics e-Prints, Cornell Univ., Ithaca, NY, Oct. 2000 [Online]. Avail-able: http://www.arxiv.org/abs/quant-ph/0010040
[24] I. M. Tsai and S. Y. Kuo, “Quantum Boolean circuit construction and layout under locality constraint,” in Proc. 1st IEEE Conf.
Nanotech-nology, 2001, pp. 111–116.
[25] S. A. Cook and D. G. Mitchell, “Finding hard instances of the satisfi-ability problem: A survey,” in Satisfisatisfi-ability Problem: Theory and
Ap-plications, Du, Gu, and Pardalos, Eds. New York: American Mathe-matical Society, 1997, vol. 35, pp. 1–17.
[26] IBMs Test-Tube Quantum Computer Makes History: First Demon-stration of Shors Historic Factoring Algorithm, IBM Research News, Yorktown, NY, Dec. 2001 [Online]. Available: http://www.domino.re-search.ibm.com/comm/pr.nsf/pages/news.20011219_quantum.html [27] D. P. DiVincenzo, “The physical implementation of quantum
89, p. 017901, 2002.
[31] R. G. Clark et al., “Progress in silicon-based quantum computing,” Roy.
Soc. London Trans. Series, vol. 361, pp. 1451–1471, 2003.
[32] P. G. Kwiat, J. R. Mitchell, P. D. D. Schwindt, and A. G. White, “Grover’s search algorithm: An optical approach,” J. Modern Opt., vol. 47, pp. 257–266, 2000.
[33] J. L. O’Brien, G. J. Pryde, A. G. White, T. C. Ralph, and D. Branning, “Demonstration of an all-optical quantum controlled-not gate,” Nature, vol. 426, pp. 264–267, 2003.
[34] N. Gershenfeld and I. Chuang, “Bulk spin-resonance quantum compu-tation,” Sci, vol. 275, no. 5298, pp. 350–356, Jan. 17, 1997. [35] T. F. Havel, S. S. Somaroo, C.-H. Tseng, and D. G. Cory, “Principles
and demonstrations of quantum information processing by NMR spec-troscopy,” Appl. Alg. Eng., Commun., Comput., vol. 10, pp. 339–374, 2000.
[36] I. M. Tsai, S. Y. Kuo, S. L. Huang, Y. C. Lin, and T. T. Chen, “Experi-mental realization of an NMR quantum switch,” in Proc. ERATO Conf.
Quantum Inf. Sci., 2004.
[37] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum
Information. Cambridge, U.K.: Cambridge Univ. Press, 2000. [38] D. DiVincenzo, “Two-bit gates are universal for quantum
computa-tion,” Phys. Rev., vol. 51, no. 2, pp. 1015–1022, Feb. 1995.
[39] A. Barenco, “A universal two-bit gate for quantum computation,” Proc.
Roy. Soc. Lond., vol. 449, pp. 679–683, 1995.
[40] Data Encryption Standard, NIST, Boulder, CO, Oct. 1999 [On-line]. Available: http://www.csrc.nist.gov/publications/fips/fips46-3/ fips46-3.pdf
[41] DES Challenge III, RSA, Bedford , MA, Jan. 1999 [Online]. Available: http://www.rsa.com/rsalabs/node.asp?id=2108
[42] Distributed.Net, Distributed Computing Technologies, Jan. 1999 [On-line]. Available: http://www.distributed.net/des
[43] Electronic Frontier Foundation, Cracking DES: Secrets of
Encryp-tion Research, Wiretap Politics and Chip Design. Sebastopol, CA: O’Reilly, 1998.
Yi-Lin Ju received the B.S. and M.S. degrees in
computer science and information engineering from National Taiwan University, Taipei, Taiwan, R.O.C., in 2000 and 2002, respectively. She is currently working toward the Ph.D. degree in the Department of Electrical Engineering at the same university.
Her current research interest is quantum informa-tion processing.
Since 1993, he has been with Chunghwa Telecom-munication Laboratories, Taoyuan, Taiwan, R.O.C., where he works on circuit design, broadband switching, information security, and network ar-chitecture evolution. His research fields include experimental and theoretical aspects of quantum computing and quantum communication.
Sy-Yen Kuo (S’85–M’88–SM’98–F’01) is a Chair
Professor and Dean of the College of Electrical and Computer Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan. He is also a Distinguished Professor at the Department of Electrical Engineering, National Taiwan University where he is currently taking a leave of absence and was the Chairman at the same department from 2001 to 2004. He received the BS (1979) in Electrical En-gineering from National Taiwan University, the MS (1982) in Electrical & Computer Engineering from the University of California at Santa Barbara, and the PhD (1987) in Computer Science from the University of Illinois at Urbana-Champaign. He spent his sab-batical years as a Visiting Professor at the Computer Science and Engineering Department, the Chinese University of Hong Kong from 2004–2005 and as a visiting researcher at AT&T Labs-Research, New Jersey from 1999 to 2000, respectively. He was the Chairman of the Department of Computer Science and Information Engineering, National Dong Hwa University, Taiwan from 1995 to 1998, a faculty member in the Department of Electrical and Computer Engineering at the University of Arizona from 1988 to 1991, and an engineer at Fairchild Semiconductor and Silvar-Lisco, both in California, from 1982 to 1984. In 1989, he also worked as a summer faculty fellow at Jet Propulsion Laboratory of California Institute of Technology. His current research interests include dependable systems and networks, software reliability engineering, mobile computing, and reliable sensor networks. Professor Kuo is an IEEE Fellow. He has published more than 270 papers in journals and conferences, and also holds several patents. He received the distinguished research award between 1997 and 2005 consecutively from the National Science Council in Taiwan and is now a Research Fellow there. He was also a recipient of the Best Paper Award in the 1996 International Symposium on Software Reliability Engineering, the Best Paper Award in the simulation and test category at the 1986 IEEE/ACM Design Automation Conference(DAC), the National Science Foundation’s Research Initiation Award in 1989, and the IEEE/ACM Design Automation Scholarship in 1990 and 1991.