國
立
交
通
大
學
電信工程研究所
碩 士 論 文
室內多入多出天線正交分頻多工系統節能演算
法之研究
A Study on Power-Saving Algorithms for Indoor
MIMO-OFDM Systems
研 究 生:鄭學璟
指導教授:黃家齊 博士
室內多入多出天線正交分頻多工系統節能演算法之研究
A Study on Power-Saving Algorithms for Indoor MIMO-OFDM
Systems
研 究 生: 鄭學璟
Student: Shiue-Jing Cheng
指導教授: 黃家齊 博士
Advisor: Chia-Chi Huang
國立交通大學
電信工程研究所
碩士論文
A Thesis
Submitted to Institute of Communications Engineering College of Electrical Engineering
National Chiao Tung University in partial Fulfillment of the Requirements
for the Degree of Master
In
Communications Engineering August 2014
Hsinchu, Taiwan, Republic of China
室內多入多出天線正交分頻多工系統節能演算法之研究
研究生:鄭學璟
指導教授:黃家齊 博士
國立交通大學電信工程研究所 碩士班
摘
要
在本論文中,多天線輸入多天線輸出正交分頻多工系統節省功率演算法被提出。我 們分別考慮兩種不同的情況:(1) 通道狀態資訊在接收端已知;(2) 通道狀態資訊在傳送端 已知。另外,以延長一個移動裝置的電池使用時間而言,我們要降低它的總功率消耗 其中包含傳送的功率消耗及電路的功率消耗。我們的設計目標是要最小化總功率消耗 同時滿足資料傳輸率和位元錯誤率的要求。此論文中揭露了單天線輸入單天線輸出系 統較適合使用在路徑損耗小的情形,而分集階數較高的方法適合使用在路徑損耗較大 的情形。除此之外,我們所提出的演算法可以利用路徑損耗決定最佳的傳送和接收方 式進而減少設計複雜度。A Study on Power-Saving Algorithms for Indoor MIMO-OFDM
Systems
Student: Shiue-Jing Cheng
Advisor: Dr. Chia-Chi Huang
Institute of Communication Engineering
National Chiao Tung University
ABSTRACT
In this thesis, power-saving algorithms for multiple-input multiple-output (MIMO) orthog-onal frequency division multiplexing (OFDM) systems are proposed. We design algorithms for two cases individually: (1)channel state information (CSI) is available at receiver; (2)CSI is available at transmitter. Besides, in order to extend the battery life of a mobile device, we should reduce the total power consumption, which includes both transmit power consump-tion and circuit power consumpconsump-tion. We aim to minimize the total power consumpconsump-tion while meeting the data rate and bit error rate (BER) requirements. It is revealed in this thesis that single-input single-output (SISO) system is preferable in small path loss situations, whereas schemes with higher diversity order are preferable in large path loss situations. Moreover, it is observed that the optimal transmit and receive schemes can be determined by path loss, thus significantly reducing design complexity.
誌
謝
在碩士班期間非常感謝指導教授黃家齊老師的春風化雨,讓我有機會以更高的視野了 解專業領域且學習以圓融的態度待人處事。另外也非常感謝馬峻楹和蕭煒翰學長,你 們就像是知識的寶庫,我在你們身上得到很多專業知識及靈感,讓我在課業及研究上 事半功倍。再來要感謝實驗室一起努力的夥伴潘駿逸、謝昕峰、鍾孟剛和尹佳樂,跟 你們一起享樂患難,豐富了我的研究所生活。另外也要感謝實驗室充滿活力的學弟們, 是你們讓實驗室生氣蓬勃,期許你們在未來的研究都能順利。最後還要感謝我的家人 和女朋友熊柔雲,你們的支持與鼓勵是我最大的動力,讓我完成研究所兩年的學業。Contents
中文摘要 i
ABSTRACT ii
誌謝 iii
List of Tables vi
List of Figures vii
1 Introduction 1
1.1 IEEE 802.11ac WLAN . . . 2
1.1.1 Multiple Antennas and Multi-User MIMO . . . 2
1.1.2 Channel Bandwidth . . . 3
1.1.3 Modulation and coding schemes . . . 3
1.2 Pre-Coding MIMO System . . . 4
1.3 Thesis Organization . . . 4
2 System Model 6 2.1 Transceiver Front-End Structure . . . 6
2.2 MIMO-OFDM Signal Model . . . 8
3 Optimal Design to Reduce Total Power Consumption with CSIR 11 3.1 Problem Formulation . . . 11
3.2 STBC and Spatial Multiplexing Signal Model . . . 13
3.3 Solving Problem . . . 19
3.4 Simulation Results . . . 20
3.4.1 Power Consumption Performance in CSIR Scenario . . . 21
3.4.2 Trends in the Power Saving Algorithm in CSIR Scenario . . . 24
4 Optimal Design to Reduce Total Power Consumption with CSIT 26 4.1 Problem Formulation . . . 26
4.2 Solving Problem . . . 28
4.2.1 Pre-coder and Decoder Weighting Design . . . 28
4.2.2 Power Loading . . . 30
4.2.3 Antenna Selection . . . 32
4.3 Complexity Reduction by Antenna Number Selection . . . 34
4.4 Simulation results . . . 35
4.4.1 Power Consumption Performance in CSIT Scenario . . . 36
4.4.2 Trends in the Power Saving Algorithm in CSIT Scenario . . . 39
4.5 Antenna Number Selection by Path Loss . . . 41
5 Conclusion 42
List of Tables
1.1 Modulation and coding schemes of IEEE 802.11ac . . . 3
1.2 Mandatory and optional features of IEEE 802.11ac . . . 4
3.1 Transmit and receive schemes for CSIR case . . . 19
3.2 System parameters. . . 21
3.3 Power consumption parameters. . . 21
4.1 System parameters. . . 35
List of Figures
2.1 MIMO-OFDM transceiver front-end structure. . . 6
2.2 MIMO-OFDM transmitter model. . . 8
2.3 MIMO-OFDM receiver model. . . 8
2.4 Pre-coded MIMO-OFDM transmitter model. . . 9
2.5 Pre-coded MIMO-OFDM receiver model. . . 10
3.1 Alamouti 2ˆ1 STBC block diagram. . . 13
3.2 Alamouti 2ˆ2 STBC block diagram. . . 14
3.3 Circuit power of each transmit and receive scheme in CSIR case. . . 22
3.4 Power of power amplifier of each transmit and receive scheme in CSIR case. . 23
3.5 Total power of each transmit and receive scheme in CSIR case. . . 23
3.6 Optimum selection for the proposed method in CSIR case. . . 25
3.7 Total power for the outperforming schemes on different path loss in CSIR case. 25 4.1 Circuit power of each transmit and receive scheme in CSIT case. . . 37
4.2 Power of power amplifier of each transmit and receive scheme in CSIT case. . 37
4.3 Total power of each transmit and receive scheme in CSIT case. . . 38
4.4 Optimum selection for antenna number selection method in CSIT case. . . 40 4.5 Total power for the outperforming schemes on different path loss in CSIT case. 40
Chapter
1
Introduction
Recently, there is an explosively growing interest on the topic of power-saving, as the issue of carbon reduction and energy conservation has been brought to public attention. Hence, the power-saving algorithms for communication systems have massively been investigated. However, in traditional designs, most attention was put on minimizing the transmit power only. In order to extend the battery life of a mobile device, not only transmit power consumption but also circuit power consumption should be minimized. As pointed out by [1], [2], the traditional belief that MIMO systems are more energy-efficient than SISO systems may be misleading when both the transmission energy and the circuit energy consumption are considered. Since Shuguang Cui published [1], [2] in year 2004, numerous power-saving algorithms that consider both transmit power consumption and circuit power consumption, e.g., [3], [4] have been proposed.
Conventional adaptive modulation and coding Schemes (AMC) attempted to achieve the highest data rate while keeping the error rate at or below a target [5]. However, the highest data rate is sometimes over the budget actually required; therefore, it is a waste on power consumption. From the power-saving point of view, we suggest to use the transmit and receive scheme having minimum power consumption while meeting the target data rate and BER.
In this work, we propose power-saving methods and apply these methods to IEEE 802.11ac which is a next-generation wireless local area network (WLAN) standard [6]. We define the terminology total power consumption, as the summation of transmit power consumption and circuit power consumption. Obviously, it is necessary to design an algorithm that jointly
considers total power consumption, data rate, and bit error rate (BER), for they are the key features affecting users’ experience. With regard to this design, we considered two scenarios. In the first scenario, we consider the case that CSI is available at receiver only. The total power consumptions of different MIMO transmission schemes, such as space-time block coding (STBC) and spatial multiplexing with different data detectors such as, zero-forcing (ZF), minimum mean square error (MMSE), and maximum likelihood (ML) can be evaluated at receiver. Afterwards, the transmit and receive scheme with minimum total power consumption is selected and used for transmission. In the second scenario, we consider the case that CSI is available at transmitter. Thus, pre-coding and power loading schemes can be used to minimize the transmit power while meeting the BER constraint. Furthermore, we used a global search method and complexity reduction methods to find the suitable transmit and receive antennas so that the total power consumption can be reduce.
1.1 IEEE 802.11ac WLAN
The next-generation standard IEEE 802.11ac, which is referred as the very high throughput (VHT) WLAN system [6], is regarded as the extension of IEEE 802.11n [7]. In the two standards mentioned above, OFDM is adopted as the major modulation scheme. Comparing to 802.11n in the 2.4 GHz band, 802.11ac provides five-fold increase on single-user throughput in the 5 GHz band. The new technologies in 802.11ac should be considered as extensions of the physical-layer techniques pioneered in 802.11n, including more antennas, more spatial streams, wider channel bandwidth, and larger modulation size [8].
1.1.1 Multiple Antennas and Multi-User MIMO
802.11n defines up to four transmit and receive antennas and four spatial streams, while 802.11ac further defines up to eight transmit and receive antennas and eight spatial streams. In addition, 802.11ac, for the first time in 802.11 standard employs downlink Multi-User MIMO (MU-MIMO) technology which allows simultaneous transmission from one access point (AP) to multiple stations (STAs). The maximum throughput of MU-MIMO is promising to reach
more than 1 Gbps [9]. It is worth to mention that the standard adds several further constraints on MU-MIMO: no more than four clients can be targeted simultaneously, no client can use more than four streams, and all streams in a downlink MU-MIMO transmission must use the same modulation and coding scheme (MCS).
1.1.2 Channel Bandwidth
It is clear that wider channel bandwidth allows higher throughput in the wireless communication systems. For 802.11n the maximum channel bandwidth is 40 MHz, the channel bandwidth is extended to 80 MHz and 160 MHz in 802.11ac. Especially, the 160 MHz bandwidth channels are defined as two contiguous or non-contiguous 80 MHz bandwidth channels.
1.1.3 Modulation and coding schemes
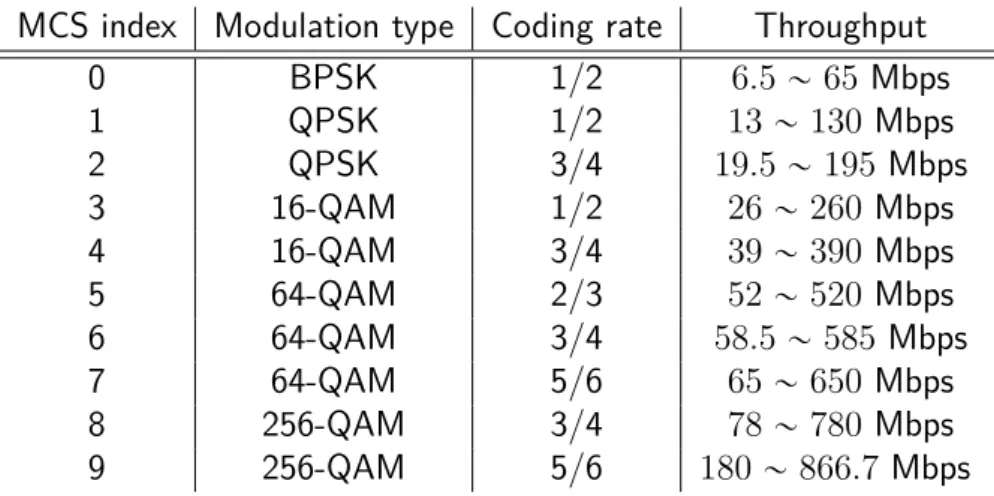
Building on the modulation, BPSK, QPSK, 16-QAM, and 64-QAM of 802.11n, 802.11ac now extends the modulation up to 256-QAM. This means that each symbol represents one of 256 possibilities on the constellation. Although the complexity of modulation and detection is increased, the number of bit number per modulation symbol also increased. In 802.11ac standard, 256-QAM, with code rate 3/4 and 5/6 are added as optional modes in MCS. Table 1.1 is the MCS of 802.11ac, and Table 1.2 summarizes the mandatory and optional features of IEEE 802.11ac.
Table 1.1: Modulation and coding schemes of IEEE 802.11ac MCS index Modulation type Coding rate Throughput
0 BPSK 1/2 6.5 „ 65 Mbps 1 QPSK 1/2 13 „ 130 Mbps 2 QPSK 3/4 19.5 „ 195 Mbps 3 16-QAM 1/2 26 „ 260 Mbps 4 16-QAM 3/4 39 „ 390 Mbps 5 64-QAM 2/3 52 „ 520 Mbps 6 64-QAM 3/4 58.5 „ 585 Mbps 7 64-QAM 5/6 65 „ 650 Mbps 8 256-QAM 3/4 78 „ 780 Mbps 9 256-QAM 5/6 180 „ 866.7 Mbps
Table 1.2: Mandatory and optional features of IEEE 802.11ac
Feature Mandatory Optional
Channel Bandwidth 20, 40, 80 MHz 160, 80+80 MHz
FFT size 64, 128, 256 512
Modulation BPSK, QPSK, 16-QAM, 64-QAM 256-QAM
MCS 0-7 8, 9
Spatial streams 1 2-8 (Support MU-MIMO)
1.2 Pre-Coding MIMO System
In the past few decades, MIMO techniques have been extensively studied to improve the capacity and/or diversity gain. Spatial multiplexing is a common technique which attempts to increase capacity by transmitting multiple bit streams on parallel MIMO channels [10]. Besides, if CSI is known at transmitter side, spatial multiplexing with linear pre-coder is employed by multiplying spatial stream vector by a pre-coding matrix which is adjusted according to the CSI. The pre-coding matrices can be designed based on different criteria, including minimizing mean square error [11], [12], maximizing signal to interference-plus-noise ratio (SINR) [13], [14], or minimize BER [15]. In [16], the authors developed an unifying framework to consider optimizing the MSE, the SINR, and the BER directly by majorization theory [17]. Clearly, it is not practical for typical pre-coding design that needs the complete knowledge of CSI. A multi-mode pre-coding method that can design the pre-coder with limited feedback is proposed in [18].
1.3 Thesis Organization
In this thesis, power-saving algorithms are proposed in the consideration of two different scenarios including channel state information at receiver (CSIR) and channel state information at transmitter (CSIT). In Chapter 2, the model for power consumption, MIMO-OFDM, and pre-coded MIMO-OFDM systems are introduced. In Chapter 3, a power-saving algorithm with CSIR is proposed. In Chapter 4, we consider the CSIT case, a pre-coding scheme is used to reduce the power consumption. Additionally, some complexity reduction methods are also
described. Lastly, conclusion is drawn in Chapter 5.
Throughout this thesis, we adopt the following notations. Matrices and vectors are denoted by capital and small boldface letters, respectively. IN is the N ˆ N identity matrix; } ¨ } is
the two norm. tr (¨), E (¨), and DFT (¨) are the trace operation, expectation, and discrete Fourier transform, respectively. (¨)H and (¨)Trepresent the transpose and conjugate transpose (Hermitian) operators, respectively.
Chapter
2
System Model
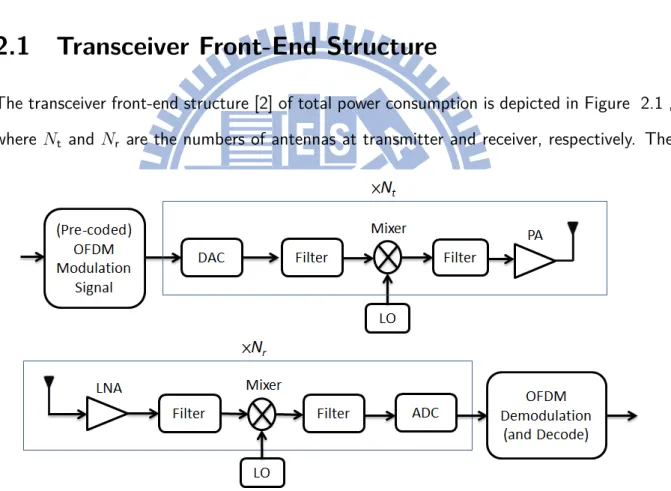
2.1 Transceiver Front-End Structure
The transceiver front-end structure [2] of total power consumption is depicted in Figure 2.1 , where Nt and Nr are the numbers of antennas at transmitter and receiver, respectively. The
Figure 2.1: MIMO-OFDM transceiver front-end structure.
baseband (pre-coded) OFDM modulation signal is first sent into the radio front-ends whose number is proportional to the number of transmit antennas. Then the baseband signal is converted into an analog signal by the digital-to-analog converter (DAC), then filtered by the low-pass filter, and modulated by the mixer. The modulated signal is then filtered again,
amplified by the power amplifier (PA) and finally transmit to the wireless channel. On the receiver side, the RF signal is first amplified by the low noise amplifier (LNA), then filtered by the filter, and down converted by mixer. The down converted signal is then filtered again before converted back to digital signal by analog-to-digital converter (ADC). Finally, the signal can be demodulated and decoded digitally. Besides, we assume that the local oscillator (LO) is shared among all the radio front-ends at transmitter and receiver.
The total power consumption Ptotal can be divided into two main components: the power
consumption of all the power amplifiers PPA and the power consumption of all other circuit
blocks Pc. Therefore, the total power consumption can be denoted as
Ptotal= PPA+ Pc. (2.1)
The power consumption of power amplifier PPA depends on the transmit power Pt, and a
parameter α (α ě 1), which is the inefficient factor of power amplifier, i.e.,
PPA = αPt (2.2)
The circuit power consumption Pc is given by
Pc= (PDAC+ Pfil_t+ Pmixer) ¨ Nt+ 2PLO+ (PLNA+ Pmixer+ Pfil_r+ PADC) ¨ Nr (2.3)
where PDAC, Pfil_t, Pmixer, PLO, PLNA, Pfil_r, and PADC, are the power consumption for DAC, filter at transmitter, mixer, LO, LNA, filter at receiver, and ADC, separately. For simplicity, we combine the parameters which is proportional to transmit and receive antennas, namely,
PC_TX and PC_RX , respectively, and the circuit power consumption can be reformulated as
2.2 MIMO-OFDM Signal Model
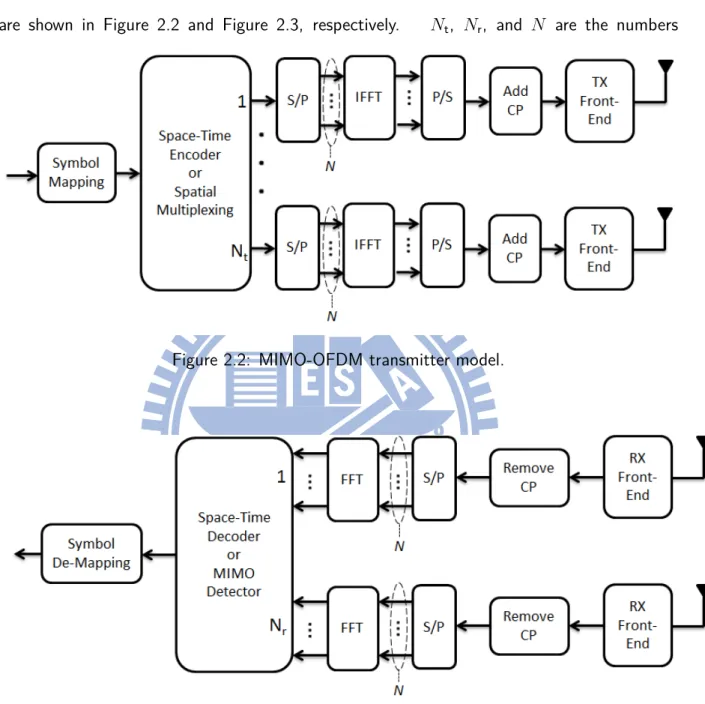
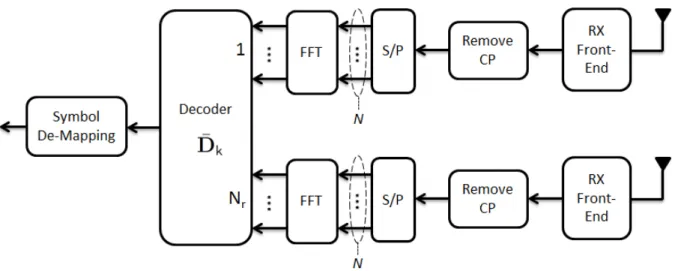
Consider a typical MIMO-OFDM system, where the block diagrams of transmitter and receiver are shown in Figure 2.2 and Figure 2.3, respectively. Nt, Nr, and N are the numbers
Figure 2.2: MIMO-OFDM transmitter model.
Figure 2.3: MIMO-OFDM receiver model.
of transmit antennas, receive antennas, and subcarriers in an OFDM symbol, respectively; besides, we use nt, nr, and k as their indexes.
For a multipath channel with NL pathes, we let h(nr,nt) =
[ h(nr,nt) 0 h (nr,nt) 1 ¨ ¨ ¨ h (nr,nt) NL´1 ] denote the multipath channel impulse response (CIR) between (nt, nr)th transmit and receive
antennas. The discrete Fourier transform (DFT) of h(nr,nt) is denoted as DFT␣h(nr,nt)( = [ H(nr,nt) 0 H (nr,nt) 1 ¨ ¨ ¨ H (nr,nt) N-1 ] . (2.5)
The OFDM frequency flat response matrix at subcarrier k can be written as
Hk = Hk(1,1) ¨ ¨ ¨ H(1,Nt) k .. . . .. ... H(Nr,1) k ¨ ¨ ¨ H (Nr,Nt) k . (2.6)
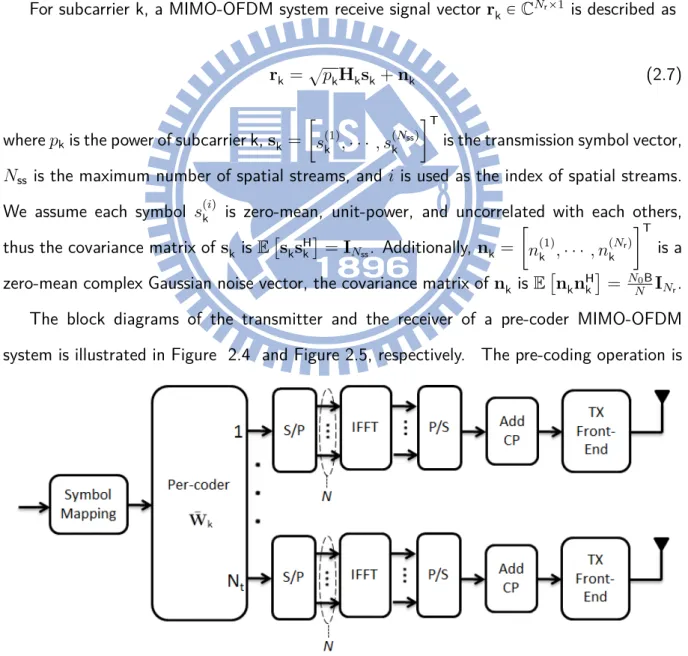
For subcarrier k, a MIMO-OFDM system receive signal vector rk PCNrˆ1 is described as
rk =?pkHksk+ nk (2.7)
where pkis the power of subcarrier k, sk =
[
s(1)k , ¨ ¨ ¨ , s(Nk ss)
]T
is the transmission symbol vector,
Nss is the maximum number of spatial streams, and i is used as the index of spatial streams.
We assume each symbol s(i)k is zero-mean, unit-power, and uncorrelated with each others, thus the covariance matrix of sk isE[sksH
k ] = INss. Additionally, nk = [ n(1)k , ¨ ¨ ¨ , n(Nr) k ]T is a zero-mean complex Gaussian noise vector, the covariance matrix of nk isE[nknH
k
]
= N0B
N INr. The block diagrams of the transmitter and the receiver of a pre-coder MIMO-OFDM system is illustrated in Figure 2.4 and Figure 2.5, respectively. The pre-coding operation is
Figure 2.5: Pre-coded MIMO-OFDM receiver model.
equivalent to multiplying the transmission symbol vector by a pre-coding matrix ¯Wk PCNtˆNss.
Therefore, the receive signal vector can be written as
rk =?pkHkW¯ ksk+ nk. (2.8)
Afterward, the equalized signal vector yk P CNrˆ1 is obtain via multiplying the the receive
signal vector by decoder matrix ¯Dk PCNrˆNss, i.e.,
Chapter
3
Optimal Design to Reduce Total Power
Consumption with CSIR
In this chapter, we would like to propose a power-saving method, assuming the CSI is available at receiver, and the selected transmission scheme information can be perfectly fed back from receiver to transmitter. The design goal is to minimize the total power consumption (2.1)-(2.4), while meeting the bit rate and BER requirements.
3.1 Problem Formulation
Contrary to conventional adaption modulation and coding methods that attempt to achieve highest signaling rate while keep the error rate at or below a target [5], we suggest that for the power-saving point of view, suitable transmit and receive schemes that have minimum power consumption while meeting the target signaling rate and BER should be employed instead.
In our formulation we would like to guarantee that the system bit rate satisfies the target bit rate. We first define the bit rate as R = Nss¨ q ¨ B ¨ r, and we hope the bit rate is larger
or equal to the target bit rate R0. So, the bit rate constraint is formulated as
Nss¨ q ¨ B ¨ r ě R0 (3.1)
code rate.
Besides, BER is a significant factor in communications, i.e., poor BER leads to either throughput reduction or additional retransmissions which strongly affect users’ experience. Thus, in our formulation, the average BER is restricted to a target BER. The general form of 2q-ary QAM modulation BER [21] on subcarrier k is denoted as
BERk,q = aqQ ( aγk,q ¨ cq ) , (3.2) where aq = $ ’ & ’ % 1 , for q = 1, 2 4 q(1 ´ 1 ? 2q) , otherwise (3.3) cq = $ ’ & ’ % ? 2 , for q = 1, 2 b 3q 2q´1 , otherwise (3.4)
and γk,q is the received SNR (Eb
N0).
We hope the average BER on a OFDM symbol is less than or equal to the target BER η, and the BER constraint can be formulated as
1 N N ´1 ÿ k=0 BERk,q ď η (3.5)
Finally, the optimization problem that minimizes total power consumption while meeting the bit rate and BER requirements is formulated as
min Ptotal= αN p + PC_TX¨ Nt+ PC_RX¨ Nr+ 2PLO s.t. Nss¨ q ¨ B ¨ r ě R0 1 N N ´1 ÿ k=0 BERk,q ď η (3.6)
where PPA = αN p is the term of power of PA, and transmit power is the summation of
pi = pj, @i ‰ j. Thus the subscript k of pk is omitted, and Pt=řN ´1k=0 pk = N p.
We will separately calculate the required total power consumption of different MIMO trans-mission schemes (STBC and spatial multiplexing) with different data detectors (ZF, MMSE, and ML) to satisfy the constraints of (3.6).
3.2 STBC and Spatial Multiplexing Signal Model
3.2.1 STBC Signal Model
STBC is a way to incorporate spatial and temporal signal processing for transmitters and receivers with multiple antennas and can get the diversity gain without getting the channel information from receiver. In this scheme, data symbols are sent in blocks with a spatial orthogonal design instead of individual. On the other hand, the receiver combine the signal in adjacent time slots to produce the original symbols.
For Alamouti STBC [19], two data signals are sent by two transmit antennas in two time slots (the code rate r = 1) and the codeword can be written in a compact matrix form:
s = s1 s2 Ñ X = s1 ´s ˚ 2 s2 s˚ 1 (3.7)
For the Alamouti 2 ˆ 1, the block diagram is shown at Figure 3.1, and the receive signals
Figure 3.1: Alamouti 2ˆ1 STBC block diagram.
in the first and second time slots are given as
r1 = r(t) = c p Nt h11s1+ c p Nt h12s2+ n1 (3.8)
r2 = r(t + T ) = ´ c p Nt h11s˚2 + c p Nt h12s˚1 + n2, (3.9)
respectively, where r1, r2, n1, and n2 are the receive signal and noise at first and second time
slot. Besides, we divide the transmit power by Nt to normalize the transmit power.
The effective receive signal vector ˜r is the combination of receive signals in the first and second time slots, i.e.,
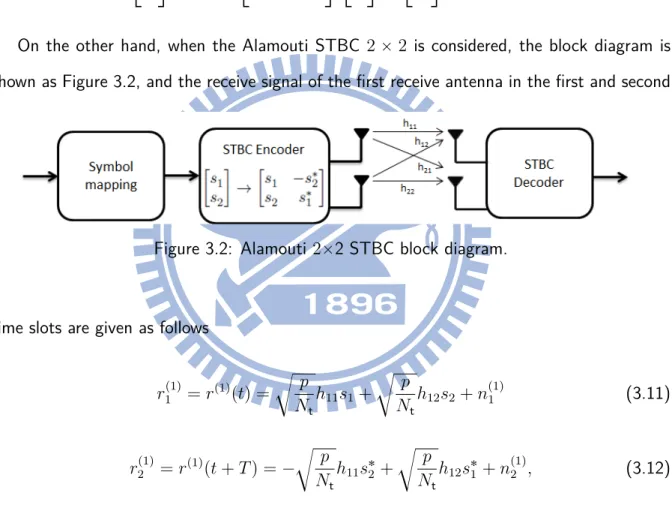
˜ r = r1 r˚ 2 =c pN t h11 h12 h˚ 12 ´h˚11 s1 s2 + n1 n˚ 2 =c pN t ˜ Hs + ˜n (3.10) On the other hand, when the Alamouti STBC 2 ˆ 2 is considered, the block diagram is shown as Figure 3.2, and the receive signal of the first receive antenna in the first and second
Figure 3.2: Alamouti 2ˆ2 STBC block diagram.
time slots are given as follows
r1(1) = r(1)(t) =c p Nth11s1+ c p Nth12s2+ n (1) 1 (3.11) r2(1) = r(1)(t + T ) = ´c p Nth11s ˚ 2 + c p Nth12s ˚ 1 + n (1) 2 , (3.12)
where the superscript denotes the receive antenna index.
For the first receive antenna, we combine the receive signal of the first and second receive time slots, i.e.,
˜ r(1) = r (1) 1 r˚(1)2 =c pN t h11 h12 h˚ 12 ´h˚11 s1 s2 + n (1) 1 n˚(1)2 =c pN t ˜ H(1)s + ˜n(1) (3.13)
slots and the receive vector can be given in the same way, i.e., r1(2) = r(2)(t) =c p Nt h21s1+ c p Nt h22s2+ n (2) 1 (3.14) r(2)2 = r(2)(t + T ) = ´c p Nth21s ˚ 2 + c p Nth22s ˚ 1 + n (2) 2 (3.15) ˜ r(2) = r (2) 1 r˚(2)2 =c pN t h21 h22 h˚ 22 ´h˚21 s1 s2 + n (2) 1 n˚(2)2 =c pN t ˜ H(2)s + ˜n(2) (3.16)
We combine the signal vectors of two receive antennas; the overall effective receive signal vector can be written as
˜r = ˜r (1) ˜ r2(2) =c pN t ˜ H(1) ˜ H(2) s1 s2 + n˜ (1) ˜ n(2) =c pN t ˜ Hs + ˜n, (3.17) where the effective channel matrix and effective noise vector in Alamouti 2 ˆ 2 are written as
˜ H = ˜ H(1) ˜ H(2) = h11 h12 h˚ 12 ´h˚11 h21 h22 h˚ 22 ´h˚21 and n =˜ n˜ (1) ˜ n(2) = n(1)1 n˚(1)2 n(2)1 n˚(2)2
The general form of Alamouti STBC effective received signal vector ˜r P C2Nrˆ1 can be
written as ˜ r =c p Nt ˜ Hs + ˜n (3.18) where H PC2NrˆNt, s PCNtˆ1, ˜n PC2Nrˆ1.
We multiply the the received signal by Hermitian of the effective channel matrix. Due to the orthogonal design, the resulting signal y is derived as
y = ˜HH˜r =c p Nt ˜ HHHs + ˜˜ HHn =˜ c p Nt ζs + ˜HHn˜ (3.19)
where ˜ HHH =˜ Nr ÿ nr=1 Nt ÿ nt=1 |hnrnt|2I2 = ζI2. (3.20) ζ = Nr ÿ nr=1 Nt ÿ nt=1 |hnrnt| 2 (3.21) From (3.19), the SNR (Eb
N0) of the Alamouti scheme which is the power of signal term divided by q and the power of noise term can be derived as
SNRk,q = γk,q = E [ }bNp tζs} 2 ] q ¨E [ } ˜HHn}˜ 2 ] = pζ2E [ tr(ssH)] qNtE [ tr(H˜Hn˜˜nHH˜)] = pζ 2tr (I 2) qNttr ( N0NBζI2 ) = pζN qNtN0B (3.22)
We now extend STBC to three transmit antennas and less than or equal to three receive antennas [20] with the following codeword, which delivers four valid symbols within eight time slots; therefore, the code rate r = 1/2.
s = s1 s2 s3 s4 Ñ X = s1 ´s2 ´s3 ´s4 s1˚ ´s˚2 ´s˚3 ´s˚4 s2 s1 s4 ´s3 s2˚ s˚1 s˚4 ´s˚3 s3 ´s4 s1 s2 s3˚ ´s˚4 s˚1 s˚2. (3.23)
The effective received signal can be gotten similarly to Alamouti STBC:
˜r =
c p
2Nt
˜
Hs + ˜n (3.24) where ˜r P C8Nrˆ1, ˜H P C8Nrˆ4, s P C4ˆ1, and ˜n P C8Nrˆ1. Besides, we divide the transmit
power by 2Nt for normalization.
For different number of receive antennas, the decoded signal y can be written as a general form: y = ˜HH˜r = c p 2Nt ˜ HHHs + ˜˜ HHn =˜ c 2p Nt ζs + ˜HHn˜ (3.25)
where ˜ HHH = 2˜ Nr ÿ nr=1 Nt ÿ nt=1 |hnrnt|2I4 = 2ζI4. (3.26) ζ = Nr ÿ nr=1 Nt ÿ nt=1 |hnrnt| 2
The SNR of the STBC using three transmit antennas can be derived as (3.27), which is identical to Alamouti STBC SNRk,q = γk,q = E[} b 2p Ntζs} 2] q ¨E [ } ˜HHn}˜ 2 ] = 2pζ2E [ tr(ssH)] qNtE [ tr(H˜Hn˜˜nHH˜)] = 2pζ 2tr (I 4) qNttr ( N0NB2ζI4 ) = pζN qNtN0B , (3.27) where ζ = Nr ÿ nr=1 Nt ÿ nt=1 |hnrnt| 2
3.2.2 Spatial Multiplexing Signal Model
For the spatial multiplexing transmission schemes, systems can support higher bit rates due to the multiple spatial channel. That is, the spatial multiplexing model can use less modulation size to achieve the bit rate constraint. It is known that lower modulation size has better BER performance (3.2)-(3.4). For the traditional belief that better BER performance leads to better (lower) transmit power consumption, we will inspect the power consumption of spatial multiplexing transmission in this section.
Spatial multiplexing MIMO detectors including ZF, MMSE, and ML are introduced in this section. In order to adjust the transmission power to meet the BER constraint, we derive the demodulated signal and the received SNR of each detection scheme. First of all, for the zero forcing demodulated signal at subcarrier k, the demodulated signal is that multiplying the received signal (2.7) by a zero forcing equalizer which is the pseudo inverse of the channel
matrix, i.e., H: k = ( HH kHk )´1 HH
k. The demodulated signal is derived as
yk = H:krk =(HHkHk)´1HHk (?pHksk+ nk) =?psk+(HHkHk)´1HHknk =?psk+ H:knk.
(3.28)
The transmit signal can be detected while accompanying with a noise enhancement term. It is obvious that SISO system is a special case of ZF whose channel matrix is a scalar. In addition, the received SNR of ZF is derived as
SNRk,q = γk,q = E[}?psk}2 ] q ¨E [ }H:knk}2 ] = p ¨E ␣tr [ sksH k ]( q ¨E!tr[H: knknHkH :H k ]) = p ¨ tr (INss) q ¨ tr [ N0NB (HH kHk )´1 HH kHk ( HH kHk )´1] = pNssN qN0B ¨ tr[(HH kHk )´1]. (3.29)
Secondly, for the MMSE equalizer at subcarrier k, i.e., Wk = ( HH kHk+ N0¨B p¨N I )´1 HH k,
the equalized signal at subcarrier k is given as
yk = Wkrk = Wk(?pHksk+ nk)
=?psk+?p (WkHk´ I) sk+ Wknk,
(3.30)
where?psk, ?p (WkHk´ I) sk, and Wknk are the signal term, interference term, and noise
term, respectively. The received SINR of MMSE equalizer can be further derived as
SINRk,q = γk,q = E[}?psk}2] q ¨E[}?p (WkHk´ I) sk+ Wknk}2 ] = p ¨ tr [ INss] q␣E[}?p (WkHk´ I) sk}2 ] +E [}Wknk}2]( = p ¨ Nss q ! p ¨ tr [ (WkHk´ I) (WkHk´ I) H] + N0NBtr[WkWH k ]) (3.31)
Lastly, we consider the ML detector. Particularly, ML detector is not a linear detector; therefore, we approximate its BER by the distance between the nearest two receive signal
vectors, i.e., dk,min = ?p minsi‰sj}Hksi´ Hksj} @i,j si, sj P {symbol set}. We note that
dk,min is the minimum distance respect to the symbol set si, sj PCNssˆ1 at subcarrier k, where
the symbol set is consisted by all the possible transmit symbols. As the result of the detection error is most likely to occur in the minimum distance case, the BER for subcarrier k using 2q-ary modulation can be approximated by
BERk,q – 1 qQ d d2 k,min¨ N 4N0¨ B (3.32)
3.3 Solving Problem
To solve the optimization problem in (3.6), the total power consumption of each transmit and receive scheme in Table 3.1 is evaluated at receiver side; moreover, the scheme with minimum
Table 3.1: Transmit and receive schemes for CSIR case Transmit scheme Receive scheme
SISO Nr = 1 Alamouti STBC Nr = 1 Nr = 2 STBC (Nt = 3) Nr = 1 Nr = 2 Nr = 3 Spatial Multiplexing(Nt) ZF(Nr) MMSE(Nr) ML(Nr)
(3.6), and it can be further reformulated as min Nt,Nr,Nss,q,p Ptotal= αN p + PC_TX¨ Nt+ PC_RX¨ Nr+ 2PLO (3.33a) s.t. Nss¨ q ¨ B ¨ r ě R0 (3.33b) 1 N N ´1 ÿ k=0 aqQ ( aγk,q¨ cq )
ď η , for STBC, Spatial multiplexing (3.33c) 1 N N ´1 ÿ k=0 1 qQ d d2 k,min¨ N 4N0¨ B ď η , for ML. (3.33d)
Discrete variables (Nt, Nr, Nss, r, and q) are determined first in this problem. Assuming certain transmit and receive schemes are decided; meanwhile, Nt, Nr, Nss, r, and Pc are also
decided. Finally, q can be decided by satisfying the bit rate constraint, i.e.,
q ě R0 Nss¨ B ¨ r
. (3.34)
Then, For each scheme, the minimum required transmit power p that satisfies the BER con-straint (3.33c), (3.33d) is calculated by using a numerical root-finding method, where dk,min and γk,q are both functions of p. The total power consumption is then calculated by adding the power of circuit and power amplifier. Under the comparison of total power consumption for each scheme, a scheme with the minimum total power consumption is regarded ar the best solution of the optimization problem. Finally, the transmit messages (transmit scheme and transmit power) are fedback to transmitter.
3.4 Simulation Results
In this section, the simulation results of the power consumption performance and the trends of proposed method in CSIR scenario are presented. We assume that carrier frequency and symbol timing are perfectly synchronized and power amplifiers, DACs, and ADCs do not cause signal distortion. The simulation parameters of the MIMO-OFDM system are listed in Table 3.2. In the simulations, the indoor channel model class B [22] is used and the power consumption of
Table 3.2: System parameters. Parameters Values Carrier frequency 5 GHz Bandwidth 80 MHz FFT size 256 CP size 64 TX antennas 3 RX antennas 3 N0 ´174 dBm/Hz Distance 10 m
Path loss exponent 3.5 Target BER (η) 10´3
Target bit rate (R0) 320 Mbps Simulation runs 1000
Table 3.3: Power consumption parameters. Parameters Values α 28.5 PDAC 1.9 ˆ 10´10ˆ B(W) PADC 2.3 ˆ 10´10ˆ B(W) Pfil_t = Pfil_r 2.5 mW PMixer 30.3 mW PLO 50 mW PLN A 20 mW
3.4.1 Power Consumption Performance in CSIR Scenario
Figure 3.3 shows the circuit power consumption of each transmit and receive scheme. The Fig-ure 3.3 indicates that the circuit power is proportional to the total number of active antennas. Naturally, SISO scheme has the least circuit power consumption, and the schemes with three transmit and receive antennas have the largest circuit power consumption. Figure 3.4 shows the power of power amplifier of each transmit and receive scheme. It is clearly mentioned that power of power amplifier is depended on the transmit power. SISO and ZF have especially high transmit power because they have low SNR caused by noise enhancement. Besides, MMSE equalizer considers both noise and interference, so it has better performance comparing to ZF. Lastly, ML detector has the relatively good performance in spatial multiplexing case, for ML
is optimum in terms of minimizing the overall error probability. On the other hand, in term of STBC, the transmit power of STBC using three transmit antennas are generally higher than Alamouti STBC due to their difference of code rate. Figure 3.5 summarizes the total power consumption of each transmit and receive scheme and the proposed method. Without doubt, the proposed method has the minimum total power consumption. In addition, Alamouti 2 ˆ 2 has the minimum total power consumption among all evaluated schemes.
Figure 3.4: Power of power amplifier of each transmit and receive scheme in CSIR case.
3.4.2 Trends in the Power Saving Algorithm in CSIR Scenario
When we consider the OFDM transmission, the small scale effect is averaged over all subcar-riers. That is, path loss is actually the decisive factor of transmit power. We now simulate the optimum selection of our algorithm based on different path loss, including transmission schemes, diversity order, and numbers of transmit and receive antennas. From Figure 3.6, we can see that one transmit and receive antennas are used in the small path loss scenario and two transmit and receive antennas are used when the path loss grows up. We can also see that only SISO system or Alamouti STBC is used in this simulation. To sum up, SISO and Alamouti STBC systems dominate in our proposed algorithm; besides, larger antenna size are preferred in large path loss scenario because more antenna number can provide higher diversity gain to combat the poor SNR caused by path loss. In Figure 3.7, the total power consumption of each scheme grows exponentially when the path loss increases. As expected, the proposed method has the minimum total power consumption. Additionally, in comparison to the existing schemes, SISO is preferable for small path loss cases, Alamouti 2 ˆ 1 is preferable for medium path loss cases, and Alamouti 2 ˆ 2 is preferable for large path loss cases.
Because path loss is actually the decisive factor of transmit power, receiver can determine transmit and receive schemes simply according to the path loss. For example, in our simulation, the path loss is about 116.24 dB. According to Figure 3.6, Alamouti 2 ˆ 2 STBC system is recommended. Consequently, we can see in Figure 3.5 the total power consumption of Alamouti 2 ˆ 2 system is lower than other existing schemes and actually not so far from the proposed method.
80 90 100 110 120 130 1 2 3 Path loss (dB) Number of TX antennas 180 90 100 110 120 130 2 3 Path loss (dB) Number of RX antennas 80 90 100 110 120 130 SISO Alamouti 2X1 Alamouti 2X2 Path loss (dB) Tramsmission scheme 80 90 100 110 120 130 1 2 3 4 Path loss (dB) Diversity order
Figure 3.6: Optimum selection for the proposed method in CSIR case.
80 85 90 95 100 105 110 115 120 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 Path loss (dB) Total Power (W) Proposed SISO Alamouti 2X1 Alamouti 2X2
Chapter
4
Optimal Design to Reduce Total Power
Consumption with CSIT
In this chapter, there are two assumptions in our design. Firstly, we assume the CSI is available at transmitter. Secondly, the designed message can be sent from transmitter to receiver via a perfect feed-forward link. Based on these assumptions, a pre-coder can be designed to minimize the total power consumption, and then the decoder information is sent from transmitter to receiver.
4.1 Problem Formulation
As we mentioned at Chapter 2, for the pre-coded MIMO-OFDM system on subcarrier k, the general form of decoded signal can be written as (2.9). In our formulation, we redefine the pre-coding matrix, ˜Wk, and the decoding matrix ˜Dk. The demodulation signal can be reformulated as
yk= ˜DH
kHkW˜ ksk+ ˜DHknk. (4.1)
The pre-coding matrix includes antenna selection matrix, A, pre-coder weighting matrix, Wk, and power loading matrix, Pk. Besides, the decoding matrix includes antenna selection matrix,
B and decoder weighting matrix, Dk, i.e., ˜
˜ Dk = BDk, (4.3) where Wk ” [ w(1)k , ¨ ¨ ¨ , w(Nss) k ] , k = 0, ¨ ¨ ¨ , N ´ 1 (4.4) Dk ” [ d(1)k , ¨ ¨ ¨ , d(Nss) k ] , k = 0, ¨ ¨ ¨ , N ´ 1 (4.5) A ” diag ( a(1), ¨ ¨ ¨ , a(Nt) ) , a(nt) P t0, 1u , n t= 1, ¨ ¨ ¨ , Nt (4.6) B ” diag ( b(1), ¨ ¨ ¨ , b(Nr) ) , b(nr) P t0, 1u , n r = 1, ¨ ¨ ¨ , Nr (4.7) Pk ” diag ( b p(1)k , ¨ ¨ ¨ , b p(Nss) k ) , k = 0, ¨ ¨ ¨ , N ´ 1 (4.8) Wk P CNtˆNss and D
k P CNrˆNss are the pre-coder and decoder weighting matrices. A P
ZNtˆNt and B PZNrˆNr are the transmit and receive antenna selection matrices. The diagonal elements a(nt)and b(nr) are either 1 or 0, for representing the active or inactive of the antennas. Lastly, Pk P RNssˆNss is the power loading matrix. The diagonal element p(i)k is the transmit
power of spatial stream i on subcarrier k.
The demodulated signal can be further denoted as (4.9), where Hck = BHkA is the
composite channel matrix according to the active antennas and n1
k = Bnk is the effective
noise vector according to the active receive antennas.
yk = DHkBHkAWkPksk+ DHkBnk
= DHkHckWkPksk+ DHkn1 k
(4.9)
Recall the power expression (2.1)-(2.4), the transmit power is denoted as the summation of all transmit power on subcarriers and spatial streams, and the circuit power is according to the number of active transmit and receive antennas. Finally, the total power consumption can be further formulated as Ptotal= α ¨ N ´1 ÿ k=0 Nss ÿ i=1 p(i)k + ( N t ÿ nt=1 a(nt) ) ¨ PC_TX+ ( N r ÿ nr=1 b(nr) ) ¨ PC_RX+ 2PLO (4.10)
rate, spatial streams, and BER constraints can be formulated as: min Ptotal = α ¨ N ´1 ÿ k=0 Nss ÿ i=1 p(i)k + ( N t ÿ nt=1 a(nt) ) ¨ PC_TX+ ( N r ÿ nr=1 b(nr) ) ¨ PC_RX+ 2PLO s.t. Nss¨ q ¨ B ¨ r ě R0 1 ď Nssď min # N t ÿ nt=1 a(nt), Nr ÿ nr=1 b(nr) + 1 N Nss N ´1 ÿ k=0 Nss ÿ i=1 BER(i)k,q ď η (4.11)
4.2 Solving Problem
For solving this problem, we first decide the active transmit and receive antennas, then we use the decided antennas to design pre-coder and decoder weighting, and the power loading. In brief, the optimization problem is solved in following three stages:
1. Antenna selection
2. Pre-coder and decoder weighting design 3. Power loading
In order to clearly express the problem-solving process, we introduce the problem-solving pro-cess in the order of 2 Ñ 3 Ñ 1.
4.2.1 Pre-coder and Decoder Weighting Design
In order to minimize the transmit power while meeting the BER constraint, we first maximize the SNR of each subcarrier. For the OFDM transmission, each subcarrier encounters inde-pendent channel fading. Maximizing the SNR of individual subcarrier implies to maximize the SNR of overall OFDM symbol. Therefore, the optimization problem for maximizing SNR is
formulated as max Wk,Dk tr ␣ }DHkHckWk}2( , k = 0, ¨ ¨ ¨ , N ´ 1 s.t. }w(i)k }2 = 1, i = 1, ¨ ¨ ¨ , Nss }d(i)k }2 = 1, i = 1, ¨ ¨ ¨ , Nss (4.12)
According to [16], to maximize SNR, Wk and Dk should be the matrices consisted by right and left singular vectors corresponding to Nss largest singular values of Hck, respectively.
We employ the result of pre-coder and decoder, i.e., the result of (4.12) into (4.9). The MIMO channel is decoupled into parallel spatial channels, and the equalized signal yk is now
yk = DHkHckWkPksk+ DHkn1 k = ΣkPksk+ ˜nk = b p(1)k σ(1)k s(1)k + ˜n(1)k ... b pk(Nss)σk(Nss)sk(Nss)+ ˜n(Nk ss), (4.13) where Σk = diag ( σ(1)k , ¨ ¨ ¨ , σ(Nss) k )
is a diagonal matrix and σk(i) is the singular value of Hck. The SNR of subcarrier k and spatial stream i using 2q-ary modulation is given below.
SNR(i)k,q = γk,q(i) = p (i) k σ 2(i) k N qN0B . (4.14)
We also recall the BER formulation(3.2)-(3.4). The The BER of subcarrier k and spatial stream i using 2q-ary QAM modulation is given below.
BER(i)k,q = aqQ (b γk,q(i) ¨ cq ) where aq= $ ’ & ’ % 1 , for q = 1, 2 4 q(1 ´ 1 ? 2q) , otherwise
cq = $ ’ & ’ % ? 2 , for q = 1, 2 b 3q 2q´1 , otherwise
4.2.2 Power Loading
After the pre-coder and decoder weighting design, we have maximized the SNR of each sub-carrier. We now design the power loading matrix Pk to minimize transmit power while meeting
the average BER constraint. The optimization problem of power loading is formulated as
min p(i)k N ´1 ÿ k=0 Nss ÿ i=1 p(i)k (4.15a) s.t. 1 N Nss N ´1 ÿ k=0 Nss ÿ i=1 BER(i)k,q ď η (4.15b) p(i)k ě 0. (4.15c)
For simplicity, we combine the subcarrier and the spatial stream indexes (k and i) in to m, m=0, ¨ ¨ ¨ , NNss´ 1, the problem is reformulated as
min pm N Nss´1 ÿ m=0 pm (4.16a) s.t. 1 N Nss N Nss´1 ÿ m=0 aqQ d pmN σ2 mc2q qN0B ď η (4.16b) pm ě 0. (4.16c)
We solve the optimization problem by the aid of Lagrange multiplier. The Lagrangian function is defined as L (tpmu) = N Nss´1 ÿ m=0 pm+ λ 1 N Nss N Nss´1 ÿ m=0 aqQ d pmN σ2 mc2q qN0B ´ η , (4.17)
where λ is a Lagrange multiplier associated with the BER constraint. The result of BL(tpmu)
Btpmu = 0 is derived as ? pm¨ e pmNσ2mc2q 2qN0B = λ ? N σmaqcq N N ?8πqN B, 0 ď m ď N Nss´ 1. (4.18)
The value at the left-hand side of (4.18) is sensitive to pm. For the sake of increasing the
convergence rate, we take natural logarithm on (4.18): 1 2ln pm+ N pmσ2 mc2q 2qN0B = ln ( λ?N σmaqcq N Nss?8πqN0B ) , 0 ď m ď N Nss´ 1 (4.19)
pm is calculated using a numerical search method, and the detail procedure is shown in Algo-rithm 1.
Algorithm 1 Transmit Power Minimization Algorithm Input: λ(0), j = 0 1: repeat 2: for m= 0 : N Nss´ 1 do 3: p‹ m Ð ! pm|12 ln pm+ N pmσ2mc2q 2qN0B = ln (λ(j)?N σ maqcq N Nss ? 8πqN0B )) 4: end for 5: BERcur = N N1 ss řN Nss´1 m=0 aqQ ( bp‹ mN σ2mc2q qN0B ) 6: Check the BER constraint(4.16b) with BERcur
7: Adjust λ(j+1) by Algorithm 2 and Algorithm 3 8: j = j + 1
9: until Stopping criterion is met Output: tp‹
mu
Algorithm 2 and Algorithm 3 are inspire by the intermediate value theorem [23], which states that:
Theorem 1 (Intermediate Value Theorem). consider an interval I = [a, b] in the real numbers
R and a continuous function f(I) Ñ R. Then, if u is a number between f(a) and f(b), i.e.,
f (a) ă u ă f (b) or f (b) ă u ă f (a) then there is a c P (a, b) such that f (c) = u.
Algorithm 2 is a coarse tune of the BER. It iteratively times or divides the current Lagrange multiplier by 2 until finding the lagrange multiplier λmax and λmin so that their corresponding
Algorithm 2 Coarse Tune of the BER Input: BERcur, λ(0) = λcur, and j = 0
1: repeat
2: if BERcurď η then
3: λmax = λ(j) 4: λ(j+1) = λ(j)/2 5: else 6: λmin = λ(j) 7: λ(j+1) = 2λ(j) 8: end if
9: update BERcur with λ(j+1)
10: j = j + 1
11: until λmin and λmax are found
According to Theorem 1, we can find a λ‹ P (λ
min, λmax) whose corresponding average
BER equals to η. Therefore, we use Algorithm 3, an iteratively fine tune process, to find λ‹.
Algorithm 3 Fine Tune of the BER
Input: BERcur, λ(0) = λcur, λmax, λmin, and j = 0
1: repeat
2: if BERcurď η then
3: λmax = λ(j) 4: λ(j+1) = λ(j)+λ min 2 5: else 6: λmin = λ(j) 7: λ(j+1) = λ(j)+λ max 2 8: end if
9: update BERcur with λ(j+1)
10: j = j + 1
11: until Stopping criterion is met
4.2.3 Antenna Selection
We note that␣a(nt)(, ␣b(nr)(, N
ss, and q are discrete variables, so we use global search methods
as min ta(nt)u,tb(nr)u,Nss,q α N ´1 ÿ k=0 Nss ÿ i=1 p(i)k + Nt ÿ nt=1 a(nt)P C_TX+ Nr ÿ nr=1 b(nr)P C_RX+ 2PLO (4.20a) s.t. Nss¨ q ¨ B ¨ r ě R0 (4.20b) 1 ď Nssď min # Nt ÿ nt=1 a(nt), Nr ÿ nr=1 b(nr) + (4.20c) 1 N Nss N ´1 ÿ k=0 Nss ÿ i=1 BER(i)k,q ď η. (4.20d)
In this problem, we hope to find the best active antennas and the transmission scheme that minimize the total power consumption. Exhaustive search is a method to get the global opti-mum solution of the optimization problem. However, the complexity of selection of antennas and spatial streams grows exponentially when the number of antennas increases. Exhaustive search is therefore computational prohibitive. Hence, we use genetic algorithm (GA) [23] to solve the antenna selection problem.
To solve the problem by GA, we first define the variable set x =(␣a(nt)( , ␣b(nr)( , N ss, q
) , which is called “chromosome.” We then randomly generate L chromosomes as the initial population set P(0)
” [
x(0)1 ¨ ¨ ¨ , x(0)L
]
. We use g = 1, ¨ ¨ ¨ , G and l = 1, ¨ ¨ ¨ , L as the indexes of generations and chromosomes. For gthgeneration,the population set can be written
as P(g). We define the total power consumption of x(g)
l as Ptotal
(
x(g)l ), and we also define
f
(
x(g)l )as the “fitness” of each chromosome:
f ( x(g)l )= max l=1,¨¨¨ ,LPtotal ( x(g)l )´ Ptotal ( x(g)l ). (4.21)
Naturally, the larger the value of the fitness represents the better the solution is. We then use “roulette-wheel scheme” to select the chromosome. The selected probabilities prob(g)l are proportional to their fitness, i.e.,
prob(g)l = f ( x(g)l ) ř lf ( x(g)l ) (4.22)
Then, the selected chromosomes are “evolved”, which includes “crossover” and “mutation” operations into next generation.
Crossover: Randomly takes a pair of selected chromosome, called “parent,” and then randomly exchange their parameters to generate a pair of “offspring.”
Mutation: Randomly changes each variable with a given probability, it is used to prevent the solution fall into local optima.
After several generations, a relative best solution would be regarded as the solution of GA.
4.3 Complexity Reduction by Antenna Number Selection
Although using GA to select the active antennas can provide a good power consumption performance, we now propose a method which has similar performance to GA but a significant reduction on complexity. As previously mentioned, antenna selection is a method to choose suitable transmit and receive antennas that maximize overall channel gain. However, when we consider the OFDM transmission, the channel gain is averaged over all subcarriers; the advantage of antenna selection is not obvious. As the result, we propose a method that has similar performance as GA but it has significant reduction in complexity. We then modify the problem by deciding “how many antennas shall be active” instead of “which antennas shall be active.” The problem can be reformulated as
min nt_act,nr_act,Nss,q α N ´1 ÿ k=0 Nss ÿ i=1
p(i)k + nt_actPC_TX+ nr_actPC_RX+ 2PLO (4.23a)
s.t. Nss¨ q ¨ B ¨ r ě R0 (4.23b)
1 ď Nss ď min tnt_act, nr_actu (4.23c)
nt_act = 1, ¨ ¨ ¨ , Nt (4.23d) nr_act = 1, ¨ ¨ ¨ , Nr (4.23e) 1 N Nss N ´1 ÿ k=0 Nss ÿ i=1 BER(i)k,q ď η (4.23f)
transmit and receive antennas are randomly assigned. Transmitter selects the minimal total power consumption one as the solution of the optimization problem and then sends the decoder information (receive antenna indexes and weights) to receiver.
4.4 Simulation results
In this section, the simulation results of the power consumption performance and the trends of proposed method in CSIT scenario are presented. We assume that carrier frequency and symbol timing are perfectly synchronized and power amplifiers, DACs, and ADCs do not cause signal distortion. The simulation parameters of the MIMO-OFDM system are listed in Table 4.1. In the simulations, the indoor channel model class B [22] is used and the power consumption of transceiver front-end elements [2] are listed in Table 4.2
Table 4.1: System parameters.
Parameters Values Carrier frequency 5 GHz Bandwidth 80 MHz FFT size 256 CP size 64 TX antennas 3 RX antennas 3 N0 ´174 dBm/Hz Distance 10 m
Path loss exponent 3.5 Target BER (η) 10´3
Target bit rate (R0) 320 Mbps Simulation runs 1000
Table 4.2: Power consumption parameters. Parameters Values α 28.5 PDAC 1.9 ˆ 10´10ˆ B(W) PADC 2.3 ˆ 10´10ˆ B(W) Pfil_t = Pfil_r 2.5 mW PMixer 30.3 mW PLO 50 mW PLN A 20 mW
4.4.1 Power Consumption Performance in CSIT Scenario
Figure 4.1 shows the circuit power consumption of each transmit and receive scheme. SISO system has the minimum circuit power consumption due to the minimum active antenna numbers it has, on the other hand, schemes with maximum active antenna numbers (MIMO 3ˆ 3) have the maximum circuit power consumption. We conclude that circuit power consumption is proportional to the total number of active antennas. The power of power amplifier of all transmit and receive schemes are shown in Figure 4.2. It is clearly that power of power amplifier depends on the transmit power. The evidence that transmit power is relative to its diversity gain can be seen in Figure 4.2. The schemes with rare diversity gain (SISO, spatial multiplexing) require especial high transmit power, whereas schemes with higher diversity order require less transmit power. Figure 4.3 summarizes the total power consumption of each transmit and receive scheme and the proposed methods. It is clear that exhaustive search is the global best solution of antenna selection problem, and GA is a suboptimal one. In addition, the result of antenna number selection method is not so far from the GA.
Figure 4.1: Circuit power of each transmit and receive scheme in CSIT case.
4.4.2 Trends in the Power Saving Algorithm in CSIT Scenario
For the previous point of view, it is clear that the small scale fading effect of OFDM trans-mission is averaged over all subcarriers. That is, path loss is actually the decisive factor of transmission power. We now simulate the trends of spatial streams, diversity order, and num-bers of transmit and receive antennas of different path loss. As shown in Figure 4.4, schemes with small number of active antennas are preferable in the small path loss cases. This is be-cause in these cases, SNR is good enough that no extra diversity gain is required and a small number of active antennas are sufficient. On the other hand, when the path loss becomes large, system suffers from the poor SNR. Therefore, larger antenna number is needed to pro-vide higher diversity order. Besides, the number of spatial streams is always one. It is easy to understand that schemes with diversity gain are preferred in this algorithm. For Figure 4.5, the total power consumption grows exponentially when the path loss increases. It is obvious that the antenna number selection method has the minimum total power consumption. Besides, schemes with low diversity order outperform in small path loss, whereas schemes with high diversity order outperform in large path loss.
80 90 100 110 120 130 0 2 4 6 8 10 Path loss (dB) Diversity order 80 90 100 110 120 130 1 2 3 Path loss (dB) Number of TX antennas 180 90 100 110 120 130 2 3 Path loss (dB) Number of RX antennas 80 90 100 110 120 130 1 2 3 Path loss (dB)
Number of spatial stream
Figure 4.4: Optimum selection for antenna number selection method in CSIT case.
90 95 100 105 110 115 120 125 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Path loss (dB) Total Power (W)
Antenna Number Selection SISO
2X1 Nss=1 3X1 Nss=1 3X2 Nss=1 3X3 Nss=1
4.5 Antenna Number Selection by Path Loss
As is mentioned earlier, path loss is actually the decisive factor of transmit power. It is reasonable to suppose that we can create a look-up table that optimum transmit and receive antenna numbers and spatial stream are determined by path loss. Transmitter can determine the active antenna numbers simply according to the path loss and then send the receive antenna indexes and weights to receiver. For example, in our simulation, the path loss is about 116.24dB. According to Figure 4.4, three transmit antennas, two receive antennas, and one spatial stream is suggested in proposed method. As a consequence, in Figure 4.3, we can see the total power consumption of 3 ˆ 2 Nss= 1 outperforms existing schemes and actually
not so far from the antenna number selection method. To sum up, antenna number selection by path loss look-up table avoids the high computation complexity of antenna selection while providing good performance.
Chapter
5
Conclusion
In this thesis, power-saving algorithms for both CSIR and CSIT cases are proposed. The design idea is that an algorithm can be utilized to select transmit and receive schemes having the minimum total power consumption while meeting data rate and BER requirements. Besides, the optimum transmit and receive schemes in terms of path loss are shown in this thesis. It is revealed that in both CSIR and CSIT cases, SISO system is preferable in small path loss situations, while schemes with higher diversity order are preferable in large path loss situations. Moreover, the path-loss-based optimum transmit and receive schemes enable a considerable reduction on the computational complexity.
REFERENCE
[1] S. Cui, A. J. Goldsmith, and A. Bahai, “Energy-efficiency of MIMO and cooperative MIMO techniques in sensor networks,” IEEE J. Sel. Areas Commun. , vol. 22, no. 6, pp. 1089-1098, Aug. 2004.
[2] S. Cui, A. J. Goldsmith, and A. Bahai, “Energy-constrained modulation optimization,”
IEEE Trans. Wireless Commun. , vol. 4, no. 5, pp. 2349-2360, Sep. 2005.
[3] H. S. Kim and B. Daneshrad, “Energy-constrained link adaptation for MIMO OFDM wireless communication systems,” IEEE Trans. Wireless Commun. , vol. 9, no. 9, pp. 2820-2832, Sep. 2010.
[4] C. Y. Ma and C C. Huang, “Energy-efficient power loading algorithms for uniform-rate OFDM systems,” Proc. IEEE Wireless Commun. Network. Conf., Apr. 2014.
[5] M. Wallace, J. R. Walton, and A. Jalali “Method and apparatus for measuring reporting channel state information in a high efficiency, high performance communications system,” U.S. Patent No. 6,473,467. 29 Oct. 2002.
[6] E. Perahia, “IEEE802.11 Wireless LANs: VHT below 6GHz PAR Plus 5C’s,” IEEE 802.11-08/0807r4, Sep. 2010.
[7] Wireless LAN medium access control (MAC) and physical layer (PHY) specification.
am-mendment 5: enhancements for higher throughput, IEEE Std. 802.11n, 2009.
[9] D. Nojima, L. Lanante, Y. Nagao, M. Kurosaki, and H, Ochi, “Performance evaluation for multi-user MIMO IEEE 802.11ac wireless LAN system,” IEEE Conf. Advan.
Com-mun. Tech. (ICACT), 2012.
[10] A. J Paulraj and C. B. Papadias, “Space-time processing for wireless communications,”
IEEE Signal Processing Magazine, vol. 14, no. 6, pp. 49-83, Nov. 1997.
[11] M. Sampath, P. Stoica, and A. Paulraj, “Generalized linear precoder and decoder design for MIMO channels using the weighted MMSE criterion,” IEEE Trans. Commun. , vol. 49, no. 12, pp. 2198-2206, Dec. 2001.
[12] J. Yang and S. Rov, “On joint transmitter and receiver optimization for multiple-input multiple-ouput (MIMO) transmission systems,” IEEE Trans. on Commun., vol. 42, no. 12, pp. 3221-3231, Dec. 1994.
[13] A. Scaglione, G. B. Giannakis, and S. Barbarossa, “Redundant filterbank precoders and equalizers Part I: Unification and optimal designs,” IEEE Trans. on Signal Process., vol. 38, no. 7, pp. 1988-2006, July 1999.
[14] R. W. Heath Jr., S. Sandhu, and A. Paulraj, “Antenna selection for spatial multiplexing with liner receivers,” IEEE Commun. Lett., vol. 5, no. 4,pp. 142-144, April 2001.
[15] S. Ohno, G. B. Giannakis, “Optimal training and redundant precoding for block trans-missions with application to wireless OFDM,” IEEE Trans. Commun., vol. 50 no. 12, pp. 2113-2123, 2002.
[16] D. P. Palomar, J. M. Cioffi, and M. A. Lagunas, “Joint Tx-Rx beamforming design mul-ticarrier MIMO channel:A unified framework for convex optimization,”IEEE Trans. Signal
Process., vol. 8, no. 12, pp. 5755-5760,Dec. 2009.
[17] D. P. Palomar and Y. Jiang MIMO transceiver design via majorization theory, Foundation and rendsr in Communications and Information Theory. vol. 3,no. 4-5, pp. 331-551, 2006.