An approximately global optimization method for assortment problems

(1)

~ ~t- E U R O P E A N

~) , ' " J O U R N A L

OF OPERATIONAL

RESEARCH

ELSEVIER

European Journal of Operational Research 105 (1998) 604-612

Theory and Methodology

An approximately global optimization method for assortment

problems

Han-Lin Li *, Ching-Ter Chang

Institute of Information Management, National Chiao Tung University, Ta Hsieh Road, Hsinshu 30050, Taiwan, ROC

Received 20 July 1996; accepted 27 January 1997

Abstract

Assortment problems occur when we want to cut a number of small rectangular pieces from a large rectangle to get the minimum area within the rectangle. Recently, Chen et al. proposed a useful model for assortment problems. Although Chen et al.'s model is quite promising to find solutions, there are two inadequacies in their model: firstly, the objective function in their model is a polynomial term, which may not lead to a globally optimal solution; secondly, too many 0-1 variables are used to formulate the non-overlapping constraints. We propose a new method to reformulate an assortment model. Our model is not only able to find the approximately global optimal solution, but involves less 0-1 variables for formulating non-overlapping constraints. 9 1998 Elsvier Science B.V.

Keywords: Assortment; Optimization

1. I n t r o d u c t i o n

A n assortment optimization problem is the problem o f placing a given set o f rectangles within a rectangle which has m i n i m u m area. Assortment problems occur when a n u m b e r o f small rectangular pieces need to be cut from a large rectangle to get m i n i m u m area. Methods for assortment p r o b l e m s can be classified as the exact approach and the heuristic approach. The exact approach guarantees to find the optimal solution, while the heuristic approach can only find solutions which are ' g o o d e n o u g h ' . This p a p e r emphasizes on discussing the exact methods o f assortment problems.

Page [5] proposed a d y n a m i c p r o g r a m m i n g for solving cutting problems o f rectangle steel bars. Beaslay [2] proposed an integer model to solve a guillotine cutting problem. Recently, Chen et al. [1] presented a mixed integer p r o g r a m m i n g for assortment problems. C o m p a r e d to previous models, Chen et a l . ' s m o d e l is more promising in solving practical problems. However, Chen at al.'s model m a y only finds locally optimal solutions. In addition, Chen et al. use many 0-1 variables to formulate non-overlapping constraints in their models, which causes an extra computational burden.

(2)

H.-L. Li, C.-T. Chang / European Journal of Operational Research 105 (1998) 604-612 6 0 5

This paper proposes a new method for solving assortment optimization problems. T w o advantages o f this method are listed below:

1. it can find the solution which can be as close as possible to the globally optimum, instead of obtaining a local optimum as found by Chen et al.'s model;

2. it adopts less 0-1 variables to reformulate the non-overlapping constraints than used in Chen et al.'s model.

2. P r o b l e m f o r m u l a t i o n

Given n rectangles with fixed lengths and widths. An assortment optimization problem is to allocate all of these rectangles within an enveloping rectangle which has minimum area. Denote x and y as the width and the length of the enveloping rectangle, the assortment optimization problem is stated briefly as follows:

Minimize xy Subject to

I. all of n rectangles are non-overlapping;

2. all of n rectangles are within the range o f x and y.

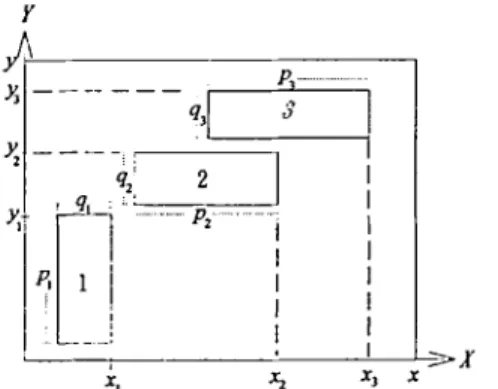
The related terminologies used in assortment models, by referring to Chen et al. [1] are described below: (Pi,qi): Dimension of rectangle i, Pi is the long side and qi is the short side. Pi and qi are constants, i ~ J , J

is the set o f given rectangles.

(xi,Yi): The top right c o m e r coordinates of rectangle i, i ~ J , x i and Yi are variables. ( x , y ) : The top right c o m e r coordinates of the enveloping rectangle, x and y are variables.

si: An orientation indicator for rectangle i, i ~ J. si = 1 if Pi (the longer dimension of rectangle i) is parallel to the x-axis; s i = 0 if p; is parallel to y-axis. Take Fig. 1 for example, s I = 0, s 2 = 1, and

5 3 = 1.

For any pair of rectangles i and k, the relative position indicators are denoted as follows:

ait:: The 'left' position indicator for rectangles i and k; aik equals 1 if rectangle i is to the left of rectangle k, and aik equals 0 otherwise.

bit::

The 'right' position indicator for rectangles i and k;

bit

equals 1 if rectangle i is to the right of rectangle k, and bit: equals 0 otherwise.

Y

I

q,l

72 . . . . i ; m q2' 2 ~ / , _qL :~"~ - - x, x~ x3 x

(3)

606 H.-L. Li, C.-T. Chang/European Journal of Operational Research 105 (1998) 604-612

cik: The 'below' position.indicator for rectangles i and k; cik equals 1 if rectangle i is to the below of rectangle k, and cik equals 0 otherwise.

d~k: The 'above' position indicator for rectangles i and k; d~k equals 1 if rectangle i is to the above of rectangle k, and d/k equals 0 otherwise.

J: Set of all rectangles within the enveloping rectangle xy.

The conditions for rectangles i and k to be non-overlapping are stated below

(1) aikq-bik-FCik-l-dik>__ 1,

(2) aik -t- bik < 2 and ci~ + dik < 2.

Take Fig. 1 for example, rectangles 1, 2 and 3 are non-overlapping, where

al2 + bl2 + c~2 + dj2 = 1 + 0 + 0 + 1 = 2 ,

and

a23 +b23 +c23 +d23 = 0 + 0 + 0 + 1 = 1.

Chen et al. [1] formulated an assortment model as follows (Fig. 1): Chen et al.'s Model:

Minimize xy

subject to, for all i, k ~ J, i < k:

x k - p k s k - q k ( 1 -- Sk) + (1 -- a i k ) M > _ x i , (1)

x i -- PiSi -- q i ( 1 -- Si) + (1 -- bik ) M ~" Xk, (2)

Yk -- qk Sk -- Pk ( 1 -- S t ) + ( 1 -- Ci~) M > Yi, (3)

Yi - q i s i -- P i ( 1 -- s i ) + ( 1 -- dik ) M > Yk, (4)

aik + bik -F cik + di~ >_ 1, (5)

where M is a large positive numbers: for all i E J:

x >__ x i, (6)

Y >-- Yi, (7)

x i - p i s i - q i ( 1 - s i ) > O, (8)

Yi - qisi - P i ( 1 - s i ) >- O, (9)

aik ,bik ,Cik ,dik = 0 or 1

for all i, k ~ J , i < k, s i = O o r l for a l l i ~ = J .

The objective function is to minimize the enveloping area. Constraints (1)-(5) ensure that the rectangles will not overlap. Constraints (6)-(9) ensure that all rectangles are within the enveloping rectangle.

Chen et al.'s model is a program with a nonlinear objective function, which is difficult to solve. By fixing the value of y in the objective function, Chen et al. solve their model to obtain the solution. Clearly, there are two defects within Chen et ai.'s model:

1. Firstly, y is assigned as a fixed value in solution process to reduce the computational complexity of the problem. Chen et al.'s model therefore may only find a locally optimal solution.

(4)

H.-L. Li, C.-T. Chang/European Journal of Operational Research 105 (1998)604-612 607 Y Y I P, I ' 2 . . . . . . . t - - - ~ X x x;

Fig. 2. Graphical illustration of proposed model.

2. Secondly, extravagant 0-1 variables are used to ensure the non-overlapping between rectangles, this will increase the computational burden in the solution process

In order to overcome above defects, we propose a new model for assortment optimization problem. First, denote x'i and Y'i below:

x'i: Distance between center o f rectangle i and original point along the x-axis, i ~ J (Fig. 2); y~: Distance between center of rectangle i and original point along the y-axis, i ~ J (Fig. 2).

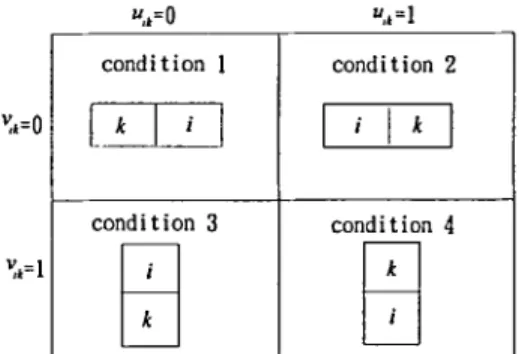
The conditions of non-overlapping between rectangles i and k can be reformulated by introducing two binary variables uik and vik as follows (Fig. 3):

C o n d i t i o n 1. uik = 0 and vik = 0 if and only if rectangle i is at the right of rectangle k. C o n d i t i o n 2. uik = 1 and vi, = 0 if and only if rectangle i is at the left of rectangle k. C o n d i t i o n 3. ui~ = 0 and v~k = 1 if and only if rectangle i is at the above o f rectangle k. C o n d i t i o n 4. uik = 1 and vi~ = 1 if and only if rectangle i is at the below o f rectangle k.

These four conditions can be represented as a proposition below:

uk=0 %=1 v,k=O v,k= | condition 1

I k l , I

condition 3 i k condition 2

I , i k l

condition 4 k ' i

(5)

608 H.-L. Li, C.-T. Chang/European Journal of Operational Research 105 (1998) 604-612

Table 1

Non-overlapping and position indication

Uik Uik Si Sk

Corresponding Coordinates paralleled conditions in to longer dimension

Fig. 3 i k 1 0 0 0 2 0 0 0 3 0 0 l 4 0 0 1 5 0 1 0 6 0 1 0 7 0 ! 1 8 0 1 1 9 1 0 0 10 1 0 0 11 1 0 1 12 1 0 1 13 1 1 0 14 1 1 0 15 1 1 l 16 i l 1 0 1 l 0 l i 2 2 2 2 0 3 3 0 3 3 4 4 4 4 y-axis y-ax~s X-axIS x-axis y-axis y2axls .x-axis .x-axis y-axis y-axis .X-axIS ,X-axIS y-axis y-axis x-axis x-axis y<LXlS x-axIs y-axis x-axis y-axis x-axis y - a x B x-axis y-axis x-axis y-axis x-axis y-axis x-axis y - a x i s x-axIs

Proposition 1. Rectangles i and k are non-overlapping i f the following conditions are satisfied:

1

( x'i - x'k) + u i t M + vikM > -~ [ pisi + qi(1 -- si) + pksk + qk(1 -- st,)] ,

1

( X' k -- X'i) + (1 -- Uik ) M + VikM > ~ [ PiSi + qi(1 -- si) + p , s k + qk(1 -- St)],

1

( Y; -- Y'k) + uikM + (1--Vik)M>__ ~ [ p i ( 1 - - S i ) + qisi + Pk(1 -- Sk) + q~Sk] ,

1

( y~ -- y;) + (1 -- Uik ) M + (1 -- Vik ) M > "~ [ pi(1 -- si) + qisi + pk(1 -- sk) + qksk], where all of variables are the same as defined before.

The corresponding binary variables uik, vik, s i and s k have 16 combinations shown in Table 1. From the basis of Proposition 1 the proposed model can be formulated as follows:

Proposed model: Minimize xy subject to

constraints ( 1 0 ) - ( 1 3 ) ,

1

Y >- Y'i + ~ [ Pi(1 - si) + qisi], i = 1,2 . . . N,

1 x>__x' i+ - Z [ p i s i + q i ( 1 - s i ) ], i = 1 , 2 . . . N, z . -

(lO)

(11) (12) (13) (14) (15) (16) (17)

(6)

H.-L. Li, C.-T. Chang/European Journal of Operational Research 105 (1998) 604-612

Table 2

Size of non-overlapping constraints and variables

609

Chen et al.'s model Proposed model

No. of 0-I variables 2n 2 - n n 2

No. of constraints } n ( n - l ) + 4 n 2n(n - l ) + 4 n

1

x ; - ~ [ P i s i + q i ( 1 - s i ) ] > 0 , i = 1 , 2 . . . N, (18)

y ; - l [ p i ( 1 - s i ) + q , si] >_0, i = 1 , 2 . . . N. (19)

The number of variables and constraints used in Chen et al.'s model ((1)-(9)) and the proposed model ((15)-(19)) is listed in Table 2. Table 2 shows that the proposed model uses less 0-1 variables to reformulate the non-overlapping constraints.

3..Linear strategies

This section aims at linearizing the polynomial term xy appear in the objective function of (14). Consider two bounded variables x, y where 0 < x < ~: and 0 < y < ~, .~ and ~ are constants, x and y can be represented as follows: G x =-~ E 2g-'Og + ~,, (20) g = l H Y=~y E 2h-'~$h + 6 , , (21) h = l

where ~ and cy are small positive variables. ~ and ~y are the pre-specified constants which are the upper bounds of e~ and ey respectively. 0 and ~ are 0-1 variables, and G, H are integers which denote the number of required 0-1 variables for representing x or y.

Proposition 2. Referring to (20)-(21), a polynomial term xy is represented as G xy = ~, E 2g-'OgY+ r g = l G H = ?~, ~7~ 2g-'OgY+-~y Y'. 2 h - l ~ h ~ ' x + g x o ~ g = l h = l

Let exy as a linear approximation of r162 expressed as

1

The error of approximating c x cy is then computed as

I _ e~ey

O < e~Y -- ~r'g" = -2 ( gxgy + -~yr ) - r162 < - 4

(22)

(7)

610 tl.-L. Li, C.-T. Chang / European Journal of Operational Research 105 (1998) 604-612

The maximal difference between exy and ~ gy is ~ c y / 4 , which occurs at

~ = T and e y = T "

S,tbstitute s ~ y in (22) by e~y its (23), the polynomial term xy in (22) with 0 < x < Yc and 0 < y <_ ~, can be approximately linearized as

G H 1

Ycy=-~ E 2g-'OgY + -~r E 2h-'6he~ + -~('~,ey + -eyr

(24)

g~l h=l

where 0 < Y~ - xy < ~ x ~ / 4 .

The term Ogy and 8h~, in (24) can be fully linearized based on Proposition 3 below

Proposition 3. An optimization problem of {Minimize O y, where 0 E (0,1), 0 < y <_ Y, Y E F ( a feasible set)} cats be linearized as Minimize z subject lo y + ~ ( O - - 1 ) < z , Z>_0, 0 ~ (0,1), y ~ F .

From the basis of Proposition 1 to Proposition 3, the proposed model of (14)-(19) can be linearized as follows: G H Minimize ~ '~. 2 g - l z g q- ~y E 2 h - l a b g = l h = l subject to z g > _ y + ~ ( O g - 1 ) , g---1,2 . . . G, zg>_O l l h ~ _ _ _ E x ' ~ - - ~ x ( a h - - l ) , h = 1,2 . . . H, It h >__ 0 , ( 1 5 ) - ( 1 9 ) , Og ,6h ~ (0,1). 4. Examples

Consider the following assortment optimization problems adopted from Chen et al. [ 1 ]: The sizes of pieces of rectangles are given in Table 3.

Minimize xy subject to

(8)

H.-L. Li, C.-T. Chang / E,,ropean Journal o f Operational Research 105 (1998) 604-612 611 Table 3 Sample data (18,3G) Rectangle 2 R e c t a n g l e 1 Rectangle 3 (31.21) !4,20) c t a n g l e 4 1 I ) I 1 x=34 (a) Result of Chert et a l . model

:3.1.36)y=31 (34.35) ( 1 6 . 3 8 ) (30,381(31.38) Rectangle 2 Rectangle 3 Rectangle I ~.20) ' :ctangh 4 j (30,22) (21,31) x=31 ~ (b) Result of proposed model Fig. 4. Solutions of Problem 1.

Problem number Number of rectangles Pi qi

1 4 2 4 20 18 16 16 14 21 7 2 6 33 I0 30 I1 25 15 18 14 18 I0 15 15 y = 3 ~ (30.35) (48.36)

y=36

!

Rectangle 2 05,25) Rectangle 8 Rectangle 3 Rectangle 4 Rectangle 5 Rectangle 1

(a) Result of Chea et a l . model

(48.34) (48.20) (48,10) i ) - - Z > x =48 (30,3G) Rectangle 2 (18,25) Rectangle 5 (33,Z5) Rectangle 4 Rectangle 6 Rectangle I J I I 1 , I Rectangle 3 (33,10)

(b) Result of proposed model Fig. 5. Solutions of Problem 2.

48,36) 48.35)

48.25)

(9)

612 H.-L. Li, C.-T. Chang/European Journal of Operational Research 105 (1998) 604-612

Table 4

Computational comparison of two models

Problem Chen et al.'s model Proposed model

number No. of 0-1 variables Objective value No. of 0-1 variables

in non-overiapping in non-overlapping

constraints constraints

Objective value

1 28 1224 16 1178

2 58 1728 36 1728

Chen et al. treated Problem 1 by fixing the value o f y as y = 36, then they solved a linear mixed 0-1 program to obtain the solution depicted in Fig. 4(a) with an objective value that equals 1224. Similarly, Chen et al. treated Problem 2 by assuming y = 36, then they solved the problem to obtain the results depicted in Fig. 5(a). By specifying ~ , = ey = 0.1, the proposed model solves these two problems by L I N D O [4] on an I B M - P C / A T 586 to find the solution shown in Fig. 4(b) and Fig. 5(b) in which we obtained an approximately global optimal solution.

Table 4 is the computational comparison o f two models, which demonstrates that 1. the proposed model is guaranteed to find a approximately global optimal solution;

2. the proposed model can solve an optimal program directly, while Chen et al.'s model needs to assign (or to guess) the value o f y; and

3. the proposed model uses less number o f 0-1 variables to formulate the non-overlapping constraints.

5. Conclusion

This paper proposes a new method to solve assortment optimization problems. By approximately linearizing the polynomial objective function, the proposed method with linear strategies can reach a solution which is close to the globally optimal solution. In addition, less 0-1 variables are used to reformulate the non-overlapping constraints of assortment optimization problems.

References

[1] C.S. Chen, S. Sarin, R. Balasubramanian, A mixed-integer programming model for a class of assortment problems, European Journal of Operational Research 63 (1993) 362-367.

[2] J.E. Beasley, An algorithm for the two-dimensional assortment problem, European Journal of Operational Research 19 (1985) 253-261. [3] A.I. Hinxman, The trim-loss and Assortment problem: A survey, European Journal of Operational Research 5 (1980) 8-18.

[4] S. Linus, UNDO release 5.3, LINDO System, Inc., 1994.