A Novel Superquadric Fitting based on Radial Euclidean Distance for 3D Objects Fitting

A Novel Superquadric Fitting based on Radial Euclidean Distance for 3D Objects Fitting

Wu-Chih Hu

Department of Computer Science and Information Engineering, National Penghu University

wchu@npu.edu.tw

Chuan-Yu Chang Department of Computer and

Communication Engineering, National Yunlin University of Science &

Technology

chuanyu@yuntech.edu.tw

Abstract

Superquadric is a very flexible primitive in computer vision, it can represent a variety of 3D shapes by varying a few parameters. In this paper, a novel superquadric fitting based on radial Euclidean distance is proposed to evaluate the parameters of a superquadric. In the proposed superquadric fitting method, the initial parameters of a superquadric are first obtained by using the superellipse fitting method based on the geometric properties of the superquadric.

Once the initial parameters are obtained, the more accurate parameters are estimated by using iterative procedure involved optimization problem. The proposed superquadric fitting method is very useful for object representation and recognition.

Keywords: Superquadric fitting; Radial Euclidean distance; Object representation.

1. Introduction

Visual perception can provide us with information and capability that makes it possible to locate and recognize objects and their interrelationships without direct physical contact. Besides, the 3D object recognition is very important in many industrial applications and research areas, such as robotics and computer vision. Therefore, it is very important to seek a meaningful and compact object description for computer vision processing. In the 3D object description, three main categories (wire frame model, cylinder model, and volumetric model) are used (Nevatia and Binford, 1977).

In wire frame model, a set of lines and their relationship are used to describe the object. Because the topology of the wire frame model is not specific, the further application of object recognition is difficult.

In cylinder model, the object is described based on the reference axis and the planar cross-section which is perpendicular to the reference axis. Using cylinder model, complex objects are not immediately described and these complex objects must be partitioned into small and suitable units. In volumetric model, a set of solid models and Boolean operators are used to

describe the object. The geometric information and topology of objects would be saved in volumetric model. Therefore, using volumetric model is useful for the further application of object recognition.

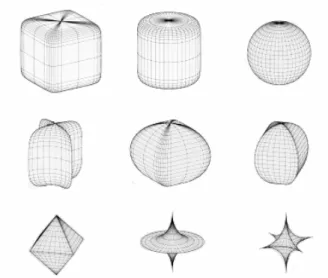
Superquadric fitting is the volumetric model, and it is also the parametric model. Parametric model is one of suitable model for computer vision processing which has been widely used in computer vision. Furthermore, superquadric has powerful capability to represent a wide variety of 3D shapes including cuboids, rounded cuboids, cylinder, ellipsoids, octahedrons, and pinched octahedrons, etc., as shown in Fig. 1.

Fig. 1. Various superquadrics (Kindlmann, 2004).

Superquadric is a very flexible primitive in computer vision, and it was popularized in computer graphics by Barr (Barr, 1981), and computer vision by Pentland (Pentland, 1986). The recovery of parametric model (deformable superquadric) was discussed from synthesized or real range images by Solina and Bajcsy (Solina and Bajcsy, 1990).

In superquadric fitting, the least-squares method is often used to solve the parameters of the superquadric.

The least-squares method is one of the well known and mostly applied tools in various disciplines of science and engineering. The least-squares method

minimizes the square sum of error-of-fit in predefined measures, and two main categories (algebraic fitting and geometric fitting) are differentiated by the respective definition of the errors between the curve and the real data.

In algebraic fitting, the superquadric is described by implicit equation, and the error is defined as deviation of the implicit equation from the expected value at each given point (Solina and Bajcsy, 1990;

Chen, et al., 1997; Liu and Yuan, 2001). The computational cost of using algebraic distance is low, but the high curvature bias (Rosin and West, 1995) is attended to generate drawback in accuracy. That is, the error from a data point to the superquadric gives a lower estimate near high curvature sections than low curvature sections for the same Euclidean distance.

In geometric fitting, the error is usually defined with the orthogonal distance from the given point to the superquadric, and it is also known as the best fitting (Wen and Yuan, 2004). Unfortunately, it is difficult to solve the associate equations, and it would be computationally expensive.

Radial Euclidean distance is another case of geometric fitting. It is defined as the Euclidean distance from the data point to the point on the superquadric along the line that passes through the data point and the center of the superquadric. Using radial Euclidean distance, the high curvature bias can be effectively reduced (Rosin and West, 1995), and the computational cost is lower than one using orthogonal distance. Besides, the objective function based on radial Euclidean distance performs much better in the experiments than the function based on the implicit definition (algebraic distance) in almost all aspects including the accuracy and fitting errors of the recovered superquadrics, robustness against noise, and convergence speed of the data fitting process (Zhang, 2003). Therefore, radial Euclidean distance is used in the proposed superquadric fitting in this paper.

In this paper, a novel superquadric fitting based on radial Euclidean distance is proposed to evaluate the parameters of a superquadric. In the proposed superquadric fitting, the initial parameters of the superquadric are first obtained by using the superellipse fitting. Two independent superellipses are found with geometric properties and they are only affected by the individual squareness parameter.

Therefore, parameters of the superquadric can be efficiently evaluated by the two independent superellipses. The superellipse fitting methods, such as 6D optimization method (Rosin and West, 1995), moment based method (Voss and Suesse, 1999), area based method, diagonal based method, 1D optimization method (Rosin, 2000), and 2D optimization method (Hu and Sheu, 2001) can all be considered to estimate the initial parameters of the superquadric. For considering the consistency, 2D optimization method is selected in this paper. Once the initial parameters are obtained, the more accurate parameters are estimated by using iterative procedure

of Powell's conjugate direction technique (Press et al., 1992).

Besides, limitations contained in this paper are summarized as follows. First, only regular superquadrics are investigated and deformable superquadrics are not addressed. Second, the 3D data points of the object surface are obtained by using the active machine vision system (Wu and Sheu, 1996), which is formed from a laser projector, rotating platform, and CCD camera.

In the remainder of this paper, review of 2D optimization method of superellipse fitting is presented in Section 2. In Section 3, the novel superquadric fitting is proposed. Section 4 presents experimental examples and evaluations of the experimental results. Finally, conclusion is made in Section 5.

2. Review of 2D optimization method of superellipse fitting

Superellipses are the 2D version of superquadrics.

Superellipses were first formulated by Gardiner (Gardiner, 1965), and curve segmentation/representation based on superellipses was first proposed by Rosin and West (Rosin and West, 1995). A superellipse centered on the origin with its axes aligned with the coordinate system can be represented by the equation (1).

1 ) ( )

(x a ^2ε + y b ^2ε = (1)

where ε is called the squareness. A superellipse with different values of the squareness ε , it can represent a wide variety of 2D shapes such as rounded rectangle, ellipse, diamond, pinched diamond, etc.

The superellipse fitting methods, such as 6D optimization method (Rosin and West, 1995), moment based method (Voss and Suesse, 1999), area based method, diagonal based method, 1D optimization method (Rosin, 2000), and 2D optimization method (Hu and Sheu, 2001) can all be considered to estimate the initial parameters of the superquadric.

The 6 parameters {x₀,y₀,θ,a ,b ,ε} of a superellipse are iteratively estimated in 6D optimization method by using the parameters of an ellipse as the initial values, thus the computational cost is very high, where {x₀ ,y₀} are the center of the superellipse, θ is the orientation, and { ba, } are the lengths of the major and the minor axes, respectively.

In moment based method, all parameters (except for squareness) of a superellipse are estimated by using moments, and the squareness is iteratively estimated.

The minimum bounding rectangle is used in the area based method, where the minimum bounding rectangle provides all the parameters of a superellipse except for the squareness. The squareness is estimated by calculating the area of the superelliptical region in the image and comparing it against the theoretical area.

But, the deviation between estimated squareness and

true squareness is high in the area based method.

In diagonal based method, the minimum bounding rectangle of the superellipse is first found, and the squareness is estimated by the intersection of the boundary with diagonal of the minimum bounding rectangle. Four estimated the squareness would be obtained by four intersection points of the boundary with the diagonals, and then the median is taken to provide some robustness to noise.

The shape of the superellipse is defined as a weighted average of an ellipse and a rectangle (for

1

0<ε≤ ) in 1D optimization method. This enables a 1D search over 0<ε ≤1. Hence, superellipse fitting is limited in 0<ε≤1.

For considering the consistency, 2D optimization method is selected in this paper. In the first scheme of 2D optimization method of superellipse fitting, 6 parameters {x₀,y₀ ,θ,a ,b,ε} of a superellipse are evaluated roughly. The zero^th harmonic of Fourier descriptor corresponds to the center of the approximated contour and the first harmonic of Fourier descriptor is an ellipse with the same orientation as the one of the approximated contour.

This research employs this fact to estimate these three parameters {x₀,y₀,θ}. The orientation estimation using the consistent symmetric axis method (Sheu, et al, 1997) is further explained below.

Since the first harmonic of a Fourier descriptor is an ellipse with the orientation of the approximated superellipse, the consistent symmetric axis method for estimating the orientation of an ellipse is exploited.

Essentially, the method involves first constructing the symmetric horizontal axis by connecting the midpoints of the horizontal scan line segments inside the ellipse, and similarly for the symmetric vertical axis. With this approach, the ellipse parameters are insensitive to noise and the computational cost is low.

Consider an ellipse as shown in Fig. 2, where the orientation θ can be estimated from the angles α and β using equation (2), and α and β are the angles of the symmetric horizontal/vertical axes PQ and P′Q′, respectively.

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛ − + − + +

= ⁻

β

β β α β α β

θ α

tan 2

tan 4 tan tan tan tan 2 1 1 tan tan tan

2 2 2 1

(2) Once the center and orientation are obtained, the

lengths of the major and the minor axes { ba, } can be easily estimated based on geometric properties and dominant points for ε≤2 and ε >2, respectively.

Finally, the squareness ε is easy evaluated from equation (3) by using the bounding rectangle model as shown in Fig. 3.

2 ln

) ln(

2 d l

=−

ε (3)

Fig. 2. An ellipse with orientation θ .

P Q d l

Fig. 3. The bounding rectangle model.

In the second scheme of 2D optimization method of superellipse fitting, the parameters of a superellipse are obtained accurately by using the iterative procedure Powell's algorithm (Press, et al., 1992). The objective function is defined as equation (4) in the iterative procedure.

∑

= ⁿ

i

di

n MSE

1

) 2

1

( (4)

where d_i is the Euclidean distance along the line passing through the estimated point and the center of the superellipse, and n is the number of total points.

For a superellipse centered on the original with axes aligned with the coordinate system, the formulas for estimating d_i are obtained from equations (5) and (6), where (x_i,y_i) is the estimated point, and

) ,

(x_e y_e is the intersection point.

2

2 ( )

)

( _{i e i e}

i x x y y

d = − + − (5)

2 2

2 ( )

) 1 (

1 ^ε

ε

ε y xb

x a

i i

e= + (6a)

) ( _{i i}

e

e x y x

y = (6b)

The iterative procedure of Powell's algorithm is as follows.

(i) Set the parameters {x₀,y₀,θ,a,b ,ε} estimated in the first scheme as the initial values.

(ii) Do a gradient descent by varying the parameter a, and ε is updated by using equation (3). Once the minimum of the objective function has been found, repeat for the parameter b.

(iii) Combine the change in the parameters { ba, } into a vector and ε is updated until minimum of the objective function is obtained by gradient descent

along this vector.

(iv) Repeat from stage (ii) until the change of { ba, } is sufficiently small.

Only two parameters { ba , } are repeatedly estimated in iterative procedure to obtain more accurate result. Hence, the superellipse fitting is a 2D optimization.

A mechanical piece shown in Fig. 4(a) is used to evaluate the performance of the 2D optimization method of superellipse fitting, and 7 superellipses are obtained successfully, as shown in Fig. 4(b).

(a)

(b)

Fig. 4. Superellipse fitting of a mechanical piece.

3. The proposed superquadric fitting

A superquadric centered on the origin with its axes aligned with the coordinate system can be represented by the equation (7).

1 ) ( ] ) ( )

[(x a ^2ε2+ y b ^{2ε2 ε2ε1}+ z c ^2ε1 = (7) Its parametric form is given by equation (8), where a, b and c are the scale factors along the x, y, and z axes, respectively. ε and 1 ε are called the 2 squareness parameters, where ε determines the 2 shape of the superquadric cross section parallel to the xy plane, while ε determines the shape of the 1 superquadric cross section in a plane perpendicular to the xy plane.

π ω π

π η π η

ω η

ω η ω

η

ω η ω

η

ε ε ε

ε ε

<

≤

−

≤

≤

⎪⎩

⎪⎨

⎧

=

=

= - 2 2

, sin

) , (

sin cos ) , (

cos cos ) , (

1 2 1

2 1

c z

b y

a x

(8)

In the novel superquadric fitting, a two-phase scheme is proposed to evaluate 11 parameters

} , , 2, 1, , , , , , ,

{x₀ y₀ z₀ a b c ε ε θ_x θ_y θ_z of a superquadric, where {x₀,y₀,z₀} are the center of a superquadric, and {θ_x,θ_y,θ_z} are the Euler angles of the x, y, and z axes, respectively. In the first phase scheme, the initial parameters {x₀,y₀,z₀,a,b,c ,ε1,ε2,θ_x,θ_y,θ_z} are first estimated by using the 2D optimization method of superellipse fitting (Hu and Sheu, 2001) with the geometric properties of the superquadric. The more accurate parameters are estimated by using iterative procedure of Powell's conjugate direction technique (Press, et al., 1992) in the second phase scheme.

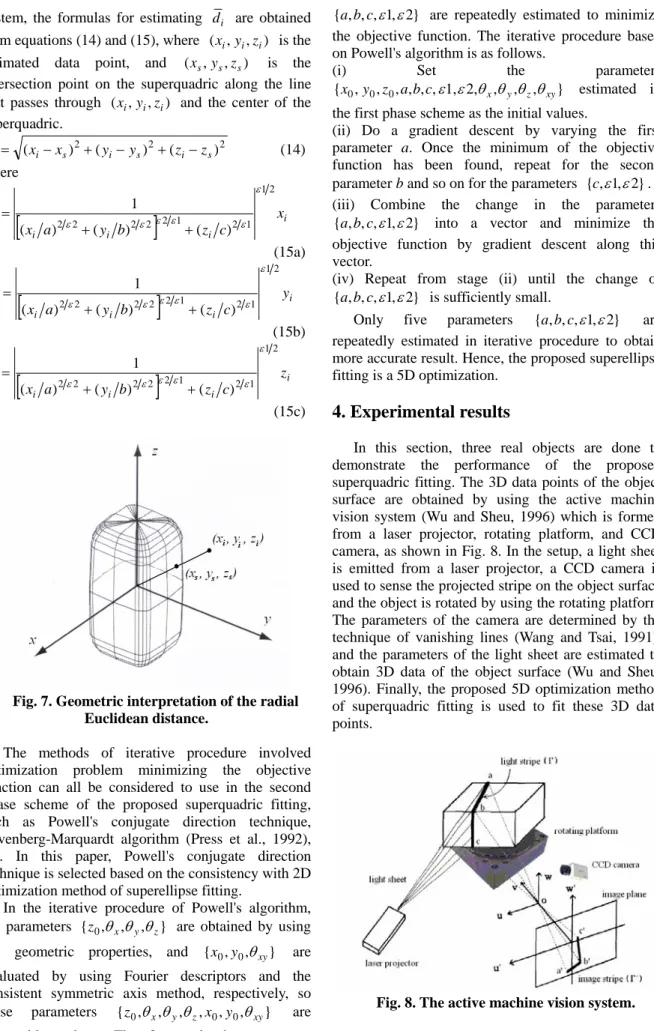
Suppose the vertical axis of the superquadric is parallel to the z axis, i.e., the superquadric is perpendicular to the xy plane, as shown in Fig. 5. In the practicality of computer vision measurement, this treatment is reasonable. Therefore, Euler angles would be θ_x =θ_y=θ_z =0; parameter c can be evaluated by taking half of the height of the superquadric, and parameter z₀ can be obtained by taking the midpoint of the two endpoints on the z axis of the superquadric.

Fig. 5. A superquadric is perpendicular to the xy plane.

In Fig. 5, two independent superellipses are found based on geometric properties and they are only affected by the individual squareness parameter.

Therefore, parameters of the superquadric can be efficiently evaluated with the two independent superellipses. The superellipse only affected by ε 2 (indicated as superellipse S_ε2, as shown in Fig. 5) is obtained from the section of the superquadric by using the horizontal plane passing z0. The parameters of superellipse S_ε2 would be estimated by using 2D optimization method (Hu and Sheu, 2001).

The parameters {x₀,y₀,a,b,ε2,θ_xy} can be evaluated by using the first scheme of 2D optimization method of superellipse fitting, where θ is the _xy orientation in xy plane. When the parameters

} , 2 , , , ,

{x₀ y₀ a b ε θ_xy are obtained, the superellipse

only affected by ε (indicated as superellipse 1 S_ε1) can be obtained from the section of the superquadric by using the vertical plane passing the center

) , ,

(x₀ y₀ z₀ and rotating θ , as shown in Fig. 6. In _xy the parameters of superellipse Sε1, only squareness parameter ε is not obtained. 1

Fig. 6. The bounding rectangle model of the superellipse S_ε1.

The squareness ε can be estimated with a closed 1 form solution by modifying the diagonal based method (Hu and Sheu, 2001). The closed form solution of the squareness ε is described as follows. 1 Consider the line segment between the center

) , , (x₀ y₀ z₀

O and a point on a superellipse along the diagonal segment, and let its length be OQ d~

= , and the length of diagonal segment is OP a₂ c₂ l~

= +

= ,

as shown in Fig. 6. The squareness 1ε is determined by equation (9).

2 ln

~) ln(~ 1=−2 d l

ε (9)

Once the initial parameters of a superquadric are obtained, the more accurate parameters are estimated by using iterative procedure with the objective function. Most superquadric fitting methods for 3D objects recover superquadrics from range images by minimizing the objective function. The objective function plays an important role to measure the accuracy of the recovered model. Algebraic fitting is often used in superquadric fitting. In algebraic fitting, the superquadric is described by implicit equation, as shown in equation (10), and the error is defined with deviation of the implicit equation from the expected value at each given point.

1 ) ( ] ) ( ) [(

) , ,

(x y z = x a ^2ε2+ y b ^{2ε2 ε2ε1}+ z c ^2ε1− F

(10) )

, , (x y z

F is also called the inside-outside function because it provides a simple test whether a given point lies inside or outside the superquadric.

<0

F , F =0, and F>0 imply that the given point lies inside the superquadric, on the surface of the superquadric, and outside the superquadric, respectively. The computational cost of using

algebraic distance is low, but the high curvature bias (Rsoin and West, 1995) is attended to generate drawback in accuracy. That is, the error from a data point to the superquadric gives a lower estimate near high curvature sections than low curvature sections for the same Euclidean distance. Therefore, Solina and Bajcsy (Solina and Bajcsy, 1990) suggested minimizing the equation (11) to find the better superquadric fitting with the minimum volume.

) , , (x y z F

abc (11)

In geometric fitting, the error is usually defined with the orthogonal distance from the given point to the superquadric. The geometric fitting is also known as the best fitting. Normal vector on the superquadric surface must be calculated in the estimation of the orthogonal distance. The normal vector nv at a point on the superquadric surface is defined as the equation (12).

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

−

−

−

=

−

−

−

− +

−

− +

−

ω ω

η η

ε ε

ω ω

η η

ε ε

ω ω

η η

ε ε

ε ε

ε

ε ε

ε

ε ε

ε

1 2 1 2 1 1 2

1 2 1

1 1 1

1 2 1

1 1 1

cos sin

cos sin 2 1

cos sin cos

sin 2 1

sin cos cos

sin 2 1

ab ac bc nv

(12) Unfortunately, it is difficult to solve equation (12)

for η and ω analytically although the values of η and ω that minimize orthogonal distance can be determined numerically by walking around the superquadric. This would be computationally expensive.

Radial Euclidean distance is another case of geometric fitting. It is defined as the Euclidean distance from the data point to the point on the superquadric along the line that passes through the data point and the center of the superquadric. Using radial Euclidean distance, the high curvature bias can be effectively reduced (Rosin and West, 1995), and the computational cost is lower than one using orthogonal distance. Besides, the objective function based on radial Euclidean distance performs much better in the experiments than the function based on the implicit definition (algebraic distance) in almost all aspects including the accuracy and fitting errors of the recovered superquadrics, robustness against noise, and convergence speed of the data fitting process (Zhang, 2003). Therefore, radial Euclidean distance is used in the proposed superquadric fitting in this paper.

In the second phase scheme of the proposed superquadric fitting, the parameters of a superquadric are accurately estimated by using the iterative procedure with the objective function defined as equation (13).

∑

= ^N

i

di

N MSE

1

) 2

1

( (13)

where d_i is the radial Euclidean distance, as shown in Fig. 7, and N is the number of total 3D data points of the object surface. For a superquadric centered on the original with axes aligned with the coordinate

system, the formulas for estimating d_i are obtained from equations (14) and (15), where (x_i,y_i,z_i) is the estimated data point, and (x_s,y_s,z_s) is the intersection point on the superquadric along the line that passes through (x_i,y_i,z_i) and the center of the superquadric.

2 2

2 ( ) ( )

)

( _{i s i s i s}

i x x y y z z

d = − + − + − (14)

where

[

]

s x

c z b

y a

x x

2 1

1 1 2

2 2 2 2

2 ( ) ( )

) (

1

ε

ε ε ε ε

ε + +

=

(15a)

[

]

s y

c z b

y a

x y

2 1

1 1 2

2 2 2 2

2 ( ) ( )

) (

1

ε

ε ε ε ε

ε + +

=

(15b)

[

]

s z

c z b

y a

x z

2 1

1 1 2

2 2 2 2

2 ( ) ( )

) (

1

ε ε ε

ε ε

ε + +

=

(15c)

Fig. 7. Geometric interpretation of the radial Euclidean distance.

The methods of iterative procedure involved optimization problem minimizing the objective function can all be considered to use in the second phase scheme of the proposed superquadric fitting, such as Powell's conjugate direction technique, Levenberg-Marquardt algorithm (Press et al., 1992), etc. In this paper, Powell's conjugate direction technique is selected based on the consistency with 2D optimization method of superellipse fitting.

In the iterative procedure of Powell's algorithm, the parameters {z₀,θ_x,θ_y,θ_z} are obtained by using the geometric properties, and {x₀,y₀,θ_xy} are evaluated by using Fourier descriptors and the consistent symmetric axis method, respectively, so these parameters {z₀,θ_x,θ_y,θ_z,x₀,y₀,θ_xy} are reasonable to keep. Therefore, only the parameters

} 2 , 1 , , ,

{a b cε ε are repeatedly estimated to minimize the objective function. The iterative procedure based on Powell's algorithm is as follows.

(i) Set the parameters }

, , , 2, 1, , , , , , ,

{x₀ y₀ z₀ abc ε ε θ_xθ_y θ_z θ_xy estimated in the first phase scheme as the initial values.

(ii) Do a gradient descent by varying the first parameter a. Once the minimum of the objective function has been found, repeat for the second parameter b and so on for the parameters {c,ε1,ε2}. (iii) Combine the change in the parameters

} 2 , 1 , , ,

{a b cε ε into a vector and minimize the objective function by gradient descent along this vector.

(iv) Repeat from stage (ii) until the change of }

2 , 1 , , ,

{a b cε ε is sufficiently small.

Only five parameters {a,b,c,ε1,ε2} are repeatedly estimated in iterative procedure to obtain more accurate result. Hence, the proposed superellipse fitting is a 5D optimization.

4. Experimental results

In this section, three real objects are done to demonstrate the performance of the proposed superquadric fitting. The 3D data points of the object surface are obtained by using the active machine vision system (Wu and Sheu, 1996) which is formed from a laser projector, rotating platform, and CCD camera, as shown in Fig. 8. In the setup, a light sheet is emitted from a laser projector, a CCD camera is used to sense the projected stripe on the object surface, and the object is rotated by using the rotating platform.

The parameters of the camera are determined by the technique of vanishing lines (Wang and Tsai, 1991), and the parameters of the light sheet are estimated to obtain 3D data of the object surface (Wu and Sheu, 1996). Finally, the proposed 5D optimization method of superquadric fitting is used to fit these 3D data points.

Fig. 8. The active machine vision system.

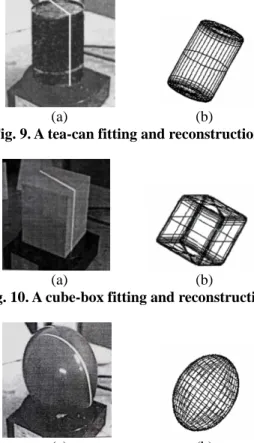
The number of total lines (light stripes) on object

surface is set as 360 n, where n is the degrees of per rotation in rotating platform. In the experiments, n is set as 2 degrees, thus the number of total lines on object surface is 180. Three real objects (a tea-can, a cube-box, and a balloon) are tested, as shown in Figs.

9(a), 10(a), and 11(a), respectively. The reconstruction results of three real objects in arbitrary pose are shown in Figs. 9(b), 10(b), and 11(b), respectively. Because Figs. 9(a) and 10(a) are the standard shapes of superquadrics, the performance of object fitting is very good by using the proposed method. Besides, traditional superquadric fitting (11D optimization method) uses the parameters of an ellipsoid as the initial parameters in the iterative procedure involved optimization problem, thus the computational cost of the proposed 5D optimization of superquadric fitting would be lower than the traditional superquadric fitting.

(a) (b)

Fig. 9. A tea-can fitting and reconstruction.

(a) (b)

Fig. 10. A cube-box fitting and reconstruction.

(a) (b)

Fig. 11. A balloon fitting and reconstruction.

Analyzing the results of Figs. 9(b), 10(b) and 11(b), the degrees of per rotation in rotating platform would affect the resolution of 3D data points of object surface. It would also affect the accuracy of superquadric fitting. Besides, the deviation of superquadric fitting is high for the object with asymmetry to the center of the object, as shown in Fig.

11(a). Therefore, the deformable superquadric (Solina and Bajcsy, 1990; Wen and Yuan, 2004) is studied for fitting the asymmetric objects. But, the tapering and bending parameters (total of additional parameters is 4) in the deformable superquadric fitting are considered

and estimated, and the computational cost would be greatly increased. However, the result of the first phase scheme of proposed superquadric fitting can be used as the initial parameters of deformable superquadric fitting to effectively reduce the computational cost.

5. Conclusion

A novel superquadric fitting based on radial Euclidean distance for 3D objects fitting is proposed successfully. The proposed method is a 5D optimization method of superquadric fitting. In the proposed superquadric fitting, a two-phase scheme is proposed to evaluate 11 parameters of a superquadric.

In the first phase scheme, the initial parameters are first obtained by using the 2D optimization method of superellipse fitting with the geometric properties of the superquadric. In this paper, two independent superellipses are found based on geometric properties and they are only affected by the individual squareness parameter. Hence, all parameters of the superquadric can be efficiently evaluated with the two independent superellipses. Furthermore, the more accurate parameters are estimated by using iterative procedure with Powell's conjugate direction technique in the second phase scheme.

The computational cost of the proposed 5D optimization of superquadric fitting would be lower than the traditional superquadric fitting. Furthermore, the parameters obtained in the first phase scheme of proposed superquadric fitting can be used as the initial parameters of deformable superquadric fitting to to increase the efficiency. Hence, the proposed superquadric fitting would be very useful for object representation and object recognition.

Acknowledgements

This paper has been supported by the National Science Council, Taiwan, ROC under Grant No. NSC 94-2213-E-346-006.

References

Barr, A. H. (1981). Superquadrics and angle-preserving transformations., IEEE Computer Graphics Applications, 1 (1), 11-23.

Chen, L. H., & Liu, Y. T., & Liao, H. Y. (1997).

Similarity measure for superquadrics. IEE Proceeding-Vision, Image and Signal Processing, 144 (4), 237-243.

Gardiner, M. (1965). The superellipse: a curve that lies between the ellipse and the rectangle. Scientific American, 21, 222-234.

Hu, W. C., & Sheu, H. T. (2001). Efficient and consistent method for superellipse detection. IEE Proceeding-Vision, Image and Signal Processing, 148 (4), 227-233.

Kindlmann, G. (2004). Superquadric tensor glyphs. in:

Proceedings of IEEE TVCG/EG Symposium on Visualization, 147-154.

Liu, W. B., & Yuan, B. Z. (2001). Superquadric based hierarchical reconstruction for virtualizing free form objects from 3D data. Chinese Journal of Electronics, 10 (1), 100-105.

Nevatia, R. & Binford, T. O. (1977). Description and recognition of curved objects. Artificial Intelligence, 8, 77-98.

Pentland, A. (1986). Perceptual organisation and the representation of natural form. Artificial Intelligence, 28, 293-331.

Press, W. H., & Teukolsky, S. A., & Vetterling, W. T.,

& Flannery, B. P. (1992). Numerical Recipes in C.

Cambridge Press, USA.

Rosin, P. L., & West, G. A. W. (1995). Curve segmentation and representation by superellipse.

IEE Proceeding-Vision, Image and Signal Proceeding, 142 (5), 280-288.

Rosin, P. L. (2000). Fitting superellipses. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22 (7), 726-732.

Sheu, H. T., & Chen, H. Y., & Hu, W.C. (1997).

Consistent symmetric axis method for robust detection of ellipses. IEE Proceeding-Vision, Image and Signal Processing, 144 (6), 332-338.

Solina, F., & Bajcsy, R. (1990). Recovery of parametric models from range images: the case for superquadrics with global deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12 (2), 131-147.

Voss, K., & Suesse, H. (1999). A new one-parametric fitting method for planar objects. IEEE Transactions on Pattern Analysis and Machine Intelligence, 21 (7), 646-651.

Wang, L. L., & Tsai, W. H. (1991). Camera calibration by vanishing lines for 3-D computer vision. IEEE Trans. Pattern Analysis and Machine Intelligence, 13 (4), 370-376.

Wen, F., & Yuan, B. (2004). Least-squares fitting for deformable superquadric model based on orthogonal distance. Pattern Recognition Letters, 25, 933-941.

Wu, M. F., & Sheu, H. T. (1996). 3D invariant estimation of axisymmetric objects using Fourier descriptors. Pattern Recognition, 29 (2), 267-280.

Zhang, Y. (2003). Experimental comparison of superquadric fitting objective functions. Pattern Recognition Letters, 24, 2185-2193.