由量測數據建構人類脊椎骨模型之理論研究

全文

(1)國立交通大學機械工程學系碩士論文. 由量測數據建構人類脊椎骨模型之理論研究 A Theoretical Construction of 3D Spinal Disk Model from Measured Geometric Data. 研究生：林於呈指導教授：陳大潘. 博士. 中華民國九十五年九月.

(2) 由量測數據建構人類脊椎骨模型之理論研究. 研究生：林於呈. Student：Yu-Chen Lin. 指導教授：陳大潘博士. Advisor：Da-Pan Chen. 國立交通大學機械工程研究所碩士論文. A Thesis Submitted to Institute of Mechanical Engineering College of Engineering National Chiao Tung University In Partial Fulfillment of the Requirements For the Degree of Master of Science in Mechanical Engineering. July 2006 Hsinchu, Taiwan, Republic of China. 中華民國九十五年九月.

(3) 由量測數據建構人類脊椎骨模型之理論研究. 研究生：林於呈. 指導教授：陳大潘博士. 國立交通大學機械工程研究所. 摘. 要. 本論文主要目的是研究人類單節脊椎骨幾何模型的建立，其中包括幾何模型原理、物體資料點間之三角化過程、以及兩模型間之組合方式討論。首先對於幾何模型原理作相關介紹，並經由實際使用參數曲面建立模型之過程，了解此方式在建立構造複雜模型時不足的地方。而後分別討論由雷射取得物體資料點以及由電腦斷層掃描圖片建立模型此兩種建模方式。其次以猶他茶壺做為範例，介紹由物體之切面輪廓建立模型的過程，並實際建立人類之單一節脊椎骨模型，最後並將不同切面的兩模型組合，以期能完整呈現物體之幾何構造。. i.

(4) A Theoretical Construction of 3D Spinal Disk Model from Measured Geometric Data Student: Yu-Chen Lin. Advisor: Dr. Da-Pan Chen. Department of Mechanical Engineering National Chiao Tung University. ABSTRACT. The aim of this research study is to apply the technique of geometric modeling to establish a human spinal disk model. The content includes geometric modeling theory, the process of triangulation between data points, and a discussion of the combination of the two models. First of all, an introduction is given on geometric modeling theory, by the way of establishing parametric model, we can realize its failures of building complicated models. After that, we compare two ways of establishing models. Secondly, we take Utah Teapot as an illustration to introduce the establishing process of the model which using the contours of the cross sections, and we apply the method to establish a human spinal model, Finally, combing the two models established by the vertical and horizontal cross sections, we can get a complete geometric structure.. ii.

(5) 誌. 謝. 時光飛逝，轉眼間就要結束了學生生涯，邁向人生的另一個旅程。本篇論文得以完成，首先要感謝父母親給予的許多包容與支持，讓我能在無後顧之憂的環境下順利完成學業。最重要的是要感謝二年來的指導教授陳大潘老師，不論是課業上或生活上，老師的教誨都讓我獲益良多。感謝學長振予在研究過程中的諸多幫助，也感謝實驗室的同學以及學弟們。感謝曾經幫助與照顧我的每一個人。. iii.

(6) 目. 錄. 頁次. 摘要……………………………………………………………………. i. ABSTRACT………………………………………………………….... ii. 誌謝……………………………………………………………………. iii. 目錄……………………………………………………………………. iv. 圖目錄…………………………………………………………………. vi. 一、緒論………………………………………………………………. 1. 1-1 前言…………………………………………………………….. 1. 1-2 研究背景……………………………………………………….. 1. 1-3 研究目的……………………………………………………….. 2. 1-4 論文架構……………………………………………………….. 3. 二、幾何模型原理基礎………………………………………………. 5. 2-1 參數曲線……………………………………………………….. 5. 2-1-1 赫米特曲線(Hermite Curves)…………………………….. 6. 2-1-2 伯濟爾曲線(Bezier curves)……………………………….. 7. 2-2 曲線之連續……………………………………………………... 8. 2-3 參數曲面……………………………………………………….. 15. 2-3-1 張量積雙三次曲面(Tensor-Product Bicubic Patch)…….... 15. 2-3-2 伯濟爾曲面(Bezier Surface)…………………………….... 17. 2-4 齊次座標轉換………………………………………………….. 18. 三、幾何模型建構方式………………………………………………. 20. 3-1 Primitive Models………………………………………………... 20. 3-2 Constructive Solid Geometry(CSG) Models…………………… 21 iv.

(7) 3-3 Triangulated surface Models……………………………………. 23. 3-4 CT Models………………………………………………………. 24. 四、茶壺模型的建立…………………………………………………. 26. 4-1 切面輪廓的取得……………………………………………….. 26. 4-2 由切面輪廓重建模型………………………………………….. 27. 4-2-1 三角元素品質(Mesh Quality)…………………………….. 27. 4-2-2 三角化連接………………………………………………... 28 4-3 CT Modeling 之缺點………………………………………… 31 五、脊椎模型的建立與重組…………………………………………. 33 5-1 脊椎模型之建立……………………………………………….. 33. 5-1-1 XY 切面所建構之脊椎骨模型…………………………… 33 5-1-2 YZ 切面所建構之脊椎骨模型…………………………… 35 5-2 模型之切割與合併…………………………………………….. 38. 5-3 結果討論……………………………………………………….. 43. 5-3-1 合併後之脊椎模型……………………………………….. 43 5-3-2 切面的影響……………………………………………….. 44. 六、結論………………………………………………………………. 46. 6-1 結論…………………………………………………………….. 46. 6-2 未來展望……………………………………………………….. 46. 參考文獻………………………………………………………………. 47. v.

(8) 圖. 目. 錄. 圖 1-1 資料點對曲線之影響……………………………………….. 2. 圖 2-1 Hermite Curve P(t)的幾何圖………………………………….... 5. v 圖 2-2 Bezier curves r (u ) 表示圖…………………………………... 圖 2-3 控制點對曲線的影響…………………………………............. 8 8. 圖 2-4 n 條 Hermite Curve 幾何圖…………………………………... 12 圖 2-5 四角孔氏綴面…………………………………......................... 15. 圖 3-1 圓球上之綴面…………………………………......................... 20. 圖 3-2 布林運算後之結果…………………………………................. 21. 圖 3-3 飛機模型…………………………………................................. 23. 圖 3-4 脊椎骨模型…………………………………............................. 24. 圖 4-1 猶他茶壺模型…………………………………......................... 26. v 圖 2-6 Bezier surfaces r (u , v ) 表示圖………………………………… 18. 圖 4-2 不同 Z 值之茶壺切面圖片…………………………………..... 27 圖 4-3 三角化過程示意圖…………………………………................. 29. 圖 4-4 改善前終點部份之三角化………………………………….... 30. 圖 4-5 改善後終點部份之三角化………………………………….... 30. 圖 4-6 茶壺模型…………………………………................................. 31. 圖 5-1 原始脊椎模型…………………………………......................... 33. 圖 5-2 不同 Z 值之脊椎切面輪廓……………………………………. 34 圖 5-3 XY 切面所建之脊椎骨模型…………………………………... 35 圖 5-4 不同 X 值之脊椎切面輪廓………………………………..…... 36 圖 5-5 YZ 切面所建之脊椎骨模型…………………………….……... 37. vi.

(9) 圖 5-6 切割與合併模型之步驟…………………………………......... 38. 圖 5-7 切割面位置…………………………………............................. 39. 圖 5-8 三角單元的存留判斷…………………………………….….... 40. 圖 5-9 切割後之脊椎模型………………………………………...….. 40. 圖 5-10 經切割面所通過的三角單元之放大圖………………..……. 41. 圖 5-11 兩模型合併時之三角化連接……………………………...… 42 圖 5-12 組合而成之脊椎模型…………………………………...….... vii. 44.

(10) 一、緒論. 1-1 前言在現代工業中，電腦輔助設計扮演了一個重要的角色，為了讓設計過程更加的快速、簡便以及精確，選擇一個可以有效率達成任務的電腦輔助設計軟體成為一個重要的課題；市面上已有許多功能強大的繪圖軟體，提供操作簡便的人機介面讓使用者大量減少繪圖時所花費的時間。但是面對整個產業的快速進步，此方面還是存在著許多發展空間值得我們去研究，也唯有通過對基礎理論的研究與了解，方可針對不足的地方加以改良與創新。. 1-2 研究背景隨著電腦效能不斷的提升，CAE(Computer aided engineering)軟體的運用也愈加廣泛，越來越多的工程師在設計以及分析時，需要 CAE 軟體的協助以尋求問題的解答。雖然 CAE 軟體擁有強大的分析功能，但大部分的 CAE 軟體其前處理的模型建立功能並不容易使用，往往必須經過繁複的步驟以及花費大量的時間才得以建構出分析用的幾何模型。若能先將模型建立後再匯入 CAE 軟體中進行分析，可大幅縮短整體分析的時間，提升工作效率。. 1.

(11) 1-3 研究目的幾何塑型的過程中，先由點而線、再由線至面，為了建立模型，最初的工作為取得物體的幾何資料。參考圖(1-1)，由赫米特曲線方程式建立一圓心為(0,0)，半徑為 1 的圓形時，圖中(a)(b)(c)分別使用了不同數量與位置的資料點。由結果可以看出，使用計算幾何的方式建立模型時，資料點對於整體結果，具有相當大的影響。. (a). (b). (c). 圖 1-1 資料點對曲線之影響. 使用參數曲面建立模型時，若物體的形狀較為簡單，經由適當的選擇資料點，可快速且正確的建構出物體之模型；而當物體的構造較為複雜時，通常的處理方式為將物體分成幾個形狀較為簡單的部份，分別建立後再將其組合為一完整的模型。隨著醫療工程的快速發展，模型的複雜程度也與日俱增，傳統的模型建立方式也因此顯得有點不足，為了能夠更加快速且精確的建立 2.

(12) 模型，許多新的建模方式也因應而生，例如經由雷射掃瞄，得到散佈於物體表面之資料點，再經由點與點之間的三角化連接，建立其幾何模型，此方式的缺點在於必須將物體放在機器中進行掃描，對於存在於人體內的各種器官，這種方式當然不可行。電腦斷層(computed tomography , CT)掃描是一種利用人體組織對 X 光吸收的程度，進而判斷組織結構是否正常的過程。它可將身體每個層面，以精確的構造影像顯現於電腦上，相較於一般 X 光檢查，電腦斷層可進一步顯示各層面之內部結構，提供更精確的診斷協助。利用電腦斷層影像建立模型的方式，已大量的使用於醫療影像的顯示與生物力學的分析工作上。然而，只由一種方向的斷層圖片所建立之模型，其與切面平行的部位往往與實體間存在著誤差；本研究之目的為使用兩不同切面，分別建立模型後，保留模型表現較好的部份，而後加以合併，以期能得到一完整表現物體幾何特性的模型。. 1-4 論文架構本篇論文共分為六章，依序為緒論、幾何模型原理基礎、幾何模型建構方式、茶壺模型的建立、脊椎模型之建立與重組以及結論。第一章緒論中，先敘述研究的背景，並說明本研究所使用的方法與最終希望達到的目的，最後對本論文架構做一簡單的介紹；第二章. 3.

(13) 幾何模型原理基礎中，簡單描述參數曲線以及曲面之基礎原理；第三章幾何模型建構方式中將分別介紹三種不同的建模方式，經由實例的探討與比較，說明本研究為何使用 CT Modeling 此種建模方式。第四章茶壺模型的建立是使用猶他茶壺做為範例，介紹由切面輪廓建立幾何模型之方法與步驟，並對此方式之缺點加以討論。第五章脊椎模型之建立與重組中，分別由兩不同切面建立脊椎模型，並經由兩模型的合併，得到更加精確的結果。最後在第六章結論中將對本研究內容與結果做一總結，並對於本研究在未來可能的發展加以探討。. 4.

(14) 二、幾何模型原理基礎. 幾何模型的構成：先由點，而後為線，再組成面。先由線談起，兩點之間使用三次曲線來模擬，是曲線摻合最常使用的方法，稱為三次參數曲線(Parametric cubic curve)。由於特定方程式所能夠產生的曲線形狀非常有限，因此就產生了一些繪製多變化曲線的方法，如 Hermite、Bezier 曲線，這些方法都有一個共同的特徵，就是採用片段連接曲線的方式，因此在相鄰的曲線片段間的連接條件就特別重要。. 2-1 參數曲線當我們要建立一條曲線時，令參數為 t，則線段上的任一點可表示為：Ｐ(t) = [ x (t), y (t), z (t)]. (座標表示法). (2-1). 或是 uv v v v uv P (t ) = a + bt + ct 2 + dt 3. 0 ≤ t ≤1. (參數表示法) uv. (2-2). 參考圖(2-1)，當 t 改變時，位置向量 P (t ) 會沿著曲線的軌跡移動。. 圖 2-1 Hermite Curve P(t)的幾何圖 5.

(15) 2-1-1 赫米特曲線(Hermite Curves) 將圖(2-1)中首尾兩端點的位置向量及切線向量共四個邊界條件代入方程式(2-2) uv v P (0) = a. (2-3a). uv v v v uv P (1) = a + b + c + d. (2-3b). uv v P(0) = b. (2-3c). uv v v uv P(1) = b + 2c + 3d. (2-3d). 重新組合可得到 uv uv uv uv uv P (t ) = F0 (t ) P (0) + F1 (t ) P(1) + F2 (t ) P(0) + F3 (t ) P(1) uv ⎡ P (0) ⎤ ⎢ uv ⎥ ⎢ P (1) ⎥ = [ F0 (t ) F1 (t ) F2 (t ) F3 (t ) ] ⎢ uv ⎥ ⎢ P (0) ⎥ ⎢ uv ⎥ ⎢ P (1) ⎥ ⎣ ⎦. (2-4). 這就是赫米特曲線的幾何模式，其中 F0 (t ) = 1 − 3t 2 + 2t 3. (2-5a). F1 (t ) = 3t 2 − 2t 3. (2-5b). F2 (t ) = t − 2t 2 + t 3. (2-5c). F3 (t ) = −t 2 + t 3. (2-5d). 是所謂的摻合函數(Blending functions)，或稱之為形狀函數(Shape functions)，若用矩陣表示方程式(2-3)，成為. 6.

(16) uv P(t ) = ⎡⎣1 t1 t 2. uv = [t ][ M ][ P]. uv ⎡ P (0) ⎤ ⎡ 1 0 0 0 ⎤ ⎢ uv ⎥ P (1) ⎥ ⎢ 0 1 0 ⎥⎥ ⎢ 3 ⎢ 0 ⎢ uv ⎥ t ⎤⎦ ⎢ −3 3 −2 −1⎥ ⎢ P (0) ⎥ ⎢ ⎥⎢ ⎥ ⎣ 2 −2 1 1 ⎦ ⎢ uv ⎥ ⎣ P (1) ⎦. (2-6). 2-1-2 伯濟爾曲線(Bezier curves) 伯濟爾曲線是一種利用趨近方式(approximation)來產生曲線的方法，所產生的曲線只有通過曲線上首尾兩個控制點而已。伯濟爾曲線曲線多項式摻合函數為 Bi ,n ( u ) ，參數曲線具有以下通式： n uv v r ( u ) = ∑ Pi Bi ,n ( u ). 0 ≤ u ≤1. (2-7). i =0. 其中 { Pi }i = 0 為控制點(Control points)， {Bi ,n ( u )}i =0 為 Bernstein 多項 n. n. 式，定義如下：. Bi ,n ( u ) = C ( n, i ) u i (1 − u ) C ( n, i ) =. n −i. (2-8). n! i !( n − i ) !. (2-9). 以 n=3 為例說明，則(2-4)式可展開為： v uv uv uv uv r (u) = (1 − u )3 P0 + 3u(1 − u)2 P1 + 3u 2 (1 − u) P2 + u 3 P3 uv. uv. uv. uv. (2-10). 如圖(2-2)所示，P 0、P 3 為端點(End points)，P1、P2 稱之為控制點(Control points)。. 7.

(17) v r 圖 2-2 Bezier curves (u ) 表示圖隨著控制點的位置改變，曲線也因此跟著改變，使用者可根據實際上需要改變控制點的位置來獲得所需模型，圖 2-3 為曲線隨著控制點而改變之表示圖。. 圖 2-3 控制點對曲線的影響. 2-2 曲線之連續有了描述兩點間線段的表示方法，本節將以赫米特曲線來進一步探討線段間的連續性，由於每一線段都是首尾相接，相接兩線段在連接點的關係，決定了曲線模型是否平順。當連接點的一次微分向量相 1. 2. 等稱為 C 連續，且二次微分向量相等稱為 C 連續。若只有一次微分向 1. 量方向相同，稱為 G 連續。. 8.

(18) 兩首尾相連之赫米特曲線可用方程式(2-4)表示為： uv uv uv uv uv P i (t ) = F0 (t ) P i + F1 (t ) P i +1 + F2 (t ) P i + F3 (t ) P i +1. (2-11a). uv uv uv uv uv P i+1 (t ) = F0 (t ) P i+1 + F1 (t ) P i + 2 + F2 (t ) P i+1 + F3 (t ) P i + 2. (2-11b). i = 0,1,2 , ... ,n − 2,n − 1, n uv. 上式共有 n 條的赫米特曲線，n+1 個連接點，其中 Pi 是資料點的位 uv. 置向量，可由實物測量或經由適當的設計來當已知值， Pi 是資料點的切線向量，是我們要求的未知數。. C1連續(First-degree parametric continuity)是前後兩條赫米特曲線的一次微分相等，也就是切線向量在連接點處相等，即 uv uv ⎧ P i +1 (0) = P i (1) ⎪ ⎨ uv uv ⎪⎩ P i +1 (0) = P i (1). (2-12). C 2 連續(Second-degree parametric continuity)除了一次微分相等，更達到連接點的二次微分相等，所以 uv uv ⎧ P i +1 (0) = P i (1) ⎪ uv ⎪ uv ⎨ P i +1 (0) = P i (1) ⎪ uv uv ⎪ P i +1 (0) = P i (1) ⎩. (2-13). 由方程式(2-11)(2-13)可以得到 uv uv uv uv uv Pi + 4 Pi+1 + Pi+ 2 = 3( Pi+ 2 − Pi ). (2-14). C 2 連續的條件下，n 條赫米特曲線得到 n-1 條類似方程式(2-14)的 ⎡ uv ⎤. 方程式，將這些方程式以矩陣方式寫成 ⎡⎣M* ⎤⎦ ⎢Ρ ⎥ = ⎡⎣ R* ⎤⎦ 即 ⎣ ⎦. 9.

(19) ⎡1 4 1 0 . . ⎢0 1 4 1 0 . ⎢ ⎢. . . . . . ⎢ ⎢. . . . . . ⎢⎣ 0 . . . . 1. ⎡ uv ⎤ ⎢ P0 ⎥ ⎢ uv ⎥ uv uv . 0 ⎤ ⎢ P1 ⎥ ⎡ 3( P 2 − P 0 ) ⎤ ⎢ ⎥ ⎢ uv uv ⎥ . 0 ⎥⎥ ⎢ uPv 2 ⎥ ⎢ 3( P 3 − P1 ) ⎥ ⎢ ⎥ ⎥ . .⎥⎢ . ⎥ = ⎢ . ⎢ ⎥ ⎥⎢ . .⎥ . ⎥ ⎢ . ⎥ ⎢ ⎥ ⎢ uv uv ⎥ 4 1 ⎦ ⎢ uv ⎥ ⎣3( P n − P n − 2 ) ⎦⎥ ⎢ P n −1 ⎥ ⎢ uv ⎥ ⎢⎣ P n ⎥⎦. (2-15). 2. 這就是 C 連續條件下，求取曲線資料點切線向量的公式。觀察方程式(2-11)，可以發現 ⎡⎣M* ⎤⎦ 是 (n − 1) × (n + 1) 矩陣， ⎡⎣ R* ⎤⎦ 是 (n − 1)× 1 矩陣， v. 而 ⎡⎣ p& ⎤⎦ 是 (n + 1)× 1 矩陣，方程式有 n-1 條，未知數卻有 n+1 個，必須再有兩條方程式才能求解，所以考慮曲線模型首尾兩端點的邊界條件，有以下的三種情形： (1)固定端點(Fixed ends) v v P& 0 = a, P& n = b. a, b 已知. (2-16a). (2)自由端點(Free ends) &v& &v& P0 (0) = 0, Pn (1) = 0. (2-16b). (3)循環端點(Cyclic ends) v v v v Pn = P0 , P& n = P&0. (2-16c). 自由端點的邊界條件可以導出 v v v v& 2P& 0 + P1 = 3(P1 − P0 ) v& v& v v 2Pn + Pn −1 = 3(Pn − Pn −1 ). (2-16d). 10.

(20) 2. 故 C 連續條件，求取曲線資料點切線向量的公式，可整理成 (1)固定端點(Fixed ends) v v v v ⎡4 1 0 . . . . 0⎤ ⎡ P&1 ⎤ ⎡ 3( P2 − P0 ) − P& 0 ⎤ v v ⎥ ⎢1 4 1 0 . . . 0⎥ ⎢ v& ⎥ ⎢ ⎢ ⎥ ⎢ P2 ⎥ ⎢ 3( P3 − P1 ) ⎥ ⎥ ⎢ . . . . . . . . ⎥⎢ . ⎥ ⎢ . ⎥=⎢ ⎥ ⎥⎢ ⎢ ⎥ ⎢ . . . . . . . . ⎥⎢v . ⎥ ⎢ v . v ⎢0 . . . 0 1 4 1 ⎥ ⎢P& ⎥ ⎢ 3( P − P ) ⎥ ⎢ ⎥ ⎢ vn − 2 ⎥ ⎢ v n −1v n − 3 v ⎥ ⎢⎣0 . . . . 0 1 4⎥⎦ ⎢⎣ P& n −1 ⎥⎦ ⎢⎣3( Pn − Pn − 2 ) − P& n ⎥⎦. (2-17) (2)自由端點(Free ends) ⎡2 1 0 . . . ⎢1 4 1 0 . . ⎢ ⎢0 1 4 1 0 . ⎢ ⎢. . . . . . ⎢. . . . . . ⎢ ⎢0 . . . 0 1 ⎢0 . . . . . ⎣. v v 0⎤ ⎡ P& 0 ⎤ ⎡ 3(P1 − P0 ) ⎤ ⎢v ⎥ ⎢ v v ⎥ . 0⎥⎥ ⎢ P&1 ⎥ ⎢ 3( P2 − P0 ) ⎥ v v v . 0⎥ ⎢ P& 2 ⎥ ⎢ 3( P3 − P1 ) ⎥ ⎥ ⎥⎢ ⎥ ⎢ . .⎥⎢ . ⎥ = ⎢ . ⎥ ⎥ . .⎥⎢ . ⎥ ⎢ . ⎥ ⎥ ⎢ v& ⎥ ⎢ v v 4 1 ⎥ ⎢Pn -1 ⎥ ⎢3( Pn − Pn − 2 )⎥ v v ⎢v ⎥ 1 2⎥⎦ ⎢⎣ P& n ⎥⎦ ⎢⎣3( Pn − Pn −1 ) ⎥⎦ .. (2-18). (3)循環端點(Cyclic ends) ⎡4 ⎢1 ⎢ ⎢0 ⎢ ⎢. ⎢. ⎢ ⎢0 ⎢1 ⎣. v v v 0 1 ⎤ ⎡ P& 0 ⎤ ⎡ 3( P1 − Pn −1 ) ⎤ v v ⎥ ⎢v ⎥ ⎢ 4 1 0 . . . 0⎥⎥ ⎢ P&1 ⎥ ⎢ 3( P2 − P0 ) ⎥ v v v 1 4 1 0 . . 0⎥ ⎢ P& 2 ⎥ ⎢ 3( P3 − P1 ) ⎥ ⎥ ⎢ ⎥ ⎥⎢ . . . . . . . ⎥⎢ . ⎥ = ⎢ . ⎥ ⎢ ⎥ ⎢ ⎥ . . . . . . .⎥ . . ⎥ v ⎥ ⎢ v& ⎥ ⎢ v . . . 0 1 4 1 ⎥ ⎢Pn - 2 ⎥ ⎢3( Pn −1 − Pn − 3 )⎥ v v ⎢v ⎥ 0 . . . 0 1 4⎥⎦ ⎢⎣ P& n -1 ⎥⎦ ⎢⎣ 3( P0 − Pn − 2 ) ⎥⎦ 1 0. .. .. .. (2-19). G1 連續(First-degree geometric continuity)是一次微分向量的方向相同，也就是連接點前後切線向量的方向一樣。如圖(2-4)， l 是弧長，曲線參數是 t 但物理意義不一定是弧長，隨. 11.

(21) v. 著 t 的改變， P (t)將在曲線軌跡上移動而掃出整條線段。. 圖 2-4 n 條 Hermite Curve 幾何圖 v. v. δP(t) δP(t) δl δl v = = T δt δ l δt δ t. (2-20a). 其中 T 是單位切線向量(Unit tangent vector)， δ l 是向量大小，當 t δt. 物理意義是弧長時 uv. uv. δ P(t ) δ P(t ) = =T δt δl. ( when. t = l). (2-20b). 如果各線段的弧長不同，即各節點的之間距不等距時，欲得到精 t l. 確之曲線，參數 t 應除弧長 l ，則令 ξ = 、 δξ =. δt l. uv *. uv. 、 P (ξ ) = P (t ) ，方程. 式(2-20)變成 uv *. uv. uv. uv. δ P (ξ ) δ P(t ) δ P(t ) δ t δ P(t ) uv = = =l = lT δξ δξ δ t δξ δt. (2-21). 所以相接的兩條線段如果弧長不一樣，則切線向量必然不等，但 v. 單位切線向量 T 一樣，所以定義 G 連續的條件為 1. uv * uv * P i +1 (0) = P i (1). (2-22a). uv * uv * P ni +1 (0) = β i P i (1). (2-22b). 模仿方程式(2-4)的做法，利用方程式(2-21)可以推得. 12.

(22) uv * P (ξ ) uv = P(t ) uv * uv * uv * uv * = F0 (ξ ) P (0) + F1 (ξ ) P (1) + F2 (ξ ) P (0) + F3 (ξ ) P (1) uv uv uv * uv * δ P(t ) δ P(t ) = F0 (ξ ) P (0) + F1 (ξ ) P (1) + F2 (ξ )l + F (ξ )l δ t t =0,ξ =0 3 δ t t =l ,ξ =1 uv * ⎡ P (0) ⎤ ⎢ uv * ⎥ ⎢ P (1) ⎥ t ⎢ ⎥ = [ F0 (ξ ) F1 (ξ ) F2 (ξ ) F3 (ξ ) ] ⎢ uv * ⎥ ; 0 ≤ξ = ≤ 1 l ⎢l P (0) ⎥ ⎢ uv ⎥ ⎢ l P* (1) ⎥ ⎣ ⎦. (2-23). 前後相連的赫米特曲線可仿照方程式(2-11)寫成 uv * uv uv uv uv P i (ξ ) = F0 (ξ ) P i + F1 (ξ ) P i +1 + F2 (ξ )li P i + F3 (ξ )l i P i +1. (2-24a). uv * uv uv uv uv P i +1 (ξ ) = F0 (ξ ) P i +1 + F1 (ξ ) P i + 2 + F2 (ξ )li +1 P i +1 + F3 (ξ )l i +1 P i + 2. (2-24b). i = 0,1, 2...n − 2. uv. uv. 其中 l 是各段的弧長， P i 是資料點的位置向量， Pi 是資料點的單位切線向量，是要求的未知數。將方程式(2-24)對 ξ 微分，前後兩段赫米特曲線的連接點處 uv * uv P ni (1) = li P i +1. (2-25a). uv * uv P ni +1 (1) = li +1 P i +1. (2-25b). 可以寫成底下的關係 uv* l uv * P ni +1 (0) = i +1 P i (1) li. (2-26). 它們的切線方向一樣，切線的大小與弧長成反比。方程式(2-14)變. 13.

(23) 成 uv 1 1 uv uv 1 uv 1 uv 3 uv 3 uv Pi + 2 Pi +1 ( + ) + Pi + 2 = 2 ( Pi + 2 − Pi +1 ) + 2 ( Pi +1 − Pi ) li li li +1 li +1 li +1 li. (2-27). 如果前後弧長 li +1 = li ，方程式(2-27)又會跟方程式(2-14)一樣。同樣的，利用 G1 連續的方法將會找到 n-1 條類似的方程式，再考慮曲線模型首尾的邊界條件，以循環式端點邊界條件為例，將會有底下的結果 1 ⎡ 1 1 0 . ⎢ 2( l + l ) l0 n −1 0 ⎢ 1 1 1 1 ⎢ 2( + ) 0 ⎢ l0 l0 l1 l1 ⎢ ⎢ 1 1 1 1 0 2( + ) ⎢ l1 l1 l2 l2 ⎢ ⎢ . . . . ⎢ . . . . ⎢ ⎢ 0 . . 0 ⎢ ⎢ ⎢ 1 0 . . ⎢ ln −1 ⎢⎣. . . 0 . . 1 ln − 3 0. 3 uv uv 3 uv uv ⎤ ⎡ ⎢ l 2 ( P1 − P 0 ) + l 2 ( P 0 − P n −1 ) ⎥ 0 n −1 ⎢ ⎥ u v u v 3 3 uv uv ⎢ ⎥ ( P 2 − P1 ) + 2 ( P1 − P 0 ) 2 ⎢ ⎥ l1 l0 ⎢ ⎥ ⎢ ⎥ 3 uv uv 3 uv uv ( P 3 − P 2 ) + 2 ( P 2 − P1 ) ⎢ ⎥ 2 l2 l1 ⎥ =⎢ ⎢ ⎥ . ⎢ ⎥ . ⎢ ⎥ ⎢ 3 uv ⎥ uv u v u v 3 ⎢ 2 ( P n −1 − P n − 2 ) + 2 ( P n − 2 − P n −3 ) ⎥ ln − 3 ⎢ ln − 2 ⎥ ⎢ 3 uv uv ⎥ u v u v 3 ⎢ 2 ( P 0 − P n −1 ) + 2 ( P n −1 − P n − 2 ) ⎥ ln − 2 ⎢⎣ ln −1 ⎥⎦. 14. ⎤ ⎥ ln −1 ⎥ ⎡ uPv ⎤ ⎥⎢ 0 ⎥ . 0 ⎥ ⎢ uv ⎥ ⎥ ⎢ P1 ⎥ ⎥ ⎢ uv ⎥ . 0 ⎥ ⎢ P2 ⎥ ⎥ ⎥⎢ . ⎢ ⎥ ⎥ . . ⎥⎢ . ⎥ . . ⎥ ⎥⎢ u v ⎢ ⎥ ⎥ 1 1 1 P n − 2 ⎢ ⎥ + 2( ) ⎥ ln − 3 ln − 2 ln − 2 ⎢ ⎥ uv ⎥ 1 1 1 ⎥ ⎢⎣ P n−1 ⎥⎦ + 2( )⎥ ln − 2 ln − 2 ln −1 ⎥⎦ 0. 1. (2-28).

(24) G2連續(Second-degree geometric continuity)是除了連接點兩端的一次微分向量方向相同外，連接點後端的二次微分向量必有一分量在前端的切線方向上、一分量在前端的法線方向上。 uv uv P i +1 (0) = βi P i (1). (2-29a). uv uv uv P i +1 (0) = βi 2 P i (1) + N i P i (1). (2-29b). 其中，β與 N 兩者皆為調整曲線形狀的控制參數。. 2-3 參數曲面 2-3-1 張量積雙三次曲面(Tensor-Product Bicubic Patch) 考慮綴面外形，三條參數曲線所組成的稱為三角綴面(Triangular patch)、四條參數曲線組成的稱為四角綴面(Rectangular patch)。孔氏 (Coons)綴面是處理組合曲面的方法之一，可用圖(2-5)解釋。. 圖 2-5 四角孔氏綴面. 15.

(25) 取 u、v 兩個獨立參數，對應某 u 值，就有一等 u 值的赫米特曲線，而且 uv uv uv uv u uv u P 0 (u ) = F0 (u ) P 00 + F1 (u ) P10 + F2 (u ) P00 + F3 (u ) P10. (2-30a). uv uv uv uv u uv u P1 (u ) = F0 (u ) P 01 + F1 (u ) P11 + F2 (u ) P 01 + F3 (u ) P11. (2-30b). uv v uv v uv v uv uv uv uv P 0 (u ) = F0 (u ) P 00 + F1 (u ) P10 + F2 (u ) P00 + F3 (u ) P10. (2-30c). uv v uv v uv v uv uv uv uv P1 (u ) = F0 (u ) P 01 + F1 (u ) P11 + F2 (u ) P 01 + F3 (u ) P11. (2-30d). uv. 式中加了上標的向量 P 是沿所標示變數方向的切線向量。必須有四個角點的資料點，其中 F (u ) 是赫米特摻合函數，根據上面章節對曲線模型的討論，可以組成一條以 v 為參數的赫米特曲線 uv uv uv uv v uv v P (u , v) = F0 (v) P 0 (u ) + F1 (v) P1 (u ) + F2 (v) P 0 (u ) + F3 (v) P1 (u ) uv uv uv v uv v ⎡ ⎤ ⎡ 1 0 0 0 ⎤ ⎢ P 00 P 01 P 00 P 01 ⎥ ⎡1 uv uv uv v uv v ⎢ 0 1 0 ⎥⎥ ⎢ P10 P11 P10 P11 ⎥ ⎢⎢ 0 2 3 ⎢ 0 = ⎡⎣1 u u u ⎤⎦ ⎢ uv uv ⎥ ⎢ 0 ⎢ −3 3 −2 −1⎥ ⎢ uPv u00 uPv u01 uPv uv P 01 ⎥ 00 ⎢ ⎥ ⎢ uv ⎥⎢ u v u v u ⎣ 2 −2 1 1 ⎦ ⎢ P u P u P uv Pv uv ⎥ ⎣ 0 11 10 11 ⎦ ⎣ 10 uv uv uv v uv v ⎡ P 00 P 01 P 00 P 01 ⎤ ⎡ F (v ) ⎤ ⎢ uv uv uv v uv v ⎥ ⎢ 0 ⎥ ⎢ P10 P11 P10 P11 ⎥ F (v) = [ F0 (u ) F1 (u ) F2 (u ) F3 (u ) ] ⎢ uv u uv u uv uv uv uv ⎥ ⎢ 1 ⎥ ⎢ P 00 P 01 P 00 P 01 ⎥ ⎢ F2 (v) ⎥ ⎢ uv u uv u uv uv uv uv ⎥ ⎢ F (v) ⎥ ⎢⎣ P10 P11 P10 P11 ⎥⎦ ⎣ 3 ⎦. = [ F (u )][Q ][ F (v)]. T. 0 −3. 2 ⎤⎡1 ⎤ 0 3 −2 ⎥⎥ ⎢⎢ v ⎥⎥ 1 −2 1 ⎥ ⎢v 2 ⎥ ⎥⎢ ⎥ 1 −1 1 ⎦ ⎣ v 3 ⎦. (2-31). 這是孔氏綴面的數學模式，又稱張量積雙三次綴面(Tensor-product. 16.

(26) 2. bicubic patch)，由三次參數曲線所建立，符合 C 的連續條件，必須有四個資料點共計 16 個已知向量來組合。. Position ⎡ ⎢ vectors ⎢ [Q ] = ⎢ ⎢ ⎢ u − direction ⎢⎣ tan gent vectors. v − direction ⎤ tangent vectors ⎥⎥ ⎥ ⎥ twist ⎥ ⎥⎦ vectors. (2-32). uv uv. 若為 Bicubic Ferguson patch， P ij = 0 ，這種簡化方式可以免除許多麻煩，卻也難免影響綴面，但程度不大，也因此 Ferguson patch 一直很受歡迎。 2-3-2 伯濟爾曲面(Bezier Surface) 將 Bezier 曲線推廣可得 Bezier 曲面，方程式如下：. r (u , v) = [1 u u 2. ⎡1⎤ ⎢ ⎥ 3 T ⎢ v ⎥ u ]MBM ⎢v 2 ⎥ ⎢ 3⎥ ⎣v ⎦. ⎡1 0 0 ⎢ −3 3 0 M =⎢ ⎢ 3 −6 3 ⎢ ⎣ −1 3 −3. 0⎤ 0 ⎥⎥ 0⎥ ⎥ 1⎦. (2-33). 其中. ,. ⎡ r00 ⎢r B = ⎢ 10 ⎢ r20 ⎢ ⎣ r30. r01. r02. r11. r12. r21 r31. r22 r32. r03 ⎤ r13 ⎥⎥ r23 ⎥ ⎥ r33 ⎦. 如(2-6)圖所示，全部資料點中只有 r00、 r03 、 r30 以及 r33 位於曲面上，其他控制點則決定了整個曲面的曲度以及外型。. 17.

(27) v r 圖 2-6 Bezier surfaces (u , v ) 表示圖. 2-4 齊次座標轉換齊次座標乃是將 n 維座標 T 向量以(n+1)維表示，使轉換公式更加簡單。以三維為例，特性如下 ⎡a ⎢d Th = ⎢ ⎢g ⎢ ⎣l. b e i m. c f j n. p⎤ q ⎥⎥ r⎥ ⎥ h⎦. (2-34). 其中 Th 旋轉 ⎡a b ⎢d e ⎢ ⎢g i ⎢ ⎣0 0. c f j 0. 縮放 0⎤ 0⎥⎥ 0⎥ ⎥ 1⎦. ⎡S x ⎢0 ⎢ ⎢0 ⎢ ⎣0. 平移 ⎡1 0 ⎢0 1 ⎢ ⎢0 0 ⎢ ⎣⎢t x t y. 0 Sy 0 0. 0 0 Sz 0. 投影. 0⎤ 0 0⎥⎥ 1 0⎥ ⎥ t z 1⎦⎥. ⎡1 ⎢0 ⎢ ⎢0 ⎢ ⎣0. 0. 18. 0 1 0 0. 0 p⎤ 0 q ⎥⎥ 1 r⎥ ⎥ 0 1⎦. 0⎤ 0⎥⎥ 0⎥ ⎥ 1⎦.

(28) 其中對 z 軸旋轉 θ ⎡ cos θ ⎢ − sin θ ⎢ ⎢ 0 ⎢ ⎣ 0. sin θ cos θ 0 0. 0 0 1 0. 0⎤ 0 ⎥⎥ 0⎥ ⎥ 1⎦. 0 sin γ cos γ 0. 0⎤ 0⎥⎥ 0⎥ ⎥ 1⎦. 對 x 軸旋轉 γ 0 ⎡1 ⎢0 cos γ ⎢ ⎢0 − sin γ ⎢ 0 ⎣0. 對 y 軸旋轉 β ⎡cos β ⎢ 0 ⎢ ⎢ sin β ⎢ ⎣ 0. 0 − sin β 1 0 0 cos β 0 0. 0⎤ 0⎥⎥ 0⎥ ⎥ 1⎦. 19.

(29) 三、幾何模型建構方式 3-1 Primitive Models 第二章中介紹了建構參數曲面之基礎理論，本節將藉由建立一圓球模型，介紹其過程與步驟。首先在圓球上選取資料點，如同第一章所描述，資料點的位置對於模型擁有相當大的影響，因此經度方向與緯度方向皆每隔 45°取一資料點。當選定資料點後，根據雙三次曲面原理，可在球面建立四角綴面，如圖(3-1)所示。. 圖 3-1 圓球上之綴面依(2-31) (2-32)式孔氏綴面之數學模式所述，建立曲面必須有四個資料點共計 16 個已知向量來組合。除了點座標外，尚需要各點之切線斜率與扭轉向量。使用循環端點的邊界條件，將各角點代入(2-19)式可得其切線斜率。由於本例是採用 Ferguson patch，故可將各角點之扭轉. 20.

(30) 向量設為零。綜合以上所得之數據並給定各綴面編號及綴面上之 u、v 參數值，依序代入(2-31)式，即可找出曲面模型上的點位置，經由電腦繪圖的程序，即可建構出圓球模型。. 3-2 Constructive Solid Geometry (CSG) Models 使用參數曲面建立外形較為複雜之模型時，為了能夠充分表現物體之幾何特性，必須將模型分為幾個形狀較為簡單的部份，其中的每一部份可由前幾個章節所介紹之計算幾何方式分別建立後，再利用彼此間的布林運算(聯集、差集、交集)，將各部分依序加入後，即可得到組合後之物體模型，如(3-2)圖所示。. 圖 3-2 布林運算後之結果. 21.

(31) 經由飛機模型的建立，可以更加清楚的了解此建模方式之理論與步驟。將飛機分為機身(fuselage)、機翼(wing)、水平尾翼與垂直尾翼 (horizontal and vertical tail)、派龍(pylon)以及引擎外殼(engine housing) 等六大部份。機身分為前中後三段，前段為駕駛艙(cockpit)，是一略為改變之圓錐，中段機艙為一圓柱，後段尾部為一圓錐，而機翼、尾翼、派龍皆是以根部及頂端兩個不同的翼截面配合上翼長(span)、弦長 (chord length)、縮小比(taper ratio)、掠角(sweep angle)、仰角(dihedral angle)等所定義，而引擎外殼則是一近似圓柱之前後內包的外形，將各部份依照前一節所介紹之方式分別建立後，以 SSI 的方式加以組合，即可得到完整之飛機模型，如(3-3)圖所示。. (a). (b). (c) 22.

(32) (d) 圖 3-3 (a)機翼相交部分(b)尾翼相交部分 (c)派龍與引擎相交部分(d)飛機模型. 3-3 Triangulated Surface Models 三維雷射掃瞄系統原理乃利用直線式雷射光投射置放於工作台上之物品，並利用一台或兩台相機擷取雷射光之影像。當雷射光源和相機兩者之間的相對位置為已知，則可以利用三角法或其它方法將影像光點位置轉換為物品上光點之 X、Y、Z 三維座標。圖(3-4)為一人類脊椎骨模型，由圖中可以看出，經雷射掃描所取得的資料點遍佈於脊椎表面，藉由資料點間的三角化處理可將模型建立。相較於傳統的建模方式，此方式可更加快速且準確的建構出外形複雜之物體模型。然而，使用雷射掃瞄取得物體資料點時，必須將實 23.

(33) 體置放於工作台中進行掃描，若要建立之模型為人體內部之器官組織，此方式顯然不可行。. (a). (b) 圖 3-4 (a)脊椎骨模型(b)局部放大圖. 3-4 CT Models 近年來利用電腦斷層影像建立模型的方式，已大量的使用於醫療影像的顯示與生物力學的分析工作上。經由對電腦斷層掃描圖片的影像處理以及影像分割後，可擷取出欲建立模型之組織輪廓，並經過三維成像的方法重建其三維模型。經由此方式，以往難以建構之人體內部器官模型，如今可快速的將其建立出來。本研究之主要目的為建立脊椎骨模型，使用計算幾何的方式雖然也可建構其模型，但由於脊椎之外形過於複雜，為了能夠精確的表現其幾何構造，必須將綴面分割得更加細小，如此一來，模型建立的過. 24.

(34) 程將變得瑣碎繁雜，故本研究將選擇使用 CT Modeling 的方式建立脊椎模型。. 25.

(35) 四、茶壺模型的建立. 本章將使用(4-1)圖中之猶他茶壺作為範例，介紹由物體切面輪廓建構幾何模型之方法與步驟，並探討此建模方式能夠加以改進的地方。. (a). (b). 圖 4-1 猶他茶壺模型(a)立體圖(b)上視圖. 4-1 切面輪廓的取得實際上經由參數曲面所建立之茶壺模型為一組資料點陣列，為了得到茶壺之切面輪廓，我們利用固定 Z 值時分布於茶壺表面之資料點連線，即可得到(4-2)圖中之茶壺切面圖片。. 26.

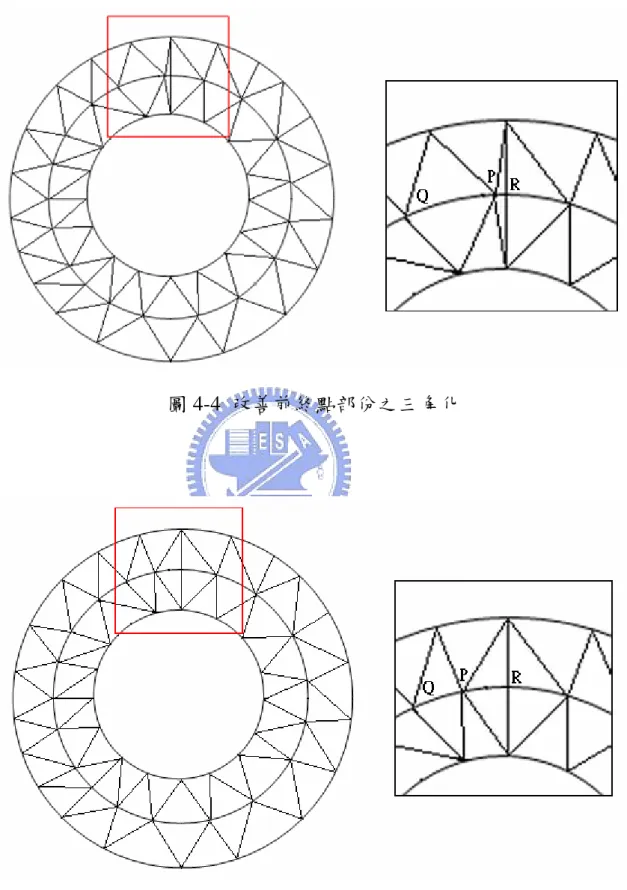
(36) C3 C2 C1 z x. (a)Z=C1. (b)Z=C2. (c)Z=C3. 圖 4-2 不同 Z 值之茶壺切面圖片. 4-2 由切面輪廓重建模型 4-2-1 三角元素品質(Mesh Quality) 為了能夠讓分布於模型表面的三角網格擁有較佳的元素品質，於建立模型前必須先設定一個判斷元素品質優劣的標準[11，林欣暐]，林欣暐以正三角形為需求，藉由使所有之三角網格趨近於正三角形，以達到改善元素品質之目的。二維之三角元素品質定義如下:. 27.

(37) Quality ( ABC ) = 2 3. A B * AC 2. 2. AB + BC + CA. 2. (4-1) =4 3. 三角元素面積三角元素的邊界平方和. 對於三角網格外形為正三角形時，可以計算得到 Quality(正三角形)=1。因此，元素品質愈接近理想值 1，就表示三角網格的外形愈接近正三角形。 4-2-2 三角化連接在得到物體之邊界資料點後，開始進行資料點間的三角化連接以建構模型，(4-3)圖為一段展開之邊界，假定 A1 及 B1 為上下兩邊界之起始點，我們可以定義 A1B1 為起始三角網格之起始邊，而為了能夠建立品質較佳之三角網格，我們將元素品質作為判定第三頂點之依據。首先將最小元素品質定為 Qmin ，利用(4-1)式之計算方式，交替的在上下邊界尋找元素品質大於 Qmin 之三角單元，假設在上邊界到達 A12 時， Quality(A1 B1 A12 ) 大於 Qmin ，則將起始三角形定為 [A1 B1 A12 ] 。由於有限. 單元計算過程的限制，且為了避免之後進行模型切割與合併時發生錯誤，對於三角單元各頂點之排列順序，在此必須先加以控制，經由固定每個三角單元之三頂點皆為逆時針排列可達成此一要求。. 28.

(38) 在尋找第三頂點的過程中我們發現，由於兩邊界之相對關係(距離、幾何形狀)之影響，每個元素所能達到之最高品質將有所限制，若將 Qmin 定得太大，將會產生無法滿足限制條件而造成程式錯誤之情況發生，但若是將 Qmin 定得過小，網格品質將因此變差，因此於建構模型前，必須先選定適當的 Qmin ，於本例中我們將 Qmin 定為 0.7。. 圖 4-3 三角化過程示意圖. 由於兩邊界長度的不同，於終點的地方將有品質無法滿足 0.7 之三角單元出現，為了改善此情況，我們必須對此部份加以單獨處理以改善此一情況。(4-4)圖為終點部份的三角化情形，由圖中可以看出，由於剩下之資料點數不足，導致終點前之三角單元並無法滿足品質大於 0.7 的要求，在此我們採用移動 P 點的方式來增加此三角單元之品質。首先將包含 P 點之六個三角單元提取出來，讓 P 點在 Q 點與 R 點之間移動，分別計算 P 點於不同位置時，此六個三角單元之平均元素品質，找出一最佳位置，令此六個單元擁有最佳的元素品質，如(4-5)圖所示。 29.

(39) 圖 4-4 改善前終點部份之三角化. 圖 4-5 改善後終點部份之三角化. 30.

(40) 經由以上所描述的步驟，對茶壺之切面逐層的進行三角化連接，即可得到(4-6)圖之茶壺模型。. 圖 4-6 茶壺模型. 4-3 CT Modeling 之缺點由(4-6)圖可以看出，模型中手把以及壺蓋其頂端表現出之外形與實際上的形狀有所不同。總括來說，由於切面與切面間之距離所造成的影響，模型中與切面平行的部份，是與實體間存在著最多差距的部份，於建構脊椎模型時，此現象的發生將使模型之精確度降低，而為了改善這種狀況，本研究採取的方式為利用兩不同切面建構模型，分別選. 31.

(41) 擇模型中表現較佳的部份加以組合，藉由此方式讓模型之幾何構造得以更加完整的呈現。. 32.

(42) 五、脊椎模型之建立與重組. 本章所使用之原始模型為經廠商掃描過後所得之一組資料點，將這些資料點輸入電腦後可得(5-1)圖。. 圖 5-1 原始脊椎模型. 5-1 脊椎模型之建立 5-1-1 XY 切面所建構之脊椎骨模型有了原始模型後，下一步要取得其切面輪廓，經由固定 Z 值，自下至上 Z 值每增加 0.1 公分取一切面輪廓。圖(5-2)為不同 Z 值之二個切面輪廓。. 33.

(43) 圖 5-2 不同 Z 值之脊椎切面輪廓. 經由第四章所描述的模型建構方式，對脊椎之邊界資料點逐層進行三角化連接，可得以下脊椎模型。. (a). 34.

(44) (b) 圖 5-3 XY 切面所建之脊椎骨模型. 由(5-3)圖可以看出，模型中與 XY 切面平行的部份結果並不理想，為了表現出此部份之真實外觀，我們嘗試使用與 XY 切面垂直的 YZ 切面建構另一模型。. 5-1-2 YZ 切面所建構之脊椎骨模型首先同樣要取得脊椎之切面輪廓，利用不同的 X 值，每 0.1 公分取一切面輪廓，(5-4)圖為不同 X 值時之二個切面輪廓。. 35.

(45) 圖 5-4 不同 X 值之脊椎切面輪廓. 再次依照第四章描述的之步驟進行三角化連接，可得到由 YZ 切面所建立的另一個脊椎模型，如圖(5-5)所示。. (a). 36.

(46) (b) 圖 5-5 YZ 切面所建之脊椎骨模型. 將圖(5-3)與圖(5-5)中之脊椎模型相互比較，我們可以發現，經由 YZ 切面所建立之模型於脊椎之上下兩面，呈現出較真實之物體輪廓，然而於此模型中，與 YZ 切面平行的部份則又出現較差之外形。綜合以上所得結論，我們可以發現，不論採用何種角度之切面建立模型，總是會有無法完整表現的部位，若是能夠保留兩不同切面所建構之模型中表現較好的部份，並去除不理想的部份後加以組合，將可得到一更加真實之組合模型。. 37.

(47) 5-2 模型之切割與合併依照(5-6)圖的步驟，對兩模型分別進行切割、邊界點的紀錄與判斷、最後再進行模型之合併，可得到一個同時具有兩模型優點之組合模型。. 決定切割面. 邊界點的排序. 切割模型. 兩模型接合. 邊界點的判斷. 完成脊椎骨模型. 圖 5-6 切割與合併模型之步驟. 為了能夠讓合併後之模型得以兼具兩種切割方式所建立的模型各自的優點，必須先選擇一適當之切割面。於圖(5-7)中，XY 切面所建立. 38.

(48) 的模型之上半部份較無法呈現真實的形狀；而 YZ 切面所建立的模型則是在下半部份較差，因此我們將切割面定為 Y=4.0 此一平面。. 圖 5-7 切割面位置. 決定切割面後接著要判斷資料點的存留與否，以 XY 切面所建立的模型為例，需要留下的部份為圖(5-7)之下半部，我們以(5-8)圖說明此時對三角網格之處理，若模型中任一個三角單元之三頂點 Y 值皆小於 4.0，則將此單元保存；反之，若三角單元的三個頂點 Y 值皆大於 4.0，便刪除此一單元；而為了能夠找出切割後所得之模型邊界點，我們先將切割面所通過之三角單元記錄起來，而對這些單元的處理將於之後詳加解釋。. 39.

(49) 對於 YZ 切面所建立的模型同樣也使用 Y=4.0 此一平面進行切割，不同的是此時要保存圖(5-7)之上半部。經此步驟後可得到(5-9)圖中之二個切割後的脊椎模型。. 圖 5-8 三角單元的存留判斷. (a). (b) 圖 5-9 切割後之脊椎模型. 40.

(50) 於切割模型時，我們已將切割面所通過之三角單元記錄下來，圖 (5-10)為這些單元之放大示意圖，若處理 XY 切面所建立之模型時，B1、 B2 … Bn 為所需要之模型邊界點，為了往後組合模型時接合處的三角化. 得以順利進行，尚需要將這些邊界點依序排列並記錄。由於之前建構脊椎模型時，已先將全部三角網格之資料點排序皆固定為逆時針排列，例如圖中之三角單元為 [ A1 B1 B2 ]、[ A1 B2 A 2 ] 至. [An. Bn-1. Bn ] ，依序檢查每一個三角單元，可找出 B1 B2 、 B2 B3 至 Bn −1 Bn 這. 些兩點皆小於 4.0 之邊界，而後只需將這些邊的兩端點首尾相連並紀錄起來，即可得到一組整齊排列的邊界點。同樣利用此方式可找出 YZ 切面所建立的模型之邊界點。. 圖 5-10 經切割面所通過的三角單元之放大圖. 最後要進行的是模型的合併，如(5-11)圖所示， H1 、 H 2 … H n 為 XY 切面所建立模型之邊界點， V1 、 V2 … Vm 為 YZ 切面所建立模型之邊界點， H1V1 為起始網格之起始邊，經由單元品質離判斷方式，我們可進 41.

(51) 行兩模型邊界點間之三角化連接。先分別計算 Quality ( H1 V1 H 2 ) 以及 Quality ( H1 V1 V2 ) ，若 Quality ( H1 V1. H 2 ) < Quality ( H1 V1 V2 ) ，則判定三. 角單元為 [ H1 V1 V2 ] ；若 Quality ( H1 V1 H 2 ) > Quality ( H1 V1 V2 ) ，則判定三角單元為 [ H1 V1 H 2 ] 。. 圖 5-11 兩模型合併時之三角化連接判別式如下：. If. Q u a lity ( H 1. V1. H. )<. [H 1. V1. V2. ]. [H 1. V1. H. 2. 2. Q u a lity ( H 1. V1. V2. ). th e n T r ia n g le = e ls e T r ia n g le =. ]. 在找出三角單元 [ H1 V1 H 2 ] 後，下一個網格之起始邊變為 H 2V1 ，重複的利用此判別方式進行三角化連接，即可完成兩模型之合併，得到一重組後之脊椎模型。. 42.

(52) 5-3 結果討論 5-3-1 合併後之脊椎模型. (a). (b). 43.

(53) (c) 圖 5-12 組合而成之脊椎模型. 由(5-12)圖可以看出，組合後的模型分別保留了兩種切面所建構模型的優點，並去除了原本不甚理想的部份，相較於使用單一切面所建構的模型，此方式可以表現出更完整的物體幾何特性。 5-3-2 切面的影響在研究的過程當中，我們發現 CT Modeling 大致受以下二個因素的影響，切面間距以及切面的角度。建構模型時，切面與切面間資料點為直線連接，也就是說，模型在切面間之曲率的變化，並無法完整的呈現，若切面間之曲率變化過大，模型並無法將此大幅度的變化表現出來。藉由縮小切面之間距雖可解決此問題，卻也因此大幅增加資 44.

(54) 料點數目，考慮到並非模型之每一部份均須如此多之切面數量方可表達，過多的資料點不僅造成了計算資源的浪費，也增加了模型建立的時間。而切面角度對模型之影響，可經由相互比較本章中所建之兩個脊椎模型得到結論，大致上來說，模型中與切面平行的部份，其所呈現出之形狀與實體間存在著較大的不同。藉由選擇適當之切面間距以及模型的合併，我們能夠更加快速且精準的建立物體模型。. 45.

(55) 六、結論. 6-1 結論幾何模型的建立在工程分析這個領域中，一直是相當重要的一部份，隨著電腦速度的不斷提升，有越來越多的方式可將模型建立。對於複雜外形的物體，建構其幾何模型仍有廣泛的發展空間。在本研究中，經由撰寫程式，對物體之切面輪廓進行三角化連接，得到其幾何模型，並對不同切面所建立之模型加以組合，提供撰寫類似程式的工具與經驗，相信可提高往後研究的效率。. 6-2 未來展望本研究尚有許多空間可以發展，包括程式的模組化，提高兩物體合併之相容性，模型的平滑處理等。展望未來，藉由此研究做為基礎，讓模型自動化建立技術得以更加完備。. 46.

(56) 參考文獻 [1] Richard H. Gallagher, “Finite Element Analysis, Fundamentals”, Prentice-Hall, Inc., 1975. [2] O. C. Zienkiewicz, R. L. Taylor“The Finite Element Method”, 4th Edition, volume 2, McGraw-Hill, 1991. [3] I.D Faux and M.J. Pratt, “Computational Geometry for Design and Manufacture”, ELLIS HORWOOD, 1979. [4] Michael E. Mortenson, “Geometric Modeling”,John Wiley and Sons, 1985. [5] Yang K.H. and Wang K.H., “Finite Element Modeling of human throax”, The Second Visible Human Project Conference, 1998. [6] David F. Roger and J.Alan Adams, “Mathematical Elements for Computer Graphics”, McGraw-Hill,inc., 1989. [7] 郭坤裕，“Geometric Local Modification with B-Spline Surface”，國立交通大學機械工程研究所碩士論文，1999。. [8] 程重光，“Computer Aided Geometric Design of Aircrafts”，國立交通大學機械工程研究所碩士論文，1993。. [9] 方文聘，“Theory and Practice of Computer-Aided Geometric Model of Aircraft”，國立交通大學機械工程研究所碩士論文，1998。. [10] 蔡明志，“Computer Aided Structural Analysis of Aircraft Wings”，國. 47.

(57) 立交通大學機械工程研究所碩士論文，1997。. [11] 林欣暐，“A Mesh Generation for Finite Element Analysis Using Delaunay Triangulation”，國立交通大學機械工程研究所碩士論文， 1998 [12] 張智星，“MATLAB 程式設計與應用”，清蔚科技出版社，2000。 [13] 繆紹綱，“數位影像處理-活用 MATLAB”，全華科技圖書股份有限公司，1999。. 48.

(58)