An efficient construction of perfect secret sharing schemes for graph-based structures

(1)

C o m p u t e r s M a t h . Applic. Vol. 31, No. 7, pp. 129-135, 1996

P e r g a m o n Copyright(~)1996 Elsevier Science Ltd

A n Efficient C o n s t r u c t i o n o f P e r f e c t S e c r e t

S h a r i n g S c h e m e s for G r a p h - B a s e d S t r u c t u r e s

H U N G - M I N S U N

Department of Information Management, Chaoyang Institute of Technology Wufeng, Taichung County, Taiwan, R.O.C.

S H I U H - P Y N G S H I E H

Department of Computer Science and Information Engineering National Chiao Tung University, Hsinchu, Taiwan, R.O.C.

(Received October 1993; revised and accepted May 1995)

A b s t r a c t - - I n this paper, we propose an efficient construction of perfect secret sharing schemes for g r a p h - b a s e d access s t r u c t u r e s where a vertex denotes a participant and a n edge does a qualified pair of participants. T h e secret sharing scheme is based on t h e a s s u m p t i o n s t h a t t h e pairs of participants corresponding to edges in t h e graph can c o m p u t e the m a s t e r key but t h e pairs of p a r t i c i p a n t s corresponding to nonedges in the graph cannot. T h e information rate of our scheme is 1 / ( n - 1), where n is t h e n u m b e r of participants. We also present an application of our scheme to t h e reduction of storage a n d c o m p u t a t i o n loads on the c o m m u n i c a t i o n granting server in a secure network.

K e y w o r d s - - S e c r e t sharing scheme, D a t a security, Cryptography, Access structure.

1. I N T R O D U C T I O N

In 1987, I t o et al. described a general method of secret sharing called secret sharing scheme (SSS) which allows a m a s t e r key to be shared among a finite set of participants in such a way t h a t only certain prespecified subsets of participants can recover the m a s t e r key [1]. Let P be the set of participants. T h e collection of subsets of participants t h a t can reconstruct the secret in this way is called the access structure (denoted by F). The collection of subsets of participants t h a t cannot obtain any information a b o u t the secret is called the prohibited structure (denoted by A) [2]. T h e n a t u r a l restriction is t h a t F is monotone increasing and A is monotone decreasing; t h a t is,

- i f A c F a n d A C _ B C _ _ P , t h e n B E F , and - i f A E A a n d B C _ A C _ P , t h e n B E A .

If A = 2 p \ F, t h e n we say the structure (F, A) is complete [2]. Let ]C be the m a s t e r key space and $ be the share space. T h e information rate for the secret sharing scheme is defined to be log 2 I1~]/log 2 ]S[ (see [3]). A construction for a secret sharing scheme is some concrete realization of the scheme. T h e concept of an (m, n)-threshold scheme, m < n, is to transform a master key, top secret, into n shares in such a way t h a t the master key cannot be reclaimed unless m or more shares are collected [4,5]. It is clear t h a t the threshold scheme is a way of constructing secret sharing schemes. A secret sharing scheme is called perfect if any set of participants in the pro- hibited structure A obtains no information regarding the master key [2,6,7]. Given any complete structure (F, A) (i.e., A = 2 P \ F), Ito et al. showed t h a t there exists a perfect secret sharing

T h i s research was s u p p o r t e d by t h e National Science Council of Republic of C h i n a under G r a n t No. NSC-84-2213- E-009-081.

T y p e s e t by ~4A/IS-TEX

(2)

scheme to realize the structure [1,8]. Benaloh and Leichter proposed a different algorithm to realize secret sharing schemes for any given monotone access structure [9]. In b o t h constructions, the information rate decreases exponentially as a function of n, the number of participants.

T h e r e are several performance and efficiency measures proposed for analyzing secret sharing schemes [1,10]. Their goal is to maximize the information rate of a secret sharing scheme. Brick- ell and Stinson studied a perfect secret sharing scheme for a graph-based structure where the monotone-increasing access structure F contains the pairs of participants corresponding to edges, and the prohibited structure A is the collection of subsets of participants corresponding to any independent set of the graph [1]. T h e y proved that, for any graph G with n vertices having max- i m u m degree d, there exists a perfect secret sharing scheme realizing G in which the information rate is at least 2 / ( d ÷ 3). In the worst case when d = n - 1, the information rate is 2 / ( n ÷ 2). T h e s t r u c t u r e of their secret sharing scheme is complete. However, their construction is difficult to use because it needs to maintain a large access check m a t r i x with at least [/CI- d rows. It is also time-consuming to recover the master key by looking up the large access check matrix.

In this paper, we propose an efficient construction of a perfect secret sharing scheme for access/prohibited structures based on a graph where the monotone-increasing access structure F contains the pairs of participants corresponding to edges, and the monotone-decreasing prohibited s t r u c t u r e A contains the pairs of participants corresponding to nonedges. T h e information rate of our scheme is 1 / ( n - 1), where n is the n u m b e r of participants. O u r scheme does not need to maintain a large access check matrix, and thus is more efficient t h a n the Brickell and Stinson's m e t h o d . We also present an application of our scheme to the reduction of storage and c o m p u t a t i o n loads on the communication granting server in a secure network.

This p a p e r is organized as follows. In Section 2, we propose a construction of perfect secret sharing schemes for graph-based access/prohibited structures. In Section 3, we discuss the application of our construction. Finally, we conclude the p a p e r in Section 4.

2. C O N S T R U C T I O N O F P E R F E C T M O N O T O N E S S S F O R G R A P H - B A S E D A C C E S S / P R O H I B I T E D S T R U C T U R E S

It is difficult to efficiently construct a secret sharing scheme for any access structure due to its irregular nature. In this paper, we focus only on the graph-based access/prohibited structures t h a t have interesting features. For convenience, we abbreviate the secret sharing scheme for g r a p h G to SSS(G). Let P be the set of participants, and G be a graph where a vertex denotes a p a r t i c i p a n t in P and an edge does a pair of participants. In a

perfect

secret sharing scheme for access/prohibited structures based on G, a pair of participants corresponding to an edge of G can c o m p u t e the m a s t e r key, while a pair of participants corresponding to a nonedge of G cannot obtain any information regarding the master key. We use E to denote the set of edges of G; N E to denote the set of nonedges of G; S to denote the set of pairs of participants corresponding to edges of G; R to denote the set of pairs of participants corresponding to nonedges of G. It is reasonable to restrict t h a t the access structure and prohibited structure are monotone. T h a t is,

- if A E S and A C_ B C_ P , B can compute the master key, and

- if A E R and B C_ A _C P , B can obtain no information regarding the m a s t e r key. Thus, the access structure F = {B [ A E S and A C_ B C P } , and the prohibited structure A = {B [ A E R and B C_ A C_ p } .

Here, we only consider the case of an access graph G which is connected. If g r a p h G is not connected, we can divide G into two or more connected components. Each component is realized by a perfect secret sharing scheme, respectively. Our access graph is based on the assumptions as Brickell and Stinson's schemes [3] t h a t graphs do not have loops or multiple edges.

In the following, we will use the conventional threshold schemes [4,5] to construct the perfect secret sharing schemes for graph-based access structures. We assume t h a t all c o m p u t a t i o n s are over

GF(q)

where q is a prime which is larger t h a n the size of the m a s t e r key space.

(3)

Perfect Secret Sharing Schemes 131

Given a connected graph G without loops, a secret sharing scheme for the access s t r u c t u r e based on the graph G is constructed as follows. Assume t h a t P = {Pl,P2 . . . . ,Pn} is the set of participants corresponding to the vertices of the graph G. We first construct n conventional (2, n)-threshold schemes [4,5], n a m e d T S 1 , T S 2 , . . . , and TSn. To avoid ambiguity, we call the m a s t e r key and the shares of each TS~ s u b m a s t e r key and subshares, respectively. For each (2, n)-TSi, let k~ be its s u b m a s t e r key and si,1, s i , 2 , . . . , si,~ be its n subshares. Thus, given any two subshares, si,j and s~,k (1 _< j < k <_ n), the s u b m a s t e r key ki can be recovered, but less t h a n two subshares provide no information a b o u t k~.

T h e m a s t e r key of the secret sharing scheme for the access structure based on the graph G is given by K = kl + k2 + . . . + kn (mod q), where ki is r a n d o m l y selected over G F ( q ) , for 1 < i < n.

T h e share of participant Pi is given by Si = (ai,1,... , a i , t , . . . ,aw~), where 1 < t < n, ai,t = kt if PiPt is an edge of G,

ai,t = st,i if PiPt is not an edge of G and t ¢ i, and

ai,t is e m p t y if t = i.

Thus, the constructed secret sharing scheme satisfies:

(1) if A E S and A C B C P , B can compute the master key;

(2) if A E R and B C_ A C_ P , B can obtain no information regarding the m a s t e r key.

THEOREM 1. I f A E S and A C B C P , B can c o m p u t e the m a s t e r k e y o f t h e c o n s t r u c t e d secret sharing s c h e m e for t h e access s t r u c t u r e based on the graph C.

PaOOF. B e c a u s e A C_ B and A E S, there e x i s t s p ~ , p j E B (i ¢ j ) such t h a t ~ E E. T h e share of Pi is S~ = (a~,l, a~,2,..., ai,~} and the share of pj is Sj = (aj,], a j , 2 , . . . , aj,n).

Because PiPj is an edge of G, we can conclude t h a t for any t, 1 < t < n, one of the following three cases holds:

(1) ai,t = St,i or kt, and aj,t = - St,j o r Ict if t ¢ i and t ~; j;

(2) ai,t = e m p t y and aj,t = kt if t = i; (3) ai,t = kt and aj,t = e m p t y if t = j.

In all these cases (1), (2), and (3), the s u b m a s t e r key k t c a n be recovered. Thus, participant Pi and participant py can recover the s u b m a s t e r keys kl, k 2 , . . . , kn and hence the m a s t e r key K . |

THEOREM 2. I f A E R and B C A C_ P , then B can obtain no information regarding t h e m a s t e r k e y o f t h e c o n s t r u c t e d secret sharing scheme for the access s t r u c t u r e based on the graph G.

PaOOF. Because

]AI

= 2 and B c_ A,

Igl

<_ 2. W i t h o u t loss of generality, we assume t h a t

B = {Pi, Pj }, where i ¢ j. Because B C__ A and A E R , ~ E N E .

T h e share of Pi is Si = (ai,1, a i , 2 , . . . , ai,n} and the share of pj is S j = (aj,1, a 3 , 2 , . . . , aj,~).

Because p i p j is not an edge of G, we can conclude t h a t for any t, 1 < t < n, one of the following three cases holds:

(1) ai,t = st,i or kt, and aj,t = 8t,j or kt if t ¢ i and t ¢ j; (2) ai,t ~- e m p t y and aj,t = st,j if t = i;

(3) ai,t -= st,i and aj, t = e m p t y if t = j.

In case (1), the s u b m a s t e r key kt can be recovered. In case (2), ai,i and aj,i can obtain only one subshare si,j of the (2, n)-TSi. Therefore, pi and pj get no information a b o u t the s u b m a s t e r key ki. In ease (3), ai,j and aj,j can obtain only one subshare sj,i of the (2, n ) - T S j . Therefore, p~ and pj get no information a b o u t the s u b m a s t e r key k j .

Because K = kl + k2 + . . . + kn (mod q), Pi and pj get no information a b o u t the m a s t e r

key K . |

T h e share of participant Pi, ( a i , 1 , . . . , a i , t . . . ai,~), is an n-dimensional vector. Except t h a t a~,i is empty, every ai,j is over G F ( q ) . Therefore, the size of the share space is q n - 1 and the size of the m a s t e r key space is q. It is clear t h a t the information rate of our secret sharing

(4)

P6

P3

P4

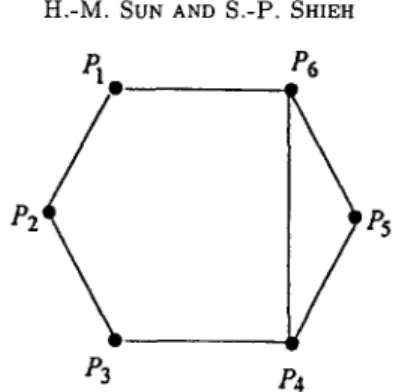
Figure 1. Graph G with six participants.

scheme for graph-based access structure is log 2 q / l o g 2 qn-m = 1 / ( n - 1), where n is the n u m b e r of participants.

We d e m o n s t r a t e the use of our m e t h o d in the following example. In Figure 1, the graph G denotes the access/prohibited structures with six participants. T h e graph G has a set of edges E and a set of nonedges N E , where

E = {PlP2,PlP6,P2P3,P3P4,P4P5,P4P6,PsP6}, and N E = {Pip3, pxP4, PiPs, p2p4, P2Ps, p2P6, P3P5, p3P6} •

T h e secret sharing scheme for the access/prohibited structures based on the g r a p h G is con- s t r u c t e d as follows. Let P = {Pl,P2,P3,P4,P5,P6}. Thus, S = {{Pl,P2},{Pl,P6},{P2,P3},{P3,P4},{P4,P5},{P4,P6},{P5,P6}} and R : {{pl,P3},{Pl,P4},{Pl,P5},{P2,Pn},{P2,P5},{P2,P6},{P3,P5},{P3,P6}}. T h e access structure F : {{pl,p2},{pl,p6},{p2,p3},{p3,p4},{p4,p5},{p4,p6},{p5,p6}, {Pl,P2,P3},{Pl,P2,P4},{Pl,P2,P5},{Pl,P2,P6},{Pl,P3,P4}, {Pl,P3,P6},{Pl,P4,P5},{Pl,Pn,P6},{Pl,P5,P6},{P2,P3,P4}, {P3,P4,P5},{P3,P4,P6},{P3,P5,P6},{P4,P5,P6},{Pl,P2,P3,P4}, {Pl,P2,P3,P5},{Pl,P2,P3,P6},{Pl,P2,P4,P5},{Pl,P2,P4,P6}, { P l , P 2 , P 5 , P 6 } , { P l , P 3 , P 4 , P 5 } , { P l , P 3 , P 4 , P 6 } , { P l , P 3 , P 5 , P 6 } , { P l , P 4 , P 5 , P 6 } , { P 2 , P 3 , P 4 , P s } , { P 2 , P 3 , P 4 , P 6 } , { P 2 , P 3 , P s , P 6 } , {P2,P4,P5,P6},{P3,P4,P5,P6},{Pl,P2,P3,P4,Ps}, { P l , P 2 , P 3 , P 4 , P 6 } , { P l , P 2 , P 3 , P 5 , P 6 } , { P l , P 2 , P 4 , P 5 , P 6 } , { P l , P 3 , P 4 , P s , P 6 } , { P 2 , P 3 , P 4 , P s , P 6 } , { P l , P 2 , P 3 , P 4 , P 5 , P 6 } } . T h e prohibited structure

A : {¢,{Pl},{P2},{P3},{P4},{Ps},{P6},{Pl,P3},{Pl,P4},

Let T S 1 , T S 2 , . . . , and TS6 be six (2,6)-threshold schemes. We assume t h a t k~ is the s u b m a s t e r key of TSi and si.1, s~,2,,.., and si,n are the subshares of TS~. Here we use Shamir's m e t h o d [5] to construct these threshold schemes. For each (2, 6)-TSi, let

(5)

Perfect Secret Sharing Schemes 133 be a secret polynomial of degree 1 over the finite field

GF(q),

where q is a prime. Let IDj denote the identity of the participant

pj.

T h e 6 subshares s i , 1 , . . . , si,6 are c o m p u t e d from

fi(x)

as follows:

si,j

= f i ( I D j ) ( m o d q ) , j = l , . . . , 6 .

Obviously, given any two subshares,

si,j and si,k, f~(x)

can be reconstructed from the Lagrange interpolating polynomial as follows [11]:

(x - IDk) (x - IDj) (mod q).

fi(x)

= si,3 (IDj - IDk) +

Si,k

(IDk - I D j )

Thus, the s u b m a s t e r key k i ( =

fi(O))

can be obtained, but less t h a n two subshares provide no information a b o u t the s u b m a s t e r key.

T h e m a s t e r key of the SSS(G) is given by K = kl + k 2 + . . - + k 6 (rood q). T h e shares of participants are given by

81 ---- (--, k2, 83,1,84,1, 85,1, k6), 82 = (kl, - , ks, s4,~, s~,2, s6,2), 83 = <sl,3, k2, - , k4, s5,3, s6,3>, S 4 • (81,4, 82,4, k3, --, k5, k6), $5 ---- {81,5, S2,5, 83,5, k4, --, k6}, S 6 ~- {kl, 82,6, 83,6, k4, k5, - } , where ' ' d e n o t e s e m p t y e n t r y .

If A = {Pl,P2} E F, A can recover the m a s t e r key K as follows.

(1) P a r t i c i p a n t Pl can obtain k2 and k6 because he owns his share S1. (2) P a r t i c i p a n t P2 can obtain kl and k3 because he owns his share $2. (3) Participants Pl and P2 can recover k4 from 84,1 of $1 and 84, 2 of S 2. (4) Participants pl and P2 can recover k5 from s5,1 of $1 and s5,2 of S~.

Therefore, participants Pl and P2 can c o m p u t e K = kl + k2 + . , . + k6 (rood q). On the other hand, if B = {Pl,P3} E A, B cannot recover either kl or k3. Therefore, B can obtain no information a b o u t the m a s t e r key K .

3 . A P P L I C A T I O N

Our secret sharing scheme for graph-based access structures can be employed in m a n y appli- cations in various areas, such as secure communication networks, and secure databases. It is particularly useful for access control (e.g., reading a file, or sending a message) in an environment where the n u m b e r of participants is large, such as a large secure network. Consider a network system with n participants, where an access control policy is enforced by a communication granting server (CGS) to restrict the communication between participants. A secure session key will not be issued unless the sender requesting the key is allowed to communicate with the receiver. T h e access control m a t r i x employed in conventional access control mechanisms can be used by the CGS to achieve the goal [12]. However, the CGS need to store and search the large access control m a t r i x of size O(n2). This size of information causes heavy storage and c o m p u t a t i o n loads on the CGS when n is large. In the worst case, the storage and c o m p u t a t i o n loads m a y make this design impractical.

In contrast, the perfect secret sharing scheme for graph-based access structures is more efficient. We can t r a n s f o r m the communication relationships into a graph where a vertex denotes a participant and an edge does a legal communication. In the network system, each participant holds a secret (which can be regarded as his private secret key). T h e secret can be t r a n s f o r m e d into the corresponding share in the secret sharing scheme by the communication granting server.

(6)

T w o participants present their secrets to the CGS when a t t e m p t i n g to communicate. If the two corresponding shares generated by the two secrets can successfully determine the m a s t e r key, the C G S will return a session key to b o t h participants. This session key will be used as b o t h encryption and decryption keys for future communication between these two participants. In the scheme, the CGS need not maintain a large access control matrix, b u t only needs to keep a single m a s t e r key.

In the following, we state the communication granting protocol for the s u p p o r t of the legal communication in detail. It is clear t h a t any access m a t r i x (communication relationships) for legal communication can be transformed into a graph where a vertex denotes a participant and an edge denotes a legal communication. Let graph G denote the access graph, Si (1 < i < n) be the share of the participant p~ in a secret sharing scheme based on the access graph G, and K be the m a s t e r key of the secret sharing scheme. We assume the communication granting server has the secret key K c a s . Each participant pi holds a Ti in secret, where Ti = { S i } K c G s (Si is e n c r y p t e d with C G S ' s secret key K c c s ) .

S e n d e r R e c e i v e r Figure 2, Communication granting protocol

Figure 2 illustrates the communication granting protocol. T h e following abbreviations are used in the protocol.

s --+ sender

r --+ receiver

K~,y -~ session key for x and y

{ M } K ~ , y --* message M encrypted with the session key shared by x and y

T h e steps of the protocol are listed in the following. {s,r,Ti }Kp i,CoS STEP 1. Pi ' CGS. { s , r , K p i , p j } K P j , C G S STEP 2. CGS ) P j . {s,r,Tj }Kpj ,c~s STEP 3. Pj ) CGS.

Then, CGS checks whether S~ and S j , derived from Ti and Tj, respectively, can recover the m a s t e r key K or not. If not, the request for communication is illegal.

{ s , r , g p i ,Pj } K P i , c o s

STEP 4. CGS ' Pi.

It is clear t h a t if the request of communication between a pair of participants is illegal, t h e n the C G S will not return a session key to the sender. Thus, the communication between the pair of participants will not be processed. Note t h a t no subset of participants can recover the m a s t e r key w i t h o u t the help of CGS.

4. C O N C L U S I O N S

In this paper, we propose an efficient construction of perfect secret sharing schemes for graph- based access structures. T h e information rate of our scheme is 1 / ( n - 1). Our scheme does not

(7)

Perfect Secret Sharing Schemes 135 n e e d t o m a i n t a i n a l a r g e a c c e s s c h e c k m a t r i x , a n d t h u s is m o r e efficient. O u r e f f i c i e n t s c h e m e c a n b e a p p l i e d t o a c c e s s c o n t r o l in a n e n v i r o n m e n t w h e r e t h e n u m b e r o f p a r t i c i p a n t s is l a r g e . T h e C G S b a s e d o n o u r s c h e m e d o e s n o t n e e d t o m a i n t a i n a l a r g e n × n a c c e s s c o n t r o l m a t r i x , b u t i n s t e a d o n l y n e e d s t o k e e p a s i n g l e m a s t e r key. T h u s , t h e s t o r a g e a n d c o m p u t a t i o n l o a d s o n t h e C G S a r e g r e a t l y r e d u c e d .

R E F E R E N C E S

1. M. Ito, A. Saito and T. Nishizeki, Secret sharing scheme realizing general access structure, Proc. I E E E

Globecom '87, 99-102 (1987).

2. W.A. Jackson, K.M. Martin and C.M. O'Keefe, Multisecret threshold schemes, In Advances in C~nyptol-

ogy--Crypto '93 Proceedings, Lecture Notes in Computer Science, Vol. 773, pp. 126 135, Springer-Verlag,

Berlin, (1994).

3. E.F. Brickell and D.R. Stinson, Some improved bounds on the information rate of perfect secret sharing schemes, Journal of Cryptology 5, 153-166 (1992).

4. G.R. Blakley, Safeguarding cryptographic keys, In Proc. A F I P s 1979 National Computer Conference, New York, Vol. 48, pp. 313-317, (1979).

5. A. Shamir, How to share a secret, Commun. of the A C M 22 (11), 612-613 (1979).

6. R.W. Hamming, Coding and Information Theory, Prentice-Hall, Englewood Cliffs, N J, (1986).

7. C.E. Shannon, Communication theory of secrecy systems, Computer Security Journal V I (2), 7-66 (1990). 8. M. Ito, A. Saito and T. Nishizeki, Multiple assignment scheme for sharing secret, Journal of Cryptology 6,

15-20 (1993).

9. J. Benaloh and J. Leichter, Generalized secret sharing and monotone functions, In Advances in Cryptol-

ogy--Crypto '88 Proceedings, Lecture Notes in Computer Science, Vol. 403, pp. 27-35, Springer-Verlag,

Berlin, (1990).

10. R..M. Capocelli, A. De Santis, L. Gargano and U. Vaccaro, On the size of shares for secret sharing schemes, In Advances in Cryptology--Crypto '91 Proceedings, Lecture Notes in Computer Science, pp. 101-113, Springer-Verlag, Berlin, (1992).

11. D.E.R. Denning, Cryptology and Data Security, Addison-Wesley, Reading, MA, (1983).

12. B.W. Lampson, Protection, Proc. 5 th Princeton Syrup. of Info. Sci. and Syst., Princeton Univ., 437-443, (March 1971); Reprinted in A C M Oper. Syst. Rev. 8 (1), 18-24 (January 1974).