Generation and evolution of spin entanglement in nonrelativistic QED
Ru-Fen Liu*and Chia-Chu Chen†Physics Department, Laboratory for Quantum Information Science, National Cheng-Kung University, 1 University Road, Tainan 70101, Taiwan, Republic of China
共Received 9 May 2003; published 13 October 2003兲
Analysis of the generation of spin entanglement from nonrelativistic QED is presented. The results of entanglement are obtained with relativistic correction to the leading order of (v/c)2. It is shown that to this
order, the degree of entanglement of a singlet state does not change under time evolution, whereas the triplet state can change.
DOI: 10.1103/PhysRevA.68.044302 PACS number共s兲: 03.67.⫺a, 03.65.Ud
The generation of entanglement states is one of the im-portant problems of quantum information science. This is due to the fact that entanglement is the essential source of quantum computing and quantum information processing. An interesting example of entanglement is the famous Einstein-Podolsky-Rosen共EPR兲 pair 关1兴 which has been sug-gested to provide secure quantum communication 关2兴. Re-cently, experimental works have produced photons which are in the entangled states and have been used to show violation of Bell’s inequality关3兴 and quantum teleportation 关4兴. How-ever, the generation of entangled states of electrons have only been suggested theoretically关5兴. By realizing the fact of the long spin dephasing time of electrons in semiconductors, the conservation of electron numbers in the nonrelativistical limit, and the rapid development in the research of quantum dot systems, it seems quite promising that electronic en-tanglement can provide a scalable approach to quantum com-puting.
Achieving quantum computation requires precise manipu-lation of the controlled Hamiltonian. In Loss and DiVincen-zo’s work关5兴, they proposed to implement quantum gates by a time dependent Heisenberg spin Hamiltonian. More re-cently, the generation of EPR states from two-electron mixed state has also been proposed in the quantum dots system关6兴. As all effective interactions in condensed matter systems are basically electromagnetic, it is therefore interesting to ad-dress the entanglement problem within the framework of quantum electrodynamics共QED兲. This approach not only has the advantage of relativistic invariance but also takes care of the problem of indistinguishable property of electrons. In a recent paper, Pachos and Solano关7兴 have discussed the prob-lem of the relativistic invariance of entangprob-lement by using QED. They have also claimed to obtain the Heisenberg Hamiltonian by considering the lowest-order scattering pro-cess of two electrons. Since magnetic interactions are of a relativistic nature, it is important to consider all the relativ-istic effects to the same order. Due to the fact that electrons are fermions, the antisymmetric nature of the state vector leads to interesting results which do not arise for nonidenti-cal particles. Moreover, there is also another aspect of en-tanglement which needs to be addressed. Namely, the effects
of interaction on the evolution of entanglement states should be investigated. The problem of entanglement and identical particles has also been addressed by Omar et al. 关8兴, how-ever, they concentrate on transferring entanglement from the internal to the spatial degrees of freedom without consider-ing interaction. In this work, we analyze the generation and evolution of entangled electron pairs within the nonrelativis-tic共NR兲 expansion by including the interaction effects to the order of (v/c)2 and using a properly antisymmetric wave function. Consistency then requires the QED corrections to O(␣2) with ␣ being the fine structure constant. Therefore, for completeness, the two-photon exchange processes are also discussed in this work.
Due to the nonrelativistic approach of this work, the state of the two-electron system can be expressed by a wave func-tion. Furthermore, with electrons being identical fermions, the total wave function of the electron system is required to be totally antisymmetric. In discussing scattering processes, the total wave function of two electrons⌿ can be expressed by the direct product of spatial wave function and spin wave function :
⌿⫽丢.
For the moment it is appropriate to introduce the concept of Schmidt’s decomposition into the spin wave function such that the entanglement analysis can be performed effectively 关9兴.
The wave function of any bipartite system is expressed as a double sum. Schmidt’s decomposition procedure asserts that the double sum can be expressed as a single sum by local unitary transformation. For example, the spin state vec-tor of two spin-1/2 particles is
兩
典
⫽兺
nm
Cnm兩n
典
A兩m典
B, 共1兲where兵兩1典,兩2典其A and兵兩1典,兩2典其B are two sets of
ortho-normal basis which belong to the spin Hilbert space of the bipartite system A and B. By applying Schmidt’s decompo-sition procedure,兩
典
can be reduced to兩
典
⫽a1兩1典A兩1典B⫹a2兩2典A兩2典B. 共2兲Here,兵兩1典,兩2典其A and兵兩1典,兩2
典
其B are the two possiblein-complete orthonormal bases of the Hilbert space, where
兵a1,a2其 are Schmidt’s coefficients which satisfy the nor-*Electronic address: fmliu@phys.ncku.edu.tw
†Electronic address: chiachu@phys.ncku.edu.tw
PHYSICAL REVIEW A 68, 044302 共2003兲
malization condition 兺i2⫽1ai2⫽1. This decomposition proce-dure is particularly useful for expressing entangled states. For this two-spin system, if all ai are nonvanishing then the
system is spin entangled, which means the state vector 兩
典
cannot be expressed as a direct product兩⬘典
A兩⬘典
B. By pick-ing a special direction as z axis, one can define a conven-tional basis兵兩↑典
,兩↓典
其 along this axis such that any spin state vector can be expanded as a linear combination of these basis vectors. A symmetrized and entangled spin vector denoted as 兩SE
典
, the general form written in the conventional basis is 兩S
E
典
⫽C兩↑↑典
⫹D共兩↑↓典
⫹兩↓↑典
)⫹G兩↓↓典
, 共3兲with D2⫽CG. By tuning the coefficients C, D, and G, three of the Bell states, 兩⌽⫾
典
⫽(1/冑
2)(兩↑↑典
⫾兩↓↓典
) and 兩⌿⫹典
⫽(1/冑
2)(兩↑↓典
⫹兩↓↑典
) can be obtained from Eq. 共3兲. If D2 ⫽CE then the state is not entangled, that is to say, by local unitary transformation the state can be written as a direct product. On the other hand, for the antisymmetric and en-tangled spin vector兩AE典
one can easily prove that the state is the remaining Bell state兩⌿⫺典
,兩A
E
典
⫽兩⌿⫺典
⫽ 1冑
2共兩↑↓典
⫺兩↓↑典
). 共4兲 It is also noted that if the spin degree of the system is not entangled, then one of Schmidt’s coefficients must vanish and the other is equal to one.By properly antisymmetrizing the total wave function and choosing the Coulomb gauge, the interaction potential 关10兴 to thev2/c2 is
U⫽UC⫹USL⫹USS, 共5兲
where UC, USL, and USS, denote the Coulomb interaction
with relativistic correction, orbital interaction, and spin-spin interaction, respectively. The form of these three inter-actions are as follows:
UC⫽ e2 r ⫺ e2ប2 4c2m2␦共r兲⫺ e2 2m2c2r
冋
p1•p2⫹ r•共r•p1兲p2 r2册
, 共6兲 ULS⫽⫺ e2ប 4m2c2r3关r⫻共p1⫺p2兲•共1⫹2兲兴, 共7兲 USS⫽ e2ប2 4m2c2再冋
8 3 ␦共r兲⫹ 1 r3册
共1•2兲⫺ 3共1•r兲共2•r兲 r5冎
. 共8兲 It is noted that all the correction terms are of the same order as the v2/c2 correction to the Coulomb potential e2/r. By applying these interacting potentials in the Born approxima-tion, a systematic analysis of entanglement can proceed. However, it is not consistent if one stops at the first Born approximation of the order ␣. As is well known in atomic physics, the energy correction due to the relativistic effect is of the same order as ␣2. Furthermore, for electronsin metal, the Fermi velocityvFis of the order of 106 m/s and
hence the ratiovF/c is of the same order as␣. Therefore, for
consistency one must consider the second Born term, which is O(␣2). This higher order analysis will be discussed later. In order to address the generation and evolution of en-tangled states of two electrons, the effects of the spatial wave function must be considered. According to the principle of quantum mechanics on identical particles, the total wave function is either symmetric or antisymmetric depending on the nature of the system. Therefore, any sensible discussions on entanglement must take into account the spatial property. This is in contrast to the conventional discussion on en-tanglement where only the spin states are involved. With this in mind the problem can be posed in the following way. If the system is prepared without spin entanglement, then after being scattered by the above interaction potentials, is it pos-sible to generate a spin entangled state? The more interesting question is what type of spin entanglement state is robust during the scattering process? These questions are addressed in the next section. Let us consider the two-electron scatter-ing process. The initial wave function can be prepared as the simultaneous eigenfunction of the Hamiltonian and total mo-mentum operators. The three possible different forms of the wave function are as follows:
兩⌿(1)
典
⫽兩 A共p1,p2兲典
丢兩S E”典
, 兩⌿(2)典
⫽兩 A共p1,p2兲典
丢兩S E典
, 兩⌿(3)典
⫽兩 S共p1,p2兲典
丢兩A E典
. 共9兲Here,兩S(p1,p2)
典
and兩A(p1,p2)典
represent the symmetric and antisymmetric wave functions of the system, respec-tively, with momenta p1 and p2. 共Such initial states in prin-ciple can be created by doubly ionizing the two electrons in the ground state of the helium atom.兲 The explicit form of these functions 兩S典
and兩A典
are as follows:兩S共p1,p2兲
典
⫽ 1 共2ប兲3/2兵e (i/ប)(p1•x1⫹p2•x2) ⫹e(i/ប)(p2•x1⫹p1•x2)其, 兩A共p1,p2兲典
⫽ 1 共2ប兲3/2兵e (i/ប)(p1•x1⫹p2•x2) ⫺e(i/ប)(p2•x1⫹p1•x2)其.The form of 兩SE
典
and 兩AE典
are given by Eqs. 共3兲 and 共4兲, respectively. The state 兩SE”典
representing the no-entangled-spin state is兩S
E”
典
⫽C兩↑↑典
⫹D共兩↑↓
典
⫹兩↓↑典
)⫹G兩↓↓典
, 共10兲 with D2⫽CG. Let the initial and final states of the system be denoted as兩⌿i(k)典
and兩⌿f(k)典
, respectively, where k rep-resents any one of the states of Eq. 共9兲. Since some of the terms of the interaction potential U, such as UC, ULS, andBRIEF REPORTS PHYSICAL REVIEW A 68, 044302 共2003兲
兵1•2其, are commuting with total spin S⫽s1⫹s2, the scat-tering process through these terms is spin angular-momentum conserving. Even though the last term of Eq.共8兲 does not commute with the total spin S, however, when act-ing on either the symmetric or antisymmetric spin state, the resulting state retains the same symmetry property. This is due to the fact that this term is symmetric. Explicitly, the forms of the resulting states are
共1•r兲共2•r兲兩A
典
⫽⫺r2
4 兩A
典
, 共11兲 共1•r兲共2•r兲兩S典
⫽1兩↑↑典
⫹2共兩↑↓典
⫹兩↓↑典
)⫹3兩↓↓典
,共12兲 whereiare some spatial factors. Then it is obvious that the
scattering between symmetric and antisymmetric spin state by this term produces zero transition amplitude. As a result the total scattering amplitude of the initial state兩⌿i
(1)
典
is具
⌿f (k)兩U兩⌿ i (1)典
再
⫽0, k⫽3 ⫽0, otherwise. 共13兲 This result shows that as the initial state is no spin tanglement, the probability for creating a spin singlet en-tangled state 兩⌿(3)f典
is zero. This result also holds for the initial state being兩⌿i(2)典
, which is an entangled spin triplet state. On the other hand, by taking the spin singlet state 兩⌿i(3)
典
as initial state, one can make use of the complex conjugate of the above results to conclude that the final state can only be the same spin entangled state. Furthermore, the results also imply that if we prepare an initial spin state as either 兩SE”
典
or 兩SE典
, the interaction potential U can change the degree of spin entanglement. For example, the spin triplet entangled state兩SE典
can scatter into a no-spin entangled state 兩SE”
典
. Therefore, one has an important conclusion that, by taking QED into account, the degree of entanglement is not an invariant concept during time evolution. From the above discussions, one may conclude that, due to the stability of entanglement of the spin-singlet state, implementation of the spin-singlet state in quantum computation is more practical. In order to justify the above conclusion, it is necessary to establish the fact that the high-order corrections do not spoil the result. Furthermore, there is also another important issue which requires at least including the next order correction. It was mentioned earlier that all correction terms are of the same order O(v2/c2) correction to the Coulomb potential e2/r. Since the magnitude of v2/c2 is the same as ␣2, the second Born approximation by the interaction potential U should be included in the discussion.
A complete␣2correction to the scattering amplitude must include also the radiative correction to the coupling constant
␣ and the electron mass. However, since this work is only considering the nonrelativistic expansion, these radiative ef-fects do not alter the results of scattering and will be ne-glected. The second Born approximation can be obtained
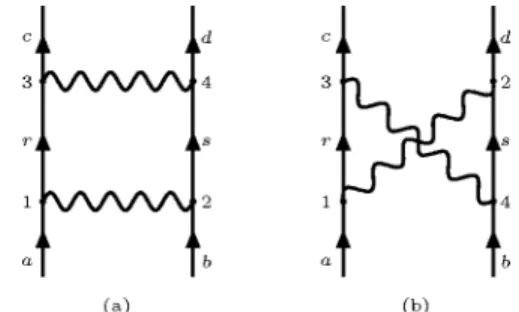
di-rectly from calculating the corresponding Feynman diagrams which are the ladder and crossed diagrams as given in Fig. 1. This approach is quite elaborate for the result of this section. Fortunately, there exists an effective way of calculating the results within the validity of the nonrelativistic expansion. It is known that the␣2 correction can be obtained by a second order potential U(2),
U(2)⫽VL(2)⫹VX(2), 共14兲 where VL(2) and VX(2) are calculated from the ladder and crossed diagrams, respectively. Even though the forms of these potentials are gauge dependent, it has been shown that the total scattering amplitudes are gauge independent 关11兴. Therefore, one can choose a convenient gauge to calculate the amplitude. In the present study the Coulomb gauge is more suitable, as will be shown later, and the leading rela-tivistic correction of the VX(2)vanishes in the Coulomb gauge. To simplify the discussion, the notation for the wave func-tion is modified slightly. All the initial states of two electrons are written as 兩ab
典
and the final states as兩cd典
. The lowest order scattering amplitude具
cd兩S(1)兩ab典
can be identified with a potential scattering with the interaction potential U given by Eq.共5兲具
cd兩S(1)兩ab典
⫽⫺2i␦共a⫹b⫺c⫺d兲
具
cd兩U12兩ab典
, 共15兲 wherea denotes the energy eigenvalue of the free electronof state a and U12is the potential of vertices 1 and 2 . The two-photon exchange contributions to the order of interest, namely O(␣2), can be expressed as the effective potentials which are given by
具
cd兩VL(2)兩ab典
⫽⫺21i兺
rs
冕
dz
⫻
具
c3d4兩U34共a⫺c⫺z兲兩r3s4典具r1s2兩U12共z兲兩a1b2典 共a⫺r⫺z⫹ir兲共b⫺s⫹z⫹is兲共16兲 and similarly for the crossed diagram
FIG. 1. 共a兲 The ladder and 共b兲 the crossed diagrams of two-photon exchange processes.
BRIEF REPORTS PHYSICAL REVIEW A 68, 044302 共2003兲
具
cd兩VX(2)兩ab典
⫽⫺ 12i
兺
rs冕
dz
具
c3s4兩U34共a⫺c⫺z兲兩r3b4典具r1sd2兩U12共z兲兩a1s2典 共a⫺r⫺z⫹ir兲共d⫺s⫹z⫹is兲. 共17兲
Here, Ui j(cq) is the Fourier transform of the potential with q being the three-dimensional momentum transfer. As shown in Lindgren’s work关11兴, the result of Eq. 共16兲 can be simplified as
具
cd兩VL (2)兩ab典
⫽1 2兺
rs 兵具
cd兩r12⫺1兩rs典具
rs兩VB M兩ab典
⫹具
cd兩VB M兩rs典具
rs兩r 12 ⫺1兩ab典
其 共a⫹b⫺r⫺s兲 . 共18兲Here, VB M is the generalized potential of Brown and Mittleman关12兴
具
rs兩VB M兩ab典
⫽12具
rs兩U共a⫺r兲⫹U共b⫺s兲兩ab典
. 共19兲Since what one needs from this calculation is the order ␣2 correction, it is obvious that one should only keep the Coulomb potential e2/r of U in the above expression for VB M. However, since the Coulomb potential does not flip the spin of electrons, VL(2)does not scatter the spin-singlet state into other spin configuration. It is now important to show that VX(2)also preserves the spin-singlet state.
For the crossed diagram, one can also simplify Eq. 共17兲 and the result is
具
cd兩VX(2)兩ab典
⫽⫺12
兺
rs兵
具
cs兩r12⫺1兩rb典具
rd兩Vdi f f兩as典
⫹具
cs兩Vdi f f兩rb典具
rd兩r12⫺1兩as典
其 共a⫹s⫺d⫺r兲, 共20兲
where Vdi f f is the difference potential
具
rs兩Vdi f f兩ab典
⫽⫺具
rs兩U共a⫺r兲⫺U共b⫺s兲兩ab典
.共21兲 Thus, within the same approximation, one should retain only the Coulomb potential and therefore a vanishing Vdi f f is obtained. As a result, to the leading relativistic order, VX(2) does not contribute to the scattering process. This completes the proof of the stability of the spin-singlet entanglement.
Recently, people have tried to control electron spin as qubit directly in some condensed matter system, such as electrons in quantum dots. It is also claimed that the interac-tion of such systems can be described by the Heisenberg Hamiltonian H⫽J(t)1•2. It is easy to check that the Bell states are stable during time evolution with this Hamiltonian. However, in this approach, spins are the only variables of the system which, in general, cannot properly describe electrons. As pointed out earlier, it is inadequate to neglect the spatial
wave function which is involved in the formalism of identi-cal particles. The effects of identiidenti-cal particle on entangle-ment can be seen from previous discussion on the fact that the entangled spin-triplet states, such as Bell states, can evolve into no-spin entangled state. As a result, the concept of entanglement for the spin-triplet state is not practical. This is in contrast to the case described solely by the Heisenberg Hamiltonian. On the other hand, as shown also in this work, the spin-singlet state which is entangled by nature is stable to a high degree of accuracy. Therefore, for any practical imple-mentation of entangled state with spin, the spin-singlet state deserves more attention. Furthermore, the result obtained here by considering the antisymmetric wave function implies that the spin-singlet entangled state cannot be generated from the other spin configuration regardless of its state of en-tanglement.
This work was supported by NSC91-2112-M-006-008.
关1兴 A. Einstein, N. Rosen, and B. Podolsky, Phys. Rev. 47, 777 共1935兲.
关2兴 C.H. Bennett and G. Brassard, in Proceedings of the IEEE
Conference on Computers, Systems and Signal Processing, Bangalore, India共IEEE, New York, 1984兲, p. 174; A.K. Ekert,
Phys. Rev. Lett. 67, 661共1991兲.
关3兴 A. Aspect, P. Grangier, and G. Roger, Phys. Rev. Lett. 47, 460 共1981兲; G. Weihs et al., ibid. 81, 5039 共1998兲.
关4兴 D. Bouwmeester et al., Nature 共London兲 390, 575 共1997兲; D. Boschi et al., Phys. Rev. Lett. 80, 1121共1998兲; A. Furusawa
et al., Science 282, 706共1998兲.
关5兴 D. Loss and D.P. DiVincenzo, Phys. Rev. A 57, 120 共1998兲. 关6兴 W.D. Oliver, F. Yamaguchi, and Y. Yamamoto, Phys. Rev. Lett.
88, 037901共2002兲.
关7兴 J. Pachos and E. Solano, Quantum Inf. Comput. 3, 115 共2003兲; e-print quant-ph/0203065.
关8兴 Y. Omar, N. Paunkovic´, S. Bose, and V. Vedral, Phys. Rev. A
65, 062305共2002兲.
关9兴 E. Schmidts, Math. Ann. 63, 433 共1907兲.
关10兴 L.D. Landau and E.M. Lifshitz, Relativistic Quantum Theory
Part I共Addison-Wesley, 1971兲, p. 284.
关11兴 I. Lindgren, J. Phys. B 23, 1085 共1990兲; C.C. Chen, ibid. 26, 599共1993兲.
关12兴 G. Brown, Philos. Mag. 43, 467 共1952兲; M.H. Mittleman, Phys. Rev. A 4, 893共1971兲; 5, 2389 共1972兲.
BRIEF REPORTS PHYSICAL REVIEW A 68, 044302 共2003兲