國立宜蘭大學土木工程學系（研究所） 碩士論文 Department of Civil Engineering National Ilan University Master Thesis

國立宜蘭大學土木工程學系（研究所）

碩士論文

Department of Civil Engineering National Ilan University

Master Thesis

以最小二乘配置法進行小區域地籍資料坐標轉換精度之研究 -以宜蘭縣壯圍鄉吉祥段為例

A Study of Coordinates Transformation in Small Area Using Least-Squares Collocation Method

-A Case of Ji-Xiang section, Zhuang-Wei village, ILan County

指導教授：崔國強 博士

Gwo-Chyang Tsuei Ph. D.

研究生：李添福

Tien-Fu Lee

以最小二乘配置法進行小區域地籍資料坐標轉換精度之研究

-以宜蘭縣壯圍鄉吉祥段為例

研究生：李添福 指導教授：崔國強 博士 國立宜蘭大學土木工程學系所

摘要

臺灣地區之地籍測量隨著坐標系統的更新，先後採用多種不同坐標系 統之測量成果，且不同測區間缺乏嚴密的關聯，常造成部分測量人員辦理 土地複丈未予查覺而誤用，在新的 TWD97 坐標系統公告後，新測之地籍測 量成果均以此系統為基準。

為了要整合不同坐標系統之圖籍資料，本研究以實驗區周遭之 10 個四 等控制點為共同點，採用最小二乘配置法進行小區域的平面坐標轉換，將 TWD67 的地籍資料坐標轉換至 TWD97 坐標系統下，並以實驗區內 125 個 圖根點為檢核點，實驗結果發現以最小二乘配置法結合四參數或六參數兩 種模式進行坐標轉換，於 125 個圖根點精度上沒有明顯的差異，125 個圖根 點中僅有 3 個點位誤差大於 2 公分，122 個點位誤差小於 2 公分，佔所有點 數 97.6％，點位誤差最大者為 2.7 公分。

以同一組轉換參數，將實驗區內之所有界址點進行坐標轉換，宗地之 界址點平均點位誤差為 0.5 公分，99.66%邊長增減在 1 公分以內，平均每筆 面積增加 0.007%，99.6%宗地面積增減在 0.1%內；由以上實驗成果可知坐 標轉換之成果均可符合地籍測量實施規則之要求，本坐標轉換可視為無誤 差，並可直接以轉換後之 TWD97 坐標進行複丈作業。

A Study of Coordinates Transformation in Small Area Using Least-Squares Collocation Method

-A Case of Ji-Xiang section, Zhuang-Wei village, ILan County

Student：Tien-Fu Lee Advisor：Dr. Gwo-Chyang Tsuei Department of Civil Engineering

National Ilan University Abstract

Some surveyors often misapply the coordinate data in performing cadastral survey, cause of the renewal of the coordinate system in Taiwan and the cadastral survey successively adopted the measurement achievements of many kinds of different coordinate systems, and lacked the tight relation with different area. After the new TWD97 coordinate system announced, the cadastral survey results are on a basis of this new system.

In order to integrate the maps of different coordinate systems, this research adopted the least squares collocation to translate the TWD67 coordinates to TWD97 coordinates on the small area, and chose 10 4th order control points around the test area as the common point and 125 control points as the checking point. The experimental results find that the least squares collocation method combines four parameters or the way of six parameters did not have obvious difference on 125 control points precision. Only 3 control points position errors are greater than 2 centimeters, 122 control points position error are smaller than 2 centimeters, account for all count 97.6% , the greatest position error is 2.7 centimeters.

Then we translated the coordinates of all parcels boundaries points using the same transformation parameters of test area, the experimental results are ： the greatest position error of parcels boundaries coordinates is 1.3 centimeters, and the land boundaries position error is 0.5 centimeters on average, 99.7% of the lengths error of parcels are within 1 centimeter, 99.6% area error of parcels are in 0.1%. So we can find that these results all conform to the cadastral survey implement law request, this coordinate transformation could be deemed to have no position error, and we can perform the cadastral survey tasks with these TWD97 coordinates directly.

誌 謝

本文承蒙恩師崔教授國強博士，於研究過程中悉心指導及在學習期間 對治學方法多方啟發，方能順利完成，測量科技文明結合圖資，作好三圖 合一（地籍圖、地形圖、都市計畫圖）統一坐標之準備而努力，藉圖資的 整合，有感我敬愛的崔教授國強博士在研究學習上的悉心指導，敦促教誨 鼓勵，讓學生學有所成，在此向恩師致上最誠摯的感謝與謝意。

衷心感謝口試委員何教授維信博士、李教授良輝博士、洪教授本善博 士、高教授書屏博士於百忙中抽空審查並細心斧正，口試時費心審核和提 供許多精闢意見及諸多見解，對論文之各項指正與提供寶貴意見修正，促 使本研究論文在實務上更臻堅實與完備，在此亦表達最誠摯之謝意。

感謝在本校俟容於求學生涯，歷經各位師長教誨，一路走來點點滴滴 感恩在心頭，研究所兩年論文的完成得以付梓，教授以測量實務操作，感 性教學新動脈，歷年學生屢次參加學校接受內政部委託宜蘭縣政府發包攸 關地理資訊建置案，如 93 年度宜蘭縣羅東鎮之千分之一數值地形圖及門牌 系統建置，委託規劃建造案。經濟部自來水公司第八區營運處，委託本校 作全宜蘭縣所有一萬四千餘處的自來水管路系統暨安全閥及消防栓，消防 止水閥等作地理資訊 GIS 資料庫建檔系統之測量監造及教育調查測量暨測 設教學，94 年延續宜蘭市之千分之一數值地形圖及門牌系統建置委託計劃 監造案，及台東縣政府、金門縣政府等委託監造案與宜蘭大學接受內政部 土地測量局委託辦理招訓地籍測量人員訓練班第三十二及三十三期培訓業 務。

最後仍要感謝我的家人的支持與鼓勵，尤其是內人全力支持配合及協 助英文翻譯繕寫，考試及測量實驗期間無論晴天或雨天甚至節慶假日全程 陪伴，在我求學期間經營事業的幫忙，無怨無悔，從不抱怨，讓我無後顧

之憂，方能完成論文之撰寫，特藉本文之一隅，獻上無限的謝意，俟容與 所有朋友分享。

謝謝大家！！

李添福 謹識 九十五年 六 月

目 錄

摘要 ...I

Abstract ... II 誌 謝 ... III

目 錄 ... V

圖 目 錄 ... VIII

表 目 錄 ... X

第一章 緒論 ... 1

1-1 前言... 1

1-2 研究動機與目的... 1

1-3 文獻回顧... 2

1-4 研究方法... 4

第二章 坐標系統... 5

2-1 地籍坐標系統... 5

2-2 TWD67... 6

2-3 TWD97... 8

第三章 坐標系統轉換模式... 12

3-1 四參數轉換... 12

3-2 六參數轉換... 13

3-3 最小二乘配置法(Least Squares Collocation)... 14

第四章 實驗與分析... 17

4-1 實驗方法... 18

4-1-1 實驗區的選擇 ... 20

4-1-2 共同點資料的預處理 ... 22

4-2 成果分析... 27

4-2-1 共同點之精度分析 ... 27

4-2-2 檢核點(圖根點)之精度分析 ... 29

4-2-3 界址點精度分析 ... 37

4-2-4 地籍圖宗地邊長及面積精度分析 ... 40

4-2-5 都市計劃樁位精度分析 ... 45

第五章 結論與建議... 50

5-1 結論... 50

5-2 建議... 51

參考文獻 ... 52

附 表 ... 54

附表 A 不同坐標轉換模式之圖根點成果比較表 ... 54

附表 B 界址點協助指界內容 ... 58

附表 C 邊界樁距離與方位角度差明細表 ... 60

附表 D 控制測量成果基線成果比較表... 61

附表 E 參數轉換成果 ... 67

圖 目 錄

圖 2-1 地籍坐標系統示意圖 ... 6

圖 3-1 四參數轉換示意圖 ... 13

圖 3-2 六參數轉換示意圖 ... 14

圖 4-1 坐標轉換作業流程圖 ... 20

圖 4-2 實驗區範圍示意圖 ... 21

圖 4-3 實驗區已知基本控制點分布圖 ... 24

圖 4-4 測區與鄰近 10 點四等點位分佈位置圖 ... 25

圖 4-5 圖根點資料處理流程圖 ... 27

圖 4-6 實驗區圖根點網絡圖 ... 31

圖 4-7 四參數轉換 N、E 向量改正數大小分佈圖... 32

圖 4-8 六參數轉換 N、E 向量改正數大小分佈圖... 33

圖 4-9 最小二乘配置法+四參數轉換 N、E 向量改正數大小分佈圖………34

圖 4-10 最小二乘配置法+六參數轉換 N、E 向量改正數大小分佈圖……..35

圖 4-11 圖根點位誤差大小分佈... 36

圖 4-12 界址點資料處理流程圖 ... 38

圖 4-13 抽樣圖根點測站位置圖 ... 39

圖 4-14 邊長誤差較大位置圖 ... 42

圖 4-15 都市計畫使用分區及都市計畫樁分佈圖 ... 47

圖 4-16 抽樣都計樁位置圖 ... 48

表 目 錄

表 2-1 TWD97 所採用的大地參數（黃華尉,2001） ... 10

表 4-1 各項作業內容 ... 18

表 4-2 實驗區資料一覽表 ... 21

表 4-3 實驗區基本控制點點號明細表 ... 22

表 4-4 四個共同點坐標轉換精度分析 ... 24

表 4-5 10 個共同點坐標轉換精度分析 ... 29

表 4-6 各種轉換精度分析表 ... 35

表 4-7 界址點誤差分析表(取絕對值)... 39

表 4-8 邊長增減分析比較表 ... 41

表 4-9 邊長較差大於 2 公分明細表 ... 41

表 4-10 宗地面積增減百分比筆數分佈表 ... 43

表 4-11 宗地面積增減百分比及增減大小範圍表 ... 43

表 4-12 6 筆宗地面積增減百分比較大之明細表 ... 43

表 4-13 實驗區都市計劃樁位明細 ... 46

表 4-14 路寬精度分析 ... 47

表 4-15 邊界樁距離與方位角比較表 ... 48

表 4-16 街廓區塊面積比較表 ... 48

第一章 緒論

1-1 前言

地籍圖係國家執行土地政策明訂土地界址位置之依據，記載著各宗土 地之方位、界址、形狀、面積等資訊，舉凡交通建設、國土規劃、土地開 發、水利設施、防災救災等等，均需使用地籍圖資料。

目前地籍測量所使用之坐標系統可概分為地籍坐標（日據時期及修測 地籍圖）、TM 三度分帶坐標（早期重測地籍圖）、TM 二度分帶坐標（69 年 內政部頒布）及 TWD97 坐標系統，且其成果計算方式又可分為改算、局部 平差、全面平差等多種成果，不同時期所採用之測量方法、測量儀器、坐 標系統、成果精度均不大相同，常造成部分測量人員辦理土地複丈未予查 覺而誤用，引起諸多困擾，因此在使用這些資料時如未經過化算，無法有 效發揮這些圖籍資料的效益。

理論上實地上同一點位於不同圖籍上，位置應相同，但由於不同圖籍 資料引用不同系統之控制點施測，且因使用圖紙之伸縮率不一致，導致各 類地籍圖間難以嚴密套合，因此如何將此等不同坐標系統、不同比例尺之 地籍圖利用數學模式，進而建立各系統間之轉換模式，予以整合應用，的 確是目前重要的課題。

1-2 研究動機與目的

早期重測、重劃區坐標系統又與都市計畫樁位系統不同，造成地籍測 量與都市計畫無法整合，形成施政規劃障礙及公務執行困難，導致人民權 益受損，糾紛案件不斷，隨著測量技術更新，臺灣地區亦將坐標系統重新 定義，並於民國 87 年公佈新的坐標系統 TWD97，新的坐標系統產生之後，

面臨到的問題就是不同坐標系統之間的轉換。

臺灣省自 78 年度起全面採用數值法辦理地籍圖重測工作，建立高精度 數值化之地籍圖資，對於後續土地複丈工作已發揮具體功效，惟當時採用 之坐標系統為 TWD67，因此吾人想利用坐標轉換方式將這些 TWD67 數值圖資 轉換成 TWD97。

一般坐標轉換的作法都採用簡單的多項式轉換，例如四參數、六參數轉 換到同一坐標系統內，但古典最小二乘法平差將兩坐標系之間視為僅含有 獨立的偶然誤差來處理，且每一個參考點在轉換後會產生剩餘誤差，即轉 換後參考點的坐標會因有改正數而改變，這在法律上和實務上是不允許的。

不同於傳統的平差法，最小二乘配置法(Least Squares Collocation) 是一種結合最小二乘法、內差與濾波平差的方法，傳統的測量平差法僅能 處理觀測量含有純粹的偶然誤差，而最小二乘配置法不但將之擴大到能處 理觀測量含有相關性的誤差以外且還能估計出未做觀測之處應有之觀測值 [1984,王蜀嘉]，地籍坐標公告後，具有法律地位，無法任意更改，故為維 持坐標轉換後，每個控制點的坐標改正數為零，四、六、七參數、多項式 轉換均無法達到，本研究係以參數轉換結合最小二乘配置法來進行坐標轉 換作業，並探討轉換後之地籍坐標精度是否符合複丈作業需求。

1-3 文獻回顧

一般常用於坐標轉換之方法有四、六、七參數、多項式、最小二乘配 置法等模式，依區域大小有分全區、小區域等不同方式，以下針對坐標轉 換摘錄幾篇相關文章及其研究成果。

在[尤瑞哲，1998]中提及要解決不同坐標系統間的轉換問題，以選取 施測區域內具有同樣兩種坐標的參考點求取轉換參數，是目前最普遍採用 的方式，但一般只適用於較小的區域。

應用在「台北市地籍資料 TWD67 與 TWD97 坐標轉換之比較研究」[許皓 寧,2004]，以台北市政府公告之三、四等衛星控制點當作共同點，以最小 二乘法平差為原則，進行不同區域大小與不同坐標轉換模式之地籍資料坐 標轉換轉換比較研究，結果顯示，以六參數坐標轉換為較佳的模式，實驗 成果顯示方位角誤差可控制在 10 秒內，距離誤差可控制在 3 公分內。

在「利用六參數平面轉換與最小二乘配置進行小區域 TWD67 與 TWD97 地籍資料坐標轉換-以台北市大安通化段為例」[戴翰國,2002]，研究中透 過六參數轉換結合最小二乘配置法的方式，進行小區域的平面坐標轉換，

將 TWD67 的地籍資料坐標轉換至 TWD97 坐標系統下，以利土地複丈作業之 進行，並將複丈後的成果轉換為 TWD67 的系統下，以更新地籍資料庫。

「TWD97與TWD67二度TM坐標轉換之研究」[黃華尉,2001]，文中利用本 文利用臺灣地區新公告之一、二等衛星控制點TWD97二度TM坐標及原有的 一、二、三等三角點TWD67二度TM坐標當作實驗資料，並將平面與高程資料 分開，僅採用平面坐標進行二維坐標轉換，研究結果顯示臺灣地區TWD97和 TWD67兩個坐標系統之間含有系統誤差，在N和E分量最大約30公分，使用最 小二乘配置法可以有效分配該系統誤差而得到較佳的轉換成果。

[李祺滄、高書屏，2005]，文中應用地震誘發之地層錯動修正模式及 六參數坐標轉換將地籍圖TWD67轉成TWD97系統方法來進行地籍圖坐標轉 換，實驗結果發現研究區內各段轉換前後之面積總和比較分析，誤差比皆 小於0.012%，轉換前後之邊長及面積差異量、精度分析並且至現場實測檢 測比較，其誤差值皆符合地籍測量實施規則要求之精度在市地界址點誤差 應小於6公分的規範。

[Fritzensmeier et al.，Vincenty，1980]中提到GPS高精度相對定位，

野外快速作業、高可靠度、施測不易受天候影響的優點，若想將GPS資料加 入傳統大地網中，可考慮下列作法，以提升精度。

1. 以衛星測得到之坐標與原有地面坐標為觀測量，以混合平差進行平 差。

2. 以衛星測得之基線距離為觀測量，加入傳統大地往進行計算。

3. 將有三角網觀測量精確化算至衛星坐標基準，再針對網形叫弱的部 分進行衛星測量補強，再重新平差計算。

4. 以衛星測量所得之基線長度與方位角加入原有的大地網進行平差計 算。

1-4 研究方法

隨著新的坐標系統 TWD97 公佈後，解決不同坐標系統間的轉換問題已 成為目前常遭遇到的問題，常用之區域性坐標轉換方法為四參數及六參數 轉換，此類作法必須於區域內找到若干具有新舊兩組坐標之共同點，據以 解算該區域之轉換參數，再利用坐標轉換參數將舊的坐標系統轉換到新的 坐標系統上，四參數轉換模式需有二個共同點以上，六參數轉換模式則需 有三個共同點以上，才得以實施，此類坐標轉換方式之成果精度則視所用 共同點坐標精度而定。

一般常用基本控制點、圖根點、都市計畫樁等點位當做坐標轉換之共 同點，但這些控制點常因年代久遠，或遭人為破壞，尤其是圖根點，多已 遺失殆盡，因此要取得這些控制點當坐標轉換之共同點有其困難。

在實際應用上常需將上級網強制附合，即共同點點位改正數為零，而 最小二乘配置法在一定的條件下有可能使每一個共同點在轉換後都沒有改 正數的優點，所以利用最小二乘配置法來處理不同坐標系統之間的轉換是 相當合適的選擇；因此本實驗採用最小二乘配置法為坐標轉換之工具，並 以 90 年度宜蘭縣政府數值重測區為實驗區域，以當年重測區外圍之四等控 制點為共同點進行坐標轉換，獲得實驗區之界址點、圖根點、都市計劃樁

等點位之 TWD97 坐標，並以圖根點為檢核點，圖根點之 TWD97 坐標系利用 當年重測區之原始觀測資料經嚴密三角三邊程式重新計算得到，並與坐標 轉換之 TWD97 坐標比較，以探討坐標轉換模式之精度，最後並利用 GIS 軟 體，將轉換後之地籍圖、都市計畫圖、航測地形圖等三圖套疊，以瞭解轉 換後各種圖籍資料是否可以正確套合。

第二章 坐標系統

所謂的坐標系統即用來描述點在空間的位置，由坐標原點的位置、坐 標軸的方位、坐標參數（如卡氏坐標之 X，Y 或球面坐標之^ϕ、^λ）等三要 素構成。一般常見的坐標系統有二維卡氏坐標系、極坐標系、地心地固坐 標系統等等。臺灣常見之坐標系統有以下幾種：

2-1 地籍坐標系統

以臺中公園內之主三等三角點八九號為原點（X＝0,Y＝0），並以對葫 蘆墩主三等三角點三○號的方向為原方位，採用平面直角坐標系，單位為

“間＂，間為日尺，約等 1.8 公尺；澎湖則自成一個系統，未與臺灣本島 聯測，以馬公主三等三角點八八一號為原點。早期地籍、水利、農林等機 關採用此系統，目前圖解地籍圖數值化辦理區域多屬本坐標系統。

圖 2-1 地籍坐標系統示意圖

2-2 TWD67

內政部於民國 69 年完成三角點檢測，並公布「中華民國臺灣地區三角 點成果表」，作為後續測量工作起算之依據，包括三角點之二度分帶橫麥卡 托投影坐標和 GRS67 橢球體之經緯度及正高，亦即目前所謂之虎子山大地 基準，又稱 TWD67 大地基準，其相關資料如下：

一、參考橢球體：採用 1967 年國際大地測量及地球物理學會（International Union of Geodesy and Geophysics 簡稱 IUGG）公布之參考橢球體(Geodetic Reference System 1967 簡稱 GRS67)，其橢球參數為：

長半徑： a = 6378160 公尺 扁 率： f = 1/298.25

二、測量原點：平面位置之原點為南投縣埔里之虎子山一等三角點 經度λ＝120°58' 25.975"

緯度φ＝ 23°58' 32.340"

對頭拒山之方位角α=323°57' 23.135"

三、經緯度及方位角的起算標準如下：

（一）經度以通過英國格林威治天文台子午儀中心之子午線起算，向 東者為正，向西者為負。

（二）緯度自赤道起算，向北者為正，向南者為負。

（三）方位角自正北起算，向東順時針方向為正，反之為負。

四、TWD67 坐標系統以虎子山原點起算時，採用以下幾個假設作為整 個系統推算的依據：

（一）坐標系統的 X、Y、Z 三軸與地心地固坐標系統之三軸平行。

（二）虎子山原點之大地經緯度與天文經緯度一致，即垂線偏差為零 且天文方位角與大地方位角一致。

TWD67 之特點（楊名,2003）﹕

‹ 採用古典大地基準定義方式實現。

‹ 定義量=^{ϕ0,λ0,ξ0,η0,H0}

+

‹ 由於普遍缺乏大地起伏(Undulation)及垂線偏差(Deflections of the Vertical)資訊，TWD67 實為一水平基準。僅有虎子山原點之三維位置 為已知（因係定義量），其餘點位之高程係由三角高程測量所得，與水 平位置分開。

‹ 由於大地計算過程中缺乏使用大地起伏及垂線偏差資料進行觀測量化 算，平差結果含有系統性影響（Systematic Effects），此變形量影響

水平位置甚鉅。

‹ 水平與高程位置之精度屬不同等級，水平精度遠優於高程精度，且不相 關。

2-3 TWD97

鑒於原有 TWD67 大地基準已使用多年，而且受到當時測量技術的限制 等各項因素導致 TWD67 基本三角點坐標成果精度不佳，早已不敷使用；GPS 衛星測量自 1980 年代興起後，其高精度之相對定位、不受天候影響等特性，

已廣泛應用於控制測量工作。

內政部為建立完整、統一、高精度之基本控制點系統，自民國 82 年起，

採用 GPS 衛星定位測量技術，辦理衛星追蹤站及一、二等衛星控制點測量，

並於民國 87 年公布新的國家坐標系統（TWD97），採用以下程序來訂定（曾 清涼,1998）：

一、 由內政部 8 個（陽明山、墾丁、鳳林、金門、北港、太麻里、馬祖、

東沙）GPS 衛星追蹤站聯合 51 個分布於全球之 IGS 國際追蹤站一起 進行追蹤站網分析。IGS 追蹤站網分成 igs1 及 igs2 兩網其中有 13 個 core station，其坐標系統為 ITRF94。

二、 所有追蹤站觀測數據為 1995 年 4 月 10 日至 1997 年 8 月 31 日的 GPS 觀測數據透過網路取得。

三、 先用 GAMIT 解算內政部 8 個追蹤站每日的基線向量，再用 GLOBK 結合 所有的單日解，解算這 8 個追蹤站 1997.0 的精確 ITRF94 站坐標值及 速度量。

四、 以 1997.0 的 8 個站坐標作為框架站來約制臺灣 105 個一等衛星控制 點的網型平差，如此可解出 105 個一等衛星控制點之 ITRF94 坐標，

以這組一等點坐標值建立臺灣新的大地基準 3D 坐標參考框架。

五、 選用 GRS80 橢球參數，作為參考橢球體以便換算大地坐標（

ϕ

λ

六、 地圖投影之平面直角坐標在臺灣、澎湖地區維持原用之二度分帶橫麥 卡托投影，在金門、馬祖地區則改採與臺灣本島相同但中央經線位置 不同之投影方式來處理。

由上整理出 TWD97 相關元素如下：

一 、 參考 框 架： 採 用國 際 地球 參 考框 架 （International Terrestrial Reference Frame ，簡稱 ITRF）。ITRF 為利用全球測站網之觀測資料 成 果 推 算 所 得 之 地 心 坐 標 系 統 ， 其 方 位 採 國 際 時 間 局 （ Bureau International de I＇Heure 簡稱 BIH）定義在 1984.0 時刻之方位。

二、參考橢球體：採用 1980 年國際大地測量及地球物理學會（IUGG）公布 之參考橢球體(GRS80)，其橢球參數為：

表 2-1 TWD97 所採用的大地參數（黃華尉,2001）

參數 數值

定義的常數

長半徑 6378137 m

地球引力常數 3986005 x10⁸m³S⁻¹ 動力模式參數J2 （不含固體潮） 108263 x10⁻⁸

地球自轉角速度w ^{7292115 x}10⁻¹¹rad S⁻¹ 推求之幾何參數

短半徑b 6356752.3141 m

第一離心率的平方e² 0.00669438002290 扁率f 1/298.257222101

平均半徑R 1 6371008.7714 m

相同表面積的球體半徑R 2 6371007.1810 m 相同體積的球體半徑R 3 6371000.7900 m 推求之物理參數

橢球正常引力位U ⁰ 850.62636860 m²S⁻² 赤道的正常重力 7803267715.9 m S⁻² 兩極的正常重力 8321863685.9 m S⁻²

三、投影方式：臺灣、琉球嶼、綠島、蘭嶼及龜山島等地區之投影方式採 用橫麥卡托投影經差二度分帶，其中央子午線為東經121 度，投影原 點向西平移250,000 公尺，中央子午線尺度比為0.9999；另澎湖、金 門及馬祖等地區之投影方式，亦採用橫麥卡托投影經差二度分帶，其 中央子午線定於東經119 度，投影原點向西平移250,000 公尺，中央 子午線尺度比為0.9999； 南沙地區則是中央子午線定於東經119 度，

投影原點向西平移250,000 公尺，中央子午線尺度比為0.9999。

TWD97 之特點（楊名,2003）﹕

‹ 三維、全球性、以地球質心為原點。

‹ 使用 IGS(International GPS Service for Geodynamics) 13 個框架點 (Fiducial Point)來定義其參考框架。

‹ TWD97 參考框架 = ITRF94（International Terrestrial Reference Frame），參考時刻 1997.0。

‹ 台灣地區共有 8 個 GPS 衛星追蹤站框架點。

‹ 框架點 ≠ 固定點，框架點先驗資料除坐標值以外並包含坐標之標準偏 差。

‹ TWD97 目前包含 105 個一等衛星控制點、621 個二等衛星控制點，以及 數千個三、四等點。

‹ 一、二等衛星控制點之平均精度：經度為±1.2 cm，緯度為±1 cm，高程 為±3.1 cm。

第三章 坐標系統轉換模式

各種不同的圖籍資料可利用地面一些共同控制點或現況測得之可靠 點，在兩個坐標系統中建立數學模式，透過這個數學模式進行坐標轉換，

一般常見的有正形轉換、仿射轉換、七參數轉換、多項式轉換、最小二乘 配置等方法。

3-1 四參數轉換

四參數轉換又稱正形轉換(Helmert Transformation)，兩坐標系間包 含一個比例尺因子、一個旋轉量及兩個平移量，其物理意義為轉換後原為 正方形之特徵物仍保持正方形狀，一般用於兩平面直角坐標系統之坐標轉 換，其轉換示意圖如圖 3-1，方程式如(3.1)。

圖 3-1 四參數轉換示意圖

⎥⎦

⎢ ⎤

⎣

⎡

+ +

−

+

= +

⎥⎦

⎢ ⎤

⎣

⎡ Δ + Δ

⎥⎦

⎢ ⎤

⎣

⎥⎡

⎦

⎢ ⎤

⎣

⎡

= −

⎥⎦

⎢ ⎤

⎣

⎡

D Ay Bx

C By Ax y

x y

S x Y X

θ θ

θ θ

cos sin

sin cos

……….(3.1) 其中

x,y:原坐標系統 X,Y:轉換後坐標系統

A、B、C、D：轉換參數

3-2 六參數轉換

六參數轉換又稱仿射轉換(Affine Trasformation)，其物理意義為兩 坐標系間包含二個比例尺因子、一個剪量變形因子、一個旋轉量及兩個平 移量，至少要三個共同點來求解，基本上大多數的坐標轉換均能以６參數 為之。其轉換示意圖如圖 3-2，方程式如(3.2)。

X Y

X Y

X Y

圖 3-2 六參數轉換示意圖

⎥⎦

⎢ ⎤

⎣

⎡

+ +

+

= +

⎥⎦

⎢ ⎤

⎣

⎡ Δ + Δ

⎥⎦

⎢ ⎤

⎣

⎥⎡

⎦

⎢ ⎤

⎣

⎡

+

⋅

−

−

⋅

= +

⎥⎦

⎢ ⎤

⎣

⎡

F Ey Dx

C By Ax y

x y

x S

S

S S

Y X

y x

y x

) cos sin

(sin sin

) cos sin (sin cos

θ θ

ε θ

θ ε θ

θ ….(3.2)

其中

[x,y]:原坐標系統 [X,Y]:轉換後坐標系統

A、B、C、D、E、F：轉換參數

3-3 最小二乘配置法

所謂的配置，以前是指組合各種資料來研究地球形狀和重力場的數學 方法，在地球形狀和重力場的研究中，配置的普遍形式是在其函數模型中，

除包含隨機部份外，還包含有系統部分的誤差，也就是說，在配置問題中，

有求定隨機信號的估值內容，也有求定非隨機參數估值的內容，在測量平 差中，將這種兼有求信號和非隨機參數的方法稱為最小二乘配置法[于宗 壽、魯林成,1982]。

不同於傳統的平差法，最小二乘配置法是一種結合最小二乘法（未知 參數的估計）、預估（計算任一點的信號 s）與濾波（雜訊 n 的移除）三種 作用的方法，傳統的測量平差法僅能處理觀測量含有純粹的偶然誤差，而 最小二乘配置法不但將之擴大到能處理觀測量含有相關性的誤差以外且還 能估計出未做觀測之處應有之觀測值，其函數模型為

n s Ax+ +

l= (3.3) 式中 x 為未知參數，s 為信號矩陣，n 為雜訊矩陣，l 為觀測量矩陣，A 為設計矩陣，若將 s 和 n 合併在一起估計即成為一個隨機量

v = s + n

l-v=Ax (3.5) 第(3.3)式中僅有觀測量的地方估計該觀測量的信號，但對於沒有觀測 量的地方，其相對應的信號也希望能被估計出來，因此廣義的最小二乘配 置法還包括內插，也就是利用信號間所存在的相關性以內插方法求出沒有 觀測量處之信號，故第(3.3)式可改為

n S B x

A

+ +

l =

上式中共有 q 個觀測量，P 個未知參數，欲內插的信號共 r 個（q+r=m）， 且

⎥⎦⎤

⎢⎣⎡

=

I 0

r

* q

*q q

,

B (3.7)

⎥⎥

⎦

⎤

⎢⎢

⎣

= ⎡

t s

1

* r

1

*

S q (3.8)

信號向量 S 包含觀測處的信號向量 s 和無觀測處的信號向量 t。

解算(3.6)式時，必須先假設兩個基本條件：

（1）v、s、t 和 n 的期望值為零；

（2）信號和雜訊獨立不相關，即

Σ

= Σ

= 0

ss nn

vv

= Σ + Σ

Σ

⎥ ⎦

⎢ ⎤

⎣

⎡

Σ Σ

Σ

= Σ Σ

tt ts

st ss

SS (3.10) 第(3.6)式基本上是條件帶未知數的平差模式，由最小二乘原理可得

min )

- n BS (Ax 2k - n n S

S^TΣ_SS^-1 + ^TΣ^-1_nn ^T + + =>

=

Φ l (3.11)

由上式可得法方程式

⎪⎩

⎪⎨

⎧

=

= Σ

= Σ

0 Aˆ k

0 kˆ ˆ -

0 B kˆ ˆ -

T T 1 - nn

T -1 SS T T

n S

(3.12)

解此法方程式可得[黃華尉,2001]

⎪⎪

⎩

⎪⎪⎨

⎧

Σ + Σ Σ

=

Σ +

⎥ Σ

⎦

⎢ ⎤

⎣

⎡ Σ

= Σ

⎥⎦

⎢ ⎤

⎣

=⎡

Σ + Σ Σ

+ Σ

=

) xˆ A - ( ) (

nˆ

) xˆ A - ( ) t (

Sˆ s

) (

A A) ) (

(A xˆ

1 - nn SS nn

1 - nn SS ts SS

-1 nn SS T -1 -1 nn SS T

l l

l

(3.13)

其中k為Lagrange聯繫數， Σ 為觀測量協變方矩陣，_nn Σ 、_ss Σ 和_st Σ 為隨機_tt 變數s和t的協變方矩陣，可從協變方函數推導而得。協變函數是一個表示 共同點與共同點間、共同點與非共同點間相關關係的函數，它可以用來計 算訊號間的相關關係。在最小二乘配置法實際應用上，可假定點位間的相 關性僅和點位間的距離有關，也就是說協變函數為一個與方向無關，同時 也和點的絕對位置無關的函數C(d) 。最常用者為高斯鐘形曲線函數

C(d)=C₂exp(−C₁d²) (3.14) 式中d 表示點位間的距離，C1、C2 為高斯鐘形曲線函數的兩個參數。

協變函數可由實際的觀測數據估計得到或事先給定之，也可以雜訊佔 歸心參考值的比例求之。

把最小二乘配置法運用於 TWD67 坐標與 TWD97 坐標之轉換，則 l 就是 TWD97 坐標值，待定參數 x 就是兩個坐標系統間之轉換參數，s 相當於系統 性誤差，可能是由於控制網形張力問題、地殼變動、投影變形以致點位位 移等問題造成，n 相當於偶然誤差，純粹由各觀測量經平差計算後產生的殘 差。

若兩組平面直角坐標系統(N,E)和(

N

E

d aE bN E

c bE aN N

+ +

−

′ =

+ +

′ =

(3.15) 式中 a、b、c、d 為轉換參數，若以六參數轉換則為：

f eE dN E

c bE aN N

+ +

′=

+ +

′=

(3.16) 式中 a、b、c、d、e、f 為轉換參數，若將(3.15)、(3.16)以(3.6)式表示 可得：

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥

⎦

⎤

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢

⎣

⎡

′

′

′

′

=

n n

E N E N

M l M

1 1

，

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

⎤

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

⎡

=

1 0 N - E

0 1 E N

1 0 N - E

0 1 E N

q q

q q

1 1

1 1

L L

L

A L

⎥⎥

⎥⎥

⎦

⎤

⎢⎢

⎢⎢

⎣

⎡

= d c b a

x (3.17)

或

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥

⎦

⎤

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢

⎣

⎡

′

′

′

′

=

n n

E N E N

M l M

1 1

，

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎦

⎤

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎣

⎡

=

1 0 E N 0 0

0 1 0 0 E N

...

...

...

...

1 0 E N 0 0

0 1 0 0 E N

q q q q

1 1 1 1

A ，

⎥⎥

⎥⎥

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢⎢

⎢⎢

⎢

⎣

⎡

=

f e d c b a

x (3.18)

由於點位坐標本身包含的誤差而產生的信號與雜訊，測量上兩坐標系統 間坐標轉換關係即可組成(3.3)式，並求出轉換參數，信號 s 與雜訊 n 也可 在計算中同時被估計出來，因此可藉由此關係將某些點位轉換至另一坐標 系統。

第四章 實驗與分析

為瞭解地籍資料不同坐標系統之間轉換模式精度，本研究以實驗區周 圍之四等控制點為共同點，採最小二乘配置法結合六參數轉換進行坐標轉 換，並以實驗區內之圖根點當作檢核點，並分析轉換後界址點的精度是否 符合地籍測量的作業規範。

4-1 實驗方法

本實驗的作業流程包括規劃準備、選定作業區、資料整理、共同點之 改算、獲得轉換參數、坐標轉換及分析、成果檢查及成果整理等步驟，本 實驗作業流程如圖 4-1，各項作業內容分敘如下：

表 4-1 各項作業內容

工 作 項 目 作 業 內 容 說 明

1.規劃準備 作業準備、資料收集

2.選定作業區 選定合適之區域當做實驗區

3.資料整理 整理原始觀測資料

4.共同點之改算 以實驗區外圍之四等控制點為共

同點進行坐標轉換

5.獲得轉換參數 獲得實驗區內一組最佳轉換參數

6.坐標轉換及分析 以同一組轉換參數進行圖根點、

界址點、都市計劃樁坐標轉換

7.成果檢查 以原始觀測資料重新計算測區圖

根點(TWD97)為檢核點，檢核轉換 後坐標之精度

8.成果整理 成果整理

圖 4-1 坐標轉換作業流程圖

4-1-1 實驗區的選擇

對於小區域而言，TWD67 與 TWD97 坐標系統可視為兩個平面，透過平面 坐標轉換模式，可將兩種坐標系統進行互換，因此本次研究採用宜蘭縣壯 圍鄉 90 年度上半年度壯圍重測區，範圍位置如圖 4-2 紅色範圍所示，重測 後分成吉祥一段、吉祥二段，以圖上藍色線為分界，重測區採數值法辦理，

坐標系統為 TWD67，選擇本實驗區係因該區為數值重測區，因此進行坐標系 統轉換時，無須考量圖紙伸縮變形之問題，且又保留當年重測時所進行之 控制測量原始資料，可供重新解算該區控制點之 TWD97 坐標，可用來分析 坐標轉換模式成果之精度。

圖 4-2 實驗區範圍示意圖

吉祥一段

吉祥二段

本實驗所需用到的資料有地籍圖、基本控制點資料、都市計畫樁位、

航測地形圖等，資料格式如表 4-2：

表 4-2 實驗區資料一覽表

資料種類 坐標系統 資料描述

地籍圖資料 TWD67 90 年上半年度宜蘭縣政府辦理 之地籍圖重測區，資料格式為 內政部土地測量局所開發之重 測系統格式。

都市計畫圖 TWD67 實驗區內計 175 個樁位。

TWD67 1. 已知基本控制點計 21 點。

2. 重測區圖根點 125 點。

已知基本控制點

TWD97 已知基本控制點計 4 點。

航測地形圖 TWD97 由宜蘭縣政府提供 1/1000 航測 地形圖，資料格式為 DWG 檔。

4-1-2 共同點資料的預處理

在進行坐標轉換時，須至少有三個點位同時具有 TWD97 及 TWD67 坐標，

以決定兩個坐標系統之間的轉換參數(6 參數)，這些同時具備二組坐標系統 之點位稱為共同點，因此進行坐標轉換時，需先清查測區附近之共同點，

做為坐標轉換之依據，一般常用之共同點有基本控制點、圖根點、都市計 畫樁等。

坐標轉換中所使用之共同點，倘存在某共同點誤差較大或錯誤，勢必 影響求得轉換參數之正確性，導致轉換後界址點坐標發生偏差，因此坐標 轉換作業時常使用多於轉換函數模式所需之最低共同點數，再以平差方法 求解，並將初步轉換結果中改正數較大之共同點剔除，再行作業。

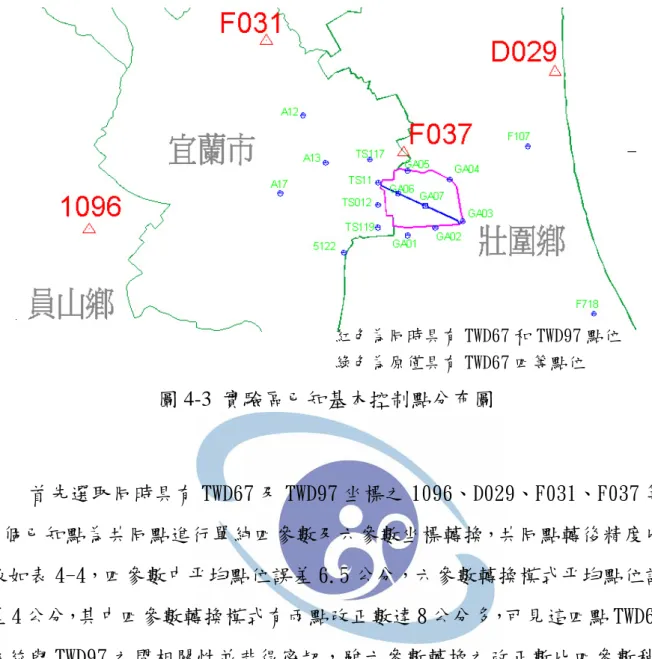
本實驗區經清查後 TWD67 系統之基本控制點有內政部二等衛星控制點 5 點、83 年度宜蘭縣宜蘭測區精密導線點 3 點及 90 年度宜蘭縣壯圍縣辦重測 區四等控制點 13 等，計 21 點，TWD97 系統之點位有 4 點，圖 4-3 為基本控 制點位分布圖，圖中紅色線為實驗區，綠色線為行政區界，點號明細表表 如表 4-3。

表 4-3 實驗區基本控制點點號明細表

坐標系統 TWD67 TWD97

點號 1096、5122、A12、A13、A17、D029、

F031、F037、F107、F718、GA01、

GA02、GA03、GA04、GA05、GA06、

GA07、TS012、TS11、TS117、TS119

1096（N496）、D029

（N629）、F031（N431）

（N431）、F037（N537）

小計 21 4

圖 4-3 實驗區已知基本控制點分布圖

首先選取同時具有 TWD67 及 TWD97 坐標之 1096、D029、F031、F037 等 4 個已知點為共同點進行單純四參數及六參數坐標轉換，共同點轉後精度比 較如表 4-4，四參數中平均點位誤差 6.5 公分，六參數轉換模式平均點位誤 差 4 公分，其中四參數轉換模式有兩點改正數達 8 公分多，可見這四點 TWD67 系統與 TWD97 之間相關性並非很密切，雖六參數轉換之改正數比四參數稍 好，惟自由度僅有 2 個，改正數仍過大，且共同點距重測區之距離也過長，

對本實驗而言這 4 個共同點精度似乎不足。

紅色為同時具有 TWD67 和 TWD97 點位 綠色為原僅具有 TWD67 四等點位

表 4-4 四個共同點坐標轉換精度分析

四參數 六參數

點號

VN VE 點位誤差 VN VE 點位誤差

1096 0.045 -0.043 0.062 -0.008 0.030 0.031

D029 0.026 -0.016 0.030 -0.013 0.048 0.050

F031 0.008 0.084 0.085 0.004 -0.016 0.016

F037 -0.078 -0.024 0.082 0.016 -0.062 0.064

平均 0.065 0.040

一般而言，坐標轉換最好有至少三個以上已知控制點分佈在測區外圍 的，由上可知 1096、D029、F031、F037 顯然無法達到我們的要求，為增進 坐標轉換精度，捨棄 1096、D029、F031、F037 等四點為共同點之作法，另 以均勻分布重測區外圍之四等控制點 GA01~GA07、TS011、TS012 及 TS119 等點位為共同點，此 10 個點位分佈圖如圖 4-4。為獲得該 10 個點位之 TWD97 坐標，吾人利用 90 年度上半年度重測區之四等控制點外業觀測之 GPS 觀測 量，將當時計算完成之基線解重新於 TWD97 之基準下進行網形平差，並強 制附合至 1096、D029、F031、F037 等 4 點上。

圖 4-4 測區與鄰近 10 點四等點位分佈位置圖

基線計算軟體為 GPSURVEY 2.35 版，嚴密網形平差軟體為 GPSURVEY 2.35 提供之 TRIMNET 模組，GPS 成果計算程序主要可分為基線計算、最小約制網 形平差計算及強制附合網形平差計算等三項。基線計算所用之相關參數設 定分述如下：

1.採用廣播星曆。

2.採用 Hopfield 模式來改正對流層遲滯效應。

3.資料篩選臨界值(Edit 值)設定為 3.0。

4.比率檢驗值(Ratio 值)設定最小為 3.0。

GPS 基線網形係先以自由網最小二乘法模式進行最小自由網網形平差 計算偵錯，經以自由網最小約制平差檢核控制網系內所有衛星測量基線求 解無誤後，最後再以 TRIMNET 進行網形強制套合約制平差，以求得控制測 量坐標成果，基線成果比較表如附表 D。

四等控制點 GA01~GA07、TS011、TS012 及 TS119 等點位經過四參數及 六參數轉換後其共同點之改正數已大大改善，故本實驗決定改採該 10 個點 位當坐標轉換之共同點，其圖根點資料處理流程如圖 4-5 所示，相關精度 分析另於下節描述。

圖 4-5 　 圖根點資料處理流程圖

4-2 成果分析

本實驗採用單純四參數、六參數及四參數、六參數結合最小二乘配置 法等四種轉換模式進行界址點、圖根點及都計樁之 TWD67 與 TWD97 坐標系 統之間轉換：

‹ 轉換模式:

(1)四參數 (2)六參數

(3)四參數+最小二乘配置法 (4)六參數+最小二乘配置法

‹ 待轉換資料：

(1)圖根點 (2)界址點

(3)都市計畫樁位

4-2-1 共同點之精度分析

本作業共同點選擇以重測時均勻分佈於測區外圍之四等控制點為主，

並採用 GA01~GA07、TS011、TS012 及 TS119 為共同點進行四參數及六參數 轉換，計算完之坐標轉換參數如下：

（一）四參數轉換參數：

區域中心座標：N0= 2737880.9179 E0= 328946.0711 E(X) = A * (E - E0) + B * (N - N0) + C

N(Y) =- B * (E - E0) + A * (N - N0) + D A= 1.00002890539757

C= 329777.4735 D= 2737676.2999

OFFSET E(X)=831.402 N(Y)=-204.618

旋轉 : - 0 度 00 分 03.8068 秒 (順正逆負) Scale : 1.00002890556789

DEGREE OF FREEDOM = 16

STANDARD ERROR = .018 [M]

（二）六參數轉換參數：

區域中心座標：N0= 2737880.9179 E0= 328946.0711 E = A * (E - E0) + B * (N - N0) + E

N = C * (E - E0) + D * (N - N0) + F A= 1.00002335070082

B= 6.27018690830682E-07 C= 3.10209729948223E-05 D= 1.00004494150684 E= 329777.4735

F= 2737676.2999

DEGREE OF FREEDOM = 14

STANDARD ERROR = .012 [M]

經轉換後發現四參數轉換模式共同點之點位誤差最小 0.4cm，最大為 4.5cm，平均點位誤差為 1.8cm，六參數轉換模式共同點之點位誤差最小 0.4cm，最大為 2.9cm，平均點位誤差為 1.2cm，六參數轉換共同點平均誤 差小於四參數轉換，但差異不大，但由四參數轉換模式改正數最大之點位

誤差 TS011 點位誤差 4.5cm，但其六參數轉換模式中其點位誤差已降至 2.9cm，顯見本實驗中六參數轉換模式較四參數轉換模式之成果好，其轉換 後各共同點之改正數如表 4-5。

表 4-5 10 個共同點坐標轉換精度分析

四參數 六參數

點號 V^N V^E 點位誤差 V^N V^E 點位誤差 GA01 0.008 0.012 0.015 -0.007 -0.003 0.008 GA02 0.007 0.006 0.009 -0.004 -0.004 0.006 GA03 0.009 0.009 0.012 0.008 -0.004 0.009 GA04 -0.001 -0.004 0.004 0.006 0.004 0.007 GA05 -0.003 -0.016 0.016 -0.013 0.011 0.017 GA06 0.000 -0.013 0.013 -0.02 0.005 0.021 GA07 -0.001 0.008 0.008 0.003 -0.003 0.004 TS011 -0.031 0.032 0.045 0.022 -0.019 0.029 TS012 -0.008 0.019 0.020 0.002 -0.004 0.004 TS119 0.023 0.025 0.034 0.002 0.018 0.018

平均 ^{0.018 0.012}

上節中以 1096、D029、F031、F037 等四點為共同點，經四參數轉換後，

共同點之平均誤差為 6.5m，六參數轉換之共同點平均誤差為 4.0cm，改成 以 GA01~GA07、TS011、TS012 及 TS119 等 10 點為共同點後，經四參數轉換 後，共同點之平均誤差降為 1.8cm，六參數轉換之共同點平均誤差降為 1.2cm，可知以這 10 個四等控制點為共同點之精度遠比上節中 1096、D029、

F031、F037 等四點佳，故以下實驗將以這 10 點為共同點進行坐標轉換後獲 得之轉換參數，據以轉換其他圖籍之坐標。

4-2-2 檢核點(圖根點)之精度分析

圖根測量係依據基本控制點之成果，在測區內佈設點位間距較短之次 級控制點，作為界址測量之依據，基於各宗地界址點與圖根點關係密切，

且本實驗區圖根點原始觀測紀錄保存良好，因此本實驗以圖根點為坐標轉

換之檢核點，用以探討轉換後地籍圖資料之精度。

本實驗區之圖根點計有 125 點，包括幹導點 78 點、支導點 47 點，引 用之精密導線點有 GA01~GA07、TS011、TS012 及 TS119 共 10 點，圖根點位 分布圖如圖 4-6 所示，125 個點位 TWD97 坐標係利用當年原始觀測資料，先 採單導線計算結成網狀，再利用三角三邊程式實施整體平差重新計算以獲 得圖根點 TWD97 坐標，並與單純四、六參數及最小二乘配置法結合四、六 參數等四種轉換模式之坐標進行比較。

圖 4-6 實驗區圖根點網絡圖

4 種模式坐標轉換之坐標與經三角三邊嚴密平差後獲得之 TWD97 坐標之 較差整理如附表 A，針對 125 個圖根點進行檢核，精度分析如下：

單純四參數轉換成果中 N 向量大於 2 公分的有 7 點，1~2 公分有 32 點，

小於 1 公分有 86 點，占所有點數 68.8%；E 向量大於 2 公分的有 5 點，1~2 公分有 30 點，小於 1 公分有 85 點，占所有點數 68%；N 方向改正數最大 2.4 公分、最小-1.3 公分，改正數變化範圍在 3.8 公分以內，E 方向改正數最

大 1.8 公分、最小-3.1 公分，改正數變化範圍在 4.9 公分以內，最大點位 誤差為 3.9 公分，平均點位位誤差為 1.1 公分，125 個圖根點 N、E 向量改 正數大小分佈圖如圖 4-7。

圖 4-7 四參數轉換 N、E 向量改正數大小分佈圖

單純六參數轉換成果中 N 向量大於 2 公分的有 5 點，1~2 公分有 28 點，

小於 1 公分有 87 點，占所有點數 69.6%；E 向量大於 2 公分的有 0 點，1~2 公分有 26 點，小於 1 公分有 99 點，占所有點數 79.2%；N 方向改正數最大 2.8 公分、最小-2 公分，改正數變化範圍在 4.8 公分以內，E 方向改正數最 大 1.6 公分、最小-1.8 公分，改正數變化範圍在 3.4 公分以內，最大點位 誤差為 2.8 公分，平均點位位誤差為 1.1 公分，125 個圖根點 N、E 向量改 正數大小分佈圖如圖 4-8。

圖 4-8 六參數轉換 N、E 向量改正數大小分佈圖

以最小二乘配置法結合四參數進行坐標轉換，轉換成果中 N 向量大於 2 公分的有 3 點，1~2 公分有 11 點，小於 1 公分有 111 點，占所有點數 88.8%；

E 向量大於 2 公分的有 0 點，1~2 公分有 10 點，小於 1 公分有 115 點，占 所有點數 92%；N 方向改正數最大 2.6 公分、最小-1.1 公分，改正數變化範 圍在 3.7 公分以內，E 方向改正數最大 1.6 公分、最小-1.2 公分，改正數 變化範圍在 2.8 公分以內，最大點位誤差為 2.7 公分，平均點位位誤差為 0.7 公分，125 個圖根點 N、E 向量改正數大小分佈圖如圖 4-9。

圖 4-9 最小二乘配置法+四參數轉換 N、E 向量改正數大小分佈圖

以最小二乘配置法結合六參數轉換成果中 N 向量大於 2 公分的有 3 點，

1~2 公分有 11 點，小於 1 公分有 111 點，占所有點數 88.8%；E 向量大於 2 公分的有 0 點，1~2 公分有 10 點，小於 1 公分有 115 點，占所有點數 92%；

N 方向改正數最大 2.6 公分、最小-1 公分，改正數變化範圍在 3.6 公分以 內，E 方向改正數最大 1.6 公分、最小-1.1 公分，改正數變化範圍在 2.7 公分以內，最大點位誤差為 2.7 公分，平均點位位誤差為 0.7 公分，125 個 圖根點 N、E 向量改正數大小分佈圖如圖 4-10。

圖 4-10 最小二乘配置法+六參數轉換 N、E 向量改正數大小分佈圖

將 4 種轉換模式之點位誤差大小分佈及精度分析整理如圖 4-11 及表 4-6，單純四、六參數轉換 N、E 向量之改正數變化範圍均在 5 公分以內，

四參數轉換點位誤差最大的為 3.9 公分，六參數轉換點位誤差最大的為 2.8 公分，平均點位誤差均為 1.1 公分；以最小二乘配置法結合四、六參數 N、

E 向量之改正數變化範圍均在 4 公分以內，點位誤差最大均為 2.7 公分，平 均點位誤差均為 0.7 公分。

另比較誤差在 2 公分以內之點位個數，單純四參數轉換中有 3 個點位

（B22、B23、B29）大於 3 公分，12 個點位誤差大於 2 公分（B20、B21、B21-1、

B28、B48、B51、B52、B53、B61、H26、H27、H31），110 個點位誤差小於 2 公分，佔所有點數 88％；單純六參數轉換中有 7 個點位（B29、B36、B48、

B49、B50、B51、B54）誤差大於 2 公分，118 個點位誤差小於 2 公分，佔所 有點數 94.4％；以最小二乘配置法結合四、六參數轉換中均僅有 3 個點位

（B47、B48、B49）誤差大於 2 公分，122 個點位誤差小於 2 公分，佔所有 點數 97.6％；可見以最小二乘配置法結合四參數或六參數兩種模式進行坐

標轉換，於 125 個圖根點精度沒有明顯的差異，且較單純四、六參數轉換 模式好。

圖 4-11 圖根點位誤差大小分佈圖 表 4-6 各種轉換精度分析表

N 向量改正數 E 向量改正數 點位誤差

轉換模式

最大值 最小值 範圍 最大值 最小值 範圍 最大值 最小值 平均值 (1)四參

數轉換坐 標

0.024 -0.013 0.038 0.018 -0.031 0.049 0.039 0.001 0.011 (2)六參

數轉換坐 標

0.028 -0.020 0.048 0.016 -0.018 0.034 0.028 0.002 0.011 (3)四參

數轉換坐 標+最小 二乘配置 法

0.026 -0.011 0.037 0.016 -0.012 0.028 0.027 0.001 0.007

(4)六參 數轉換坐 標+最小 二乘配置 法

0.026 -0.010 0.036 0.016 -0.011 0.027 0.027 0.000 0.007

由以上數據發現誤差最大之點位為 B47、B48、B49，該點位係由 B14 導

線計算得到，該導線內容如下，導線總邊長 1597.848 公尺，距離閉合差 0.063 公尺，導線點數計有 9 點，為所有導線長度最長、點數最多，點與點之間 的距離有些已拉到 200 多公尺，且又無多餘觀測，可能因此造成誤差累積 在導線中間的 3 點上。

從以上分析可知採用四等控制點為共同點，利用最小二乘配置法進行 地籍資料之坐標轉換，並以實驗區內 125 個圖根點檢核，轉換後之平均點 位誤差為 0.7 公分，97.6％之點數誤差小於 2 公分，應可符合地籍測量實 施規則之要求。

導 線 名 稱 ： B14

點 號 水平角 方位角 距 離 縱 座 標 橫 座 標 平差後方位角 平差後距離 點 號

(B24 ) 2738562.239 328845.928 (B24 ) 16 55 58 16 55 58

B33 71 32 10 -3 2738372.261 328788.090 B33 88 28 5 273.093 10 -3 88 27 57 273.090

B45 181 36 5 -3 2738379.572 329061.082 B45 90 4 7 144.591 5 -2 90 3 59 144.589

B46 183 35 58 -3 2738379.404 329205.672 B46 93 40 2 133.363 5 -2 93 39 54 133.361

B47 173 43 9 -3 2738370.879 329338.760 B47 87 23 8 180.080 7 -2 87 23 0 180.078

B48 230 52 50 -3 2738379.100 329518.651 B48 138 15 55 144.770 5 -2 138 15 52 144.765

B49 202 45 0 -3 2738271.073 329615.020 B49 161 0 52 156.036 6 -2 161 0 52 156.030

B50 182 5 42 -3 2738123.531 329665.781 B50 163 6 31 159.556 6 -2 163 6 31 159.550

B51 177 48 56 -3 2737970.865 329712.140 B51 160 55 24 154.987 6 -2 160 55 24 154.981

B52 180 39 10 -4 2737824.395 329762.793 B52 161 34 30 96.276 4 -1 161 34 30 96.272

B53 182 33 56 -3 2737733.058 329793.221 B53 164 8 23 155.096 6 -2 164 8 23 155.090

B44 128 10 32 -3 2737583.872 329835.606 B44 112 18 52 112 18 52

(GA03 ) 2737516.898 329998.788 (GA03 )

角 度 閉 合 差 = 34. 秒

導 線 總 邊 長 = 1597.848

距 離 閉 合 差 = .063 縱 距 閉 合 差 = -.060 橫 距 閉 合 差 = 018

位 置 閉 合 差 = 1/ 25562.

4-2-3 界址點精度分析

由以上圖根點精度分析可知，本實驗區以最小二乘配置法較單純利用 四六參數進行坐標轉換之精度好，且最小二乘配置法結合四參數或六參數 轉換模式精度無明顯差異，因此本實驗以實驗區外圍之 10 個四等控制點為 共同點，採用最小二乘配置法結合六參數轉換模式進行坐標轉換，獲得一 組轉換參數後，再以同一組轉換參數將實驗區之界址點一併進行坐標轉 換，以獲得實驗區內 3,546 個界址點 TWD97 坐標。界址點資料處理流程如 圖 4-12。

圖 4-12 界址點資料處理流程圖

基於各宗地界址點與圖根點關係密切，因此本實驗藉比較 TWD67 與 TWD97 兩坐標系統之圖根點與界址點間之水平夾角與水平距離等協助指界 資料，作為檢核轉換後界址點坐標之精度，本實驗隨機取樣測區 5 個圖根 點，界址點位置如圖 4-13。每個圖根點各放樣 10 個界址點，計有 50 個界 址點，其 TWD67 坐標系統與 TWD97 之協助指界資料比較如附表 B，並將 50 個界址點之精度分析整理如表 4-7。

5 個測站中以 H21 測站所放樣之界址點與原 TWD67 系統之較差最大，10 個放樣點誤差均大於 1 公分，最大之界址點誤差達 1.3 公分，其他四個站 之誤差均小於 1 公分，平均點位誤差為 0.5 公分。

圖 4-13 抽樣圖根點測站位置圖

表 4-7 界址點誤差分析表(取絕對值)

角度誤差(秒) 距離誤差(公分) 點位誤差(公分)

測站 標定點

最大 最小 最大 最小 最大 最小 平均

B45 H9 21 0 0.5 0 0.5 0.1 0.3

H21 H20 141 43 1.1 0.3 1.3 1.1 1.2

B32 B31 90 5 0.3 0.0 0.4 0.2 0.3

B44 B7 14 1 0.5 0.2 0.7 0.2 0.4

B47 B48 11 0 0.7 0 0.7 0.1 0.4

平均 0.5

依據地籍測量實施規則圖根點與界址點之位置誤差相關規定，本實驗取 樣之 50 個界址點中誤差最大者為 1.3 公分，尚符合第 247 條第 1 款 0.005 公尺√S ＋0.04 公尺及第 73 條第 1 款標準誤差 2 公分之規定，顯示本實驗 採用之坐標轉換模式所得到界址點 TWD97 坐標系統，均符合複丈之相關精 度規範，可視為無誤差。

第 73 條 戶地測量採數值法測繪者，其圖根點至界址點之位置誤差不 得超過下列限制：

一 市地：標準誤差二公分，最大誤差六公分。

二 農地：標準誤差七公分，最大誤差二十公分。

三 山地：標準誤差十五公分，最大誤差四十五公分。

第 247 條 複丈應以圖根點或界址點作為依據，並應先檢測圖根點及界址 點，所測得點位間之距離與由坐標反算之距離，其差不得超過下列限制：

一 市地：0.005 公尺√S ＋0.04 公尺 (S 係邊長，以公尺為單位) 。 二 農地：0.01 公尺√S ＋0.08 公尺。

三 山地：0.02 公尺√S ＋0.08 公尺。

前項之檢測應由縱橫二方向實施之。

4-2-4 地籍圖宗地邊長及面積精度分析

經坐標轉換後除界址點是否位移之問題受到矚目外，轉換後之宗地是 否變形？面積是否有增減？亦是民眾所關心的重大問題，因此除了以上以 圖根點、界址點當檢核點外，本節比較了轉換前 TWD67 及轉換後地籍圖之 每筆宗地邊長及面積之增減，探討是否可符合地籍測量的作業規範。

本實驗區有吉祥一段及吉祥二段，以吉祥一段為地籍測試區，其段代 碼 GB0541，範圍約 2km X 1km 大小之區域，計有 1479 筆宗地，面積為總計 為 98.864408 公頃，其宗地之邊長數總計有 4948 條。

轉後前總邊長為 110542.284 公尺，經最小二乘配置法坐標轉換後總邊 長為 110546.254 公尺，總邊長增加 3.07 公尺，平均每段邊長增加 0.001 公尺，增減最大值為 0.027 公尺，最小值為-0.001 公尺， 99.66%邊長增減 在 1 公分以內，1~2 公分者有 12 段，大於 2 公分者有 5 段。

另依據地籍測量實施規則第 74 條規定，界址點間坐標計算邊長與實測 邊長之差於市地不得超過 2 公分＋0.3 公分√S (S 係邊長，以公尺為單 位)，本實驗區計有 5 段超過 2 公分，分析其原因，發現該 5 段邊長皆大於 700 公尺，尚符合 2 公分＋0.3 公分√S 之標準，惟一筆宗地之邊長有 700 公尺似乎不合理，經查確有該筆宗地存在，地號為 164，界址點數有 49 個，

登記面積 464 平方公尺，為狹長之道路用地地號，詳見圖 4-14 地籍邊長面 積誤差較大分佈位置圖。建議地政機關於地籍整理時可將諸類狹長宗地逕 行分割成較小之宗地，除較好管理外，也可減少複丈時因長距離所造成之 誤差。邊長增減分析及邊長大於 5 公分之彙整表如表 4-8、4-9。

圖 4-14 　 邊長誤差較大位置圖

第 74 條戶地測量採數值法測繪者，其界址點間坐標計算邊長與實測邊長之 差不得超過下列限制：

一 市地：2 公分＋0.3 公分√S (S 係邊長，以公尺為單位) 二 農地：4 公分＋1 公分√S

三 山地：8 公分＋2 公分√S

表 4-8 邊長增減分析比較表

TWD67 總邊長 110542.284m 誤差大小(公分) 邊長數量 百分比

TWD97 總邊長 110546.254m -1~0 50 1.01%

總邊長增減 3.97m 0~1 4881 98.65%

平均增減 0.001m 1~2 12 0.24%

最大值 0.027m >2 5 0.10%

最小值 -0.001 合計 4948 100.00%

表 4-9 邊長較差大於 2 公分明細表 紅色為誤差較大的邊長

起始界址點號 結束界址點號 TWD67 邊長 TWD97 邊長 較差(公尺) 百分比 1241 1915 731.941 731.962 0.021 0.003%

1235 1920 732.194 732.215 0.021 0.003%

1714 4839 725.632 725.659 0.027 0.004%

1499 4841 723.703 723.73 0.027 0.004%

1320 4806 721.088 721.115 0.027 0.004%

本實驗區計有 1479 筆宗地經最小二乘配置法坐標轉換後，重新計算每 一筆宗地面積，TWD97 坐標系統之總面積 988716.81 平方公尺，較原 TWD67 坐標系統 988644.08 平方公尺增加 72.73 平方公尺，面積增加最多之比率 為 0.228％，減少最多的為 0.685％，平均每筆面積增加 0.007%，宗地面積 增加最大者為 1.23 平方公尺，減少最多的為 0.15 平方公尺，面積增減均 在 0.1%內，占總筆數的 99.6%，面積增減百分比筆數分佈及增減百分比及 增減大小範圍表如表 4-10、4-11；因宗地筆數眾多，無法詳列每一筆宗地 面積變化情形，僅列出其餘 6 筆面積增減較大之資料，發現面積增減百分 比較大之宗地皆屬較小面積之宗地，且其面積增減大小皆為 0.01 平方公 尺，該微小之面積增減量因宗地面積小使其面積增減百分比之量級較其他 宗地來的大，該 6 筆宗地資料如表 4-12。

依據地籍測量實施規則第 243 條對於土地分割面積之限制應符合 F

F ) 02 . 0 10 . 0

( + ⁴ (F 為一筆土地之宗地面積，以平方公尺為單位)之規範，

本實驗區經坐標轉換後之面積皆符合上開規定，即利用轉換後坐標進行土 地分割時，並無與原登記面積差異過大需進行面積配賦問題。

表 4-10 宗地面積增減百分比筆數分佈表 面積增減

百分比(%)

>0.2 0.1 ~0.2 0~0.1 -0.1~0 -0.7~-0.6 合計

筆數 1 4 1024 449 1 1479

比率 0.07% 0.27% 69.24% 30.36% 0.07% 100%

表 4-11 宗地面積增減百分比及增減大小範圍表

範 圍 最大值 最小值 平均值

面積增減百分比(%) 0.228% -0.685% 0.007%

面積增減大小(平方公尺) 1.230 -0.150 0.049

表 4-12 6 筆宗地面積增減百分比較大之明細表

宗地地號 TWD67 面積

(平方公尺)

TWD97 面積 (平方公尺)

面積較差

(平方公尺) 較差百分比

1289 1.45 1.46 -0.01 -0.6849%

1124 7.16 7.15 0.01 0.1399%

974 6.60 6.59 0.01 0.1517%

614 6.37 6.36 0.01 0.1572%

969 6.16 6.15 0.01 0.1626%

948 4.39 4.38 0.01 0.2283%

第 243 條 分割土地面積之計算，依下列規定辦理：

一、一宗土地分割為數宗土地，該分割後數宗土地面積之總和，須與原土 地面積相符。如有差數，經將圖紙伸縮成數除去後，其增減在下列公式計 算值以下者，應按各地號土地面積比例配賦；在下列公式計算值以上者，

應就原測量及計算作必要之檢核，經檢核無誤後依第二百三十二條規定辦 理。