國 立 交 通 大 學
應用數學系
碩 士 論 文
弦環式網路的邊刪除直徑不變性質
The Diameter-edge-invariant Property
of Chordal Ring Networks
研 究 生:黃信菖
指導教授:陳秋媛 教授
弦環式網路的邊刪除直徑不變性質
The Diameter-edge-invariant Property
of Chordal Ring Networks
研 究 生:黃信菖 Student: Hsin-Chang Huang
指導教授:陳秋媛
Advisor: Chiuyuan Chen
國 立 交 通 大 學
應 用 數 學 系
碩 士 論 文
A Thesis
Submitted to Department of Applied Mathematics
College of Science
National Chiao Tung University
in Partial Fulfillment of the Requirements
for the Degree of
Master
in
Applied Mathematics
January 2009
Hsinchu, Taiwan, Republic of China
弦環式網路的邊刪除直徑不變性質
研究生:黃信菖
指導老師:陳秋媛 教授
國 立 交 通 大 學
應 用 數 學 系
摘 要
環狀網路是最簡單的網路架構,然而,環狀網路的可靠度低、傳輸延遲高,因此, 以環狀網路為基礎的混合式環狀網路相繼被提出,以提高其可靠度與降低傳輸延 遲。Arden 和 Lee [1]在 1981 年提出了以環狀網路延伸而成的弦環式網路。弦環 式網路是在環狀網路的結構中增加弦,使得其可靠度提高、直徑降低。更具體的 來說,一個弦環式網路CR N w 具有( , ) N個點(N為偶數,點的編號為0至N−1) 與3N 2條邊,邊的連線方式為: i 連至(i+1)modN,∀ =i 0,1,…,N−1,及 i 連至(i+w)modN,∀ =i 1,3,…,N−1, 其中w為不大於N 2的奇數。弦環式網路為 3-正則圖,它與環狀網路一樣具有漢 彌爾頓圈,而且比環狀網路擁有更好的直徑。在 1987 年,Lee 和 Tanoto [14 , 15] 提 出 了 邊 刪 除 直 徑 不 變 圖 的 概 念 。 令 D(G)為 圖G 的 直 徑 。 一 個 圖G 為 diameter-edge-invariant 若它滿足D(G−e)=D(G),∀e∈E(G)。本篇論文之目的 在於研究弦環式網路CR N w 的邊刪除直徑不變性質,特別是在( , ) w∈{3,5, 7, 9} 時,我們判斷出所有的CR N w 是否為邊刪除直徑不變圖。 ( , ) 關鍵詞:環狀網路、弦環式網路、連接網路、直徑、邊刪除、正則圖。 中 華 民 國 九 十 八 年 一 月The Diameter-edge-invariant Property
of Chordal Ring Networks
Student: Hsin-Chang Huang
Advisor: Chiuyuan Chen
Department of Applied Mathematics National Chiao Tung University
Hsinchu, Taiwan 30050
Abstract
One of the simplest topologies for interconnection networks is the ring network. However, the ring network has poor reliability (any failure in a node or link destroys the function of the network) and it has high transmission delay (large diameter). As a result, hybrid topologies utilizing the ring network as a basis for synthesizing richer interconnection schemes have been proposed to improve the reliability and reduce the transmission delay. The chordal ring network, proposed by Arden and Lee [1] in 1981, is a commonly used extension for the ring network. The chordal ring network is considered to be obtained by adding chords to a cycle (a ring network) so that the diameter can be reduced and the reliability can be increased. More specifically, a chordal ring network CR(N, w), where N is a positive even integer and w is a positive odd integer such that w ≤ N/2, is a graph with N nodes 0, 1, . . . , N − 1 and 3N/2 links of the form:
(i, (i + 1) mod N ), i = 0, 1, 2, . . . , N − 1, (i, (i + w) mod N ), i = 1, 3, 5, . . . , N − 1.
The chordal ring network is 3-regular, preserves the Hamiltonian cycle from the ring network, and has a better diameter than the ring network. In 1987, Lee and Tanoto [14, 15] proposed diameter-edge-invariant graphs. Let D(G) denote the diameter of a graph G. G is diameter-edge-invariant (dei) if D(G − e) = D(G) for all e ∈ E(G). The purpose of this thesis is to study the dei property of chordal ring networks. In particular, we determine if CR(N, w) is dei for all w ∈ {3, 5, 7, 9}.
Keywords: ring network, chordal ring network, interconnection network, di-ameter, edge deletion, regular graph.
誌 謝
時光匆匆、光陰似箭,兩年的碩士生活就在撰寫完論文的同時劃下了句點。 在這過程當中,要感謝許多的人提攜與幫助,才能讓信菖如期的完成學業。首先 必須感謝指導教授陳秋媛老師,除了用心的督促與指導之外,對待學生更是視如 己出、無微不至。在老師辛勤叮嚀論文的進度之下,論文才能夠如期的完成。再 來要感謝兩位口試委員翁志文老師與廖勝強老師的建議與指教,才能使論文的內 容更加豐富。更要感謝教過信菖的每一位師長,讓我獲得了許多學科上的新知。 研究室裡的每一位同窗都將成為日後的回憶,國元學長、鈺傑學長、志文、 子鴻、慧棻、松育、宜君、士慶及碩一的學弟們,謝謝你們這段日子以來對信菖 的照顧,未來的日子裡彼此多珍重。還有許多伴我成長的朋友們,因為有你們, 我才能有今天的成果。 謝謝一位曾經相知相惜的朋友─佩瑾。是你教會了我用輕盈的腳步,滑過生 命中所有猶豫與不確定。 特別感謝我的父母親含辛茹苦地將我拉拔長大。你們是我心目中的太陽,希 望我能成為你們的驕傲。 黃信菖 謹誌于交通大學 2009 年 1 月Contents
Abstract (in Chinese) i
Abstract (in English) ii
Acknowledgement iii
Contents iv
List of Figures v
1 Introduction 1
2 Preliminaries 4
3 Counterexamples for Theorem 3 7
4 The dei property of chordal ring networks 9
4.1 CR(N, w) with w = 3 . . . 11 4.2 CR(N, w) with (N = 2w or 2w + 2) and w ≥ 5 . . . 12 4.3 CR(N, w) with 2w + 4 ≤ N ≤ (w − 5)(w + 1) and w = 9 . . . 13 4.4 CR(N, w) with (w − 5)(w + 1) + 2 ≤ N ≤ (w − 3)(w + 1) . . . 15 4.5 CR(N, w) with N ≥ (w − 3)(w + 1) + 2 . . . 23 5 Concluding remarks 26
List of Figures
1 CR(26, 11): the chordal ring with N = 26 and w = 11. The number inside
parentheses is the distance to node 0. . . 3
2 CR(22, 9) and its associated triangular grid representation. . . 11
3 CR(16, 3). . . 12
4 The graph H = G − e, where G = CR(18, 7) and e = (0, 11). The number inside parentheses is the distance to node 0. . . 15
5 (a) The triangular grid representation and the first shaded area. (b) The second shaded area. . . 16
6 The triangular grid representation of CR(42, 9). . . 16
7 (a) The third shaded area. (b) The fourth shaded area. . . 17
8 Those shaded boundary nodes need additional discussion. . . 18
9 The shaded nodes in (a) are identical; those in (b) are also identical. . . 18
10 The shaded nodes in (a) are identical; those in (b) are also identical. . . 19
11 The shaded nodes in (a) are identical; those in (b) are also identical. . . 19
12 The shaded nodes in (a) are identical; those in (b) are also identical. . . 20
13 The shaded nodes in (a) are identical; those in (b) are also identical. . . 20
14 Those shaded boundary nodes need additional discussion. . . 22
15 The graph H = G − e, where G = CR(16, 5) and e = (0, 1). The number inside parentheses is the distance to node 0. . . 24
1
Introduction
Our graph terminology and notation are standard; see [3] and [21] except as indicated. In this thesis, a graph is always undirected, without multiple edges and loops. For con-venience, vertices of a graph are also called nodes. Let G be a graph with vertex set V (G) and edge set E(G). The distance dG(u, v) between two nodes u, v ∈ V (G) is the
length of a shortest path joining u, v. The eccentricity e(v) of a vertex v ∈ V (G) is the distance between v and a farthest node from v. The diameter D(G) and the radius r(G) of G are the maximum and the minimum eccentricities of all nodes of G, respectively. Let e ∈ E(G) and v ∈ V (G). G − e, G + e and G − v denote the graph obtained by deleting e, adding e, and deleting v, respectively.
Ore [17] first considered graphs G with the property D(G) > D(G+e) for all e 6∈ E(G). Almost at the same time, Glivjak [6] initiated the study of graphs G with the property D(G − e) > D(G) for all e ∈ E(G). G is called diameter-minimal if D(G − e) > D(G) for all e ∈ E(G). A lot of researches have been done on the above two concepts; see [7, 8, 9, 10, 18]. In particular, Glivjak showed that every graph can be embedded as an induced subgraph in a diameter-minimal graph with diameter 2 [6]; thus finding a forbidden subgraph characterization for diameter-minimal graphs becomes impossible.
A network can be modeled by a graph. The diameter of a network represents the maximum transmission delay between two nodes. In general, the failure of a link will increase the diameter of the network. It is therefore an interesting problem to design a network such that the diameter is invariant under any link failure. Based on this idea, in [14], Lee proposed the the definition: A graph G is diameter-edge-invariant (dei) if D(G − e) = D(G) for all e ∈ E(G). For convenience, in this thesis, if G is not dei, then we simply write G is non-dei.
It is clear that there is no dei graphs with diameter 1. It is also clear that if a graph is dei, then it is 2-edge-connected. However, there exists 2-edge-connected graphs that are non-dei; K2 × C3 is an example. In [14], Lee proposed some constructions for dei
prod-uct method and the edge expansion constrprod-uction. Lee also proved that every connected graph is an induced subgraph of a dei graph with diameter ≥ 2. Thus finding a forbidden subgraph characterization for dei graphs becomes impossible. In [15], Lee and Tanoto constructed three classes of planar dei networks: the young tableau graphs, the young tableau graphs with diagonal crossing and the reverse young tableau graph with diagonal crossing. Recently, in [20], Walikar et al. proved that for any two nonnegative integers n and q, where 0 ≤ n ≤ q, there exists a connected graph G having q edges, precisely n of which are diameter-increasing except for some n, q. They proved that every graph can be embedded as an induced subgraph in a diameter-edge-invariant graph. They also provided a characterization for dei graphs that has diameter 2 and a characterization for dei graphs that has radius 1.
The following variations of dei graphs have been discussed in the literatures: critical dei graphs, cocritical dei graphs, radius-edge-invariant graphs, diameter-vertex-invariant graphs and diameter-adding-invariant graphs. More precisely, a graph G is critical dei (resp. cocritical dei) if G is dei and G − v is non-dei (resp. still dei) for all v ∈ V (G); see [16]. A graph G is radius-edge-invariant if r(G − e) = r(G) for all e ∈ E(G); see [5, 20]. A graph G is diameter-vertex-invariant if D(G − v) = D(G) for all v ∈ V (G) and diameter-adding-invariantif D(G + e) = D(e) for all edges e of the complement of G; see [19].
The ring network is one of the simplest topologies for interconnection networks. It has many attractive properties such as simplicity, extendibility, low degree, and ease of implementation. It has drawbacks as well: it has poor reliability (any failure in an interface or communication link destroys the function of the network) and it has high transmission delay. As a result, a lot of hybrid topologies utilizing the ring network as a basis for synthesizing richer interconnection schemes have been proposed to improve the reliability and reduce the transmission delay [1, 2, 4, 11, 12, 22]. One example of the commonly used extensions for the ring network is the multi-loop network, which was first proposed by Wong and Coppersmith in [22] for organizing multi-module memory services.
Another example of the commonly used extensions for the ring network is the chordal ring networkand is formally defined below.
The chordal ring network was first proposed by Arden and Lee [1]. It is considered to be obtained by adding chords to a cycle (a ring network) so that the diameter can be decreased and the reliability can be increased. More specifically, a chordal ring network CR(N, w), where N is a positive even integer and w is a positive odd integer such that w ≤ N/2, is a graph with N nodes 0, 1, . . . , N − 1 and 3N/2 links of the form:
(i, (i + 1) mod N), i = 0, 1, 2, . . . , N − 1, (i, (i + w) mod N), i = 1, 3, 5, . . . , N − 1.
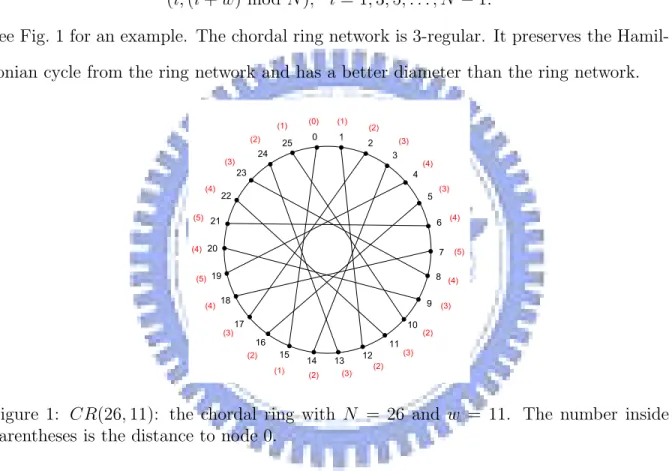
See Fig. 1 for an example. The chordal ring network is 3-regular. It preserves the Hamil-tonian cycle from the ring network and has a better diameter than the ring network.
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 0 1 2 3 4 5 6 7 (0) (1) (1) (1) (2) (2) (2) (2) (2) (2) (3) (3) (3) (3) (3) (3) (3) (4) (4) (4) (4) (4) (4) (5) (5) (5)
Figure 1: CR(26, 11): the chordal ring with N = 26 and w = 11. The number inside parentheses is the distance to node 0.
A network is usually been evaluated by its maximum transmission delay (diameter) and by it fault-tolerant capability. Therefore a network with the dei property is preferred than those without the property. The purpose of this thesis is to study the dei property of chordal ring networks CR(N, w). So far as we know, nobody has ever studied the dei property for this kind of networks. In particular, we will determine if CR(N, w) is dei for all w ∈ {3, 5, 7, 9}. In [1], Arden and Lee proposed a formula for computing the diameter of CR(N, w). Unfortunately, their formula is not always correct. In this thesis, we will
prove that for each N ≥ 26, there exists a w such that Arden and Lee’s formula is not correct. We will also fix the formula for two of the faulty cases.
This thesis is organized as follows. Section 2 gives some preliminaries. Section 3 gives counterexamples for Arden and Lee’s diameter formulas. Section 4 contains our dei results for chordal ring networks. The concluding remarks are given in the last section.
2
Preliminaries
Throughout this thesis, nodes in a graph are assumed taken modulo N. As an example, u + v is the node (u + v) mod N and u − v is the node (u − v) mod N. An edge between nodes u and v is denoted by (u, v). The following definitions will be used throughout this thesis. For each odd-numbered node i, we call a chordal traversal from node i to node i + w a clockwise chordal traversal. Similarly, for each even-numbered node j, we call a chordal traversal from node j to node j − w a counterclockwise chordal traversal. A path from node u to node v is called a clockwise path if it consists of clockwise chordal traversals (possibly zero) plus appropriate ring-edge traversals. Similarly, a path from node u to node v is called a counterclockwise path if it consists of counterclockwise chordal traversals (possibly zero) plus appropriate ring-edge traversals. Let distG,R(u, v) (resp. distG,L(u, v))
denote the length of a shortest clockwise (resp. counterclockwise) path from u to v in G. In [1], Arden and Lee had proven that
dG(u, v) = min{distG,R(u, v), distG,L(u, v)}.
Take CR(26, 11) in Fig. 1 as an example. Then distG,R(0, 11) = 3 and two clockwise
paths with such a distance are 0 → 1 → 12 → 11 and 0 → 25 → 10 → 11. Also, distG,L(0, 11) = 5; three counterclockwise paths with such a distance is 0 → 15 → 14 →
13 → 12 → 11, 0 → 25 → 24 → 23 → 22 → 11, and 0 → 25 → 24 → 13 → 12 → 11. Form the above, dG(0, 5) = 3.
It is obvious that in a chordal ring network, all even-numbered nodes are symmetric; also, all odd-numbered nodes are symmetric. If we flip a chordal ring network vertically,
then it is not difficult to see that node 1 is symmetric to node 0, node 2 is symmetric to node N − 1, node 3 is symmetric to node N − 2, and so on. Thus a chordal ring network is vertex-transitive and consequently,
D(G) = max{dG(0, v)}.
By using the vertex-transitive property, we obtain the following identities, which will be used in the remaining proof.
• distG,R(u, v) = distG,L(v, u).
• For u even, dG(u, v) = dG(0, v − u).
• For u even, distG,R(u, v) = distG,R(0, v − u) and distG,L(u, v) = distG,L(0, v − u).
• For u odd, dG(u, v) = dG(0, u − v).
• For u odd, distG,R(u, v) = distG,L(0, u − v) and distG,L(u, v) = distG,R(0, u − v)
In [1], Arden and Lee provided the following formula for computing distG,R(0, v).
Theorem 1. [1] Suppose G = CR(N, w) and v is a node in G. Let g = ⌈ v
w+1⌉, △v =
v mod (w + 1), and define ϕ(v) = 0 if v is even and ϕ(v) = 1 if v is odd. Then
(i) When g ≥ w−1 2 , distG,R(0, v) = ( 2g − 1 if △v = 1, 2g + ϕ(v) if △v = 0 or 2 ≤ △v ≤ w. (ii) When g < w−1 2 , distG,R(0, v) = 2(g−1)+△v if 1 ≤ △v ≤ w+12 − g, w + 1 − △v if w+32 − g ≤ △v ≤ w − 2g, 2g + ϕ(v) if △v = 0 or w−2g+1 ≤ △v ≤ w.
Arden and Lee did not provide an explicit formula for computing distG,L(0, v) and the
readers are asked to refer to the dissertation in [13]. For completeness of this thesis, we now provide such a formula.
Theorem 2. Suppose G = CR(N, w) and v is a node in G. Then
(i) When N − w +w−1
(ii) When N − w ≤ v ≤ N − w +w−1
2 , distG,L(0, v) = 1 + v − (N − w).
(iii) When v < N − w, distG,L(0, v) = min{v, 1 + distG,R(0, N − w − v)}.
Proof. To calculate distG,L(0, v), we divide the nodes in CR(N, w) into several
counter-clockwise intervals each of size w + 1 (except possibly the last interval). The first interval contains node 0, N −1, N −2, . . . , N −w. Obviously, the length of a shortest counterclock-wise path from node 0 to node N − w is 1. The length of a shortest counterclockcounterclock-wise path from node 0 to any node v ∈ {N −1, N −2, . . . , N −w+w−1
2 +1} is N −v and one such path is
0 → N −1 → N −2 · · · → v. On the other hand, the length of a shortest counterclockwise path from node 0 to any node v ∈ {N −w+w−1
2 , N −w+w−12 −1, . . . , N −w} is 1+v−(N −w)
and one such path is via the chord (0, N − w) and then follows the ring-edges, that is, 0 → N − w → N − w + 1 · · · → N − w + 2 → v. Since a chordal ring network is vertex-transitive, by Theorem 1 and by the observation that distG,L(u, v) = distG,R(0, u − v) if u
is odd, we have distG,L(N − w, v) = distG,R(0, N − w − v). When v < N − w, node 0 can
get to node v by using only ring-edges or by using the chord (0, N − w) and appropriate ring-edges; therefore distG,L(0, v) = min{v, 1 + distG,R(0, N − w − v)}.
In [1], Arden and Lee also provided a formula for computing the diameter of a chordal ring network; see the following theorem. For convenience, call this theorem the Diameter Theorem.
Theorem 3. [1] (The Diameter Theorem) SupposeG = CR(N, w), i = ⌈ N 2(w+1)⌉, and △ = N 2 mod (w + 1). Then Case 1. When i ≥w−12 , D(G) = 2i − 1 if △ = 1, 2i if 2 ≤ △ ≤ w+32 , 2i + 1 if △ = 0 or w+32 ≤ △ ≤ w. Case 2. When i =w−3 2 , D(G) = ( w − 3 if 1 ≤ △ ≤ 2, w − 2 if △ = 0 or 3 ≤ △ ≤ w. Case 3. When i ≤w−5 2 , D(G) = ( i+w−3 2 if 1 ≤ △ ≤ w+1 2 −i or w+5 2 −i ≤ △ ≤ w − i, i+w−1 2 if △ = 0 or △ = w+3 2 −i or w−i+1 ≤ △ ≤ w.
Before closing this section, we have to mention that Theorems 1 and 2 hold when 2w ≤ N ≤ 2w + 2 and when N ≥ (w−1
4 )(w + 1) − 2; for 2w + 4 ≤ N ≤ (w−14 )(w + 1) − 4,
these two theorems may not hold. The incorrectness of the Diameter Theorem might come from the use of Theorem 1 for N such that 2w + 4 ≤ N ≤ (w−1
4 )(w + 1) − 4.
3
Counterexamples for Theorem 3
Let Ni denote the set of nodes in a chordal ring network whose distance to node 0
is i. We now give a counterexample for the Diameter Theorem. Consider CR(26, 11) shown in Fig. 1. It is not difficult to see that CR(26, 11) has N0 = {0}, N1 = {1, 15, 25},
N2 = {2, 10, 12, 14, 16, 24}, N3 = {3, 5, 9, 11, 13, 17, 23}, N4 = {4, 6, 8, 18, 20, 22}, and
N5 = {7, 19, 21}. Since S5i=1Ni = {0, 1, . . . , 25}, D(CR(26, 11)) = 5. However, the
Diameter Theorem obtains D(CR(26, 11)) = 6.
We have run computer programs to obtain the diameters of chordal ring networks CR(N, w) for N = 6, 8, . . . , 5000, and for each N, we test all possible chord lengths w. Our experimental results show that the Diameter Theorem is correct if w ∈ {3, 5, 7, 9}, the first fault occurs at CR(26, 11), and for each N ≥ 26 (and N even), there exists a chord length w such that the Diameter Theorem is wrong for CR(N, w). For example, the Diameter Theorem is wrong for CR(28, 11), CR(30, 13), CR(32, 13), CR(34, 15), and so on. Moreover, our experimental shows that Cases 1 and 2 of the Diameter Theorem are correct and faults occur in Case 3.
Recall that the Diameter Theorem is correct if w ∈ {3, 5, 7, 9} and the first fault of the Diameter Theorem occurs at CR(26, 11). The chordal ring network CR(26, 11) satisfies N = 2w + 4. While we are unable to fix all the faults in the Diameter Theorem, we do fix this theorem for the N = 2w + 4 and N = 2w + 6 cases. See the following for details. For G = CR(2w + 4, w), the Diameter Theorem obtains D(G) = w+12 . However, in Theorem 4, we show that this result is incorrect. For G = CR(2w + 6, w), the Diameter Theorem obtains D(G) = w+12 . In Theorem 5, we show that this result is also incorrect. Do notice that Theorems 4 and 5 together show that for all N ≥ 26, there exists a w such
that the Diameter Theorem is incorrect.
Theorem 4. Suppose N = 2w + 4 and w ≥ 11. Write w in the form w = 12t + p, where t is a positive integer and p is an odd integer such that −1 ≤ p ≤ 9. Then
D(CR(N, w)) = ( w+3 2 − 2t if −1 ≤ p ≤ 3 w+1 2 − 2t if 5 ≤ p ≤ 9.
Proof. Let G = CR(N, w). Then N0 = {0}, N1 = {1, w + 4, 2w + 3}, N2 = {2, w −
1, w + 1, w + 3, w + 5, 2w + 2}, and N3 = {3, 5, w − 2, w, w + 2, w + 6, 2w + 1}. Each node
in N3 (except w + 2) has at least one neighbor v such that node 0 can not reach node v
in three edges. In particular, node 0 can reach node 4 via node 3, reach node 6 via node 5, reach node w − 3 via node w − 2, reach node w + 7 via node w + 6, and reach node 2w via node w or 2w + 1. Thus N4 = {4, 6, w − 3, w + 7, 2w − 2, 2w}. In general, we can
obtain Ni for i ≥ 4 + 4j as follows. Let j ≥ 0. Then
N4+4j = {4 + 6j, 6 + 6j, w − 3 − 6j, w + 7 + 6j, 2w − 2 − 6j, 2w − 6j},
N5+4j = {7 + 6j, w − 4 − 6j, w + 8 + 6j, w + 10 + 6j, 2w − 1 − 6j, 2w − 3 − 6j},
N6+4j = {8 + 6j, w − 7 − 6j, w − 5 − 6j, w + 9 + 6j, w + 11 + 6j, 2w − 4 − 6j}, and
N7+4j = {9 + 6j, 11 + 6j, w − 8 − 6j, w − 6 − 6j, w + 12 + 6j, 2w − 5 − 6j}.
We now calculate D(G) according to the value of p. (i) Suppose p = −1. Then w = 12t − 1. Let j = w−11
12 . Then
N4+4j = {w−32 ,w+12 ,w+52 ,3w+32 ,3w+72 ,3w+112 } and N5+4j = {w+32 ,3w+52 ,3w+92 }.
Since N6+4j = {w−32 ,w+12 ,w+52 ,3w+72 ,3w+32 }, clearly N6+4j ⊆ N4+4j and therefore D(G) ≤
5 + 4j. Since {w+32 ,3w+52 ,3w+92 } 6⊆S4+4j
i=1 Ni, Thus D(G) = 5 + 4j = w+32 − 2t.
(ii) Suppose p = 1. Then w = 12t + 1. Let j = w−13
12 . Then
N4+4j = {w−12 ,w−52 ,w+72 ,3w+12 ,3w+92 ,3w+132 } , N5+4j = {w+12 ,w+52 ,3w+32 ,3w+72 ,3w+112 } ,
Note that {w−3 2 , w+9 2 } ⊆ N7+4j and {w−32 , w+9 2 } 6⊆ N5+4j. Since {w−32 , w+9 2 } ⊆ N3+4j, dG(0,w−32 ) = dG(0,w+92 ) = 3 + 4j, therefore D(G) ≤ 6 + 4j. Since {w+32 ,3w+52 } ⊆ N6+4j and {w+32 ,3w+52 } 6⊆S5+4j i=1 Ni, Thus D(G) = 6 + 4j = w+32 − 2t.
(iii) Suppose p = 3. Then w = 12t + 3. Let j = w−15
12 . Then N5+4j = {w−12 ,w+72 ,3w+12 ,3w+52 ,3w+92 ,3w+132 } , N6+4j = {w+12 ,w+52 ,3w+32 ,3w+72 } , N7+4j = {w−12 ,w+32 ,w+72 ,3w+52 ,3w+92 } and N8+4j = {w−32 ,w+52 ,w+92 ,3w−12 ,3w+112 ,3w+32 }. Note that {w−3 2 , w+9 2 , 3w−1 2 , 3w+11 2 } ⊆ N8+4j and {w−32 , w+9 2 , 3w−1 2 , 3w+11 2 } 6⊆ N6+4j. Since {w+92 ,w−3 2 , 3w+11 2 } ⊆ N4+4j, dG(0, w+9 2 ) = dG(0,w−32 ) = dG(0, 3w+11 2 ) = dG(0, 3w−1 2 ) =
4 + 4j, therefore D(G) ≤ 7 + 4j. Sincew+32 ∈ N7+4j and w+32 6∈ S6+4ji=1 Ni, Thus D(G) =
7 + 4j = w+32 − 2t.
(iv) Suppose p = 5. Then w = 12t + 5. Let j = w−17
12 . The proof is similar to case (i).
The farthest nodes from node 0 is in N7+4j and D(G) = w+43 = w+12 − 2t.
(v) Suppose p = 7. Then w = 12t + 7. Let j = w−19
12 . The proof is similar to case (ii).
The farthest nodes from node 0 is in N4+4j and D(G) = w+53 = w+12 − 2t.
(vi) Suppose p = 9. Then w = 12t + 9. Let j = w−21
12 . The proof is similar to case
(iii). The farthest nodes from node 0 is in N5+4j and D(G) = w+63 = w+12 − 2t.
Theorem 5. Suppose N = 2w + 6 and w ≥ 11. Write w in the form w = 8t + p, where t is a positive integer and p is an odd integer such that −1 ≤ p ≤ 5. Then
D(CR(N, w)) = (
2t + 2 = w+9
4 if p = −1
2t + 3 = w−p+124 if 1 ≤ p ≤ 5. Proof. Similar to that of Theorem 4.
4
The dei property of chordal ring networks
In this section, we will discuss the dei property of chordal ring networks. Notice that N satisfies Case 1 of Theorem 3 if N ≥ (w − 3)(w + 1) + 2, Case 2 of Theorem 3 if (w − 5)(w + 1) + 2 ≤ N ≤ (w − 3)(w + 1), and Case 3 of Theorem 3 if 2w ≤ N ≤
(w − 5)(w + 1). The discussions in this section are grouped according to the value of the chord length w and the above ranges of N.
The following lemma provides a sufficient condition for a chordal ring network to be dei. For convenience, call this lemma the DEI Lemma.
Lemma 6. (The DEI Lemma) Let G = CR(N, w). If for all v ∈ V (G), there are always two edge-disjoint paths P1, P2 between node 0 and node v such that |Pi| ≤ D(G)
for i = 1, 2, then G is dei.
Proof. Since CR(N, w) is vertex-transitive and there are always two edge-disjoint paths P1, P2 between node 0 and node v such that |Pi| ≤ D(G) for i = 1, 2, deleting any edge
will not raise the diameter. Hence we have this lemma.
Let e be an edge of G = CR(N, w) and H = G − e. To prove that G is non-dei, it suffices to prove that
D(G − e) ≥ dH(0, x) > D(G). (1)
This inequality is used heavily in the remaining proofs.
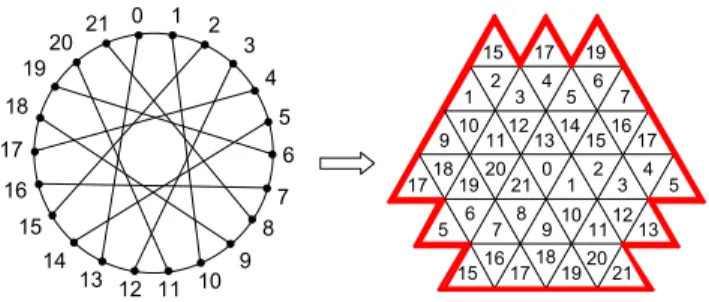
Before going further, we introduce the triangular grid representation for a chordal ring network CR(N, w). See Fig. 2 for an illustration. Consider the triangular grid on the plane. We associate CR(N, w) a labeling on the cells of the triangular grid as follows (all the labels are assumed taken modulo N). Label 0 to an arbitrary downward triangle. Once a downward triangle is labeled i, label its three neighboring triangles by i + 1, i − 1, and i − w in such a way that the triangle to the right of it receives i + 1, to the left of it receives i − 1, and above it receives i − w. Once a upward triangle is labeled j, label its three neighboring triangles by j + 1, j − 1, and j + w in such a way that the triangle to the right of it receives j + 1, to the left of it receives j − 1, and below it receives j + w. Note that in this thesis, only nodes within distance D(CR(N, w)) will be shown in the triangular grid representation.
For clarity, the remaining part of this section is divided into subsections. Subsection 4.1 considers CR(N, w) with w = 3.
9 10 11 12 13 14 15 16 17 18 19 20 21 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 21 20 19 18 17 10 11121314151617 9 5 4 3 2 1 6 7 17 15 19 7 6 5 8 910111213 17 16 15 18192021
Figure 2: CR(22, 9) and its associated triangular grid representation.
Subsection 4.2 considers CR(N, w) with (N = 2w or 2w + 2) and w ≥ 5.
Subsection 4.3 considers CR(N, w) with 2w + 4 ≤ N ≤ (w − 5)(w + 1) and w = 9. Subsection 4.4 considers CR(N, w) with (w − 5)(w + 1) + 2 ≤ N ≤ (w − 3)(w + 1). Subsection 4.5 considers CR(N, w) with N ≥ (w − 3)(w + 1) + 2.
4.1
CR(N, w) with w = 3
For chordal ring networks with w = 3, we have the following result.
Theorem 7. CR(N, 3) is non-dei if N = 4k + 6 and dei if N = 4k + 8, where k ≥ 0.
Proof. Let G = CR(N, 3). First assume that N = 4k + 6. Let e denote the edge (0, N − 3) and let H = G − e. Consider the node x = N
2 + 1 if k is odd and x = N
2 if k is
even. Since any shortest clockwise path from 0 to x in G does not use the edge e,
distH,R(0, x) = distG,R(0, x)
by Theorem 1
= k + 3.
Since any shortest counterclockwise path from 0 to x in H must traverse via node N − 2, distH,L(0, x) = 2 + distH,L(N − 2, x)
= 2 + distG,L(0, x − (N − 2))
by Theorem 2
= k + 3.
Thus dH(0, x) = min{distH,R(0, x), distH,L(0, x)} = k + 3. By Theorem 3, D(G) = k + 2.
By (1), G is non-dei.
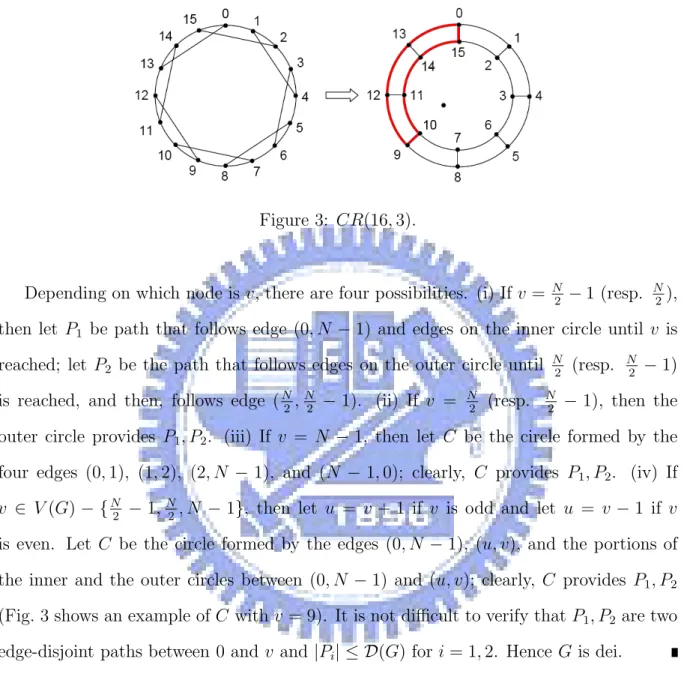
Now assume that N = 4k + 8. Then G can be drawn as two concentric circles in such a way that half of the nodes are on the inner circle and half of them, the outer circle. (See Fig. 3 for an example.) By Theorems 1 and 2, when k is even (resp. odd), the node that
is farthest from node 0 is N
2 − 1 (resp. N
2). By Theorem 3, D(G) = k + 3. We now prove
that for all v ∈ V (G), there are two edge-disjoint paths P1, P2 between 0 and v such that
|Pi| ≤ D(G) for i = 1, 2. See Fig. 3 for an illustration.
Figure 3: CR(16, 3).
Depending on which node is v, there are four possibilities. (i) If v = N
2 − 1 (resp. N
2),
then let P1 be path that follows edge (0, N − 1) and edges on the inner circle until v is
reached; let P2 be the path that follows edges on the outer circle until N2 (resp. N2 − 1)
is reached, and then, follows edge (N 2, N 2 − 1). (ii) If v = N 2 (resp. N 2 − 1), then the
outer circle provides P1, P2. (iii) If v = N − 1, then let C be the circle formed by the
four edges (0, 1), (1, 2), (2, N − 1), and (N − 1, 0); clearly, C provides P1, P2. (iv) If
v ∈ V (G) − {N 2 − 1,
N
2, N − 1}, then let u = v + 1 if v is odd and let u = v − 1 if v
is even. Let C be the circle formed by the edges (0, N − 1), (u, v), and the portions of the inner and the outer circles between (0, N − 1) and (u, v); clearly, C provides P1, P2
(Fig. 3 shows an example of C with v = 9). It is not difficult to verify that P1, P2 are two
edge-disjoint paths between 0 and v and |Pi| ≤ D(G) for i = 1, 2. Hence G is dei.
4.2
CR(N, w) with (N = 2w or 2w + 2) and w ≥ 5
For chordal ring networks with N = 2w or 2w + 2, we have the following result.
Theorem 8. CR(N, w) is non-dei if (N = 2w or 2w + 2) and w ≥ 5.
Proof. Let G = CR(N, w). First assume that N = 2w and w ≥ 5. Set e = (0, 1) and H = G − e for easy writing. Consider the node x = w−1. Since any shortest clockwise
path from 0 to x in H must use the edges (0, N − 1) and (N − 1, w − 1),
distH,R(0, x) = 2 + distG,R(w − 1, x) = 2 + distG,R(0, x − (w − 1))
by Theorem 1
= 2 + w−1 2 .
Since any shortest counterclockwise path from 0 to x in G does not use the edge e,
distH,L(0, x) = distG,L(0, x)
by Theorem 2
= w+32 .
Thus dH(0, x) = w+32 . By Theorem 3, D(G) = w+12 . By (1), G is non-dei.
Now assume that N = 2w + 2 and w ≥ 5. Let e = (0, N − 1) and H = G − e. Consider the node x = w+32 . Since any shortest clockwise path from 0 to x in H must use the edges (0, 1) and (1, 2) or the edges (0, 1) and (1, 1 + w),
distH,R(0, x) = 2 + min{distH,R(2, x), distH,R(1 + w, x)}
= 2 + min{distG,R(2, x), distG,R(1 + w, x)}
by Theorem2
= w+3 2 .
Since any shortest counterclockwise path from 0 to x in G must use the edge (0, N − w),
distH,L(0, x) = 1 + distH,L(N − w, x) = 1 + distG,R(0, N − w − x)
by Theorem 1
= w+3 2 .
Thus dH(0, x) = w+32 . By Theorem 3, D(G) = w+12 . By (1), G is non-dei.
4.3
CR(N, w) with 2w + 4 ≤ N ≤ (w − 5)(w + 1) and w = 9
For chordal ring networks with w = 9, we have the following result.
Theorem 9. CR(N, 9) is dei if N ∈ {22, 24, 40} and non-dei if N ∈ {26, 28, 30, 32, 34, 36, 38}.
Proof. First assume that N ∈ {22, 24, 40}. Let G = CR(22, 9). By Theorem 3, D(G) = 5. All the nodes that can be reached from node 0 in D(G) edges are shown in the triangular grid representation in Fig. 2. As was shown in this figure, for all v ∈ V (G), there are always two paths P1, P2 satisfying the DEI Lemma. Hence G is dei. Similarly,
we can prove that CR(24, 9) and CR(40, 9) are dei.
Case 1: N ∈ {26, 28, 30, 32, 34}. Let e = (0, N − 1) and H = G − e. Consider the node x = N − 4. Since any shortest clockwise path from 0 to x in H must use the edges (0, 1) and (1, 2) or the edges (0, 1) and (1, 10),
distH,R(0, x) = 2 + min{distH,R(2, x), distH,R(10, x)}
= 2 + min{distG,R(2, x), distG,R(10, x)}
by Theorem 1
= 6.
Since any shortest counterclockwise path from 0 to x in G must use the edge (0, N − 9),
distH,L(0, x) = 1 + distH,L(N − 9, x) = 1 + distG,L(0, −5)
by Theorem 2
= 6.
Thus dH(0, x) = 6. By Theorem 3, D(G) = 5. By (1), CR(N, 9) is non-dei if N ∈
{26, 28, 30, 32, 34}.
Case 2: N = 36. Let e = (0, 1) and H = G − e. Consider the node x = 13. Since any shortest clockwise path from 0 to x in H must use the edges (0, 35) and (35, 8),
distH,R(0, x) = 2 + distG,R(8, x) = 2 + distG,R(0, 5)
by Theorem 1
= 7.
Since any shortest shortest counterclockwise path from 0 to x in G does not use edge e,
distH,L(0, x) = distG,L(0, x)
by Theorem 2
= 7.
Thus dH(0, x) = 7. By Theorem 3, D(G) = 6. By (1), CR(36, 9) is non-dei.
Case 3: N = 38. Let e = (0, 37) and H = G − e. Consider the node x = 15. Since any shortest clockwise path from 0 to x in H must use the edges (0, 1) and (1, 2) or the edges (0, 1) and (1, 10),
distH,R(0, x) = 2 + min{distH,R(2, x), distH,R(10, x)}
= 2 + min{distG,R(2, x), distG,R(10, x)}
by Theorem 1
= 7. Since any shortest counterclockwise path from 0 to x in G must use the edge (0, 29),
distH,L(0, x) = 1 + distH,L(29, x) = 1 + distG,L(0, 14)
by Theorem 2
= 7.
4.4
CR(N, w) with (w − 5)(w + 1) + 2 ≤ N ≤ (w − 3)(w + 1)
When (w − 5)(w + 1) + 2 ≤ N ≤ (w − 3)(w + 1), Case 2 of the Diameter Theorem occurs and we have the following result.
Theorem 10. For (w − 5)(w + 1) + 2 ≤ N ≤ (w − 3)(w + 1), we have:
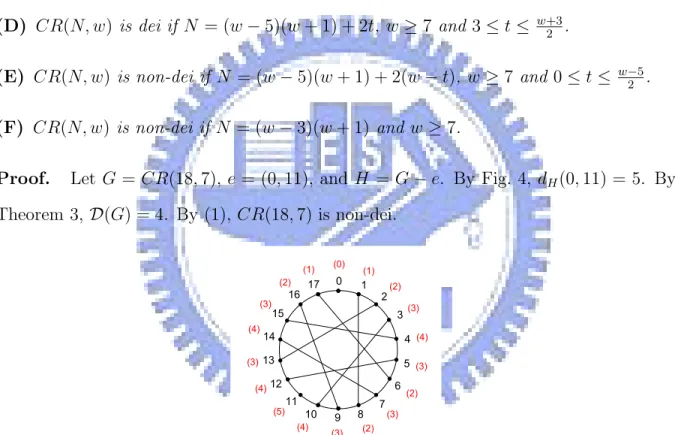
(A) CR(18, 7) is non-dei.
(B) CR(N, w) is dei if N = (w − 5)(w + 1) + 2 and w ≥ 9.
(C) CR(N, w) is non-dei if N = (w − 5)(w + 1) + 4 and w ≥ 7.
(D) CR(N, w) is dei if N = (w − 5)(w + 1) + 2t, w ≥ 7 and 3 ≤ t ≤ w+32 .
(E) CR(N, w) is non-dei if N = (w − 5)(w + 1) + 2(w − t), w ≥ 7 and 0 ≤ t ≤ w−5 2 .
(F) CR(N, w) is non-dei if N = (w − 3)(w + 1) and w ≥ 7.
Proof. Let G = CR(18, 7), e = (0, 11), and H = G − e. By Fig. 4, dH(0, 11) = 5. By
Theorem 3, D(G) = 4. By (1), CR(18, 7) is non-dei. (5) (4) (4) (4) (4) (3) (3) (3) (3) (3) (3) (2) (2) (2) (2) (1) (1) (0) 8 14 5 17 11 2 15 6 0 9 12 3 16 7 1 10 13 4
Figure 4: The graph H = G − e, where G = CR(18, 7) and e = (0, 11). The number inside parentheses is the distance to node 0.
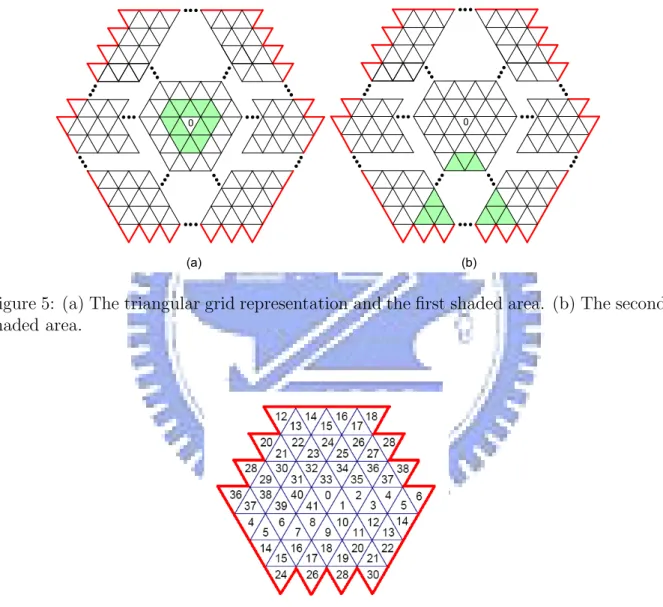
We now prove (B). Let G = CR(N, w). By Theorem 3, D(G) = w − 3, which is an even number. The triangular grid representation of G is of the form shown in Fig. 5(a). In the following, we will consider the triangular grid representation of G as the combination of several shaded areas. For each shaded area, we will prove that for each node v in that
shaded area, there are always two paths P1, P2 satisfying the DEI Lemma. See also Fig. 6
for a specific triangular grid representation.
First consider the shaded area shown in Fig. 5(a). Since D(G) ≥ 6, for each node v in this shaded area, there are always two paths P1, P2 satisfying the DEI Lemma. Now
consider the shaded area shown in Fig. 5(b). Obviously, for each node v in in this shaded area, there are always two paths P1, P2 satisfy the DEI Lemma.
0 0
(a) (b)
Figure 5: (a) The triangular grid representation and the first shaded area. (b) The second shaded area.
Figure 6: The triangular grid representation of CR(42, 9).
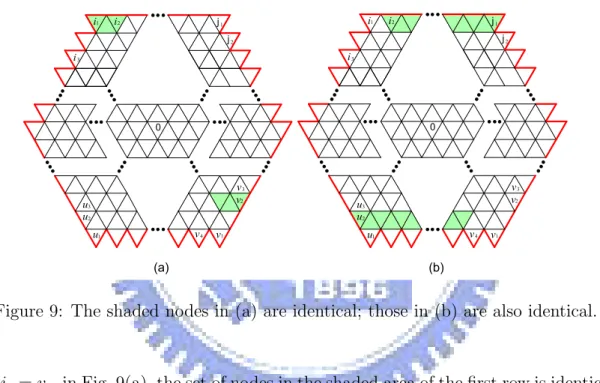
Consider the shaded area shown in Fig. 7(a). For convenience, let a denote the node w + 1. Clearly, dG(0, a) = 2. Each node v in this shaded area has dG(0, v) = dG(a, v)
Consequently, for each node v in in this shaded area, there are always two paths P1, P2
satisfy the DEI Lemma. Consider the shaded area shown in Fig. 7(b). For convenience, let b denote the node N − w − 1. Clearly, dG(0, b) = 2. Each node v in this shaded area
has dG(0, v) = dG(b, v) and the distance from node 0 to any node in this shaded area is
at most D(G) − 2. Consequently, for each node v in in this shaded area, there are always two paths P1, P2 satisfy the DEI Lemma.
a
0
b
0
(a) (b)
Figure 7: (a) The third shaded area. (b) The fourth shaded area.
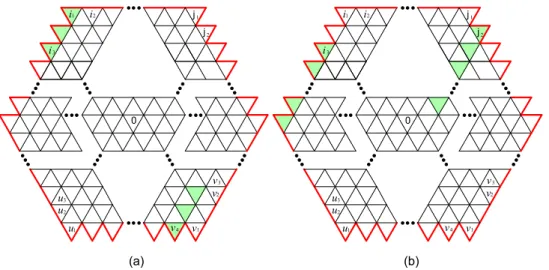
By similar arguments, for each node v, except those in the shaded area of Fig. 8, there are always two paths P1, P2 satisfying the DEI Lemma. We now consider nodes in the
shaded area of Fig. 8. See Figs. 9-13 for an illustration.
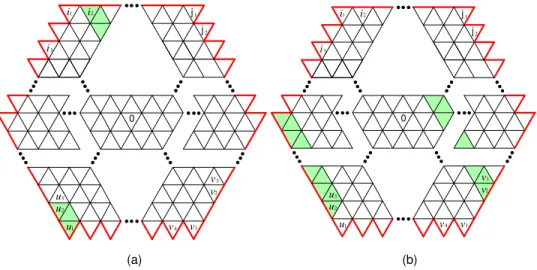
First consider Fig. 9 and the cells labeled i1, i2, u1, u2, v1, v2, in this figure. The label
i1 is in the leftmost cell of the first row; thus i1 = N − (w+12 )(w − 3) = w
2 −6w−3 2 . Therefore i2 = i1 + 2 = w 2 −6w+1
2 . The label u1 is in the leftmost cell of the last row; thus u1 =
(w−1
2 )(w − 3) = w2
−4w+3
2 . The label u2 is in the rightmost node of the reciprocal second
row; therefore u2 = u1 − (w + 1) = w
2
−6w+1
2 . The label v1 is in the rightmost cell of the
last row; thus v1 = (w+12 )(w − 3) = w
2
−2w−3
2 . The label v2 is in the rightmost node of the
reciprocal third row; therefore v2 = v1− 2(w − 1) = w
2
−6w+1
2 . From the above,
j 3 v 2 j1 1 v 2 v 3 u 3 i u2 1 u 2 i 1 i v4 0
Figure 8: Those shaded boundary nodes need additional discussion.
v4 j 3 v 3 u 3 i 2 j1 1 v 2 v u2 1 u 2 i 1 i 0 v4 j 3 v 3 u 3 i 2 j1 1 v 2 v u2 1 u 2 i 1 i 0 (a) (b)
Figure 9: The shaded nodes in (a) are identical; those in (b) are also identical.
Since i2 = v2, in Fig. 9(a), the set of nodes in the shaded area of the first row is identical to
the set of nodes in the shaded area of the reciprocal third row. Since i2 = u2, in Fig. 9(b),
the set of nodes in the shaded area of the first row is identical to the set of nodes in the shaded area of the reciprocal second row. By similar arguments, the sets of nodes in the two shaded areas in Figs. 10(a), 10(b), 11(a) and 11(b) are identical, too.
Now consider Fig. 12 and the cells labeled i3, j1, j2, v4 in this figure. The label i3 is
in the leftmost cell of the third row; thus i3 = i1 + 2(w − 1) = w
2
−2w−7
2 . The label j1 is
in the rightmost cell of the first row; thus j1 = N − (w−12 )(w − 3) = w
2
−4w−9
(a) (b) v4 j 3 v 3 u 3 i 2 j1 1 v 2 v u2 1 u 2 i 1 i 0 j 3 v 2 j1 1 v 2 v 3 u 3 i u2 1 u 2 i 1 i v4 0
Figure 10: The shaded nodes in (a) are identical; those in (b) are also identical.
j 3 v 2 j1 1 v 2 v 3 u 3 i u2 1 u 2 i 1 i v4 0 j 3 v 2 j1 1 v 2 v 3 u 3 i u2 1 u 2 i 1 i v4 0 (a) (b)
Figure 11: The shaded nodes in (a) are identical; those in (b) are also identical.
j2 = j1+ (w + 1) = w 2−2w−7 2 . Since v1 = w2−2w−3 2 , v4 = v1− 2 = w2−2w−7
2 . From the above,
i3 = j2 = v4. (3)
Thus the sets of nodes in the two shaded areas in Figs. 12(a), 12(b), 13(a) and 13(b) are identical, too.
From the above discussion, for each node v in the shaded area of Fig. 8, except the five nodes in {i2− 1, i2, i2+ 1, u3, i3}, there are always two paths P1, P2 satisfying the DEI
Lemma. For each of the five nodes in the set, we now use (i)-(v) to prove that there are also two paths P1, P2 satisfying the DEI Lemma.
j 3 v 2 j1 1 v 2 v 3 u 3 i u2 1 u 2 i 1 i v4 0 j 3 v 2 j1 1 v 2 v 3 u 3 i u2 1 u 2 i 1 i v4 0 (a) (b)
Figure 12: The shaded nodes in (a) are identical; those in (b) are also identical.
j 3 v 2 j1 1 v 2 v 3 u 3 i u2 1 u 2 i 1 i v4 0 0 (a) (b)
Figure 13: The shaded nodes in (a) are identical; those in (b) are also identical.
(i) Consider node i2− 1. By (2), i2− 1 = v2− 1. Let P1 = 0−w→ N − w → N − (w + 1)−1 −w→
N − (2w + 1) −1 → N − (2w + 2) −w → N − (3w + 2) −1 → N − (3w + 3) −w → · · · −1 → N − (w−5 2 )(w + 1) −w → N − (w−5 2 )(w + 1) − w = i2 − 1. Let P2 = 0 +1 → 1 +w→ w + 1 → w + 2+1 +w→ 2w + 2 → 2w + 3+1 +w→ 3w + 3 → · · ·+1 +w→ (w−7 2 )(w + 1) +1 → (w−7 2 )(w + 1) + 1 +1 → (w−7 2 )(w + 1) + 2 +1 → (w−7 2 )(w + 1) + 3 = v2 − 1. See Fig. 6
for an illustration. Then i2− 1 = 13, P1 = 0 → 33 → 32 → 23 → 22 → 13 and
P2 = 0 → 1 → 10 → 11 → 12 → 13.
N − (2w + 1) −1 → N − (2w + 2) −w → N − (3w + 2) −1 → N − (3w + 3) −w → · · · −1 → N − (w−7 2 )(w + 1) −w → N − (w−7 2 )(w + 1) − w +1 → N − (w−7 2 )(w + 1) − w + 1 −w → N − (w−7 2 )(w + 1) − 2w + 1 −1 → N − (w−7 2 )(w + 1) − 2w = i2. Let P2 = 0 +1 → 1 +w→ w + 1 +1→ w + 2 +w→ 2w + 2 → 2w + 3+1 +w→ 3w + 3 +1→ · · · +w→ (w−7 2 )(w + 1) +1 → (w−7 2 )(w + 1) + 1 +1 → (w−7 2 )(w + 1) + 2 +1 → (w−7 2 )(w + 1) + 3 +1 → (w−7 2 )(w + 1) + 4 = v2.
Again, see Fig. 6. Then i2 = 14, P1 = 0 → 33 → 32 → 23 → 24 → 15 → 14 and
P2 = 0 → 1 → 10 → 11 → 12 → 13 → 14.
(iii) Consider node i2+ 1. By (2), i2+ 1 = u2+ 1. Let P1 = 0−w→ N − w→ N − (w + 1)−1 −w→
N − (2w + 1) −1 → N − (2w + 2) −w → N − (3w + 2) −1 → N − (3w + 3) −w → · · · −1 → N − (w−7 2 )(w + 1) −w → N − (w−7 2 )(w + 1) − w +1 → N − (w−7 2 )(w + 1) − w + 1 −w → N − (w−7 2 )(w + 1) − 2w + 1 = i2 = 1. Let P2 = 0 −1 → N − 1 +w→ w − 1 −1 → w − 2 +w→ 2w − 2 −1 → 2w − 3 +w→ 3w − 3 −1 → · · ·+w→ (w−5 2 )(w − 1) −1 → (w−5 2 )(w − 1) − 1 = u2 + 1.
See Fig.6 for an example. Then i2 + 1 = 15, P1 = 0 → 33 → 32 → 23 → 24 → 15
and P2 = 0 → 41 → 8 → 7 → 16 → 15.
(iv) Consider node u3. By (2), i2 + 1 = u2 + 1; thus u3 = v3. Let P1 = 0 +1 → 1 → 2+1 →+1 3→ 4+1 → 5+1 +w→ 5 + w → 5 + (w + 1)+1 +w→ 5 + (2w + 1)→ 5 + (2w + 2)+1 +w→ 5 + (3w + 2)→+1 5 + (3w + 3) +w→ · · · → 5 + (+1 w−9 2 )(w + 1) = v3. Let P2 = 0 −1 → N − 1 +w→ w − 1 −1 → w − 2+w→ 2w − 2 −1 → 2w − 3+w→ 3w − 3 −1 → · · ·+w→ (w−72 )(w − 1)−1 → (w−72 )(w − 1) − 1−1 → (w−7 2 )(w − 1) − 2 −1 → (w−7
2 )(w − 1) − 3 = u3. Again, see Fig. 6. Then u3 = 5,
P1 = 0 → 1 → 2 → 3 → 4 → 5 and P2 = 0 → 41 → 8 → 7 → 6 → 5.
(v) Consider node i3. By (3), i3 = v4. Let P1 = 0−w→ N − w → N − (w + 1)−1 −w→ N − (2w +
1)−1 → N − (2w + 2)−w → N − (3w + 2) −1 → N − (3w + 3)−w → · · · −1 → N − (w−7 2 )(w + 1) −1 → N −(w−7 2 )(w+1)−1 −1 → N −(w−7 2 )(w+1)−2 −1 → N −(w−7 2 )(w+1)−3 −1 → N −(w−7 2 )(w+ 1) − 4 = i3. Let P2 = 0 +1 → 1+w→ w + 1→ w + 2+1 +w→ 2w + 2→ 2w + 3+1 +w→ 3w + 3→+1 · · ·+w→ (w−5 2 )(w + 1) −1 → (w−5 2 )(w + 1) − 1 +w → (w−5 2 )(w + 1) − 1 + w = v4. Take Fig. 6
for an example again. Then i3 = 28, P1 = 0 → 33 → 32 → 31 → 30 → 29 → 28
In (i)-(iii) and (v), P1 is a counterclockwise path, P2 is a clockwise path and P1, P2 are
edge-disjoint. In (iv), P1 and P2 are both clockwise paths and they are edge-disjoint. It
is not difficult to verify that P1, P2 satisfy the DEI Lemma. We now complete the proof
of (B).
Consider (C). Let G = CR(N, w), e = (0, 1), and H = G − e. Consider the node x = N
2 − 1. Note that dH(0, x) = min{distH,R(0, x), distH,L(0, x)}. Since any shortest
counterclockwise path from 0 to x in G will not use the edge e,
distH,L(0, x) = distG,L(0, x)
by Theorem 2
= w − 2.
Since any shortest clockwise path from 0 to x in H must use the edge (0, N − 1),
distH,R(0, x) = 2 + distG,R(w − 1, x) = 2 + distG,R(0, x − (w − 1))
by Theorem 1
= 2 + w − 4.
Thus dH(0, x) = w − 2. By Theorem 3, D(G) = w − 3. By (1), G is non-dei.
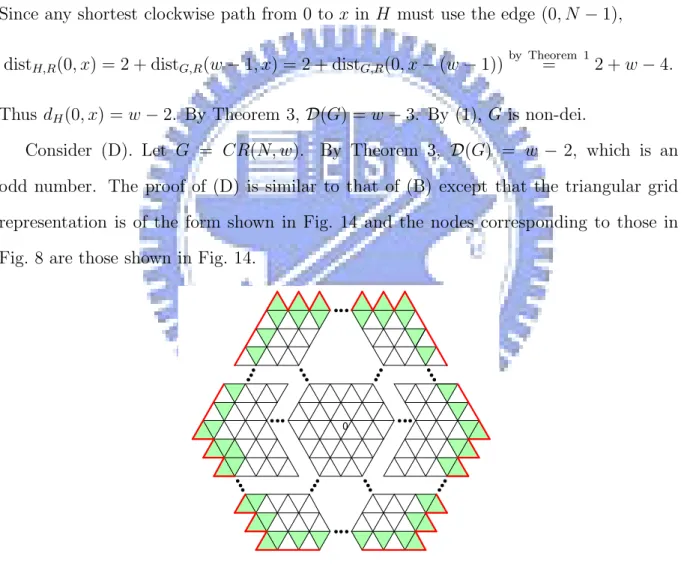
Consider (D). Let G = CR(N, w). By Theorem 3, D(G) = w − 2, which is an odd number. The proof of (D) is similar to that of (B) except that the triangular grid representation is of the form shown in Fig. 14 and the nodes corresponding to those in Fig. 8 are those shown in Fig. 14.
0
Figure 14: Those shaded boundary nodes need additional discussion.
Consider (E). Let G = CR(N, w), e = (0, 1), and H = G − e. Consider the node x = N + t + 2 − w. Since any shortest counterclockwise path from 0 to x in G will not
use the edge e,
distH,L(0, x) = distG,L(0, x)
by Theorem 2
= w − 1.
Since any shortest clockwise path from 0 to x in H must use the edge (0, N − 1),
distH,R(0, x) = 2 + distG,R(w − 1, x) = 2 + distG,R(0, x − (w − 1))
by Theorem 1
= 2 + w − 3.
Thus dH(0, x) = w − 1. By Theorem 3, D(G) = w − 2. By (1), CR(N, w) is non-dei.
Consider (F). Let G = CR(N, w), e = (0, N − w), and H = G − e. Consider the node x = N
2 − 2. Since any shortest clockwise path from 0 to x in G will not use the edge e,
distH,R(0, x) = distG,R(0, x)
by Theorem 1
= w + 2k.
Since any shortest counterclockwise path from 0 to x in H must travel via node N − 2, distH,L(0, x) = 2 + distH,L(n − 2, x) = 2 + distH,L(0, x − (n − 2))
by Theorem 2
= 2 + w − 3.
Thus dH(0, x) = w − 1. By Theorem 3, D(G) = w − 2. By (1), CR(N, w) is non-dei.
4.5
CR(N, w) with N ≥ (w − 3)(w + 1) + 2
When N ≥ (w − 3)(w + 1) + 2, Case 1 of the Diameter Theorem occurs and we have the following result.
Theorem 11. For N ≥ (w − 3)(w + 1) + 2, we have:
(a) CR(N, w) is non-dei if N = (w − 3)(w + 1) + 2 + 2k(w + 1), w ≥ 5 and k ≥ 0.
(b) CR(16, 5) is non-dei.
(c) CR(N, w) is dei if N = (w − 3)(w + 1) + 4 + 2k(w + 1) and (w = 5 and k ≥ 1) or (w ≥ 7 and k ≥ 0).
(d) CR(N, w) is non-dei if N = (w − 3)(w + 1) + 2t + 2k(w + 1), w ≥ 5, 3 ≤ t ≤ w+3 2
and k ≥ 0.
(f) CR(N, w) is non-dei if N = (w −3)(w + 1) + 2(w −t) + 2k(w + 1), w ≥ 7, 0 ≤ t ≤ w−7 2
and k ≥ 0.
(g) CR(N, w) is non-dei if N = (w − 1 + 2k)(w + 1), w ≥ 5 and k ≥ 0.
Proof. Consider (a). Let G = CR(N, w), e = (0, 1), and H = G − e. Consider the node x = N2 − 1. Since any shortest counterclockwise path from 0 to x in G will not use the edge e,
distH,L(0, x) = distG,L(0, x)
by Theorem 2
= w − 1 + 2k.
Since any shortest clockwise path from 0 to x in H must use the edge (0, N − 1),
distH,R(0, x) = 2 + distG,R(w − 1, x) = 2 + distG,R(0, x − (w − 1))
by Theorem 1
= 2 + w − 3 + 2k.
Thus dH(0, x) = w − 1 + 2k. By Theorem 3, D(G) = w − 2 + 2k. By (1), G is non-dei.
Consider (b). Let G = CR(16, 5), e = (0, 1), and H = G − e. It is not difficult to see from Fig. 15 that dH(0, 1) = 5. By Theorem 3, D(G) = 4. By (1), CR(16, 5) is non-dei.
Figure 15: The graph H = G − e, where G = CR(16, 5) and e = (0, 1). The number inside parentheses is the distance to node 0.
The proofs of (c) and (e) are similar to that of Theorem 10(B) and we omit them. Consider (d). Let G = CR(N, w), e = (0, N − w), and H = G − e. Consider the node x = N
2 − t + 3. Since any shortest clockwise path from 0 to x in G does not use edge e,
distH,R(0, x) = distG,R(0, x)
by Theorem 1
Since any shortest counterclockwise path from 0 to x in H must travel via node N − 2, distH,L(0, x) = 2 + distH,L(N − 2, x) = 2 + distH,L(0, x − (N − 2))
by Theorem 2
= 2 + w − 2 + 2k.
Thus dH(0, x) = w + 2k. By Theorem 3, D(G) = w − 1 + 2k. By (1), G is non-dei.
Consider (f). Let G = CR(N, w), e = (0, N − w), and H = G − e. Consider the node x = N
2 + t + 3. Since any shortest clockwise path from 0 to x in G will not use the edge e,
distH,R(0, x) = distG,R(0, x)
by Theorem 1
= w + 2k.
Since any shortest counterclockwise path from 0 to x in H must travel via node N − 2, distH,L(0, x) = 2 + distH,L(N − 2, x) = 2 + distH,L(0, x − (N − 2))
by Theorem 2
= 2 + w − 1 + 2k.
Thus dH(0, x) = w + 2k + 1. By Theorem 3, D(G) = w + 2k. By (1), G is non-dei.
Consider (g). Let G = CR(N, w), e = (0, N − w), and H = G − e. Consider the node x = N
2 + 2. Since any shortest clockwise path from 0 to x in G will not use the edge e,
distH,R(0, x) = distG,R(0, x)
by Theorem 1
= w + 2k.
Since any shortest counterclockwise path from 0 to x in H must travel via node N − 2, distH,L(0, x) = 2 + distH,L(N − 2, x) = 2 + distH,L(0, x − (N − 2))
by Theorem 2
= 2 + w − 1 + 2k.
5
Concluding remarks
The purpose of the thesis is to discuss the dei property of chordal ring networks. The chordal ring network is a commonly used extension of the ring network. In [1], Arden and Lee proposed a formula for computing the diameter of a chordal ring network CR(N, w). In this thesis, we have shown that this formula is incorrect. We have successfully de-termined if CR(N, w) is dei for all w ∈ {3, 5, 7, 9}. Arden and Lee’s formula actually contains three cases: Cases 1 and 2 are correct and Case 3 is incorrect (see the Diameter Theorem for details). In this thesis, we have successfully determined if CR(N, w) is dei for Cases 1 and 2 and some special cases of Case 3.
Before ending this thesis, we list the dei results for chordal ring networks CR(N, w) with N ≤ 200 and w ≤ 11 in the following table. For clarity, we omit the word “non-dei”, and “?” means “not determined yet”. From this table, it is easy to see that
when w = 3 and N ≥ 8, there is a dei graph whenever N increases w + 1; when w = 5 and N ≥ 22, there is a dei graph whenever N increases w + 1; and when w ≥ 7 and N ≥ (w − 3)(w + 1) + 4, there is a dei graph if N increased w + 1.
N \ w 3 5 7 9 11 6 Thm 7 8 dei Thm 7 10 Thm 7 Thm 8 12 dei Thm 7 Thm 8 14 Thm 7 Thm 11 Thm 8 16 dei Thm 7 Thm 11 Thm 8 18 Thm 7 Thm 11 Thm 10 Thm 8 20 dei Thm 7 Thm 11 Thm 10 Thm 8
22 Thm 7 dei Thm 11 dei Thm 10 dei Thm 9 Thm 8 24 dei Thm 7 Thm 11 dei Thm 10 dei Thm 9 Thm 8 26 Thm 7 Thm 11 dei Thm 10 Thm 9 ? 28 dei Thm 7 dei Thm 11 Thm 10 Thm 9 ? 30 Thm 7 Thm 11 Thm 10 Thm 9 ? 32 dei Thm 7 Thm 11 Thm 10 Thm 9 ? 34 Thm 7 dei Thm 11 Thm 11 Thm 9 ? 36 dei Thm 7 Thm 11 dei Thm 11 Thm 9 ? 38 Thm 7 Thm 11 Thm 11 Thm 9 ? 40 dei Thm 7 dei Thm 11 Thm 11 dei Thm 9 ? 42 Thm 7 Thm 11 Thm 11 dei Thm 10 ? 44 dei Thm 7 Thm 11 dei Thm 11 Thm 10 ? 46 Thm 7 dei Thm 11 Thm 11 dei Thm 10 ? 48 dei Thm 7 Thm 11 Thm 11 dei Thm 10 ? 50 Thm 7 Thm 11 Thm 11 dei Thm 10 ? 52 dei Thm 7 dei Thm 11 dei Thm 11 dei Thm 10 ? 54 Thm 7 Thm 11 Thm 11 Thm 10 ? 56 dei Thm 7 Thm 11 Thm 11 Thm 10 ? 58 Thm 7 dei Thm 11 Thm 11 Thm 10 ? 60 dei Thm 7 Thm 11 dei Thm 11 Thm 10 ? 62 Thm 7 Thm 11 Thm 11 Thm 11 ? 64 dei Thm 7 dei Thm 11 Thm 11 dei Thm 11 ? 66 Thm 7 Thm 11 Thm 11 Thm 11 ? 68 dei Thm 7 Thm 11 dei Thm 11 Thm 11 ? 70 Thm 7 dei Thm 11 Thm 11 Thm 11 ? 72 dei Thm 7 Thm 11 Thm 11 Thm 11 ? 74 Thm 7 Thm 11 Thm 11 dei Thm 11 dei Thm 10 76 dei Thm 7 dei Thm 11 dei Thm 11 Thm 11 Thm 10 78 Thm 7 Thm 11 Thm 11 Thm 11 dei Thm 10 80 dei Thm 7 Thm 11 Thm 11 Thm 11 dei Thm 10 82 Thm 7 dei Thm 11 Thm 11 Thm 11 dei Thm 10 84 dei Thm 7 Thm 11 dei Thm 11 dei Thm 11 dei Thm 10 86 Thm 7 Thm 11 Thm 11 Thm 11 dei Thm 10 88 dei Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 10 90 Thm 7 Thm 11 Thm 11 Thm 11 Thm 10 92 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 10 94 Thm 7 dei Thm 11 Thm 11 dei Thm 11 Thm 10 96 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 10 98 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 100 dei Thm 7 dei Thm 11 dei Thm 11 Thm 11 dei Thm 11 102 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11
N \ w 3 5 7 9 11 104 dei Thm 7 Thm 11 Thm 11 dei Thm 11 Thm 11 106 Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 11 108 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 11 110 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 112 dei Thm 7 dei Thm 11 Thm 11 Thm 11 dei Thm 11 114 Thm 7 Thm 11 Thm 11 dei Thm 11 Thm 11 116 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 11 118 Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 11 120 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 122 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 124 dei Thm 7 dei Thm 11 dei Thm 11 dei Thm 11 dei Thm 11 126 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 128 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 130 Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 11 132 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 11 134 Thm 7 Thm 11 Thm 11 dei Thm 11 Thm 11 136 dei Thm 7 dei Thm 11 Thm 11 Thm 11 dei Thm 11 138 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 140 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 11 142 Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 11 144 dei Thm 7 Thm 11 Thm 11 dei Thm 11 Thm 11 146 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 148 dei Thm 7 dei Thm 11 dei Thm 11 Thm 11 dei Thm 11 150 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 152 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 154 Thm 7 dei Thm 11 Thm 11 dei Thm 11 Thm 11 156 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 11 158 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 160 dei Thm 7 dei Thm 11 Thm 11 Thm 11 dei Thm 11 162 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 164 dei Thm 7 Thm 11 dei Thm 11 dei Thm 11 Thm 11 166 Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 11 168 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 170 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 172 dei Thm 7 dei Thm 11 dei Thm 11 Thm 11 dei Thm 11 174 Thm 7 Thm 11 Thm 11 dei Thm 11 Thm 11 176 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 178 Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 11 180 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 11 182 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 186 dei Thm 7 dei Thm 11 Thm 11 dei Thm 11 dei Thm 11 186 Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 188 dei Thm 7 Thm 11 dei Thm 11 Thm 11 Thm 11 190 Thm 7 dei Thm 11 Thm 11 Thm 11 Thm 11 192 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 11 194 Thm 7 Thm 11 Thm 11 dei Thm 11 Thm 11 196 dei Thm 7 dei Thm 11 dei Thm 11 Thm 11 dei Thm 11 198 dei Thm 7 Thm 11 Thm 11 Thm 11 Thm 11
References
[1] B. W. Arden and H. Lee, Analysis of chordal ring network networks, IEEE Trans. Comput. C-30 (1981) 291-295.
[2] J. C. Bermond, F. Comellas, and D. F. Hsu, Distributed loop computer-networks - a survey, J. Parallel and Distrib. Comput. 24(1) (1995) 2-10.
[3] G. Chartrand and L. Lensniak, Graph and Digraphs, Wadsworth, Monterey, CA, 1981.
[4] S. K. Chen, F. K. Hwang, and Y. C. Liu, Some Combinatorial Properties of Mixed chordal ring networks, Journal of Interconnection Networks 4 (2003) 3-16.
[5] R. D. Dutton, S. R. Medidi, R. C. Brigham, Changing and unchanging of the radius of a grapg, Linear Algebra Appl. 217 (1995) 67-82.
[6] F. Glivjak, On certain classes of graphs of diameter two without superfluous edges, Acta F.R.N. Univ. Comen. Math. 21 (1968) 39-48.
[7] F. Glivjak, On certain edge-critical graphs of a given diameter, Mat. Casopis Sloven Akad Vied. 25 (1975) 249-263.
[8] F. Glivjak, On the impossibility to construct diametrically critical graphs by exten-sions, Arch. Math. (Brno) 11 (1975) 131-137.
[9] D. Greenwill and P. Johnson, On subgraphs of critical graphs of diameter k, Proc. 10th S-E Conf. Combinatorics, Graph Theory and Computing (1979) 465-467.
[10] J. Hartman and I Rubin, On Diameter Stability of graphs, in Theory and Applica-tions of Graphs, Eds. Y. Alavi and D. R. Lick, Springer Lecture Notes in Mathematics, vol. 642 (1978) 247-254.
[11] F. K. Hwang, A complementary survey on double-loop networks, Theor. Comput. Sci. 263(1-2) (2001) 211-229.
[12] F. K. Hwang and P. E. Wright, Survival reliability of some double-loop networks and chordal ring networks, IEEE Trans. Comput. 44(12) (1995) 1468-1471.
[13] H. Lee, Modeling of multi-microcomputer networks, Ph. D. dissertation, Princeton Univ., Princeton NJ, Nov. 1979.
[14] S. M. Lee, Design of diameter e-invariant networks, Congr. Numer. 65 (1988) 89-102.
[15] S. M. Lee and R. Tanoto, Three classes of diameter edge-invariant graphs, Commen-tationes Mathematics Univ. Carolinae 28 (1987) 227-232.
[16] S. M. Lee and A. Y. Wang, On critical and cocritical diameter edge-invariant net-works, in Graph Theory, Combinatorics and Applications, vol. 2, Kalamazoo 1988, Wiley, New York, 1991, 753-763.
[17] O. Ore, Diameter in graph, J. Comb. Theory Ser. B 5 (1968) 75-81.
[18] A. A. Schone, H. L. Bodlaender and J. van Leeuwen, Diameter increase caused by edge deletion, J. Graph Theory 11 (1987) 409-427.
[19] O. Vacek, Diameter-invariant graphs, Mathematica Bohemica 130(4) (2005) 355-370.
[20] H. B. Walikar, F. Buckley, and M. K. Itagi, Radius-edge-invariant and diameter-edge-invariant graphs, Discret. Math. 272 (2003) 119-126.
[21] D. B. West, Introduction to Graph Theory, 2nd ed. Prentice Hall, Upper Saddle River, NJ, 2001.
[22] C. K. Wong and D. Coppersmith, A combinatorial problem related to multimodule memory organizations, J. ACM 21(3) (1974) 392-402.