Performance Evaluation of Multimedia Services over Rayleigh Fading Channel

全文

(1)Int. Computer Symposium, Dec. 15-17, 2004, Taipei, Taiwan.. 1. Performance Evaluation of Multimedia Services over Rayleigh Fading Channel Yung-Chung Wang EE, NTUT Taipei 106, Taiwan ycwang@ee.ntut.edu.tw. Abstract— With the increasing number of wireless network infrastructure deployment and the popularity of portable computing devices, more and more internet users are experiencing ubiquitous mobility using both these computing devices and the wireless networks to access the Internet. Therefore, it is necessary to study the loss behavior of the multimedia applications such as Web Browsing, VoIP, Teleconferencing, over wireless networks. This paper applies a matrix-analytic approach to analyze the loss probability of multimedia services over a Rayleigh fading channel. Due to the versatility of Discrete-time Markovian arrival process (D-BMAP) as an input process, the queuing model of the Burst-error communication channel is a D-BMAP/D/1/K queue, where K is the buffer capacity. Keywords— Rayleigh fading channel, Discrete-time Markovian arrival process (D-BMAP), Finite-state Markov Model.. I. I NTRODUCTION With the increasing number of wireless network infrastructure deployment and the popularity of portable computing devices such as PDA, handset and notebook computer, more and more internet users are experiencing ubiquitous mobility using both these computing devices and the wireless networks to access the Internet. According to this growth, the applications in the wire Internet such as Web browsing, voice over IP (VoIP), Teleconferencing etc. are moving gradually toward the wireless environment. However, the characteristics of the wireless environment are very different from the wireline networks. There are different Burst-error properties in the wireless network due to the multipath fading channel and the mobility property of the communication device in the wireless environment [24]. Therefore, it is necessary to study the loss behavior of the multimedia applications such as Web Browsing, VoIP, Teleconferencing, over wireless networks. The error process of the wireless channel has memory property due to the multipath fading channel effect and the mobility of the communication device in the wireless networks. This memory property of the error process is the main factor to determine the performance of the Rayleigh fading channel. So far, much research attention has focused on the mathematical model of the varied Burst-error property of the wireless networks. Among them, the Hidden Markov model is universally applied to model the Rayleigh fading channel [3][7][20][21][22][24]. For example, Elliott [6] and Gilbert [8] applied a two-state. Gilbert-Elliot channel to model wireless environment. However, this two-state Gilbert-Elliot channel is not adequate to model the wireless networks because the channel quality can vary dramatically. Thus it is necessary to extend the two-state Gilbert-Elliot model to a finite-state one, which is called finitestate Markov channel (FSMC) model [3][21][22]. In this paper, the wireless channel is regarded as a finite-state Markov channel model. So far, much research attention has applied the hidden Markov chain model to describe the Rayleigh fading channel property and analyzed the performance over different kind protocols [17][18][19][25]. All of the above papers consider the input process as traditional Markov process such as Poisson process. Because the traditional Markov model can not adequately capture the property of the complex multimedia traffic, such as Web Browsing, VoIP, Teleconferencing, it is necessary to propose a suitable traffic model to describe the multimedia applications over the wireless networks. Thus the packet stream is considered to follow a discrete-time Batch Markovian arrival process (D-BMAP)[2][10][11][12][13]. The queueing model of the multimedia services over a Rayleigh fading channel can be modeled as D-BMAP/D/1/K. We apply a matrix-analytic approach to analyze both the long-term loss behavior of multimedia services over a Rayleigh fading channel [1][4][14][16][23]. This paper is organized as follows: In Section II, the finite state Markov chain model for Rayleigh fading channel is briefly introduced. In Section III, the Discrete-time Batch Markovian arrival process as the input traffic model of multimedia services over a Rayleigh fading channel system is briefly introduced. In Section IV, the loss behavior of the D-BMAP/D/1/K queueing system for the Rayleigh fading channel is analyzed. Experimental numerical results are computed and discussed in Section V to reveal the computational tractability of our analysis and to develop better understanding of the multimedia applications over a Rayleigh fading channel. Concluding remarks are given in Section VI.. II. FSMC FOR THE R AYLEIGH FADING C HANNEL In many cases, modeling a Rayleigh fading channel as a two-state Gilbert-Elliot channel [8] is not adequate because the channel quality can vary dramatically. Thus it is necessary to extend the two-state model to a finite-state one, which is called finite-state Markov channel (FSMC) model [22]. FSMC This work was supported by the National Science Council, Taiwan, under Contract NSC92-2213-E-027-047. The author is with the Department of Elec- model comes from the fact that the use of received signaltrical Engineering, National Taipei University of Technology, Taipei, Taiwan. to-noise ration (SNR) as the side information in cellular net989.

(2) 2. Int. Computer Symposium, Dec. 15-17, 2004, Taipei, Taiwan. works is highly time-varying. FSMC provides a mathematically tractable model for time-varying channels and use only the received SNR of the mobile host. Since a typical time-varying channel, namely the Rayleigh fading channel, produces time-varying received SNR, by partitioning the range of the received SNR into a finite number of intervals, a FSMC model can be built for the Rayleigh fading channel. A finite state Markov Chain channel is defined by its transition probabilities and crossover probability matrix. We denote our discrete-time Markov Chain by {R(t)}t≥0 with sate space {1, . . . , M } and transition probability matrix H = [hi,j ]. Let A denote the received SNR that is proportional to the square of the signal envelop. The probability density function (PDF) of A is exponential [15] and can be written as fA (x) =. 1 − xξ e ξ. (1). where ξ is the expected value of A. Let 0 = A0 < A1 < · · · < AM −1 < AM = ∞ be the thresholds of the received SNR. Then the Rayleigh fading is said to be in state k, k = 1, 2, · · · , M , if the received SNR is in the interval [Ak−1 , Ak ). Let Nk , k ∈ {1, · · · , M }, be the expected number of times per second the received SNR passes downward across the threshold Ak . We have s Ak 2πAk (2) fm e− ξ , k = 1, · · · , M Nk = ξ where fm is the maximum Doppler frequency. To determine the transition probability matrix of R(t), we note that secondorder or high-order Markov model is unnecessary for R(t), that is, the element of H has the following result hi,j = 0, ∀ |i − j| > 1. (3). Consider a communication system with a transmission rate of C packet per second. The average packets per second transmitted during which the radio channel is in state k is C (k) = C × ψk. (4). where the steady state probability for each state is Z. Ak. Ak−1 Ak 1 − xξ e dx = e− ξ − e− ξ k = 1, 2, · · · , M. Ak−1 ξ (5) Based on the slow fading assumption of the Rayleigh fading channel, the level crossing rate should be much smaller than the value of C (k) at SNR threshold Ak . Thus we can get the approximated value of R(t) transition probabilities as follows. ψk =. hk,k+1. ≈. hk,k−1. ≈. hk,k h1,1. = = =. hM,M. Nk+1 , k ∈ {1, 2, · · · , M − 1} C (k) Nk , k ∈ {2, · · · , M } C (k) 1 − hk,k−1 − hk,k+1 , k ∈ {2, · · · , M − 1} 1 − h1,2 1 − hM,M −1. Associated with each state, there is a binary symmetric channel with crossover probability ek , which is related to the received SNR thresholds. Generally the binary phase shift keying (BPSK) is assumed with coherent demodulation. The error probability as a function of the received SNR can be written as p (6) e(x) = 1 − erf c( (2x)) where. Z. x. p. erf c(x) = −∞. 1 (2π). e−. x2 2. dx. (7). With the PDF of the received SNR as in (1), the crossover probability for each state is ´ p R Ak 1 − x ³ e ξ 1 − erf c( (2x)) dx Ak−1 ξ , k = 1, 2, · · · , M. ek = R Ak 1 x e ξ dx Ak−1 ξ (8) Note ek is actually the packet error probability for each particular channel state. And the error probability matrix Ee is define as Ec = Diag(e1 , e2 , · · · , eM ). And the success probability matrix Ec is equal to I − Ee . III. T RAFFIC M ODEL It is illustrated in [13] that traffic with certain bursty features can be qualitatively modeled by a generic Markovian arrival process, called the batch Markovian arrival process (BMAP). BMAP is a generalization of the batch Poisson process which allows for non-exponential inter-arrival times of batches, while still preserving an underlying Markovian structure. It is a point process with group arrivals generated at the transition epochs of a particular type of m-state Markov process. Many familiar processes such as MMPP, PH-renewal process and MAP can be considered as special cases of BMAP [10][13]. The application of discrete-time BMAP (D-BMAP) is proposed in [5] to model video sources. The arrival processes discussed in this paper are assumed to be D-BMAPs since time is assumed to be slotted. A D-BMAP can be described by a special type of discretetime Markov chain. Let {(N (t), J(t))}t≥0 be a discrete-time Markov chain with two-dimensional state space {(l, j)| l ≥ 0, 1 ≤ j ≤ m} and transition probability matrix   D0.  0 0. D1 D0 0. D2 D1 D0. D3 D2 D1 .. ... ... ... .... . where N (t) stands for a counting variable, J(t) represents an auxiliary state or phase variable, and Di ’s are non-negative m× m matrices whose entries are between 0 and 1, called parameter matrices. The transition probability from state (l, j) to state (l+i, j 0 ), which corresponds to the arrival of a batch of size i, is the (j, j 0 )th entry (Di )j,j 0 of the m×m matrix Di . (Di )j,j 0 may depend on phases j and j 0 . The sum of all parameter matrices D=. 990. ∞ X i=0. Di. (9).

(3) 3. Int. Computer Symposium, Dec. 15-17, 2004, Taipei, Taiwan. is an m × m stochastic matrix which is the transition probability matrix of the underlying Markovian structure {J(t)}t≥0 with respect to the D-BMAP. (I − D0 ) is assumed to be nonsingular such that the sojourn time at any state of the state space {(l, j)| l ≥ 0, 1 ≤ j ≤ m} is finite with probability 1, thus guaranteeing that the process never terminates. The fundamental arrival rate λ of this D-BMAP can then be defined as λ = π(. ∞ X. iDi )e. (10). i=1. where π is the stationary probability vector of D in (9), i.e. πD = π, πe = 1, and e is assumed in this paper to be the all-1 column vector with the designated dimension. IV. L OSS B EHAVIOR OF M ULTIMEDIA S ERVICES OVER W IRELESS L INK As demonstrated in the previous section, traffics will be modeled by D-BMAPs. Determining the characterizing parameter matrices for a D-BMAP is, of course, an essential problem. This obstacle is not dealt with here since a large class of variable bit rate (VBR) sources and their superpositions have already been studied in [5]. In this section, the proposed basic model is described, and used to examine the related loss information. We consider a single server queue with a buffer size K. With time slotted and service time assumed to be constant for each packet, the queue with finite buffer capacity K (packets) can be modeled by a D-BMAP/D/1/K queue. Consider the embedded Markov chain {(L(t), J(t), R(t))}t≥0 of the queueing system, which can be described as a particular type of semi-Markov process where the state jumps regularly at a constant slot time. This is considered in the state space {0, 1, . . . , K} × {1, 2, . . . , m} × {1, 2, . . . , M }, where L(t), J(t), and R(t) denote the buffer occupancy, the phase of the D-BMAP, and the state of the wireless channel respectively at the end of the t-th time slot. For convenience, the queueing system is said to be at a level j if its buffer occupancy is equal to j. The embedded Markov chain now has an irreducible transition probability matrix of the following block form  P∞ D0 ⊗ H D1 ⊗ H ··· Di ⊗ H i=K P ∞  D0 ⊗ Ec H D0 ⊗ Ee H + D1 ⊗ Ec H · · · P∞i=K Fi  0 D0 ⊗ Ec H ··· F  i=K−1 i Q= . . . .  . . .. . . .  P∞.  0 0 ··· F i=2 i P∞ 0. 0. ···. i=1. Fi. (11) where Fi = Di−1 ⊗ Ee H + Di ⊗ Ec H and ⊗ is the Kronecker product [9]. Each block is of dimension mM × mM and corresponds to the transition from one buffer level to another buffer level. ¯ = [x0 , x1 , . . . , xK ] Let x with xk = [xk,1,1 , xk,1,2 , . . . , xk,m,M ] ∀k, be the steady-state proba¯Q = x ¯ and x ¯ e = 1. bility vector of the queueing system, i.e. x Let Lloss denote the number of packets lost during a time slot, with only long-term packet loss probability considered as significant. Now, the expected value E[Lloss ] of Lloss can be. evaluated as E[Lloss ] = x0. Ã∞ X. ! iDK+i ⊗ H. e. i=1. +. K X. xk. Ã∞ X. ! i(DK−k+i ⊗ Ee H + DK−k+1+i ⊗ Ec H) e.. i=1. k=1. Consequently, the long-term packet loss probability, denoted by Ploss , is E[Lloss ] (12) Ploss = λ where λ is the fundamental arrival rate of the packet stream as in (10). V. N UMERICAL R ESULTS In this section, we will investigate and discuss the numerical results from a wireless link queueing system. The time is slotted such that the unit time is equal to the packet transmission time, which is equal to (500 bits)/(C kbits/s), where C kbits/s is the link capacity of the wireless channel. The numerical results are computed by the algorithm developed in the previous section. In this paper, the arrival process has the mean rate µ kbits/s, the standard deviation of the rate σ kbits/s, and the autocovariance function of the rate r(τ ) = σ 2 e−aτ . By the methods proposed in [5] to model the arrival process by a D-BMAP, the underlying Markovian structure for the traffic is assumed to be an m-state birth-and-death process, where each of the m states (i.e. phases) corresponds to a level in the uniform quantization of the rate, from 0 to m − 1, with the transition probability matrix  1 − (m − 1)p  (m − 1)p ··· 0  D= . q 0 .. . 0. 1 − q − (m − 2)p 2q .. . 0. ··· ··· .. . ···. 0 0 .. . 1 − (m − 1)q.   . in which p = a/[1 + (1/(m − 1))(µ2 /σ 2 )] and q = a/[1 + (m − 1)(σ 2 /µ2 )]. And the sequences {Di }i≥0 of parameter matrices for the packet traffic are  a (0)  0 ··· 0 i  0 a (1) · · · 0 i   . . Di =  ..  D, ∀i ≥ 0 ..  .. .. .  .  0 0 · · · ai (m − 1)   µ ¶   k respectively, where ai (k) = η i (1 − η)k−i with η = i (µ/(m − 1) + σ 2 /µ)/C. Note that Di = 0 for all i ≥ m. In this example, the arrival process has the mean rate µ = 600 kbits/s, the standard deviation of the rate σ = 250 kbits/s, and the autocovariance function of the rate r(τ ) = 2502 e−0.025τ . In this study, we have selected m = 10 such that the highest level of rate of the birthand-death underlying Markovian structure corresponds to the peak rate of the traffic. By the way, we have selected 8 thresholds of the received SNR of fading channel. The maximum Doppler frequency fm will be adjusted such that the fading channel has different conditions. The capacity C 991.

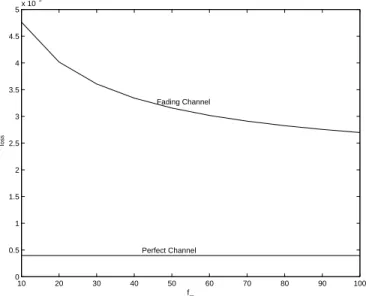
(4) 4. Int. Computer Symposium, Dec. 15-17, 2004, Taipei, Taiwan. −3. 5. x 10. 4.5. 4. 3.5 Fading Channel. loss. 3. P. kbits/s of the fading channel is 1000 kbits/s that the system has load condition ρ = 0.6. Based on theses setting, we have the transition probability matrix H = [hi,j ] of the fading channel as shown in Table I and II and the error probability matrix Ee = Diag(0.3272, 0.1968, 0.1256, 0.0768, 0.0432, 0.0216, 0.008, 0.0008). The buffer capacity K is taken to be 30 due to the practical application. In Figure 1, we can find that the loss probability Ploss in the fading channel is higher than the loss probability Ploss in the perfect channel.. 2.5. 2. 1.5. VI. C ONCLUSIONS 1. This paper applies matrix-analytic approach to investigate the loss behavior of multimedia services over a Rayleigh fading channel. We have examined the packet loss probabilities. We use this queuing model to quantify the effects of multimedia services over a Rayleigh fading channel.. 0.5. 0 10. Perfect Channel. 20. 30. 40. 50. 60. 70. 80. 90. 100. fm. Fig. 1. Long-term loss probability in a wireless link queueing system with fading channel.. R EFERENCES [1] H. Akaike, “Block Toeplitz matrix inversion,” SIAM J. Appl. Math., vol. 24, no. 2, pp. 234–241, Mar. 1973. [2] N. Akar, N. C. Oguz, and K. Sohraby, “Matrix-geometric solutions of M/G/1-type Markov chains: A unifying generalized state-space approach,” IEEE J. Select. Areas Commun., vol. 16, no. 5, pp. 626–639, June 1998. [3] F. Babich, O. E. Kelly, and G. Lombardi, “A variable-order discrete model for the mobile propagation channel,” Broadband Wireless Channels, pp. 259–266, 1998. [4] R. Bellman, Introduction to Matrix Analysis, 2nd edn. New York: McGraw-Hill, 1970. [5] C. Blondia and O. Casals, “Statistical multiplexing of VBR sources — A matrix-analytic approach,” Performance Evaluation, 16, pp. 5–20, 1992. [6] E. O. Elliott, “Estimates of error rates for codes on burst-noise channels,” Bell. Syst. Tech. J., vol. 42, pp. 1977-1997, Sep. 1963. [7] B. D. Fritchman, “A binary channel characterization using partitioned Markov chains,” IEEE Trans. Inform. Theory, vol. IT-13, pp. 221-227, Apr. 1967. [8] E. N. Gilbert, “Capacity of a burst-noise channel,“ Bell. Syst. Tech. J., vol. 39, No. 5, pp. 1253-1265, Sep. 1960. [9] A. Graham, Kronecker Products and Matrix Calculus with Applications. New York: Horwood Halsted Press, 1981. [10] D. M. Lucantoni, “New results on the single server queue with a batch Markovian arrival process,” Commun. Statist. Stochastic Models, 7(1), pp. 1–46, 1991. [11] M. F. Neuts, Matrix-Geometric Solutions in Stochastic Models — An Algorithmic Approach. Baltimore and London: The Johns Hopkins University Press, 1981. [12] M. F. Neuts, Structured Stochastic Matrices of M/G/1 Type and Their Applications. New York: Marcel Dekker, 1989. [13] M. F. Neuts, “Models based on the Markovian arrival process,” IEICE Trans. Commun., vol. E75-B, no. 12, pp. 1255–1265, Dec. 1992. [14] D. V. Ouellette, “Schur complements and statistics,” Linear Algebra and its Applications, 36, pp. 187–295, March 1981. [15] J. G. Proakia, Digital Communications 2nd ed. New York: McGraw Hill, 1989 [16] E. Seneta, Nonnegative Matrices and Markov Chains, 2nd ed. New York: Springer-Verlag, 1981. [17] D. Towsley, “A statistical analysis of ARQ protocols operating in a nonindependent error environment,” IEEE Trans. Commun., Vol. COM-29, pp. 971-981, July 1981. [18] D. Towsley, “The analysis of a statistical multiplexer with nonindependent arrivala and error,” IEEE Trans. Commun., Vol. COM-28, pp. 65-72, Jan. 1980. [19] W. Turin, and M. Zorzi, “Performance Analysis of Delay-Constrained Communications Over Slow Rayleigh Fading Channels,” IEEE Trans. Wireless Commun., vol. 1, No. 4, pp. 801–807, Oct. 2002. [20] W. Turin, Digital transmission systems: performance analysis and modeling, New York: McGraw-Hill, 1998. [21] W. Turin, and M. M. Sondhi, “Modeling error sources in digital channels,” IEEE J. Select. Areas in Commun., vol. 11, No. 3, pp. 340–347, Apr. 1993.. [22] H. S. Wang, and N. Moayeri “Finite-state Markov channel – a useful model for radio communication channels,” IEEE Trans. on Vehicular Tech., vol. 44, no.1, pp. 163–171, Feb. 1995. [23] Y.-C. Wang, and C.-C. Lu, “Loss behavior in space priority queue with batch Markovian arrival process –Discrete-time case,” Performance Evaluation, 41, 269-293, 2000. [24] M. Zorzi, R. R. Rao, “On channel modeling for delay analysis of packet communications over wireless links,” Proc. 36th Annual Allerton Conference, Sep. 1998. [25] M. Zorzi, “Packet dropping statistics of a data-link protocol for wireless local communication,” Proc. ICUPC’97, pp. 536-540, Oct. 1997.. 992.

(5) 5. Int. Computer Symposium, Dec. 15-17, 2004, Taipei, Taiwan.. TABLE I. TABLE II. A NALYSIS VALUES OF THE TRANSITION PROBABILITIES MATRIX FOR EIGHT- STATE M ARKOV CHANNEL (fm = 10 ∼ 50H Z ). A NALYSIS VALUES OF THE TRANSITION PROBABILITIES MATRIX FOR EIGHT- STATE M ARKOV CHANNEL (fm = 60 ∼ 100H Z ). fm =10Hz. fm =20Hz. fm =30Hz. fm =40Hz. fm =50Hz. k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8. hk,k−1 0.03205 0.04035 0.04295 0.04175 0.03725 0.0295 0.01805 hk,k−1 0.0641 0.0807 0.0859 0.08350 0.07450 0.0590 0.0361 hk,k−1 0.09615 0.12105 0.12885 0.12525 0.11175 0.0885 0.05415 hk,k−1 0.1282 0.1614 0.1718 0.167 0.15 0.118 0.0722 hk,k−1 0.16025 0.20175 0.21475 0.20875 0.18625 0.1475 0.09025. hk,k 0.96795 0.9276 0.9167 0.9153 0.921 0.93325 0.95245 0.98195 hk,k 0.9359 0.8552 0.8334 0.8306 0.842 0.8665 0.9049 0.9639 hk,k 0.90385 0.7828 0.7501 0.7459 0.763 0.79975 0.85735 0.94585 hk,k 0.8718 0.7104 0.6668 0.6612 0.683 0.732 0.8098 0.9278 hk,k 0.83975 0.638 0.5835 0.5765 0.605 0.66625 0.76225 0.90975. hk,k+1 0.03205 0.04035 0.04295 0.04175 0.03725 0.0295 0.01805 hk,k+1 0.0641 0.0807 0.0859 0.08350 0.07450 0.0590 0.0361 hk,k+1 0.09615 0.12105 0.12885 0.12525 0.11175 0.0885 0.05415 hk,k+1 0.1282 0.1614 0.1718 0.167 0.15 0.118 0.0722 hk,k+1 0.16025 0.20175 0.21475 0.20875 0.18625 0.1475 0.09025 -. fm =60Hz. fm =70Hz. fm =80Hz. fm =90Hz. fm =100Hz. 993. k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8. hk,k−1 0.1923 0.2421 0.2577 0.2505 0.2235 0.1770 0.1083 hk,k−1 0.22435 0.28245 0.30065 0.29225 0.26075 0.2065 0.12635 hk,k−1 0.2564 0.3228 0.3436 0.334 0.298 0.236 0.1444 hk,k−1 0.28845 0.36315 0.38655 0.37575 0.33525 0.2655 0.16245 hk,k−1 0.3205 0.4035 0.4295 0.4175 0.3725 0.295 0.1805. hk,k 0.8077 0.5656 0.5002 0.4918 0.526 0.5995 0.7147 0.8917 hk,k 0.77565 0.4932 0.4169 0.4071 0.447 0.53275 0.66715 0.87365 hk,k 0.7436 0.4208 0.3336 0.3224 0.368 0.466 0.6196 0.8556 hk,k 0.71155 0.3484 0.2503 0.2377 0.289 0.39925 0.57205 0.83755 hk,k 0.6795 0.276 0.167 0.153 0.21 0.3325 0.5245 0.8195. hk,k+1 0.1923 0.2421 0.2577 0.2505 0.2235 0.1770 0.1083 hk,k+1 0.22435 0.28245 0.30065 0.29225 0.26075 0.2065 0.12635 hk,k+1 0.2564 0.3228 0.3436 0.334 0.298 0.236 0.1444 hk,k+1 0.28845 0.36315 0.38655 0.37575 0.33525 0.2655 0.16245 hk,k+1 0.3205 0.4035 0.4295 0.4175 0.3725 0.295 0.1805 -.

(6)