單迴路積分三角類比數位轉換器之積分器充電雜訊與諧波功率模型

國

立

交

通

大

學

電機與控制工程系

碩

士

論

文

單迴路積分三角類比數位轉換器之積分

器充電雜訊與諧波功率模型

Analytical Settling Noise and Distortion Power Models

of Sigma-Delta ADCs

研 究 生：黃俊傑

指導教授：陳福川 教授

單迴路積分三角類比數位轉換器之積分器充電雜訊

與諧波功率模型

Analytical Settling Noise and Distortion Power Models

of Sigma-Delta ADCs

研 究 生：黃俊傑 Student：Chun-Chieh Huang

指導教授：陳福川 Advisor：Fu-Chuang Chen

國 立 交 通 大 學

電 機 與 控 制 工 程 系

碩 士 論 文

A Thesis

Submitted to Department of Electrical and Control Engineering College of Electrical Engineering

National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master

In

Electrical and Control Engineering September 2008

Hsinchu, Taiwan, Republic of China

單迴路積分三角類比數位轉換器之

積分器充電雜訊與諧波功率模型

研究生：黃俊傑 指導教授：陳福川 教授 國立交通大學 電機與控制工程研究所

摘要

交換式電容積分器是積分三角轉換器中基本的建構成份。其電容不完全的充 放電轉換特性(積分器充放電問題)為積分三角轉換器中一個主要影響輸出誤差 的來源。而因為積分器充放電問題的高複雜性,相關的誤差和失真的解析模型實 際上是不存在的。在此篇論文中,我們的目的在於經由非線性擬合方法和輸出端 頻譜預測技術來分析積分器充放電問題。由上法,積分器充放電問題誤差和失真 的封閉解可獲得,且可使用積分三角轉換器中的系統參數來組成函數以呈獻出 來。同時我們使用了行為層的模擬以及HSPICE 電路的模擬來驗證此解析模型的 正確性,驗證結果顯示出我們的解析模型是足夠精確的。

Analytical Settling Noise and Distortion Power

Models of Single-Loop Sigma-Delta ADCs

Student：Chun-Chieh Huang Advisor：Dr. Fu-Chuang Chen

Institute of Electrical and Control Engineering Nation Chiao Tung University

ABSTRACT

Switch-capacitor (SC) integrator is the basic building component for sigma-delta ( ) modulators and its incomplete charge transfer (settling problem) constitutes one of the dominant error sources in

ΣΔ

ΣΔ modulators. Due to the complexity of settling problem, analytic models for related noises and distortions are virtually non-existent. In this paper, we aim to analyze the settling problems by employing nonlinear fitting methods and output spectrum prediction techniques. Closed forms of settling error and settling distortion models are obtained, and are represented as functions of modulator system parameters. Both behavior simulations and HSPICE circuits are employed to verify these analytical models, and the results show that our analytical models are sufficiently accurate.

Contents

中文摘要 ... I English Abstract...II Acknowledgment...III Contents ...IV Lists of Tables ...VII Lists of Figures ...IX List of Symbols ...XIII

Chapter1 Introduction...1

1.1 Current Status and Background...1

1.2 Motivation and Aims...3

1.3 Organization...4

Chapter2 Formulation of ΣΔ Modulators Settling Problems...5

2.1Settling Noise of Sampling Phase and Integration phase...6

2.2 Properties of V_S... ………...8

2.3 Performance Metrics for a ΣΔ Modulator ...11

Chapter3 Derivation of Sigma-Delta Modulator Settling noise Power Model…..…14

3.1Settling Errors of Sampling Phase...14

3.2Settling Errors of Integration Phase...14

Chapter4 Derivations of Sigma-Delta Modulators Settling Distortion…………....24

Chapter5 Simulation Results and Validation………..31

Lists of Tables

Table 2.1 Standard deviations of VS vs. different quantizer bit numbers

………..9 Table.3.1 Coefficients obtained in three cases

………..19 Table.4.1 Minimum SR and GBW required w. r. t. OSR

………....29 Table.5.1 Simulation parameters in Fig. 5.3

………33 Table.5.2Minimum SR and GBW required w. r. t. OSR

Lists of Figures

Fig. 2.1 Single loop second order ΣΔ modulator...5

Fig. 2.2 A typical SC integrator with DAC branches...5

Fig. 2.3 Switched capacitor integrator diagrams （a）Sampling phase （b）Integration phase...7

Fig. 2.4 Simulated results of VS distribution...9

Fig. 2.5 PSD of VS...10

Fig. 2.6 Simulated results of VS with AVS = 0.5, OSR = 16, and different Bits………11

Fig. 2.7 Performance characteristic of a ΣΔ converter………...13

Fig 3.1 Distribution of VS obtained in three cases………18

Fig.3.2 VS versus settling error in three cases……...19

Fig.3.3 The distribution of angle of VS……...19

Fig.3.4. the expect value of (3.16) and the behavior model simulation result……….21

Fig.3.5. The expect value of VS 3 and the simulation result by behavior model……...22

Fig. 3.6. The expect value of VS 5 and the simulation result by behavior model……..22

Fig. 4.1 3D plot of（4.3）………...25

Fig. 4.2 Output spectrum of a second-order ΣΔ modulator with harmonic distortion………...………26

Fig. 4.3 GBW v.s HD3……….27

Fig. 4.4 SR v.s HD3...…28

Fig. 5.1 Circuit-level schematic of spice simulation………29

Fig. 5.2 Quantizer of spice simulation……….29

Fig. 5.3 Comparison of our theoretical result with transistor-level and behavior simulation result………...………30

Fig. 5.4 PSD of settling noise obtained from transistor-level simulation and previous established model……….32

List of Symbols

Symbols

VLSB Quantizer step size

OS

V Maximum output swing of op-amp

OSR OverSampling Ratio

n Order of the Sigma-Delta modulator

B Number of bits in the quantizer

S

f

Sampling Frequency

B

f Signal Bandwidth

ref

V Reference Voltage of the quantizer

0

A Finite Gain of OTA

in

f Frequency of the input signal

i

φ ith phase of a nonoverlap clock

in

A

Amplitude of input signal

.

jit

σ standard deviation of clock jitter

S

C

Sampling capacitor

I

C

Integrating capacitor

L

C

Load capacitor of OTA

Logic

C

The loading capacitors of CMOS logic gates

gate

C The gate capacitances of all CMOS transmission gates

OX

C The capacitance per unit area of the gate oxide

S

V Input signal plus feedback DAC signal

1

τ Time constant of input branch

VS

σ Standard deviation of V_S

2

τ Time constant of integrator output settling

i

η percentage of the bottom plate parasitic

T Absolute temperature R Switch ON resistance

N quantizer levels

gm1 Amplifier transconductance Pr() Probability of some condition

.

cap

σ Mismatch of unit capacitance

k Boltzmann’s constant (1.38×10−23) J/K

α OTA noise factor []

Erf Error Function

OTA

I

Total current of the OTA

B

I Bias current of each transistor of the input differential pair of OTA

OTA

k The ratio of the total current of the OTA to this bias current 2

cl

f The GBW of the OTA

reff

V The overdrive voltage of the transistor of the input differential pair of

OTA

Cs

k The ratio between the summation capacitance of in all stages and

the one in the first stage

S

C

0

ε

The permittivity of free space

S

1.Introduction

1.1 Current Status and Background

Sigma-delta( ) A/D converters have been widely used for implementation of analog-to-digital conversion with high-resolution and low-to-moderate bandwidth ranging from 100Hz to 10MHz like audio [1-3], precision measurement [4], mobile communications [5], worldwide interoperability microwave access (WiMAX) system [6], and broadband wireline application like ADSL [7, 8]. Compared to the traditional converters, modulators have several advantages such as superior linearity and accuracy, simple realization, and low sensitivity to circuit imperfection [9], so modulators have become more suitable for high-resolution and low-power designs.

ΣΔ

ΣΔ

ΣΔ

Switched-capacitor (SC) integrators are basic building components for implementation of circuits. Its incomplete transfer of charge and the slewing effect degrade drastically the performance of

ΣΔ

ΣΔ modulators and remains as the most crucial factor that restricts the performance of ΣΔ modulators. The influence increases as sampling frequency increases, since higher sampling frequency shortens the operating time of the integrator so that the integrator settling error rises. Due to the complexity of settling problem, analytic models for related noises and distortions are virtually non-existent. Recently papers considered transient transfer of charge in SC integrators and proposed several time-domain-based behavioral descriptions [10-12], which can be used in behavior simulations. Behavior simulations are time-consuming, indirect, and difficult to separate settling noises from other noises. On the other hand, analytical efforts are actually seen before. In [18-20], a detailed transient analysis for the charge-transfer error was carried out, but only for linear systems. In [21], the distortion due to operational transconductance amplifier (OTA) dynamics has been

analyzed and modeled. It uses power expansion and nonlinear fitting to obtain analytical model to represent harmonic distortion as a function of the slew-rate (SR), gain-bandwidth (GBW), and nonlinear DC gain, but the settling noise was not discussed. It is coarsely assumed in [13] that the settling noise is white and the associated power spectral density (PSD) is constant in the sampling interval, but this is far from reality.

1.2 Motivation and Aim

Designing of modulators is a very complex process. Recently modulator designing based on numerical optimization [13-15] (behavior simulation) is becoming popular, which requires many computing iterations until best performance is achieved. If the best performance achieved still can not meet the design specification, this approach can provide little clue about the dominating noise or distortion. In contrast, design and optimization based on analytical noise and distortion models can be a more efficient and dependable approach [16, 17], as long as all of the important noise and distortion models are available. Although many noise and distortion models are well derived for

ΣΔ ΣΔ

ΣΔ modulators [], analytical model for switched-capacitor(SC) integrators settling noise is never seen in the literature. For the reasons provided in this and previous paragraphs, the major goal of this paper is to provide the settling noise model.

The settling problems of the SC integrators are mainly caused by non-idealities of OTA such as finite dc gain, finite GBW, and SR limitations. Our research shows that these non-idealities create nonlinear transfer characteristics, which not only cause signal distortions, but also reflect high-frequency noises into base band. By employing nonlinear fitting methods and output spectrum prediction techniques, closed forms of settling error and settling distortion analytical models are obtained, and are represented as functions of ΣΔ modulator system parameters. Both behavior simulations and HSPICE circuits are employed to verify these analytical models, and the results show that our analytical models are sufficiently accurate.

1.3 Organization

This paper is organized as follows. In section II, the motivation of modulators settling effect and properties of the input for SC integrator are discussed. The formulation of analytical settling noise power model is presented in section III with an analytical discussion. In section IV, we develop the model to the settling distortion and discuss the relevance with system parameters. In section V, simulation results including transistor-level and behavior model are used to validate the model do an analytical discussion. in section VI, we provide some conclusions.

2.

Formulation of

ΣΔ

Modulators Settling

Problems

There are two purposes in this section. The first is to clearly define the settling error in switched-capacitor integrators. The second is to explore the properties of VS, which

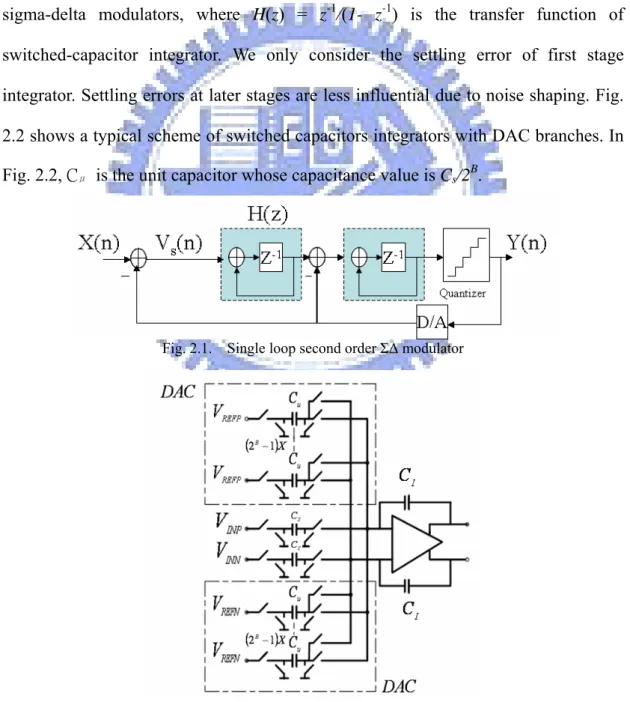
is the input to SC integrator. Fig. 2.1 indicates a standard architecture of second order sigma-delta modulators, where H(z) = z-1

/(1- z-1) is the transfer function of

switched-capacitor integrator. We only consider the settling error of first stage integrator. Settling errors at later stages are less influential due to noise shaping. Fig. 2.2 shows a typical scheme of switched capacitors integrators with DAC branches. In Fig. 2.2, Cμ is the unit capacitor whose capacitance value is C_s/2B.

Fig. 2.1. Single loop second order ΣΔ modulator

2.1 Settling Noise of Sampling Phase and Integration Phase

Sampling and integration phase will be analyzed separately. Fig. 2.3 illustrates sampling and integration phase of SC integrators with the MOS switched on-resistance R and the transconductance of OTA, gm1. Let the output parasitic capacitor be C_L ≅η⋅C_I , where η is the percentage of bottom plate parasitic,

assumed to be 20%[22]. In Fig. 2.3(a), the voltage VS represents the difference

between the sinusoid input signal and the feedback signal from DAC:

)

(

)

(

)

(

z

X

z

Y

z

V

_S

=

−

(2.1)

In a second-order modulator, modulator output signal Y(z) is the time delay

version of X(z) plus high-pass filtered (noise shaped) quantization noise (1-z-1)2E(z).

Therefore, ΣΔ (2.2)

)

(

)

1

(

)

(

)

(

2 1 2

z

E

z

z

X

z

z

Y

=

−

+

−

−

Combining（2.1）and（2.2）, VS (z) can be written as

[

1

]

(

1

)

(

)

)

(

)

(

2 1 2

z

E

z

z

z

X

z

V

_S

=

−

−

−

−

− (2.3)

It is sampled by Cs, so Cs is charged in the half clock period T/2 to the voltage

VCS: )] 2 exp( 1 [ 1 τ ⋅ − − ⋅ =V T V_{CS S} (2.4)

where is the time constant of the sampling phase in the input branch. So the setting error during the sampling phase is:

s s C R ⋅ = 1 τ

) 2 exp( 1 1 _τ ε ⋅ − ⋅ =V_S T (2.5) S C S V I C L C VO S V ₁ gm I C L C S C R O V S C DAC

(a) Sampling phase (b) Integration phase Fig. 2.3 Switched capacitor integrator diagrams

Next, we consider the integration phase shown in Fig. 2.3(b), where the 2B unit capacitors are combined into Cs, and the 2B DAC switches are neglected. The charge

stored in sampling capacitor will be added to the integration capacitor and this charge current is supplied by OTA. So when the slew rate and gain bandwidth are not large enough, the settling error ε₂ will appear. According to absolute value of VS, three

types of settling conditions can happen in the integrator output during this phase, and the corresponding voltage errors of these three conditions are [11]:

1. Linear settling: When the initial change rate of the integrator output voltage (Vo) is

smaller than the OTA slew rate (SR).

) 2 exp( 2 1 2 _τ ε ⋅ − ⋅ ⋅ =a VS T , when ₂ 1 1 0< < ⋅SR⋅τ a V_S (2.6)

2. Partial slewing: The initial change rate of Vo is larger than SR, but it gradually

decreases until it is below the slew rate.

1) 2 exp( 2 2 1 2 2 _⋅ − − ⋅ ⋅ ⋅ = τ τ τ ε T SR V a SR S , when 1 2 2 1 ) 2 ( 1 a SR T V SR a ⋅ ⋅τ < S < +τ (2.7)

above SR in the 2 T interval. 2 1 2 T SR V a ⋅ _S − ⋅ = ε when ) 2 ( 2 1 τ + > T a SR VS (2.8)

where SR is the slew rate of OTA, and

GBW Cs R GBW ⋅ ⋅ ⋅ ⋅ + = π π τ 2 2 1 2 [23] is the time

constant in the integration phase, with GBW being the equivalent gain bandwidth in the integration phase. The capacitor loading in OTA output during this phase is heavier than in the sampling phase, and is [17]

I S I L S L C C C C C C 2 2 (2 ) + ⋅ + = (2.9) The GBW is given by π 2 2⋅ = L C gm1 GBW （2.10）

2.2 Properties of

VS

In this section, we separately discuss the time-domain and frequency-domain properties of VS to find out the time-domain probability distribution and the P.S.D of.

These properties will be used to do nonlinear fitting and spectrum construction of settling noise in section III.

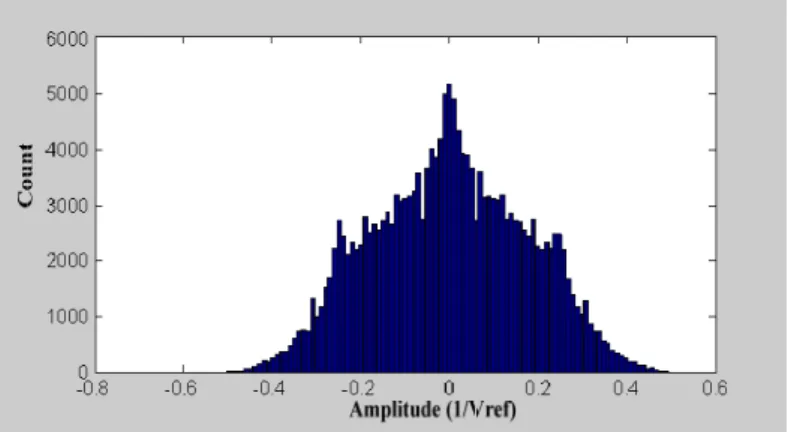
Firstly, we need to find the VS time-domain statistical property. Simulations results

(using SIMULINK) on a second-order ΣΔ modulator with a1 = 0.5, a2 = 2, 10-level

quantization, reference voltage Vref = 1, and a full scale sinusoidal input signal, are

shown in Fig. 2.4. The result is close to a Gaussian distribution. Therefore, we assume

VS is Gaussian distributed with a zero mean. The standard deviations σVS of VS under

different quantizer levels are tabulated in Table 2.1 We observed that when the quantizer level N increases, σ_VS decreases. From this table, the relation between standard deviation σ_VS and quantizer levels 2B can be approximated by

Fig. 2.4. Simulated results of VS distribution

TABLE 2.1

Standard deviations of VS vs. different quantizer bit numbers

Std. deviation (σVS) Variance Quantizer level (N) Bit number (B) 0.706 0.498 2 1 0.476 0.227 3 1.585 0.282 0.080 5 2.322 0.198 0.040 7 2.808 0.152 0.023 9 3.17 0.124 0.016 11 3.46 0.047 0.002 31 4.95

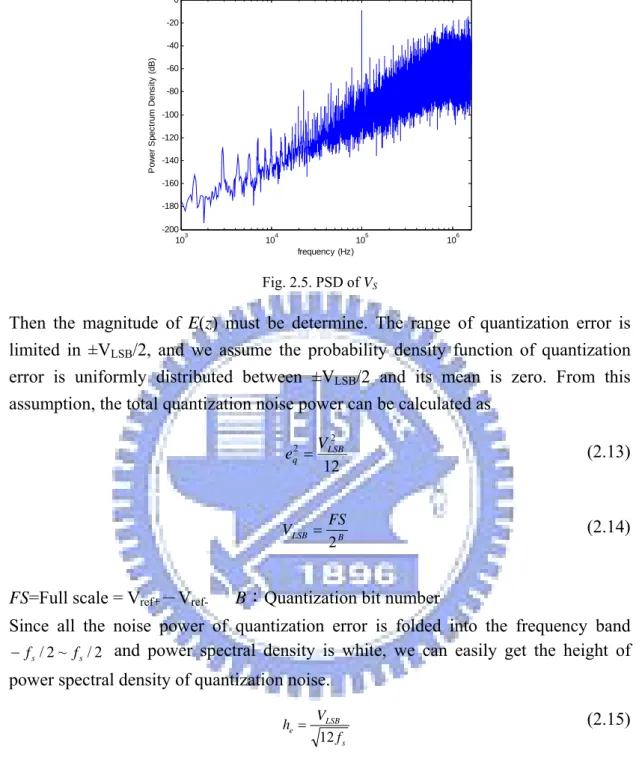
Next, we must determine the P.S.D of VS. Am expression for VS has been given in

(2.3)

[

1

]

(1 ) ( ) ) ( ) ( 2 1 2 z E z z z X z VS − − _{− −} − =

The PSD of VS of second order ΣΔ modulator which simulates with OSR = 16, SR =

60V/μs, GBW = 130M, and a 100kHz sinusoidal input signal is plotted in Fig. 2.5. In

order to calculate the PSD of VS, we separately discuss the part of E(z) and X(z). We

firstly ignore X(z) in (2.3) and express VS as

(2.12) ) ( ) 1 ( ) ( 1 2 z E z z VS − − =

103 104 105 106 -200 -180 -160 -140 -120 -100 -80 -60 -40 -20 0 frequency (Hz) P o w e r S pec tr um D e ns it y (dB ) Fig. 2.5. PSD of VS

Then the magnitude of E(z) must be determine. The range of quantization error is limited in ±VLSB/2, and we assume the probability density function of quantization error is uniformly distributed between ±VLSB/2 and its mean is zero. From this assumption, the total quantization noise power can be calculated as

12 2 2 LSB q V e = (2.13) B LSB FS V 2 = (2.14)

FS=Full scale = Vref+－Vref- B：Quantization bit number

Since all the noise power of quantization error is folded into the frequency band and power spectral density is white, we can easily get the height of power spectral density of quantization noise.

2 / ~ 2 / s s f f − s LSB e f V h 12 = (2.15)

Then we substitute z with _ej2πf/fs in (2.12) and magnitude of VS can be defined as

s B s s f FS f f f V 12 2 sin 2 ) ( 2 ⋅ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ = π (2.16)

So the relationship between the magnitude of VS and the bits number translates to a

Fig. 2.6. Simulated results of VS with AVS = 0.5, OSR = 16, and different Bits

Then we consider the part of X(z) and ignore the E(z) in (2.3) to express VS as

(2.17) ) ( ) 1 ( ) ( 2 z X z z VS − − =

Take the inverse z-transform to （2.17）

) T t ( u ) T t ( x ) t ( x ) t ( V_S = − −2 −2 ) 2 ( )) 2 ( sin( ) sin( t A t T u t T Ain − in − ⋅ − = ω ω _（2.18）

Then, the amplitude of VS can be obtained as

T A T A T x T V A_VS = _S(2 )= (2 )= _insin(

ω

⋅2 )≅2 _in⋅

ω

⋅ （2.19）

Note that AVS is not related to quantizer bit number B. The result has been verified by

behavior simulation under different B values, as shown in Fig. 2.6. From（2.19）, we can see that input signal amplitude Ain, input signal frequency ω and sampling time

T are the critical parameters to impact the harmonic distortion.

2.3 Performance Metrics for a

ΣΔ

Modulator

․Signal to Noise Ratio: The SNR of a data converter is the ratio of the signal power to the noise power, measured at the output of the converter for certain input amplitude. The maximum SNR that a converter can achieve is called the peak

SNR.

․Signal to Noise and Distortion Ratio: The SNDR of a converter is the ratio of the signal power to the power of the noise and the distortion components, measured at the output of the converter for certain input amplitude. The maximum SNDR that a converter can achieve is called the peak SNDR.

․Dynamic Range at the input: The DRi is the ratio between the power of the largest input signal that can be applied without significantly degrading the performance of the converter, and the power of the smallest detectable input signal. The level of significantly degrading the performance is defined as the point where the SNDR is 6 dB bellow the peak SNDR. The smallest detectable input signal is determined by the noise floor of the converter.

․Dynamic Range at the output: The dynamic range can also be considered at the output of the converter. The ratio between maximum and minimum output power is the dynamic range at the output DRo, which is exactly equal to peak SNR.

․Effective Number of Bits: ENOB gives an indication of how many bits would be required in an ideal quantizer to get the same performance as the converter. This numbers also includes the distortion components and can be calculated as

02 . 6 76 . 1 ENOB= SNR− (2.20)

․Overload Level: OL is defined as the relative input amplitude where the SNDR is decreased by 6dB compared to peak SNDR

Typically, these specifications are reported using plots like Fig. 2.7. This figure shows the SNR and SNDR of the ΣΔ converter versus the amplitude of the sinusoidal wave applied to the input of the converter. For small input levels, the

the SNDR and SNR curves coincide for small input levels. When the input level increases, the distortion components start to degrade the modulator performance. Therefore, the SNDR will be smaller than the SNR for large input signals. Note that these specifications are dependent on the frequency of the input signal and the clock frequency of the converter. Fig. 2.7 also shows that SNDR curves drop very fast once the overload point is achieved. This is due to the overloading effect of the quantizer which results in instabilities.

3.

Derivation of Sigma-Delta Modulator

Settling noise Power Model

In this section, models of settling noises which appear at ΣΔ modulator output will be derived and expressed in noise power form. This derivation is divided into sampling phase and integration phase.

3.1 Settling Errors of Sampling Phase

From (15) and (17), we can get magnitude of N_TF(z) in frequency domain. By

calculating the sum of in-band noise power, settling error of sampling phase can be acquired.

∫

∫

− − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − × = = B B B B f f 2 s s s LSB f f e TF df T f f f V df f N f S P ) 2 exp( ) ( sin 4 12 ) ( ) ( 1 2 2 2 1

τ

π

ε (3.1)

3.2 Settling Errors of Integration Phase

As discussed in section II, there are three settling conditions depending on the absolute value of VS. The full slewing case is not considered here because it is not

significant. Note that VS at end of each integration interval can be written as

⎪

⎩

⎪

⎨

⎧

>

−

≤

−

=

₋ L S V V S L S L S S S i

V

V

e

e

V

V

V

a

V

V

V

a

V

g

L S

)

;

1

(

;

)

1

(

)

(

₁ 1 1

β

β

(3.2)

where β =exp(−T_s/2τ₂) and V_L =SRτ₂/ a₁

From（3.2）,the settling error of integration phase can be calculated as following expression: ⎪⎩ ⎪ ⎨ ⎧ > ≤ = − L S V V L S L S S S V V e e V V a V V V a V L S ; ) sgn( ; ) ( 1 1 1 2

β

β

ε

(3.3)

To approximate (3.3), we apply least square method and neglect the even terms by reasons of symmetry of (3.3). Then (3.3) can be approximated by

(3.4) 5 5 3 3 1 ) ( S S S S i V V V V p =α +α +α

The pi(VS) should be fitted through all the points in that specific interval so that the

sum of the squares of the distances of those points from the pi(VS) is minimum. The

sum of the squares is

[

]

S V S S p V dV V q=

∫

H − 0 2 2( ) ( ) ε (3.5)

[

S V S S S S a V a V a V dV V H 2 0 5 5 1 3 3 1 1 1 2( )

∫

− − − =

ε

α

α

α

]

With above method, the determination of coefficients in （3.4） for q to be minimum becomes the solution of follow equations.

[

]

[

]

[

]

⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = − ∂ ∂ = − ∂ ∂ = − ∂ ∂

∫

∫

∫

0 ] ) ( ) ( [ 0 ] ) ( ) ( [ 0 ] ) ( ) ( [ 0 2 2 5 0 2 2 3 0 2 2 1 S V S S S V S S S V S S dV V p V dV V p V dV V p V H H H ε α ε α ε α (3.6)

Note that (3.7) only takes into account the nonlinear curve in (3.7), whereas errors derived from the distribution of VS are omitted. This may lead to a worse estimation of

assumed to be uniformed distributed in the specific integral interval. Nevertheless, the distribution of VS should be defined as Gaussian distribution and the weighting

function that indicates the probability of VS in the specific interval must be considered

so that (3.6) should be de revised as:

[

]

{

}

[

]

{

}

[

]

{

}

⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = × − ∂ ∂ = × − ∂ ∂ = × − ∂ ∂

∫

∫

∫

0 ) ( ) ( ) ( 0 ) ( ) ( ) ( 0 ) ( ) ( ) ( 0 2 2 5 0 2 2 3 0 2 2 1 S S V S S S S V S S S S V S S dV V W V p V dV V W V p V dV V W V p V H H H ε α ε α ε α (3.7)

where W(VS) represents the weighting function of VS. Since the settling noise is highly

depends on the distribution of VS, the probability of VS in the specific interval must be

defined. As discussed in section II, the VS can be assumed to be Gaussian distribution

and the relation between standard deviation σ_VS and quantizer levels 2B can be approximated by ref vs B V 1.4⋅ ≈ ⋅σ 2 (3.8) From（3.8）, the p.d.f of VS is ) 2 exp( 2 1 ) ( ₂ S S V s V s V V f

σ

σ

π

− = (3.9)

However, since the integral interval is 0 ~ VH, the p.d.f of VS should be redefined as

) 2 exp( 2 1 ) 2 exp( 2 1 1 ) ( ₂ 0 2 S S H V s V V s s s V dV V V f

σ

σ

π

σ

π

− − =

∫

(3.10)

where VH is defined as 2Vref. Then (3.11) is normalized and the weighting function can

) 2 exp( 2 1 ) 2 exp( 2 1 2 0 2 2 S S H V s V V s s H V dV V V k

σ

σ

π

σ

π

− − =

∫

(3.11)

Taking into account (3.11), (3.8) can be re-written as

[

]

{

}

[

{

]

}

[

]

{

}

⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = × − − − ∂ ∂ = × − − − ∂ ∂ = × − − − ∂ ∂

∫

∫

∫

0 ) ( 0 ) ( 0 ) ( 2 0 2 5 5 1 3 3 1 1 1 2 5 2 0 2 5 5 1 3 3 1 1 1 2 3 2 0 2 5 5 1 3 3 1 1 1 2 1 S V S S S S S V S S S S S V S S S S dV k V a V a V a V dV k V a V a V a V dV k V a V a V a V H H H α α α ε α α α α ε α α α α ε α

[

]

[

]

[

]

⎪

⎪

⎩

⎪

⎪

⎨

⎧

=

−

×

−

−

−

=

−

×

−

−

−

=

−

×

−

−

−

⇒

∫

∫

∫

0

)

2

(

)

(

0

)

2

(

)

(

0

)

2

(

)

(

2 5 1 0 5 5 1 3 3 1 1 1 2 2 3 1 0 5 5 1 3 3 1 1 1 2 2 1 0 5 5 1 3 3 1 1 1 2 S S V S S S S S S V S S S S S S V S S S S

dV

k

V

a

V

a

V

a

V

a

V

dV

k

V

a

V

a

V

a

V

a

V

dV

k

V

a

V

a

V

a

V

a

V

H H H

α

α

α

ε

α

α

α

ε

α

α

α

ε

[

]

[

]

[

]

⎪

⎪

⎩

⎪

⎪

⎨

⎧

=

×

+

+

=

×

+

+

=

×

+

+

⇒

∫

∫

∫

∫

∫

∫

H H H H H H V S S S S V S S S V S S S S V S S S V S S S S V S S S

dV

k

V

dV

k

V

V

a

V

a

V

a

dV

k

V

dV

k

V

V

a

V

a

V

a

dV

k

V

dV

k

V

V

a

V

a

V

a

0 2 5 2 2 5 0 5 5 1 3 3 1 1 1 0 2 3 2 2 3 0 5 5 1 3 3 1 1 1 0 2 2 2 0 5 5 1 3 3 1 1 1

)

(

)

(

)

(

ε

α

α

α

ε

α

α

α

ε

α

α

α

[

]

[

]

[

]

⎪

⎪

⎪

⎪

⎪

⎪

⎩

⎪

⎪

⎪

⎪

⎪

⎪

⎨

⎧

+

=

×

+

+

+

=

×

+

+

+

=

×

+

+

⇒

∫

∫

∫

∫

∫

∫

∫

∫

∫

− − − H L L S L H H L L S L H H L L S L H V V S S V V L V S S S V S S S V V S S V V L V S S S V S S S V V S S V V L V S S S V S S S

dV

k

V

e

e

V

dV

k

V

dV

k

V

V

V

dV

k

V

e

e

V

dV

k

V

dV

k

V

V

V

dV

k

V

e

e

V

dV

k

V

dV

k

V

V

V

2 5 1 0 2 6 2 0 10 5 8 3 6 1 2 3 1 0 2 4 2 0 8 5 6 3 4 1 2 1 0 2 2 2 0 6 5 4 3 2 1

β

β

α

α

α

β

β

α

α

α

β

β

α

α

α

Then the values of the coefficients are: × ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ −

∫

∫

∫

∫

∫

∫

∫

∫

∫

V k V k V k V k V k V k V k V k V k Vh S Vh S Vh S Vh S Vh S Vh S Vh S Vh S Vh S 1 0 10 2 0 8 2 0 6 2 0 8 2 0 6 2 0 4 2 0 6 2 0 4 2 0 2 2 5 3 1 α α α ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⋅ + ⋅ +

∫

∫

∫

∫

∫

∫

− − − L h L L S L h L L S L h L L S V V V S S V V L S S V V V S S V V L S S V V V S S V V L S S dV V e e V k dV V k dV V e e V k dV V k dV V e e V k dV V k 0 5 1 2 6 2 0 3 1 2 4 2 0 1 2 2 2 β β β β β β (3.12)

In order to validate (3.12), we apply least square to the VS in three cases. In case one,

simulations was carried for a ΣΔ modulator with 3-Bits, OSR = 120, SR = 40V /μs,

and GBW = 100MHz and the VS was obtained. The coefficients,α1,α3, and , can be

determined by applying least square method to above VS and compare with the ones

obtained by another two cases, with Gaussian distribution, and no Gaussian distribution. Fig. 3.1 and Table 3.1 show the VS and coefficients obtained in three

cases. The case applied Gaussian distribution show a good fit when compared to the one by simulation. In Fig 3.2, the fitting results in three cases were illustrated and the case with Gaussian distribution is closer to the one simulated than another case. Note that the VL in this case is 0.1681 and the probability of nonlinear operation is respectively 0.35, 0.34, and 0.9 in three cases. This result shows that applying Gaussian distribution to VS plays a crucial role in calculating settling noise.

5 α -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 0 2000 4000 6000 8000 10000 12000 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 200 400 600 800 1000 1200 1400

(a) Behavioral model (b) with Gaussian distribution (c) No Gaussian distribution Fig. 3.1. Distribution of VS obtained in three cases

TABLE 3.1

Coefficients obtained in three cases Behavioral model with Gaussian distribution no Gaussian distribution 1 α 0.958 0.94 835.67 3 α 1.239 1.609 -1532.7 5 α 19.677 16.357 567.25 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -8000 -6000 -4000 -2000 0 2000 4000 6000 8000 Vs s et tl ing er ro r Behavioral model

with Gaussian distribution no Gaussian distribution

Fig. 3.2. VS versus settling error in three cases

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 200 400 600 800 1000 1200 1400

Fig. 3.3. The distribution of angle of VS

With

α

3 and

α

5 , the next step of calculating settling noise power is the

determination of the P.S.D of VS 3 by using the P.S.D of VS.

The height of the power spectral density of VS in frequency domain can be expressed as α

π

i s s LSB e

e

f

f

f

V

f

h

_⎥

×

⎦

⎤

⎢

⎣

⎡

=

2

)

sin(

2

12

)

(

_(3.13)

where α represents the angle of VS. In Fig. 3.3, simulation result shows that the

angle of VS is close to a uniform distribution. Therefore, α is considerably assumed

to be a arbitrary value in 0~2π. To demonstrate the P.S.D of VS 3, we will begin by

considering the square of VS. Since the P.S.D VS has been verify in above discussion,

we can use modulation of DTFT Theorems and apply circular convolution to realize square of VS. We can expressed the height of the power spectral density of the square

of VS in frequency domain as

)

(

)

(

)

(

2

f

h

f

h

f

h

_e

=

_e

⊗

_e

θ

θ

π

πθ

α d e f f f V f f V f i s s LSB f f s s LSB s s s × ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =

∫

− 2 2 2 2 ) ) ( sin( 2 12 ) sin( 2 12 1 (3.13)

In order to compute the expect value of (3.13), we express (3.13) as a sum of different absolute value with a arbitrary value:

...

+

+

+

β γ α i i i

ce

Be

Ae

| i A i A i A ... )) sin( ) (cos( )) sin( ) (cos( )) sin( ) (cos( | + + + + + + = γ γ β β α α

[

]

0.5 2 2 2 ) cos( ) cos( ) cos( ... ... AB AB AB C B A + − + − + − + + + + = α γ γ β β α (3.14)

...

2 2 2

₊

₊

₊

C

B

A

(3.15)

Then the expect value of the height of spectral density of square of VS can be defined

as

θ

θ

π

πθ

d f f f f V f f h s f f s s LSB s e s s ) ) ( ( sin ) ( sin 9 16 1 ) ( ₂ 4 2 4 4 2 − =

∫

− (3.16)

Fig 3.4 shows that the expect value of (3.16) and behavior model simulation with = 20MHz, Bit = 1. S f 104 105 106 107 0.5 1 1.5 2 2.5x 10 -4 A m p lit u d e frequency (Hz)

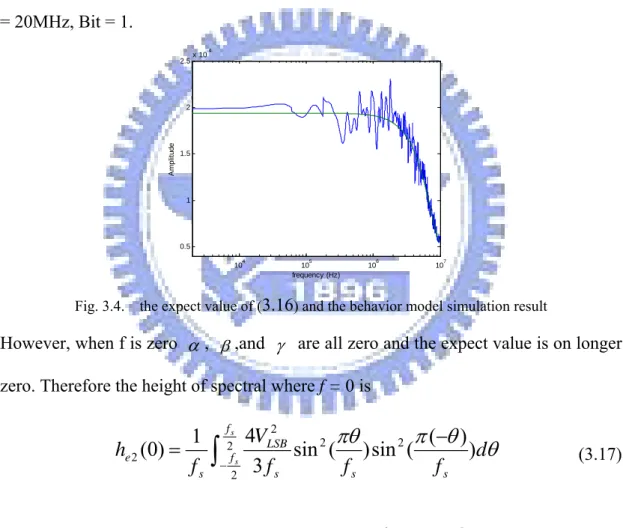
Fig. 3.4. the expect value of (3.16) and the behavior model simulation result

However, when f is zero α , β,and γ are all zero and the expect value is on longer zero. Therefore the height of spectral where f = 0 is

θ

θ

π

πθ

d

f

f

f

V

f

h

s f f s s LSB s e s s

)

)

(

(

sin

)

(

sin

3

4

1

)

0

(

₂ 2 2 2 2 2

−

=

∫

− (3.17)

( )

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎤ ⎢ ⎢ ⎡ + − + ≅ ) ( cos 8 ) ( cos 136 173 0642 . 0 ) ( sin 879 . 0 2 1 2 4 2 2 2 2 3 3 f f f f f f f f f h s s B e π π π

( )

5 . 0 4 4 2 2 2 2 5 5 ) ( sin 8 . 15 ) ( cos 23 . 3 ) ( sin 6 . 55 ) ( cos 11 . 18 ) ( sin ) ( cos 97 . 16 2 . 9 2 0396 . 0 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + + ≅ s s s s s s B s e f f f f f f f f f f f f f f h π π π π π π

Fig. 3.5 and Fig. 3.6shows that the expect value of VS 3 and VS 5 compared with

simulation results by behavior model.

103 104 105 106 107 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5x 10 -4 A m pl it ude frequency (Hz)

Fig. 3.5 The expect value of VS 3 and the simulation result by behavior model

103 104 105 106 107 1 2 3 4 5 6 7 8 9 10x 10 -4 frequency (Hz) A m pl it ud e

Then the expect value of the height of spectral density of settling noise of integration phase can be defined as

5 5 3 3 1 1

)

(

f

h

_e

h

_e

h

_e

h

=

α

+

α

+

α

(3.18)

So the settling noise in base band± f_Bof integration phase can be obtained by

integrating (38): (3.19)

df

f

h

f

h

f

h

P

B B f f e e e

∫

−

+

+

=

2 5 5 3 3 1 1 2

(

α

(

)

α

(

)

α

(

))

ε

Then total settling noise is

2

1 ε

ε

ε

P

P

P

=

+

(3.20)

Note the low frequency region of third and fifth power is absolutely flat and means that the in band noise power will increase if the α₃ and α₅ in (3.11) increase.

Therefore, the nonlinearity of settling will make an amount increase on noise power. It is worth noting that settling noise is highly dependent on the high frequency noise. Due to the noise shaping nature, the high frequency amplitude of VS is great and will

4.

Derivations of Sigma-Delta Modulators

Settling Distortion

In analysis of settling noise, the input of integrator, VS, is define as a function of

quantization noise and (13) is used to derivate settling noise. However, the VS in this

section is defined as a sinusoid and the quantization noise is ignored.

The technique applied in section 3 will be used to calculate settling distortion. Since the input signal is a sinusoid and the distribution is uniformed distributed in - ~ , the weighting function would not be considered and the coefficients were determined by (25). Then the coefficients were expressed as

VS A AVS ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⋅ − − + ⋅ − − + − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⋅ ⋅ − ⋅ ⋅ − ⋅ ⋅ − ⋅ ⋅ − ⋅ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡

∫

∫

∫

∫

∫

∫

VL A VL S S V V S L S S VL A VL S S V V S L S S VL A VL S V V S L S VS L S VS L S VS _{S L} dV V e V V dV V e dV V e V V dV V e dV e V V dV e Vh Vh Vh Vh Vh Vh Vh Vh Vh 0 4 4 0 2 2 0 9 7 5 7 5 3 5 3 5 3 1 ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( 64 11025 32 4725 64 945 32 4725 16 2205 32 525 64 945 32 525 64 225 β β β β β β α α α (4.1) where AVS has defined in (2.19). Note that the validation of the calculation is

VS

L A

V < , otherwise, the settling will operate linearly and has no distortion at output

node. V_S ≤V_L can be further derived as:

L S V V ≤ 5 . 0 2A

ω

T ≤ SR

τ

⇒

GBW RC GBW SR OSR BW f A S in _⋅ ⋅ ⋅ + ⋅ ≤ × × ⋅ ⋅ ⋅ ⇒ π π π 2 2 1 5 . 0 2 1 2 2 SR RC GBW GBW BW f A OSR S in 5 . 0 2 1 2 2 1 2 2 ⋅ ⋅ + ⋅ × ⋅ ⋅ ⋅ ⋅ ≥ ⇒ π π π (4.2) Assumingfin=BW,R= 300Ω, CS F 12 10 2_× −

= , it leads to the following equation:

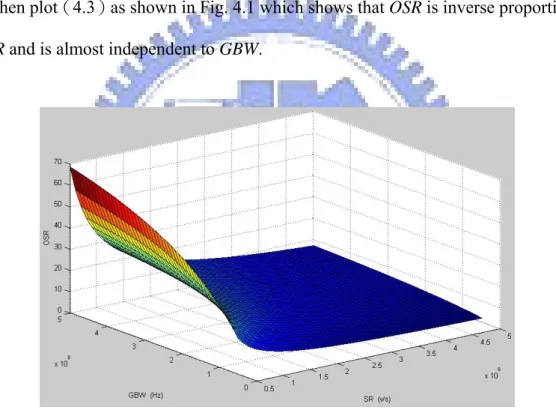
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ ×} ⋅ ≥ −10 10 6 2 1 GBW SR OSR π π (4.3) We then plot（4.3）as shown in Fig. 4.1 which shows that OSR is inverse proportional

to SR and is almost independent to GBW.

Fig. 4.1 3D plot of（4.3）

Fig. 4.1 indicates that if we design SR and GBW above the curve with desired OSR, the modulator would have no harmonic distortion. It shows that the op-amp slew rate needs to be at least 200V/us, then the modulator can have no harmonic distortions with OSR larger than 15. Although op-amps operate in linear region can have no harmonic distortion, it may consume more power dissipation (because large slew rate).

Therefore, there has a trade off between power consumption and harmonic distortion. In general, one can choose smaller slew rate to let power consumption lower and have negligible harmonic distortions.

In order to verify the result in （4.1）, we use SIMULINK to build a second-order modulator with a multi-bit quantizer. The behavioral settling model in [11] is employed. We assume that SR = 70

ΣΔ

s

V/μ , GBW = 100MHz, R = 300Ω , OSR = 16,

= 1MHz and = 2pF, and a 1MHz sinusoidal input signal is used. After performing FFT to the output data of the modulator, we obtain the simulated P.S.D which is shown in Fig. 4.2 It shows that HD3 is -115.1dB and HD5 is -119.9dB. The theoretical harmonic powers calculated from（4.1） are HD3 = -116.4dB and HD5 = -120.3dB. The simulated and theoretical results are very close, and this confirms that our settling distortion model is reasonably precise.

B f S C ΣΔ 106 107 -250 -200 -150 -100 -50 0 X: 3e+006 Y: -115.1 X: 5e+006 Y: -119.9 frequency (Hz) P o w e r Dens it y (d B )

Fig. 4.2 Output spectrum of a second-order ΣΔ modulator with harmonic distortion

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 4 2 1 log 20 ) ( 3 3 3 VS settling A dB HD α

₂₀

[

_{log log}

₍

₂

₎

3 _{log4 2}

]

3 + −

= α AωT

_{=20logα3 −60logOSR+30.095} （4.4） 15 . 48 log 100 log 20 ) ( 5 dB = 5 − OSR+ HD _settling α

From （4.4） we can see that OSR can effectively influence settling harmonic powers. The（4.4）reveals that α₃ and α₅ are functions of T, GBW, R, and SR. In order to place much more emphasis on relationship between GBW and the settling distortion, Fig 4.3 shows HD3 with SR=50V/us, R = 300

S C

Ω , OSR = 16, fB= 1MHz and Cs = 2pF,

and a 1MHz sinusoidal input signal. Similarly, Fig. 4.4 shows SR vs. HD3 with

GBW=50MHz. 50 100 150 200 -160 -150 -140 -130 -120 -110 -100 -90 -80 GBW (MHz) HD3 (d B ) Fig. 4.3 GBW v.s HD3

10 15 20 25 30 35 40 45 50 -160 -140 -120 -100 -80 -60 -40 -20 0 SR(V/us) H D 3( dB ) Fig. 4.4 SR v.s HD3

The simulated and theoretical results are very close, and this confirms that our settling distortion model is reasonably precise.

In general, harmonic distortion less than -110dB can be ignored because it is below the noise floor of modulator output spectrum. From（39）, Fig. 4.4 and Fig. 4.5, we can obtain the minimum required SR and GBW w. r. t. a specific OSR. The results are summarized in Table 4.4.

It is clear from Table 4.1 that as OSR decreases, SR have to increase dramatically so that the effect of settling distortion can be contained. This can be explained by（39）, since T increases when OSR decreases.

TABLE 4.1

Minimum SR and GBW required w. r. t. OSR

OSR HD3(dB) SR ) / (V μs GBW (MHz) 2 20logα3 -24 ≥180 ≥430 4 20logα3 -42 ≥150 ≥400 8 20logα3 -60 ≥120 ≥370 16 20logα3 -72 ≥100 ≥350 32 20logα3 -78 ≥80 ≥340 64 20logα3 -89 ≥50 ≥320 100 20logα3 -90 ≥30 ≥300

Fig. 5.1 Circuit-level schematic of spice simulation

104 105 106 107 -140 -120 -100 -80 -60 -40 -20 frequency (Hz) P ow e r S p ec tr um D e ns it y ( d B ) Behavior Simulation Spice simulation our model (a) 103 104 105 106 107 -120 -100 -80 -60 -40 -20 Behavior Simulation Spice Simulation our model (b) 103 104 105 106 107 -110 -100 -90 -80 -70 -60 -50 -40 -30 -20 -10 frequency (Hz) P o w er S p ec tr um D ens it y ( d B ) Behavior Simulation Spice Simulation Our model (c)

5.

Simulation Results and Validation

In order to demonstrate the validity the model presented in previous section, we use the spice simulation shown in Fig. 5.1 and Fig. 5.2 The relevant parameters were:

kHz, OSR = 100, CS = 0.5pf, Ci = 1pf, and a 100 kHz sinusoidal input signal. Additional parameters used in the simulation of Fig. 5.3 are listed in Table 5.1. Fig. 5.3 shows the settling noise obtained by presented model and simulated output by transistor-level and behavior model. The theoretical noise power by previous model is obtained by adding the previous settling noise power to the theoretical quantization noise power. The output shows a good agreement between the transistor-level modeled and presented modeled modulator.

100 =

B

f

Notice that increase OSR will increase settling noise and reduce SNR. Then we do the same simulation with different OSR. Fig. 5.4 indicates the noise power at modulator output, which is a combination of quantization noise and settling noise. Notice that increasing SR and GBW will reduce settling noise and increase SNR, but will also increase analog power consumption and the design challenges. On the other hand, multi-bit quantizers can reduce the slew rate requirement, since a multi-bit structure makes the output feedback signal closer to the input signal.

20 40 60 80 100 120 140 160 180 -75 -70 -65 -60 -55 -50 -45 -40 In B and N o is e P ow er (dB ) OSR spice simulation presented model

Fig. 5.4 P.S.D of settling noise obtained from transistor-level simulation and previous established model

The previous study reveals that as non-idealities or OSR increases, the settling noise will rise dramatically and degrade the performance of ΣΔ modulator. Because high non-idealities reflect high-frequency noises into base band, first order modulator maybe is a more efficient architecture than second order. In order to make an efficient choice between first and second order, we calculate the minimum required SR and

GBW w. r. t. a specific OSR. The results are summarized in Table 5.2. Table 5.1

indicates that as OSR increase, the bigger SR and GBW are needed to cope with the settling noise.

TABLE 5.1

SIMULATION PARAMETERS IN FIG.5.3

Parameter Fig. 5.3(a) Fig. 5.3(b) Fig. 5.3(c)

SR(V /μ s) 160 80 60

GBW(MHz) 160 127 95

ε

P (dB) -85.4 -68.48 -49.2

TABLE 5.2

MINIMUM SR AND GBW REQUIRED W. R. T.OSR

OSR PQ of fist order

modulator ΣΔ SR ) / (V μ s GBW (MHz) 16 6.69×10−5 ≥6 ≥20 32 8.37_×10−6 ≥₂₀ ≥₄₀ 64 1.05×10−6 ≥50 ≥75 80 5.35×10−7 ≥60 ≥120 100 2.74×10−7 ≥100 ≥140 120 1.59_×10−7 ≥₁₄₀ ≥₁₆₀ 140 1×10−7 ≥200 ≥220

6.

Conclusions and Future Works

The analytical model of settling noise of ΣΔ ADCs is never derived in the literature to date and can only be performed through time-domain behavior simulations due to the complex dynamic behavior. In this paper, we have established an analytical model with nonlinear slewing behavior to adequately estimate the ADCs in-band noise power as a function of

ΣΔ ΣΔ modulator system parameters. Once the system parameters such as OSR, GBW, and SR are known, the model gives a expect value of PSD. Both behavior simulations and HSPICE circuits are employed to verify these analytical models, and the results show that our analytical models are sufficiently accurate. Measurement results suggest that for high order ADCs with high OSR and low Bit-number the settling noise will be bigger than other noises and becomes dominate noise source.

References

[1] J. Candy, "A Use of Double Integration in Sigma Delta Modulation," Communications, IEEE Transactions on [legacy, pre - 1988], vol. 33, pp. 249-258, 1985.

[2] B. P. Brandt, D. E. Wingard, and B. A. Wooley, "Second-order sigma-delta modulation for digital-audio signal acquisition," Solid-State Circuits, IEEE Journal of, vol. 26, pp. 618-627, 1991.

[3] B. E. Boser and B. A. Wooley, "The design of sigma-delta modulation analog-to-digital converters," Solid-State Circuits, IEEE Journal of, vol. 23, pp. 1298-1308, 1988. [4] B. DelSignore, D. Kerth, N. Sooch, and E. Swanson, "A monolithic 20 b delta-sigma

A/D converter," in Solid-State Circuits Conference, 1990. Digest of Technical Papers. 37th ISSCC., 1990 IEEE International, 1990, pp. 170-171, 293.

[5] J. Grilo, I. Galton, K. Wang, and R. G. Montemayor, "A 12-mW ADC delta-sigma modulator with 80 dB of dynamic range integrated in a single-chip Bluetooth transceiver," Solid-State Circuits, IEEE Journal of, vol. 37, pp. 271-278, 2002. [6] B. J. Farahani and M. Ismail, "Adaptive Sigma Delta ADC for WiMAX fixed point

wireless applications," Circuits and Systems, 2005. 48th Midwest Symposium on, pp. 692-695, 2005.

[7] R. Gaggl, A. Wiesbauer, G. Fritz, C. Schranz, and P. Pessl, "A 85-dB dynamic range multibit delta-sigma ADC for ADSL-CO applications in 0.18-/spl mu/m CMOS," Solid-State Circuits, IEEE Journal of, vol. 38, pp. 1105-1114, 2003.

[8] R. del Rio, J. M. de la Rosa, B. Perez-Verdu, M. Delgado-Restituto, R.

Dominguez-Castro, F. Medeiro, and A. Rodriguez-Vazquez, "Highly linear 2.5-V CMOS /spl Sigma//spl Delta/ modulator for ADSL+," Circuits and Systems I: Regular Papers, IEEE Transactions on [Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on], vol. 51, pp. 47-62, 2004.

[9] S. R. Norsworthy, R. Schreier, and G. C. Temes, Delta-Sigma data converters: theory, design, and simulation: New York: IEEE Press: Wiley-Interscience, 1997.

[10] G. Suarez, M. Jimenez, and F. O. Fernandez, "Behavioral Modeling of Switched Capacitor Integrators with Application to 聶聶 Modulators," in Circuits and Systems, 2006. MWSCAS '06. 49th IEEE International Midwest Symposium on, 2006, pp. 709-713.

[11] P. Malcovati, S. Brigati, F. Francesconi, F. Maloberti, P. Cusinato, and A. Baschirotto, "Behavioral modeling of switched-capacitor sigma-delta modulators," Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on [see also

Circuits and Systems I: Regular Papers, IEEE Transactions on], vol. 50, pp. 352-364, 2003.

[12] G. Suarez, M. Jimenez, and F. O. Fernandez, "Behavioral Modeling Methods for Switched-Capacitor &#931;&#8710; Modulators," Circuits and Systems I: Regular Papers, IEEE Transactions on [Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on], vol. 54, pp. 1236-1244, 2007.

[13] F. Medeiro, A. Perez-Verdu, and A. Rodriguez-Vazquez, Top-Down Design of High-Performance Sigma-Delta Modulators: Kluwer Academic Publishers, 1999. [14] S. Loeda, H. M. Reekie, and B. Mulgrew, "On the design of high-performance

wide-band continuous-time sigma-delta converters using numerical optimization," Circuits and Systems I: Regular Papers, IEEE Transactions on [Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on], vol. 53, pp. 802-810, 2006.

[15] O. Bajdechi and J. H. Huijsing, Systematic Design Of Sigma-delta Analog-to-digital Converters: Springer, 2004.

[16] G. I. Bourdopoulos, Delta-SIGMA Modulators: Modeling, Design and Applications: Imperial College Press, 2003.

[17] Y. Geerts, M. Steyaert, and W. M. C. Sansen, Design of Multi-Bit Delta-SIGMA A/D Converters: Kluwer Academic Publishers, 2002.

[18] W. M. C. Sansen, H. Qiuting, and K. A. I. Halonen, "Transient analysis of charge-transfer in SC filters-gain error and distortion," Solid-State Circuits, IEEE Journal of, vol. 22, pp. 268-276, 1987.

[19] K. L. Lee and R. G. Mayer, "Low-distortion switched-capacitor filter design techniques," Solid-State Circuits, IEEE Journal of, vol. 20, pp. 1103-1113, 1985. [20] J. C. Candy and G. C. Temes, "Oversampling Delta-Sigma Data Converters: Theory,

Design and Simulation," IEEE, New York, 1992.

[21] F. Medeiro, B. Perez-Verdu, A. Rodriguez-Vazquez, and J. L. Huertas, "Modeling opamp-induced harmonic distortion for switched-capacitor &Sigma;&Delta; modulator design," in Circuits and Systems, 1994. ISCAS '94., 1994 IEEE International

Symposium on, 1994, pp. 445-448 vol.5.

[22] S. Rabii and B. A. Wooley, The design of low-voltage, low-power sigma-delta modulators: Kluwer Academic Publishers Norwell, MA, USA, 1998.

[23] R. Rio Fernandez, F. Medeiro, B. Perez Verdu, J. M. Rosa Utrera, and A. Rodriguez Vazquez, "CMOS Cascade Sigma-Delta Modulators for Sensors and Telecom: Error Analysis and Practical Design," 2008.

Systems, 1999. ISCAS'99. Proceedings of the 1999 IEEE International Symposium on, vol. 2, 1999.