A New LMI-Based Approach to Relaxed Quadratic
Stabilization of T–S Fuzzy Control Systems
Chun-Hsiung Fang, Senior Member, IEEE, Yung-Sheng Liu, Shih-Wei Kau, Lin Hong, and Ching-Hsiang Lee
Abstract—This paper proposes a new quadratic stabilization condition for Takagi–Sugeno (T–S) fuzzy control systems. The condition is represented in the form of linear matrix inequalities (LMIs) and is shown to be less conservative than some relaxed quadratic stabilization conditions published recently in the litera-ture. A rigorous theoretic proof is given to show that the proposed condition can include previous results as special cases. In compar-ison with conventional conditions, the proposed condition is not only suitable for designing fuzzy state feedback controllers but also convenient for fuzzy static output feedback controller design. The latter design work is quite hard for T–S fuzzy control systems. Based on the LMI-based conditions derived, one can easily syn-thesize controllers for stabilizing T–S fuzzy control systems. Since only a set of LMIs is involved, the controller design is quite simple and numerically tractable. Finally, the validity and applicability of the proposed approach are successfully demonstrated in the control of a continuous-time nonlinear system.
Index Terms—Fuzzy feedback controller, linear matrix in-equality, relaxed quadratic stability, stabilization, Takagi–Sugeno (T–S) fuzzy systems.
I. INTRODUCTION
F
UZZY control technique represents a means of collecting human knowledge and expertise. It has been applied to various industrial fields [12], [17]. Although the method has been practically successful, it has proved extremely difficult to develop a general analysis and design theory for conventional fuzzy control systems. Recently, based on Takagi–Sugeno (T–S) fuzzy model [13], [14], there have appeared in the literature a great number of results concerning stability analysis and design [1]–[3], [10], [14]–[17].Reference [10] proposed a so-called relaxed stabilization con-dition and then applied the concon-dition to design fuzzy controllers for T–S fuzzy systems. In [4], an interesting quadratic stabiliza-tion condistabiliza-tion was reported to release the conservatism of the condition of [10] by collecting the interactions in a single ma-trix. Very recently, a more relaxed stabilization condition was proposed in [8]. It admits more freedom in guaranteeing the sta-bility of T–S fuzzy control systems than the one of [4].
[10] as special cases. By a numerical example, one can see that the new stabilization condition significantly relaxes the conser-vativeness of existing ones. The present condition is also very useful for fuzzy controller design. Once the condition is fea-sible, a state feedback controller for stabilizing T–S fuzzy sys-tems can be easily obtained. Unlike conventional approaches [4], [8], [10] which are mainly suitable for designing fuzzy state feedback controllers, the approach used in this paper can be also applied to solve the fuzzy static output feedback stabilization problems. In practical, fuzzy static output feedback control is very useful and more realistic since it can be easily implemented with low cost. However, the problem is essentially hard for T–S fuzzy systems and, thus, rarely studied in the literature [5], [6]. By the proposed approach, a fuzzy static output feedback con-troller for stabilizing T–S fuzzy systems can be synthesized with ease.
The paper is organized as follows: Some results published recently are briefly reviewed in Section II for a clear overview of related research and further comparison with our contribu-tions. Section III contains main results of the paper, in which both continuous-time and discrete-time cases are investigated. The comparison of relaxation between main results and existing ones mentioned in Section II is also made in this section. Sec-tion IV presents a numerical example which illustrates the va-lidity and applicability of the proposed approach in the control of a continuous-time nonlinear system. The conclusion is lo-cated in Section V.
In this paper, “continuous-time fuzzy systems” and “discrete-time fuzzy systems” are abbreviated as CFS and DFS, respec-tively. Other notations used are fair standard. For example,
(or ) means the matrix is symmetric and negative definite (or symmetric and negative semidefinite). denotes the transpose of . The symbol (or ) represents the identity matrix with appropriate dimension (or dimension ).
where represents an operator. For CFS cases means
and for DFS cases represents . In (1),
is the fuzzy set and
is the number of IF–THENrules. , are the
premise variables. is the state vector, is the
input vector. Assume and . Given
a pair of , the final output of the fuzzy system is inferred as follows:
(2)
where ,
, is the grade of membership of
in , and represents the weight of the th
rule. It is easy to check that , , and
. Let the controller be
Controller Rule If is and and is
Then (3)
where . The designed fuzzy controller shares
the same fuzzy sets in the premise parts with the plant and has local linear controllers in the consequent parts. The output of the fuzzy state feedback controller is given by
(4) By substituting (4) into (2), the closed-loop fuzzy system can be represented as
(5)
Definition 1 [12]: The fuzzy system (2) is said to be quadrat-ically stabilizable if there exists a controller as in (4) such that
the closed-loop system (5) is quadratically stable.
B. Basic Stabilization Conditions
In this subsection, two basic stabilization conditions for CFS and DFS are reviewed in Theorems 1 and 2, respectively. In the subsequent discussion, the origin is assumed to be the only equilibrium point of the fuzzy control system.
Theorem 1 [4]: The equilibrium of the CFS of (2) is
quadrat-ically stabilizable via the fuzzy controller (4) if there exist
ma-trices , , , and , such that (6) (7) .. . ... . .. ... (8)
Moreover, in this case, the fuzzy local feedback gains are
, .
Theorem 2 [4]: The equilibrium of the of (2) is quadratically stabilizable via the fuzzy controller (4) if
there exist matrices , , , and ,
such that (9)–(11), as shown at the bottom of the page, hold. Moreover, in this case, the fuzzy local feedback
gains are , .
It has been shown in [4] that Theorems 1 and 2 are more re-laxed than the famous rere-laxed stabilization conditions proposed in [10] and [11].
C. Relaxed Stabilization Conditions
The basic stabilization conditions stated in the Section II-B
may be conservative since all , ,
are required to be symmetric. To release the con-servatism, the following relaxed stabilization conditions were reported recently in [8], in which each is not required to be symmetric.
Theorem 3 [8], [18]: The equilibrium of the CFS of (2) is
quadratically stabilizable via the fuzzy controller (4) if there
exist matrices , , , and ,
, such that (12) (13) (9) (10) .. . ... . .. ... (11)
..
. ... . .. ... (14)
Moreover, in this case, the fuzzy local feedback gains are
, .
Theorem 4 [8], [18]: The equilibrium of the DFS of (2) is
quadratically stabilizable via the fuzzy controller (4) if there
exist matrices , , , and ,
, such that (15)–(17), as
shown at the bottom of the page, hold. Moreover, in this case, the
fuzzy local feedback gains are , .
Remark 1: When this paper was submitted, [18] was not yet
available in the open literature. However, its conference paper [8] had been cited in our initial submission. For completing the references, the paper [18] was added in reference section when this paper was revised.
Obviously, if set , Theorems 3 and 4 reduce to Theorems 1 and 2. Thus Theorems 1 and 2 are particular cases of Theorems 3 and 4, respectively. In next section, new conditions that are more relaxed than Theorems 3 and 4 will be proposed. Actually, Theorems 3 and 4 are shown to be particular cases of the proposed conditions.
III. MAINRESULTS
In this section, two kinds of stabilization conditions are pre-sented. One is for fuzzy state feedback stabilization problem. The other one is for fuzzy static output feedback stabilization problem. The latter problem is essentially hard for T–S fuzzy models but very useful in practice. To the best of authors’ knowl-edge, very little effort has been paid to this problem for T–S fuzzy control systems.
A. LMI-Based Stabilization Condition for Fuzzy State Feedback Control
In this subsection, the state feedback case is considered firstly. New stabilization conditions for CFS and DFS are derived and expressed in terms of a set of LMIs. These conditions are more relaxed than Theorems 1–4. It can be shown that Theorems 1–4 are our special cases.
Theorem 5: The equilibrium of the of (2) is quadrati-cally stabilizable via the fuzzy controller (4) if there exist
ma-trices ; , ; , ;
and , , , and
, , , ,
, satisfying the following
LMIs: (18) (19) (20) .. . ... . .. ... (21)
Moreover, in this case, the fuzzy local state feedback gains are
, .
Proof: For simplicity, we will use , , and in place of , , and , respectively. Consider a
can-didate of quadratic function . The
equi-librium of CFS (5) is quadratically stable if
(22)
From (22), the equilibrium of CFS (5) is quadratically stable if
Let , . Premultiply and postmultiply (23) by , we have the first equation shown at bottom of page. If (18)–(20) are feasible .. . ... ... . .. ... ... .. . ... ... . .. ... ... .. . ... ... . .. ... ... .. . ... ... . .. ... ...
Thus, if (21) holds, . In other words, the equilibrium of the of (2) is quadratically stabilizable via the fuzzy controller (4).
Theorem 6: The equilibrium of the DFS of (2) is
quadrati-cally stabilizable via the fuzzy controller (4) if there exist
ma-trices ; , ; , ;
and , , , and
, , , ,
, satisfying the LMIs shown
in (24)–(27) at the bottom of the page. Moreover, in this case, the
fuzzy local feedback gains are , .
(24)
(25)
(26)
..
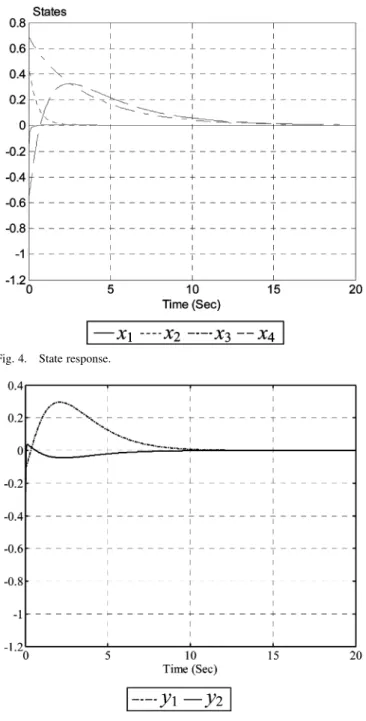
Fig. 4. State response.
Fig. 5. Output response.
In this simulation, assume and . By Theorem 9, we obtain
that it can be also applied to solve fuzzy static output feedback stabilization problems which are hard in essence for T–S fuzzy systems but useful and important in practice.
REFERENCES
[1] W. J. Wang and C. S. Sun, “Relaxed stability condition for T–S fuzzy discrete system,” in Proc. FUZZ-IEEE’02, 2002, pp. 244–249. [2] , “Relaxed stability conditions for T–S fuzzy systems,” in Proc. 9th
IFSA World Congress, 2001, pp. 221–226.
[3] J. Joh, Y. H. Chen, and R. Langari, “On the stability issues of linear Takagi–Sugeno fuzzy models,” IEEE Trans. Fuzzy Syst., vol. 6, no. 3, pp. 402–410, Aug. 1998.
[4] E. Kim and H. Lee, “New approaches to relaxed quadratic stability con-dition of fuzzy control systems,” IEEE Trans. Fuzzy Syst., vol. 8, no. 5, pp. 523–534, Oct. 2000.
[5] S.-W. Kau, Y.-S. Liu, C.-H. Lee, L. Hong, and C.-H. Fang, “Static output feedback fuzzy controller design for T–S fuzzy descriptor systems,” Int.
J. Fuzzy Syst., vol. 6, no. 4, pp. 187–193, Dec. 2004.
[6] , “H control of nonlinear systems via fuzzy static output feed-back—an LMI approach,” Int. J. Elect. Eng., vol. 12, no. 2, pp. 125–131, 2005.
[7] K. Kim, J. Joh, R. Langari, and W. Kwon, “LMI-based design of Takagi-Sugeno fuzzy controllers for nonlinear dynamic systems using fuzzy estimators,” Int. J. Fuzzy Syst., vol. 1, no. 2, pp. 133–144, Dec. 1999. [8] X. Liu and Q. Zhang, “H output feedback control designs for T–S
fuzzy dynamic systems via LMI,” in Proc. 41st IEEE Conf. Decision
and Control, 2002, pp. 2153–2158.
[9] K. Tanaka and H. O. Wang, “Fuzzy regulators and fuzzy observers: a linear matrix inequality approach,” in Proc. 36th IEEE Conf. Decision
and Control, 1997, pp. 1315–1320.
[10] K. Tanaka, T. Ikeda, and H. O. Wang, “Fuzzy regulators and fuzzy observers: relaxed stability conditions and LMI-based designs,” IEEE
Trans. Fuzzy Syst., vol. 6, no. 2, pp. 250–265, May 1998.
[11] , “An LMI approach to fuzzy controller designs based on the relaxed stability conditions,” in Proc. IEEE Int. Conf. Fuzzy Systems
(FUZZ/IEEE), 1997, pp. 171–176.
[12] K. Tanaka and H. O. Wang, Fuzzy Control Systems Design and
Anal-ysis. New York: Wiley, 2001.
[13] T. Takagi and M. Sugeno, “Fuzzy identification of systems and its appli-cation to modeling and control,” IEEE Trans. Syst., Man, Cybern., vol. SMC-15, no. 1, pp. 116–132, Feb. 1985.
[14] K. Tanaka and M. Sugeno, “Stability analysis and design of fuzzy control systems,” Fuzzy Sets Syst., vol. 45, pp. 135–156, 1992.
[15] K. Tanaka, T. Ikeda, and H. Wang, “Design of fuzzy control systems based on relaxed LMI stability conditions,” in Proc. 35th IEEE Conf.
Decision and Control, 1996, pp. 598–603.
[16] H. O. Wang, K. Tanaka, and M. F. Griffin, “An approach to fuzzy control of nonlinear systems: Stability and design issues,” IEEE Trans. Fuzzy
Syst., vol. 4, no. 1, pp. 14–23, Feb. 1996.
[17] L.-X. Wang, A Course in Fuzzy Systems and Control. London, U.K.: Prentice-Hall, 1997.
[18] X. Liu and Q. Zhang, “New approaches toH controller designs based on fuzzy observers for T–S fuzzy systems via LMI,” Automatica, vol. 39, no. 5, pp. 1571–1582, Oct. 2003.
[19] M. C. M. Teixeira, E. Assuncao, and R. G. Avellar, “On relaxed LMI-based designs for fuzzy regulators and fuzzy observers,” IEEE Trans.
Yung-Sheng Liu was born in Hsin-Chu, Taiwan, in
1980. He received the B.S. degree from the Depart-ment of Electrical Engineering, Naitonal Yunlin Uni-versity of Science and Technology, Yunlin, Taiwan, in 2002, and the M.S. degree from the Department of Electrical Engineering, National Kaohsiung Uni-versity of Applied Sciences, Kaohsiung, Taiwan, in 2004.
Currently, he is with Ingrasys Technology Inc., Tao-Yuan, Taiwan. His research interests include, fuzzy control, linear system control, and singular systems.
Shih-Wei Kau was born in Taichung, Taiwan, in
1950. He received the diploma from the National Kaohsiung Normal University,Kaohsiung, Taiwan, in 1974. He received research scholarship of DSE for industry control from Mamhann University, Mamhann, Germany, in 1980 and 1981. Currently, he is working toward the Ph.D. degree at Strathclyde University, Glasgow, U.K.
From 1974 to 1979, he served as a Teaching As-sistant with the Electrical Engineering Department at National Kaohsiung Institute of Technology (NKIT). In 1982, he returned to NKIT and served as an Instructor of Electrical Engi-neering and also as the Chair of Computer Center at NKIT. Now, he is with National Kaohsiung University of Applied Sciences. His research interests are in the areas of neural genetic application in industry, control system integrated in remote control using neuron chip, PLC control system, etc.
Lin Hong was born in Changhwa, Taiwan in 1947.
He received the B.S. degree in engineering sci-ence from National Cheng-Kung University, Tainan, Taiwan, and the M.S. degree in electrical engineering from Pennsylvania State University, State College.
Since 1977, he has been an Instructor with the Electrical Engineering Department at National Kaohsiung Institute of Technology, Kaohsiung, Taiwan, and then was promoted to Associate Pro-fessor. From August 1982 to December 1982, he was a Visiting Scholar at Cuyahoga Community College, Cleveland, OH. Currently, he is an Associate Professor with the Electrical En-gineering Department at National Kaohsiung University of Applied Sciences, Kaohsiung, Taiwan. His research interests are in the areas of adaptive control, digital controller design, and real-time control.
Ching-Hsiang Lee was born in Taipei, Taiwan. He
received the B.S. degree from Feng-Chia University, Tahchung, Taiwan, the M.S. degree from Chiao-Tung University, Hsiun-Chu, Taiwan, and the Ph.D. degree from Tsing-Hua University, Hsiun-Chu, Taiwan.
He served as a Lecturer at National Kaohsiung Institute of Technology, Kaohsiung, Taiwan, from 1981 to 1997. Currently, he is an Associate Professor with the National Kaohsiung University of Applied Sciences, Kaohsiung, Taiwan. His areas of research interest are stability theory, nonlinear control, and adaptive fuzzy control.