The Edge-Orientation Problem and Its Variants on Some Classes of Graphs

全文

(1)The Edge-Orientation Problem and Its Variants on Some Classes of Graphs1 (Submitted to ICS2002-Workshop on Algorithms and Computational Molecular Biology). William Chung-Kung Yen Department of Graphic Communications and Technology, Shih Hsin University, Taipei, Taiwan, ROC. Corresponding address: Chung-Kung Yen, Associate Professor Department of Graphic Communications and Technology, Shih Hsin University, Taipei, Taiwan 116, ROC E-mail address: ckyen001@ms7.hinet.net 1. This research was supported by National Science Council, Taiwan, R.O.C., under the contract number NSC-90-2213-E-128-001.

(2) The Edge-Orientation Problem and Its Variants on Some Classes of Graphs William Chung-Kung Yen Dept. of Graphic Communications and Technology Shih Hsin University, Taipei, Taiwan (e-mail: ckyen001@ms7.hinet.net). Abstract This paper considers the Edge-Orientation Problem (EOP) and its variants on weighted undirected graphs. Let G(V, E, C, W) be a graph in which V is the set of n vertices and E is the set of m edges. Each vertex v is associated a real cost C(v) and each edge e = (u, v) is associated with two real weights: W(u → v) and W(u → v). The problem involves assigning an orientation to each edge such that G becomes a directed graph. First, the significance and motivations of the EOP and some practical variants are addressed. Then, nontrivial efficient algorithms for solving its two variants, the Out-Degree EOP and the Vertex-Weighted EOP, on general graphs are designed, respectively. Finally, the EOP is proven to be NP-hard on bipartite graphs and then an O(nlgn) time algorithm on weighted trees is proposed. In general, the used techniques and the algorithmic results of this paper may have great help for implementing the Weighted Fair Queuing (WFQ) on real networks. The major goal of the WFQ is to assign effective weight for each queue or flow that can enhance link utilization. Consequently, the findings here can be easily extended to other classes of graphs, such as cactus graphs, block graphs, interval graphs, etc.. Keywords:. undirected graph v.s. directed graph, the Edge-Orientation Problem, WFQ, trees, NP-hard. 1. Introduction and Motivations. 1.

(3) In the research on graph theory and graph algorithms, graphs are often classified into two categories: undirected graphs and directed graphs. For many problems on graphs, researchers often assume that the input graphs are either undirected or directed. This research starts with a new point of view that focuses on transforming an undirected graph to a directed graph (digraph). In short, the major task is to assign each edge e = (u, v) an orientation, either from u to v or from v to u, to obtain a digraph. Meanwhile, the motivations and significance of our research can be described from practical aspects as follows. The modern information networks provide easy and efficient manners to access information for people. The major concerns of various information services over networks, including Internet, private Intranets and Extranets, are to achieve high efficiency, quality, and throughput. Many fundamental problems, such as resource allocations (e.g. replication of data objects on a distributed database), Quality of Service (QoS) and various routing, load balancing, and flow controls, have been received much interest and attention [1, 4, 7, 8, 10 – 13, 20]. In [15, 16], we have proposed the Link-Orientation Problem (the LOP) which is highly related to assign flow orientations of links of a network. In many applications of real flow control, each link of a network is effectively assigned a weight correspond to the switch router for representing the fair of the buffers. A switch router often uses the peer-link to determine the effective weights for each queue (flow). Many useful and powerful approaches for flow control and related issues in QoS monitoring have been proposed [3, 9, 10, 19]. Among these various approaches, a variant of the Fair Queuing (FQ), called the Weighted Fair Queuing (WFQ), has been studied by many researchers [14]. The WFQ wants to achieve two major objectives: to allocate resource in a fairer manner and to enhance link utilization. Basically, a router performing WFQ must learn what weights to be assigned to each flow (queue). Many previous works often assumed that it is possible to split the flow based on the actual weight of each link. The direction of message flows within any link e = (u, v) can be either oriented from u to v or from v to u. The essential issue is to determine which orientation will be the 2.

(4) most helpful for the WFQ and other network applications such as routing and load balancing. It is the time to define our problem formally. Let G(V, E) be a graph in which V is the set of n vertices and E is the set of m edges. In many real-world environments, resources are often allocated at vertices. The cost of placing resources at each vertex might be very different. Thus, each vertex v is associated with a real cost C(v) to indicate this fact. Besides the cost of allocating resources at vertices, another key issue is to minimize the communication cost in a computer network. For any edge e = (u, v), the communication costs from u to v and from v to u should be greatly different. The communication cost will be accumulated to the total cost of u if the message flow is from u to v, and vice versa. This means that each edge e = (u, v) should be assigned an orientation either from u to v or from v to u. There are 2m different ways for assigning the orientations of all edges. Each way for assigning the orientations of all edges is called an edge-orientation scheme. Since the costs of the orientations, u → v and v → u, are different, it is worthy to determine which edgeorientation scheme is the most suitable for the concerned real application. This paper proposes very useful and meaningful measurements as well as efficient algorithms for selecting edge-orientation schemes of a weighted undirected graph. This issue is called the Edge-Orientation Problem (EOP) and is defined as follows [15].. The Edge-Orientation Problem (The EOP): Let G(V, E, C, W) be a connected undirected graph. Meanwhile, each vertex v is associated with a real cost C(v) and each edge e = (u, v) is associated with two real weights: W(u → v) and W(v → u). For each edge-orientation scheme A, denote µ(A) as maxx∈V{C(x) + The value. ∑. x→ z. ∑. x→ z. W ( x → z ) }.. W ( x → z ) is defined to be zero if outdeg(x) = 0 within A, where. outdeg(x) is the out-degree of the vertex x. The objective of the problem is to identify an edge-orientation scheme A* such that µ(A*) is minimized. We denote µ(G) as min{µ(A) | A is an edge-orientation scheme of G} hereafter.. 3.

(5) A special form of the EOP has been further proposed and studied in [15].. The Vertex-Weighted Edge-Orientation Problem (The Vertex-Weighted EOP): Given a weighted undirected graph G(V, E, C), for any edge-orientation scheme A, denote π(A) as maxx∈V{C(x) + outdeg(x)}. The aim of the problem is to identify an edge-orientation scheme A* such that π(A*) is minimized. We denote π(G) as min{π(A) | A is an edge-orientation scheme of G} hereafter.. The Vertex-Weighted EOP is just the problem called the Edge-Direction Assignment problem (the EDA problem) which is originally proposed and studied by the authors in [17, 18]. We have successfully applied the EDA problem to design linear-time optimal algorithms for solving the Searchlight Guarding Problem on weighted cographs and weighted interval graphs, respectively. In addition, the VertexWeighted EOP is also the LOP addressed in [16] and linear-time algorithms for the problem on weighted complete networks and weighted trees have been proposed. To investigate the inner spirit and the significance of our research, another simpler version of the EOP has been established [15].. The Out-Degree Edge-Orientation Problem (The Out-Degree EOP): Given a connected undirected graph G(V, E), let θ(A) denote the value maxx∈V{outdeg(x)} for any link-orientation orientation A. The objective of the problem is to derive an edgeorientation scheme A* such that θ(A*) is minimized. We denote θ(G) as min{θ(A) | A is an edge-orientation scheme of G} hereafter.. The Out-Degree EOP has a very close relation to the Bottleneck Searchlight Guarding Problem [15]. The author in [15] has proposed an important strategy for solving bottleneck minimization problems, called the threshold-value binary search, and a linear-time algorithm has also been designed for solving the EOP on weighted complete-split graphs. The strategy used is the recursive greedy approach [2]. 4.

(6) The rest of this paper is organized as follows. An O(m) time algorithm for the Out-Degree EOP on general graphs will be proposed in Section 2. Section 3 will design an O(m + nlgn) time algorithm for the Vertex-Weighted EOP on general graphs. Section 4 will show that the EOP is NP-hard on bipartite graphs. Then, an O(nlgn) time algorithm for the EOP on weighted trees will be designed in Section 5. Finally, the conclusions and future research directions will be addressed in Section 6.. 2. A Time-Optimal Algorithm for Solving the Out-Degree EOP on General Graphs This section will propose an O(m) time algorithm for solving the Out-Degree EOP on general graphs. It is clear that the lower bound of the problem is O(m) since each edge must be examined at least once in order to derive an optimal edgeorientation scheme. Therefore, our algorithm is time-optimal in worst-case. To solve the Out-Degree EOP, a corresponding decision problem is proposed.. The Out-Degree Bounded Edge-Orientation Problem (The Out-Degree Bounded EOP): Given a connected undirected graph G(V, E) and an integer constant 1 ≤ k ≤ max{deg(v) | v ∈ V} in which deg(v) means the degree of the vertex v, determine whether there exists an edge-orientation scheme A* such that θ(A*) ≤ k.. Lemma 1: The answer of the Out-Degree Bounded EOP is 'YES' iff k * n ≥ m. proof: Suppose that the answer of the Out-Degree Bounded EOP is 'YES', i.e., there exists an edge-orientation scheme A such that θ(A*) ≤ k. This implies that outdeg(v) ≤ k, for all v ∈ V. According to the definition of edge-orientation schemes, we must have. ∑. v∈V. outdeg(v) = m. This can directly derive that. ∑. v∈V. outdeg(v) = m ≤ k * n.. Next, consider the case that k * n ≥ m. Note that the out-degree of each vertex can be at most k after assigning the orientations of all edges. A partial edgeorientation scheme H can be obtained by executing the following code segment.. 5.

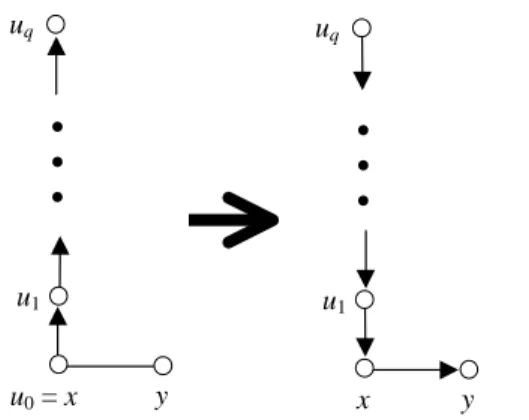
(7) for each vertex u outdeg(u) = 0; for each edge e = (u, v) incident with u if (outdeg(u) < k) and (the orientation of e is not determined) { assign the orientation of e from u to v; outdeg(u)++; } else discard e; endif endfor endfor. It is simple to verify that if the orientations of all edges have been determined within H, then θ(H) ≤ k and the answer of the Out-Degree Bounded EOP is 'YES'. So, the task left is to handle the situation when there exist edges whose orientations are still undetermined after executing the above code segment. Suppose that the orientation of some edge e = (x, y) is left undetermined. The following observations can be directly established by examining the above code segment.. Observation 1: outdeg(x) = outdeg(y) = k.. Observation 2: There must exist a vertex z such that outdeg(z) < k.. Since we assume that G is connected, a directed path P: x = u0 → u1 → u2 … → uq-1 → uq in which outdeg(uj) = k, 0 ≤ j ≤ q - 1, and outdeg(uq) < k can be found by performing the following loop.. P = {x}; s = x; loop u = select(s); /* u is any vertex such that s → u within H. */ P = P ∪ {u}; if outdeg(u) < k { output P; exit; 6.

(8) } endif s = u; endloop. When the directed path P has been obtained, we simply reverse the orientations of all edges in P and assign the orientation of the edge (x, y) as x → y. Figure 1 illustrates this change. Verifying that the out-degree of each vertex is still smaller than or equal to k is an easy job. uq. uq • • •. • • •. u1 u0 = x. u1 y. x. y. Fig. 1. A directed path P from x to uq, where outdeg(uj) = k, 0 ≤ j ≤ q - 1, and outdeg(uq) < k. Note that u1 may be the vertex y.. The task for finding a directed path P as stated above can be performed in iterative manner until the orientations of all edges have been assigned. Combining all reasoning so far, we can conclude that k * n ≥ m iff the answer of the Out-Degree Bounded EOP is 'YES'. Thus, we complete our proof. g. Based on Lemma 1, the following algorithm can be design to solve the OutDegree EOP correctly and Theorem 1 will be established. Algorithm Out-Degree-EOP Input: A connected undirected graph G(V, E) with n vertices and m edges. Output: An edge-orientation scheme A* such that θ(A*) = maxx∈V{outdeg(x)} is minimized. Method: Step 1: max-degree = maxv∈V{deg(v)}; 7.

(9) Step 2: k = smallestk(m, n, max-degree); /* smalestk(m, n, max-degree) returns the smallest integer k such that 1 ≤ k ≤ max-degree and k * n ≥ m. */ Step 3: find a partial edge-orientation scheme H such that θ(H) ≤ k; Step 4: for each edge e = (x, y) whose orientation has not been determined Step 5: find a directed path P: x = u0 → u1 → u2 … → uq-1→ uq such that all selected edges are "unused" and outdeg(uj) = k, 0 ≤ j ≤ q - 1, and outdeg(uq) < k; Step 6: reverse the orientations of all edges in P; Step 7: mark all edges in P to be "used"; Step 8: assign the orientation of the edge e from x to y; Step 9: outdeg(x)++; Step 10:endfor End Out-Degree-EOP Theorem 1: The Out-Degree EOP can be solved in O(m) time on general graphs. proof: The task is to examine the time-complexity of Algorithm Out-Degree-EOP. It is easy to ascertain that Step 1 through Step 3 can be done in O(m) time. Assume that e1, …, eh are the edges whose orientations left undetermined after performing Step 3 and they are examined sequentially during the for loop from Step 4 to Step 10. Let Pj denote the directed path found corresponding to ej, 1 ≤ j ≤ h. Step 6 reverses the orientations of all edges in Pi and these edges will not be used while constructing Pi+1, 1 ≤ i ≤ h - 1. The path Pi+1 always can be found if k ≥ 2 and the case k = 1 can be solved by trivial way. It implies that each edge of G will be examined at most one time during the execution of the for loop. Therefore, the for loop can be done in O(m) time and the total time-complexity is clear O(m). g. 3. An O(m + nlgn) Algorithm for Solving the Vertex-Weighted EOP on General Graphs This section will generalize the algorithmic result of the Out-Degree EOP to the Vertex-Weighted EOP. First, the following lemma can be directly obtained according to the results of Section 2.. 8.

(10) Lemma 2: Let A* be an edge-orientation scheme of the Out-Degree EOP such that θ(A*) is minimized. Then, θ(A*) is equal to the smallest integer k such that 1 ≤ k ≤ max-degree and k * n ≥ m.. Suppose that G(V, E, C) is an input instance of the Vertex-Weighted EOP and assume β = maxv∈V{C(v)}. Another graph G*(V*, E*, C*) can be obtained via executing the following code segment.. sort the vertices of G into non-decreasing order using their costs as keys; /* C(v1) ≤ … ≤ C(vn) after sorting */ V* = V; E* = E; C* = C; for each vertex vj, j = 1, …, n if (C*(vj) < β) for each edge e = (vj, x) incident with vj if (C*(vj) + 1 < β) { assign the orientation of e from vj to x; C*(vj)++; deg(vj)--; deg(x)--; E* = E* - {e}; } endif endfor endif if (deg(vj) == 0) V* = V* - {vj}; endif endfor. The following lemma can be easily verified.. Lemma 3: The graph G*(V*, E*, C*) can be constructed from the original input graph G(V, E, C) in O(m) time and C*(x) - C*(y) < 1, for all x ≠ y.. The problem that we should handle becomes the problem of solving the Vertex-Weighted EOP on G*(V*, E*, C*). In the following, the graph considered is G*(V*, E*, C*). Let {H1, …, Ht} be all edge-orientation schemes such that θ(Hj) = η is 9.

(11) minimized, i.e., H1, …, and Ht are all optimal solutions of the Out-Degree EOP. The following lemma is established.. Lemma 4: Suppose that Q is an optimal solution of the Vertex-Weighted EOP. Then, Q ∈ {H1, …, Ht}. proof: Since H1, …, and Ht are all optimal solutions of the Out-Degree EOP, it implies that η is the smallest integer such that η * V* ≥ E*. According to Lemma 2, θ(Q) must be greater than or equal to η. First, it is clear that each Hi is a feasible solution of the Vertex-Weighted EOP with π(Hi) = maxv∈V*{C*(v) + outdeg(v)} = C*(y) + η, for some vertex y. Since Q is an optimal solution of the Vertex-Weighted EOP, we already have π(Q) ≤ π(Hi), for all i. Furthermore, if Q ∉ {H1, …, Ht}, then θ(Q) ≥ (η + 1). We can derive the following equations. π(Q) = maxv∈V*{C*(v) + outdeg(v)} = maxv∈V*{maxoutdeg(v)>η{C*(v) + outdeg(v)}, maxoutdeg(v)≤η{C*(v) + outdeg(v)}} (*) Lemma 3 has stated that C*(x) - C*(y) < 1, for all x ≠ y. Thus, there must exist a vertex u such that the equation (*) can be reduced to C*(u) + θ(Q) ≥ C*(u) + (η + 1). This means that π(Q) > π(Hi), for all i. A contradiction occurs. g. Now, the following algorithm can be designed for solving the VertexWeighted EOP and its correctness can be easily verified. Algorithm Vertex-Weighted-EOP Input: A weighted connected undirected graph G(V, E, C) with n vertices and m edges. Output: An edge-orientation scheme A* such that π(A*) = maxx∈V{C(x) + outdeg(x)} is minimized. Method: 10.

(12) Step 1: construct the graph G*(V*, E*, C*) such that C*(x) - C*(y) < 1, for all x ≠ y, as described in the previous paragraphs; Step 2: max-degree = maxv∈V{deg(v)}; Step 3: k = smallestk(m, n, max-degree); /* smalestk(m, n, max-degree) returns the smallest integer k such that 1 ≤ k ≤ max-degree and k * n ≥ m. */ Step 4: sort the vertices of G* into non-decreasing order using their costs as keys; /* C*(x1) ≤ … ≤ C*(xs) after sorting */ Step 5: find a partial edge-orientation scheme H such that θ(H) ≤ k by examining the vertices x1, …, xs sequentially; Step 6: for each edge e = (x, y) whose orientation has not been determined Step 7: find a directed path P: x = u0 → u1 → u2 … → uq-1→ uq such that all selected edges are "unused" and outdeg(uj) = k, 0 ≤ j ≤ q - 1, and outdeg(uq) < k; Step 8: reverse the orientations of all edges in P; Step 9: mark all edges in P to be "used"; Step 10: assign the orientation of the edge e from x to y; Step 11: outdeg(x)++; Step 12:endfor End Vertex-Weighted-EOP. Theorem 2: The Vertex-Weighted EOP can be solved in O(m + nlgn) time on general graphs. proof: The needed task is to examine the time-complexity of Algorithm VertexWeighted-EOP. It is easy to see that Step 1 through Step 3 can be done in O(m) time. Step 4 involves sorting of at most n numbers and the time-complexity is O(nlgn). Step 6 through Step 12 can be perform in O(m) time as reasoning in Theorem 1. Therefore, the total time-complexity is O(m + nlgn). g. 4. NP-hardness of the EOP on Bipartite Graphs This section will propose a very different algorithmic result than previous sections: the EOP is NP-hard on bipartite graphs. A graph G(V, E) is called a bipartite graph [6] if V consists of two disjoint sets X and Y such that (u, v) ∈ E implies that either (u ∈ X and v ∈ Y) or (u ∈ Y and v ∈ X). A bipartite graph with V = X ∪ Y will be denoted by G(X ∪ Y, E) hereafter. Now, another special version of the EOP and one of its corresponding decision problems are proposed 11.

(13) The Edge-Weighted Only Edge-Orientation Problem (The Edge-Weighted Only EOP): Let G(V, E, W) be a connected undirected graph in which each edge e = (u, v) is associated with two positive real weights: W(u → v) and W(v → u). For each edgeorientation scheme A, denote σ(A) as maxx∈V{ ∑ x → z W ( x → z ) }. Identify an edgeorientation scheme A* such that σ(A*) is minimized. We denote σ(G) as min{σ(A) | A is an edge-orientation scheme of G} hereafter.. The Edge-Weighted Bounded Edge-Orientation Problem (The Edge-Weighted Bounded EOP): Given a positive-edge-weighted graph G(V, E, W) and a positive real constant k, determine whether there exists an edge-orientation scheme A* such that maxx∈V{ ∑ x → z W ( x → z ) } ≤ k.. The following NP-Complete problem is used for reduction.. The Monotone Three Satisfiability problem (The M3SAT problem) [5]: Given a set C of Boolean clauses in the conjunctive normal form in which each clause can contain either only positive literals, say ui′s, or only negative literals, say u i ′s, and each clause contains exactly three literals. The task requires determining whether the given Boolean formula is satisfiable or not.. Lemma 5: The Edge-Weighted Bounded EOP is NP-Complete on bipartite graphs. proof: Suppose that there is an instance of the M3SAT problem with h variable-set U = {u1, …, uh} and the clause-set C = CP ∪ CN, where CP = { c P 1 , …, c P a } is the set of clauses containing only positive literals and CN = { c N 1 , …, c N b } is the set of clauses containing only negative literals. Let U = { u1 , …, u h }. Given any positive real constant k, a positive-edge-weighted bipartite graph G(X ∪ Y, E, W) can be constructed as follows:. 12.

(14) X = U ∪ CN and Y = U ∪ CP, E = {( c P s , uj)  c P s contains uj, 1 ≤ s ≤ a and 1 ≤ j ≤ h} ∪ {(ui, u i )  1 ≤ i ≤ h} ∪ {( c N t , u i )  c N t contains u i , 1 ≤ t ≤ b and 1 ≤ i ≤ h}, W(ui → u i ) = W( u i → ui) = k, for all edges (ui, u i ), W( c P s → uj) = k / 2 and W(uj → c P s ) = k / deg(uj), 1 ≤ s ≤ a and 1 ≤ j ≤ h, W( c N t → u i ) = k / 2 and W( u i → c N t ) = k / deg( u i ), 1 ≤ t ≤ b and 1 ≤ i ≤ h.. It is clear that G is a bipartite graph and deg( c P s ) = deg( c N t ) = 3, for all 1 ≤ s ≤ a and 1 ≤ t ≤ b. The remaining task is to show that there exists an edge-orientation scheme H such that maxx∈V{ ∑ x → z W ( x → z ) } ≤ k in G if and only if the given Boolean formula c P 1 • ... • c P a • c N 1 • ... • c N b is satisfiable. First, assume that there is an assignment satisfying the input Boolean formula. Let u z1 = ... = u zα = TRUE and u w1 = ... = u wε = FALSE, where α + ε = h. Then, zi ≠ wj, for any i and j. An edge-orientation cheme H can be obtained via executing the following code segment. UT = { u z1 , ... , u zα }; UF = { u w1 , ... , u wε }; for each e = ( u zi , u zi ), 1 ≤ i ≤ α assign the orientation of e from u zi to u zi ; endfor for each e = ( u w j , u w j ), 1 ≤ j ≤ ε assign the orientation of e from u w j to u w j ; endfor for each e = (c, u), c ∈ CP and u ∈ U if u ∈ UT assign the orientation of e from u to c; else assign the orientation of e from c to u; endfor for each e = (c, u), c ∈ CN and u ∈ U if u ∈ UF assign the orientation of e from u to c; else 13.

(15) assign the orientation of e from c to u; endfor The task of verifying that maxx∈V{ ∑ x → z W ( x → z ) } ≤ k can be achieved based on the following reasoning. 1. Each clause c must contain at least one true literal in this true assignment. This implies that indeg(c) ≥ 1 within H, for all clause vertices c. Since deg(c) = 3, for all clauses c, we can further claim that. ∑. c →u. W (c → u ) ≤ outdeg(c) * (k / 2) ≤ 2 *. (k / 2) = k. 2. According to the above codes, it is easy to see that outdeg(v) = 0, for all v ∈ (U ∪ U ) - (UT ∪ UF). 3.. ∑. v →c. W (v → c) ≤ outdeg(v) * (k / deg(v)) ≤ deg(v) * (k / deg(v)) = k, for all v ∈. (UT ∪ UF).. Second, if there exists an edge-orientation scheme. H such. that. maxx∈V{ ∑ x → z W ( x → z ) } ≤ k. For each edge (ui, u i ), it is clear that either outdeg(ui) = 0 or outdeg( u i ) = 0 since W(ui → u i ) = W( u i → ui) = k. Meanwhile, for each clause c contains the literal v, W(c, v) = k / 2 implies that outdeg(c) ≤ 2, i.e., there must exist a literal y in c such that the orientation of the edge (c, y) is from y to c. Let S = {v ∈ (U ∪ U )  outdeg(v) > 0}. Take the assignment that the literals corresponding to S are assigned to be TRUE. Ascertaining that this assignment will satisfy the input Boolean formula is a simple matter. g. Consequently, the following main theorem can be established based upon the reasoning so far.. Theorem 3: The EOP is NP-hard on bipartite graphs.. 14.

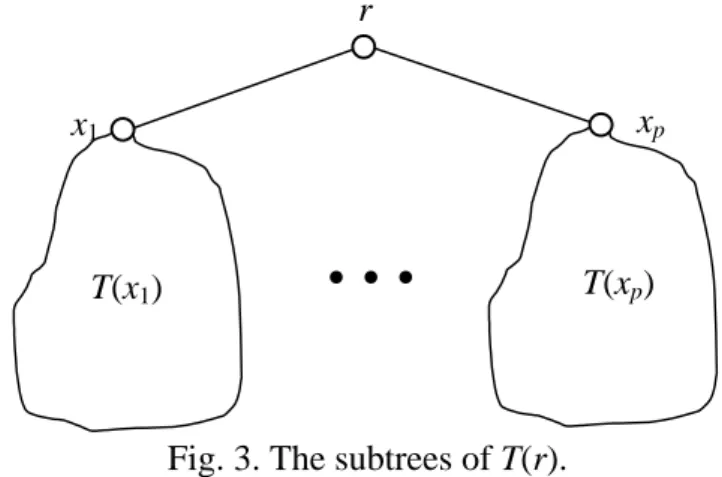
(16) 5. An O(nlgn) Algorithm for Solving the EOP on Weighted Trees This section will propose an O(nlgn) time algorithm for solving the EOP on weighted trees. Given a tree T and any vertex r, the tree will be denoted by T(r) hereafter. Figure 3 shows a general tree T(r) and its subtrees. r xp. x1. T(xr 1). • • •. T(xp). Fig. 3. The subtrees of T(r).. Consider each subtree T(xj), the orientation of the edge (r, xj) can be either from r to xj or from xj to r. If the orientation is from r to xj, then the weight W(r → xj) will be added to the total cost of r and an optimal edge-orientation scheme of T(xj) can be solved recursively and independently. We denote that µ(T(xj, r → xj)) = min{µ(A)  A is an edge-orientation scheme of T(xj) in which the orientation of the edge (r, xj) is from r to xj.} Otherwise, the orientation is from xj to r. By the definition of the EOP, the weight W(xj → r) must be added to the total cost of xj. Replace C(xj) by C(xj) + W(xj → r) and then recursively find an optimal edge-orientation scheme of T(xj). We denote that µ(T(xj, xj → r)) = min{µ(A)  A is an edge-orientation scheme of T(xj) in which the orientation of the edge (r, xj) is from xj to r.} The boundary condition is that the subtree T(xj) only consists of {xj}. It is clear that µ(T(xj, r → xj)) = C(xj) and µ(T(xj, xj → r)) = C(xj) + C(r). Now, a feasible edge-orientation scheme H of T(r) can be obtained via assigning orientations of each edge (r, xj) from xj to r and the following formula can be easily derived.. 15.

(17) µ(T(r)) ≤ µ(H) = max{C(r), max1≤j≤pµ(T(xj, xj → r))} (5.1). The task left is to determine a subset Q = {(r, x q1 ), …, (r, x qα )} (may be empty) of {(r, x1), …, (r, xp)} such that reversing the orientations of all edges in Q can obtain µ(T(r)). The following code segment is designed for identifying such a set. Q = empty set; K = {T(x1), …, T(xp)}; currentµ = max{C(r), max1≤j≤pµ(T(xj, xj → r))}; sort T(xj) into non-decreasing order using µ(T(xj, xj → r)) as keys; while (Q ≠ K) maxµ = max{µ(T(xz, xz → r))  T(xz) ∈ K - Q}; H = {T(xs) ∈ K - Q  µ(T(xs, xs → r)) is equal to maxµ}; newµ = max{C(r) + ∑T ( x )∈H W (r → x s ) , s. max{µ(T(xz, xz → r))  T(xz) ∈ K - (H ∪ Q)}}; if newµ < currentµ { C(r) = C(r) + ∑T ( x )∈H W (r → x s ) ; s. Q = Q ∪ H; currentµ = newµ; } else exit; endif endwhile Lemma 6: Let Qs denote the set derived after the sth iteration of the while loop in the above code segment. Then, max{C(r) + ∑T ( x )∈Q W (r → x z ) , max{µ(T(xz, xz → r))  z. T(xz) ∈ K - Qs} ≤ max{C(r) +. ∑. T ( x z )∈Qs +1. s. W (r → x z ) , max{µ(T(xz, xz → r))  T(xz) ∈. K - Qs+1}.. Lemma 7: Let Q be the set obtained after terminating the above code segment. Then, max{C(r) + ∑T ( x )∈Q W (r → x z ) , max{µ(T(xz, xz → r))  T(xz) ∈ K - Q} ≤ max{C(r) z. +. ∑. T ( x z )∈H. W (r → x z ) , max{µ(T(xz, xz → r))  T(xz) ∈ K - H}, for each subset H of. {T(x1), …, T(xp)}.. Theorem 4: The EOP can be solved in O(nlgn) time on weighted trees. 16.

(18) proof: Lemma 6 and Lemma 7 imply that an optimal edge-orientation scheme of T(r) can be obtained by recursively deriving µ(T(xj, r → xj)) and µ(T(xj, xj → r)) for each subtree T(xj) and then examine each child of r constant times after sorting all subtrees T(xj). Let Time(n) denote the time-complexity for T(r). The following equations can be established, where V(T(xj)) means the vertex-set of each subtree T(xj). p. Time(n) =. ∑ Time( V (T ( x j =1. j. )) ) + O( p lg p ) = O(nlgn). g. 6. Conclusions This paper has open a new research fields that transforms an undirected graphs to digraphs under minimization of some practical cost measurements. The issue is called Edge-Orientation Problem (EOP) here. Nontrivial efficient algorithms for solving its two variants, the Out-Degree EOP and the Vertex-Weighted EOP, on general graphs has been designed, respectively. Furthermore, the EOP itself has been shown to be NP-hard on bipartite graphs and an O(nlgn) time algorithm on weighted trees has also been proposed. The followings are some research directions that deserve us to further work. 1. Basically, the used techniques and the algorithmic results may have great help for implementing the WFQ on real networks to enhance link utilization. Studying how to really apply the EOP for the WFQ as well as network flow control will be an interesting and meaningful job. 2. Extend the findings of this paper to solve the EOP on other classes of graphs, such as cactus graphs, block graphs, interval graphs, etc. 3. Identify the properties with great help for solving fundamental problems such as shortest paths and domination on digraphs via examining the EOP and its variants in detail.. 17.

(19) References [1]. S. N. Bhatt. and J. Crowcroft, “QoS Sensitive Flows: Issues in IP packet Handling,” IEEE Internet Computing Journal, Vol. 4, No. 4, pp. 48-57, 2000.. [2]. T. H. Cormen, C. E. Leiserson, and R. L. Rivest, Introduction to Algorithms, The MIT Press, New York, 1990.. [3]. W. C. Feng, D. D. Kandlur, D. Saha, and K. G. Shin, “Understanding and Improving TCP Performance over Networks with Minimum Rate Guarantees,” IEEEE/ACM Transactions on Networking Journal, Vol. 7, No. 2, pp. 173-187, 1999.. [4]. M. L. Fisher and D. S. Hochbaum, “Database Location in Computer Network,” Journal of Association Computer Machine, Vol. 27, No. 4, pp. 781735, 1980.. [5]. M. R. Garey and David S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, Bell Laboratories, Murray Hill, Freeman & Co., N. J., 1978.. [6]. M. C. Golumbics, Algorithmic Graph Theory and Perfect Graphs, Academic Press, Inc., New York, 1980.. [7]. S. L. Hakimi and E. F. Schmeichel, “Locating Replicas of a Database on a Network,” Networks, Vol. 30, No. 1, pp. 31-36, 1997.. [8]. X. Jia, “A Distributed Algorithm of Delay Bounded Multicast Routing for Multimedia Applications in Wide Area Networks,” IEEE/ACM Transactions on Networking Journal, Vol. 6, No. 6, pp. 828-837, 1998.. [9]. Y. Jiang, C. K. Tham, and C. C. Ko, “Challenges and Approaches in Providing QoS Monitoring,” International Journal of Network Management, Vol. 10, No. 6, pp. 323-334, 2000.. [10]. W. Korfhage, “Dynamically Load Balancing Prioritized Processes in Distributed Systems,” ISCA Journal, Vol. 2, No. 3, pp. 137-144, 1995.. 18.

(20) [11]. H. Lorenz and A. Orda, “QoS Routing in Networks with Uncertain Parameters,” IEEE/ACM Transactions on Networking Journal, Vol. 6, No. 6, pp. 768-778, 1998.. [12]. D. Medihi, “Models for Network Design, Servicing, and Monitoring of ATM Networks Based on the Virtual Path Concept,” Computer Networks and ISDN Systems Journal, Vol. 29, pp. 373-386, 1997.. [13]. D. L. Mills, “Adaptive Hybrid Clock Discipline Algorithm for the Network Time Protocol,” IEEE/ACM Transactions on Networking Journal, Vol. 6, No. 5, 1998.. [14]. L. L. Peterson and B. S. Davie, “Computer Networks: A Systems Approach,” Morgan Kaufmann Publishers, CA. USA, 2nd Ed., 2000.. [15]. W. C-K Yen, “The Link-Orientation Problem and Its Variants with Applications”, Shih Hsin University Journal, Vol. 11, pp. 265-285, 2001.. [16]. W. C. K. Yen and S-J Yang, "The Link-Orientation Problem on Weighted Networks", Proceedings of the 16th International Conference on Computer and Their Applications (CATA-2001), Seattle, Washington, USA, pp. 325-329, 2001.. [17]. W. C. K. Yen and C. Y. Tang, “The Searchlight Guarding Problem on Weighted Split Graphs and Weighted Cographs”, Networks, Vol. 35 No. 4, pp. 195-206, 2000.. [18]. W. C. K. Yen and C. Y. Tang, “An Optimal Algorithm for Solving the Searchlight Guarding Problem on Weighted Interval Graphs”, Information Sciences, Vol. 100, pp. 1-25, 1997.. [19]. C. K. Tham, Y. Jiang, and C. C. Ko, “Monitoring QoS Distribution in Distributed Multimedia Networks,” International Journal of Network Management, Vol. 10, No. 2, pp. 75-90, 2000.. [20]. T. Tsichiya and T. Kikuno, “Dependable Evaluation of the Weighted Voting System in the Presence of Node and Link Facilities,” International Journal of Computer Systems Science & Engineering, Vol. 15, No. 3, pp. 181-190, 2000. 19.

(21)