Cognitive Conflicts as a Teaching Strategy to Enhance the Need of Mathematical Proofs with Technology Support

全文

(1)Cognitive Conflicts as a Teaching Strategy to Enhance the Need of Mathematical Proofs with Technology Support. Chun-Yi Lee & Ming-Puu Chen Graduate Institute of Information and Computer Education National Taiwan Normal University 162 He-Ping East Road, Section 1, Taipei City, Taiwan 106 Telephone: 886-2-23622841#21 E-mail:mpchen@ice.ntnu.edu.tw. ABSTRACT. believed that a mathematical proof is a universal symbolic. In solving mathematical problems, students can feel. script, which allows one to distinguish clearly between. that the universality of a conjecture or a formula is. truth and falsity [2]. Through logic and inductive. validated by their experiments and experiences. In. reasoning, proofs provide students with other learning. contrast, students generally do not feel that deductive. opportunities to enhance their mathematical understanding. explanations strengthen their conviction that a conjecture. from a rigorous perspective. Therefore teaching proofs is a. or a formula is true. In order to cope with students’. common activity in mathematics classroom of high school. conviction based on empirical experience only and to. students, which is unique and different from other sciences. create a need for deductive explanations, we developed a. teaching.. teaching activity with technology support intended to. Proving is a complex and difficult task for high. cause cognitive conflicts. In this paper, we describe the. school students and the attempts to teach it were generally. conducting process throughout this activity that led. not successful in the past [3]. Euclidean geometry was just. students to contradictions between original conjectures. used as such a vehicle to teach formal mathematical proofs. and new findings. The teacher could create familiar. in high schools, and a great deal of time was devoted to it.. problem situations and use students’ naïve inductive. Many students derived little or even no benefit from the. approaches to make students think mathematically and. geometry courses, and they could not distinguish between. establish the necessity for proofs via technology support.. empirical evidence and deductive proofs [4]. It was very common for students to stop at the stage in which they had found a formula, and they could not feel the necessity of. 1: INTRODUCTION. producing proofs. Students constructed a proof just because the teacher asked them to do so [5]. Even worse,. For mathematicians, proofs have been considered as tools for verifying mathematical statements and explaining. many people thought of proofs as a part of geometry rather than a general mathematical process [6].. the reasons that support these statements [1]. Leibniz. - 1443 -. Therefore, how to have students engage in proving.

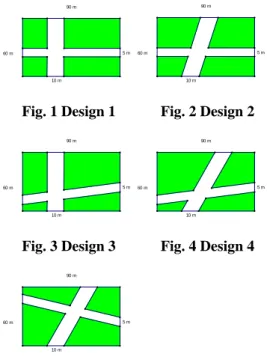
(2) processes and let them see any reason or feel any need for. providing solutions, which may vary from group to group,. it is an important issue in mathematics education [7]. In. students’ strategies of heuristics may increase and thus be. this paper, a teaching activity that raises students’. used on subsequent problem solving tasks. With skillful. consciousness. old. teaching, a variety of ideas may be discussed, which can. conjectures and new findings through technology support. be linked in an effort to enhance mathematical. will be described. This activity created the setting and. understanding. One other advantage of this reporting back. atmosphere from which the contradictions arose and left. stage is that students sometimes learn more easily from. the findings unresolved. The need to explain and prove the. each other than they do from the teacher. The most. findings students explored by themselves thus emerged. important objective of this stage is to integrate different. quite naturally [1].. strategies and solutions, demonstrate general applicability. of. cognitive. conflicts. between. of problem solving strategies, and show how problem. 2: INSTRUCTIONAL FRAMEWORK. features may influence solving approach.. In this paper, the teaching activity was divided into. 3: THE PASTURE PROBLEM. three stages: introduction, exploration in groups, and reporting back [8]. In the introduction stage, the teacher. Many students arriving at university level still does. created the problem situation and had students read the. not even realize that fitting a formula to a pattern is not the. problem. Then the teacher discussed words or phrases. same thing as proving it. How to help students bridge the. students may not understand or led whole-class discussion. gap from the conjecture to a proof and make them feel the. to focus on the importance of understanding the problem.. need of proving is an important issue in a well-designed. The main goal of this stage is to illustrate the importance. mathematics curriculum. Cognitive conflicts can provide. of reading carefully, and to focus on special vocabulary,. just the new medium we need for teaching proofs. For this. important data, and clarification process. In the second. to be successful, however, we need a bank of good. stage, exploration in groups, groups of size of three or. examples. The rest of this paper is devoted to one such,. four tried to solve problems by interacting with each other.. and the example of teaching the pasture problem will be. During this stage, the teacher moved from group to group. described and presented based on the above teaching. providing hints as needed, observed and questioned. framework.. students about where they were, provided problem. The Pasture Problem: A shepherd has a rectangular. extensions in the right time, and required students who. pasture with a length of 90 meters and a width of 60. had obtained a solution to answer the question. The. meters. The shepherd wants to construct a cross street on. primary intention of this stage is to diagnose strengths and. the pasture. Here are five designs (see Fig. 1 to Fig. 5).. weaknesses of students’ problem-solving process, and help. Do the following five figures have the same leftover area. students overcome blockages they encounter during this. of the pasture? If not, which one of them would have the. stage. In the final stage, reporting back, a member of each. maximum leftover area of the pasture?. group would report back to the whole class. It is important that this stage is more than just presenting answers. By. - 1444 -.

(3) into a large rectangle with a length of (90-10) meters and a. 90 m. 90 m. width of (60-5) meters. This conjecture students gained 5m. 60 m. plays an important role during introduction stage because. 5m. 60 m. 10 m. 10 m. Fig. 1 Design 1. it will lead students to generate cognitive conflicts during the next teaching stage.. Fig. 2 Design 2. 90 m. 90 m. 3.2: TEACHING STAGE 2: EXPLORATION IN 5m. 60 m. 5m. 60 m. 10 m. GROUPS. 10 m. Fig. 3 Design 3. The purpose of this teaching stage is to make students. Fig. 4 Design 4. plan how to proceed and to execute the solution according. 90 m. to the plan, consisting of identifying goals and sub-goals, 5m. 60 m. making and implementing a global plan, monitoring and. 10 m. controlling the progress of a solution plan. The teacher divided the class into eight groups. There were four. Fig. 5 Design 5. students with heterogonous in the mathematical ability in. 3.1: TEACHING STAGE 1: INTRODUCTION. each group. Then the teacher provided each group the computer tool [9] which could simulate the pasture. The purpose of this teaching stage is to make students. problem, help students explore it, and guide them to form. understand the pasture problem, including reading and. new conjectures. Students used this tool to investigate the. rereading. subsequent. nature of the pasture problem, and to monitor progress of. representations of the problem, analysis of the information. their plan of the solution (Fig. 6, Fig. 7, and Fig.8 are the. and conditions of the problem, and assessment of. displays of operations of this computer tool). The teacher. difficulty in the problem. The teacher has to create the. also had to move from group to group providing assistance. problem situation and pose the pasture problem described. via scaffolding. Through group discussion and technology. above and then he or she must consider students’ ability to. support, almost each group of students found the. identify the problem and define it. Students will code the. following facts: (a) the four leftover pastures can combine. important elements from the problem situation. They will. into a big rectangle in the first three figures (see Fig. 6). (b). represent the characteristics of the pasture problem. In the fourth figure, the four leftover pastures can combine. mentally,. acquired. into a big rectangle, but there is a small overlap of a. information to the previously acquired information. Then. parallelogram in the middle of the big rectangle (see Fig.. the teacher gives every student a chance to guess the. 7). (c) In the final figure, the four leftover pastures can. answer and judge the reason. Almost ninety five percent of. combine into a big rectangle, but there is a small gap of a. students in the class would consider that the five figures. parallelogram in the middle of the big rectangle (see Fig.. all have the same leftover area, 440 m . This is because. 8).. the. problem,. involving. initial. relating. and. the. newly. 2. they think that the four leftover pastures could combine. - 1445 -.

(4) 3.3: TEACHING STAGE 3: REPORTING BACK The purpose of this teaching stage is to make students evaluate what they know about their performance, encompassing the interaction of a person, a solution and a strategy. In this final stage, the representatives of each. Fig. 6 The finding in condition 1. group will report back to the whole class. Each group would get the new conjecture of the contradictory phenomenon and everyone concerned not only the fact of this. phenomenon. but. also. the. reason. why. this. phenomenon occurred. The teacher would need to listen carefully to the reports of the members who represent their. Fig. 7 The finding in condition 2. groups and discuss the key points of their solutions. After all the representatives have finished their reporting, the teacher needed to summarize different approaches to the pasture problem, eventually leading to a final solution that might be more elegant. However, only two of the eight groups in a class could build a model to solve this problem. Fig. 8 The finding in condition 3 Fact (a) is an expected result whereas fact (b) and. and explain the results of the contradictions and surprise.. fact (c) are surprising findings. This is because students. The following is the solution provided by one of the two. hypothesized that the four leftover pastures could combine. successful groups in explaining the strange phenomenon.. into a big rectangle in all five figures and this intuitive. Because the area of the two roads is always fixed. belief was quite strong especially when the first three. according to the problem situation, we can get the sum of. figures are checked using the computer tool. But the. the area of the four leftover pastures by subtracting the. findings of the last two figures didn’t support their. area of the two roads, IJKL, EFGH from the area of. judgment and original conjecture. Therefore they were. rectangle ABCD, and then adding the area of the. much surprised about the strange phenomenon occurred in. parallelogram MNOP, the intersection of the two roads. their exploration via computer support. The teacher should. (see Fig. 9). Therefore the larger the area of MNOP is; the. utilize the above three facts to guide students to resolve. greater the sum of the area of the four leftover pastures is.. the contradictions. Cognitive conflicts resulting from these. We define that the width of the vertical road is x (i.e.. contradictions while checking their original conjectures. IJ =x), and the width of the horizontal road is y (i.e.. might trigger a need for explanations and proofs. Students. EF =y). It is supposed that the included angle of the two. in the same group started to discuss why these surprising. roads is θ (i.e. ∠MPO=θ), and the included angle of the. phenomena occur and they desired to build a mathematical. vertical road IJKL and. model to address this issue.. AD is α (i.e. ∠PMR=α). We. also construct that OQ is perpendicular to MP ,. - 1446 -. MR is.

(5) parallel to AD , and OS is parallel to AB . Observing. △MPR, we can find that. observing. △ QSO,. IJ × EF (i.e. x × y) on account of. sin(α + θ ) sin 90° = cos(90° − θ ) × sin θ sin θ 1 = sin θ × =1 sin θ. cos α ×. y MP = sin θ sin(180° − α − θ ) y × sin(α + θ ) ⇒ MP = sin θ Similarly. equal to. we. can. get. that. 4: Conclusion. x OQ = ⇒ OQ = x × cos α . Hence sin 90° sin(90° − α ). In this paper, we exemplified a teaching design which. the area of the parallelogram MNOP is equal to. students encountered cognitive conflicts with computer. sin(α + θ ) sin θ sin α cos θ + cos α sin θ = x × y × cos α × sin θ = x × y × cos α × (sin α cot θ + cos α ). support and had the opportunities for feeling the need to. x × y × cos α ×. prove, rather than considering proving as unnecessary. Cognitive conflicts occur when expectations are not fulfilled. Our task for the pasture problem takes cognitive conflicts as a teaching strategy to encourage students to explore more and to bridge the gap between a conjecture and a proof. In the beginning, students made a conjecture concerning the solution of the pasture problem and found a reason why it was true. The reason was often rooted in common sense or based on previous learning. Through computer-supported cognitive conflicts, our teaching activity led students to more than accepting the correctness of the new conjecture; it led them to construct a new explanation for this new conjecture naturally. It is believed that in this task students were guided to use. Fig. 9 The draft of the formal proof From this formula, we could consider the following conditions of the pasture problem.. deductive reasoning to construct reasons to support the new conjecture that motivated them to solve the pasture. (1) When the included angle α of vertical road and. AD. problem.. is fixed, we could find that the larger the included angle θ. Technology makes students engage in exploration. is, the smaller the area of parallelogram MNOP becomes.. more easily in this activity and enable them to try various. This is because when θ increases, cot θ decreases.. possibilities of solving the problem. Like a jungle. AD (i.e.. adventure, students explore uncertainties and encounter. α=0°), the area of parallelogram MNOP is equal to. different new things during this process. They discover. IJ × EF (i.e. x × y).. that something is not as predicted as they originally. (2) When the vertical road EFGH is parallel to. AB. considered. Consequently students will think about how to. (i.e. α + θ = 90° ), the area of parallelogram MNOP is. explain this phenomenon and finally develop a better. (3) When the horizontal road IJKL is parallel to. - 1447 -.

(6) solution integrating the previous experiences. The design. Council of Teachers of Mathematics, U.S.A.. with technology support has brought proofs into the realm. [6] Holton, D., Oldnow, A., Porkness, R. & Stripp. of student activity and argument; that is, proofs have been. C. (2004). Investigations, proofs and reports.. engaged naturally in true mathematical activities. And. Teaching mathematics and its applications, 23. indeed in this task, students ceased to be recipients of. (2), 97-105.. formal proofs, but were engaged in an activity of. [7] Balacheff, N. (1991). The benefits and limits of. construction and evaluation of conjectures where certainty. social interaction: The case of mathematical. and understanding were not clear, and they had to use their. proof. In A. J. Bishop, S. Mellin-Olsen & J. Van. mathematical knowledge to explain contradictions and. Dormolen (Eds.), Mathematical Knowledge: Its. overcome uncertainties with computer support [1].. Growth Through Teaching (pp. 175-192). Dordrecht, Netherlands: Kluwer Academic. References. Publishers. [8] Holton, D., Anderson, J., Thomas, B., & Fletcher, D. (1999). Mathematical problem. [1] Hadas, N., Hershlowitz, R., & Schwarz, B. B. (2000). The role of contradiction anduncertainty. solving in support of the curriculum?. in promoting the need to prove in dynamic. International Journal of Mathematical. geometry environments. Educational studies in. Education in Science and Technology, 30 (3),. Mathematics, 44, 127-150.. 351-371. [9] Yuan, Y., & Lee, C. Y. (2004, July). Designing. [2] Hanna, G. (2000). Proofs, explanations, and exploration: An overview. Educational studies. instructional tools by Flash MX to teach basic. in Mathematics, 44, 5-23.. geometry concepts. In Proceedings of the TIME-2004 Symposium. Montreal, CA.. [3] Clements, D. H., & Battista, M. T. (1992). Geometry and spatial reasoning. In D.A. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning (pp. 420-464). New York: Mac- Millan. [4] Chazan, D. (1993). Instructional implications of students' understandings of the differences between empirical verification and mathematical proof. In J. Schwartz, M. Yerushalmy & B. Wilson (Eds.), The Geometric Supposer: What is it a Case of? (pp. 107-116). Hillsadle, NJ: Lawrence Eribaum Associates. [5] Balacheff, N. (1988). A study of students' proving processes at the junior high school level. Paper presented at the 66th Annual Meeting of the National. - 1448 -.

(7)