Iterative ML estimation for frequency offset and time synchronization in OFDM systems

Proceedings of the 2004 IEEE

International Conference on Networking. Sensing & Control Taipei, Taiwan, March 21-23, 2004

Iterative

ML

Estimation for Frequency Offset and

Time Synchronization in OFDM Systems

Chien-Chih

Chen

Electrical Engineering Department National Taiwan University

Taipei, Taiwan 106, R.

0.

C. coolmail@tpts5 .seed.net.tw

.

Abstract

-

In recent years, orthogonal frequency division multiplexing (OFDM) technique has become attractive and important in both wireline and wireless communications. One of the well-known problems in OFDM systems is its vulnerability to frequency and time offset. This paper develops an iterative maximum-likelihood (ML) estimation algorithm for correction ofbothfrequency and time offset in OFDM systems. Because of the complicated characteristics

of log-likelihood function, not every chosen initial point for iteration procedure can always converge to the values resulting in acquisition of the global maximum of log- likelihood function. This implies that some of the selected initial points can on!v converge to the values which yield local maxima of log-likelihood function. According to the proposed iterative approaching algorithm, the global maximum of log-likelihoodfunction can be definitely found to achieve both frequency and time synchronization. In

addition, the seeking time for this global maximum in the iteration procedure is able to be reduced and evaluated. Keywords: Maximum-likelihood estimation, frequency offset, time synchronization, iterative approaching algorithm, OFDM systems.

1 Introduction

Olthogonal frequency division multiplexing (OFDM) is a powerful modulation scheme for high rate wireless communication systems because of its superior property to overcome frequency selective fading in multipath environments. In Europe, OFDM has been standardized for digital audio broadcasting (DAB) and digital video broadcasting television [I]. Recently, OFDM has also been applied to wireless local area network (WLAN) such as IEEE 802.11a [Z] in United States and Hiperlad2 in Europe.

In recent years, OFDM technique attracts increasing interests because of its excellent property in wireless communications. Since each subcarrier in OFDM is narrowband with respect to coherent bandwidth, an OFDM system is capable of coping with frequency-selective fading and narrow band noise. The other advantage in OFDM system is its efiicient modulation and demodulation schemes. Inverse discrete Fourier transform (IDFT) and discrete Fourier transform (DFT) can be implemented with inverse fast Fourier transform (IFFT) and fast Fourier

Jung-Shan Lin

Electrical Engineering Department National Chi

Nan

University Nantou, Taiwan 545, R.

0.

C.

j slin@ncnu.edu.tw

transform (FFT) which can be realized by specific hardware to speed up signal processing.

However, one of well-known problems in OFDM system is its sensitivity to synchronization errors, including both frequency and time. It is very sensitive to frequency offset compared with other single-carrier modulation schemes. All of the subcarriers in the OFDM system are overlapped and orthogonal to each other. Minor carrier frequency offset will make these subcarriers lose their orthogonality [3]. Like the sample time offset in time domain causing inter-symbol interference (ISI), frequency offset will significantly degrade the system performance and cause inter-carrier interference (ICI). For this reason, how to detect carrier frequency and time offset is a crucial problem in OFDM systems.

In general, frequency and time offset correction algorithms are classified into two folds based on using the additional data or not and what kind of additional data they exploit. The data-aided schemes are suitable for the applications that require fast and reliable synchronization because of their redundancy of the OFDM data frame. Training symbols (or called training sequence) and pilot subcarriers are the two redundancy data that usually he exploited. Training symbols are two or more consecutive and identical symbols, and were used to estimate frequency or time offset in [3]. The other redundancy data, pilot subcarrier, was first analyzed in single carrier system in [6J In multicarrier systems, the related synchronization methods were proposed in [7] and [SI. The drawback of data-aided method is the loss of data rate due to the overhead.

The non-data-aided, or called blind, schemes relying on the nature structure of OFDM frames to estimate frequency offset. In [9] and [IO], the authors took advantage of the presence of virtual carriers in OFDM signaling to solve problem. Virtual subcarriers are the carriers that are not modulated in order to avoid the transmit filtering; hence, information-bearing subchannel is smaller than the size of FFT block. How to select the null subcarriers to result in better performance is discussed in [ I l l . Another blind method is first proposed in [I21 and [13], which were based on the correlation of the received data samples. An adaptive algorithm is used to minimize the mean square frequency offset error.

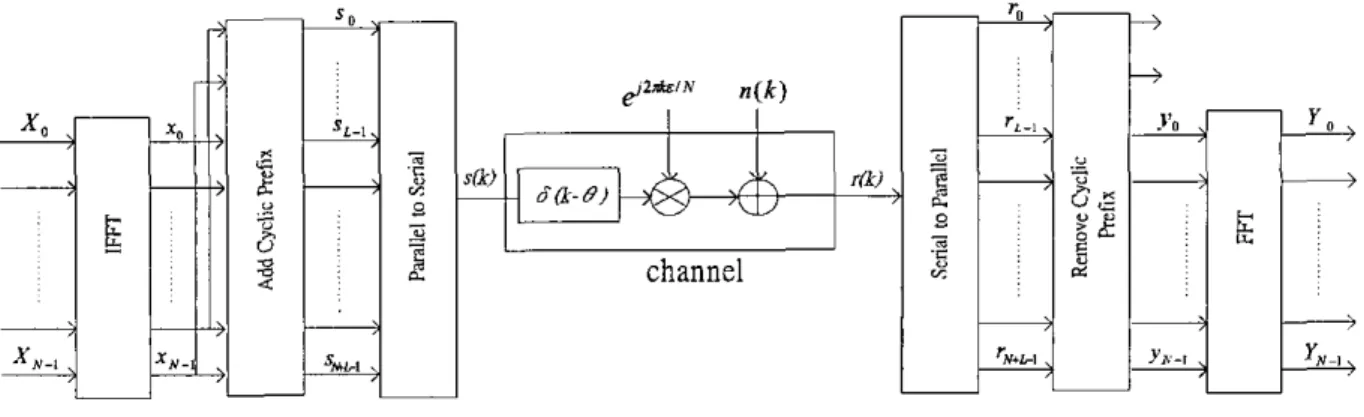
Figure 1. An OFDM system structure

The other synchronization method for carrier- frequency and time offset is to maximize the average log- likelihood function [ 141 with inserting the cyclic extension. At the receiver side, the received signal with cyclic prefix is used to obtain the joint likelihood function for estimation of symbol frame and frequency offset. If the maximum of ML function can be reached, then the actual values of frequency and time offset can be simultaneously obtained. Our work proposes an iterative approaching algorithm to maximize the ML function and acquire the

time and frequency offset. A suggestion is also provided to choose the starting point of iterative that can reduce the trial-and-emor times of iteration and ensure to find the correct global maximum of likelihood function.

The remainder of this paper is organized as follows. In Section 2, the basic shucture of an OFDM system model is introduced and analyzed. In Section 3, the analysis of the joint ML estimation for frequency and time offset in the receiver end is presented and investigated. The methodology of our iterative approaching algorithm for the synchronization in both frequency and time is derived and proposed in Section 4. Finally, some concluding remarks are given in Section 5.

2

OFDM

System

Model

A discrete-time FFTilFFT-based OFDM system is considered and its typical structure of block diagram is shown in Figure 1. Each modulated symbol

X,

is assumed to be an independent complex random variable. Signal X k is composed as N symbols

X,

by inverse discrete Fourier transform (IDFT), that is,

In wireless communications, inter symbol interference

(1%) caused by multipath effect usually happens. To

eliminate this effect and maintain the orthogonality of OFDM signals, guard interval is usually inserted before

transmission. The guard interval, also called cyclic prefix

(CP), is a copy of last L samples of xk appending to OFDM symbols as a preamble. After inserting the cyclic prefix, the transmitted frame becomes sk ,defined by

X N + ~ , k=O,

...,

L - l

x ~ - L , k = L

,....

N + L - I ' (2)

sk = {

An OFDM frame is depicted in detail in Figure 2. Finally, the parallel signals sk are transferred to serial signal s ( k ) for transmission. Frame k

I

1

k d

j

' lorcnd FFr wmdou an OFDM blah

Figure 2. The symbol h u e of OFDM systems.

At the receiver side, r ( k ) is received and transferred to a parallel signal rk as a reverse of transmitter doing. Then, remove the first L samples of frame

rx

, the relation between yk and rk can be written as

yk = rk+L,

k

= 0, ..., N - 1 ₍₃₎ After that, through yk to the N-point discrete Fourier

transform (DFT) as follows: - j 2 h / N 1 N - l yn =-

c

Yke

f i

n=O (4)

If the orthogonal property of each subcarrier is preserved, the original data will be retrieved.

However, because of the non-stability of local oscillators and Doppler effects, each subcarrier has a small frequency offset mismatch between transmitter and receiver. Besides, at the receiver side, there exists uncertainty in symbol arrival time, so the time offset is leaded. In discrete time system, frequency offset is presented as a fraction of frequency spacing and denoted

as E , where

I

E

I<

0.5. Assume all subcarrier experience the same offset, frequency offset can be modeled

as

e j2*” in mathematically and multiply it to each s(k)

.

As to another non-ideal effect, time offset, ‘is modeled as a step delay S ( k - 8 ) in the channel. In this aticle, transmitted signals are assumed only suffer complex additive white Gaussian noise (AWGN) n(k) with variance un 2 , the received signal may be written as

r ( k ) = s(k - 8)e jZnkE”

+

n ( k ) . (5) When the length of block N is enough, from central limit theory, X k or sk can be seen as complex Gaussian

random variables with independent identical distribution (iid). And the sequence of transmitted signal, s(k)

,

is a

complex Gaussian random process but not white due to cyclic prefm insertion. The variance or the average energy of s ( k ) is u:,

3 ML Estimation Analysis

From the conclusion of [14], the log-likelihood function can be expressed as

A(@,&) =/

4

(8)

I

C O S P E + (8))

-

PA2 (@),

₍₆₎

where B+L-l Al(8)=

1

r ( k ) r * ( k + N ) ,

k=e

and

(7)

The magnitude of the correlation coefficient between

rk

and

rHN

is

and

SNR

is defmed as 0:/c:. The estimated frequency

offset

8,

and time offset OML are the argument of 8 and

E that maximum this log-likelihood function, the answer may be written as

(B^ML,;ML)=

a r g m a x A ( 8 , ~ ) . (10)

( 0 6 )

The article [14] argues the maximum value happened when the cosine in ( 6 ) is equal to zero, then the closed form can be derived as

(11) 8, = argmax{~1(8)-pA2(8)]

e

and

In another point of view, ( 6 ) is a function with two variables or axis, time and frequency. The function is unlimited in time axis and is periodic in frequency axis because of the periodicity of cosine function, cos(&& + LAl (8)). If we concern only N+2L samples, the question becomes finding a maximum point of (6) in the range of 8 E

[0

L] and E E [-0.5 0.51.

4

Iterative Approaching Algorithm

In order to maximize the log-likelihood function defmed in (6), utilizing iterative method with separation of

two variables is an appropriate and reasonable approach to this question. In the log-likelihood function A ( ~ , E )

,

frequency offset E is continuous, but time offset 8 is discrete and only has fmite samples from 0 to N + L- 1 . Hence, choosing 0 as the starting variable for the iteration procedure is better than starting at the axis of frequency offset E

.

We

define

ei,j

is the im time-offset iteration result whose initial seed is

eo,j

at the time sample j ,

j = 0 , - - - , N + L - 1

.

That is to say, eo,j is the fust choice we made to sfart the iteration procedure. Then, (12) can be used to obtain the frequency-offset as below:

where denotes the i‘h frequency-offset iteration result whose initial seed is

eo,j

at time sample j

.

Then, based on the known value of (6) becomes

-

(14)

A(@)=l2,(@)

I

cos(2n~,,j + LA,(@))-

PA,(^.

Therefore, the log-likelihood function 4 8 , ~ ) with two variables becomes x(8) which depends only on

0 .

Then the fEst iteration result is the argument that maximizes the function x ( S ) , and can be written as

should be substituted into (12) again and these steps must he applied recursively, so we can obtain ~ 2 , ~ , B z r j ,

E ~ , ~ , and so on. This iteration procedure continues

until the result of

n

-th time iteration is equal to that of (n

+

1) -th time iteration, which can he expressed as

As a result, the fmal iterative convergence pair (ICP), written as (e;,&:), must be equal to ( 8 n , j , ~ m , j ) , that is, 0; = f f , , j and s; = E ~ , ~ . If the initial seed Bo,j is chosen

appropriately, ICP will be the correct time and frequency offset we want to retrieve.

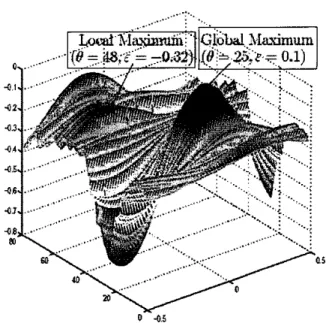
However, not all the initial seeds converge to the correct values of frequency and time offset, and different choices are possible to yield different results. Consider an OFDM system with N = 64 (number of the subcarriers) and L = 16 (CP length) on an AWGN channel. Assume that the real frequency and time offset are 0.1 and 25, and SM is equal to 25,The log-likeliiood function A(ff,&) of the 6" symbol frame is plotted in Figure 3. Clearly, we can see that the global maximum occurs at the point ( B = 2 5 , & = 0 . 1 ) , a n d t h e p o i n t ( B = 4 8 , & = - 0 . 3 2 ) i s a local maximum. Using the previous mentioned iteration method directly without taking notice of the selection of initial seeds, the estimated values of time and frequency offset are possible to converge to local maximum points and retrieve incorrect results.

In order to overcome this mistake, we can try every initial point Bo,j and find a set of ICP

(e;,&;)

from j = 0 to j = N + L - I . Substihlte these pairs into equation (6), the value of ML function with respect to each ICP can he evaluated and defmed by

* *

(17) C . = A(Bj,Ej) j = O...N+ L - 1.

I

From all C j 's, choose the maximum value Cmax among them that is,

The argument (ff;,.;) corresponding to ,C is definitely the correct result for frequency and time offset. Nevertheless, searching every possible point is tedious and wastes too much time. We have to find a way to reduce the seeking time for the actual values of frequency and time offset if possible.

~

Figure 3. ML function surface, 6" frame, frequency offset==O.l,time offset=25,SNR=25. ~

Let us observe all the ICP values for every possible initial seed over a symbol frame in Figure 4. The seed is chosen from 0 to N + L - 1, which is 79 in this case. The actual time offset (TOS) and frequency offset (FOS) are still 25 and 0.1, S M = 2 5 , and the observation frame is the 6"symbol. As long as the initial seed is chosen at the range that the dotted and solid lines overlap, the proposed iteration method has the ability to achieve the correct ICP.

In any frame j , the maximum successive length that the dotted and solid lines overlap together is defmed as the maximum iteration length d j . Therefore, d6 is equal to 30 in this case.

However, because of noise and the randomized transmitted signal s(k)

,

the maximum iteration length is not always the same for evety frame symbol. This

phenomenon can be observed in Figure 5. In this figure, we plot the maximum iteration length of first 30 symhols with various subcarriers in an OFDM system. In general, every symbol's maximum iteration length d i is usually different. If we can fmd the exact iteration length d

,

which is defined as the smallest d j among all frames, choosing initial seed once every d point, such as

ffo,j,B,,j+d,B,,jizd..., and so forth, is enough to obtain the actual values of frequency and time offset. According to this rule, there must be at least one seed staying in the region of maximum iteration length of each frame, and therefore the seeking time can be reduced and evaluated in the procedure.

I

b

-04'

o i o m 30 40 m a 70 m

Figure 4. The distribution of correct convergence region at ream-

a symbol frame.

fane i'dex

Figure 5. The maximum iteration length for each frame. To estimate the exact iteration length

d ,

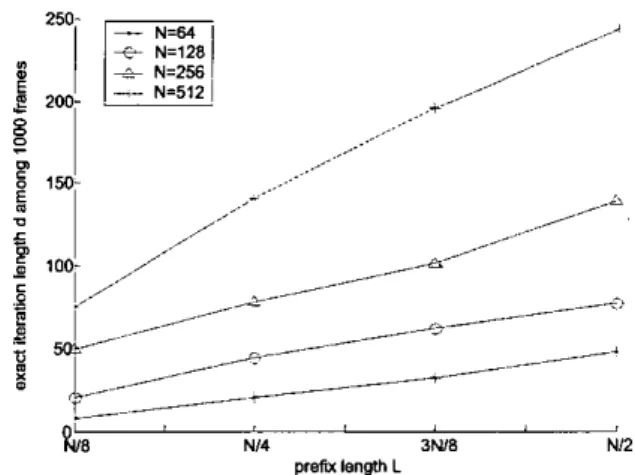
we simulate OFDM system with different N and different CP. The minimum iteration length over 1000 frames is listed in Table 1 and plotted in Figure 6. It can be shown that these exact iteration lengths have almost linear relationship and all of them are larger

than

or equal to the length of CP, which is L. As a result, choosing the exact iteration length d as L is a conservative assumption to guarantee acquisition of the global maximum of ML function, and then achievement of the synchronization of frequency and time.

Table 1: The exact iteration length over 1000 frames.

256 49 78 101 139

512 141 I96 251

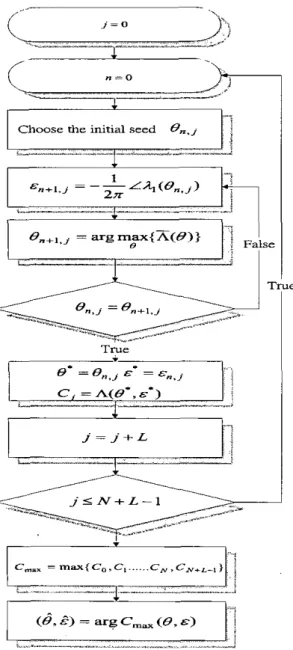
Figure 6.The exact iteration length with various CP lengths To sum up, the proposed iterative approaching algorithm is summarized as following steps and the flow chart of this algorithm is illustrated in the Figure 7. Siep 1: Choose the initial seed to be

Siep 2: Substitute tbe initial seed BOJ into (13), and use (13)-(15) iteratively to find out the corresponding , and set j = 0 .

.

ICP

(s;,.;)

.

Step 3: Substitute the ICP ( O ; , E ; ) into (17) to determine the value of log-likelihood function Ci

.

Step4: Increase j by L (the length of CP), that is,

j =

j + L .

If the index j < N + L - l , then go

back to Step 2. Otherwise, go to Step 5.

Step 5: Determine the maximum from all the values of

cj

's that are obtained in Step 3. The specific ICP associated with this largest

c j

is the actual answer for the values of frequency and time offset

5

Concluding

Remarks

In

this paper,

we

have developed the

maximum-

likelihood estimation with iterative approaching algorithm for correction of both frequency and time offset in OFDM systems. According to the proposed iterative approaching algorithm, the global maximum of log-likelihood function can be definitely found to achieve both frequency and time synchronization. In addition, we provided a method to reduce the seeking time for the global maximum of log-

likelihood function in the iteration procedure.

Although this algorithm is only applied in the AWGN channel here, we believe that our iterative approaching algorithm can be extended to Rayleigb fading channels and multipath channels. As long as the ML functions

associated with various channel models can be analyzed and derived, our algorithm proposed here should have the potentials to maximize the log-likelihood functions and then achieve the synchronization in both carrier frequency and frame arrival time.

.

? , I i .>

-

_i I t

Figure 7. The flow chart of the iterative approaching algorithm.

References

[I1

H.

Sari, G . Karam, and L. Jeanclaude, “Transmission techniques for digital terrestrial TV broadcasting,” in IEEE Communications Mazazine, vol. 33, pp. 100-

109,1995.

121 R. V. Nee, “A new OFDM standard for high rate wireless LAN in the 5 GHz band,” IEEE Vehicular

Technology Conference, vol. 1 , pp. 258-262,1999

PI P. H. Moose, “A technique for orthogonal frequency division multiplexing frequency offset correction,” IEEE Transactions Communications, vol. 42, pp. 2908 -2914, Oct. 1994.

PI

M.-H. Hsieh and C.-H. Wei, “A frequency acquisition scheme for OFDM systems,” Personal, Indoor and Mobile Radio Communications, Seventh IEEE International Svmposium, vol. 13, pp. 843-847, Oct.

1996.

[SI

T. M.

S. a. D. C. Cox, “Robust frequency and timing synchronization for OFDM,” IEEE Transactions on Communications, vol. 45, no. 12, pp. 1613-1621, Dec. 1997.

[GI J. K. Cavers, “An analysis of pilot symbol assisted modulation for Rayleigh fading channels,” IEEE Trans. on Vehic. Technol, vol. 40, pp. 686-693, Nov.

1991.

[’I M. J. Fernandez-Getino, 0. Garcia-Edfors, and J. M. Paez-Borrallo, “Frequency offset correction for coherent OFDM in wireless systems,” IEEE Transactions on Consumer Electronics, vol. 47, pp.

187-193,Feb. 2001.

PI D. Landstrom, S. K. Wilson, J.-J. van de Beek, P. Odling, and P. 0. Bojesson, ‘‘Symbol time offset estimation in coherent OFDM systems,” IEEE Transactions on Communications, vol. 50, pp. 545- 549, Apr 2002.

P I H. Liu and U. Tureli, “A high efficiency carrier estimator for OFDM communications,” IEEE Comm.

Letter, pp.104 -106, Apr. 1998.

I101 U. Tureil, H. Liu, and M. D. Zoltowski, “OFDM blind carrier offset estimation: ESPRIT,’’ IEEE Trans.

Comm, pp. 1459 -1461, Setp. 2000.

[ I l l M. Ghogho, A. Swami, and G. B. Giannaki,

“Optimized null-subcarrier selection for CFO estimation in OFDM over frequency-selective fading channels,” IEEE Global Telecommunications, pp. 202 -206,2001.

[121

M.

A. Visser, 2. Pingping, and Y. Bar-Ness, “A novel

method for blind frequency offset correction in an OFDM system,” Personal, Indoor and Mobile Radio Communications, vol. 2, pp. 816-820, Sep. 1998. B . 4 . Chen and C.-L. Tsai, “Frequency offset estimation in an OFDM system,” IEEE Signal processing Workshop on Signal Processing Advance in wireless Communications, pp. 150-1 53, March 2001

[‘4l J.-J. van de Beek, M. Sandell, and P. 0. Bojesson, “ML estimation of time and frequency offset in OFDM systems,” IEEE Transactions on Signal Processing, vol. 45,pp. 1800-1805, Jul. 1997