144 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, VOL. 26, NO. 5 , OCTOBER 1996
J
Chin-Teng Lin, Member,
Abstract-A neural fuzzy system learning with fuzzy training data (fuzzy if-then rules) is proposed in this paper. This system is able to process and learn numerical information as well as linguistic information. At first, we propose a five-layered neural network for the connectionist realization of a fuzzy inference system. The connectionist structure can house fuzzy logic rules and membership functions for fuzzy inference. We use a-level sets of fuzzy numbers to represent linguistic information. The inputs, outputs, and weights of the proposed network can be fuzzy numbers of any shape. Furthermore, they can be hybrid of fuzzy numbers and numerical numbers through the use of fuzzy singletons. Based on interval arithmetics, a fumy supervised learning algorithm is developed for the proposed system. It extends the normal supervised learning techniques to the learning problems where only linguistic teaching signals are available. The fuzzy supervised learning scheme can train the proposed system with desired fuzzy input-output pairs which are fuzzy numbers instead of the normal numerical values. With fuzzy supervised learning, the proposed system can be used for rule base concentration to reduce the number of rules in a fuzzy rule base. Simulation results are presented to illustrate the performance and applicability of the proposed system.
I. INTRODUCTION
OME observations obtained from a system are precise, while some cannot be measured at all. Namely, two kinds of information are available. One is numerical information from measuring instruments, and the other is linguistic infor- mation from human experts. However, some of data obtained in this manner are hybrid; that is, their components are not homogeneous but a blend of precise and fuzzy information.
Neural networks adopt numerical computations with fault- tolerance, massively parallel computing, and trainable prop- erties. However, numerical quantities evidently suffer from a lack of representation power. Therefore, it is useful for neural networks to be capable of symbolic processing. Most learning methods in neural networks are designed for real vectors. There are many applications that the information cannot be represented meaningfully or measured directly as real vectors. That is, we have to deal with fuzzy information in the learning process of neural networks. Fuzzy set is a good representation form for linguistic data. Therefore, combining neural networks with fuzzy set could combine the advantages of symbolic and numerical processing. In this paper, we propose a new model
Manuscript received February 4, 1995; revised July 25, 1995. This work was supported by the National Science Council, R.O.C., under Grant NSC 84-2212-E-009-034.
The authors are with the Department of Control Engineering, Na- tional Chiao-Tung University, Hsinchu, Taiwan, R.O.C. (e-mail: chinteng @ ecn.purdue.edu).
Publisher Item Identifier S 1083-4419(96)05364-2.
U IEEE, and Ya-Ching
Lu
of neural fuzzy system that can process the hybrid of numerical and fuzzy information. The main task is to develop a fuzzy supervised learning algorithm for the proposed neural fuzzy system.
Most of the supervised learning methods of neural net- works, e.g., the perceptron [ 11, the BP (backpropagation) algorithm [ 2 ] , [3], process only numerical data. Some ap- proaches have been proposed to process linguistic information with fuzzy inputs, fuzzy outputs, or fuzzy weights. Tanaka and his colleagues have proposed a series of approaches and applications with the capacity of processing linguistic input or/and linguistic output [4]-[6]. In their methods, the weights, inputs, and outputs of the neural network are fuzzified using fuzzy numbers represented by a-level sets. In [4], learning methods of neural networks were proposed to utilize not only numerical data but also expert knowledge represented by fuzzy if-then rules. In order to handle linguistic informations in neural networks, they proposed an architecture of multilayer feedforward neural network that can deal with fuzzy input vectors. The fuzzy data are viewed as convex and normal fuzzy sets represented by a-level sets. Since the a-level sets of fuzzy numbers are intervals, the operations of real number in the traditional neural networks are extended to the closed intervals in their proposed model. The characteristics of their proposed architecture are as follows:
1) fuzzy numbers are propagated through neural networks; 2) a single unit is employed for representing a fuzzy
3) the weights and biases in neural networks are still real
Tanaka et al. [5], [6], also proposed an architecture of fuzzy neural network with fuzzy weights and fuzzy biases, and derived its learning algorithm from the modeling of nonlinear fuzzy systems which map a real input vector to a fuzzy output. The architecture of fuzzy neural network is the same as that in [4], except that the numerical weights and biases have been replaced by the fuzzy weights and biases. The calculations in the fuzzy neural network are performed by using interval arithmetic operations for a-level sets. Also, the learning algorithm is derived from a cost function defined by the a-level sets of a actual fuzzy output and a target fuzzy output. Furthermore, they show that the learning algorithm can be applied to the case of fuzzy input vectors and fuzzy target outputs by slightly modifying it. They use sypmetric triangular (or trapzzoidal) fuzzy numbers for fuzzy weights and fuzzy biases and a learning algorithm is derived from a nonfuzzy cost function.
number;
numbers.
LIN AND L U NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING
~
145
Hayashi et al. [7] presented a similar method with fuzzy signals and fuzzy weights by using triangular fuzzy numbers. A similar learning algorithm is derived from a nonfuzzy cost function. Hayashi et al. [:3] also proposed a similar architecture of neural network with fuzzy weights and fuzzy signals, but the learning algorithv was completely different from the proposed methods of Tanaka. In [8
1,
the BP learning algorithm is directly fuzzified based on a fuzzy-valued cost function; i.e., the rule for changing fuzzy weights is also defined by fuzzy numbers. The common points of the above approaches are summa- rized as follows:1) a-level sets of fuzpy numbers represent linguistic inputs, linguistic outputs, fuzzy weights, or fuzzy biases; 2) the operations in n1:ural network are performed by using
interval arithmetic operations for a-level sets;
3) fuzzy numbers are propagated through neural networks; 4) fuzzy weights are usually triangular or trapezoidal fuzzy
Because the real number arithmetic operations in the tra- ditional neural network!, are extended to interval arithmetic operations for a-level seits in the above fuzzified networks, the computations become colmplex (e.g., multiplication of interval) and time-consuming. Moreover, since the fuzzy numbers are propagated through the whole neural networks, the time of computations and the required memory capacities are 2h times of those in the traditional neural networks, where h represents the number of a-level sets. In this paper, we attack this problem by allowing numerical signals to flow in the proposed network internally and reach the same purpose of processing fuzzy numbers.
The objective of this paper is to explore the approach to supervised learning of neural fuzzy systems which receive only linguistic teaching signals. At first, we propose a five- layered feedforward network for the network realization of a fuzzy inference system. 'This connectionist structure can house fuzzy logic rules and membership functions, and perform fuzzy inference. We use a-level sets of,fuzzy numbers to represent linguistic information. 'The inputs, outputs, and weights of the proposed network can be fuzzy numbers of any shape. Since numerical values can be represented by fuzzy singletons, the proposed system c m in fact process and learn hybrid of fuzzy numbers and niumerical numbers. Based on interval arithmetics, a fuzzy s u p w i s e d learning scheme is developed for the proposed system. It generalizes the normal supervised learning techniques to the learning problems where only linguistic teaching signals are available. The fuzzy supervised learning scheme can train the proposed network with desired fuzzy input-output pair,; (or, equivalently, desired fuzzy if- then rules) represented tly fuzzy numbers instead of numerical values. With supervised learning, the proposed system can be used for rule base concentration to reduce the number of rules in a fuzzy rule base.
This paper is organized as follows: Section I1 describes the fundamental properties and operations of fuzzy numbers and their a-level sets. There operations and properties will be used in later derivation. In Section 111, the structure of our neural fuzzy system is proposed. A fuzzy supervised learning
numbers.
algorithm for the proposed system is presented in Section IV. The learning algorithm contains structure and parameter learning phases. In Section V, simulations are performed to illustrate the performance of the proposed system. Finally, conclusions and future research are summarized in the last section.
11. REPRESENTATION OF LINGUISTIC INFORMATION When constructing information processing systems such as classifier and controllers, two kinds of information are available. One is numerical information from measuring in- struments and the other is linguistic information from human experts. We can naturally indicate the numerical information using real numbers. But, how to represent the linguistic data? It has been popular for using fuzzy sets defined by discretized (pointwise) membership functions to represent lin- guistic information. Fuzzy sets, however, can be defined by the families of their a-level sets according to the resolution identity theorem. In our model, we use a-level sets of fuzzy numbers (i.e., convex and normal fuzzy sets) to represent linguistic information due to their several good properties such as closeness and good representation form. In using
&-
level sets, we consider a fuzzy number to be an extension of the concept of the interval of confidence [9]. Instead of considering the interval of confidence at one unique level, it is considered at several levels and more generally at all levels from 0 to 1. Namely, the level of presumption a , a E [0,1]gives an interval of confidence A, = [ a y ) , a?)], which is a monotonical decreasing function of a ; that is,
(1)
(d
>
a ) -+ ( A Q /c
A m )for every a , a' E [0,1].
The expressions level of presumption are well suited to the concept of fuzzy numbers. Moreover the intervals of confidence at all level from 0 to 1 are the same as the a-level sets of fuzzy number. In-this paper, we use a- level sets of fuzzy number to indicate linguistic information because of their advantages in both theoretical and practical considerations [ 101. These advantages will be explained in details in subsection 11-C.
A. Basic Dejinitions of Fuzzy Numbers
Some notations and basic definitions are given in this subsection. We use the uppercase letter to represent a fuzzy set and the lowercase letter to represent a real number.
Let x be an element in a universe of discourse X . A fuzzy set, P , is defined by a membership function, p p ( ~ ) , as
When X is continuum rather than a countable or finite set, the fuzzy set P is represented as
746 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B CYBERNETICS, VOL 26, NO 5, OCTOBER 1996 where z E X. When X is a countable or finite set
z
where x , E X . We call the form in the above equation as a discretized or pointwise membership function.
A fuzzy set, P , is normal when its membership function, p p ( x ) , satisfies
maxpLp(z) 2 = 1. ( 6 )
A fuzzy set is convex if and only if each of its a-level sets is a convex set. Equivalently, we may say that a fuzzy set P is convex if and only if
where 0
5
Q5
1 , x E X .A fuzzy set P is convex if and only if every P, is convex; that is, P, is a closed interval of
R.
It can be represented byP, = [ P P ' , P P ) ] (9)
where a E [0,1]. A convex and normalized fuzzy set whose membership function is piecewise continuous is called a fuzzy number. Thus, a fuzzy number can be considered as containing the real numbers within some interval to varying degrees. Namely, a fuzzy number P may be decomposed into its ai- level sets, P,, according to the resolution idenlity theorem
[ l l ] as follows:
B. Basic Operations of Fuzzy Numbers
In this subsection, we introduce some basic operations of a-level sets of fuzzy numbers. These operations will be used in the derivation of our model in the following section. More detailed operations of fuzzy numbers can be found in [9].
Addition: Let A and B be two fuzzy numbers and A ,
and B, their a-level sets, A =
U,
aA, =U,
a [ a p ) , a?)],B
=U,
OB,
=U,
a[h?),/I?)]
Then we can writewhere a E [0,1].
the definition of subtraction as follows:
Subtraction: The definition of addition can be extended to
where a E [ O , l ] .
Multiplication by an Ordinary Number: Let A be a fuzzy number in
R
and k an ordinary number k ER.
We haveMultiplication: Here we consider multiplication of fuzzy numbers in ?I?+. Consider two fuzzy numbers A and B in ?I?+. For the level cu of presumption, we have
The reader is referred to [9] for the general case that A and B are fuzzy numbers in
R.
The operations on fuzzy numbers can be performed on the basis of the extension principle. Let G ( A , B) be an operation on fuzzy numbers A and B by giving a function g(z, y). The membership function of G ( A , B), ~ G ( A , B ) ( z ) , is obtained by extension principle as follows:
(15) where x E A , y E
B,x
E 2.If G(.) is addition, subtraction, or multiplication as above, the result can be easily obtained by using the a-level sets of A
and
B
as above operations. It can be proved easily that these operations based on a-level sets and the extension principle are equivalent [9]. When G ( . ) is one of the operations given above, if A and B are fuzzy numbers inR,
then G ( A , B ) is also a fuzzy number. Owing to this closed property and good representation form, we use fuzzy numbers rather than general fuzzy sets to represent linguistic information in our model.Difference: We can compute the difference between fuzzy numbers A and B by
1 2
diff(A,B) =
-1
[(ay' - b P ) ) ' + (a?) - b p ) ) ' ] . (16)0
Fuzzification: Fuzzification is a subjective valuation to transform a measurement crisp value into a valuation of a subjective value. Hence, it can be defined as a mapping from an observed input space to labels of fuzzy sets in a specified input universe of discourse. In this paper, we intuitively consider fuzzification to be an operation that calculates the membership grade of z, p p ( x ) , to a given fuzzy number P .
The values p p ( z ) can be easily obtained by using the follow- ing procedure. In this procedure, the notation h represents the number of quantized membership grade.
Procedure: FuzziJication Search
Inputs}: The order set S = { p ~ ) , p j l / h ) , p ~ / h ) ,
. . .
, p l (1),
p a l ) ,
. .
. ,PPI} and a numerical value z, where S represents the a-level sets of the interested fuzzy number P and x is the input numerical value to be fuzzified.Output}:& indicating the membership grade of ic, p p ( x ) , to fuzzy number P .
LIN AND LU: NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING
membership grade
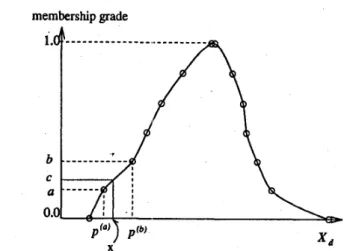
Fig. 1.
equal to 6).
Illustration of the fuzzification search procedure (the value of c is
Step 1: Use binaly smrch to find the correct position of II: in S ; that is, to find
d")
and p @ ) such that p ( a ) 5 I(:5
p @ ) , p ( " ) , p @ ) E S . In the binary search, we compare first x to the entry in the middle of the list S. If II: is larger, it is in the second half; with one comparison the entire first half of the list is eliminated from consideration. Conversely, if II: is smaller than the entry in the middle of the list, the second half the list is eliminated from consideration. This process continues until the right interval that I(: locates is found.
Step 2: Compute the membership degree by & = a
+
(II: -Step 3: Output &, and stop.
After this recursive calculation, the value & is equal to the value of p p ( ~ ( : ) as shown in Fig. 1. If we use the binary search method, the processing tiime with this procedure is proportional to logz h. If we use the sequential search method, the process- ing time is O ( h ) . Therefore, performing this procedure is very easy and not time consuming. Another method to find pp(x) can be found in [lo].
Defuzzification: In many practical applications such as con- trol and classification, numerical (crisp) data are required. That is, it is essential to transform a fuzzy number to a numerical value. The process mapping a fuzzy number into a nonfuzzy number is called "defuzzification". Various defuzzification strategies have been suggested in [12], [13]. In this subsection, we describe two methods (MOM, COA) that transform a fuzzy number in the form of o(-level sets into a crisp value.
p'"') b-a
p ( b ) - p ( a ) '
Mean of Maximum Method ( M O M )
The mean of maximum method (MOM) generates a crisp value by averaging 1 he support values whose membership values reach the mauimum. For a discrete universe of dis- course, this is calculated based on membership function by
1
(17) where I is the number of quantized z values which reach their maximum membership value.
For a fuzzy number 2 in the form of a-level sets, the defuzzification method can be expressed according to
E,=,
z.7zo =
-
1
741
(17) as
where defuzziJier represents a defuzzification operation. Center of Area Method (COA)
Assuming that a fuzzy number with a pointwise member- ship p~ has been produced, the center of area method calculates the center of gravity of the distribution for the nonfuzzy value. Assuming a discrete universe of discourse, we have
For a fuzzy number 2 with the representation form of a-level sets, it can be approximately expressed according to (19) as
C. Advantages of Using a-Level Sets of Fuzzy Numbers Fuzzy sets have been studied actively and applied in a wide variety of areas such as system control, modeling, signal processing, and expert systems. In this paper, we also use fuzzy numbers to represent linguistic data. Conventionally, fuzzy numbers are defined by membership functions, such as bell shaped functions, triangular functions, trapezoidal functions, etc. In these forms, we only need a few simple parameters (e.g., the center-and the width) to define them, but they can only display some normal situations. In this paper, we use a-level sets to define fuzzy number owing to the following advantages [ lo]:
a) Theoretical
It effectively studies the effects of the position in a universe of discourse and the fuzziness of a fuzzy number.
b) Practical
It provides fast inference computations by using hardware construction in parallel and requires less memory capacity for fuzzy numbers defined in uni- verses of discourse with a large number of elements. It easily interfaces with two-valued logic.
It allows good matching with systems that include fuzzy number operations based on the extension principle.
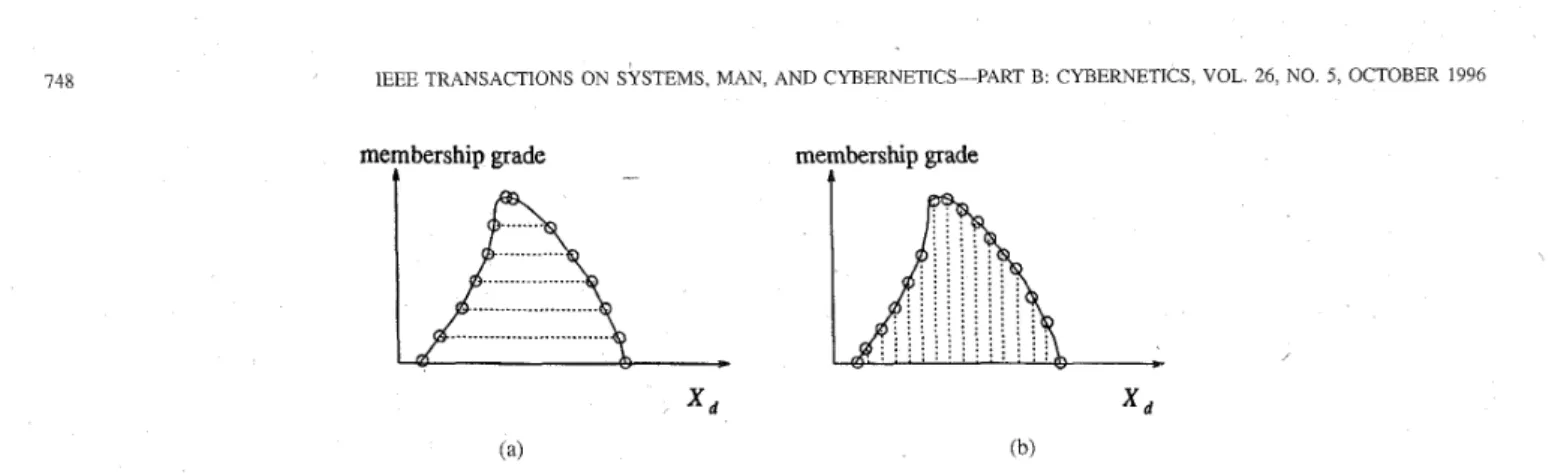
These advantages are explained in details below. Fig. 2(b)
illustfates a discretized membership function for a fuzzy number in a universe of discourse with a discrete space xd.
In this figure, the discretized membership function does not explicitly give the position of the fuzzy number in the universe of discourse and the fuzziness. In contrast, the a-level sets in Fig. 2(a) are more effective representation forms of fuzzy numbers. The left and right limits of one of the a-level sets directly give the position of the fuzzy number, and the width of
148 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, membership grade
VOL. 26, NO. 5. OCTOBER 1 996
‘ d ‘ d
(4 (b)
Fig 2 Representatlons of fuzzy number (a) a-level sets of fuzzy number, and (b) discretized (pointwise) membership function
the a-level set is directly related to the fuzziness and converge of the fuzzy number in the universe of discourse. If fuzzy- inference operations can be represented using parameters that define a-level sets, namely, the left and right limits mentioned above, the relation between the given facts and the inferred consequent might easily be derived with direct information on the position and fuzziness of fuzzy numbers.
Providing hardware-related advantages is also important for a-level-set-based formulation. Hardware systems for fuzzy inference have been developed and studied [14] owing to the development of fast and cost-effective fuzzy-inference engines. In conventional fuzzy propositions based on regular membership functions such as triangular or trapezoidal forms, the fuzzy-inference consequent is not always triangular or trapezoidal if fuzzy relation is adopted. As a result, the hardware may have complex structure. Also, the required memory capacity for discretized membership functions must be proportional to the number of elements in the universe of discourse. This facts also means that fuzzy inference operations are time-consuming processes because calculations for inference have to be conducted for “all elements” to which membership grades are assigned. Due to the above reasons, the fuzzy-logic hardware based on discretized membership functions has a disadvantage in the required memory capacity and processing time.
In the scheme based on a-level sets, the required mem- ory capacity and processing time depend on the number of membership-grade levels instead of the number of elements in the universe of discourse. It is clear that the number of elements in a universe of discourse is much larger than the required number of membership-grade levels. Hence hardware systems based on a-level sets have the advantage in required memory capacity and processing time. These advantages al$o
exist in adaptive fuzzy inference systems where fuzzy numbers are adjusted in the learning process. These advantages are considered in greater details in [lo].
Fuzzy inference based on a-level sets interfaces well with two-valued logic because a-level sets themselves are crisp sets. This interface is useful, for example, when two-valued decision making is needed for inference consequents. More- over, the operations on fuzzy numbers based on the extension principle, such as the addition and multiplication of fuzzy numbers, can be performed efficiently using a-level sets. Consequently, efficient calculation may be possible for both fuzzy-inference operations.
Due to the above advantages, more and more authors rep- resent fuzzy numbers using a-level sets rather than pointwise membership functions [15], [16]. In this paper, the a-level sets are also used to represent fuzzy numbers in the proposed neural fuzzy systems. It will be oberved that the use of a - level sets also simplifies the learning rules for updating fuzzy weights in the network.
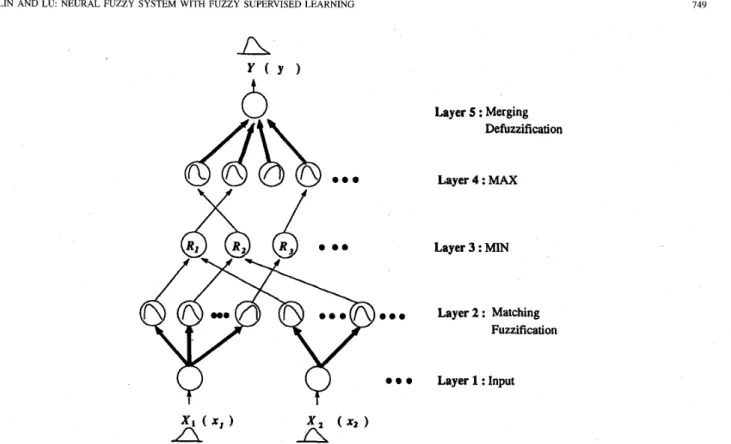
111. BASIC STRUCTURE OF THE NEURAL FUZZY SYSTEM
In this section, we construct an architecture of neural fuzzy system that can process fuzzy and crisp information. Fig. 3 shows the proposed network structure which has a total of five layers. This five-layered connectionist structure performs fuzzy inference effectively. Similar architectures have been proposed in [17], [IS], and [19]. Nodes at layer one are input nodes whose inputs are fuzzy numbers or crisp numbers. Each input node corresponds to one input linguistic variable. Layer five consists of output nodes whose output are also fuzzy numbers or crisp numbers. Each output node corresponds to
one output linguistic variable. Nodes at layers two and four are term nodes which define membership functions representing the fuzzy terms of the respective linguistic variable. Only the nodes at layer two and five have fuzzy weights (as shown by bold lines in Fig. 3). The other weights are numerical (as shown by plain lines in Fig. 3). Each node in layer two executes a “match” action to find the match degree between the input fuzzy number and the fuzzy weight if the input is linguistic information. If the input is a crisp number, they execute a “fuzzification” operation to map the input value from an observed input space to the fuzzy weights in nodes at layer two. Each node at layer three is a rule node which represents one fuzzy rule. Hence, all the layer-three nodes form a fuzzy rule base. Links from layers two to three define the preconditions of the fuzzy rules, and links from layer three to four define the consequents of the fuzzy rules. Therefore, for each rule node, there is at most one link (maybe none) from or to some term node of a linguistic node. This is true both for precondition links and consequent links. The links at layers two and five are fully connected between linguistic nodes and their corresponding term nodes. If linguistic outputs are expected, each node in layer five “merges” all fuzzy weights connected to it, scaled by the output values of layer four, to produce a new fuzzy number. If numerical output values are required, each layer-5 node execute a “defuzzification” operation to obtain a crisp decision.
LIN AND L U NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING 149
Fig. 3. The five-layered architecture of the proposed neural fuzzy system. indicate the links with numerical weights.
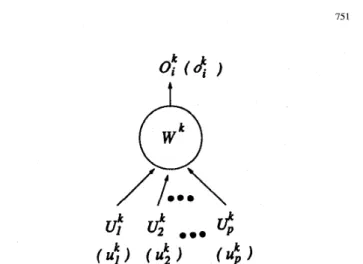
We shall next descrihe the signal propagation in the pro- posed network layer by layer following the arrow directions shown in Fig. 3. This is done by defining the transfer function of a node in each layer. Signal may flow in the reverse direction in the learnin): process as we shall discuss in the following sections. In the following description, we shall consider the case of single output node for clarity. It can be easily extended to the case of multiple output nodes. A typical neural network consists of nodes, each of which has some finite fan-in of connecticins represented by weight values from other nodes and fan-out of connections to other nodes (see Fig. 4). The notations U and U represent the input crisp and
fuzzy numbers of the node, respectively. The notations o and 0 represent, respectively, the output crisp and fuzzy numbers. The superscript in the following formulas indicates the layer number.
Layer 1 (Znput): If the input is a fuzzy number, each node in this layer only transmits input fuzzy number
X,
to the next layer directly. No computation is done in this layer. That is,If the input is a crisp number
xi,
it can be viewed as a fuzzy singleton, i.e.,Note that there is no weight to be adjusted in this layer.
Layer 5 : Merging Defbzzification Layer 4 : MAX Layer 3 : MIN Layer 2 : Matching Fuzzification Layer 1 : Input
The bold lines indicate the links with fuzzy weights and the plain lines
Layer 2 (Matching/FuzziJication): Each node in this layer has exactly one input from some input linguistic node, and feeds its output to rule node(s). For each layer-2 node, the input is a fuzzy number and the output is a numerical number. The weight in this layer is a fuzzy number WX,,. The index i, j means the j t h term of the ith input linguistic variable X,.
The transfer function of each layer-2 node is
where a2 is the variance of the activation function U ( . ) . It is a constant given in advance. The activation function U ( .) is a nonnegative, monotonically decreasing function of f & E [O,oo], and a ( 0 ) is equal to 1. For example, U ( . ) can also be given alternatively as
where 0
<
r<
1, orwhere X is a nonnegative constant.
Layer 3 (MZN): The input and output of the node in this layer are both numerical. The links in this layer perform pre- condition matching of fuzzy logic rules. Hence, the rule nodes should perform fuzzy AND operation. The most commonly
750 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B CYBERNETICS, VOL 26, NO 5, OCTOBER 1996
used fuzzy AND operations are intersection and algebraic product [ 131. If intersection is used, we have
(27)
o,” = min (u:,u:, . . . , u k ) . 3
On the other hand, if algebraic product is used, we have
3 3 3 3
0, = u1u2 ‘ .
.
U kSimilar to layer one, there is no weight to be adjusted in this layer.
Layer 4 (MAX): The nodes in this layer should perform fuzzy OR operation to integrate the fired rules which have the same consequent. The most commonly used fuzzy OR
operations are union and bounded sum [13]. If the union operation is used in this model, we have
o$ = max (ut, U ; ,
. . .
, U : ) If the bounded sum is used, we have0: = min ( I , U:
+
U ;+
. . .+
U : ) . (30) The output and input of each layer-4 node are both numerical values.Layer 5 (Merging/Defuzz$cation): In this layer, each node has a fuzzy weight W E . There are two kinds of operations in this layer. When we need a fuzzy output . - Y , the following formula is executed to perform a “merging” action:
Namely,
cv
cy
where
If the output of the neural fuzzy system is required to be a numerical value, the output node executes the defuzzification action. The following formulas simulate the Tsukamoto’s defuzzification method [ZO]
-
internally from layer two to layer four in the FCLO and FCNO. This makes the operations in our proposed network less time-consuming as compared to the neural networks that can also process fuzzy input/output data but require fuzzy signals flowing in it. It is noted that (see subsection 11-A) the linguistic output Y must be a fuzzy number; that is, it must be convex and normal. To guarantee this, we have to keep the fuzzy weights in our network convex and normal. This constraint should be satisfied in deriving weight update rules in the following section.
(31)
(32)
where
fuzzy numbers and numerical numbers by viewing the latter as fuzzy singletons. It is noted that although the topology of the proposed network is almost the same as that of the conventional ones such as [17]-[19] (i.e., they are all five- layer fuzzy inference networks), their functions are quite diffcrcnt. Especially, the fuzzy weights used in our netwoi-k allow the proposed system to process and adapt fuzzy data in addition to numerical data. However, the conventional fuzzy inference networks can only process numerical data. Although some normal multilayer neural networks have been proposed for processing and learning fuzzy and numerical data (e.g., [4]-[8]), they suffer the inherited problem of neural networks-the hidden layers are opaque to the user. Hence the outside observer cannot understand what the network has learned exactly. This makes the normal multilayer networks difficult to be used for rule extraction from fuzzy training data, and for fuzzy rule base concentration.
In the rest of this paper, we call the above proposed five-layered neural network with fuzzy output as “Fuzzy Connectionist Architecture with Linguistic Output” (FCLO), and that with numerical output as “Fuzzy Connectionist Ar- chitecture with Numerical Output” (FCNO). From the above description we observe that only layer-1 inputs and layer-5 outputs of the FCLO and FCNO are possibly fuzzy numbers (in the form of a-level sets). Real numbers are propagated
IV. SUPERVISED LEARNING ALGORITHM
( 3 3 ) In this section, we shall derive a supervised learning al- gorithm for the proposed neural fuzzy system (FCLO and FCNO). This algorithm is applicable to the situations that pairs of input-output training data are available. We allow the training data (either input or output) to be numerical values
(34)
(37)
(vectors), fuzzy numbers, or mixture of them. When the system is trained to be a fuzzy controller or fuzzy classifier, the input and desired output are usually numerical values. On the other hand, when the system is trained to be a fuzzy expert system, the input and desired output are usually fuzzy numbers (linguistic information). In this case, the fuzzy input- output training pairs can be regarded as fuzzy if-then rules and the trained neural fuzzy system is like a (condensed) fuzzy knowledge base. Consider for example the following two training fuzzy if-then rules:
R I : IF x1 is small and x2 is large, THEN y is good Ra: IF x1 is large and 2 2 is small, THEN y is bad. According to the function processing of the proposed net-
work described in the above, our network can process both
Then the corresponding two input-output training pairs are “(small, large; good)” and “(large, small; bad),” where the
LIN AND LU: NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING
~
75 1
fuzzy terms are defined by given fuzzy numbers in the form of ai-level sets. In general, the fuzzy rules for trainging are
is Yp R,: IF x1 is X,, and and
xp
is X,,, THENwhere p = 1 , 2 , .
.
,,
m, and m is the total number of train- ing rules. These fuzzy if-then rules can be viewed as the fuzzy input-output pairs, ( X p l , X p 2 , . . .,
Xp,; Y p ) , where p =1 , 2 , .
.
.
, m . if the input or output are crisp data, the corre- sponding fuzzy elements in the training pairs become numer- ical elements.With the supervised learning algorithm that we shall de- velop, the proposed system can learn fuzzy if-then rules from numerical data. Moreover, it can learn fuzzy if-then rules from experts' linguistic Icnowledge represented by fuzzy if- then rules. This means that it can learn to represent a set of training fuzzy if-then rules using another smaller set of fuzzy if-then rules. This is a novel and efficient approach to rule combination. The proposed neural fuzzy system can thus be used for rule bast concentration to reduce the number
of rules. This provides a useful tool for designing a fuzzy knowledge base. A knowledge base is usually contributed by several domain experts, so duplication of if-then rules is inevitable. Hence, we usually need to compress the rule base by combining similar rules into representative rules.
Before the learning of the neural fuzzy system, an initial network structure is first constructed. Then during the learning process, some nodes and links in the initial network are deleted or combined to form the final structure of the network. At first, the number of input (output) nodes is set equal to the number of input (output) linguistic variables. The number of nodes in the second layer is decided by the number of fuzzy partitions of each input linguistic variable x,, IT(x2)1, which must be assigned by the user. Thc fuzzy weights W X , , in layer two are initialized randomly as fuzzy numbers. One better way is to distribute the initial fuzzy weights evenly on the interested domain of the corresponding input linguistic variable. As for layer three of the initial network, there are
n,
IT(z,)I rule nodes with the inputs of each rule node coming from one possible combination of the terms of input linguistic variables under the constraint that only one term in a term set can be a rule node's input. This gives the preconditions of initial fuzzy rules.Finally, let us considcr the structure of layer four in the initial network. This is equivalent to determining the conse- quents of initial fuzzy rules. We propose two approaches to initializing the layer-4 nodes and the links from layer-3 nodes to layer-4 nodes.
Method I : The first method uses the self-organized learn- ing technique. To use this method, the number of fuzzy partitions of the output linguistic variable y, lT(y)l, must be given in advance. The initial fuzzy weights WY, in layer five are distributed evenly on the output space, We let the layer- 5 nodes to perform up.down transmission. in the up-down transmission, the desired outputs are pumped into the network from its output side and the operations in layer five are the same as those in layer two. Signals from both external sides of the network can thus reach the output points of term nodes at layer two and layer four. Since the outputs of term nodes at
t
Fig. 4. Basic structure of a node in the proposed neural fuzzy system.
layer two can be transmitted to rule nodes through the initial architecture of layer-3 links, we can obtain the output (firing strength) of each rule node. Based on the firing strengths of rule nodes
(09)
and the outputs of term nodes at layer four (o,"), we can decide the correct consequent links of each rule node by unsupervised (self-organized) learning method [21]. The links at layer four are fully connected initially. We denote the weight on the link from the ith rule node to the j t h output term node as w , ~ . The Hebbian learning law is used to update these weights for each training data set. The learning rule is described asA W Z 3 = c0;o; (38)
where c is a positive constant. After the learning, only one link with the biggest weight in the fan-out of a layer-3 (rule) node is remained as its consequent.
Method 2: This method is simpler than Method 1, but it requires a larger memory capacity. First, let the number of nodes in layer four be the same as the number of rule nodes in layer three. Also, the fuzzy weights in layer five are assigned randomlpThe mapping from layer-3 nodes to layer-4 nodes is one-to-one initially. That is, each layer-3 node connects to its respective layer-4 node. Some of layer-4 links and nodes will be eliminated properly in the structure learning process which will be described in subsections IV-B.
With the above initialization process, the network is ready for learning. We shall next propose a two-phase supervised learning algorithm for our five-layered neural fuzzy system. In phase one, a parameter learning scheme is used to adjust the fuzzy weights. In phase two, a structure learning scheme is
used to delete or combine some nodes and links in the neural fuzzy system.
A. Parameter Learning Phase
A gradient-descent-based backpropagation algorithm [21],
[22] is employed to adjust fuzzy weights in layer two and layer five of the proposed network. If the FCLO is used, the error function to be minimized is
152 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B. CYBERNETICS, VOL 26, NO 5 , OCTOBER 1996
Layer 5 :
Layer 4 : --3e
Layer 3 :
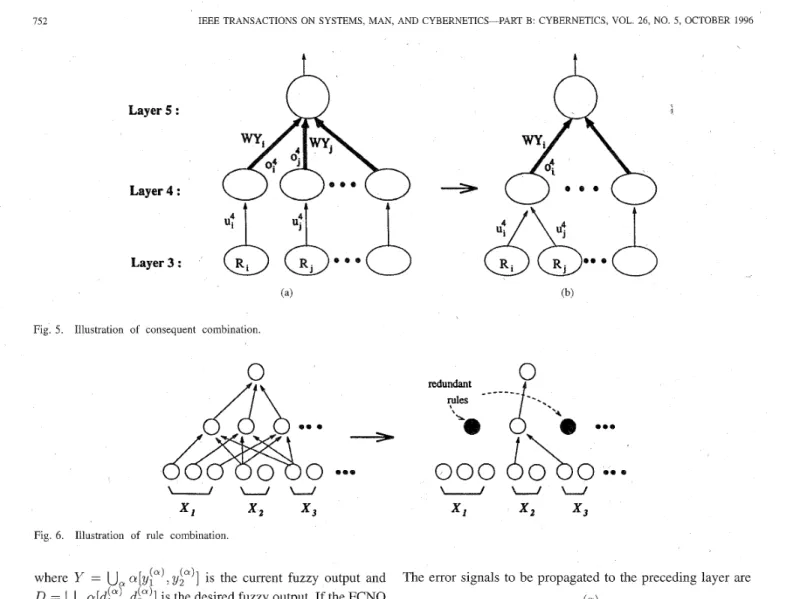
Fig. 5. Illustration of consequent combination.
redundant
0
u
u
u
X l x2 x3
Fig. 6 . Illustration of rule combination
where Y =
U,
cy[yla), y p ' ] is the current fuzzy output and D =U,
a [ d p ) , d p ) ] is the desired fuzzy output. If the FCNO is used, the error function to be minimized isThe error signals to be propagated to the preceding layer are
(44) d e dei") 1 ay1 @") ao5(") ~ - - ~ ) (, = (y?) - d p ) ) 1 2 e - ( d - y) 2
where y i s the current output and d is the desired output. We assume that W =
U,
a [ w p ) . w p ' ] is the adjustable fuzzy weights means to update the parameters w p ) and w p ) . Weby layer based on the general learning rule
where
parameter in layer two and layer five. Then to update fuzzy
shall next derive the update rules for these parameters layer
(46)
(47) If an FCNO is used and the desired output is numerical value y, the update rules of the parameters are derived from (35) and (36) as follows: w ( t
+
1) = w ( t )+
7 (41) (4@ d e - de ay ay - -- (..) = (Y - d)- aw y!;) where w represents wj"i) or tup), and rj is the learning rate. awy!p) - ay dwy,,ay
+--
Layer 5: If an FCLO i s used and the desired output is fuzzy number Y , the update rules of wy!:) and wy$' are derived from (33) and (34) as follows:
where
dY a f z am2
awy!p)
-af2
awyz(p)
3~awyy!;)
U,"l& cyE,
U3J2 2E,
a ~ _ _ _ - - d eLIN AND L U NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING 153
lnplt
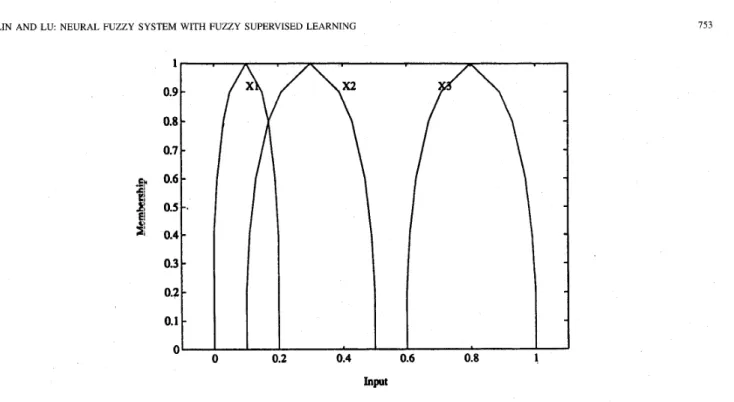
Fig. 7. The membership functions of the input linguistic value “very small” ( X l ) , “small” (X2), “large” ( X 3 ) ,in Example 1.
iterations Fig. 8. The learning curve iri Example 1.
and The error signal to be propagated to the preceding layer is
where
Layer 4: In this layer, there is no weights to be adjusted. Only the error signals need to be computed and propagated. If an FCLO is used, the error signal
:
6
is derived from (29)154 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, VOL. 26, NO. 5 , OCTOBER 1996
Desind (-)/Actual (..I output
Fig 9. The actual fuzzy outputs, Y1, Y 2 , Y 3 , of the learned neural fuzzy system and the corresponding desired fuzzy outputs, D l , D 2 , 0 3 , in Example 1
:I
0.4,,,!
0.3 0.2 0.1 0 0 0.8 1 Weight X (-),Weight Y (..) Fig. 10. The learned fuzzy weights of the FCLO in Example 1where If FCNO is used, the error signal
Sf
is derived from (29)as follows:
Layer3: As in layer four, only the erros signals need to
be computed. According to (27), this error signal 6: can be derived as
LIN AND LU: NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING 15s
" 0 0.2 0.4 0.6 0.8
The change in Weights WXl(..), W(-) (a)
" 0 0.2 0.4 0.6 0.8
Ihe change in weights WY l(..), WY2(-) (b)
Fig. 11.
W Y l , W Y 2 , during the learning process in Example 1.
(a) Time evolving graph of fuzzy weights WX1, W X 2 , during the learning process in Example 1. (b) Time evolving graph of fuzzy weights
where 1 if o : ~ = min(u:, . . .
,
U ; ) (60) (57) ={
f
if o: = max (ut,.. .
, U ; ) otherwise.Layer 2: In this layer, there are fuzzy weights W X to be adjusted. The update rules can be derived from (23) and (24) as follows:
and
a e ij(7,3 80% - ss do3 do2
~ - (61) ( 5 8 ) r j - - d e awx!;? 80: dwx(") 23 1 awz!;?
756 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, VOL. 26, NO. 5, OCTOBER 1996 :final state :initial state
I
I 4 x2''ak2L-
Fig. 12. The neural fuzzy system before and after learning in Example 1
When fuzzy weights are adjusted by (42)-(62), two unde- sirable situations may happen. That is, the lower limits of the
they are legal fuzzy numbers after updating. This process is described as follows: ..
a-level sets of fuzzy weights may exceed the upper limits, and the updated fuzzy weighted may become nonconvex. In order
to coDe with these undesirable situations, we do necessary
Procedure: Fuzzy Number Restoration
Inputs:) Fuzzy weights
w
=U,
a[w!a),w?)l adjustedLIN AND L U NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING 151
Inputs
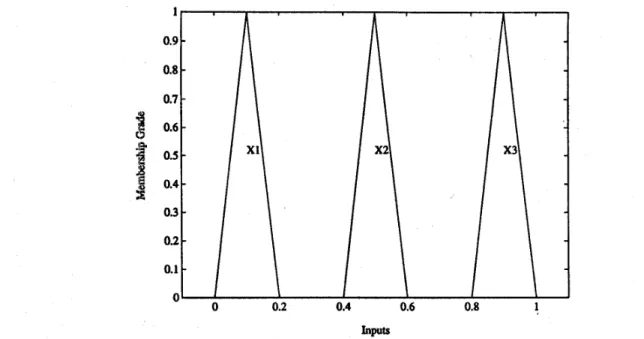
Fig. 13. The membership functions of the input linguistic values Xl,X2,X3, in Example 2.
Fig. 14. The learning curve in Example 2.
k + l k + l
Outputs:} The modified fuzzy weights
r/i/
= ifwr/h)
<
G ~ T ) then 6 r l h ) = w2 - ( T - )U,
a [ w p ) . wp)] which are legal fuzzynumbers. Step 3:
else ~ r / h ) = w2 ( k j h )
.
Output
e,
and stop. Step 1:and
B. Structure Learning Phase
In this subsection, we propose a structure learning algorithm for the proposed neural fuzzy system to reduce its node and link number. This structure learning algorithm is divided into two parts: One is to merge the fuzzy terms of input and output linguistic variables (term-node combination). The other is to do rule combination to reduce the number of rules. We shall discuss these two parts separately below.
758
1 -
U -
46
4 4
IEEE TRANSACTIONS ON SYSTEMS, MAN,
-
-
AND CYBERNETICS-PART B: CYBERNETICS, VOL. 26, NO. 5 , OCTOBER 1996
(-Y- 0
Fig. 15. The actual fuzzy outputs, Y1, Y 2 . Y 3 , of the learned neural fuzzy system and the corresponding desired fuzzy outputs, 0 1 . 0 2 . 0 3 , in Example 2.
wsiobc x (-Wsiobc Y (I)
Fig. 16. The learned fuzzy weights of the FCLO in Example 2.
Term-Node Combination Scheme: Term-node combination is to combine similar terms in the term sets of input and output linguistic variables. We shall present this technique for the term set of output linguistic variables. It is applied to the term set of input linguistic variables in exactly the same way. We have proposed two methods to initialize the nodes and links in layer four of FCLO and FCNO in the initialization process. If Method 1 is used, the consequents of the rule nodes have been established by self-organized learning in the initialization process. Hence no further structure learning is necessary in the consequent parts of the rule nodes if Method 1 of initialization process is used. On the other hand, if Method 2 is used, further actions should be taken to eliminate redundant nodes and links in layer four. The whole learning procedure using Method 2 of initialization is described as follows:
Step I : Perform parameter learning until the output erroi- is smaller than a given value; i.e., e
5
errordimit, where errordimit is a small positive constant.Step 2: diff (WU,, WU,)
5
similardimit and similardimit is a given positive constant, remove term node J with fuzzy weight W r / , and its fan-out links, and connect rule node j in layer 3 to term node i in layer four (see Fig. 5).Step 3; Perform the parameter learning again to optimally adjust the network weights.
The term-node combination scheme in Step 2 can automat- ically find the number of fuzzy partitions of output linguistic variables. The rationale of this step is described mathemati- cally in the followings. Let us consider the supervised learning of FCLO. If Step 2 is not performed (see Fig. 5(a)), FCLO does the following operations in layer 4
( 6 3 )
4
0, = U $ , 0; = U ;
where c is the sum of other input values and C is the sum of the other products of the input values and fuzzy weights in layer four. I ' 1
I
0I
.
I
a4 a6 0.8 ! uipr- 0 03Fig. 17. Generalization test of the learned neural fuzzy system in Example 2
On the other hand, if Step 2 is performed (see Fig. 5(b)), FCLO does the following operations:
If U:
+
U," 5 1, thenNotice that in (65). the bounded sum is used for fuzzy OR operation. From (64) and (66), we find that if WU, is very similar to WU, (as the required condition in Step 2) and (U:
+
U 3 )<
- 1, then Y, M Y b . This means that the networks before and after the rule combination process is nearly equivalent. We can obtain the same result for the supervised learning of FCNO. Hence, the proposed term-node combination scheme is appropriate and accurate. The operations in Step 2 can be equally applied to the term set of input linguistic variables.Rule Combination Scheme: After the fuzzy parameters and the consequents of the rule nodes are determined, the rule combination scheme is performed to reduce the number of rules. The idea of rule combination is easily understood
759
LIN AND LU: NEURAL FUZZY SlYSTEM WITH FUZZY SUPERVISED LEARNING
Fig. The training Pairs
(x)
y , in the form Of d e v e l in Fig. 20. Generalization test of the learned neural fuzzy system in Example 3. Example 3.i
Fig. 19. a6i
lml
a4. a:.@ 0 m y l x The learned fuzzy weights in Example 3.Y Y
A
A
k
f
(a) (b)
Fig. 21. The structures before and after learning of the FCLO in Example 4. through the following example. Consider a system contains
the following fuzzy if-then rules: If some rule nodes satisfy these three conditions, then these rules can be combined into a single rule. An illustration in shown in Fig. 6. It should be noted that the proposed rule combination scheme is exactly only for max-min composition.
V. ILLUSTRATIVE EXAMPLES
R I : IF z1 is small and x2 is small, THEN y is good
R2: IF z1 is medium arid 22 is small, THEN
R3: IF 2 1 is large and :e2 is small, THEN y is good is good
where the fuzzy partitions of input linguistic variable z1 are “small,” “medium,” and “‘large”. The three rules R1, R2 and R3 can be merged to one rule as follows:
R: IF x2 is small, THEN y is good.
That is, the input variable 21 is not necessary in this situa- tion. The conditions for applying rule combination has been explored in [17] and are given as below.
1) These rule nodes have exactly the same consequents. 2) Some preconditions ,are common to all the rule nodes,
that is, the rule nodes are associated with the same term nodes.
3) The union of other preconditions of these rule nodes composes the whole terms set of some input linguistic variables.
In this section, we shall use some examples to illustrate the performance of the proposed fuzzy supervised learning algorithm on FCLO and FCNO. All the following simulations are run on a Sun SPARCstation.
Example 1
-
Fuzzy Input and Fuzzy Output: Consider the following three fuzzy if-then rules for training:R I : IF 2 is very small (Xl), THEN y is very large (Dl)
R2: IF 2 is small (X2), THEN y is large (D2)
RY:
IF 2 is large (X3), THEN y is small (D3)where the fuzzy numbers “small,” “large,” “very small” are given in Fig. 7. Because input and desired output are linguis- tic, an FCLO is used in this example. Using Method 2 of initialization process, we set up an FCLO with two layer-2 nodes and two layer-4 nodes (and thus, two layer-3 (rule) nodes). Fig. 8 shows the learning curve. The total learning time is 0.853 s. The error tolerance is 0.0001 and the number
760 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, VOL. 26, NO. 5, OCTOBER 1996
0 0.2 0.4 0.6 0.8 1
Input
Fig 22. The training data pairs in Example 4.
0.8
--
a
8
0.6-.
1
4
0.4-
0.2-
0 - 0 0.2 0.4Fig. 23. The actual outputs of the learned FCLO in Example 4.
of a-cuts is 6. After supervised learning, the fuzzy outputs of the learned FCLO and the corresponding desired outputs are shown in Fig. 9. The figure shows that they match closely. The two learned (representative) fuzzy rules after learning (condensing) are
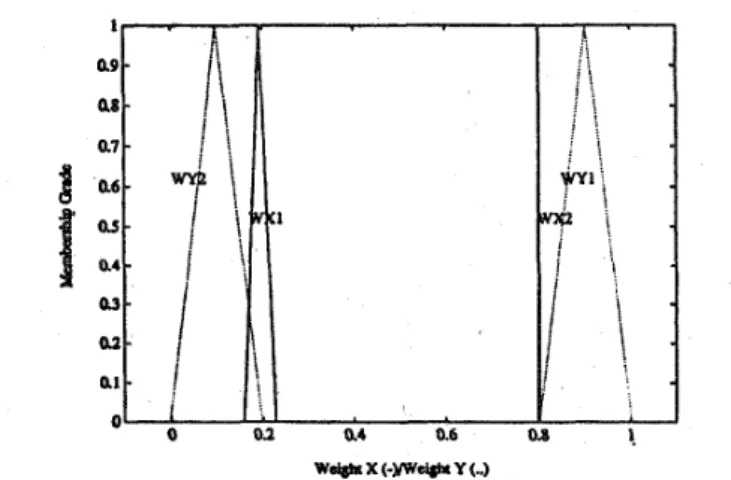
IF z is WX1, THEN y is IVY1 and
IF 2 is W X 2 , THEN y is W Y 2
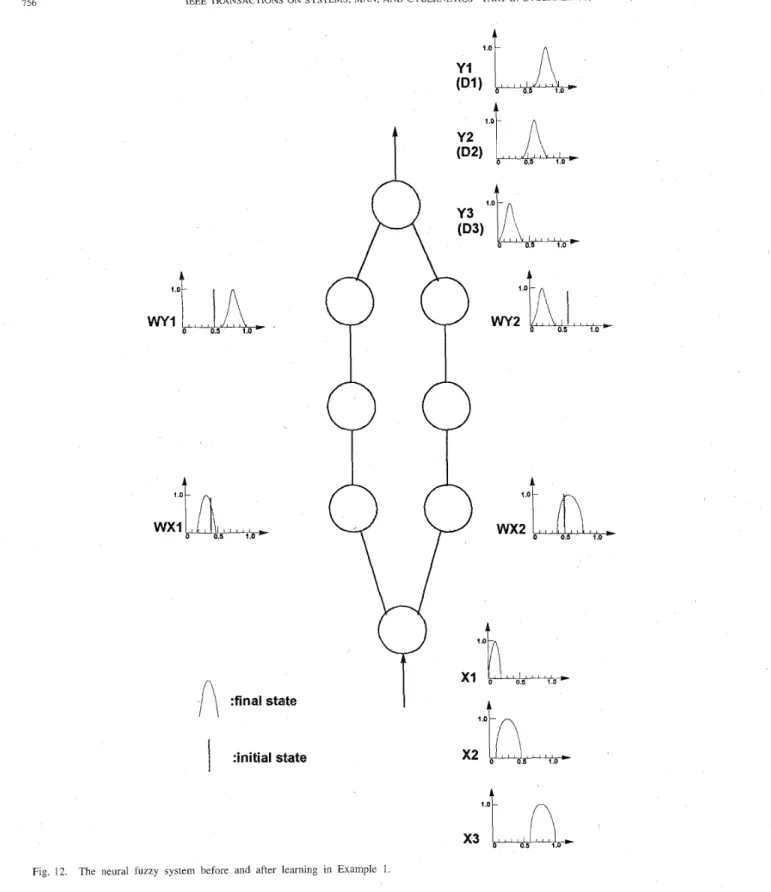
where the fuzzy weights after learning are shown in Fig. 10. For illustration, Fig. 11 shows the change of fuzzy weights in the learning process. The five-layered network structure of the neural fuzzy system used in this example is shown in Fig. 12. In the figure, the fuzzy weights before and after learning
0.6 0.8
are shown, where the exact fuzzy weights after learning can be found in Fig. 10. It is observed that these weights grow to fuzzy numbers from the initial numerical numbers (fuzzy singletons) when the network is trained with fuzzy inputloutput data. Three fuzzy input numbers and the corresponding fuzzy output numbers are also shown in Fig. 12 for illustration. Hence the original three fuzzy rules have been condensed to two rules, and these two sets of rules represent equivalent knowledge. As a comparison, when we solved the problem in this example using the approach in [4], the learning time needed to obtain the same learning result is 2.455 s. There are two major reasons that the proposed system can learn faster than the compared one. First, the proposed system allows numerical signals to flow in the network. Second,
LIN AND LU: NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING 16 1
0 0.2 0.4 0.6 0.8 1
weight
x
Fig. 24. The learned fuzzy weights in Example 4.A
Y
Y
Fig. 25. The structure of the FCNO in Example 5 .
the proposed system is a structured neural network (a fuzzy inference network), but the one in [4] is a normal multilayer neural network.
Example 2 - Fuzzy Input and Fuzzy Output: In this simula- tion, we train an FCLO having the same structure as that in Example 1 using fuzzy training data { ( X l J l ) , ( X 2 , 0 2 ) , ( X 3 , 0 3 ) } shown in Figs. 13 and
15. Here we set the number of ai-level sets as 2; i.e., a = (0, l} to emulate the triangular membership function that is used widely. The learning curve shown in Fig. 14 indicates that it takes a little bit more iterations to converge for smaller number of quantized membership grade. The total learning time is 1.572 s. (The learning time needed for the approach in [4] is 4.828 s.) The fuzzy outputs ( Y l 1 Y 2 , Y 3 ) of the learned FCLO and the corresponding desired outputs are shown in Fig. 15. The figure shows that they match perfectly. The learned fuzzy weights are shown in Fig. 16. We also use novel fuzzy inputs to test the generalization capability of
the learned FCLO. The results shown in Fig. 17 demonstrate its good interpolation and extrapolation capability, where the squares correspond to the Q = 0 level sets.
Example 3 - Fuzzy Input and Fuzzy Output: In this exam- ple, we train an FCLO with five training fuzzy number pairs shown in Fig. 18. In this figure, the stacked rectangles represent different a-level sets. Five level sets corresponding to a = 0,0.25,0.5,0.75,1 are used for each fuzzy number. In the initial FCLO, there are four nodes in each of layers 2,
3, and 4. That is, there are four fuzzy rules initially. After the structure and parameter learning, we obtain an FCLO containing three fuzzy rules (i.e., there are three nodes in each of layers 2, 3, and 4). The total learning time is 2.627 s. (The learning time needed for the approach in [4] is 8.422 s.) Fig. 19 shows the learned fuzzy weights. In order to examine the generalization capability of the trained FCLO, we present three novel fuzzy numbers to its input nodes for testing. The results shown in Fig. 20 (the dashed rectangles) indicate the good generalization capability of the learned FCLO.
Example 4
-
Crisp Input and Fuzzy Output: In this exam- ple, we train an FCLO with training pairs containing numer- ical inputs and fuzzy outputs. With Method 2 of initializa- tion process, the initial structure of the FCLO is shown in Fig. 21(a). The eleven training data pairs are shown in Fig. 22, where each input is a point, and the desired output is repre- sented by the interval corresponding to the level set of Q = 0. Five level sets corresponding to cy = 0,0.25,0.5,0.75,1 are used for each fuzzy number. After learning, the final FCLO is shown in Fig. 21(b), and its the actual outputs with respect to the training inputs are shown in Fig. 23. The total learning time is 2.392 s. (The learning time needed for the approach in [4] is 7.348 s.) The learned weights are shown in Fig. 24, where the layer-2 weights are crispy, and the layer-4 weights are fuzzy.Example 5 - Crisp Input and Crisp Output: In this exam- ple, we train an FCNO with numerical training data pairs.
162 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS-PART B: CYBERNETICS, VOL. 26, NO. 5 , OCTOBER 1996
8 . 2 0 0 2 0.4 0.6 0.8 1 1.2
x1 Fig. 26. The training data pairs in Example 5.
Lr*huCIz) w w r
Fig 27 The learning curve in Example 5 Fig 29 The learned output fuzzy weights in Example 5
shown in Fig. 26, where the circle has desired output of 0 and the star has desired output of 1. Eleven level sets are used in this example. The learning curve is shown in Fig. 27. The total learning time is 5.841 s. (The learning time needed for the approach in [4] is 16.2 s.) The learned weights are shown in Figs. 28 and 29. It is observed that the final learned weights could be fuzzy numbers even though the training data are all numerical.
VI. CONCLUSION
In this paper, we proposed a neural fuzzy system that can process both numerical and linguistic information. The proposed system has some characteristics and advantages:
1) The inputs and outputs can be fuzzy numbers or numer-
2) The weights of the proposed neural fuzzy system are w w x
Fig. 28 The learned input fuzzy weights in Example 5.
ical numbers.
fuzzy weights. With Method 1 of initialization process, the structure of the
LIN AND LU: NEURAL FUZZY SYSTEM WITH FUZZY SUPERVISED LEARNING 163
3) Owing to the representation forms of the a-level sets, the fuzzy weights, fuzzy inputs, and fuzzy outputs can be fuzzy numbers of any shape.
4) Except the input and output layers, numerical numbers are propagated through the whole neural fuzzy system; thus the operations in the proposed neural fuzzy sys- tem are not time-consuming and the required memory capacity is small.
The proposed system has fuzzy supervised learning capability. With fuzzy supervised learning, the proposed system can be used for a fuzzy expert system, fuzzy system modeling, or rule base concentration. When learning with numerical values (real vectors), the proposed system can be used for an adaptive fuzzy controller. Computer simulations satisfactorily verified the performance of the proposed neural fuzzy system. We are currently extending the fuzzy supervised learning scheme proposed in this paper to a fuzzy reinforcement learning scheme with the expectation that a neural fuzzy system can learn teacher’s oral (linguistic) instructions.
]REFERENCES
S. K. Pal and S. Mitra, “Multilayer perceptron, fuzzy sets and clas-
sification,” IEEE Trans. Neural Networks, vol. 3, no. 5, pp. 683-696,
1992.
J. M. Keller and H. Tahani. “Backpropagation neural networks for fuzzy
logic,” In$ Sci., vol. 62, pp. 205-221, 1992.
S. Horikawa, T. Furuhashi, and Y. Uchikawa, “On fuzzy modeling using
fuzzy neural networks with the backpropagation algorithm,” IEEE Trans. Neural Networks, vol. 3, no. 5, pp. 801-806, 1992.
H. Ishibuchi, R. Fujioka, and H. Tanaka, “Neural networks that learn from fuzzy if-then rules,” IEEE Trans. Fuzzy Syst., vol. I , no. 2, pp.
85-97, 1993.
H. Ishibuchi and H. Tanaka, “Fuzzy regression analysis using neural networks,” Fuzzy Sets and Systems, vol. 50, pp. 257-265, 1992.
H. Ishibuchi, H. Tanaka, and H. Okada, “Fuzzy neural networks with fuzzy weights and fuzzy biases,” in Proc. Int. Joint Cont Neural Networks, San Francisco, CA, 1993, pp. 1650-1655.
Y. Hayashi, J. J. Buckley, and E. Czogula, “Fuzzy neural network,”
International Journal of Intelligent Systems, vol. 8 , pp. 527-537, 1993.
- , “Systems engineering application of fuzzy neural networks,” in Proc. Int. Joint Con$ Neural Networks, Baltimore, MD, 1992, pp.
4 13-4 18.
A. Kaufmann and M. M. Gupta, Introduction to Fuzzy Arithmetic. New
York: Van Nostrand, 1985.
K. Uehara and M. Eujise, “Fuzzy inference based on families of a-level sets,” IEEE Trans. Fuzzy Syst., vol. I , no. 2, pp. 111-124, 1993. L. A. Zadeh, “The concept of a linguistic truth variable and its application to approximate reasoning-I, 11,” In$. Sci., vol. 8 , pp. M. Braae and D. A. Rutherford, “Fuzzy relations in a control setting,”
Kyberbetes, vol. 7, no. 3, pp. 185-188, 1978.
C. C. Lee, “Fuzzy logic in control systems: Fuzzy logic controller-Part I & 11,” IEEE Trans. Syst. Man, Cybern., vol. 20, no. 2, pp. 404-435,
1990.
199-249, 301-357, 1975.
[ 141 T. Yamakawa and T. Miki, “The current mode fuzzy logic integrated cir- cuits fabricated by the standard CMOS process,” IEEE Trans. Comput.,
vol. C-35, no. 2, pp. 161-167, 1986.
[15j K. Uehara, “Computational efficiency of fuzzy inference based on level sets,” in Proc. 1989 Spring Nut. Conv. Rec., IEICE, Japan, p. D-400.
[ 161 -, “Fast operation of fuzzy inference based on level sets,” in Proc. 38th Ann. Conv. Rec. IPS Japan Rec., 1989, p. 3G-3.
[17] C. T. Lin and C. S. G. Lee, “Neural-network-based fuzzy logic control
and decision system,” ZEEE Trans. Cornput., vol. 40, no. 12, pp. [ 181 - , “Reinforcement structure/parameter learning for neural-network- based fuzzy logic control systems,” IEEE Trans. Fuzzy Syst., vol. 2, no.
1, pp. 46-63, 1995.
[ 191 J.-S. Jang “Self-learning fuzzy controllers based on temporal back propagation,” IEEE Trans. Neural Networks, vol. 3 , no. 5, pp. 714-723,
1992.
[20] T. Tsukamoto, “An approach to fuzzy reasoning method,” in Advances in Fuzzy Set Theory and Applications, M. M. Gupta, R. K. Regade, and R. R. Yager, Eds.
[21] J. M. Zurada, Introduction to ArtiJicial Neural Systems. New York:
West, 1992.
[22] G. E. Hinton, “Connectionist learning procedure,” Art$cial Intelligence, vol. 40, no. 1, pp. 143-150, 1989.
[23] R. Keller, Expert System Technology-Development and Application.
Englewood Cliffs, NJ: Prentice-Hall, 1987. 1320-1336, 1991.
North-Holland, Amsterdam, 1979.
Chin-Teng Lin (S’88-M’91) received the B.S. de-
gree in control engineering from the National Chiao- Tung University, Taiwan, R.O.C., in 1986 and the M.S.E.E. and Ph.D. degrees in electrical engineering from Purdue University, West Lafayette, IN, in 1989 and 1992, respectively.
Since August 1992, he has been with the College of Electrical Engineering and Computer Science, the National Chiao-Tung University, Hsinchu, Taiwan, where he is currently an Associate Professor of Control Eneineerine. His current research interests
-
are fuzzy systems, neural networks, intelligent control, human-machine in- terface, and video and audio processing. He is the author of Neural FuzzyControl Systems with Structure and Parameter Learning (World Scientific),
and coauthor of Neural Fuzzy Systems: A Neuro-Fuzzy Synergism to Intelligent Systems (Englewood Cliffs, NJ: Prentice-Hall).
Dr. Lin is a member of Tau Beta Pi and Eta Kappa Nu.
Ya-Ching Lu was born in Tainan, Taiwan, R.O.C., in 1970. She received the B.S. and M.S. degrees in computer and information science from the National Chiao-Tung University, Hsinchu, Taiwan, R.O.C., in 1992 and 1994, respectively.
Since July 1994, she has been with the Academia Sinica, Taiwan, where she is currently an Assistant Researcher in the Institute of Information Science. Her current research interests include fuzzy systems, neural networks, and pattern recognition.