A combined evolutionary algorithm for real parameters optimization

A Combined Evolutionary Algorithm for

Real Parameters OptimizatiLon

Jinn-Moon

Yang

-

and C.Y. Kao*

Department of Computer Science and Information Engineering National Taiwan University

Taipei, Taiwan

E-mail: moon@solab.csie.ntu.edu.tw

Abstract

-

The real coded genetic algorithms (RCGA) have proved to be more efficient than traditional bit-string genetic algorithm in parameter optimization, but the RCGA focuses on crossover operators and less on the mutation operator for local search

.

Evolution strategies (ESs) and evolutionary programming (EP) only concern the Gaussian mutation operators. This paper proposes a technique, called combined evolutionary algorithm (CEA), by incorporating the ideas of EP and GAS into ES. Simultaneously, we add the local competition into the CEA in order to reduce the complexity and maintain the diversity. Over 20 benchmark function optimization problems are taken as benchmark problems. The results indicate that the CEA approach is a very powerful optimization technique.

I. Introduction

The function optimization problems have widespread application domain, including those of optimizing models, solving systems of nonlinear equations and control problem. Recently, the technique has been applied to train the weight of neural networks[ 11.

The Function optimization problems can be generalized in the following standard form[ 11:

Minimize f ( x i 7 XZ,. .. , x,,)

or

Maximize f ( X I , x 2 . . . . , x , ~ )

where xi is a real parameter subject to CL 4 x, I b,

a, nnd b, are some constant constraint

Evolutionary computations, based on natural selection in Darwin's theory, are studied and applied in three standard formats: genetic algorithms, evolution strategies, and evolutionary programming [3][4].

These methodologies have great robustness and problem independence; therefore, they are powerful optimization techniques in many applied domains, such as combinatorial optimization[6], function optimization [ 1][2][9][8], control, and machine learning[3,4]. Genetics algonthms[4][ 1 11, the most known and discussed in USA, stress chromosomal operator, such as crossover operator. Evolution strategies[9][ 151 and evolutionary programming [2][3] emphasize mutation operation for the behavioral link between parents and offspring, rather than the genetic link which is stressed in genetic algorithms.

Traditional GAS use bit-string to represent problem domains, but this representation is not suitable and not natural in some application domains, such as real-coded. In recent years, some authors[ 1,121 suggested the real-coded GA to represent the problem and proved this approach could gain better performance, but they focused on some modified crossover operators called blend crossover only . Basically,

the operator may be viewed as a simple heuristic crossover in real-coded parameters. The imain power and operators of GAS are crossover operators. Some studies[2.3,16,17] argued over the power of crossover operators. They explained and indicated that these operator are inappropriate i n some applications. So far, the CiAs lack fine local tuning capabilities

.

Schwefel[9] extended the ( 1 +p)-ES towards a (p+k)-ES and (p,?L)-ES for numerical optimization and proposed an algorithm for the capability of self-adapting step size. Both methods were all the same except the selection philosophy. The Ip.+h)-ES selected the top p population. based on fitness value, form p (parents) and

h

(children). but the (p.L)-ES selected the top p population form the h (children) only. That is, the lifetime for each individual is only one generation in the (p,h)-ES. The selection of the ESs is strictly deterministic and elicited policy. with the possibility of causing the premature convergence.

The Gaussian mutation operator[9], [ 151, could be viewed as heuristic mutation operator, the main power of ESs. The main strategies parameter in ESs is the mutation size and the step size control. Many studies discussed the operator and parameters control.

Fogel[3] wrote "there are two essential differences between ESs and EP, I . ESs rely on strict deterministic selection. E P typically emphasizes the probability nature of selection by conducting a stochastic tournament for survival at each generation ,... 2. . _ _ , ESs may use recombination operators to generate new trials, but EP does not, as there is no sexual communication between species."

Generally, the typical ESs use a parentsioffspring ratio of 1/6 (Cl/h=1/6) as opposed to the 1 ratio used in the EP. So, the EP can be viewed as (p+p)-ES when excluding the tournament selection operator.

11. The Combined Evolutionary Algorithm

The CEA technique combines the philosophy of ESs,GAs and EP. The detai!ed algorithm is shown in Fig. 1 . The basic idea of CEA is similar to the evolution strategies. However, there are three essential differences between CEA and ESs.

1) CEA incorporates the E P stochastic tournament selection[3] to replace the ES deterministic and elicited selection.

2) CEA views the blend crossover[ 121 as big-step-size mutation, and the crossover rate must decease dynamically. This operator is responsible for global search in the beginning phase. At the initial phase. we hope this operator can guide the search direction approximately in order to reduce the unnecessary search and concentrate on the interesting area as possibly as. The combination operator of ESs focuses on the step size only[lS].

3) CEA Incorporates the local competition as GESA[6] i n order to avoid the ill effect of greediness. The children, generated from the same parent by the Gaussian mutation operator, compete with each other, and only the best child survives and participates in the selection operators . That is, only (p+,u) individuals have the probability to become population of the next generation. Respectively, Both (p+h)-

ES and (p,h)-ES select from all children.

Initially, the CEA generates 2*P feasible solutions by uniform distribution in the feasible search space. Using the EP tournament selection (each member competes against k (general k=10) others, chosen at random based on the corresponding fitness value. Then, each member is assigned a score w(O<=w<=k) based on the number of the competition wins. Select P members with the most wins to be the parents for the next generation) to select P members. These selected members become the parents of blend crossover (BLX-0.5). The BLX-0.5 randomly selects a point from the line

connecting two parents extension of half the distance of the parents ate each end. In the BLX-0.5, we use the GA tournament selection(size=2) to select two parents and to generate one child by the BLX-0.5. In the process, the BLX- 0.5 generates P candidates. These candidates become the parents of the Gaussian mutation operators. Each parent generates n children, based on Gaussian mutation operator(i.e x'=x+G*N(O, 1). The children generated by the same candidate are viewed as a family. In each family only one best child, based on evaluated value, can survive. Therefore, exactly, two members (the parent and the best child) are put into the population pool in each family. Thus, the population size is invariant(2"P individuals).

The original real-code GAS use blend crossover and random mutation, so they lack fine local tuning capabilities. The Gaussian mutation operator is good local search method[7]. We suggest the combination of the blend crossover and Gaussian mutation operator. Initially, the crossover operator finds the approximated solution and the mutation operator adjusts the bias. The crossover may reduce the performance when near the optimal and the mutation become the main power, respectively. Therefore, we increase the length of Gaussian mutation and decrease the crossover rate dynamically. This strategy will improve the quality greatly.

The local competition of Gaussian mutation search can avoid early superstar domination the whole of population. Exactly one child in the same family can survive in CEA but at most h children can survive in ES. respectively. The EP selection tournament strategy plus the local competition can maintain the diversity. To reduce the complexity of EP tournaments selection is another benefit of local competition. The complexity of EP-selection is TS

*

P

+

P log P where P is the population size and the TS is the tournament size (times of the competition ). The size in CEA is 2p and 8p in general (p+h)-ES, respectively. Therefore, the local completion can reduce the complexity.

The CEA technique has three phases i n the evolutionary search.

I)

initial phase: The primary purpose in the phase is to find the approximate solution and to reduce the search space. The crossover operator is the main operator for global search and mutation operator for adjusting the bias. The phase takes about 10% of the computing time.

2) middle phase: Both mutation and crossover are equal important. This phase takes about 20% of computing time.

3) last phase: The main purpose in the phase is to tune the solution i n order to find the best solution . The Gaussian mutation is primary operator and very little disturbance is made by crossover operator. The phase spends about 70% computing time.

1. Set the strategy parameters: Local-Search-Length Cross-O\,er-Rate and CaussianMutationSize(

s)

2. Randomly generates 2 *P candidates by uniform distribution f o r m feasible solution

3. Compute the fitness of each candidates. ( E(Xi) ,i=lv...v2P)

4. Select X i ( i = l ,...,Pi parents by EP tournament selection from X [ ( i = l ,..., 2 P )

5 For each X i ( i = l ,..., P ) execute blend crossover(BLX-0.5) generate a child C

if

E ( C I < E ( X i j then replace X i else keep Xi ( when

minimize the fitness function)

6. Generate Xi(i=P+l ,..., 2 P ) f o r each Xi(i=l ,..., P){

generate Local-Search-Length "offspring" through Gaussian mutation operator (xt=x+6*N(0, I)) f r o m the same parent

select the best offspring based on fitness as the child

(X,(

i = P i- 1,. 1. 2 P ) .

I

7 Change the parameters f o r next generation when satisjj some constraints {

Cross-Ove r-Rate= Cross-Ove r-Rate

-

0. OS;

Local-Search-Length=Local-Search-Length i- I ;

6=

0.95

*

6

}

8. r f discovery sufficient solution or exhaust the available time then terminate else goto step 3

parameters setting: (for all benchmark problems)

Local-Search-Length: initial = 3, MaxLen = IO, increase by 1 for each 10 generations CrossOverRate: initital = 0.5, MinRate = 0.05,

decrease by 0.05 for 10 generations decrease rate = 0.95.

6 : ' initial=0.2*abs(Max-Constraint-MinConstraint), ' .

Poplation-size = 50

Fig 1. The Combined Evolutionary Algorithm.

111.

The

CEA

Approach

to

Function

Optimization: Empirical Results, findings and

discussions

We have implemented the CEA algorithm on function optimization. The strategy parameters (Local-Search-Length, Gaussian-Mutation-Size, and CrossOverRate) were given the value as in the fig 1 for all testing function. At first, we compared the CEA technique with other evolutionary algorithms for over 20 benchmark problems. The CEA always gained better results. The CEA is also robust i n various problems. We discuss the effect and influence of strategy parameters, and try to explain the reasons.

CEA's performance has been compared with traditional GA. real-code GA and EP. We select over 20 benchmark

functions and these test functions are given in the table I . The

FI

to F7 and

t

9

have been studied by De Jong[ll], Schaffer[lO] and Wright[ 11. These problems are benchmark functions in GAS. Yip[6] studied the

F8

and compared with simulated evolution. F11 to

FI

9 were collected and studied for EP by Koon[8]. These functions are the benchmark function in the SIAM journal on Scientific Computing. The F21 to F23 are studied in McDonnell [13]. The three functions have 30 dimensions and studied in ES. Above all, F23 is very complex function and high dimensions(30). Fig 2 shows one-dimensional slice of F23. All these functions search for the global minimum..

F18 I I 10 1.6.0 1-5.534 IF8ofG.H. Koon

O L ' ' Y , , , ,

-30 -20 -10 _{10 20}

30

K

First. i n order to compare with EP, the functions from

F11 to Fli) were executed with over 50 runs by CEA. We started the parameters as i n the fig 1 and terminated the process after 1000 generations(ab0ut 480,000 function evaluations). The CEA found all function global minimums at 200 generations (about 86,000 function evaluation) in each run. We used F15 as an example to shows the convergence curve and given i n Fig 3. The summary of these experiment are given i n Table 2. The EP, after executing 2000 generations (about 100,000 function evaluations), cannot find the giobal minimum for complexity functions (F12,F13.F14 and F15). As shown in Table 2, the CEA outperforms the EP on these benchmark problems..

Function

#

Table 2. Comparison with EP[G.H.Koon][B] on F11 to F19(benchmark problem in the Journal on Scientific Computing. For each function the CEA runs 50 times (terminated 1000 generations(ab0ut 480000) and finds the global minimum about 200 generations(about 86,000

Real-code GA Traditional GA CEA(mean) Optimal function evaluations). F1 000004 FZ 00207 F3 05730 F4 - 1 0906 . . F13 1-156 119* 1-156 665 1-156.665 F14 (0.00Ib 10 10

I

I ! 0 0062 0 0 1 0 1 9 2 0 0 I 1 7 1 0 0 0 9 7 3 1 1 0 0

*: EP cannot find the global rmnimum of the function. and CEA can find the global minimum all functions

F l j . P i f " C \ S I - l u n c t l s n E I I l U I L i " "

I 3 1 7 2 1 2 5 2 V 3 3 3 7 4 1 I < I V 5 3 5 7 d l 6 5

r u cII I t i ,,

Fig 3: The convergent curve of F15

Table 3 compares the performance of CEA with that of the traditional GA and real-coded GA[l] for F1 to F7 and F9. This result indicates that CEA outperforms the traditional GA and real-coded GA. The CEA can find the global minimum for all except function F7 (mean different value about equal 1E-6). CEA needed about 50 generations(ab0ut 13.000 function evaluations) for F5 and F9, while other functions needed about 200 generations (about 86,000 function evaluations). The convergent curve of the more complex function F5 was given i n fig 4. In these experiments we found the real-coded GA to converge optimal faster than CEA. But the real-code GA could not find the global optimum when it trapped into the local optimal. This result implies that the blend crossover has poor ability for local search. Fig 6 indicates and also explains that the blend crossover is not suitable for local search in the real-coded GA.

the CEA cannot find the global mnimum

The GESA[6] approach incorporates the local competition i n the same family and the authors use the F8 as a benchmark problem to compare with simulated evolution. The GESA needed about 500,000 function evaluations to find the global optimum in each runs. In the same search space, the CEA executes 50 runs and table 4 shows the result. Fig 5 shows the convergence curve. Each experiment of the

CEA finds the global minimum and needs 330,000 function evaluation on average. The main reason may be the local competition length. Each parent i n GESA generates 20 children to compete on average, but the CEA only generates 3 to 10 children. Maybe the crossover and EP-selection cause the result

I '

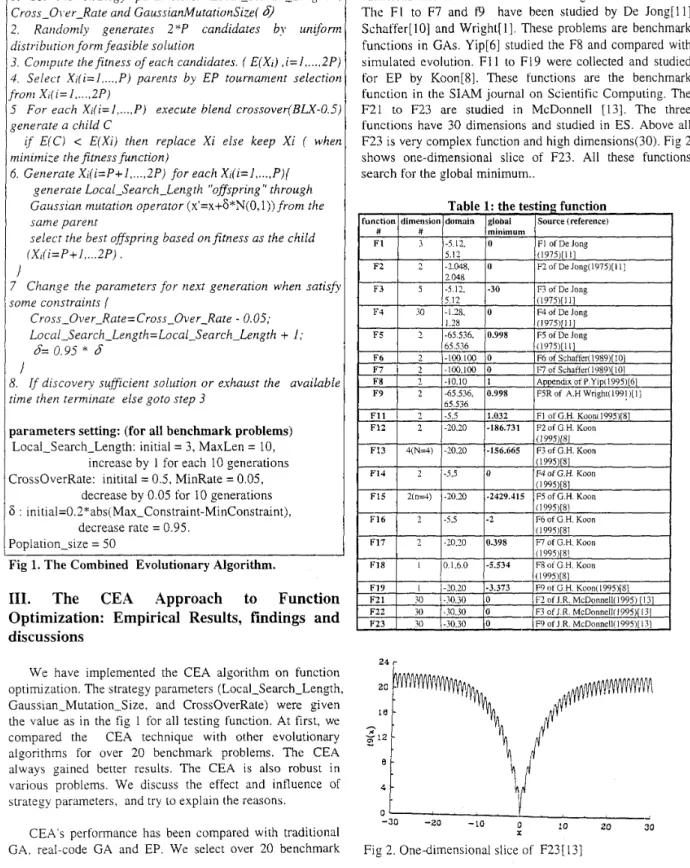
In order to explain the effect of blend crossover in real coded representation, we set the crossover rate to 1 and fixed the rate. Table 4 indicates the high and fixed crossover rate policy will reduce the performance when the function is complex. The result may be caused by two main factors.

I ) The crossover operator is a larger step search than Gaussian mutation and is not suitable for the fine tuning when the solution is near the optimal. Therefore. in the last phase, the crossover must be inhibited or reduced to very low probability.

2) The Gaussian mutation is main role in the last phase and has excellent ability for fine tuning.

Function #

Table 4. A comparison of blend crossover rate strategy: high and fixed rate policy vs. lower and dynamic rate policy (mean value of 50 runs)

search CEA: dynamic search Optimal length =1 length from 3 to 10

Function # F1 F2 _ - F6 ]0.0003 10

10

F8 \1.001329 I I 11

static: CEA: dynamic: crossover rate Optimal crossover (from 0.5 to 0.05 decease by rate =1 0.05) 0 0 0 0 0 0 F22 1228.4286 10 10 F23

I

11,72984 I1.82E-07 10 +

iu

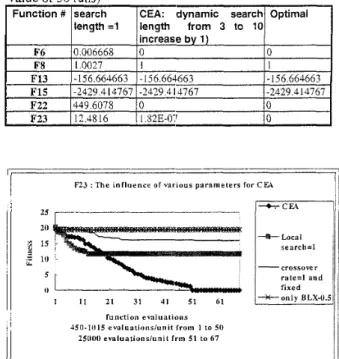
Loca I search=l I crossover r a t e d and fixed

The step size of Gaussian mutation is the most important parameter for ESs and EP. Therefore, many studies have discussed the control of the step size. In this paper, we use very

a

simple rule, fixed decreasing rate, to control the steps size. Table 5 indicates the influence of the Gaussian mutation size in CEA. Primarily, This experiment showed that this simple rule is enough good when the initial step size is not small enough. Because small mutation size makes the CEA too greedy, it causes the premature convergence.

Function initial-size =0.05'(Max-Const

I

# iraint

-

In order to explain and prove the power of local competition, we used only the mutation operator and local competition. For each function, randomly execute 50 runs. We discovered that the results were almost as well as the original CEA almost except the F8 and F23. This result might be caused by the complexity of function and lack of BLX-0.5 crossover operator.

initial-size raint

Table 5 . The effect and influence of Gaussian mutation size(mean value of 50 runs)

F5 F6 Min-Constraint) Min-Constraint) 2.09841 0.998 0 998 0 0 0 F8 11 F9 2 19549 F22 12.78935 F23 . 9 52435 I I 0 998 0 998 0 0 1 S E 0 7 0

Using Gaussian mutation as a search operator, the typical search length for EP and ESs is 1 and 7, respectively. CEA views the search length as competition numbers. Table 5

indicates the influence of the Gaussian local search length. With more variables (e.g. F22 and

F23)

and complex functions the search length must be longer. The local search spent most computing time in CEA. Search length over 10 is not worthwhile considering the the tradeoff between search time and quality. The effect of CEA's parameters, based on the complex and high dimensions F23, is showed in fig. 6.

- 156.664663 -2429.4 14761

F7.3 : T h e influence of various parameters for CEX 20 2 15 '1: I O 5 I1 2 1 11 31 3 1 4 1 5 1 61 function evaluations 351100 evaluationsiunit frm 51 to 61 45(1-1015 evaluatiansiunit from 1 to 50 I ' > ,

Fig 6. The convergent curve for various parameters based on F23

IV.

Coriclusion

Incorporating the ideas of EP and GAS into evolution strategies, CEA was found to 'oe a very powerful optimization technique. As demonstrated with the use of the 20 benchmark function problems, the CEA outperformed other simulated evolutionary algorithms, including the EP,ESs, traditional GA and real-coded. GA. The CEA uses the same parameters with small population size and simple control rule to solve all functions and converge to the optimum or point very near the optimal(mean different value lower than 1E-6).

The eialutionary search process of CEA can be viewed i n three phases. In the first phase, use crossover (BLX-0.5) as a global j z x c h operator i n order to find approximate solutions. The Gaussian mutation can be viewed as a local search operator to adjust the bias. In the second phase, both the crossover operator and mutation operator are equally important. in order to explore and exploit the search information. In the last phase, the crossover becomes less important and mutation becomes the main operator.

[IO]. J.D. Schaffer, etal. " A Study of Control Parameters

Affect On-line Performance of Genetic Algorithm for Function Optimal," in Proc of the Third ICGA, Morgan Kaufmann, 1989, pp 51-60.

[ 111. K.A. De Jong. Analysis of the behavior of a class of genetic Adaptive System, Ph.D. Dissertation, Department of Computer and Communication Science,University of Michigan, 1975.

In the future research, we will use CEA to solve NP-Hard [12]. L.J Eshelman & J.D. Schaffer, " Real-coded Genetic

Algorithms and Interval-Schemata," in Proc. FOGA '93. combinatorial optimization problems.

reference:

[ 131. Mcdonnell and D.E. Wagen,"An Empirical Study of Recombination in Evolutionary Search," in Proc Evolutionary Programming IV 1995, pp 465-448.

[I]. A.H. Wright,"Genetic Algorithm for real Parameter [ I d ] . P.J.B. Hancock. "An Empirical Comparison of Optimization", in Proc FOGA '9 1, pp 205-2 18. Selection methods in the evolutionary algorithms," in Proc.

of the First International Conference on Parallel Problem

[ 2 ] . D.B. Fogel and J.W. Atmar, "Comparing Genetic Solving from Natural, 1991 , PP 81-94. Operators with Gaussian Mutations in Simulated

Evolutionary Processes Using linear Systems," Biological [151. T. Back, F. Hoffmeister and H.P. Schwefel, " A survey

Cybernetic, vol, 63, 1993. pp 11 1-1 14. of Evolution Strategies," in Proc. ICGA' 91 , pp 2-9.

[ 3 ] . D.B. Fogel ,"An Introduction to Simulated Evolutionary [161. D.B. Fogel ,"An Evolutionary Approach to traveling Optimization", JEEE trans. Neural Networks, VO] 5,no. 1, Salesman Problem," Biological Cybernetic, vol. 60, 1988, pp

Jan. 1994. pp 3-14 139-144.

[4]. D,E. goldberg, Genetic Algorithms in search, [ 171. P.J. Angeline, G.lM. Saunders, and J.B.Pollack ,"An Optimization & Machine Learning, Reading. MA: Addison- Evolutionary Algorithm that Constructs Recurrent Neural Welsley. 1989. Networks," IEEE trans. on Neural Networks, vol 5,no. 1 ,

Jan. 1994, pp 54-65. [SI.

D.E.

goldberg and K.Deb," A Comparative Analysis of

Selection Schemes Used i n Genetic Algorithms," in Proc. FOGA 9 2 , ~ ~ 69-93.

161. D. Yip and Y.H. Pao, "Combinatorial Optimization with Use of Guided Evolutionary Simulated Annealing," IEEE trans. Neural Networks, vol. 6,no. 2, Mar 1995, pp 290-295 [7]. F. Hoffmeister and T. Back."Genetic Algorithms and Evolution Strategies: Similarities and difference," in Proc. of the First International Conference on Parallel Problem Solving from Natural, 1991 , pp 455-470.

[SI. G.H. Koon and A. V. Sebald, "Some interesting Functions for Evaluating Evolutionary Programming Strate,oies." in Proc Evolutionary Programming IV 1995, pp 479-499

[9].

H P Schwefel, Numerical Optimization for Computer Models Chichester, UK:wiley 198 1 .