On the arrangement graph

(1)

On the arrangement graph

Wei-Kuo Chiang a,*, Rong-Jaye Chen b

a Computer Telephony Applications Department, Computer & Communication Research Laboratories, Industrial Technology Research Institute, K200 CCL Bldg. 51, 195-11 Sec. 4, Chung Hsing Road, Chutung, Hsinchu, Taiwan 310

b Department of Computer Science and Information Engineering, National Chiao Tung University 1001 Ta Hsueh Road, Hsinchu, Taiwan 300

Received 27 August 1996 Communicated by F. Dehne

Abstract

The arrangement graph was proposed as a generalization of the star graph topology. In this paper we investigate the topological properties of the (n, k)-arrangement graph &k. It has been shown that the (n, n - 2)arrangement graph An,+2 is isomorphic to the n-alternating group graph AGn In addition, the exact value of average distance of A,,& has been derived. 0 1998 Published by Elsevier Science B.V. All rights reserved.

Keywords: Interconnection networks; Graph isomorphism; Average distance

1. Introduction

Recently, a widely studied interconnection network

topology called the star graph was proposed by Akers et al. [2]. It has been known as an attractive alternative to the hypercube [ 11. The star graph is node and edge symmetric, and strongly hierarchical as is the case of the hypercube. The n-star graph S, is regular of degree n - 1, the number of nodes n!, and diameter

[3(n - 1)/2]. For a similar number of nodes, the star graph has a lower node degree, a shorter diameter, and a smaller average distance than the comparable hypercube.

In addition, .low et al. presented another interconnection scheme based on the Cayley graph of the alternating group, called the alternating group graph [8]. The n-alternating group graph AG, is regular of de- gree 2(n - 2), the number of nodes n!/2, and diameter

* Corresponding author. Email: wkchiang@dcs.ccl.itri.org.tw.

13 (n - 2)/2J . The alternating group graph is also node and edge symmetric.

A common drawback of & and AG, is the restric- tion on the number of nodes: n! for S,, and n!/2 for AG, . The set of values of n! (or n!/2) is spread widely over the set of integers; so, one may be faced with the choice of either too few or too many available nodes.

Even before [8] was published, Day and Tripathi [5] proposed a generalized star graph, called the arrangement graph, as an attractive interconnection scheme for massively parallel systems. An arrangement graph is specified by two parameters n and k, satisfying

1 < k < n - 1. The (n, k)-arrangement graph An,k is regular of degree k(n - k), the number of nodes n!/(n - k)!, and diameter [3k/2]. The (n, n - l)- arrangement graph An,n-l is isomorphic to the n-star graph S, [6]. The arrangement graph provides more flexibility than the star graph in terms of choosing the major design parameters: degree, diameter, and number of nodes. The arrangement graph has been shown 0020.0190/98/$19.00 0 1998 Published by Elsevier Science B.V. All rights reserved

(2)

216 W-K. Chiang, R.-J. Chen /Information Processing Letters 66 (1998) 215-219

to be node and edge symmetric, strongly hierarchical, maximally fault tolerant, and strongly resilient [5].

In this paper we further look into the topological properties of the arrangement graph. We first show that the (n, n -2)arrangement graph An,n-2 is isomorphic to the n-alternating group graph AG,. Then, we derive the exact value for the average distance of An,k. Due to the isomorphism between A,,+_2 and AG,, the average distance derived here for the arrangement graph as well as those discussed in the literature [4-71 can be applied directly to the alternating group graph. Therefore, we solve two of four open problems for the alternating group graph listed in [ 81:

(1) enumeration of the node disjoint paths; and (2) exact value of the average distance.

2. Graph definitions and basic properties

In this section we introduce the definitions and notations of the arrangement graph and the alternating group graph, and address their basic topological properties.

2. I. Graph definitions

For simplicity, let (n) = { 1,2, . . . , n) and (k) = (1,2,. . .,k).

Definition 1 [5]. The (n, k)-arrangement graph A n,k=Wl,El), I<k<n-1, is defined as follows: V~={p~p2...p~I~~~(~)andp~#pjfori#j}, and Et={(p,q))pandqinVtandforsomeiin(k), pi#q;andpj=qjforj#i].

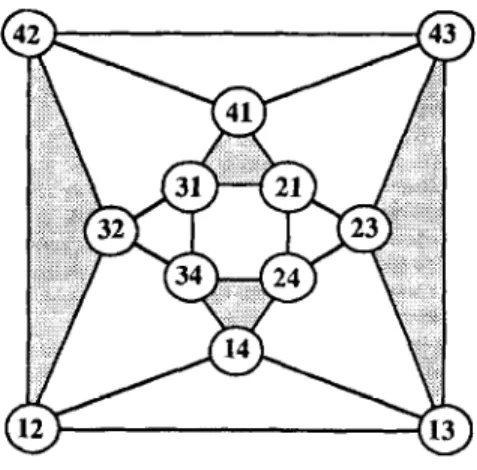
That is, the nodes of A,,k are the arrangements of k elements out of the n symbols (n), and the edges of An,k connect arrangements which differ in exactly one of their k positions. An edge of A,,k connecting two arrangements which differ only in position i is called an i-edge. An example of A,,,k for n = 4 and k = 2 is given in Fig. 1.

Fig. 1. A (4,2)-arrangement graph.

To define the alternating group graph, we describe some terminologies and notations for ease of exposi- tion.Inapermutationp=ptp~...pi...pj...p,,the

pair (i, j), i < j, is said to constitute an inversion if pi > pj. A permutation p is called even or odd de- pending on the number of inversions in p being even or odd. The alternating group A,, is defined as the set of all even permutations of n elements [3].

Let

g+ = (1 2 i), gi = (1 i 2), n=(g’13~i6n)U(gi13~i~n},

where 0 is known to be a generator set for A, [8]. Let cj denote the transposition that swaps the elements at positions i and j, then g+ = Tl7_ . T2i and gi = T2i ’ Tl2 for 3 < i < n.

Definition 2 [S]. The n-alternating group graph AG, = (V2, E2) is defined as follows:

Vz = A,, and

E2 = {(P, q) I p, q E h, and

where “0” is the composition operator. The nodes of AG, are even permutations of the n symbols (n). An edge of AG,, connecting two even permutations p and qiscalledani-edgeifq=pogpanda=+or-.

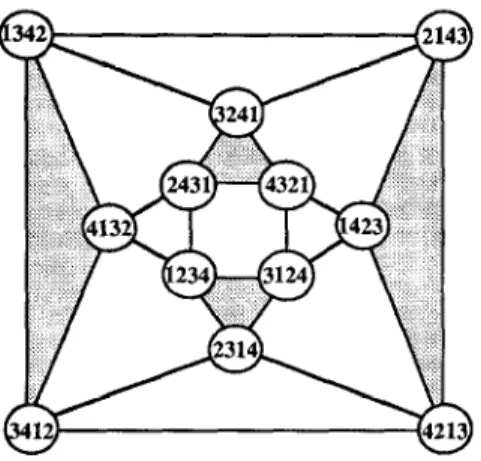
Note that q = p o gt if and only if p = q o gi. An example of AG, for n = 4 is given in Fig. 2.

(3)

Fig. 2. A 4dtemating group graph AG4.

2.2. Basic properties

There are (n - l)!/(n - k)! nodes in An,k which have element i in position j, for any fixed i and j (1 < i < n, 1 < j < k). These nodes are interconnected in a manner identical to an An_t,k_t graph. For a fixed position j, an A,,k can be partitioned into n node- disjoint copies of An-t,k_t. This partitioning of A,,k into n copies of An_t,k_t can be done in k different ways corresponding to the k possible values of j (1 < j < k) and can be carried out recursively. Fig. 1 shows that A4,2 can be viewed as an interconnection of four A~,J’s by fixing the symbol in position 2.

Due to the node symmetry of the (n, k)-arrangement graph, the problem of routing between two arbitrary nodes in An,k is reduced to the problem of routing between an arbitrary node and the identity node &. In order to solve the problem of the routing, a cycle representation for the label of each node in An,k was in- troduced in [5]. The cycle representation of a node p with c cycles including e external cycles can be de- noted as

C(p) = Cl, c2, . . ., ce, c:,, 1 c:,,, . . .t cl,

where Ct,Cz,..., C, are external cycles and CL,, , c;+2,. . . , CL are internal cycles. Let m denote the total number of elements in these cycles. It has been shown in [5] that the distance d(p) from node p to the identity node Ik in A,,,k is given by:

d(p)=c+m-2e. (1)

In addition, it has been presented in [5] that the connectivity K(An,k) of An,k is k(n - k) and the fault-

diameter Df(An,k) of An& is at most [3k/2J + 4. In [6], it has been known that the arrangement graph A ,,k, for 1 < k < n - 2, contains cycles of any arbitrary length L, 3 < L < ]An,kl, where ]An,kl is the number of nodes in An,k. Furthermore, it has been shown in [7] that an (n - k + 1) x (n - k + 2) x . . x (n - 1) x n grid can be embedded into An,k with unit expansion and dilation three.

3. Isomorphism between An,n_:! and AG,

In this section, we show the alternating group graph is a spatial arrangement graph. Before proving it, we give a formal definition of isomorphism between two graphs in the following.

Definition 3. Two graphs Gt and G2 are isomorphic if there is a one-to-one function f from V(G1) onto V(G2) such that (p,q) E E(G1) if and only if (f(p), f(s)> E E(Gd, where f(p) is the image

of p.

Theorem 4. The (n, n - 2)-arrangementgraph An,*_2 is isomorphic to the n-alternating group graph AG,. Proof. To prove that AG, and An,n_2 are isomorphic, we define a one-to-one function ft from the nodes of AC,, to those of An,n_2 by:

fi(PlPZP3.~ .Pn-lPn)=P3...Pn-lPn.

Note that .f-‘(43.. .qn-144 = aq2q3.. .qn-lqn or q2qtq3... qn_lq,, depending on which one is an even permutation.

Now, we prove fr preserves adjacency. Let p and q be two nodes linked with an i-edge in AG,, . Then fl(p) and fl(q) are linked with an (i - 2)-edge in An,n_2. Conversely, let s and t be two nodes linked with a (j - 2)-edge in An,+2, i.e.,

s = s3 . . . Sj_lSjSj+] . . .S, and t = s3 . . .Sj_ltjSj+l . . .Sn.

Without loss of generality, assume s is an even permutation, then

fi-‘(S) = SlS2S3.. .Sj_lSjSj+l . . .Sn and

(4)

218 WK. Chiang, R.-J. Chen /Information Processing Letters 66 (1998) 215-219

where st < s2 and tj = ~1, and thus fi_’ (t) = fi-’ (s) o g;. That is, fi_‘(t) and fi-‘(s) are linked with a j- edge in AG,, . q

The example for A4,2 in Fig. 1 is the resulting graph when ft is applied to AG4 in Fig. 2.

The next corollary solves one of four open problems listed in [S]. We get the result by using Theorem 4 and the fact that for any two nodes of i&k, there exists k(n - k) node-disjoint paths of length at most four plus the distance between the two nodes [4].

Corollary 5. Given any distinct nodes s and t in an n- alternating group graph AG,, there are 2(n - 2) node- disjoint paths of length at most four plus the distance between the two nodes. That is, the connectivity K(AGn) of AG, is 2(n - 2) and the fault-diameter Df (AGn) of AG, is at most [3(n - 2)/2J + 4.

The following corollary describes the routing distance in AG, . Although the result was discussed in [8], here we get it directly by applying Eq. (1) with Theo- rem 4.

Corollary 6. The distance d(p) from node p to the identity node I,, in AG, is:

I nfk-1, if p1 = 1 and p2 = 2, n+k-l-2, tfpl # 1 and p2 = 2, d(p)= n-tk-l-2, ifpl=landp2#2, n+k-1-3, ifland2ECt, n+k-l-4, iflECiand2ECj,

where k and 1 denote the numbers of cycles and invariants in C(p).

Proof. The distance from p = plp2p3 . . . pn to In = 123.. n in AG, is equivalent to the distance from p” = p3 . . . p,, to I{ = 3. . .n in An,n_2. Let c”, m”, and e” denote the number of cycles, the total number of elements in these cycles, and the number of external cycles in C(p”) with respect to I:; that is, d(p) = d(p”) = c” + m” - 2e”. Note that symbols 1 and 2 with respect to Z: are foreign symbols.

(a) If p1 = 1 and pz = 2, then c” = k, m” = n - 1, e” = 0, and d(p”) = n + k - 1.

(b) If p1 # 1 and p2 = 2, then c” = k, m” = n - 1, e” = 1, and d(p”) = n + k - 1 - 2.

(c) If pt = 1 and p2 # 2, then c” = k, m” = n - 1, e” = 1, and d(p”) = n + k - 1 - 2.

(d) For 1,2 E Ci, if either p1 = 2, or p2 = 1, c” = k, m” = n - 1 - 1, e” = 1; otherwise, c” = k + 1, m” = n - 1, e” = 2. Therefore, d(p”) = n + k - l-3.

(e) If 1 E Ci and 2 E Cj, c” = k, m” = n - 1, and

e”=2;so,d(p”)=n+k-l-4. q

4. Average distance

In this section, we derive the exact values for the av- erage distances of the (n, k)-arrangement graph An,k and the n-alternating group graph AG,. The average distance of a symmetric interconnection network is de- termined by the summation of distances of all nodes from a given node over the total number of nodes. Average distance is a better indicator of the average message delay in an interconnection network than its diameter. Since &k is node-symmetric, its average distance among all pairs of nodes p and 4 (possibly p = q) equals the average distance from the identity node fk to all nodes.

Let B(An,k) denote the average distance of An,k. The value of this measure for the (n, k)-arrangement graph is

D(&,k) =

c

d(p)lN(n, k),

P-&k

where N(n, k) = n!/(n -k)!.

It is known that the average number of cycles including invariants in a permutation of n symbols is H,, where Hn = c?‘=l l/i denotes the nth Harmonic number [9]. Here, we show the average number of cycles including invariants in a permutation of k elements out of n symbols is Hk.

Lemma 7. The average number of cycles including invariants in a permutation of k elements out of n symbols is Hk.

Proof. We consider a permutation p formed by choos- ing arbitrarily k elements out of the n symbols (n) . Let p’ be the permutation obtained from replacing each foreign element of p with its corresponding nonfor- eign element. Then the total number of cycles of C(p) is equal to that of C(p’). The number of cycles in all permutations of the k symbols (k) is k! x Hk. There-

(5)

fore, the total number of cycles in all permutations of k elements out of the n symbols (n) is

x k! x Hk.

Dividing it by the total number of permutations of k elements out of the n symbols (n), we derive the average number of cycles in a permutation as Hk. 0 Given a node p, let u be the total number of in- variants, c* be the total number of cycles including invariants, and m* be the total number of misplaced symbols, i.e., m* = k - u. In Eq. (l), c denotes the to- tal number of cycles of C(p) excluding invariants, and m denotes the total number of elements in these cycles including the corresponding nonforeign elements for the external cycles. It then follows that for c and m as defined above, c = c* - u and m = m* + e. Similar to the argument of Theorem 2 in [l], we rewrite Eq. (1) as

d(p)=k+c*-e-2u. (2)

The following theorem gives the exact value for the average distance of &k, which is obtained by computing the total value of Eq. (2) for each node in An,k and then dividing by n!/(n - k)!.

Theorem 8. The average distance B(A,,k) of the (n, k)-arrangement graph is given by:

H

+W-2)

k -. n

Proof. The first term in the summation of Eq. (2) over all nodes of &k is k x n!/(n - k)!, and the second term is Hk x n!/(n - k)!. The third term is the total number of foreign symbols in all nodes of An,k, i.e., k x (n -k) x (n - l)!/(n - k)!. The final term is the total number of symbols in the correct position for all nodes multiplied by -2, i.e., -2 x k x (n - l)!/(n - k)!. Therefore,

D(A,,J = k + Hk - k x (n - k)/n - 2k/n

=Hk+kx(k-2)/n. u

The next corollary solves another open problem listed in [S]. That is, the exact value for the average distance of AG, is found while the result for the average distance of AG, proposed in [8] is just an upper bound.

Corollary 9. The average distance D(AG,) oj’the n- alternating group graphs is

n+H,fl- - 1 -6. n n-l

Proof. By applying Eq. (3) with Theorem 4, D(AG~) = D(A,,,_~). q

References

[l] S.B. Akers, D. Horel, B. Krishnamurthy, The star graph: An attractive alternative to the n-cube, in: Proc. Internat. Conf. on Parallel Processing, 1987, pp. 3931100.

[2] S.B. Akers, B. Krishnamurthy, A group theoretical model for symmetric interconnection networks, in: Proc. Intemat. Conf. on Parallel Processing, 1986, pp. 216-233.

131 C. Berge, Principles of Combinatorics, Academic Press, New York, 1971, Chapter 4.

[4] K. Day, A. Tripathi, Characterization of node-disjoint paths in arrangement graphs, Tech. Rept. TR 91-43, Dept. of Computer Science, University of Minnesota, 1991.

151 K. Day, A. Tripathi, Arrangement graphs: A class of generalized star graphs, Inform. Process. Lett. 42 (1992) 235-241. 161 K. Day, A. Tripathi, Embedding of cycles in arrangement

graphs, IEEE Trans. Comput. 42 (1993) 1002-1006.

[7] K. Day, A. Tripathi, Embedding grids, hypercubes, and trees in arrangement graphs, in: Proc. Internat. Conf. on Parallel Processing, 1993, pp. 65-72.

[8] J. Jwo, S. Lakshmivamhan, SK. Dhall, A new class of interconnection networks based on the alternating group, Networks 23 (1993) 315-326.

[9] D.E. Knuth, The Art of Computer Programming, Vol. I, Addison-Wesley, Reading, MA, 1973.