Health Econ. 9: 319 – 326 (2000)
ECONOMIC EVALUATION
MOTHER’S WILLINGNESS TO PAY FOR HER
OWN AND HER CHILD’S HEALTH: A
CONTINGENT VALUATION STUDY IN TAIWAN
JIN-TAN LIUa, JAMES K. HAMMITTb,*, JUNG-DER WANGcAND JIN-LONG LIUd aDepartment of Economics, National Taiwan Uni6ersity, Taiwan
bCenter for Risk Analysis, Har6ard School of Public Health, USA cSchool of Public Health, National Taiwan Uni6ersity, Taiwan dInstitute of Industrial Economics, National Central Uni6ersity, Taiwan
SUMMARY
We use the contingent valuation (CV) method to estimate mothers’ willingness to pay (WTP) to protect themselves and their children from suffering a minor illness — a cold — in Taiwan. WTP is specified as a hedonic function of the duration and severity of the cold (measured alternatively by symptoms experienced and the Quality of Well-Being (QWB) index) and of respondents’ socioeconomic characteristics. The average mother is willing to pay more to protect her child than herself from suffering a cold. Median WTP to avoid the average mother’s and child’s colds are US$37 and US$57, respectively. Adjusting for the greater duration and severity of the average mother’s cold suggests that WTP to prevent comparable illnesses is approximately twice as large for the child as for the mother. We also find that mother’s WTP is about 20% greater to prevent a son’s than a daughter’s illness. Copyright © 2000 John Wiley & Sons, Ltd.
KEY WORDS— contingent valuation; willingness to pay; morbidity; altruism
INTRODUCTION
We estimate the values to Taiwanese mothers of protecting themselves and their children from suf-fering a minor illness — a cold — and examine how the values depend on the severity and duration of the cold. Values are elicited using contingent valu-ation (CV). We find that willingness to pay (WTP) to prevent a cold is positively associated with the severity of symptoms and their duration. Moreover, mothers’ altruistic WTP to protect their children from a cold is approximately twice as large as their private WTP to protect them-selves from a cold of equivalent duration and severity. That is, mothers value their children’s health more than their own.
Several previous studies have estimated the value to an individual of preventing her own minor illness, but few studies have examined WTP to protect another person’s health [1,2]. Viscusi et
al. [3] used CV to estimate WTP to prevent the
risk of injury associated with household pesti-cides. They found that WTP to reduce risks to one’s children exceeds WTP to reduce risks to oneself but could not distinguish the effects of parental altruism and injury severity. Agee and Crocker [4] estimated parental WTP to reduce the risk of neurological impairments due to childhood exposure to lead using a revealed-preference ap-proach based on the parents’ decision to obtain chelation therapy for their child. They did not examine WTP to reduce risks of neurotoxicity to
* Correspondence to: Center for Risk Analysis, Harvard School of Public Health, 718 Huntington Ave., Boston, MA 02115, USA. Tel.: + 1 617 432 4497; fax: + 1 617 432 0190; e-mail: James –Hammitt@Harvard.edu
adults (which are much smaller than risks to children).
Several studies have used CV in USA popula-tions to estimate WTP to reduce one’s own minor illness [5 – 11]. These studies estimated values for 1-day avoidance of various symptoms between US$12 and US$154 (1993 dollars). Johnson et al. [12] combined five CV studies of short-term mor-bidity in a meta-analysis using the Quality of Well-Being (QWB) index to control for severity. They estimated WTP for avoiding 1 day of vari-ous symptoms as US$19 – 72. The only previvari-ous study for a developing country (Taiwan) is by Alberini et al. [13]. They estimated the median WTP to avoid recurrence of the average respon-dent’s most-recent episode of acute illness (5.3 days, 2.2 symptoms) as approximately US$40.
The remainder of the paper is organized as follows. The next section presents the survey method and data. The third introduces the empir-ical models and the fourth section presents the WTP estimates. The conclusion is in the last section.
DATA COLLECTION
The data were collected in a December 1995 in-person survey conducted in four areas repre-senting diverse regions of Taiwan: Metropolitan Taipei, Kaushung, Miaoli, and Yunlin. Taipei is the capital and largest city in Taiwan. It is located near the northern tip of the island. Kaushung and Miaoli are sites of major petrochemical com-plexes. Kaushung is a major industrial city in southwest Taiwan and Miaoli is in a northern rural area. Yunlin is located on the central west coast of the island and is relatively unpolluted. The sample is a stratified random sample. Pri-mary schools were randomly selected within each region and 700 of the 4500 students enrolled in these schools were randomly selected. Profession-ally trained interviewers went to the selected stu-dents’ homes to interview each student’s mother. Results from a focus group and two pretests confirmed that Taiwanese mothers are more knowledgeable about their children’s health than are fathers and are much more likely to be the one accompanying a child who visits a doctor. Inter-views were completed with 650 mothers. Deleting the observations with missing income and other socioeconomic variables leaves 598 observations that are used in the analysis.
The survey instrument includes questions on socioeconomic characteristics, health status, mother’s and child’s most recent colds, and valua-tion. Our hypothetical market good is prevention of one of the most common illnesses, a cold, which is easily understood by respondents. We asked each respondent to describe her own and her child’s most recent cold, including the dura-tion and symptoms experienced. The respondent was then asked to value prevention of a cold with the characteristics she had described. Alberini et
al. [13] used a similar approach. In contrast, most
previous studies have specified the symptoms to be valued [5,7,14,15]. The older approach may not account for averting behaviour (e.g. taking medicine to reduce symptom severity) and may pose double-counting problems when evaluating an illness that includes multiple symptoms.
After asking the respondent to describe her own and her child’s most recent cold, we asked her to value prevention of a similar cold. For her own illness, the following question was asked (the question for the child’s illness is similar):
When you get a cold, your loss includes: (1) in-creased medical expenditures, (2) spending time visit-ing the doctor or hospital, (3) poor workvisit-ing performance, (4) missing leisure time and daily activ-ities. We are now going to ask you a hypothetical question. Suppose you were told that, within the next few days, you would experience a recurrence of the cold episode you have described for us. Assume you can purchase a special preventive medicine to avoid getting this cold again. How much are you willing to pay for this medicine? Bear in mind if you purchase this medicine, you have to give up some other use of this money. For example, you may reduce your expenditures for recreation or education.
WTP was elicited using binary-choice ques-tions. Each respondent was randomly assigned to one of three initial WTP values (NT$300, 700 and 1000). (The 1995 exchange rate was 27.265 New Taiwanese dollars per US$.) Each respondent re-ceived the same initial bid for the mother and child questions. The use of a common initial bid limits the effect of any starting-point bias on the difference between values for the mother’s and child’s illness but risks anchoring the value for preventing the child’s illness on the value of pre-venting the mother’s illness. As in [13], two fol-low-up questions were asked yielding a triple-bounded binary-choice format. Adding a single follow-up to an initial dichotomous-choice ques-tion substantially improves statistical efficiency [16].
EMPIRICAL MODELS
WTP to avoid a cold is modelled as a linear function of the respondent’s characteristics and the severity of the cold. The model is estimated by the maximum-likelihood method under the as-sumption that WTP is lognormally distributed [17]. Alternative distributional assumptions (log-logistic, exponential, and Weibull) are rejected in favour of the log-normal distribution using a likelihood-ratio test.
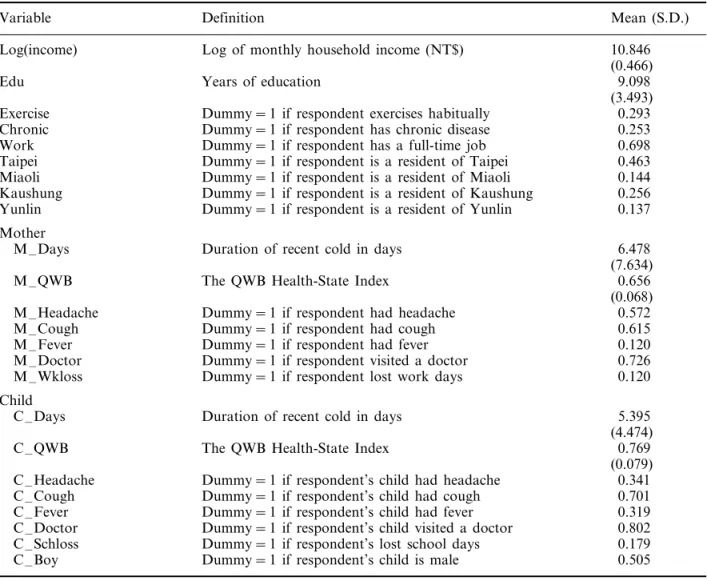
The explanatory variables are defined and sum-mary statistics reported in Table 1. Socioeco-nomic characteristics include income, education, and age. The effect of income is anticipated to be
positive. Education and age may also affect the respondent’s WTP for health, although the direc-tion of the effects is not apparent a priori.
Overall health status is represented by a dummy variable indicating whether the individual had a chronic disease (Chronic). Respondents with chronic disease are expected to exhibit higher WTP to avoid a cold if the marginal disutility of poor health is increasing [18]. Whether or not the respondent exercises habitually is represented as a dummy variable (Exercise). This variable may be interpreted as another indicator of health (health-ier people are more likely to exercise) or as a proxy for the respondent’s health preference (peo-ple with a stronger preference for health are more Table 1. Definitions of variables and basic statistics
Variable Definition Mean (S.D.)
10.846 Log(income) Log of monthly household income (NT$)
(0.466) Years of education
Edu 9.098
(3.493) 0.293 Dummy = 1 if respondent exercises habitually
Exercise
Dummy = 1 if respondent has chronic disease
Chronic 0.253
Work Dummy = 1 if respondent has a full-time job 0.698
0.463 Dummy = 1 if respondent is a resident of Taipei
Taipei
Miaoli Dummy = 1 if respondent is a resident of Miaoli 0.144 Dummy = 1 if respondent is a resident of Kaushung 0.256 Kaushung
Yunlin Dummy = 1 if respondent is a resident of Yunlin 0.137 Mother
M –Days Duration of recent cold in days 6.478
(7.634)
M –QWB The QWB Health-State Index 0.656
(0.068) Dummy = 1 if respondent had headache 0.572 M –Headache
M –Cough Dummy = 1 if respondent had cough 0.615
M –Fever Dummy = 1 if respondent had fever 0.120
M –Doctor Dummy = 1 if respondent visited a doctor 0.726
0.120 M –Wkloss Dummy = 1 if respondent lost work days
Child
Duration of recent cold in days 5.395
C –Days
(4.474) 0.769 The QWB Health-State Index
C –QWB
(0.079) 0.341 Dummy = 1 if respondent’s child had headache
C –Headache
C –Cough Dummy = 1 if respondent’s child had cough 0.701
0.319 C –Fever Dummy = 1 if respondent’s child had fever
C –Doctor Dummy = 1 if respondent’s child visited a doctor 0.802 Dummy = 1 if respondent’s lost school days
C –Schloss 0.179
C –Boy Dummy = 1 if respondent’s child is male 0.505
Note: S.D. values for dummy variables are omitted since they can be calculated from (m−m2)1/2, where m is the fraction in the
likely to exercise). Consequently, there is no pre-diction for the sign of its coefficient. The child’s sex is introduced in the child WTP equation to measure gender differences in the intrahousehold distribution of resources. Mothers may have dif-ferential preferences with respect to investments in boys and girls. Dummy variables for the respon-dent’s place of residence, Taipei, Kaushung, and Miaoli, are used to capture regional differences in preferences, the cost of living, and other factors.
WTP for symptom relief consists of two terms: the monetary cost and disutility of any actions taken to mitigate the illness and the disutility of illness after mitigation [19]. We include variables to represent each component in the regression. Because all respondents have national health in-surance which covers most of their medical ex-penses, expenditures do not vary greatly. As an alternative, a dummy variable indicating whether the respondent visited a doctor (Doctor) is used to represent mitigating behaviour.
The disutility of illness should increase with severity and duration. Duration is measured by (the logarithm of) the number of days of illness (LogM –days, LogC–days). Severity is measured by a dummy variable indicating whether the mother missed work or the child missed school (M –Wkloss and C–Schloss) and, alternatively, by dummy variables representing the occurrence of specified symptoms (headache, cough, fever) and by the QWB index (M –QWB, C–QWB). The QWB is a health-state index that rates the respon-dent’s health state from 0 to 1, where 0 represents death and 1 represents perfect health. This rating scale provides a simple technique for assigning numerical values to each symptom. To our knowl-edge, it has never been administered in a develop-ing country and so its validity in such countries is untested. We follow Johnson et al. [12] in using the community-based weights in Kaplan et al. [20] for our analysis. The QWB value is based on the symptoms reported in the questionnaire as the most serious. For example, QWB values are 0.743 for fever and mild cough, 0.682 for severe cough, 0.756 for headache, 0.83 for runny nose, and 0.769 for sinus congestion.
EMPIRICAL RESULTS
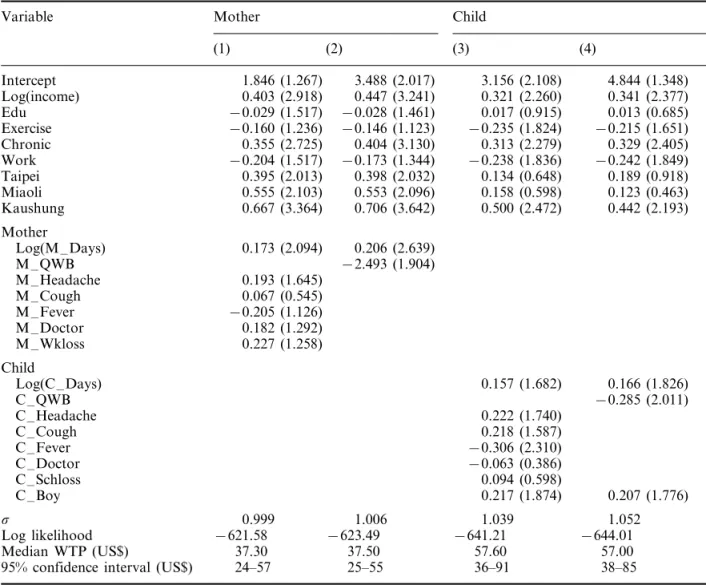
Regression estimates are reported in Table 2. As anticipated, the results indicate that WTP in-creases with the duration and severity of illness.
The coefficients of log duration, 0.173 – 0.206 for the mother and 0.157 – 0.166 for her child, suggest that the increase in WTP is much less than pro-portionate to the increase in duration. Both vari-ables are significantly different from zero (WTP increases with duration) and also from one (WTP is less than proportionate to duration). Other studies also find that WTP is less than propor-tionate to the duration of illness [5,7,13].
Severity of the illness is captured by several variables: whether the respondent missed work or her child missed school, whether she or her child went to the doctor, and alternatively dummy vari-ables for selected symptoms (headache, cough, and fever) in specifications (1) and (3) and the QWB index in specifications (2) and (4). The coefficients on work- and school-loss and doctor visits have the expected positive sign (except for the variable indicating the child was taken to the doctor) but are not significantly different from zero.
The signs of the estimated coefficients on the symptom variables are consistent between mother and child equations although most are not signifi-cantly different from zero. These estimates suggest that WTP increases with headache and cough and, contrary to expectation, decreases with fever. The coefficients of the QWB variables (M –QWB and C –QWB) are both negative and statistically significant, suggesting that QWB provides a useful measure of severity. Although the magnitudes of the coefficients on the symptom variables are similar in mother and child equations, the esti-mated coefficient on QWB is much larger for the mother than the child which suggests that the QWB is a more accurate indicator of severity for adults than for children.
To determine whether the effects of illness du-ration and severity on WTP differ between moth-er’s and child’s illness, we use a likelihood-ratio test for equality of the illness coefficients between comparable specifications. The x2 statistic for
comparing duration, symptom, doctor-visit and work- or school-loss coefficients in specifications (1) and (3) is 30.84 (six degrees of freedom). For comparing duration and QWB coefficients in specifications (2) and (4) the value is 30.31 (two degrees of freedom). Both values are much larger than the appropriate critical values so the hypoth-esis of parameter homogeneity in own and child WTP equations is rejected.
Table 2. Estimated WTP equations based on triple-bounded responses
Variable Mother Child
(1) (2) (3) (4) Intercept 1.846 (1.267) 3.488 (2.017) 3.156 (2.108) 4.844 (1.348) Log(income) 0.403 (2.918) 0.447 (3.241) 0.321 (2.260) 0.341 (2.377) Edu −0.029 (1.517) −0.028 (1.461) 0.017 (0.915) 0.013 (0.685) Exercise −0.160 (1.236) −0.146 (1.123) −0.235 (1.824) −0.215 (1.651) Chronic 0.355 (2.725) 0.404 (3.130) 0.313 (2.279) 0.329 (2.405) Work −0.204 (1.517) −0.173 (1.344) −0.238 (1.836) −0.242 (1.849) Taipei 0.395 (2.013) 0.398 (2.032) 0.134 (0.648) 0.189 (0.918) Miaoli 0.555 (2.103) 0.553 (2.096) 0.158 (0.598) 0.123 (0.463) Kaushung 0.667 (3.364) 0.706 (3.642) 0.500 (2.472) 0.442 (2.193) Mother Log(M –Days) 0.173 (2.094) 0.206 (2.639) M –QWB −2.493 (1.904) M –Headache 0.193 (1.645) M –Cough 0.067 (0.545) M –Fever −0.205 (1.126) M –Doctor 0.182 (1.292) M –Wkloss 0.227 (1.258) Child Log(C –Days) 0.157 (1.682) 0.166 (1.826) C –QWB −0.285 (2.011) C –Headache 0.222 (1.740) C –Cough 0.218 (1.587) C –Fever −0.306 (2.310) C –Doctor −0.063 (0.386) C –Schloss 0.094 (0.598) C –Boy 0.217 (1.874) 0.207 (1.776) s 0.999 1.006 1.039 1.052 Log likelihood −621.58 −623.49 −641.21 −644.01 Median WTP (US$) 37.30 37.50 57.60 57.00
95% confidence interval (US$) 24–57 25–55 36–91 38–85
Note: Absolute value of asymptotic t-statistics in parentheses. Dependent variable: log(WTP).
We next consider the effects of socioeconomic variables on WTP. Family income has the ex-pected positive sign and is significantly different from zero for all specifications. The estimated income elasticities are about 0.4 for mother her-self and 0.3 for her child. These elasticities are not significantly different from each other (the t-statistic for a difference between them is 0.59). Our elasticity estimates are comparable to previ-ous estimates. Loehman and De [14] found in-come elasticities of 0.3 for minor coughing and sneezing/eye irritation complex and 0.6 for severe shortness of breath. Alberini et al. [13] estimated that the income elasticity of WTP to avoid an acute illness episode is about 0.3. In contrast, Brien et al. [15] found that the effects of income
on WTP to avoid seven specified symptoms were very small or even negative, and not statistically significant.
None of the education coefficients are signifi-cantly different from zero. Turning to the health-status variables, the coefficients of Chronic are positive and statistically significant in all specifi-cations. Respondents with chronic disease have 37 – 50% higher WTP in both own and child equa-tions. Although we expect respondents with chronic disease to have higher WTP for them-selves, it is not clear that this preference should also be reflected in WTP to prevent their child’s illness unless it serves as an indicator of sympa-thy. The coefficient of the Exercise dummy is negative in all equations and significant in the
child equations. Habitual exercise reduces WTP to prevent the child’s illness by about 20%. The child’s sex dummy is statistically significant and indicates that mothers’ WTP is about 20% higher for a son than for a daughter. Perhaps reflecting cultural differences, this result differs from the finding that Brazilian mothers prefer to devote resources to improving the nutritional status of their daughters [21].
The regional dummy variables are statistically significant in the mother equations but only the Kaushung dummy is significant in the child equa-tions. The coefficients indicate that residents of Kaushung and Miaoli, the two locations with large petrochemical complexes, have higher WTP than those of the other two areas, Taipei and Yunlin.
WTP estimates
We calculate the median WTP for mother and child at the corresponding sample averages of the independent variables (i.e. the predicted WTP equals exp(x¯b.) where x¯ is the sample mean of the regressors and b. is the estimated coefficient vec-tor). As reported in Table 2, WTP to prevent a recurrence of the cold is about US$37 for the mother and US$57 for her child. These figures represent WTP to avoid a cold of 6.5 days (mother) or 5.4 days (child). The values exceed the corresponding mean out-of-pocket costs (US$20.11 and US$22.49, respectively), consistent with theory [22] and other empirical estimates [6,23].
The estimate for the mother’s illness is com-parable to the Alberini et al. [13] estimate for Taiwanese adults’ own WTP to avoid a similar illness episode, about US$40 for an average dura-tion of 5.3 days and 2.2 symptoms. The illness episodes valued in Alberini et al. [13] appear to be quite similar to the mother’s illness valued here. Sixty-nine percent of respondents in the previous study described their illness as a cold. Compared with the current study, the average duration of the episodes was slightly shorter (5.3 versus 6.5 days), a smaller fraction of respondents visited a doctor (54% versus 73%) or experienced headache (39% versus 57%), and a slightly larger fraction of respondents experienced fever (15% versus 12%).
The average mother’s illness is longer than the average child’s illness. Based on the QWB score, it
is also more severe. Adjusting for these differences yields an even larger difference in WTP. WTP to prevent a child’s illness as long and severe as the average mother’s illness is estimated as US$74.90 and US$70.50 using the symptom-specific and QWB equations (regressions (3) and (4)), respec-tively. These values are 1.9 – 2.0 times larger than the mother’s WTP to prevent her own illness. Conversely, the average mother’s WTP to prevent an illness as long and severe as the average child’s illness is estimated as US$29.40 and US$22.60 (using symptoms and QWB, regressions (1) and (2), respectively). WTP to prevent the child’s ill-ness is 2.0 – 2.5 times larger than these values. Both adjustments suggest that mother’s WTP to prevent her child from suffering a cold is about twice as large as her WTP to prevent herself from suffering a cold of comparable duration and severity.
The comparison of adjusted values using symp-tom-specific and QWB regressions suggests some consistency between these two methods of ac-counting for severity. Consistent with the larger estimated coefficient on QWB for the mother’s illness than the child’s, the adjustment of WTP to avoid the child’s illness is larger using the symp-tom-specific model and the adjustment for the mother’s illness is larger using the QWB model.
We test for the effect of starting-point bias on estimated WTP by adding dummy variables repre-senting the initial bid to specifications (1) and (3) (these models are not presented). Compared with our highest initial bid (NT$1000), we find no evidence of starting-point bias using our interme-diate initial bid (NT$700) but a statistically sig-nificant effect using our smallest initial bid (NT$300). The magnitude of the effect is modest: estimated WTP is about 25% smaller for both mother’s and child’s cold using the smallest rather than the largest initial bid. The estimated coeffi-cients and absolute t-statistics of the dummy vari-ables for the small and intermediate initial bids are − 0.317 (2.269) and − 0.003 (0.024) for the mother’s illness and − 0.277 (1.949) and − 0.077 (0.555) for her child’s illness.
CONCLUSION
Most previous CV studies of acute illness have used data for industrialized countries and have asked respondents to value a specified set of symptoms. Our study uses data from a developing
country and estimates values for an illness de-scribed by the respondent. The illness we value — a cold — is one of the most familiar acute illnesses and is presumably relatively easy for a respondent to recall.
Our results are consistent with the expected increasing disutility of illness: respondents express higher WTP to avoid an illness of greater dura-tion or severity as measured by symptoms or the QWB index. The regression analysis suggests a strong relationship between family income, health status, and WTP. The average mother’s WTP for her child is higher than for herself. Median esti-mates of the mother’s WTP to avoid a recurrence of the average cold are US$37 for herself and US$57 for her child; adjusting for differences in average duration and severity yields an even larger difference. We also find evidence of gender preference: mothers are willing to devote more resources to the health of their sons than their daughters. These measures of health values provide a foundation for evaluating public health or environmental regulations that may influence the prevalence of minor morbidity in a developing country.
ACKNOWLEDGEMENTS
The authors thank the Survey Research Office of Academia Sinica for assistance with data collection and the referees for helpful comments. This work was supported by the Taiwan Environmental Protection Agency under grant number EPA-84-1401-09-30.
REFERENCES
1. Becker G. Altruism in the family and selfishness in the market. Economica 1981; 48: 1 – 15.
2. Johansson P-O. Altruism and the value of statisti-cal life: empiristatisti-cal implications. J Health Econ 1994;
13: 111 – 118.
3. Viscusi WK, Magat WA, Huber J. An investigation of the rationality of consumer valuations of multi-ple health risks. RAND J Econ 1987; 18: 465 – 479. 4. Agee DM, Crocker TD. Parental altruism and child lead exposure: inferences from the demand for chelation therapy. J Human Resources 1996; 31: 677 – 691.
5. Loehman ET, Berg SV, Arroyo AA, Hedinger RA, Schwartz JM, Shaw ME, Fahien RW, De VH, Fishe RP, Rio DE, Rossley WF, Green AES.
Dis-tributional analysis of regional benefits and cost of air quality control. J En6iron Econ Manage 1979; 6: 222 – 243.
6. Rowe RD, Chestnut LG. Oxidants and asthmatics in Los Angeles: a benefits analysis, 1985. Final Report for US EPA. Document No. EPA-230-7-85-010.
7. Tolley G, Babcock L, Berger M, Bilotti A, Blomquist G, Brien M, Fabian R, Fishelson G, Kahn C, Kelly A, Kenkel D, Krumm R, Miller T, Ohsfeldt R, Rosen S, Webb W, Wilson W, Zelder M. Valuation of reductions in human health symp-toms and risk. In Contingent Valuation Study of Light Symptoms and Angina, 1986; 3. Final Report for US EPA.
8. Dickie M, Gerking S, Brookshire D, Coursey D, Schulze W, Coulson A, Tashkin D. Reconciling averting behavior and contingent valuation benefit estimates of reducing symptoms of ozone exposure. In Impro6ing Accuracy and Reducing Costs of En6i-ronmental Benefit Assessment. US EnviEn6i-ronmental Protection Agency: Washington, DC, 1987. 9. Chestnut LG, Colome SD, Keller LR, Lambert
WE, Ostro B, Rowe RD, Wojciechowski SL. Heart disease patients’ averting behavior, costs of illness, and willingness to pay to avoid angina episodes, 1988. Final Report for US Environmental Protec-tion Agency. Document No. EPA-230-10-88-042. 10. Gerking S, de Haan M, Schulze W. The marginal
value of job safety: a contingent valuation study. J Risk Uncertainty 1988; 1: 185 – 199.
11. Tolley G, Kenkel D, Fabian R. State-of-the-art health values. In Valuing Health for Policy: An Economic Approach, Tolley G, Kenkel D, Fabian R (eds). University of Chicago Press: Chicago, 1994; 167 – 190.
12. Johnson FR, Fries EE, Banzhaf HS. Valuing mor-bidity: an integration of the willingness-to-pay and health-status index literatures. J Health Econ 1997;
16: 641 – 665.
13. Alberini A, Cropper M, Fu T-T, Krupnick A, Liu J-T, Shaw D, Harrington W. What is the value of reduced morbidity in Taiwan? In The Economics of Pollution Control in the Asia Pacific, Mendelsohn R, Shaw D (eds). Edward Elgar Publishing: Cheltenham, UK, 1996; 108 – 149.
14. Loehman E, De VH. Application of stochastic choice modeling to policy analysis of public goods: a case study of air quality improvements. Re6 Econ Stat 1982; 64: 474 – 480.
15. Brien M, Kenkel D, Kelly A, Fabian R. Empirical results from household personal interviews. In Valuing Health for Policy: An Economic Approach, Tolley G, Kenkel D, Fabian R (eds). University of Chicago Press: Chicago, 1994; 167 – 190.
16. Hanemann M, Loomis J, Kanninen B. Statistical efficiency of double-bounded dichotomous choice contingent valuation. Am J Agric Econ 1991; 73: 1255 – 1263.
17. Alberini A. Efficiency vs bias of willingness-to-pay estimates: bivariate and interval-data models. J En-6iron Econ Manage 1995; 29: 169–180.
18. Grossman M. On the concept of health capital and the demand for health. J Politic Econ 1972; 80: 223 – 255.
19. Cropper ML, Freeman AM. III. Environmental health conditions. In Measuring the Demand for En6ironmental Quality, Braden JB, Kolstad CD (eds). North Holland: Amsterdam, 1991.
20. Kaplan RM, Anderson JP, Ganiats TG. The qual-ity of well-being scale: rationale for a single qualqual-ity of life index. In Quality of Life Assessment: Key
Issues in the1990s, Walker SR, Rosser RM (eds). Kluwer Academic Publishers: Dordrecht, 1993. 21. Thomas D. Intra-household resource allocation: an
inferential approach. J Human Resources 1990; 25: 635 – 664.
22. Harrington W, Portney P. Valuing the benefits of health and safety regulation. J Urban Econ 1987;
22: 101 – 112.
23. Kenkel D, Berger M, Blomquist G. Contingent valuation of health. In Valuing Health for Policy: An Economic Approach, Tolley G, Kenkel D, Fa-bian R (eds). University of Chicago Press: Chicago, 1994; 72 – 104.