植基於群體廣播橢圓曲線系統

全文

(1)A Multicasting System based on the Elliptic Curve Cryptosystem Ming-Chang Wu1. Tzer-Shyong Chen2. Institute of Electrical Engineering,. Department of Information Management,. National Chung Cheng University. Tunghai University. WMC@wireless.ee.ccu.edu.tw. arden@mail.thu.edu.tw. Jun-Lin Liu. 3. Jyh-Horng Wen4. Computer & Communications Research Lab, Industrial Technologies Research Institute. Institute of Electrical Engineering, National Chung Cheng University. jun-lin@itri.org.tw. wen@ee.ccu.edu.tw . 2000, the usage of secure filter in the multicasting system to solve its security problems and ensure the safety of the group key. This is described in details below.. Abstract With the growth of Internet technology and its popularization, numerous users can share a single package in the multicasting system, making networking more efficient and also reduces the bandwidth. The system is, however, constructed by different groups, making secret sharing complex. Therefore, the construction of a secure multicasting system through the use of information security protocol is an important topic of discussion.. The secure filter is built on a polynomial x with restrictions GF ( p) , where p is a public natural prime number. If S = {k1 , k2 , K , kn } is the set of the secret keys of all the members in the group, while gk is the group key, and the tuple of S , and gk , are all contained in the integer Zp , then the CA shall first retrieve the hash function from the secret keys of all the members of the group, and then construct the secure filter as:. All members under the same multicasting system share a group key. Therefore, all broadcasted messages can be enciphered and deciphered using this key. Consequently, only legitimate members have access to the messages. However, if any member were to join or leave the group, the group key must be changed to ensure environment security. Thus, the security of the multicasting system is absolutely dependent on the security of the group key. It is also the biggest problem in the construction of a secure multicasting system.. SF ( x) = ( x − h(k1 ))( x − h(k2 ))L ( x − h(kn )) + gk. L (1). in which h is a randomly selected one-way hash function. From the secure filter polynomial SF ( x) , it is known that when ki ∈ S , SF (h(ki )) = gk . This means that the group members can enter their secret key ki , and through the processing of the secure filter, retrieve the group key gk ; as for the non-multicasting members, because of their inability to make ( x − h(ki )) of the secure filter polynomial SF ( x) zero, are unable to obtain the group key gk . Besides, for safety reasons, when sending the secure filter polynomial SF ( x) through the internet, the polynomial can be send in the expanded form an x n + an −1 x n −1 + L + a1 x + a0 . Thus avoiding the risk of having non-multicasting members directly using the secure filter polynomial SF ( x). Kuen-Pin Wu proposed the use of the secure filter method to solve the security problems of the system, but it was still lacking. We shall, however, use the elliptic curve to construct a new framework to solve this problem and then compared it with the secure filter. Keywords: Multicasting, elliptic curve cryptosystem, access control, secure filter, group key. I. An Introduction to Kuen-Pin Wu’s proposal Kuen-Pin Wu [1] proposed in the year 1.

(2) then could y 2 = x3 + ax + b mod p , be used as the decrypting elliptic curve [2].. to retrieve the group key gk . When there is a change in the members of the multicasting system, the following operations are performed:. Before we introduce the addition operation of the elliptic curve [3-5], we need to first introduce a special point O, known as the point of infinity and it satisfies the following properties:. 1. When a new member joins the multicasting system. 1. If P, Q are two points on the elliptic curve, O is the point of infinity, then P ＋O＝O+P=P. 2. O＝-O. 3. If Q is not equal to point (-P), then P＋ Q＝O. 4. If P≠O, Q≠O, then P＋Q＝-R.. Suppose the secret key of user un +1 is kn +1 , then, kn +1 is a tuple in the set of the secret keys S ′ of the new members. When user un +1 joins the multicasting system, the CA has to change to a new group key gk ' in order to construct a new secure filter polynomial as:. According to the addition operation of the elliptic curve, if there are two points P = ( x1 , y1 ) and Q = ( x2 , y2 ) on the elliptic curve, and if P≠-Q, then P + Q = ( x3 , y3 ) ,. SF '( x) = ( x − h(k1 ))( x − h(k2 ))L ( x − h(kn )) ( x − h(kn +1 )) + gk ' L (2). The CA shall then send SF '( x) and the one-way hash function h to the group members. The group members on receiving SF '( x) , shall enter their secret keys ki , 1 ≤ i ≤ n + 1 , and through the processing of SF '( x) , obtain the group key gk ' . Non-members are unable to obtain a message through decryption.. x3 = λ 2 − x1 − x2 mod m. ，. y3 = λ ( x1 − x3 ) − y1 mod m , where  y2 − y1 x −x  2 1 λ= 2  3 x1 + a  2 y1. 2. When a member leaves the multicasting system. , if P ≠ Q , if P = Q. If there is a point G on the elliptic curve, and this point is the base point, then the operation on nG has the following properties, 1G=G, 2G=G ＋ G, 3G=G ＋ G ＋ G=2G ＋ G, ... , (n-1)G=G＋G+ ... ＋G with a total of (n-1) G, nG=O, (n＋1)G=G. Thus the nG is n×G formal, meaning addition operations of the elliptic curve, and not the general multiplication operation, are continuously performed on n number of G’s. Suppose that user ul has secret key kl , 1 ≤ l ≤ n , then kl is a tuple of the multicasting member’s secret key set S . When the user ul leaves the multicasting system, the CA has to change to a new group key gk " in order to construct a new secure filter polynomial as: SF ′′( x) = [( x − h(k1 ))( x − h(k2 ))L. For example: A, B both have chosen to use the elliptic curve y 2 = x3 + x + 6 for communip as 11, then cating, taking. ( x − h(kn ))] /( x − h(kl )) + gk ′′ L (3). The CA shall then send SF "( x) and the one-way hash function h to the group members. The members on receiving SF "(ki ) , shall enter their secret keys ki , ki ∈ S − kl , and through the processing of SF″(h( ki )), obtain the group key gk " . Non-members are unable to obtain the message through decryption.. D = 4a 3 + 27b 2 mod11 = 8 mod11 ≠ 0 , hence it is. proved that the points on the elliptic curve are (2, 4), (2, 7), (3, 5), (3, 6), (5, 2), (5, 9), (7, 2), (7, 9), (8, 3), (8, 8), (10, 2), (10, 9). If A, B both chose the point (2, 7) as G (Generator point), and performs the addition operation of the elliptic curve, then G=(2, 7), 2G=G＋G=(5, 2), 3G=2G ＋G=(8, 3), 4G=(10, 2), 5G=(3, 6), 6G=(7, 9), 7G=(7, 2), 8G=(3, 5), 9G=(10, 9), 10G=(8, 8), 11G=(5, 9), 12G=(2, 4), 13G=O, 14G=(2, 7).. II. An Introduction to the Elliptic Curve Cryptosystem. III. The Multicasting Secure Filter System. The general equation for the elliptic curve is y = x3 + ax + b mod p , p is a natural prime number, and the value of a, b should satisfy the discriminant D = 4a 3 + 27b 2 ≠ 0 mod p . Only 2. 1. The construction of the multicasting secure filter system 2.

(3) Step. l:. On. the. elliptic. curve. members on receiving ECF '( x) , shall enter their secret keys ki , 1 ≤ i ≤ n + 1 , and through the processing of ECF ′( f (ki G′)) , obtain the group. y 2 = x3 + ax + b mod p , select a point G. that. satisfies. the. D = 4a 3 + 27b 2 ≠ 0 mod p condition as the. key gk ' . Non-members are unable to obtain a message through decryption.. base point. Step 2: p is a public natural prime number,. 2. The departure of members from the system. while S = {k1 , k2 , K , kn } is a set of the secret keys of all the group member, gk is the group key, and the tuple of S , and gk , are all contained in the integer Zp , then the multicasting elliptic curve secure filter system constructed by the CA shall be:. Suppose that user ul has secret key kl , 1 ≤ l ≤ n , then kl is a tuple of the multicasting. member’s secret key set S . When the user ul leaves the multicasting system, the CA has to change to a new group key gk " in order to construct a new secure filter polynomial as: ECF "( x) = ( x − f (k1G "))( x − f (k2 G "))L. ECF ( x) = ( x − f (k1G ))( x − f (k2 G ))L. ( x − f (kn G ")) /( x − f (kl G ")) + gk "mod p L (6). ( x − f (kn G )) + gk mod p L (4). The CA shall then send ECF "( x) and G " to the group members. The members on receiving ECF "( x) , shall enter their secret keys ki , ki ∈ S − kl , and through the processing of ECF ′′( f (ki G′′)) , obtain the group key gk " . Non-members are unable to obtain the message through decryption.. where ki G = ( xi , yi ) and f (ki G ) is xi ⊕ yi ，for safety reasons, when sending the secure filter polynomial ECF ( x) through the internet, the polynomial can be send in the expanded form, an x n + an −1 x n −1 + L + a1 x + a0 . Step 3: The CA shall then send ECF ( x) and point G , to the group members.. V. Security Analysis. 2. The retrieval of the group key gk by the group members. (i) There are two security drawbacks in Wu’s proposal. On receiving ECF ( x) , the group members shall each enter their secret keys ki , and through the processing of ECF ( f (ki G )) , ki ∈ S , obtain the group key gk , and retrieve the message through decryption. Non-members are unable to perform the above operations.. 1. Drawback 1 If the multicasting system has only two members, then the secure filter polynomial shall be: SF ( x) = ( x − h(k1 ))( x − h(k2 )) + gk mod p L (7). Member u1 can use his secret key k1 to enter the secure filter polynomial SF ( x) and obtain the group key gk , and then calculate h(k2 ) = [ SF (0) − gk ] / h(k1 ) . When member u1 leaves the system, as long as u2 is still a member, the departing member u1 can obtain the group key gk ' through the new secure filter polynomial. IV. The entrance and the departure of members in the system 1. The entrance of new members into the system Suppose the secret key of user un +1 is kn +1 , then, kn +1 is a tuple in the set of the secret keys S ' of the new members. When user un +1 joins the multicasting system, the CA has to change to a new group key gk ' in order to construct a new secure filter polynomial:. SF '( x) = ( x − h(k2 ))L ( x − h(kn )) + gk '. L (8). Hence, the secure filter polynomial system becomes unsafe. 2. Drawback 2. ECF '( x) = ( x − f (k1G '))( x − f (k2 G '))L. If among the n system members, n − 1 members conspire, by taking x = 0 , they shall be able to obtain from the secure filter polynomial,. ( x − f (kn G '))( x − f (kn +1G ')) + gk ' mod p L (5). The CA shall then send ECF '( x) and point G ' to the group members. The group 3.

(4) SF (0) = (h(k1 ))(h(k2 ))L (h(kn )) + gk L (9). SF "(0) = (h(k1 ))(h(k2 ))L (h(kn ))(h(k s )). + gk " L (14). The n − 1 members can use their secret key ki to enter the secure filter polynomial (1) and obtain the group key gk , and then calculate. From the n − 1 members, a member can enter his secret key ki into the secure filter polynomial (13) and obtain the group key gk " and then calculate:. h(ki ) = [ SF (0) − gk ] /[(h(k1 )(h(k2 )L (h(kn ) / h(ki )]. L (10). h(ki )h(k s ) = [ SF (0) − gk ] /[(h(k1 )(h(k2 )L. Thus, they shall be able to know the h(ki ) , of the remaining member. When the conspiring members leaves the system, as long as ui is still a member of the new system, any of the conspiring members or any non-members who knows the message, can obtain the group key gk " through the new secure filter polynomial,. (h(kn ) / h(ki )h(k s )] L (15). From h(ki )h(k s ) , because the virtual member’s h(ks ) is unknown, the h(ki ) , of the remaining member cannot be obtained. Therefore non-new members are unable to retrieve the group key gk " from the new secure filter polynomial SF "( x) .. SF "( x) = ( x − h(k1 ))( x − h(k2 ))L ( x − h(ki ))L ( x − h(kn )) + gk ". mod p. L (11). 3. The third method Use the multicasting elliptic curve cryptosystem to construct a new multicasting elliptic curve secure filter polynomial:. Hence, the secure filter polynomial system becomes unsafe. (ii) Reform Strategy. ECF '( x) = ( x − f (k1G '))( x − f (k2 G '))L. 1. The first method. ( x − f (kn G ')) + gk ' mod p L (16). When there is entrance of new members or departure of members, at the time of constructing a new secure filter polynomial, the one-way hash function h should be changed to h ' , and h ' becomes the new one-way hash function. Thus, the new secure filter polynomial becomes:. When there are entrance or exit of members from the group, although the attackers, can obtain ECF (0) and the group key, gk , but for the obtained f (ki G ) , because ECF ( x) has already been changed to ECF '( x) , and G to G ' , the attacker is unable to log in through ECF '( x) and obtain the group key gk ' .. SF '( x) = ( x − h '(k1 ))( x − h '(k2 ))L ( x − h '(kn )) + gk '. L (12). We summarize Wu′s method and comparison of the security of the proposal in the table 1.. Since the new one-way hash function h of the new secure filter polynomial isn’t the h of the former secure filter polynomial, non-members of the new system are unable to decode the new polynomial and obtain the new group key gk ' .. VI. Improvement on Operation speed When there is entrance or departure of members from the system, the CA will need to construct a new secure filter polynomial, causing a huge operation overload and slow operation speed, which in turn, consumes a lot of time. Hence, a group-division method has been proposed in order to save computation time and reduce computation load, by dividing all the group members into sub-groups, forming unequal sub-groups; each of these sub-groups shall have their own secure filter polynomial as well as different group keys.. 2. The second method When there is entrance of new members or departure of members, at the time of constructing a new secure filter polynomial, a virtual member can be added to the group, with secret key as ks , and secure filter polynomial as SF "( x) = ( x − h(k1 ))( x − h(k2 ))L ( x − h(kn )) ( x − h(ks )) + gk " L (13). where ks is a random number contained in the integer Zp . If in the new polynomial, the group has n members, and there are n − 1 members conspiring, although they can, from the secure filter polynomial (13), make x = 0 , and obtain:. Suppose that the system has n members, these members can be divided into m subgroups, and each subgroup shall have different group keys sgk1 , sgk2 , K , sgkm , if 4.

(5) S = {k1 , k2 , K , kn } is the set of secret keys of all the members, and gk is the group key, then the CA can build the secure filter polynomial in accordance to the different subgroups as:. parent-group’s group key gk . When a member ni leaves the system, the CA shall first find out which subgroup sgi , 1 ≤ i ≤ m , the departing member belonged to, and then change the Gi of that subgroup to Gi ' and the new group key to sgki ' , and then construct a new secure filter polynomial ECFi '( x) , 1 ≤ i ≤ m + 1 . Like in the above example, member n2 of subgroup sg1 has left the system. The CA shall then build the secure filter polynomial in accordance to the different subgroups as:. ECF1 (x) = (x − f (k1G1 ))(x − f (k2G1 ))L(x − f (kn / mG1 )). + sgk1 mod p1 ECF2 (x) = (x − f (kn / m +1G2 ))L(x − f (k2n / mG2 )). + sgk2. mod p2. L(17). M M ECFm (x) = (x − f (k(m−1)n / m +1Gm ))L(x − f (knGm )). + sgkm. mod pm. ECF1 '( x) = ( x − f (k1G1 '))( x − f (k3G1 ')). ECFm+1 (x) = (x − f (sgk1Gm+1 ))(x − f (sgk2Gm+1 ))L. + sgk1' mod p1. (x − f (sgkmGm+1 )) + gk mod pm+1. ECF2 ( x) = ( x − f (k4 G2 ))( x − f (k5 G2 )) ( x − f (k6 G2 )) + sgk2 mod p2 L (19). In the equation, pi is a heterogeneous prime number, Gi satisfies a base point on the elliptic curve E p i (ai , bi ) , where 1 ≤ i ≤ m + 1 .. ECF3 ( x) = ( x − f (k7 G3 ))( x − f (k8 G3 )) ( x − f (k9 G3 )) + sgk3 mod p3 ECF4 '( x) = ( x − f ( sgk1 ' G4 '))( x − f ( sgk2 G4 ')). The CA shall then send the different subgroup’s secure filter polynomial ECFi ( x ) and Gi , 1 ≤ i ≤ m + 1 , to the members of the subgroups. Each subgroup members on receiving ECFi ( x ) and Gi , 1 ≤ i ≤ m + 1 , can enter their subgroup keys sgki , 1 ≤ i ≤ m and obtain the parent-group’s group key gk . For example, if there are a total of nine group members, n1 , n2 , K ,n9 , and S = {k1 , k2 , K, k9 } is the set of secret keys of the group members, if the group is divided into subgroups sg1 , sg 2 , sg3 , where n1 , n2 , n3 belong to sg1 , n4 , n5 , n6 belong to sg 2 , n7 , n8 , n9 belong to sg3 , then the CA can build the secure filter polynomial in accordance to the different subgroups as:. ( x − f ( sgk3G4 ')) + gk ' mod p4. The CA shall send the different new secure filter polynomials ECFi '( x) and Gi ' , i = {1, 4} , to the their subgroups. Each member of the subgroup can enter their secret key and obtain the parent-group’s group key gk '. When a new member un +1 joins the system, the CA shall put the new member in one of the subgroups sgi , 1 ≤ i ≤ m , then change the Gi of that subgroup to Gi " and the subgroup key to sgki " , in order to build a new subgroup secure filter polynomial ECFi "( x) . Like in the above example, user u10 is a new member, if the subgroup he’d been put into is sg 2 ，then the CA shall build the secure filter polynomial in accordance to the different subgroups as:. ECF1 ( x) = ( x − f (k1G1 ))( x − f (k2 G1 )) ( x − f (k3G1 )) + sgk1 mod p1. ECF1 ( x) = ( x − f (k1G1 ))( x − f (k2G1 ))( x − f (k3G1 )). ECF2 ( x) = ( x − f (k4 G2 ))( x − f (k5G2 )). + sgk1 mod p1. ( x − f (k6 G2 )) + sgk2 mod p2 L (18). L(20). ECF2 "( x) = ( x − f (k4G2 "))( x − f (k5G2 ")). ECF3 ( x) = ( x − f (k7 G3 ))( x − f (k8G3 )). ( x − f (k6G2 "))( x − f (k10G2 ")) + sgk2" mod p2. ( x − f (k9 G3 ) + sgk3 mod p3. ECF3 ( x) = ( x − f (k7 G3 ))( x − f (k8G3 ))( x − f (k9G3 )). ECF4 ( x) = ( x − f ( sgk1G4 ))( x − f ( sgk2 G4 )). + sgk3 mod p3. ( x − f ( sgk3G4 )) + k mod p4. ECF4 "( x) = ( x − f (sgk1G4 "))( x − f (sgk2 "G4 ")) ( x − f (sgk3G4 ")) + gk " mod p4. The CA shall send the different subgroup’s secure filter polynomial ECFi ( x) and Gi , i = {1, 2,3, 4} , to each of the subgroup members. The subgroup members can then enter their secret keys sgki , i = {1, 2,3} and obtain the. The CA shall send the different group’s new secure filter polynomial ECFi "( x) and Gi " , i = {2, 4} , to the different members. Each member can enter their secret key and obtain the 5.

(6) SF '( x ) = ( x − h ( k1 ))( x − h ( k 2 )) L. parent group’s group key gk " .. ( x − h ( k n ))( x − h ( k n +1 )) + gk '. VII. A probe into the Operating time. The required computation time is (n+1) TH +n TMUL；. Comparison of time complexity:. ECF '( x) = ( x − f (k1G '))( x − f (k2G '))L. 1. Parameter definitions. ( x − f (knG '))( x − f (kn+1G ')) + gk ' mod p. (1). TMUL : the time required to perform a 1024 bit multiplication operation. (2). TADD : the time required to perform a 1024 bit addition operation. (3). TSUB : the time required to perform a 1024 bit subtraction operation. (4). TH : the time required to perform a 160 bit hash function operation. (5). TEC-MUL: the time required to perform a 160 bit elliptic curve multiplication operation. (6). x − f (ki Gi ) sets all as 160 bits using the elliptic curve related parameters (7). TADD、TSUB and XOR: No time complexity calculation is done on this. From references [6], it is known that (8). TEC-MUL≈29 TMUL.. The required (30n+29)TMUL.. time. is. (4). The retrieval of the new group key: gk ′ = SF ′(h(ki )), 1 ≤ i ≤ n + 1 ；. The required computation time of each member is 2TH, then the required computation time for all members will be 2(n+1)TH, gk ' = ECF '( f (ki G ')) , 1 ≤ i ≤ n + 1 ;. The required computation time of each member is 58 TMUL, then, the required computation time for all members will be 58 (n+1) TMUL. The analysis of the production of the group key and time complexity of SF ( x) and ECF ( x) are listed in table 2.. 2. Analysis of the polynomial operating time of Wu’s polynomial SF ( x) and the polynomial ECF ( x) used herein. 3. Comparison of the operating speeds before and after the improvements. (1). The production of the polynomials SF ( x) and ECF ( x) :. (1). The mial ECF ( x) :. SF ( x) = ( x − h(k1 ))( x − h(k2 ))L ( x − h(kn )) + gk. computation. production. of. the. polyno-. ECF ( x) = ( x − f (k1G ))( x − f (k2 G ))L. mod p. ( x − f (kn G )) + gk mod p. The required computation time is n TH + (n-1) TMUL;. The time required before the improvement of the operating speed is (30n-1)TMUL. ECF ( x) = ( x − f (k1G ))( x − f (k2 G ))L. ECF1 ( x) = ( x − f (k1G1 ))( x − f (k2G1 ))L. ( x − f (kn G )) + gk mod p. ( x − f (kn / m G1 )) + sgk1 mod p1. The required computation time is (30n-1). ECF2 ( x) = ( x − f (kn / m +1G2 ))L( x − f (k2n / m G2 )). TMUL.. + sgk2. (2). The retrieval of the group key:. mod p2. M M ECFm ( x) = ( x − f (k(m−1) n / m +1Gm ))L( x − f (knGm )). gk = SF ( h ( ki )), 1 ≤ i ≤ n The required computation time of each member is 2 TH, then the required computation time for all members will be 2n TH,. + sgkm. mod pm. ECFm+1 ( x) = ( x − f (sgk1Gm+1 ))( x − f (sgk2Gm+1 ))L ( x − f (sgkmGm+1 )) + gk mod pm+1. gk = ECF ( f (ki G )) , 1 ≤ i ≤ n ;. The required computation time of each member is 58TMUL, then, the required computation time for all members will be 58n TMUL.. After improvements were made, the time required became (30n+29m-1)TMUL, the time difference is -(29m)TMUL.. (3). The production of polynomials SF ( x) and ECF ( x) on the entrance of new members:. (2). Retrieval of the group key: gk = ECF ( f (ki G )). Before improvement, the time requirement 6.

(7) been made herein with regard to the production of group keys and retrieval of group keys. The results are listed in table 3.. for each member was 58TMUL, and that for all members was 58n TMUL: gk = ECFm +1 ( f ( sgki Gm +1 )). VIII. Conclusion. After improvements were made, the time requirement for a single member became 58TMUL, and that for all members is now 58m TMUL, the time difference is 58(n-m) TMUL.. Three solutions were presented with regard to the security problem in Wu’s proposal. The first solution was to change the hash function from h to h ' , h ' is the new one-way hash function, to construct a new secure filter polynomial. The second solution was to add a virtual new member to the group at the time of the construction of a new secure filter polynomial. The third was to use the elliptic curve encryption method to build the new polynomial ECF ( x) . The difference in the above methods being, the changing to h ' which will ensure the security, and that attackers will not be able to crack it. Besides this, there is the subgroup method, which saves on time and computation load to improve operating speed and increase efficiency.. (3). The production of polynomial ECF ( x) on the entrance of new members: ECF '( x ) = ( x − f ( k1G '))( x − f ( k2 G ')) L ( x − f ( k n G '))( x − f ( k n +1G ')) + gk ' mod p. Before improvement, the time requirement was (30n+29)TMUL.. ECFm '( x) = ( x − f (k( m −1) n / m +1Gm '))L . . ( x − f (kn Gm '))( x − f (kn +1Gm ')) + sgkm ' mod pm ECFm +1 '( x) = ( x − f (sgk1Gm +1 '))( x − f (sgk2Gm +1 ')) L( x − f (sgkm ' Gm +1 ')) + gk 'mod pm +1 After improvement, the time required be-. References. came: y=(n+1)-[(m-1)  n / m  +1]+1= (n+1)-(m-1)  n / m  ， Taking. [1]. Kuen-Pin Wu, Shanq-Jang Ruan, Feipei Lai and Chih-Kuang Tseng, “On Key Distribution in Secure Multicasting,” Proceedings 25th annual IEEE Conference on Local Computer Networks, pp. 208-212, 2000.. [2]. Alferd J. Menezes, “Elliptic Curve Public Key Cryptosystem,” Anburn, pp.19-21, 1997.. [3]. Anthong-w.knapp, “Elliptic Curve,” Princeton University Prece, pp. 67-74, 1992.. [4]. Joseph H. Silverman, John Tate, “Rational Points on Elliptic Curves,” Springer-Verlag New York, pp. 28-32, 1992.. [5]. Joseph H. Silverman, “The Arithmetic of Elliptic Curves,” Springer-Verlag new work , pp. 55-63,1986.. [6]. N. Koblitz, A. Menezes and S. Vanstone, “The State of Elliptic Curve Cryptography,” Design, Codes and Cryptography, Vol.19, pp. 173-193, 2000.. Y= y+m=(n+m+1)-(m-1)  n / m  [30(Y)-2] TMUL； After improvement, the time required became {-30[(m+1)+(m-1)  n / m  ]+31}TMUL. (4). The retrieval of the new group key: gk ' = ECF '( f (ki G ')). Before improvement, the time requirement for a single member was 58TMUL, and that for all members was 58(n+1)TMUL: gk ' = ECF 'm +1 ( f ( sgki Gm +1 ')). After improvement, the time requirement for a single member became58TMUL, and that for all members is now 58m TMUL, so the time difference is 58(n-m+1)TMUL. We can deduce from the above analysis and examples that computing only a portion takes a lot less time than computing the whole thing. At the same time, the greater the number of subgroups, the more the computation time saved. Hence, effective improvement has indeed. 7.

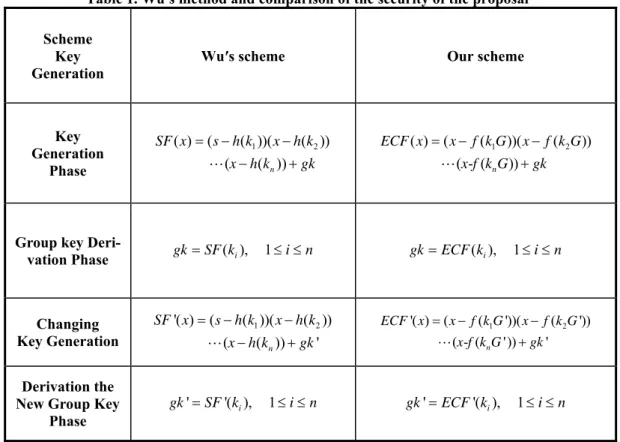
(8) Table 1. Wu′s method and comparison of the security of the proposal Scheme Key Generation. Key Generation Phase. Group key Derivation Phase. Changing Key Generation Derivation the New Group Key Phase. Wu′s scheme. Our scheme. SF ( x) = ( s − h(k1 ))( x − h(k2 )). ECF ( x) = ( x − f (k1G ))( x − f ( k2 G )) L (x-f (kn G )) + gk. L (x − h(kn )) + gk. gk = SF (ki ),. 1≤ i ≤ n. gk = ECF (ki ),. SF '( x) = ( s − h(k1 ))( x − h(k2 )). ECF '( x) = ( x − f (k1G '))( x − f (k2 G ')). L (x − h(kn )) + gk ' gk ' = SF '(ki ),. 1≤ i ≤ n. L (x-f (kn G ')) + gk '. 1≤ i ≤ n. gk ' = ECF '(ki ),. 1≤ i ≤ n. Table 2. The analysis of the production of the group key and time complexity of SF ( x) and ECF ( x) Scheme Wu′s scheme. Key Generation. Our scheme. The production of polynomials SF ( x) and ECF ( x). n TH+(n-1) TMUL. (30 n -1)TMUL. Retrieving of the group key. 2 n TH. 58 n TMUL. Production of polynomials SF ( x) and ECF ( x) at the time of addition of new members. (n +1) TH + n TMUL. (30 n +29) TMUL. The retrieving of the new group key. 2(n +1) TH. 58(n +1) TMUL. 8.

(9) Table 3. Comparison of time complexity in relation to the production and retrieval of group keys before and after the improvement were made herein. Scheme. The time difference after the improvement of operation speed. Key Generation. The production of the polynomial ECF ( x). -(29m) TMUL. The retrieving of the group key. 58(n-m) TMUL. The production of the polynomial ECF ( x). {-30[(m+1)+(m-1)  n / m  ]+31} TMUL. at the time of addition of new members. 58(n-m +1) TMUL. The retrieving of the new group key. 9.

(10)