H-Bridge Buck-Boost Converter with Dual Feedforward Control
Abstract -- This paper presents a new control method for H- bridge buck-boost converter regulated by single voltage feedback and dual feedforward controls. This converter has two pairs of the switch, one acts as a synchronous buck and another as a synchronous boost operations, and therefore is suited for battery powered applications to provide an output voltage that is below or above the input voltage. In order to realize good transient performance not only with high conversion efficiency but also with seamless circuitry transitions between the buck and buck-boost regions of operation, it is proposed that the voltage feedback is only applied to the buck section and the input voltage and the road current feedforward signals are applied to the boost section. As a result, excellent transient performances for the step load change are obtained without spoiling the efficiency for wide range of the input voltage.
Index Terms— H-bridge, Synchronous Buck-Boost Converter, Feedforward Control
I. INTRODUCTION
With recent progress of large-scale integrated circuits, various kinds of portable devices powered by batteries have widely spread in consumer electronics. In order to enable longer operation of such portable devices, it is preferable to use the battery at the lowest possible supply voltage. The terminal voltage of the battery varies considerably depending on the state of its charging condition. For example, a single Li-ion battery is fully charged to 4.2 V but it drops to 2.4 V before fully discharged. Therefore electronic circuits in the portable devices require a power converter both step-down and step-up functions. A conventional inverting buck-boost converter has such a capability with single switch and diode, but the polarity of the output voltage is opposite to the input.
A flyback converter is also able to step-up and step-down the input voltage and to isolate the input and the output. However, it is not suitable for the portable applications since the converter uses a transformer.
H-bridge DC-DC converter is a noninverting buck-boost converter that works as a buck or a boost converter by controlling two pair of switches. Since the flexibility against wide range of the input voltage, this topology is suitable for applications powered by batteries such as portable devices. In addition, since the polarity of the output voltage is the same with the supply voltage, it is easy to construct the control circuit together with the paper stage. Some families of the
circuit topology related to the noninverting buck-boost converter and their switch voltage stress are examined [1].
Several studies on the control method for this converter have been reported but the most of them are still complicated and need a number of devices [2, 3].
This paper proposes a new control method that provides excellent stability and transient performance over the wide range of the input voltage with keeping higher conversion efficiency. The feedback control is only applied to the buck section to obtain good stability and two feedforward controls are employed to the boost section to improve the transient response in case that the input voltage is lower than the output.
II. STEADY STATE PERFORMANCE
Fig.1 shows the H-bridge synchronous buck-boost converter with single inductor-capacitor and two pairs of the switch. A pair of switch S1 and S3 works as asynchronous buck mode and that of S2 and S4 works as boost mode. Fig.2
Vi
S1
S3
L
S2 S4
C R vo
iL
io
D2 D1
Driver Driver
Fig. 1. Circuit configuration of H-bridge buck-boost converter.
φ (deg) S1
S2
ON OFF
ON OFF
Fig. 2. Timing chart of drive signals.
Keiko Muro
1, Takashi Nabeshima
1, Terukazu Sato
1, Kimihiro Nishijima
1and Shinichi Yoshida
21Oita University 2Renesas Technology 700 Dannoharu 5-20-1 Josuihon-cho, Kodaira Oita 870-1192, Japan Tokyo 187-8588, Japan nabesima@eee.oita-u.ac.jp
PEDS2009
shows the timing chart of drive signals of the switch S1 and S2. This circuit is able to operate under different switching frequencies of both pairs of switch but some beat phenomena appear on the output voltage in this case. Therefore it is assumed that both switch are driven with same frequency in this paper.
A. Circuit Analysis
As can be seen from the time chart of Fig. 2, there are four states in the circuit depending on the condition of switches such as duty ratios D1, D2 of the switch S1, S2 and the phase difference φ.
Applying the state-space averaging method, the following state equation is obtained.
Vi
+ dt =
d x Ax b (1)
( )
( )
( ) ( )
C
S L C C
L S o L
r R
R
r r r D r D
r r r
LD D CR
C
L D L
r v
i
= +
+ +
⋅ +
⋅
−
− +
=
⎥⎥
⎥
⎦
⎤
⎢⎢
⎢
⎣
⎡
⎥ =
⎥⎥
⎦
⎤
⎢⎢
⎢
⎣
⎡
−
−
−
−
= −
⎥⎦
⎢ ⎤
⎣
=⎡
α
α α
φ
α α
α
2 )
2 4 (
0 1 , 1
1 ,
2 1
1
2
2 b
A x
Where symbols rS, rC and rL designate the on resistance of the switches, ESR of the capacitor C and the resistance of the inductor winding, respectively. Neglecting all internal resistances of the circuit, the steady-state output voltage and output current are expressed as
o L
i o
I D I
D V V D
⋅
−
=
− ⋅
=
) 1 ( 1
2 2 1
(2)
It is obvious that the phase difference φ does not affect the
output voltage. Only the duty ratios D1 and D2 determine the output voltage similar to the buck and the boost converters, respectively.
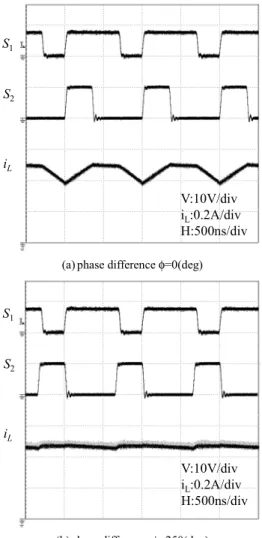
Fig.3 shows the waveforms of the drive signals and the inductor current iL for phase difference. In this figure, (a) is the case with no phase difference between S1 and S2 while with that of 250 degrees in (b). After S1 is turned off during the turn off of S2, the inductor current circulates through S2 and S3. The inductor current keeps constant value in this period. It is observed that the ripple current of (b) is well reduced compared to the case of (a). When the smaller ripple current of the inductor is required, it is effective to introduce the duration of current circulation by shifting the driving pulse of boost section. Main parameters used in the paper are L=10 μH, C=47 μF, Vo=3.3 V and 1 MHz of the switching frequency.
S1
S2
iL
V:10V/div iL:0.2A/div H:500ns/div (a) phase difference φ=0(deg)
S1
S2
iL
V:10V/div iL:0.2A/div H:500ns/div
(b) phase difference φ=250(deg)
Fig. 3. Waveforms of drive signals and inductor current.
(Vi = 3.3V, Io = 0.3 A) B. Conversion Efficiencies
It is important to investigate the relationship between the conversion efficiency and operating conditions of the switch.
Initially the influence on the efficiency due to the phase difference was examined. Fig. 4 shows the efficiency characteristics for the load current taking the phase difference as a parameter. It is observed that efficiencies with both 0 and 250 degrees of the phase difference show almost the same from the light load to the heavy one. This means that the converter operating with the period of current circulation does not spoil the efficiency.
From the viewpoint of the conversion efficiency, on the other hand, the duty ratio D1 of the buck section should be larger and that of boost section D2 should be smaller as possible when the input voltage is below the output. This is confirmed by the experimental results of efficiency characteristics shown in Fig.5 in case that the supply voltage is equal to the output and below it. It is obvious that the duty ratio D2 of the boost section should be small as possible for obtaining higher efficiency.
PEDS2009
0.7 0.8 0.9 1
0 0.2 0.4 0.6 0.8 1
Efficiency
Io(A)
φ=0(deg) φ=250(deg)
φ= 0(deg) φ= 250(deg)
Fig. 4. Conversion efficiencies for load current taking phase difference φ as a parameter.
0.7 0.8 0.9 1
0 0.2 0.4 0.6 0.8 1
Efficiency
Io(A)
D2=0.2 D2=0.36 D2=0.5
D2=0.37 D2=0.5 D2=0.6
(a) Vi = 3.3V, Io = 0.3 A
0.7 0.8 0.9 1
0 0.2 0.4 0.6 0.8 1
Efficiency
Io(A)
D2=0.2 D2=0.36 D2=0.5
D2=0.37 D2=0.5 D2=0.6
(b) Vi = 2.5V, Io = 0.3 A
Fig. 5. Conversion efficiencies for load current taking D2 as a parameter.
III. CONTROL SCHEME A. Transfer Function
This circuit has two control variables D1 and D2. Applying the small signal analysis to the state equation of (1), two open loop transfer functions are obtained as follows:
2 1 1
1( ) {1 / ( / ) }
) (
vdz o o
o
s s
N s
D s
V ω
ω ω
δ +
= + Δ
Δ (3)
2 2 2
2 2
2 2 1 1
2 3 1
) 1 (
) 1 1 (
1 /
) 1 ( )
1 (
1
) 1 ) ( 2 ( 2
) 1 )(
/ 1 (
D Z r
R Z LC D
R Z
L C Z D C
L R D
Z D R
D r r
D R
Z N V
o o o
o
o o
L vdz s
o i
= −
− +
=
+ + −
= −
− + +
+
=−
−
= +
α ω α
α δ α
ω
α α
) }(
) / ( / 1 ) { (
) (
2 2 2
2 vdz
o o
o s
s s
N s
D s
V ω
ω ω
δ −
+
= + Δ
Δ (4)
L
D D
R r r r r
R D R Z R Z
V N LD
C L vdz s
o o
i
) 1 )}(
1 ( 2
4 {
) 1 )(
/ 1 )(
/ 1 (
2 2 2
2 4 2 1
−
− + + +
= −
− +
+
= −
α ω α
α
α
It is seen form (3) that the transfer function from the duty ratio D1 to the output voltage is obviously same with the buck converter. From (4), on the other hand, the transfer function from D2 has a zero in the right half plane such as boost converter. This is confirmed from the experimental results shown in Fig. 6 in which the phase curve of the transfer
-270 -180 -90 0 90 180 270
-80 -60 -40 -20 0 20 40
0.01 0.10 1.0 10.0 100.0
phase[deg]
gain[dB]
frequency [kHz]
Phase Gain
D1to vo
D2to vo
Phase Gain
D1to vo
D2to vo
Fig. 6. Frequency responses of loop transfer function.
PEDS2009
function from D2 shifts -180 degrees higher than the resonant frequency. Therefore it is not easy to realize the excellent stability and dynamic performance only by controlling the duty ratio D2.
B. Control Scheme
When the input voltage is higher than the output, this converter operates as the buck one. This means the duty ratio D2 is zero at this mode. In the region under the output voltage, the converter must change its operation to the boost or buck- boost mode. If the converter operates as the boost one, D1 is fixed as 1 and only D2 is controlled to regulate the output.
However when the converter operates as the buck-boost mode at the input voltage near or lower than the output, both duty ratios can be employed as the control variable. As described in the preceding section, it is not preferable to use D2 as a feedback control variable.
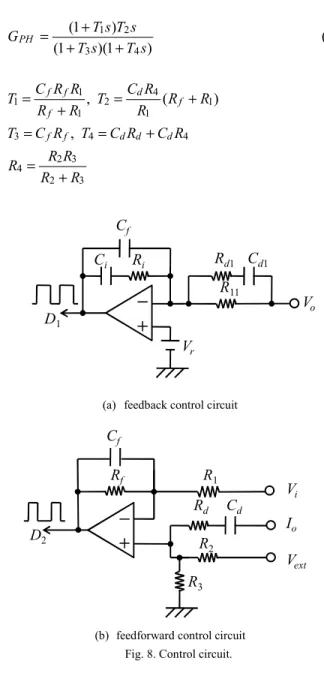
This paper proposes that the duty ratio D1 is controlled by the feedback signal from the output while D2 is controlled by two feedforward signals from the input voltage and the load current as shown in the block diagram of Fig. 7. In the range of the input voltage from slightly higher than the output to its possible lower operating voltage, D2 is adjusted by the feedforward signal from the input voltage through an element Fv so that D1 in the steady state stays at a certain value such as 0.8 or 0.9 for example. This means that when the maximum duty ratio of D1 in the steady state is assigned as D1M, D2 is determined by the following equation:
o M
PH i D
V
G =1−V 1 (5)
For example, when D1M is chosen as 0.85, D2 becomes 0 for the input voltage Vi higher than about 1.2 Vo and the converter operates just as the buck mode in this case. At the input voltage is 0.75Vo with the same condition of D1M, D2 is determined as 0.37 from (6). This function is performed by the element Fv in Fig. 7.
D2
D1
v o
Fv GHP(s)
PWM2
H-Bridge Convertor
PWM1 V i
Vr io
- +
+ feed back -
feed forward
Error amp with phase compensation
Fig. 7. Block diagram of proposed control scheme.
Another feature of the control method proposed here is the load current feedforward. The voltage feedback control of the buck section for the input voltage higher than the output works well such as the conventional buck converter. Even for the input voltage lower than the output, the transient output voltage for small load variation is also well regulated by the buck section. However, in case of the large variation of the load condition especially from the light load to heavy one, the duty ratio D1 easily reaches maximum value such as 1 due to the large undershoot voltage and then the transient voltage is no longer reduced by controlling the buck section. The role of the load current feedforward is to reduce the transient voltage in such a case by controlling the duty ratio D2 and its function only needs to work for a certain duration of the transient period. Therefore a high pass filter defined by the following equation is employed in the feedforward path.
) 1 )(
1 (
) 1 (
4 3
2 1
s T s T
s T s GPH T
+ +
= + (6)
3 2
3 4 2
4 4
3
1 1
2 4 1 1 1
,
) (
,
R R
R R R
R C R C T R C T
R R R
R T C R R
R R T C
d d d f
f
d f f
f f
= +
+
=
=
+ + =
=
+
-
D1 Vo
Vr R11 Rd1 Ri
Cf
Cd1 Ci
(a) feedback control circuit
D2 Io
Vi
Vext R1
Rd Rf
Cf
Cd R2 R3
+
-
(b) feedforward control circuit Fig. 8. Control circuit.
PEDS2009
Fig. 8 (a) shows the feedback circuit for the buck section and (b) is the feedforward circuit used in the experiments.
The phase compensation network is designed as the same way with the conventional buck converter. The resistances R1, Rf and the external voltage Vext in (b) are determined by (5).Basically the load current feedforward does not affect the system stability but the time constant T1 should be carefully designed to improve the transient response.
C. Transient Performances
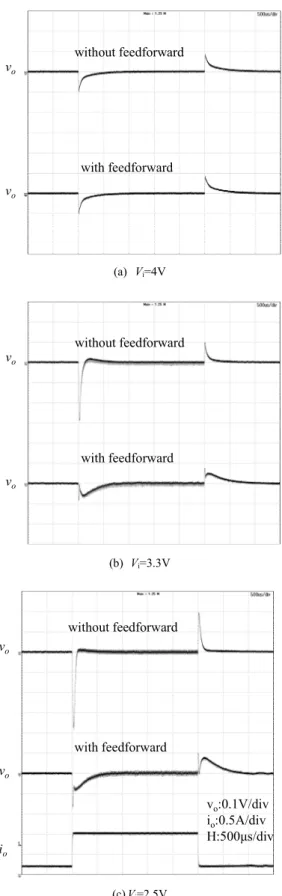
In order to verify the effectiveness of the dual feedforward control, the H-bridge converter shown in Fig. 1 together with the control circuit of Fig. 8 was experimented. The transient performances were examined by the step load change from 0.2 A to 1 A with 3.3 V of output voltage and 0.85 of D1M.
For the input voltage variation from 4 V to 3 V, the mode of operation changes from the buck to buck-boost in this range, less than 20 mV of transient output voltage was observed. The feedforward from the input voltage to the boost section enable the seamless circuitry transitions between the buck and buck-boost regions of operation.
The transient output voltages for the step load change are compared in Fig. 9 where the operation of the converter is (a) the buck mode, (b) and (c) the buck-boost mode. When the converter is in the buck mode, D2 = 0 in this case, less than 100 mV of the transient voltage is realized and no difference of the transient voltage is observed by applying the load current feedforward. In figures (b) and (c), on the other hand, large undershoot voltages appear on the output, about -380 mV of the peak voltage in (c). However these large transient voltages are effectively reduced by the load current feedforward not only for the undershoot but also for the overshoot. The conversion efficiencies at 1 A of the load current are 96 % in (a), 95 % in (b) and 93 % in (c), respectively. As can be seen from these results that the dual feedforward control method proposed in the paper well improves the transient performance for the wide range of the input voltage with keeping high efficiency.
IV. CONCLUSIONS
A new control scheme for H-bridge buck-boost converter with single feedback to buck section and dual feedforward to boost section has been proposed in this paper. This control method provides not only the seamless transitions of operating mode according to the input voltage level but also the excellent transient performance for wide range of the input voltage without spoiling the high efficiency. In order to obtain good transient performances for the load current variation, it is important to design parameters of the high pass filter GHP(s) in the feedforward path. The analytical approach to design the high pass filter is now being investigated.
vo
vo
without feedforward
with feedforward
(a) Vi=4V
vo
vo
without feedforward
with feedforward
(b) Vi=3.3V
io vo
vo
without feedforward
with feedforward without feedforward
vo:0.1V/div io:0.5A/div H:500μs/div
(c) Vi=2.5V
Fig. 9. Comparison of transient response for load step change from 0.2 A to 1 A.
(T1=0.43μs, T2=4.73μs, T3=0.54μs, T4=3.83μs)
PEDS2009
REFERENCES
[1] J. Chen, D. Maksimovic, and R. Erickson, “Buck-Boost PWM Converters Having Two Independently Controlled Switches,” PESC 2001 Record, pp.736-741, June 2001.
[2] A. A. Boora, F. Zare, G. Ledwich, and A. Ghosh, ”A Genaral Approach to Control a Positive Buck-Boost Convertor to Achieve Robustness against Input Voltage Fluctuation and Load Changes,”
PESC 2008 Record,pp.2011-2017.June 2008.
[3] B. Sahu and G. A. Ghosh, ”A General Approach to Control a Positive Buck –Boost Converter to Achieve Robustness against Input Voltage Fluctuations and Load Changes,” PESC 2008 Record,pp.2011- 2017,June 2008
PEDS2009