自然科學中的數學概念

國

立

交

通

大

學

理學院碩士在職專班網路學習組

碩士論文

自然科學中的數學概念

Mathematical concept in natural science

研究生：李金航

指導教授：陳永富教授

自然科學中的數學概念

研究生：李金航 指導教授：陳永富教授

國立交通大學理學院碩士在職專班

網路學習組

摘要 我們利用自然科學中一些週期性運動及雙螺旋排列的現象，比較不同情況下 軌跡的特性。利用不同參數的彈子球檯及李賽羅圖形探索有理數、無理數、同餘 及完全剩餘系的關係。並利用雙螺旋圖形研究輾轉相除法、漸近分數與黃金比例 的概念。透過自然科學系統的視覺化呈現，我們希望學習者可以更欣賞並學習更 進一步的自然科學與數學。

Mathematical concept in the natural science

Student: Chin Hang Li Advisor: Yung-Fu Chen

ABSTRACT

We use some natural phenomenon as the periodic motion and the dual-spiral phyllotaxis picture to contrast the different behavior of their curve. Explore rational, irrational number, Residues and complete residue system by the billiards and the lissajous pictures with different value of parameter. Use the dual-spiral graphs to study the relation between the approximating fractions and the golden number. Through visualizing the character of natural system, we wish students can better appreciate the distinction and come to gain more sophisticated intuitions about natural science and mathematics.

誌謝

首先要感謝陳永富老師的指導，為我開啟了一扇窗，讓我見識到科學之美， 還有專班許多老師。明璋老師的教導讓我在職場上的專業知能有大幅的增進。 還要感謝實驗室中那麼多的學長姐及夥伴，梁興弛學長給了我許多協助並解決我 許多學習上的問題。陸亭樺學姐、陳建誠及老大也幫了很多的忙。周鴻案則教了 我這小老弟許多人生的啟發。 最後要感謝我的父母、明軒及惠雯，感謝你們在我分身乏術的時侯給予我的 支持，感謝明軒一年多來晚上不吵不鬧的配合，還有惠雯幫我打理日常生活的大 小事物，讓我得以全力以赴。我愛你！！ 謝謝大家！！

目錄

中文摘要 ……… i 英文摘要 ……… ii 誌謝 ……… iii 目錄 ……… iv 圖表目錄 ……… v 第一章 簡介……… 1 1.1 研究動機……… 1 1.2 論文架構……… 1 第二章 數學的基本概念……… 2 2.1 何謂曲線……… 2 2.2 從同餘出發……… 10 2.3 完全剩餘系的性質……… 11 2.4 尤拉函數的引入……… 12 2.5 有理數與無理數……… 14 2.5.1 無理數的特性……… 15 2.5.2 連分數與輾轉相除法……… 16 2.5.3 黃金比例與無理數逼近……… 17 第三章 週期性軌道的曲線……… 20 3.1 古典粒子的二維週期性運動……… 20 3.1.1 方形彈子球檯……… 21 3.1.2 二維簡諧運動的李賽羅圖形……… 25 3.2 二維封閉波動系統的束縛態……… 34 3.2.1 本徵態與軌跡……… 34 3.2.2 波的干涉……… 39 3.2.3 對應於彈子球檯的波函數……… 46 3.2.4 對應於李賽羅圖形的波函數……… 52 第四章 開放式彈子球檯與漸近分數……… 59 4.1 圓式彈子球檯內的古典粒子……… 59 4.2 開放式彈子球檯……… 64 第五章 結論與展望……… 74 參考文獻 ……… 75

圖表目錄

圖 2.1.1 直角座標系上的直線……… 5 圖 2.1.2 圓錐曲線與截平面……… 6 圖 2.1.3 切點與平面上的圓錐曲線……… 7 圖 2.1.4 直角座標系上的圓……… 8 圖 2.1.5 圓與 sin 函數……… 8 圖 2.1.6 阿基米德與 logarithmic 螺旋……… 9 圖 2.5.1 葉原體移動排列示意圖……… 19 圖 2.5.2 自然界的雙螺旋……… 19 圖 3.1.1 一維方形 billiard 邊界……… 22 圖 3.1.2 一維彈子球檯位置對時間變化……… 23 圖 3.1.3 二維方形 billiard 邊界……… 23 圖 3.1.4 一維簡諧運動示意圖……… 28 圖 3.1.5 二維簡諧運動示意圖……… 29 圖 3.1.6 二維 billiard 位置隨時間變化……… 33 圖 3.2.1 一維 billiard 的波函數……… 35 圖 3.2.2 波動性干涉示意……… 42 圖 3.2.3 行進波相化變化示意……… 42 圖 3.2.4 不同相位差對波包的影響……… 43 圖 3.2.5 不同振幅分佈對波包的影響……… 44 圖 3.2.6 不同 mode 對波包的影響……… 45 圖 3.2.7 一維 billiard 內波包位置隨時間變化……… 48 圖 3.2.8 二維 billiard 內波包位置隨時間變化……… 49 圖 3.2.9 一維拋物線位能井的波函數……… 53 圖 3.2.10 一維簡諧運動波函數位置隨時間變化……… 55 圖 4.1.1 二維圓形 billiard 邊界……… 61 圖 4.1.2 二維開放式圓形 billiard……… 66 圖 4.1.3 二維封閉、開放式圓形 billiard 比較……… 67 圖 4.1.4 開放式圓形 billiard 圖形中的雙螺旋……… 68 圖 4.1.5 不同(p,q)開放式圓形 billiard 圖形……… 69 圖 4.1.6 二維開放式圓形 billiard 與完全剩餘系……… 70 圖 4.1.7 二維開放式圓形 billiard 與天然雙螺旋……… 71 圖 4.1.8 高階漸近分數二維開放式圓形 billiard 圖形……… 73 表 2.2.1 同餘在答數上的表示……… 10 表 2.3.1 完全剩餘系在月曆上的表示……… 11 表 2.4.1 尤拉函數示意……… 13 表 3.1.1 (p:q) 為有理數之二維 billiard 軌跡……… 24

表 3.1.2 (p:q)為有理數之二維李賽羅軌跡……… 30 表 3.1.3 二維 billiard 和李賽羅軌跡比較……… 31 表 3.1.4 (p:q)為無理數之二維 billiard 軌跡……… 32 表 3.1.5 (p:q)為無理數之二維李賽羅軌跡……… 32 表 3.2.1 二維 billiard 的波函數……… 37 表 3.2.2 圓形邊界形成鼓面的駐波……… 38 表 3.2.3 二維 billiard 波函數所組成的 PO……… 50

表 3.2.4 不同 mode 二維 billiard 波函數所組成的 PO……… 51

表 3.2.5 二維拋物線位能井的駐波函數……… 57

表 3.2.6 二維李賽羅波函數所組成的 PO ……… 58

表 4.1.1 圓形彈子球檯與完全剩餘系……… 62

表 4.1.2 無理數圓形彈子球檯……… 63

第一章緒論

1.1. 研究動機

大至天體運動，小至晶格原子振盪，自然界中充斥著週期性的運動，而 自然科學中，粒子模型常用於探討氣體分子、簡諧運動則是最常見的週期運 動、雙螺旋排列則出現在植物花葉序及晶體微結構中[1-3]，其週期性軌道 (periodic orbits, P.O.)：彈子球檯、李賽羅圖形[4]具有一定的規律，隱含了豐 富的數學概念。數學上利用幾何和曲線[5-8]表達許多數學上的抽象概念，而 同餘與完全剩餘系[9]、有理數與無理數等，例如： 2為無理數的証明、黃 金比例、π 的性質、無限連分數及輾轉相除法的使用[10-18]。 如何藉由簡單、視覺化的科學現象及二維週期性軌道圖形[20]，了解分 數、有理數與無理數，是我們的研究動機。而粒子與波更是物理學中的重要 課題，更進一步能否以駐波、波包的形式呈現古典粒子的週期性軌道[21-28]。

1.2. 本論文組識

本論文第二章探討基本數論中的幾個概念：由同餘概念出發，並探討有 理數、無理數、輾轉相除法、漸近分數與黃金比例。第三章針對古典粒子與 波型式的彈子球檯、李賽羅圖形的運動特性，並和有理數、無理數比較。第 四章則討論特徵長度、封閉與開放的圓型彈子球檯與完全剩餘系的關係。第 五章則為結論及可能的發展方向。

第二章 數學的基本概念

自然界的週期性運動對於科學始終是一個令人著迷的問題，虎克發現虎克定 律，一個彈簧上振盪的小球所受的力和彈簧伸長量成正比。克卜勒寫下了宇宙的秘 密，敘述天體是循一個軌道的週期性運動，牛頓則發現了萬有引力，小至蘋果大至 星體，都依循著相同的規律，成功地解釋天體間的運動狀態，更造成當時極大的振 奮。為了探討這些週期性運動的數學特性，我們先需要一些數學的基本概念： 1、 何謂曲線 2、 同餘的概念 3、 完全剩餘系的性質 4、 尤拉函數 5、 有理數與無理數的概念

2.1. 何謂曲線

數學上最簡單的曲面是平面，而平面上最簡單的曲線則是直線及圓[5]。幾何學 發展的相當的早，早在兩河流域及古埃及時代，就有幾何學的發展。便是應用尺規 作圖，使用簡單的直線及圓規，推演其他幾何圖形的性質並廣泛的應用在面積測量、 建築及器具製作等相關領域。至笛卡克，發展了座標系的概念，函數與圖形得以結 合，以圖形的方式描述函數，創建了解析幾何的領域。而不同座標系的發展，也演 譯了許多不同的函數圖形[6]。並以此奠立了物理、化學等科學的發展。而曲線在自 然界中更是隨處可見，無論是蝸牛、螺貝、羊角上的螺線，天體運行軌跡形成的楕 圓、雙曲線。一個落下物體所形成的直線及拋物線。都是曲線的一種。[7] 平面中的特定兩點可以決定一條直線(圖 2.1.1)，利用函數的概念，可以延伸得 到一個直線的函數，可由兩個特定點決定，又稱作兩點式，而線上任一點皆需符合 直線方程式： 0 1 y−y ₌ y−y (2.1)

因為直線是具有方向性的線條，故一個點加上方向，也可以決定一條直線，而這個 方式，則以斜率表現，故直線方程式又可以”點鈄式”表示。

(

y−y0

)

=m x

(

−x0

)

(2.2) 而斜截式則是點斜式的特例，由 y 軸上的截距和斜率決定一條直線。 0 y−y =mx (2..3) 而圓錐曲線的發現(圖 2.1.2)，在幾何學中是一個重要的發現。利用一個立體圓錐體 的模型，將平面上的圓、楕圓、拋物線及雙曲線幾個平面曲線，統整在一起。四個 曲線，都可以視為一個截面與圓錐體相截的曲線。若將圓錐體內放入和圓錐體及截 面相切的球體並得切點(圖 2.1.3)，則可得到平面上圓錐曲線的性質。 圓形具有半徑為定值的性質(圖 2.1.4)，故可利用畢式定理得到其函數：圓上一點, 和 圓心(x0,y0)連線為半徑，故可得：

(

) (

2

)

2 0 0 2 2 1 x x y y r r − − + = (2.4) 極座標則可以表示為 r=c (2.5) 楕圓則具有長軸 a，短軸 b 兩個軸，曲線上一點(x,y)，可寫成：

(

) (

2

)

2 0 0 2 2 1 x x y y a b − − + = (2.6) 拋物線則寫成：

(

)

(

)

2 0 0 y−y =a x−x (2.7) 雙曲線的方程式則為：

(

) (

2

)

2 0 0 2 2 1 x x y y a b − − − = (2.8) 若畫一個單位圓並引入三角函數，將 sin(θ)隨θ變化作圖，可得 sin 函數的曲 線。以一個軌跡為圓曲線的等速率的圓周運動為例：可發現其角度隨時間變化，而 位置對圓心呈等距的函數關係。若將其函數對 x 軸作投影，可以發現其 x 軸位置與 時間的關係形成了 sin 函數(圖 2.1.5)。而這樣的運動即稱作簡諧運動。

改以極座標表示，而 r 與θ具有一特殊的關係，則形成所謂的螺旋線(圖 2.1.6)。其 中阿基米德螺線其半徑隨著角度變大而增大，並具有正比的關係，可表示成： r= ⋅a θ (2.9) 故在阿基米德螺旋上取θ 為等差數列，則對應之半徑 r 將亦呈等差數列。 而 Logarithmic spiral 則為： b r= ⋅a eθ (2.10) 或改寫為 ln r b a θ ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ (2.11)

圖 2.1.1 直角座標系上的直線

(x,y)

(x

0

,y

0

)

(x

1

,y

1

)

X軸

Y軸

斜率=m

(a)圓 (b)拋物線

(c)楕圓 (d)雙曲線

切點

切點

圖 2.1.5 圓與 sin 函數 X軸 Y軸 (x,0) r=1 θ Sin(θ) 0 5 10 15 1 -1 -0.5 0.5 0 θ Sin(θ) X軸 Y軸 (x,0) (0,y) (x,y) r=c 圖 2.1.4 直角座標系上的圓

圖 2.1.6 阿基米德與 logarithmic 螺旋[4] X軸 Y軸 X軸 Y軸 (a)阿基米德螺旋 (b)Logarithmic

2.2. 從同餘出發

同餘這個概念是由高斯所提出的[8,9]，可以先從幾個簡單的除式問題出發，藉 此以了解什麼叫同餘。 例 1：一群軍士 45 人，以一至九為一班依序報數，若某軍士番號為 28 則答數為何 多少？ 因為每數到九就重新循環，28÷9=3…1，或寫成 28=9×3+1，所以答數是 1。 例 2：若答數為 1 者為班長，則除了 28 號外，還有那些人是班長？ 由第一題我們知道，計有：{1、10、19、33} 一 二 三 四 五 六 七 八 九 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 表 2.2.1 同餘在答數上的表示 在日常生活中，類似的問題很多，例如：今天是星期一、過了 15 日是星期幾？ 早上八點上課，一節課 45 分鐘，上了四節課是幾點幾分？這些問題本質上都是將總 數除了一個固定的除數，求餘數的問題。因此產生了同餘的概念，以第二題為例： {1、10、19、28、33}。這些數的共同點為除於 9 的餘數相同，皆為 1。其實同餘就 是餘數相同的數。不只是同餘的概念，高斯還引進了新的符號，讓許多計算有更方 便的方式，而同餘的定義為： 給定一個正整數 m，如果用 m 去除 a，b 所得的餘數相同，則稱 a 與 b 對模 m 同餘， 記作 ， 並讀作 a 同餘 b，模 m。例： 、 。則。 若 a 與 b 對模 m 同餘，設 ， 得， ， 。反之，若 ，設 ， 10 1 3 7 = ⋅⋅⋅

(

mod

)

a≡b m 3 0 3 7 = ⋅⋅⋅

(

)

10≡3 mod 7 a=m q ₁ + r b=m q ₂ + r

(

)

a− =b m q −q m a| −b m a| −b a=m q + r

2 2 b=m q + ，r 0≤r₁ , r₂ ≤ − ，則有m 1 m r| ₁ − ，因r₂ |r₁ −r₂ |≤ m− ，故1 r₁− = ，r₂ 0 即r₁ = 。於是得到同餘的另一等價定義。 r₂ 在引進了≣符號後，在運算上也有了改變。首先： 若a≡b

(

modm

)

，c≡d

(

modm

)

加法： a+ ≡ +c b d

(

modm

)

(2.7) 減法： a c− ≡ −b d

(

modm

)

(2.8) 乘法： ac≡bd

(

modm

)

(2.9) 除法：if ak mod≡bk

(

m

)

，

(

k m,

)

=1，同除於 k 時a≡b

(

modm

)

(2.10) if ak mod≡bk

(

m

)

，

(

k m,

)

=d，同除於 k 時a b modm d ⎛ ⎞ ≡ ⎜_⎝ ⎟_⎠ (2.11) 引入的新的符號後，同餘的概念更應用在十進位制、八進位制等轉換、密碼編譯等 領域。

2.3. 完全剩餘系的性質

完全剩餘系在同餘理論中是一個非常重要的概念，我們也可以從一個簡單的例 子了解完全剩餘系： 日 一 二 三 四 五 六 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 表 2.3.1 完全剩餘系在月曆上的表示

這是某個月份的日曆，我們可以將一個月分，以 7 天一周作為一個單位，可以分成 數周。在表內我們可以發現。周日的日期分別為{4、11、18、25}號，都對模 7 同餘， 餘數為 4，則我們將{4、11、18、25}，稱作模 7 的一個剩餘類，即屬於周日為一個 剩餘類。一周有七天，故可分為周日、周一、周二、周三、周四、周五、周六 7 個 剩餘類。再將周日至周六，各挑一個數字出來，例：{4、5、6、7、8、9、10}，則 這些整數將涵蓋周日至周六每一類。則，這樣的整數集合，我們即稱作完全剩餘系。 由此可知，若一個以 m 正整數為模的完全剩餘系，具有下列特性： (1)一個完全剩餘系有 m 個整數組成的元素。 (2)完全剩餘系的元素，關於兩兩不同餘。 (3) ，x 為 m 的完全剩餘系，則 也是 m 的完全剩餘系。 例： ，則 為同一類， 成為一個完全剩餘系。 若 ， 則 發現 各剩餘類的排列不同，但仍為一個完全剩餘系。這在圓形的 billiard 中，具有相當重 要的應用。

2.4. 尤拉函數的引入

由上節特性(3)： ，x 為 m 的完全剩餘系，則ax+b也是 m 的完全剩餘 系出發，在小於 m 的情況下，有多少個數符合這樣的性質？這時必需引入尤拉函數， 尤拉函數表示為 ，又稱 totient function，指的是比 m 來的得小，且和 m 互質的 正整數個數。例如 ：有 4 個數 1,3,7,9 符合，則 。首先我們從一個表 開始：

(

a m,

)

=1 ax+b

{

}

{

} {

}

2 0,1, 2, 3, 4, 5, 6⋅ + =3 3, 5, 7, 9,11,13,15 = 3, 5, 0, 2, 4, 6,1 3 b= 2 a= 7 m=

(

1,8,15, 22⋅⋅⋅

)

{

0,1, 2, 3, 4, 5, 6

}

(

a m,

)

=1

( )

m φ

( )

10 φ φ

( )

10 =4

1 _{2 3 4 5} 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 表 2.4.1 尤拉函數示意 設一個質數為 5 時，可得到和 5 互質的數有 5-1=4 個。 52=25，將 25 個數字排列如表，可將之分為 5 類，分別以 5 餘是餘數為{1，2，3，4， 0}，而 25 的因數是在<25 的情況下，所有 5 的倍數，即將餘數為 0 的一類劃去，由 完全剩餘系的性質可知，和 25 互質的有 5-1=4 類。整理歸納可得： 當 m= 為一個質數時，則和 p 互質的數有 1,2,….p-1，可得p φ

( )

p = −p 1 當 m= pα是一個質數的α 次方，則我們可以得到

( )

(

)

1 1 1 a 1 p p p p p α α φ _{= −} − ₌ ⎛ ₋ ⎞ ⎜ ⎟ ⎝ ⎠ (2.12) 當

(

n m,

)

=1，φ

(

n m⋅

)

=φ

( ) ( )

n ⋅φ m (2.13) 綜合以上三點，我們將 m 先化作質因數的標準式 即 ei i i m=

∏

p (2.14) 則 可得，當時e_i > 0 (2.15) 例： 3 2 72=2 ⋅ ，3 φ

( ) (

72 = 2 1 2− ⋅

)

3 1− ⋅ −

(

3 1 3

)

2 1− =24，我們將小於 72 所有的互質數 列出如下表：

{

1, 5, 7,11,13,17,19, 23, 25, 29, 31, 35, 37, 41, 43, 47, 49, 53, 55, 59, 61, 65, 67, 71

}

得計 24 個。 而一個圓形 billiard 內，存有幾種模式，可以以尤拉函數作為驗証。 p-1 類 pα-1 項

( )

(

)

1 1 1 ei 1 i i i i i m p p m p φ _{= −} − ₌ ⎛ ₋ ⎞ ⎜ ⎟ ⎝ ⎠

∏

∏

2.5. 有理數與無理數

畢達哥拉斯學派中有一句話說：萬物皆數。認為萬物皆可以用有單位的數表現 也就是以分數或有理數表現。畢氏曾發現，不同重量的鎯頭，敲擊發出的聲音不同， 若一把鎯頭的重量是另一把的一半，則會發出兩倍高的聲音，高一個八度音程，不 僅於鎯頭，所有簡單樂器大致都以相同的方式運作，無論是敲擊、撥絃還是吹管樂 器，而在天文中也有類似的現象，木星和土星的週期比為 2:5，天王星、海王星、冥 王星的週期比則為 1:2:3，在自然界中，充斥著許許多多的現象，彼此間都存在著簡 單整數比的關係。用來表示簡單整數比的數，就是有理數。 有理數稱作 ratio number，在原意是比例的意思，數學上即為一個整數 p 和一個非零 整數 q 的比，可寫作 p q，正是簡單整數比的意義，故又稱作分數。若將所有有理數 的集合稱作 Q ，則可寫成： : , , 0 p Q p Z q Z q q ⎧ ⎫ =_⎨ ∈ ∈ ≠ _⎬ ⎩ ⎭ 將有理數改以小數的方式表示，則可發現為有限小數或是循環小數。在此先了解什 麼叫作算術系。算術系由皮亞諾公理及五條運算法則組成，其中皮亞諾公理[10]是 這樣的： 1、1 是自然數 2、N 是自然數集，a∈N，a必有一個後繼數a′， a′ = +a 1 3、1 不是任何自然數的後繼數 4、一個數b∈N，即 ,a b 若a′=b′，則a=b 5、歸納法公理：任一自然數集S，若1∈S，∀ ∈a S，a+ ∈1 S，則S包含所有自然 數。

五條運算法則為： 加法交換律： a+ = +b b a 加法結合律： (a+b)+ = +c a (b+ c) 乘法交換律： a b× = ×b a 乘法結合律： (a b× × = × × ) c a (b c) 加乘分配律： a× + = × + × (b c) a b a c 只要滿足五條公理及五條運算法則的系統則稱為算術系統，而標度性在此有重 要的地位，我們可以將”1”視為一個單位，而單位”1”具有可分性和可加性，例：分 數q p，當 p ， q 為整數，可將其視為”1”分為 p 等分，1 份為 1 p，再利用可加性得 1 p p q = × ，類似的q 1 2 1 2 2 1 1 2 1 2 p p p q p q p q q p p q + + = = ，仍是可分性和可加性概念的延伸。 2.5.1 無理數的特性 然 2的出現卻造成了深深的震撼，希帕索斯為畢達哥拉斯學派，卻用畢氏定 理發現了 2無法以任何簡單整數組成的分數 p q 表示。我們考慮一個邊長為 1 的直 角三角形，我們設斜邊的長度為有理數 p q的最簡分數，依畢達哥拉斯定理可得 2 2 2 2 1 1 2 p q = + = ，則 2 2 2 p = q ，得2 p，設p=2k，則 2 2 4 p = k ， 2 2 4k =2q ， 2 2 2k =q ， 得2q，則 p q 有公因數 2， p q非最簡分數，與假設不合，故 2無法以一個最簡分數 表示[11-13]，即不具有標度性，無法以任何一個具有特定單位的數表示。在天文中 也發現，水星繞日的軌道無法形成一個封閉的軌道，似乎有理數無法完全解釋這個 世界的規律。

2.5.2 連分數與輾轉相除法 有理數和無理數間的關係，可以以數學方法表示，其中連分數與輾轉相除法 [15-18]是一個簡單、方便且類似的方法。輾轉相除法的定義是這樣的： 若有兩正整數a和b，用b除以a得商a ，餘數₀ r，寫成式子a= × + ， a₀ b r 0≤ <r b 若r=0，則b可以除盡a，a和b的最大公因數為b 若r≠0，則再用 r 除b，得商a ，餘數₁ r ₁ 1 0≤ <r r 1 1 2 b= × +a r r 如果r ＝0，則 r 可以除盡₁ b，也可以除盡a，r 為a和b的最大公因數。倘若r₁≠ ，0 以r 除 r ，得商₁ a ，餘數₂ r ₂ 2 1 2 r= × +a r r 2 1 0≤ <r r 如此延續由於b> > > >r r₁ r₂ ...(≥ ，疊代最終的結果，將找到一個式子，其餘式0) 為 0，代表其除數及被除數同餘，其故可以找出 a、b 的最大公因數。即為輾轉相除 法。 若換以分數形式操作輾轉相除法，以 42879 和 18644 兩數作輾轉相除法為例： 42897 5609 1 2 2 18644 18644 18644 5609 = + = + 1 1 2 2 1817 1 3 3 158 5609 3 1817 = + = + + + + 1 2 1 3 1 3 79 11 158 = + + + + 1 2 1 3 1 3 1 11 2 = + + + + 表示成 1 1 1 1 2 3 3 11 2 + + + + 或

[

2, 3, 3,11, 2

]

則稱作連分數。通常以 其中 2 ， 1 2 3 + ，2 1 1 3 3 + + ， ₁ 2 1 3 1 3 11 + + + 稱為 543/236 的漸近分數。其中第一個漸近 分數比 543/236 小，第二個漸近分數比 543/236 大。依序類推。

2.5.3 黃金比例與無理數逼近 在實數系中，任一質數的平方根為無理數。利用反証法，設 p 為一個質數， a p b = 或 2 2 pb =a 為一個有理數，其中_a和_b互質的整數。若_a質因數分解為 1 2 n a=a a⋅ ⋅⋅⋅ ，a _b的質因數分解為b= ⋅ ⋅⋅⋅ 。則b b_{1 2} b_m 2 a 為2n個質因數乘積，b 為2 2m 個質因數乘積。然， 2 2 pb =a 左式為奇數個質因數乘積，右式為偶數個質因數乘積， 彼此矛盾，故得証。而黃金比例代表的是 1 1 τ τ τ + = 成立時的比值，其中

(

)

1 1 5 2 τ = + [14]正是一個含有質數平方根的無理數。 黃金比例這個無理數在數學及美術中不但具有特殊的角色，也反覆的出現在自 然現象中。湯普生就以向日葵的排列方向說明黃金比例和費伯納希數列，說明植物 花葉序和黃金比例的關係[1-3]。在向日葵中，每一片花瓣由一葉原體長出，而葉原 體會依序排列組成一個弧狀的「生長螺線」，因為較早產生的會移的較遠，而形成順、 逆兩組雙螺線，並且可以緊密的互相套合。[1-2] 而順、逆螺線的數量彼此間具有特定的關係，大多數的向日葵順、逆螺線的比例為 (34:55)，有些品種的比例更達到(89:144)，並且其他植物中也發現了類似現象，鳳梨 鱗片形成(8:13)的雙螺旋排列，雲果的毬果則形成(3:5)的雙螺旋。 要了解黃金比例，首先我們要了解如何將一個無理數α 以連分數展開：因為無理數 無法以分數的方式表示，故此連分數將是一個無窮連分數，可以表示成 0 1 2 3 1 1 1 1 n a a a a α + + + +⋅⋅⋅ ，或是

[

a a a a0, 1, 2, 3...,αn

]

。在此命 n n p q 為第 n 個漸近分數，則 可以得到前三個漸近分數 0 0 p q ， 1 1 p q ， 2 2 p q ： 分別為 0 1 a ， 1 0 1 1 a a a + ， 2 1 0 0 2 1 ( 1) 1 a a a a a a + + + 。 亦可推得 1 2 1 2 n n n n n n n n p a p p q a q q − − − − + = + 以相同方式將τ 以連分數展開，可得 1 1 1 τ τ = + ，利用疊代：

可得 1 1 1 1 1 + + + ⋅⋅⋅ 或

[

1,1,1,⋅⋅⋅

]

。 分別列出 qn和 pn

{ }

q_n =1,1, 2, 3, 5,8,13,⋅⋅⋅

{ }

p_n =1, 2, 3, 5,8,13, 21,⋅⋅⋅ 其漸近分數則可表示為 1 2 3 5 8 13 21, , , , , , , 1 1 2 3 5 8 13 ⎧ _⋅⋅⋅⎫ ⎨ ⎬ ⎩ _⎭ 若和費伯那希數列比較，費氏數例的特性為： 1 1 F = ，F₂ = 1 1 2 n n n F =F₋ +F₋ 。 列出首幾項為：

{

1,1, 2, 3, 5,8,13,⋅⋅⋅

}

，可發現費氏數列相鄰兩數的比值即是黃金比例 的漸近分數。 寫成。 ₁ ( 1)1` / 1;1, ,1 n n n s F₊ F − ⎡ ⎤ =_⎢ ⋅⋅⋅ _⎥ ⎣ ⎦ 而向日葵等植物的花葉序(3,5)(8,13)(21,34)(34,55)(89,144)，都是費伯納希數列的數 項、黃金比例的漸近分數。而以連分數得到的漸近分數，經過証明，可以發現幾個 性質： 1、 1 2 1 2 n n n n n n n n p a p p q a q q − − − − + = + ，漸近分數可依循推出。 2、 2 2 n n p q < ，α 2 1 2 1 n n p q α + + > ，奇項漸近分數大於真值、偶項漸近分數小於真值。 3、 1 1 n n n n p p q q α α − − − < − ，越後項的漸近分數，越逼近真值。 4、 p P q Q α − < −α ， Q q< 。在不大於 q 的情況下，漸近分數為最佳逼近。

圖 2.5.2 自然界的雙螺旋 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 (a)向日葵 (b)松果 (c)鳳梨 圖 2.5.1 葉原體移動排列示意圖

第三章 週期性軌跡的曲線

週期性的運動常會形成一個封閉性的週期性軌道(periodic orbits,PO) 形成特 定的曲線，其中彈子球檯圖形及李賽羅圖形[4,20]，最為人們熟悉。在此藉由彈 子球檯及李賽羅的曲線圖形，探討有理數與週期性軌道的關係。然量子力學的發 展，波粒二元性及物質波的發現，粒子與波之間的關係，逐漸浮現。故在此進一 步探討以波的形式，重現古典粒子週期性軌道。

3.1. 古典粒子的二維週期性運動

彈子球的模型在物理及化學中，應用的非常早，約在 16、17 世紀，人們就 有空氣是由許許多多的小粒子所組成的概念。而後原子、分子的概念漸為人所接 受。對於氣體溫度與壓力、體積間變化的也越發的清楚。而此時的熱力學仍停留 在觀察的階段，並沒有辦法提出具有預測性、完整性的理論解釋。然伯努力 (

Bernoulli)

提出壓力來自粒子對於壁面的碰撞。克勞修斯(

Clausius)

引入統計 方法、提出自由度及平均自由徑的觀念，麥斯威爾(Maxwell)則發現氣體分子的 速度分佈，將一個巨觀的系統，視為一群粒子的整體表現。成功的解釋，粒子動 能、溫度與壓力之間的關係。 由此延伸發展了：固、液、氣態變化的粒子模型。物質內電阻係數的粒子模 型。粒子能量分佈的探討。至此，大量統計技巧引入，由微觀的粒子出發，探討 眾多複雜系統的科學現象，促發了統計力學等領域的發展。 自然界中最常見的週期性運動便是簡諧運動，而李賽羅圖形則是最為奇妙的 一種，這由 19 世紀中期法國數學家李賽羅(Lissajou)所設計的一種實驗，將鏡子 黏著於音叉末端，以光線對準音叉後敲擊音叉，經過鏡面的投射可以在屏幕上出 現正弦波的圖形，若將兩個已黏著鏡子的音叉，以垂直的方式置放，則可以獲得 李賽羅圖形。這個實驗將無法以視覺感受的聲音，以光線和屏幕展現出來，故又 稱”看得見的聲音”。大量的應用在頻率測量、電子學等相關領域。

3.1.1 方形彈子球檯

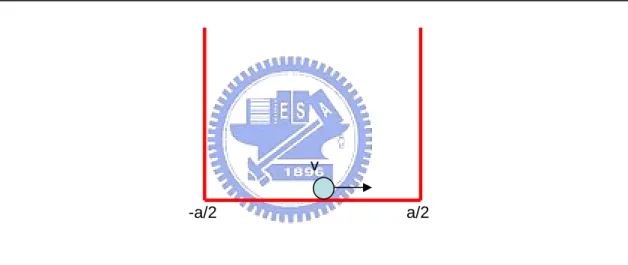
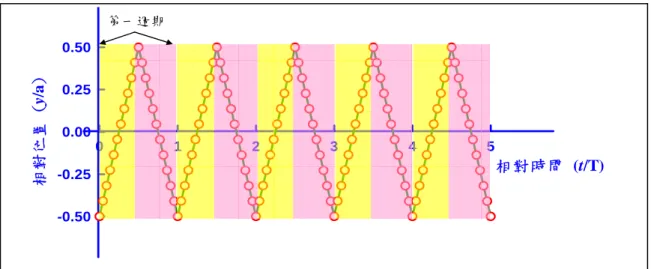
首先討論一個粒子在一個一維封閉的盒內的狀況，其邊界為 (圖 3.1.1)，粒子位置無法出現在邊界外，形成一個無限位能井，若彈子球的初速度 為v_{，且彈子球與盒壁間的碰撞為彈性碰撞，即無能量耗損，則彈子球將在邊界} 內來回碰撞，且速度不變。而彈子球的位置 x_{和時間 t 的關係(圖 3.1.2)(設} 時)，在第一週期，可以兩個方程式表示。 1 , 0 2 2 3 , 2 2 T x vt a t T x vt a t T ⎧ = − ≤ < ⎪⎪ ⎨ ⎪ = − + ≤ < ⎪⎩ _(3.1) 在此引入同餘的觀念，可得並類推至其他週期可得： 1 ( mod ) , 0 ( mod ) 2 2 3 ( mod ) , ( mod ) 2 2 T x v t T a t T T x v t T a t T T ⎧ = × − ≤ < ⎪⎪ ⎨ ⎪ = − × + ≤ < ⎪⎩ _(3.2) 形成一個振幅為 ，週期為 的三角波。 一個二維的彈子球檯(圖 3.1.3)，則可以視為 x、y 二個方向垂直且獨立的彈 子球運動，則在 x 方向速度為 vx，其位置和時間關係，將符合上式的三角波函數， 週期為 a/vx，在 y 方向速度為 vy，其位置、時間關係，亦要符合三角波函數，週 期為 a/vy。x、y 兩方向運動的合成則形成了 2 維彈子球檯的圖形。 在此考慮 3 個參數 ， 其中。ψ 則代表 彈子球出發的起始位置(表 3.1.1)。試著改變不同的參數比較 billiard 的軌跡是否 有所變化。當初始位置不是在原點且兩者互質時，則和 x 軸、y 軸碰撞的次數 和 有關， p 為和 x 軸方向碰撞的次數， q 為和 y 軸碰撞的次數，而比值為有 理數時，則整個圖形成為一個封閉的圖形，或是結束於邊界的端點，當 提高 至(5,13)，可發現整個圖形會碰撞邊界更多次，但最終仍會形成一個封閉性的週 期性軌道(periodic orbit,P.O.)。 2 a 2a v ~ 2 2 a a −

(

− ≤ ≤π φ π

)

(

p q, ,φ

)

2 a x=− 0 t = : : y x v v = p q , p q , p q

圖 3.1.1 一維方形 billiard 邊界 a/2 -a/2

圖 3.1.3 二維方形 billiard 邊界 相對時間 (t/T) 0 1 2 3 4 5 相對位置 ( y /a) -0.50 -0.25 0.00 0.25 0.50 第一週期 相對時間 (t/T) 0 1 2 3 4 5 相對位置 ( y /a) -0.50 -0.25 0.00 0.25 0.50 第一週期 圖 3.1.2 一維彈子球檯位置對時間變化 (a/2,a/2) (a/2,-a/2) (-a/2,-a/2) (-a/2,a/2) v _v y vx x y

表 3.1.1(p:q) 為有理數之二維 billiard 軌跡 (p,q) (1,1) (2,1) (3,2) Different phase

3.1.2 二維簡諧運動的李賽羅圖形

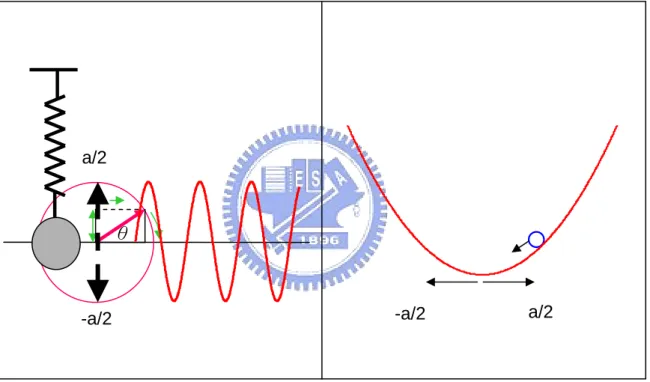
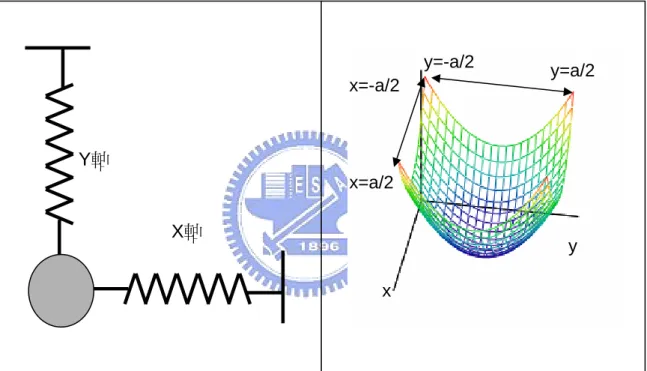
若改以一維簡諧運動、彈簧的往復運動出發(圖 3.1.4)。將一個彈簧掛吊一 個質點後，自然垂下，至整個系統平衡靜止。將質點拉離平衡點後放開，則質點 會作一個上下的往復運動。 依照彈簧的特性可知：一、質點受力情況遵守虎克定律，即F = ⋅k x。二、 位能形式為： 。三、位移和時間的關係為一個正弦函數 。 以彈子球和位能井的形式表示，簡諧運動的位能形式為 ，可視為一 個具有光滑平面的拋物線位能井，在邊界 a/2 處，放入一個彈子球，設彈子球不 受摩擦力等影響，即無能量耗損，球則會沿邊界移動，當球離最低點高度極小， 則球在 x 的方向的運動，形成一個一維的簡諧運動。 比較一維 billiard 和簡諧運動的邊界條件和位移，可以發現兩個具有幾個特 性：一、彈子球皆在靠近位能最低點的附近作週期性的運動。二、位移和時間的 關係，無論是三角波還是 sin 波，皆為一個固定週期的波函數。若考慮二維的簡 諧運動(圖 3.1.5)，可將一個質點，其 x 方向和 y 方向分別接上一個彈簧，其 x 方 向的動能、位能和 y 方向的動能位能無關。形成兩個互相垂直且獨立的簡諧運動。 則二維簡諧運動的位能形式(圖 3.1.5)為 x、y 方向垂直的拋物線圖形，可以看到， 在四個角落的位能最大，在平衡點的位能最小。而二維的簡諧運動，其位移和時 間的函數可以寫成：

(

)

(

)

sin sin x x y y y x A t y A t ω ω φ ⎧ = ⋅ ⋅ ⎪ ⎨ = ⋅ ⋅ + ⎪⎩ (3.3) 而這樣的圖形即為李賽羅圖形。 設ω_x= ⋅ 、q ω ω_y = ⋅ 則函數可改寫成： p ω

(

)

(

)

sin sin x y y x A q t y A p t ω ω φ ⎧ = ⋅ ⋅ ⎪ ⎨ = ⋅ ⋅ + ⎪⎩ (3.4) 2 1 2 U = k x⋅ _{x= Asin(}ω_⋅t) 2 1 2 U = k x⋅

同樣的我們考慮三個參數 (表 3.1.2) ，可以發現，當起始位置不為 0 及π時，p,q 分別代表和 x 軸、y 軸的接觸次數比例。當比例為(1,1)時，整個圖 形呈現一直線或是一個楕圓，比較特殊的(p,q)=(3,2)的圖形有兩個圖形，雖起始 位置不同，但卻是在同一條路徑上。若和 billiard 比較可以發現(表 3.1.3)，李賽 羅圖形在

(

p q, ,φ 和 billiard 相同的情況下，圖形的方向和形狀有著類似的性質，

)

但和邊界的接觸點不同。這是因為，兩者都是由兩個互相垂直、獨立的周期波所 組合而成。 但 ,p q 比值為無理數時(表 3.1.4 表 3.1.5)，x 軸的碰撞次數和 y 軸的碰撞次數 無法呈一個固定的比例，則隨著碰撞次數的增加，形成越來越密的軌跡，最後佈 滿整個邊界。 前面週期波的性質，可以解釋在彈子球檯及李賽羅圖形中有理數及無理數會 形成軌跡是否封閉。已知一個二維的彈子球檯，可視為一個方向為 x 軸，一個方 向為 y 軸的二個三角波疊和，一個李賽羅圖形，則可視為二個正弦波於 x 軸及 y 軸疊和。故在此以二個三角波位置隨時間變化為例。 首先以時間軸作 x 軸作兩個三角波的比較(圖 3.1.6)，週期分別是 ， ， 此時我們可以將其中一個三角波的週期 T 視為一個單位長，兩個週期比值為 ， 則另一個波長的週期為 pT q ，當 為有理數時，由最小公倍數可知，當t= p q T. . 時 會形成一個循環。當 為無理數時，由數學定義可知，一個無理數無法以單位 長度表示，即 pT q 無法由單位長 T 表示，這代表 p T q 與 T，沒有公倍數，在時間 軸上永不重合。故無論所經過時間多長，皆無法形成一個循環，圖形不會出現重 覆。 即得到了當 t 形成循環時，2 維彈子球檯及李賽羅的軌跡圖形必定重覆，也就 是將形成一個封閉的圖形。t 無法形成循環時，軌跡無法重合，必是一個開放的 圖形，最終佈滿整個彈子球檯。在此可以發現，一個古典粒子在有理數的情況下 1 2a v ₂ 2a v p q p q p q

(

p q, ,φ

)

形，無法形成可供辨識或有特定規律的軌跡。故後來量子力學中，以波動解釋粒 子運動，與古典彈子球檯作連結時，也特別著重於週期性軌道的研究與發展。

圖 3.1.4 一維簡諧運動示意圖 (a)一維簡諧運動 (b)位能井形式 a/2 -a/2 -a/2 a/2 θ

圖 3.1.5 二維簡諧運動示意圖 X軸 Y軸 x y x=a/2 x=-a/2 y=-a/2 _y=a/2 (a)彈簧的二維簡諧運動 (b)二維簡諧運動邊界條件

表 3.1.2 (p:q)為有理數之二維李賽羅軌跡 (1,1) (2,1) (3,2) (5,13 (p,q) Different phase

表 3.1.3 二維 billiard 和李賽羅軌跡比較

(p,q) _{(2,1) (3,2)}

billiard

李賽羅

表 3.1.5 (p:q)為無理數之二維李賽羅軌跡 (p,qψ) t 2 2,1, 3π ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ 2T 4T 8T 16T 32T (p,qψ) t 2 2,1, 3π ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ 2T 4T 8T 16T 32T 表 3.1.4 (p:q)為無理數之二維 billiard 軌跡

圖 3.1.6 二維 billiard 位置隨時間變化 相 對 時 間 (t/T_y) 0 1 2 3 4 相 對位置 ( x/a , y /a) -0.50 -0.25 0.00 0.25 0.50 T_x=2/5 ; T_y=1

T=2

相 對 時 間 (t/T_y) 0 1 2 3 4 相 對位置 ( x/a , y /a) -0.50 -0.25 0.00 0.25 0.50 T_x=2/5 ; T_y=1

T=2

3.2. 二維封閉波動系統的束縛態

馬克思威四條方程式及電磁波概念的確立，人們對於波的理解，由單純的機 械波，進展到不需要介質傳遞的電磁波。而有關於邊界內本徵態的了解也更進一 步。而後光電效應發現，將光視為一個粒子，碰撞一個活性大的金屬後可以游離 電子。則是光與粒子結合的開端。愛因斯坦為此提出了”波粒二元性的概念”，即 電磁輻射除了具有波的性質外，也同時具有粒子的性質。直至德布羅依則更進一 步提出，一個物質粒子也具有波動性，稱之為”物質波” [21-22]。 物質波屬於一種機率波，即在某地發現某粒子的機率密度將呈波函數的形式 分佈。在電子繞射實驗中，可以發現，電子在通過晶格狹縫後的電子密度，可形 成波的干涉條紋，証明了粒子也具有波動的性質。至此，粒子與波動獲得連結。 然粒子性具有明確的位置和速度，放入封閉的邊界內會形成特定的軌跡(PO)，則 一個波動系統在一個封閉的邊界內，波動性會如何呈現[23]？是否也具有特定軌 跡？ 3.2.1

本徵態與軌跡

無論是機械波、電磁波或是物質波，在固定邊界的條件下，必需以駐波的形 式才能穩定的存在。故必需符合特定的波函數，而這些波函數，即稱為”本徵態” 兩端固定的琴弦所發出的機械波、在無限位能井中電子的物質波，或是在一維的 billiard 駐波[24-25]，若 x 軸方向的邊界為 0~a，則不含時間的波函數(圖 3.2.1) 可寫成：

( )

2 sin( ) x n n x x a a π ψ = (3.5)

圖 3.2.1 一維 billiard 的波函數 n=0 n=2 n=4 n=1 n=3 n=5 n=30 n=6

在量子力學物質波的概念中，波函數的振幅可代表粒子出現的機率。若和古 典彈子球比較，在方形的位能井中彈子球，因保持等速運動，各點發現的機率都 相同。而 n 值極小時，其本徵態振幅集中在位能井中間，和古典情況不同，然隨 著 n 值逐漸加大，波形逐漸緊密，其振幅逐漸平均分佈於位能井內，即符合量子 力學在大尺度的情況下，其結果與古典粒子在方形位能井內各點的發現機率接近 的假設。 改考慮一個二維方形的 billard(表 3.2.1)，設 x 軸方向的邊界為 0~a，y 軸方 向的邊界為 0~a，而波在邊界內同樣必需以駐波的形式存在。又 x、y 方向的波 函數彼此獨立，故 2 維波函數表示成： , x y x y ψ =ψ ψ⋅ (3.6) , 2 sin( ) sin( ) x y n m x y a a a π π ψ = ⋅ (3.7) 形成一個以 x、y 軸對軸的波函數圖形。同樣的在(n,m)極小時，其強度分佈 集中於中間，然隨著(n,m)值變化，整個振幅也漸平均分佈於整個邊界內，代表 一個古典粒子在方形 billiard 內的隨機軌跡。 若改變不同的邊界條件，可知駐波波函數也依不同的邊界條件而有所不同 (表 3.2.2)，以聲波、音律為例：畢氏學派就已經發現不同長短、大小、形狀的物 體，產生的聲音高低及音色不同，目前已經了解，這和不同邊界所擁有的本徵態 有關。以圓形的鼓面振動為例，給予敲擊時，因為邊界是固定的，振動需符合邊 界振幅零的邊界條件，而形成駐波，而不同的駐波形式，具有不同的頻率，故敲 擊鼓面所發出的聲音，並不為單一頻率的振動，而是含有數個不同頻率，形成所 謂的”音色”，但具有較高能量，較易觀測的，多為低階、簡單的駐波形式，即為 所謂的”基頻”。在樂器上所形成的駐波形式，早期多屬於工匠的技巧及經驗累 積，經過廣泛的研究，才令人對機械波的形成有進一步的認識。

表 3.2.1 二維 billiard 的波函數 Eigenstate

(n,m) Eigenstate Intensity (n,m) Intensity

(0,0) (1,0) (1,1) (1,2) (1,3) (0,1) (0,2) (2,2) (3,0) (20,20)

表 3.2.2 圓形邊界形成鼓面的駐波 (1,2) (2,1) (0,3) (0,2) (1,1) Intensity Eigenstate (n,m) Intensity Eigenstate (0,0)

3.2.2

波的干涉

然不同的本徵態如何彼此疊加、干涉？很早之前，人們就已發現粒子在相遇 時，要不兩者結合，要不兩者分開但兩組不同的水波，在相遇時，會彼此干涉， 並造成亮暗相間的條紋，則稱為干涉(圖 3.2.2)。 數學上所謂的疊加原理表示：一個線性函數其變項值相加的函數值=各函數 值的相加。即 1 2 1 2 ( ...) ( ) ( ) ... F x + +x =F x +F x + (3.8) 故一個線性的波函數可以視為許多波函數的疊加。利用這樣的概念，所有的波 形，我們都可以利用傅利葉轉換，視為許多正弦波疊加而成。不同的波函數疊加 在空間上一點形成振幅加成或抵消的效果，則稱作建設性干涉與破壞性干涉。_一 維的方形邊界內，由(3.5)式得可存在的本徵函數，若加以疊加得：

( )

0 0 2 sin sin N M n n N A n n v n n v x x t x t NA a a a a a π π _φ π π _φ + = ⎛ ⎛ ⎞ ⎛ ⎞⎞ Ψ = ⋅ _{⎜ ⎜} + + _⎟+ _⎜ − + _⎟⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠

∑

(3.9) 其中A 為每個波函數的振幅，_n NA則是正交規一化的係數。 0 0 2 2 N M n n N NA A + = =

∑

(3.10) 在此若固定時間 t=0，即不考慮時間項一個波包可以寫成

( )

0 0 2 2 sin N M n n N A n A x x NA a a π ψ + φ = ⎛ ⎛ ⎞⎞ = _{⎜ ⎜} + _⎟⎟ ⎝ ⎠ ⎝ ⎠

∑

(3.11) 使得一個局部區域，有明顯的值，則形成一個波包。若視一個極狹窄的波包，可 以發現其具有明確的位置和速度，漸具有粒子的性質。 一個波包的形成受到幾個因素影響. 一、組成正弦波的相位。 二、組成正弦波的振幅。 三、組成正弦波的數量(mode)。

一、波包與相位的關係

一個行進波，可以視為一個固定的波形，其每一點振輻隨著時間改變，在此 我們引入複數平面的概念(圖 3.2.3)，以一個正弦波為例：若某一點 P 其振幅為 A 在原地振盪，其位置函數可寫為 y=Acos(θ)，代入ei⋅θ =cos( )θ +isin( )θ ，可得

i y= ⋅A eθ，其中若其相位隨著時間變化即θ ω= ⋅t，則隨時間函數即為 i t y= ⋅A eω φ+ ，故隨位置波函數若為 ( )Ψ x ，則隨時間的波函數則為 ( , ) ( ) i t x t x eω φ+ Φ = Ψ ⋅ ，其中相位差φ代表波函數的初始位置，相位變化則代表波 函數隨時間的移動變化。 若我們在固定時間條件下，比較兩個相位分佈不同的波包(圖 3.2.4)

( )

0 0 2 2 sin N M n A n n N A n x x A NA a a π ψ + φ = ⎛ ⎛ ⎞⎞ = _{⎜ ⎜} + _⎟⎟ ⎝ ⎠ ⎝ ⎠

∑

(3.12)

( )

0 0 2 2 sin N M n B n n N B n x x B NB a a π ψ + φ = ⎛ ⎛ ⎞⎞ = _{⎜ ⎜} + _⎟⎟ ⎝ ⎠ ⎝ ⎠

∑

(3.13)

其中N₀ =100，M =20，A_n =B_n ⇒normal distribution，φA= ， B rondom0 φ = ， 即 Aψ 彼此間的相位差為 0， Bψ 彼此間相位前為隨機分佈。可以發現， Aψ 的組 成波會彼此建設性干涉，形成的波包會很明顯的局顯在一個區域。但是 Bψ ，則 無法明顯的形成一個波包並局限在一個小區域中。

二、波包與振幅的關係

同樣地若比較將兩個同相位的波包，其中的 Aψ 振幅成高斯分佈，而 Cψ 振 幅為隨機分佈(圖 3.2.5)，即

( )

0 0 2 2 sin N M n A n n N A n x x A NA a a π ψ + φ = ⎛ ⎛ ⎞⎞ = _{⎜ ⎜} + _⎟⎟ ⎝ ⎠ ⎝ ⎠

∑

(3.14)

( )

0 0 2 2 sin N M n C n n N C n x x C NC a a π ψ + φ = ⎛ ⎛ ⎞⎞ = _{⎜ ⎜} + _⎟⎟ ⎝ ⎠ ⎝ ⎠

∑

(3.15)

rondom distribution n C ⇒ ，φC = 0 可以發現 Cψ 波包的峰值較小，分佈的也比較寬，甚至有另外的小波峰出 現，而 Aψ 波包分佈的較窄，振幅的峰值亦較大，能量較局限於特定的位置上， 形成一個較佳的波包。在實驗上以高斯分佈、等比重分佈、possion 分佈等特定 的分佈方式，也會得到較好的結果。 而不同相位和不同振幅分佈的圖形，比較可以得到一個明顯的差異，在同相 位分佈時，無論組成波振幅的分佈為何，兩個波包必定有峰值是重疊的，這是因 為振幅分佈代表各個波函數組成的比例，不同的比例組成不同的波包，具有不同 的波包寬度，而相位差隨機分佈，則會造成兩個波包無法重合，這是因為相位代 表著每個波函數間彼此的起始位置，不同的相位，即代表起始位置不同。

三、波包與 mode 的關係

當二個波包，其組成波函數的數量不同時，會對波包的形成造成什麼樣的影 響？在此取一個波包了方便起見，在此取 Dψ 和 Aψ 作比較(圖 3.2.6)，其中：

( )

0 0 2 2 sin A N M n A n n N A n x x A NA a a π ψ + φ = ⎛ ⎛ ⎞⎞ = _{⎜ ⎜} + _⎟⎟ ⎝ ⎠ ⎝ ⎠

∑

(3.16)

( )

0 0 2 2 sin d N M n D n n N D n x x D ND a a π ψ + φ = ⎛ ⎛ ⎞⎞ = _{⎜ ⎜} + _⎟⎟ ⎝ ⎠ ⎝ ⎠

∑

(3.17) normal distribution n n A =D ⇒ ，φA=φD= 0 MA=20 ， MD=10 可以發現，若一個波包所組成的 mode 越多，則這個波包越是集中，反之組 成的 mode 越少，則波包的分佈則越寬，而波包分佈越寬，代表其位置和速度的 不確定性越高，反之，波包分佈越是局限在一個區域內，代表其能量越集中，其 位置的不確定性越低，如同一個質點，在此我們可以視為一個由許多 mode 所組 成的波包，將範圍集中於一個非常小的位置上。

圖 3.2.3 行進波相化變化示意 A*eiθ i*A*sin(θ) A*cos(θ) θ P(x0,y0) (x0,yt) Δt

圖 3.2.2 波動性干涉示意

圖 3.2.4 不同相位差對波包的影響 2 A

ψ

2 B

ψ

0a 0.2a 0.4a _x 0.6a 0.8a 1a

120 (a)波包振幅與距離關係 100 105 110 115 120 100 105 110 115 n A _Bn (b)ψ_A的相位分佈 (c) ψ_B的相位分佈 0 0 8 8

圖 3.2.5 不同振幅分佈對波包的影響 (a)波包振幅與距離關係 (b)ψ_A的振幅分佈 (c) ψ_B的振幅分佈 2 A

ψ

2 C

ψ

0 0.2a 0.4a 0.6 0.8 1a x 120 n A 100 105 110 115 120 n 100 105 110 115 n n c

圖 3.2.6 不同 mode 對波包的影響 波包振幅與距離關係 2 A

ψ

2 D

ψ

0a 0.2a 0.4a 0.6a 0.8a 1a

3.2.3

對應於彈子球檯的波函數

現在將波包的概念引入方形彈子球檯的波函數中。若有 m 個波疊加，形成波 包，nx為一個特定 Nx 開始，則 nx=Nx+mx則包含時間的波函數則為：

( )

1 0 1 2 sin( ) x x x x M im x x i t m x N m x e x e a a M φ ω ψ π − − = + Φ =

∑

⋅ ⋅ (3.18) 若將波包依時間作圖(圖 3.2.7)，可發現波包依時間在邊界內反覆移動，其 移動如同彈子球在一維 billiard 的運動。然值得注意的是：在古典彈子球的 billiard 中，彈子球本身不會因位置和時間有所改變，而波包在靠近 x=0、x=a 的邊界時， 波包的呈遽烈的振盪，且極值會急遽的增大至 2 倍左右。這是因為在邊界，可視 為入射波和反射波互相干涉、疊加。當 t=T/6，可以發現波包的位置在 L/3，而 無限位能井內的古典粒子，在方形的邊界內行彈性碰撞，保持等速率的往復運 動，一個週期的路徑長為 2L，而經過 T/6 則通過 2L/6 的距離，剛好在 L/3 的位 置上，兩者相互符合。 但改以波包方式疊加：x 方向疊加的數量比 y 方向疊加的數量為 mx:my=p:q 即mx=pm，my=qm，則不含時間的波函數可寫成，可依 2 維波函數表示成： 0 0 0 0 , x y N pm N qm x y x y x y n N n N ψ ψ + + = = Ψ = Ψ ⋅ Ψ =

∑ ∑

⋅ (3.19) 含時間的波函數則是： , x y x y Φ = Φ ⋅Φ (3.20) 依時間將波包位置畫下，可得到(圖 3.2.9)，此時波包的運動狀態和一個粒子的 運動狀態相同。 若我們將波包在二維 billiard 的非時間項取出，畫出軌跡圖(表 3.2.3)，可得 到下表，下圖和二維粒子彈子球台的圖形相似，但差異在於，粒子彈子球台的軌 跡為一狹窄實線，代表粒子在軌跡出現的機率為一個連續的分佈，但波包形成的

撞點及軌跡交會處，顯然的節點是由許多波疊加、干涉出來的結果，而節點的出 現代表波包在軌跡上出現的機率為一個不連續的分佈。這在古典力學和量子力學 中是一個很大的差異。至此，已成功的將波以疊加的方式，組成古典彈子球檯的 軌跡。但改變觀察的尺度，疊加的波函數數量不同(表 3.2.4)。可以發現，當疊加 的數量較少時，得到的軌跡較寬，無法呈現直線的軌跡，而是以波的狀態呈現， 且具明顯的干涉條紋。但隨著疊加的數量增加，所得到的軌跡寬度越窄，也越接 近直線，粒子的出現機率也越限制在特定軌跡上，即越接近古典粒子的結果，符 合量子力學在大尺度的情況下，必需接近古典力學結果的條件，也是古典力學與 量子力學得以結合的部分。 當疊加的波函數越多，能量越是集中於一個點上，波長則逐漸縮短，可以發 現其波的表現逐漸帶有粒子的性質。這便是波、粒二重性。由德布羅依的公式的 物質波概念，可以了解，當一個粒子在尺度接近，也應呈現波動的形式。 而古典軌跡出現與否，不在於觀測事物的大小，無論是一個固定邊界的機械 波、波導內的電磁波抑或位能井內電子形成的物質波，只要數量級夠大，疊加的 波函數夠多，波動也能和粒子結合呈現粒子性。

圖 3.2.7 一維 billiard 內波包位置隨時間變化 t=0T t=1/4T t=1/2T t=3/4T X=0 X=L t=1/6T t=2/6T t=4/6T t=5/6T

圖 3.2.8 二維 billiard 內波包位置隨時間變化 t=0 t=1 t=2 t=3 4 5 6 7 8 9 10 11 12 13 14 15 t=3 t=3 x=a x=0

(5,13) (3,2) (2,1) (1,1) (p,q) Different phase 表 3.2.3 二維 billiard 波函數所組成的 P.O.

表 3.2.4 不同 mode 情況下，二維 billiard 波函數所組成的 P.O. m (1,1) (2,1) (3,2) 10 20 5 15 (p,q)

3.2.4 對應於李賽羅圖形的波函數

若以波的形式探討李賽羅圖形[27-28]，會是如何呢？一維簡諧運動的位能形 式和 billiard 的無限位能井並不相同，但波在邊界內仍是以駐波的形式存在。而 在導入一維簡諧運動駐波的波函數前，先要了解 Hermite 函數。 Hermite 是一個具有強烈特色的數學家，一個不會考試的數學家，天生跛足 但仍十分樂觀，從小的成績就不佳，尤其是數學成績不佳，非常痛恨學校中呆板 的數學課程，卻不放棄繼續升學，雖在年輕時就有良好的數學成就，卻五次落榜 才考上大學，因為跛足無法進入工科學系，而就讀文學。享富盛名，卻因大學成 績不佳，無法繼續升學，只能在學校擔任助教長達 25 年。直至四十九歲，巴黎 大學請他擔任教授，而後幾乎所有的法國大數學家都是他的門下。雖然求學經過 不順利，但他的數學成就卻十分驚人，而量子力學領域中，也廣泛的應用他的數 學成果。在拋物線的位能井中，駐波是以 Hermite Function 的形式存在。

( )

2 2 ( ) 1 n n _{x x} n d Hn x e e dx − = − (3.21) 波函數的形式為：

( )

( )

2 2 1 ! 2 x n n n x e H x n ψ π − = ⋅ ⋅ ⋅ (3.22) 形成的駐波為(圖 3.39)

圖 3.2.9 一維拋物線位能井的波函數 n=0 n=2 n=1 n=3 n=5 n=2 n=30

在一維拋物線的邊界中，我們可以發現，當 n 值較小時，其產生的波函數， 峰值集中於中間地帶，但當 n 值漸漸加大時，其產生的波函數中間部分漸凹，兩 端則較高。若以此與古典粒子在一維拋物線邊界內運動的位置機率分佈比較。可 以發現古典粒子在兩側邊界的位罝機率較高，在中間地帶的出現機率較低，這是 因為粒子在兩側的速度較慢，所待時間較長的緣故，正好符合 n 值極大的情況。 同樣的，我們將許多波函數疊加，形成波包並將其依時間的變化紀錄，可得 到下列圖形，可發現此波包和 billiard 同樣在邊界內週期性的運動，但觀察 t=1/6T 時圖形可發現，在 billiard 中，波包的位置在 1/3 處，而在拋物線的邊界條件中， 則是在 a/4 處。若比較一維簡諧運動。 2 sin( ) x A t T π = ⋅ (3.23) 此時 2 a A= ， 1 6 t= T代入，得 4 a x= 可以發現波包在邊界內，並非以等速率作週期性的運動，而是行簡諧運動， 其運動方式及軌跡，如同一個粒子在拋物線邊界內的表現。

圖 3.2.10 一維簡諧運動波函數位置隨時間變化

t=0

t=1/6

t=1/4

t=2/6

t=1/2

t=5/6

t=3/4

t=4/6

t=T

若在二維拋物線邊界內的波包，會有什麼樣的運動狀態？首先討論在一個二 維拋物線內的波函數為何？首先此邊界為 x、y 方向互相獨立的二組拋物線形成 的二維邊界，由前可知，拋物線內可允許的駐波形式為 Hermite function， 因為 x、y 方向互相獨立，故波函數可視為 x、y 方向獨立的波函數疊合(表 3.2.5)，即 ( , )x y ψ_n( )x ψ_m( )y Ψ = ⋅

( )

( )

2 2 2 2 , 1 1 ! 2 ! 2 x y n m n m n m e H x e H y n π m π − − Ψ = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ (3.24) 在電射光學中，也可發現類似的圖形，這是因為雷射共振腔中，共振用的反 射介質，常使用凹面鏡作為共振邊界，而凹面鏡的鏡面邊界，正是一個二維的拋 物面。形成所謂的 TEM。 二維的波包，因波函數為線性獨立的函數，故可以 x、y 方向的波包疊加得到(表 3.2.6)： Φ=ΨxΨy (3.25) 可得到在一個 billiard 的邊界條件中，粒子行等速運動，則干涉、疊加後產生的 波包，也隨著時間行等速運動，形成古典 billiard 的軌跡。在一個拋物線的邊界 條件中，粒子行簡諧運動，則波包也隨著時間行簡諧運動。形成李賽羅圖形。

表 3.2.5 二維拋物線位能井的駐波函數 (3,3) (2,2) (2,1) (1,1) (3,0) (2,0) (1,0) (0,0) Intensity eigenstate (n,m) Intensity eigenstate (n,m)

表 3.2.6 二維李賽羅波函數所組成的 P.O.

(3,2) (2,1) (1,1)

第四章 開放式圓形彈子球檯與漸近分數

圓形的彈子球檯與方形的彈子球檯屬於軸對稱的邊界不同，具有點對稱的性 質，故圓形彈子球檯能表現與方形彈子球檯不同的數學性質。然開放性的彈子球 檯，其圖形隨著開放的範圍有所改變，試以探討無理數中漸近分數，尤其是黃金 比例，在視覺上的呈現。

4.1. 圓形彈子球檯內的古典粒子

若我們改變邊界條件，改以一個圓形的彈子球檯[24,28]，探討彈子球的軌 跡。則先假定彈子球在球檯中為彈性碰撞，即每次的碰撞不會損失能量，可以簡 單的幾何證明，彈子球在不同的初始條件下，在經過連續的碰撞入射角及反射角 維持一個定值。每次的碰撞距離也是固定的。將碰撞距離視為圓中的一弦，可發 現，每弦的圓心角α為定值。 在此命 p q α = π 。可將 q 視為將圓心均分為 q 等分，在圓周上打上 q 個點， 而 p 代表每隔幾個點畫上連線(表 4.1.1)。當 p=1 時隨著 q 的增加，可以發現，畫 成一個多邊形，而且其圖形越接近圓形的邊界。引入完全剩餘系的性質，我們將 circle billiard 的軌跡視為一個以 q 為模的剩餘系，而所有的碰撞點組成一個完全 剩餘系，則 ,p q 兩個為互質的整數時，代入不同的 p 仍會是一個完全剩餘系，表 現在圖形上則仍是一個封閉且完整的路徑。 我們也可以計算當給定一個固定 q 值時，有幾種圖形的呈現，在此我們引入 尤拉函數，計算在小於 q 的情況下，有幾個 p 值被允許，在此因為碰撞點排列可 有順時鐘、逆時鐘兩個方向，然在圖形表現在並沒有差別。故可得： ( ) 2 q n=φ 以 q=11 時為例：

(

11 1

)

5 2 n= − = ，計有五種表示。

若 p,q 的值為無理數(表 4.1.2)，無法等切割圓時，則會發現，隨著碰撞次數 的增加軌跡也會越來越密，且不形成封閉的路徑，但和方形 billiard 不同的事， 彈子球隨著不同的初始條件，會有不同半徑的同心圓為禁止區域。形成包若線的 圓形。

圖 4.1.1 二維圓形 billiard 邊界

α

α

(1,5)

(1,11)

(1,4)

(1,3)

(1,1)

(4,11)

(5,11)

(3,11)

(2,11)

(1,11)

表 4.1.1 圓形彈子球檯與完全剩餘系

(80 hits)

(160 hits)

(40 hits)

(20 hits)

(10 hits)

α和圓周角比值為無理數 表 4.1.2 無理數圓形彈子球檯

4.2. 開放式彈子球檯

若我們取一個圓形球檯，連續散出彈子球後(圖 4.1.2)，打開其球檯的邊界， 則彈子球會向外散出，則越早散出的彈子球，離圓心越遠，則會形成一個發散狀 的圖形，其角度變化可形成一個等差級數，其離圓心的半徑變化亦可形成等差級 數。引入阿基米德螺旋，可以知道其角度變化與半徑成正比，故可以發現，各個 彈子球其連線將形成阿基米德螺旋。 我們先比較一個 close 和 open 的圓形彈子球檯的差異(圖 4.1.3)，可以發現封 閉的圓形彈子球檯，若 p:q 為簡單整數比時，可以形成一個封閉的圖形，而 q 值 漸大時整個圖形越趨近於圓形的邊界，而圖形也越單調越不明顯，若是 p:q 為無 理數時，都是呈現一個同心圓狀的圖形，但放入一個開放的彈子球檯時，圖形則 變的十分複雜而有變化。故試以一個開放的彈子球檯對於呈現 q 很大的彈子球性 質，比較 q 值很大及無理數時的圖形。 首先我們模擬(P,Q)其中 Q=89，0<P<45，可以發現，當(P,Q)=(34,89)時，不 但出現雙螺旋(圖 4.1.4)的現象且最為明顯、清楚。當(P,Q)=(32,89)時(圖 4.1.5)， 雖也有雙旋轉的現象，但注意中心部分，可以看到中心是呈現三個支臂的順時針 螺旋。而接近的(33,89)、(35,89)都無法出現雙螺旋的圖形。 探究雙螺旋的圖形效果，源來自於花葉序的排列觀察，其中葉原體的排列角 度正為黃金比例。而開放的圓形彈子球檯，彈子球離中心的距離隨時間而改變， 與植物花葉離中心遠近依照生長時間長短變化的方式類似。若觀察上圖可以發現 出現雙螺旋的 33/89 正是黃金比例的漸近分數之一。已知漸近分數是一個無理數 在分母不大於 P 的情況下的最佳逼近。故當(P,Q)為黃金比例的漸近分數時，應 呈現雙螺旋的圖形效果。 然若 P 選擇的範圍>45 會如何(圖 4.1.6)？由圓子彈子球檯中完全剩餘系的性 質可知，(P,Q)可視以 Q 為模的完全剩餘系，可得表示方式的數量為 (89) / 2φ ，這

(p,q)=(q-p,p)。然在一個開放的邊界中，順、逆時鐘排列是不同的排列方式，故 圖形會具有對稱、但旋轉方向不同的圖形。(34,89)具有雙螺旋的性質，由完全剩 餘系的性質可知，(89-34,89)=(55,89)也具有雙螺旋但旋轉方向不同的性質。而費 式數列的特性為： 1 2 n n n F =F₋ +F₋ ，經移項可得 2 1 n n n F −F₋ =F₋ 可以發現{34,55,89}皆是費伯納希數列的數項。也都具有雙螺旋的視覺特 性。若以連分數逼近無理數取漸近分數，從性質可知：可依次得到不同的漸近分 數 n n p q ，且 n 越大、越是高階的的漸近分數越是逼近無理數的真值。 3 1 2 1 2 3 1 2 3 5 8 13 21 34 89 , , , , , , , , , , , 1 1 2 3 5 8 13 21 55 p p p q q q ⎧ _{⎫ ⎧ ⎫} ⋅⋅⋅ = ⋅⋅⋅ ⎨ ⎬ ⎨ ⎬ ⎩ ⎭ ⎩ ⎭ 若我們取幾個不同的漸近分數(表 4.1.3)，比較不同 n 值得到的漸近分數，在 開放圓形彈子球檯內的情況。可以發現 1、漸近分數，在點數很多的情況下，會 呈現發散狀的直線排列，這是因為彈子球本來就是直線的向外發散，而雙螺旋則 是因為密集排列造成的視覺感受。2、若 n 值越大越是接近無理數的漸近分數， 在點數高的情況下，越能保持雙螺旋的視覺感受。當我們取漸近分數 (4181 ,10946)(圖 4.1.8)作圖，取 1000 點仍可以發現雙螺旋的圖形，符合 n 值越大 漸近分數越逼近無理數，圖形也越接近的特性。

1 2 3 4 5 圖 4.1.2 二維開放式圓形 billiard

順螺旋 逆螺旋

圖 4.1.5 不同(p,q)開放式圓形 billiard 圖形 (1,89) (2,89) (3,89) (4,89) (5,89) (6,89) (7,89) (8,89) (9,89) _{(10,89) (11,89) (12,89)} (13,89) (14,89) (15,89) (16,89) (17,89) (18,89) (19,89) (20,89) (21,89) (22,89) (23,89) (24,89) (25,89) (26,89) (27,89) (28,89) (29,89) (30,89) (37,89) (38,89) (39,89) (40,89) (41,89) (42,89) (43,89) (44,89) (31,89) (32,89) (33,89) (34,89) (35,89) (36,89)