五年級資優生在非例行性數線問題解題表現的個案研究

通訊作者：劉祥通，e-mail：shiangtungliu@gmail.com 收稿：2019 年 7 月 18 日；接受刊登：2019 年 12 月 3 日。 劉祥通、洪筱柟（2020）。 五年級資優生在非例行性數線問題解題表現的個案研究。 臺灣數學教師，41（1），1-25 doi: 10.6610/TJMT.202004_41(1).0001

五年級資優生在非例行性數線問題解題表現的

個案研究

劉祥通1 洪筱柟2 1_{國立嘉義大學數理教育所} 2 臺北市私立東山高中 本研究主要目的在探討一位五年級資優生在數線問題的解題表現。為了深入了解 個案的解題表現，本研究採用個案研究法。研究者根據學生的課程進度自行編製 「非例行性數線問題任務單」給個案進行解題，藉由個案學生在任務單上的解題 表現作為訪談的基礎，又依據 Schoenfeld 所提出的資源、捷思、控制與信念四個 項目分析個案的解題表現。本研究有下列發現：1. 能利用「等值分數」的概念以 及「利用兩點之間距離當作基準量」為個案學生解題的重要資源、2. 能 展 現 多 元的策略，以解不同的數線題型、3. 個案學生以「高、低階兩單位並用」方式 找尋目標點與「數間隔數」等方法來控制答案的合理性、4. 個案學生在解題之 初，持有「數線上越左邊的坐標越小、越右邊的坐標越大」以及解題之後，發展 出「距離參考點一定長度時，會有左右兩個目標點」的信念。 關鍵詞：小學數學、資優生、解題表現、數線問題

壹、 研究背景與目的

近年來，許多的數學教育人士都同意「將數學視為解題」。舉例來說，美國數學督 導學會（National Council of Supervisors of Mathematics, [NCSM], 1977）指出「學習解題 是研讀數學的主要目的」；接著美國數學教師協會（National Council of Teachers of Mathematics, [NCTM], 1980）在行動綱領亦強調「解題是數學教育的中心」；1989 年 NCTM 在 其 出 版 的 中 小 學 數 學 課 程 及 評 量 標 準 中 第 一 項 即 提 出 「 數 學 即 是 解 題 （mathematics as problem solving）」；之後在 NCTM（2000）所公佈的數學課程原則與標 準中，也把「問題解決（problem solving）」列為重點之一。再者，我國 108 課綱除了強 調數學素養以外，數學教育的課程目標有強調：培養運用數學思考問題、分析問題和解 決問題的能力， 以及培養日常生活應用與學習其他領域/科目所需的數學知能。由此可 見，數學解題在數學課程中所受到的重視。 眾多的學者都以解題歷程來分析解題的行為，唯獨 Schoenfeld（1985）以影響解題 的變項來探討解題的表現，因此研究者挑選 Schoenfeld（1985）所強調數學解題研究方 向所需要考慮的四個變項，以詮釋個案的解題表現，此四個變項分別為資源、捷思、控 制與信念，其中主要的原因在於 Schoenfeld 認為在四個變項中，控制因素居於較為關鍵 的地位，因為如何有效的運用資源、如何採用適當的捷思策略，常常是由控制因素所主 導（Schoenfeld, 1985）。在研究者的課室中，發現許多學生最嚴重缺乏的就是控制答案 的能力，許多小朋友只執著於算出答案而忽略掉答案的合理性，研究者也想經由此研究， 了解資優生是否在解題上能有優異地控制答案的能力。 數線就是一種數字符號與視覺結合而成的表示法，它可以表示出數線上的一個數值， 或是一個線段長；數線具有相同的單位長及等分段的特徵，只要標示兩個參考點的數字， 就能找出其他點所表示的值，且數線可以當作是一把尺，因為數線是連續的，任兩個數 之間必定有一個數存在的稠密性質。數線問題具有以上多種性質，所以研究者選擇數線 問題作為研究的題材，以考驗解題者解決問題時是否能利用上述性質已克服解題的障礙？ 數線也是問題表徵的重要項目之一，學生如何在數現表徵他們的想法，可以透過外顯的 落筆順序來判斷，也可以輔之以訪談來追問。Mayer（1992）指出，學生的解題困難主 要是發生在問題表徵（problem representation）階段，而非在問題解決（problem solving） 階段，如果能在國小階段讓學童具備數線表徵關鍵能力，相信對學童的數學解題能力會 有事半功倍之效。

本研究選擇研究參與者為通過瑞文氏黑白圖形補充測驗且百分等級為九十九的五 年級資優生小貞（化名）。哇，難得出現一位百分等級是九九的學生，除了聰明、活潑、 開朗，好學、好奇的特質以外，而且個案在解決非例行性的問題時，勇於嘗試運用自己 方式來解題，也很有耐心面對難題，並清楚寫下數學算式並解釋原因，表達能力也是十 分清楚，所以更可以突顯其解題想法的原創性。值得一提的是，她解有關「文字題型」 的數線問題都能迎刃而解，本文因而再以「標數題型」挑戰她，以探討她的解題表現。 如果在數線上標示兩個參考點的位置與數值，其他點的位置與數值，就已經被定位 了。個案既然如此優秀，任務單就給定二個分數的參考點，如何尋找第三個點？也給二 個點，如何尋找原點位置？再者，如果告訴已知的二點（A、B）距離，再提供 C 點位 置，且𝐴𝐵̅̅̅̅ = 𝐶𝐷̅̅̅̅，如何找出 D 點的多個位置？以上問題都是非例行性問題，課堂與課外 的老師都沒有介紹過，研究者好奇小貞是否能解答非例行任務單呢？ 本研究旨在探討個案小貞在數線問題的解題表現。研究者認為資優生在拿到非例行 性問題時，常採取自發性的策略來解決問題，面對陌生且無法用直接的算則來解決的題 目，能夠觀察題目所提供的線索而思考出自行的解決方式，因此其所運用的解題策略、 直觀方法，控制能力與所持的數學信念等，是值得我們探索與解析的課題。

貳、 文獻探討

本研究主要的目的在於探究資優生的解題表現，以數學解題與影響因素、資優生的 解題特質、數線問題，作為研究者研究時的理論與依據。

一、數學解題與影響因素

近年來，我國及世界各國對於數學解題能力都相當的重視，Kilpatrick（1985）指出， 所有的數學都是在形成問題及解決問題的過程中被創造出來的。在 NCTM（2000）所公 佈的數學教育原則與標準（Principles and Standard for School Mathematics）中提出，數 學即解題、推理與證明、溝通、連結、表徵，可見數學解題是數學學習的核心之一。 Mayer 與 Hegarty（1996）認為數學問題的型態有二：「例行性問題（routine problem）」 與「非例行性問題（non-routine problem）」。「例行性問題」是指問題解決者已經知道解 決這個問題的方法；「非例行性問題」是指解題者有了問題，卻不能立刻知道如何解決。 NCTM 於 2000 年再次提出「解題」是非常重要的課題，尤其是解非例行性的問題（NCTM,

2000）。 國內學者黃敏晃（1991）在「淺談數學解題」中也談到數學解題就是解決數學問題， 對解題者而言，只有當數學問題為非例行性問題（non-routine problem）時，才有解題行 為的發生，在解題過程中，需要用到數學相關概念、知識、技能、經驗等。因此，研究 者認為學習者遇到一個非例行性的數學問題或是一個情境不熟悉的數學問題時，利用其 舊有的知識與經驗，經過反覆的思考、邏輯推理與歸納後，所提出的一個解決問題的方 法或策略，就是數學解題。 依照時間先後，先介紹 Polya（1957）數學解題歷程的四個步驟，其次介紹 Schoenfeld （1985）解題的四個變項，再者，Mayer（1992）從認知心理學的觀點來看數學解題的 過程。 (一)Polya（1957）是最早有系統提出解題策略的學者，他在其著作「怎樣解題」（How to

solve it）書中，強調教導學生啟發知識（Heuristic knowledge）與解題的重要性，並將解 題歷程分為四個步驟如下：

1. 了解問題（understanding the problem）：解題者必須了解題意，並識別已知數與 未知數，以及題意中所能運用的條件。

2. 擬定計畫（devising a plan）：解題者根據題意，從自我的舊經驗中搜尋相關性 的問題或數學概念，而後設計一個具有可能成功的計畫。

3. 執行計畫（carrying out the plan）：解題者將計畫付諸實行，並校核明白步驟的 正確性與否。 4. 驗算與回顧（looking back）：解題者根據題意的條件，對答案再做一次的驗算 或回顧答案是否合理。 研究者認為正確了解題意是解決問題的必要條件，其次擬定一個可行且正確的解題 策略，是一個重要的解題關鍵。正如 Polya（1957）解題歷程中的第二階段擬定解題計 劃，計劃可能是逐漸地形成，也可能是瞬間突然產生的靈感（inspiration）。在擬訂計畫 中，學生往往用畫圖表示，國內外學者所提出的解題策略，發現有多位學者皆提出「畫 圖表徵」的解題策略，可見畫圖表徵是一個學生經常使用的解題方式（Kilpatrick, 1967； Sander, 1973；Larson, 1983；李佩樺、劉祥通，2008；劉哲源、劉祥通，2008；張祥瑞， 2009）。 (二)Schoenfeld（1985）強調數學解題的研究方向需要從以下四個類別（catogories）來考

慮： 1. 資源（resources）：解題者所擁有的相關數學知識，包含了數學定義、運算程序 及相關技巧等訊息。 2. 捷思（heuristics）：解題者解非例行性問題所利用的策略與技巧，例如：簡化 問題、畫表格、尋找組型等。 3. 控制（control）：解題者在解題時，如何決定計畫、如何選擇目標和次目標， 以及如何評估解題結果等方面，包括計畫、決策的評估與有意識的後設認知 （metacognition）。 4. 信念系統（belief system）：解題者對於數學的觀點，而解題者所擁有的數學觀 點將會影響其解題行為。 Polya 也主張，捷思的目標是研究發現與創新的方法與規則，作為一個形容詞，捷 思意味著為了發現的服務（Heuristic, as an adjective, means“serving to discover”）（Polya, 1957）。 Schoenfeld 發現如何有效的運用資源、如何採用適當的捷思策略，常常是由控制因 素所主導，至於信念系統影響解題更是顯著，是 Schoenfeld 獨到的見解。 Schoenfeld（1985）又依據 Polya（1957）的解題理論，提出的解題歷程模式包括， 閱讀：解題者開始讀題；分析：解題者簡化或重述問題以分析問題；探索：解題者探求 問題已知和未知間的關係；計畫：訂定解題計畫，並評估其適當性；執行：執行解題計 畫，並檢查是否依解題計畫執行；驗證：檢查解題結果是否正確合理。 Schoenfeld（1985）的解題歷程模式，描述每一階段的解題行為，著重每一決策點， 即後設認知行為發生處的分析，在驗證方面，提出用不同方法檢查解法，不僅評估解題 過程，同時評估解題者自己對解題結果的信心（李心儀，2016）。 (三)Mayer（1992）從認知心理學的觀點來看數學解題的過程，將其區分成：問題轉譯

（problem translation）、問題整合（problem integration）、解題計畫及監控（solution planning and monitoring）、解題執行（solution execution）四階段。Mayer（1992）也強調解文字題 時，問題轉譯依賴語言（linguistic）知識與語意（semantic）知識，問題整合要有基模 （schematic）知識，解題計畫及監控要有策略（strategies）知識，解題執行則要有程序性 （procedural）知識。研究者認為 Mayer（1992）主張：監控的行為不僅是解題之後，在 解題計畫的過程中即發生，這樣的觀點不同於 Polya，研究者同意監控的行為與思考在解

題過程中隨時在發生是合理的。

二、資優生的能力特質

資優生特質分成以下幾個文獻來說明：

(一)Krutetskii（1976）認為資優生的能力特質有以下四點：

1. 靈活性（flexibility）：在處理數學題目資訊的過程中，透過反向思考（reverse train of thought)達到快速重新建構的能力。

2. 壓縮（curtailment）：透過簡化（curtail）數學的過程，力求清晰（clarity）、簡 潔（simplicity, economy）且合理的解法。

3. 邏輯思維（logical thought）：會出現在數量（quantitative）和空間（spatial）關 係、數字和字母符號的範圍內的邏輯思維。 4. 形式化（formalization）：包含快速的掌握問題結構，與察覺（perception）數學 材料，具備這兩種能力，找到廣泛概括其中的數學材料、關係與方法，稱之為 形式化。 (二)Rogers（1986）發現在認知過程中資優生於下列優於普通生的特質： 1. 辨認（recognize）出欲解決的問題。 2. 預備好（readily）、自發性（spontaneously）地產生一串解決問題的方法。 3. 解決問題時所採取的方法先設定好優先順序（set priorities）。 4. 如專家一般的選擇表徵（select representation）資訊方式。 5. 能夠分配（allocate）解決某項問題時所需要的資源。

6. 有系統性地監控解答的過程（monitor solutions systematically）。

7. 解決問題時運用較長的醞釀思考時間（pre-conceptual time）。 Steiner（2006）也有類似的研究發現：資優生，當面對較新奇的非例行性的問題情 境時，資優生較一般生能選擇正確的解題策略，在解題策略的運用上，資優生會使用其 原先所具備的概念作基礎，進行有效率的策略與分析，建構自己的解題計畫。 (三)Davis 與 Rimm（2004）指出許多資優生的特質，其中與解題較有關的特質整理如下： 1. 優異的分析能力與卓越的推理、解題能力。 2. 使用抽象、複雜與具邏輯性的高層次思考能力與有效率的解題策略。

3. 具有洞察力、看見問題的架構、歸納規律並推廣到其他問題。 4. 自我反思、較佳的自覺與後設認知能力。 5. 具有創意與想像力，探究為何（why）以及如何（how）。 Cai（2005）也指出兒童發明解法的過程則是植基於他們深層的直覺與自然思考方 式，雖然這樣結合正式與非正式數學經驗的解題方法與過程，並不完全是有效用或是有 效率的，也常會有錯誤的結果發生，但經由學生自行發明的解題策略是具有原創性的。 而這樣自發性的解題策略是一種無價的資產，並可作為教師了解學生想法的一扇窗，更 是一種無價的工具（Yackel, 2005）。 Olson（齊若蘭譯，2007）的研究發現，美國六位參加 2001 年國際數學奧林匹亞競 賽選手的解題，無庸置疑的，這些數學解題高手所展現出來的特質，除了天份與多元的 興趣之外，更提到洞察力與創造力，其中洞察力在於觀察到問題的結構與困難點，而創 造力則是在現有的知識裡，找到一個乾淨俐落的解決方法。由上述所統整的解題特質可 以發現，資優生富有發現問題結構的洞察力。

資優教育學者 Renzulli（1978）提出資賦優異的三環理論（Theory of three rings）， 他主張資賦優異的行為表現要同時具備三種條件才有優異的行為表現，分別是：1.中等 以上的智能（above average ability）、2.工作投入（task commitment）以及 3.創造力 （creativity）等三種條件。Renzulli（1978）的以上論點，告訴世人不要過度迷信智商， 反而要強調專注工作的重要，也鼓勵創造，不要因循舊制，才會有傑出的表現，也告訴 教師鼓勵學生要有面對困難的堅持，並期勉學生全心投入，以及求新求變的表現。同樣 的，Griggs（1991）歸納出資優生有以下幾點認知特質：獨立學習、內控的、堅持的、 知覺強（perceptually strong）、非從眾的（nonconforming）和高度的學習動機，此堅持 的特質與工作投入，非從眾的特質與創造力，與 Renzulli（1978）的主張有「異詞同工」 之妙。 綜合以上學者所述，研究者認為資優生在遇到數學問題時，具有天生的直觀力來發 現其解題的步驟，並能簡化問題、找尋解答的方向；資優生還具有敏銳的洞察力來發現 題意的關鍵與歸納、推廣其解題過程；最後，資優生所具有的新穎創造力，能夠創造出 異於傳統制式化而具有創意的解答方式，利用自身所擁有的舊知識與舊經驗，創新解題 的過程，此類的解題不但可做為教師了解學生想法的參考，也能作為教師在設計題型時 的參考依據。

三、數線問題

在我國的中小學數學教材中，數線的概念在國小課程中便已出現，但直到國中階段 才有其專屬的課程單元。數線在教學上不僅只是標示出數在一條線上的位置，還有線段 上的合成與分割概念，因此在教學上是一種容易讓學生了解題意的表徵方式。本節針對 數線問題分別探討：（一）數線的意義、（二）數線問題相關的教材、（三）數線問題的 研究。 (一)數線的意義

有關數線的特徵，Bright、Behr 與 Post 與 Wachsmuth（1988）提出以下 4 點做說明： 1. 數線必須標上數字符號，並定義出兩個參考點（reference points），才能根據參 考點所顯示出的單位狀況找出其他點所代表的數值。 2. 數線是利用長度來代表單位，不僅單位可以重複（iteration）分割，且每一單 位（unit）均相等。 3. 數線是一種連續（continuous）模式，數線上任兩個數之間必定有另一數存在， 顯示實數具有連續性與稠密性。 4. 數線不像面積及離散量屬於單純的視覺組合。數線上必須標記兩點才構成意義， 就是說數線有賴視覺及符號兩種訊息整合。 綜合以上四點說明，研究者認為數線就是一種數字符號與視覺結合而成的表示法， 它可以表示出數線上的一個數值，或是一個線段長；數線具有相同的單位長及等分段的 特徵，同時必須標示兩個參考點的數字，才能找出其他點所表示的值，且數線可以當作 是一把尺，因為數線是連續的，任兩個數之間必定有一個數存在的稠密性質。 (二)數線問題相關的教材分布 教育部（2003）公布的九年一貫數學課程正式綱要中，將數線問題歸類於五大數學 主題中的「數與量」，雖然數線問題的基本概念在國小階段即開始出現，但是直到國中 階段才有「數線」的正式課程。 本研究的研究參與者是國小高年級學生，因此文獻只探討康軒版（個案就讀的學校 用康軒版）的課本有關數線問題的教材，尤其是比較深入的部分，以方便讀者連結教材 與任務單的關聯與差異（變異）： 在國小高年級時，開始正式引入數線問題，從五年級上學期第 1 單元「小數與分數」

就教導學生如何在數線上標示出其代表的分數或小數數值。 圖 1 康軒第九冊第 1 單元「分數」圖片（引自康軒出版社，2009） 圖 2 康軒第九冊第 1 單元「小數」圖片（引自康軒出版社，2009） 以上二圖是該版本代表性的問題，圖 1 告訴我們學生可以利用等分的概念，找出分 數的位置；圖 2 告訴我們學生可以從學習小數的百分位進階到千分位，找出千分位的位 置，而本文的任務單與以上教材的任務大不同。 (三)數線問題的研究 Skemp（1976）強調二種數學理解，一是工具性的理解（instrumental understanding）， 二是關係性的理解（relational understanding）。工具性的理解相當於程序性知識，而關係 性的理解相當於概念性知識。Skemp（1976）以 4 5 × 2 3 為例，學生能計算出 8 15 是屬於 工具性理解，而能瞭解 4₅ × 2₃ 的意義是 4₅ 的 2₃，則屬於關係性理解。研究者認為一旦 有了關係性理解就容易從 4₅ 找出 4₅ × 2₃ 的位置，也就是關係性理論有助於分數關係位 置的表徵。 劉祥通、康淑娟（2012）的研究（以 11₆ ÷ 4₃ 為例）強調：如果學生會計算 11₆ ÷ 4 3 = 11 6 ÷ 8 6 = 1 3 8，此乃程序性知識，也稱為工具性理解，但要知道以 4 3 當做基準量（1）， 比較量 11₆ 變成 13₈，能夠理解與熟悉這種知識是關係性理解。 Shaughnessy（2011）指出學生在一條數線上指認分數與小數位置點的困難，尤其是 在使用非約定的記號（unconventional notation）。但是有關資優生在數線問題的尋找分數 或小數位置的文獻卻是闕如。

參、 研究方法

本章旨在說明本研究所採取的研究方法與程序，內容共分成研究方法與研究架構、 研究參與者、研究工具等四個部分敘述如下：

一、研究方法

本研究主要目的在於探討國小五年級資優生在數線問題中的解題表現，研究者為了 充分了解研究參與者的初始想法與解題表現，預定全心投入心力與時間探索，因此採取 「個案研究法（case study）」來進行研究。

二、研究工具

本節研究工具分為研究者本身與任務單，任務單的問題，既非課本的例題、練習題， 也非市面上參考書所能見到的題目，以尋找數線上的定位點，稱為標數問題作為主軸， 並以個案學生任務單的寫作為基礎，再深入訪談其真實想法。分別敘述如下： (一)研究者

本研究屬於質性研究，在研究過程中，研究者本身即為研究工具（Guba & Lincoln, 1981）。因為在質性研究的過程中，充滿了不確定性和可變性，只有研究者本身作為研 究工作才能順應這種多變的研究情境（Lincoln & Guba, 1985），尤其在數線問題中，學 生在數線上下筆順序與塗改部份會影響研究者對個案解題的分析，因此研究者必須特別 仔細觀察學生的下筆與修改的情況。

研究者即教學者（researcher as teacher），研究者應從教學者的角色去了解與分析學 生的解題表現，進行訪談時，應適時的發揮教學者的角色，透過教學互動，才能更深入 了解個案學生的想法；研究者即模型的建造者（researcher as model builder），不斷地修 正與建立自己對受試者解題的看法（Cobb & Steffe, 1983）。

(二)非例行性數線問題任務單 任務單的設計是以尋找數線上的定位點為主軸，研究者參考數線相關文獻與國內各 版本數學教材，以及國內外各項數學競試試題，為了研究需要，研究者自行編製「非例 行性數線問題任務單」，分成「文字題型」與「標數題型」（在數線上標坐標點），本文 只呈現「標數題型」以挑戰個案學生，所謂非例行性問題對於學生是陌生的、不熟悉的、 也沒有解過的問題。為確認任務單問題的適切性，二位研究者於任務單擬定後，特別商 請一位具有多年資優班數學教學經驗的教師，共同檢視每道題目，進一步提供有效的觀

點來做適度的修正，以建立本研究任務單的專家效度。 在「標數題型」中，研究者依問題性質分為「尋找目標點」、「尋找原點」、「尋找多 個目標點」三大類。 「尋找目標點」的挑戰在於給定的二點，此二點是異分母的分數，挑戰學生如何找 到二點距離，並以此距離當作基準量，進而尋找比較量（目標點）的距離與位置。 例行性問題都是給定原點與另外一點，尋找第三個點，本任務單設計「尋找原點」 問題以挑戰學生，也可說是非例行性的問題。 已知某二點的距離是多少，但未註明二點的位置關係，這樣的問題有二種可能，因 此「尋找多個目標點」，對個案是個考驗，考驗她如何周全的解題，甚至監控答案的合 理等等。 以上三類型分別設計易、中、難各 1 個問題，共三類 9 題（參見附錄）。難易度的 主要的區分為坐標點是整數與分數，其次，分數又分成分母是倍數關係與否（例如 5₆ 與 4₃ ， 2 5 與 4 3 ）。限於篇幅，並未每題都討論。

三、研究參與者

本研究的研究參與者為通過瑞文氏黑白圖形補充測驗且百分等級為九十九的五年 級資優生小貞（化名），學籍在雲林縣。根據班級導師在訪談中的描述，此個案學生面 對數學問題具有高度的挑戰熱誠，能以積極的態度面對挑戰，在解決問題時，可以清楚 了解數學題目所表達的意涵，也能明白的寫下數學算式並解釋原因，勇於嘗試運用自己 方式來解題，且表達能力也是十分清楚，也很有耐心向艱難問題挑戰，另外，小貞的解 題想法更可以突顯其自發性與原創性。再者，她解有關數線問題的「文字題型」，都能 迎刃而解，所以本文再以「標數題型」（附錄），以觀察她的解題表現。

四、資料的分析

資料的來源主要是研究者所設計的任務單，藉此瞭解個案資優生在數線問題上的解 題表現和解題想法。學生的表現往往超乎研究者的預期，分析她的表現不在於驗證是否 符合文獻所說的特質，而是在於從哪種向度來看比較有意義。Schoenfeld（1985）所提 出的解題的影響因素「資源、捷思、控制與信念系統」，此觀點層面甚廣， 包括了先備 知識、策略的推演、監控解題計畫與結果的正確，還有對於數學的本質，自己的解題信 心，以及問題的看法等。Schoenfeld（1985）的理論可謂匠心獨具，因此本文從此四個

向度分析。 對個案資優生在任務單上的解題逐一分析；再以個案學生在非例行性數線問題任務 單的解題表現為基礎，採結構式任務單為基礎的訪談技巧進行訪談，而訪談的問題卻是 依照學生的解題表現與訪談現場學生對解題想法的解釋作調整。 為增加本研究的效度，包含文字或符號敘述、解題運算（通分與擴分）、畫圖表徵、 標位置圖的順序、任務單為基礎的晤談等等，進行資料的三角校正。 為了增進資料分析與詮釋上的信度，研究者不同的問題，利用重複的情結考驗個案 的解題想法，例如若是個案依賴直尺實測，她可能是利用比例的方法解決問題，研究者 會要求她，如果不依賴用直尺實測，您有甚麼方法呢？藉以了解個案解題時所用的資源， 與持續地了解個案所採用的解題策略，包括她如何監控答案的合理性，以增加研究的信 度。

肆、 研究結果與討論

本章的內容以個案學生的任務單解題與訪談內容為基礎，再將資料依據 Schoenfeld （1985）所提出的資源、捷思、控制、與信念系統四個類別做分析架構，分析個案學生 解題的表現。

一、標數題型的解題分析

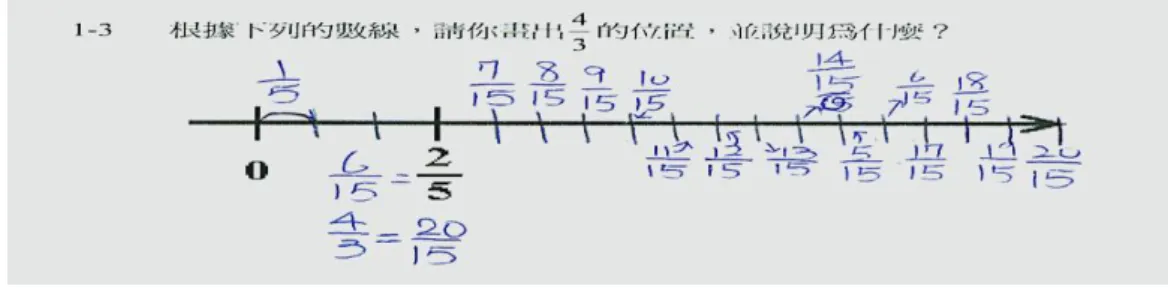
本節依標數題型分類為尋找目標點、尋找原點與尋找多個目標點三個部分，礙於篇 幅，研究者以呈現「尋找目標點之題目 1-3、找尋原點之題目 2-3、尋找多個目標點之題 目 3-2 與 3-3」，分別敘述如下： (一)尋找目標點 題目 1-3 根據下列的數線，請你畫出 4/3 的位置，並說明為什麼？ 個案的解題表現分析（一）

圖 3 個案小貞在題目 1-3 的初始解題 個案小貞對分數的通分的嫻熟，可見等值分數概念是她的解題的資源，將「4₃ 與 2₅ 通分成 20 15 與 6 15 」，再將數線上 0 到 2 5 的距離分成三等份，並註明上 1 5 的記號，發生 了等分的錯誤；她再利用 1₅ 的距離從 2₅ 往後畫，並標上坐標 ₁₅7、₁₅8、₁₅9…，造成解題 上的錯誤。 研究者詢問小貞的解題步驟時，她自己發現在「0 到 2 5 的距離分成三等份」的步驟 上發生錯誤，因此研究者推論她是不小心將 1₅ 與 ₁₅1 搞混，可以說是當下控制欠佳的表 現。 研究者請小貞再次解題，她一樣先將題目的兩個分數通分成 20₁₅ 與 ₁₅6，然後將 0 到 2 5 的距離分成兩等份，並標示出 1 5 的位置，但是她再次將 1 5 與 1 15 搞混，於是研究者 想確定學生是否了解「0 到 2₅ 分成一半的距離為 1₅」的觀念。研究者便以引導她理解 1₅ 與 ₁₅1 的倍數關係，小貞利用分數擴分寫下「1₅=₁₅3」的算式，並解釋「因為 1₅ 等於 ₁₅3 ，所 以是 1 15 的 3 倍」，她且能反推「把 1 5 分成 3 格，一格便是 1 15」的觀念；研究者因此認 為此題的重要關鍵小貞已完全理解，所以請她又再次解題。 圖 4 個案小貞在題目 1-3 經教學後的解題表現 個案小貞先將 0 到 2 5 的距離平分成兩段得到 1 5，再將 1 5 平分成三等份得到 1 15 ， 所以將一小格標示出 ₁₅1，將一大格標示出 1₅ ；研究者認為這裡的等分步驟已經成為學 生解此題的資源。接著，個案小貞再利用 1₅ 的距離推出 3₅、4₅、1 與 11₅ 的位置，並瞭 解 11₅ 就是 18₁₅，發現再 ₁₅2 就能到達目標點，於是利用 ₁₅1 的距離找到 20₁₅ 的位置；研

究者認為個案反覆利用 1₅ 與 ₁₅1 兩者的距離（6 次 1₅ 的距離， 2 次 ₁₅1 的距離），以找 出 4₃ ，可見她解題時能將所學學習遷移，此是其捷思的策略。 最後，研究者再次請她確認 4 3 的位置，小貞利用 1 5與 1 15 二個高低階單位，找到 4 3 就 是 20₁₅ ，學生終於發揮了優秀的控制能力。如此有系統性地監控解答的過程（monitor solutions systematically）是 Rogers（1986）發現資優生解決問題的在認知過程中的一項 優於普通生的一項重要的特質。 (二)尋找原點 題目 2-3 根據下列的數線，請你畫出原點 0 的位置，並說明為什麼？ 個案的解題表現分析（二） 圖 5 個案小貞在題目 2-3 的解題表現 小貞利用等值分數的概念將「2 5 和 2 3 通分成同分母，得到 6 15 和 10 15」，並發現兩數 之間相差 4 個單位長度（₁₅1），於是把「2₅ 和 2₃ 之間平分成 4 格」 ₁₅4 得到單位長度為 1 15，這些皆為小貞所具備的解題資源；接著問她，「你怎麼找到 0 的？」，回答「這裡是 1 15，從 2 5 就是 6 15，往左推就找到了。」；其次，她從 4 格的間距往相反方向去找 6 格， 得到原點的位置，研究者認為，基準化的能力是她擁有的解題資源；再者，她在數線上 持有「數線上越左邊的坐標越小、越右邊的坐標越大」的信念系統（也是先備知識）， 因此在尋找原點時，都是從給予的參考點往左邊找原點位置，找到了原點 0 的位置，以 前她從未解決過找原點的問題，面對此一非典型問題（非例行性問題），她直覺就能解 決，此點能力也呼應 Griggs（1991）所點出的資優生具有知覺強（perceptually strong） 的認知特質；最後，研究者再次詢問個案「為何往前推 6 格就是原點的位置？」，她回 答「我往前數就是 ₁₅5、₁₅4、₁₅3、₁₅2、₁₅1，接下來就是 0 了」。研究者認為，她從 ₁₅6 利用

往後數 4 個 ₁₅1，得到 10₁₅，同樣的推理，往前數 6 個 ₁₅1，得到 0。研究者認為：往前找 原點的活動，是前所未有的課題，而且 將 ₁₅4 與₁₅6 看成 4 個 ₁₅1，與 6 個 ₁₅1，把 ₁₅1 的 單位具象化與物件化了，此項能力也呼應了 Krutetskii（1976）所主張：資優生解決問題 時擁有壓縮（curtailment）的能力。研究者發現個案小貞解題時，是先標示 0 的位置， 在最後檢查答案的時候才將 ₁₅5、₁₅4、₁₅3、₁₅2、₁₅1 標示上去，用數格子的方式將每個標數 都表示出來，證明原點的位置正確，並點數自己推得的格子數是否正確，這些都是她所 具備的監控能力。 (三)尋找多個目標點 題目 3-2 根據下列的數線，已知知𝐴𝐵̅̅̅̅ = 𝐶𝐷̅̅̅̅（A、B 兩點的距離等於 C、D 兩點的 距離），請在下列數線上畫出 D 點的位置，並說明為什麼？ 個案的解題表現分析（三） 圖 6 個案小貞在題目 3-2 的初始解題 3-1 問題（參見附錄），給定 P 點(13)，請劃出與 P 點相距 5 的位置。小貞直接在參 考點前後標示， 標示 5 個單位，8 與 18 的位置。 在解 3-2 的問題時，研究者預期小貞在數線 14 的坐標左右 4 個單位，直接標示出 10 與 18。但是，從圖 6 來看小貞是選擇「用尺量」的方式，研究者詢問「你為何麼要 用尺量呢？」，小貞直接回答「測得 A、B 兩點的距離是 2.6 公分，然後認為 C、D 兩點 的距離也是 2.6 公分」，她為了精確找出 D 的位置，利用量尺求出兩點實際的距離，找 出單位長度後，再找出目標點的相對位置，研究者認為此為她意圖得到距離的真確性， 研究者認為她解讀題意的當下，認為題目要求畫出精確距離，這個面向是 Mayer 所稱的 問題轉譯， 也可以說是 Polya 所說的理解題意。而她以等距離觀念解題，此為她解題前

所擁有的解題資源。 她初始用選擇「用尺量」與等比例的方式解題，接著她自己又採取坐標點的資源解 題：因為 A、B 兩點差 4 個單位長，所以 D 點就是 14 往右移動 4 個單位長，也就是 18 的位置，研究者認為以上就是她所運用的捷思策略，利用坐標的觀念，以 4 個單位長的 距離，直接平移至參考點 C 點上。但在題目 3-2 中，目標點應該有兩個，她在初始解題 中只畫出 C 點右側的目標點，研究者猜測認為有二種可能：1. 是 A、B 兩點的相對位 置關係，使得個案學生在解此題目當下一時忽略了 C 點左右兩邊都有目標點的關鍵；2. 沒有充分詮釋線段符號𝐴𝐵̅̅̅̅ = 𝐶𝐷̅̅̅̅，此符號也等同於𝐴𝐵̅̅̅̅ = 𝐷𝐶̅̅̅̅，所以 D 點可以在 C 點左右 二個位置。 進一步推論，小貞可能在長度平移時，因為參考長度 B 點在 A 點的右側，因此影 響到學生在作答時，直覺的畫出 D 點也在 C 點右側的答案，因而忽略 C 點左側的目標 點。研究者認為，她並沒有完全地成功解題，第一個原因可能是題目增加其他條件而影 響作答；第二個原因可能是她並未使用其控制答案的能力，因此造成解題的不完整。 研究者提出「如果你不用尺去量的話，你覺得還有什麼方法可以做？」的問題，小 貞受訪時回答「我是利用數線上坐標點來判斷兩點的距離」。題目雖然提供了資訊，但 是解讀資訊，是靠解題者的先備知識，也就是她擁有解題資源。 她接著回答「可以用平分等分的方法」，她將 A 點到 B 點的距離 4 個單位長平分成 4 個間隔，作為解題的捷思策略（如圖 7）。 研究者提問「這次為什麼會出現兩個點？」，她回答「距離參考點一定長度時，會 有左右兩個目標點」（研究者認為這是屬於解題的資源，也是發展成為信念系統的一部 分），看出 D 點有 2 個。她接著說「C 點往前數 4 格，往後也數 4 格」，將 4 格以畫圖表 徵的方式是監控的行為，在數線上 C 點左右各標示 4 個單位長，分別為 10 和 18。 圖 7 個案小貞在題目 3-2 使用另一策略的解題表現 題目 3-3 已知 P 點的坐標為 10，且 P 點和 Q 點距離 2 個單位長，若 M 點坐標比 Q 點大，且 M 點和 Q 點距離 3 個單位長，請在下列數線上畫出 M 點的位置，並說明為什

麼？ 個案的解題表現分析（四） 圖 8 個案小貞在題目 3-3 的解題表現 小貞從解 3-1、3-2 的解題中得到的經驗，此解題經驗已發展成為「距離參考點一定 長度時，會有兩個目標點」的信念，發現在題目 3-3 中，能直覺的發現 Q 點也是會有兩 個可能，研究者認為此信念亦可視為她從經驗中提取出的解題資源，因此利用題目給的 題意「P 點和 Q 點距離 2 個單位長」，從參考點 P 往左找 2 公分找到 Q 點位置為坐標 8， 往右找 2 公分找到 Q 點位置為坐標 12；研究者認為小貞利用量尺的刻度當作解題捷思 策略，小貞先找到 Q 點的二個位置（子目標），接著，個案小貞繼續找目標點 M 點的位 置，繼續以 1 公分當作一個單位長，這也代表學生擁「有在同一個數線上，一個單位長 的長度是固定不變的」的信念；因此小貞從坐標為 8 的 Q 點，依照題意往右找 3 公分（也 就是 3 個單位長），到達 M 點坐標 11；又從坐標為 12 的 Q 點往右找 3 公分（也是 3 個 單位長），到達 M 點坐標 15，又得到二個 M 點（終極目標）。正如，Steiner（2006）的 研究發現：在解題策略的運用上，資優生會使用其原先所具備的概念作基礎，進行有效 率的策略與分析，建構自己的解題計畫。 研究者又詢問小貞「為什麼 M 你只找右邊的點，沒有找左邊的呢？」她回答「因 為題目說 M 的坐標比 Q 大，數線右邊的點比較大」。更確定她了解「數線上點的位置」 觀念。在尋找目標點 M 點的位置時，小貞利用其「數線上越右邊的點越大」的概念控 制其答案，只找 Q 點右邊的目標點，不需找 Q 點左邊較小的點，因此研究者認為，她

具有良好的數線概念來控制其答案的正確性。也如同 Davis 與 Rimm（2004）所強調的 特質，資優生擁有較佳的後設認知能力。

伍、 結論與討論

本研究目的為藉由研究者設計的非例行性數線問題任務單，探討國小五年級資優生 在數線問題的解題表現，並針對小貞解題表現，分析資優生如何有效運用資源（resources）、 如何採用適當的捷思（heuristics）策略、如何控制（control）過程，以及如何利用信念 性統（belief system）得到答案之四個變項做討論。因此，本章分兩個部份，第一節針 對研究結果，綜合論述個案資優生解非例行性數線問題的解題表現，作為本研究的結論； 第二節則依據研究結論提出相關之建議。

一、結論

本節依據個案資優生的解題表現，分為資源（resources）、捷思（heuristics）、控制 （control）、信念系統（belief system）四個變項，分述如下： (一)資源（resources） 「等值分數」的概念以及「利用兩點之間距離當作基準量」為個案學生解標數題型所運 用的重要解題資源 本研究結果發現，在題目 2-3 中，小貞能利用「等值分數」的概念，將參考點 2₅ 以 及目標點 2₃ 化為同分母的分數，再進行等分線段長度的步驟。在題目 3-2 她利用在數線 上坐標點來定位與判斷兩點的距離。因此研究者認為她是能夠善用自身所擁的有數學知 識和解題經驗當作其解題資源。 (二)捷思（heuristics） 個案學生能展現多元策略，以解不同的數線題型 從本研究結果發現，小貞在題目 2-3 中，能利用等分線段的方式找出目標點，也能 利用比例原則，從 ₁₅4 與 ₁₅6 看出是 4：6 關係，找出原點位置， 此乃基準化能力的展 現；在題目 3-2 中，分別用「量尺」的方式與數線上坐標點來定位與判斷兩點的距離的 方法作為其解題的捷思策略。從研究者所設計的數線問題中，其所分別需要的解題策略

大不相同，因此可以看出個案學生在解題時所運用策略的多元性。 (三)控制（control） 個案學生以「高、低階兩單位並用」方式找尋目標點與「數間隔數」等方法來控制答案 的合理性 從本研究結果發現，在解數線問題的 1-3 任務單中，找 4₃ 的位置，小貞利用 1₅ 與 ₁₅1 二 個高低階單位，找到 4₃ 就是 20₁₅ ，她發揮了優秀的控制能力，以監控解答的準確性，並 能利用有別於原來的方法來驗證自己的答案，或是利用觀念來檢視答案的正確性，更能 利用概念來控制答案的可能性。例如她會利用「數間隔數」的方式關係來確認自己答案 是否正確，研究者認為此為學生最容易運用來檢驗自己答案的方式；另外，她也能運用 數線上兩點之間的距離來檢驗答案的正確性，利用求出的答案坐標來反推與另一目標點 的距離，確認是否與題意相同；又或者利用其先備知識「數線上越右邊的點越大」來控 制自己所運用的策略，只找出題意上可能的目標點。 (四)信念系統（belief system） 個案學生在解題之初，持有「數線上越左邊的坐標越小、越右邊的坐標越大」以及解題 之後，發展出「距離參考點一定長度時，會有左右兩個目標點」的信念 本研究結果發現，在題目 2-3 中，小貞在解題的開始以「數線上越左邊的坐標越小、 越右邊的坐標越大」的信念（也是先備知識），先判斷原點的位置，0 會落在小的數 2₅ 的 左邊。在解完 3-1 的題目後 3-2 她能利用「距離參考點一定長度時，會有左右兩個目標 點」的信念，接著透過在數線上坐標點來定位與判斷兩點的距離，在題目 3-3 她持有「有 在同一個數線上，一個單位長的長度是固定不變的」的信念。研究者認為，因為她擁有 的正確信念系統，所以能有效率幫助其解題上的流暢。

二、建議

研究者將於本節針對此研究中，個案資優生在任務單上的解題表現、訪談內容與綜 合分析結果所獲得的收穫、回饋和反思，提出相關之建議，分述如下： (一)鼓勵學生解題時採取多元的解法 從個案小貞的解題表現發現，她在面對非例行性數線問題時，為了答案的正確性，

她利用不同的策略來解題，並能清楚的寫下運算過程，藉由自己的先備知識來思考或驗 證答案的合理性，此行為不但提高了學生在解題時的正確率，也能讓學生自己清楚的知 道每一個算式或步驟代表的涵義為何。以上是一個個案面對非例行性問題解題時能採用 多元的解題策略，卻也證實了 Krutetskii（1976）所歸納的資優生解決問題時的靈活性 （flexible）特質。建議教師教解題時最好多鼓勵學生發表不一樣的方法，相信資優生們 各自會貢獻不一樣的解題想法與策略，如此百花齊放，學生對於數學的愛好與學習動機 會更強烈。 (二)關於資優生的學習內容，建議教師嘗試設計與安置非例行性問題 解題能力的增加，可以從自己的解題經驗中累積，若只是單純的例行性問題，學生 只模仿老師的解法，對學生的解題經驗成長並未有太大的幫助。在個案小貞解非例行性 數線問題時，因對於不熟悉的題目可以反覆的思考，搜尋自己所具備的先備知識與數學 相關的舊經驗，透過自身所發展出的解題策略來成功解題，在學習上，學生自行發展出 的解題策略會比老師所教學的策略來得牢靠，在經驗的成長上，此次利用的解題策略也 將成為以後解題所運用的資源。因此，在資優生的數學學習上，除了加深、加廣的課程 外，可嘗試設計與加入非例行性問題當作學生學習新知的教學內容，以挑戰學生的能力， 進而發展學生解決問題的能力。 (三)任務單的設計可再加入負數概念等題材，以加深任務單的難度 從研究結果發現，此任務單對個案小貞來說，似乎顯得較容易發揮，原本研究者認 為數線單元為學生較少碰觸的題型，但研究結果發現個案小貞在數線問題上並未遇到太 大的困難，因此研究者認為若在未來的研究上面，可加深任務單的難度，例如增加負數 概念，舉例來說，在「尋找原點」題型中，因研究者的任務單只有正數的參考點，因此 學生只需往數線左邊找原點的位置，若加入負數的概念，學生可能很自然理解：數線上 正數在原點右側，負數在原點左側的概念。

誌謝

感謝科技部計畫（NSC 98-2511-S-415-003-MY3）的經費補助，本文只代表二位研 究者的意見，不代表科技部的觀點。也感謝投稿過程中匿名審查人的辛苦付出與寶貴意 見，使得本文得以較完善的面貌，與同道分享。

參考文獻

李心儀（2016）。不同解題歷程模式中的回顧。臺灣教育評論月刊，5（8），157-161。 李佩樺、劉祥通（2008）。分析國小資優生解連比問題之自發性策略。資優教育季刊， 106，8-17。 康軒出版社（2009）。國民小學數學第九冊。臺北市：康軒文教。 張祥瑞（2009）。分析資優生解速率問題之研究。（未出版之碩士論文）。國立嘉義大學 數學教育研究所，嘉義縣。 教育部（2003）。國民中小學九年一貫課程正式綱要。臺北市：教育部。 黃敏晃（1991）。淺談數學解題。教與學，23，2-15。 劉哲源、劉祥通（2008）。國一資優生對因倍數問題的解題分析。資優教育研究，8（1）， 47-66。 doi: 10.7089/JGE.200806.0047 劉祥通、康淑娟（2012）。小美在數線上關於分數基準化問題的解題表現。科學教育學 刊，20（1），23-29。 doi: 10.6173/CJSE.2012.2001.02 Olson, S.著。齊若蘭譯（2007）。數學高手特訓班。臺北市：遠流。（原著出版於 2004 年）

Bright, G. W., Behr, M. J., Post, T. R., & Wachsmuth, I. (1988). Identifying fractions on

number line. Journal for Research in Mathematics Education, 19(3), 215-232. doi:

10.2307/749066

Cai, J. (2005). What research tells us about teaching mathematics through problem solving. In F. K. Lester & R. I. Carles (Eds.), Teaching mathematics through problem solving (pp.

241-253). Reston, VA: VCTM.

Cobb, P., & Steffe, L. P. (1983). The constructivism researcher as teacher and model builder.

Journal for Research in Mathematics Education, 14(2), 83-94. doi: 10.2307/748576

Davis, G. A., & Rimm, S. B. (2004). Education of the gifted and talented(5th ed.). Boston: Pearson/ A and B.

Guba, E. G., & Lincoln, Y. S. (1981). Effective evaluation: Improving the usefulness of

evaluation results through responsive and naturalistic approaches. San Francisco:

Kilpatrick, J. (1967). Analyzing the solution of word problems in mathematics: An

exploratory study. Dissertation Abstracts International, 28, 4380A. University

Microfilms No. 68-6442.

Kilpatrick, J. (1985). A retrospective account of the past 25 years of research on teaching

mathematical problem solving. In E. A. silver (Ed.), Teaching and learning mathematical

problem solving: Multiple research perspectives (pp. 1-15). Hillsdale, NJ: Lawrence

Erlbaum Associates.

Krutetskii, V. A.(1976). The Psychology of Mathematical Abilities in Schoolchildren.

Thanslated from the Russian by Joan Teller, edited by Jeremy Kilpatrick and Izaak Wirzup. Chicago: The University of Chicago Press. (Original work published 1968.)

Larson, L. C. (1983). Problem-solving through problems. New York: Springer.

Lincoln, Y. S., & Guba, E. G. (1985). Naturalistic inquiry. Beverly Hill, CA: Sage. doi:

10.1016/0147-1767(85)90062-8

Mayer, R. E. & Hegarty, M. (1996). The process of understanding mathematical problems. In

R. J. Sternberg & T. Ben-Zeev (Eds.), The nature of mathematical thinking. NJ:

Lawrence Erlbaum Associates, Inc.

Mayer, R. E. (1992). Thinking, problem solving, cognition, (2nd ed. ). NY

:

Freeman.

National Council of Supervisors of Mathematics. (1977). Position paper on basic mathematical skills. Arithmetric Teacher, 25, 19-22.

National Council of Teachers of Mathematics (2000). Principles and standards for school

mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.

National Council of Teachers of Mathematics. (1980). An Agenda for Action:

Recommendations for school mathematics of the 1980’s. Reston, VA: Author.

National Council of Teachers of Mathematics. (1989). Curriculum and Evaluation Standards

for school mathematics. Reston, VA: Author.

Polya, G. (1957). How to solve it (2nd ed.). Garden City, NY: Doubleday and Co., Inc.

Renzulli, J. S. (1978). What makes giftedness? Reexamining a definition. Phi Delta Kappan,

Rogers, M. T. (1986). A comparative study of developmental traits of gifted and average

children. Unpublished doctoral dissertation, University of Denver.

Sander, V. A. (1973). Arithmetic problem-solving strategies of fourth grades children.

Doctoral dissertation, Wayne State University.

Schoenfeld, A. H. (1985). Mathematical problem solving. Orlando, FL: Academic Press. doi:

10.1016/B978-0-12-628870-4.50008-6

Shaughnessy, M. M. (2011). Identify fractions and decimals on a number line. Teaching

Children Mathematics, 17(7), 428-434.

Skemp, R. R. (1976). Relational understanding and instrumental understanding. Mathematics

Teaching, 77, 20-26.

Steiner, H. H. (2006). A micro genetic analysis of strategic variability in gifted and average-ability children. Gifted Child Quarterly, 50(1) ， 62-74. doi: 10.1177/001698620605000107

Yackel, E. (2005). Listening to Children: Informing us and guiding our instruction. In F. K.

Lester & R. I. Carles (Eds.), Teaching mathematics through problem solving (pp. 107-121). Reston, VA: VCTM.

親愛的小朋友，您好： 這是一份關於數線問題的工作單，請運用你所學過的數學知識，儘可能地在每一個 題目下方的空白處（或數線上）寫下您的想法和計算過程，此份試題並不會在學業 成績上做參考，請您放心作答。您的填寫對於此方面的研究相當寶貴，請認真作答，謝謝 您！

附錄 數線問題工作單

姓名： 1-1 根據下列的數線，請你畫出12 5 的位置，並說明為什麼？ 1-2 根據下列的數線，請你畫出 5₆ 的位置，並說明為什麼？ 1-3 根據下列的數線，請你畫出 4₃ 的位置，並說明為什麼？ 2-1 根據下列的數線，請你畫出原點 0 的位置，並說明為什麼？

2-2 根據下列的數線，請你畫出原點 0 的位置，並說明為什麼？ 2-3 根據下列的數線，請你畫出原點 0 的位置，並說明為什麼？ 3-1 根據下列的數線，請你畫出與 P 點相距 5 的位置？ 3-2 根據下列的數線，已知 𝐴𝐵̅̅̅̅ = 𝐶𝐷̅̅̅̅（A、B 兩點的距離等於 C、D 兩點的距離），請在下 列數線上畫出 D 點的位置，並說明為什麼？ 3-3 已知 P 點的座標為 10，且 P 點和 Q 點距離 2 個單位長，若 M 點座標比 Q 點 大，且 M 點和 Q 點距離 3 個單位長，請在下列數線上畫出 M 點的位置，並說明 為什麼？