動態幾何軟體GSP支援下之數學探究

全文

(1)國立交通大學理學院網路學習學程碩士論文. 動態幾何軟體 GSP 支援下之數學探究 Mathematical Exploring Supported by GSP. 研究生：陳佳煌指導教授：黃大原. 博士. 中華民國九十六年六月.

(2) 動態幾何軟體 GSP 支援下之數學探究 Mathematical Exploring Supported by GSP. 研究生：陳佳煌. Student：Jia-Huang Chen. 指導教授：黃大原. Advisor：Tayuan Huang. 國立交通大學理學院網路學習學程碩士論文. A Thesis Submitted to Degree Program of E-Learning College of Science National Chiao Tung University in partial Fulfillment of the Requirements for the Degree of Master in. Degree Program of E-Learning June 2007 Hsinchu, Taiwan, Republic of China. 中華民國九十六年六月.

(3) 動態幾何軟體 GSP 支援下之數學探究學生：陳佳煌. 指導教授：黃大原博士國立交通大學理學院網路學習碩士在職專班. 摘. 要. 傳統的高中數學課程，主要以紙筆為工具進行抽象思考與推理的訓練。資訊科技融入教學的實施，則希望創造一個多元且互動性高的教學環境，不但能改進老師的教學方法，增進學生的學習效果，也能培養學生主動探索的精神及解決問題的能力。很多人學習數學的歷程，都是直接從教科書或老師身上獲得數學公式及定理，然後努力學習證明及解題的技巧，過程中總是缺少由問題出發的探索經驗。本研究透過動態幾何軟體 GSP 所提供的環境，引導學生從事數學探究的活動，讓學生有機會體驗數學的求知活動中，由問題出發到實驗、觀察、猜測與驗證的完整過程。我們從高中數學教材中選取三個主題，作為研究的題材。第三章透過數學實驗探索兩個分別與距離及面積有關的極值問題，並且透過兩個動態「圖說證明」的例子，將抽象的正餘弦函數疊合的概念以具體的動態圖形呈現。第四章探索利用軌跡及參數式作出圓錐曲線圖形的方法，以及多項函數圖形的作法。第五章從幾何的觀點探索複數的幾何性質，包括複數平面、複數的四則運算及複數的 n 次方根，並舉出幾個例子，說明這些幾何性質如何應用在解決平面幾何的問題上。數學教育應該提供機會，讓學生體驗數學知識創造的過程，並享受發現的樂趣。動態幾何軟體 GSP 具有可操作、互動性高及可模擬問題情境的特性，我們相信運用 GSP 在數學的教學與學習活動上，將有助於提高學生學習數學的意願，並激發學生研究數學的興趣。. 【關鍵字】動態幾何、GSP、數學探究、數學實驗. i.

(4) Mathematical Exploring Supported by GSP Student: Jia-Huang Chen. Advisor: Dr. Tayuan Huang. Degree Program of E-Learning National Chiao Tung University. Abstract Traditionally, senior-high mathematical courses make students go into training in their abstract thinking and reasoning by pens and papers. The application of information technology to teaching attempts to create a multiple and highly-interactive teaching environment. This environment can not only improve teachers’ instructive methods but also cultivate students’ spirits of active exploring and abilities of solving problems. In the process of learning mathematics, many people directly acquire mathematical formulas and theorems from textbooks or teachers, and then strive to gain the skills in proving and problem solving. In this way, they always lack the exploring experiences triggered by problems. In the environment of GSP, this study aims to lead students to explore mathematics. In mathematical acquisition, students have better chances to experience the complete procedures for experimenting, observing, conjecturing and verifying, all initiated by problems. From senior-high mathematical materials, three subjects are selected as the topic in this study. In Chapter 3, two extremum problems are explored, related to distance and area by mathematical experiments. With two examples of dynamic “proof without words”, the abstract concept of the superposition of sine and cosine is demonstrated in concrete dynamic graphs. Chapter 4 probes the approaches to draw out the graphs of conic sections with locus and parametric equation as well as the approaches to create the graphs of polynomials. In Chapter 5, in geometric perspectives, the geometric properties of complex numbers are explored, including complex plane, four arithmetic operations of complex numbers and nth root of a complex number. It is also exemplified how these geometric properties are applied to solving the problems of plane geometry. Mathematical education is supposed to offer opportunities for students to go through the creation of mathematical knowledge and enjoy the pleasure of discovery. In the environment of GSP, learners can operate, highly interact and simulate some situations in question. We believe applying GSP to teaching and learning activities in mathematics will contribute to boosting students’ motivation for learning mathematics and further inspire their interest in studying mathematics.. Keywords: dynamic geometry, GSP, mathematical exploring, mathematical experiment. ii.

(5) 誌. 謝. 我要感謝指導教授黃大原老師，謝謝他適時對我伸出援手，不厭其煩地指導我，幫助我順利完成論文。黃老師教學時敬業與嚴謹的態度，以及指導學生時無私奉獻的精神，令我十分敬佩與感動。有幸成為黃老師的學生之一，使我受惠良多，在此由衷地表達最真誠的謝意。我要感謝陳明璋老師，謝謝他從我進入專班到論文完成這段時間的熱心指導，讓我收穫很多。同時要感謝專班主任莊祚敏教授，謝謝他在課業及行政方面的協助。此外，我也要感謝國立大里高中孟主安老師，謝謝他提供我在論文寫作方面的意見，以及往返台中與新竹之間的交通協助，感激不盡。我最感謝內人文娟，由於她的支持與體諒，我才能順利完成學業。這些年來，謝謝她對我生活上的照顧，以及精神上的加油鼓勵，再多的言詞也不足以表達我對她的感謝。如果這篇論文的完成能為我帶來任何小小的成就，那肯定都要歸功於她。最後，我要感謝這些年來家人的關心，師長的教誨，同學的勉勵，朋友的打氣，以及所有關心我、幫助過我的人，在此一併感謝。. iii.

(6) 目. 錄. 中文摘要 .....................................................................................................................................i 英文摘要 ....................................................................................................................................ii 誌謝 ...........................................................................................................................................iii 目錄 ...........................................................................................................................................iv 表目錄 ........................................................................................................................................v 圖目錄 .......................................................................................................................................vi 第一章緒論 ..............................................................................................................................1 1-1 研究背景.....................................................................................................................1 1-2 研究動機與目的.........................................................................................................1 1-3 論文結構.....................................................................................................................2 第二章文獻探討 ......................................................................................................................4 2-1 資訊科技融入教學.....................................................................................................4 2-2 數學探究.....................................................................................................................5 2-3 動態幾何.....................................................................................................................6 2-4 動態幾何軟體 GSP ....................................................................................................7 第三章探索極值問題 ..............................................................................................................8 3-1 直線上一點到線外兩定點的最小距離和.................................................................9 3-2 圓及橢圓內接三角形的最大面積...........................................................................15 3-3 正餘弦函數疊合的極值...........................................................................................22 第四章探索軌跡問題 ............................................................................................................29 4-1 圓錐曲線的等分線描點作圖...................................................................................30 4-2 圓錐曲線的參數式作圖...........................................................................................38 4-3 通過已知定點的多項函數圖形...............................................................................46 第五章探索複數的幾何性質 ................................................................................................51 5-1 複數平面...................................................................................................................52 5-2 複數四則運算的幾何意義.......................................................................................55 5-3 複數 n 次方根的幾何意義.......................................................................................58 5-4 應用複數解平面幾何問題實例...............................................................................61 參考文獻 ..................................................................................................................................65. iv.

(7) 表. 目. 錄. 表 3-2-1 圓內接三角形的三內角及面積 ..............................................................................16 表 3-2-2 橢圓內接三角形的三內角及面積 ..........................................................................19. v.

(8) 圖. 目. 錄. 圖 3-1-1 圖 3-1-2 圖 3-1-3 圖 3-1-4 圖 3-1-5 圖 3-1-6 圖 3-1-7 圖 3-1-8 圖 3-1-9. 一直線及線外兩定點（異側） ................................................................................9 一直線及線外兩定點（同側） ..............................................................................10 最小距離和實驗 ......................................................................................................10 最小距離和 .............................................................................................................. 11 B′ 是 B 對直線 L 的對稱點 ..................................................................................... 11 最小距離和的證明 ..................................................................................................12 最小距離和的作法（一直線） ..............................................................................12 兩相交直線及線外兩定點 ......................................................................................13 B1 是 B 對直線 L2 的對稱點 .....................................................................................13 圖 3-1-10 B2 是 B1 對直線 L1 的對稱點...................................................................................14 圖 3-1-11 最小距離和的作法（兩相交直線）.....................................................................14 圖 3-2-1 圓內接三角形實驗 ..................................................................................................15 圖 3-2-2 圓內接三角形的最大面積 ......................................................................................16 圖 3-2-3 一邊固定的圓內接三角形 ......................................................................................17 圖 3-2-4 圓內接銳角等腰三角形 ..........................................................................................17 圖 3-2-5 橢圓內接三角形實驗 ..............................................................................................18 圖 3-2-6 橢圓內接三角形的最大面積 ..................................................................................19 圖 3-2-7 橢圓內接 ∆PQR 及圓內接 ∆P′Q′R′ .........................................................................20 圖 3-3-1 函數 y = sin x + cos x 的圖形 ....................................................................................22 圖 3-3-2 正餘弦函數疊合的圖說證明（ sin ） ....................................................................24 圖 3-3-3 正餘弦函數疊合的圖說證明（ cos ）....................................................................24 圖 3-3-4 a sin θ + b cos θ 化成 r sin(θ + φ ) 形式的說明 ..........................................................25 圖 3-3-5 a sin θ + b cos θ 化成 r cos(θ + φ ) 形式的說明 .........................................................26 圖 3-3-6 函數 y = a sin x + b cos x 的圖形 ...............................................................................27 圖 4-1-1 過 P 且平行於直線 BA 的直線與直線 OQ 的交點 R .............................................30 圖 4-1-2 R 的軌跡實驗（拋物線） ........................................................................................31 圖 4-1-3 R 的軌跡為一拋物線的證明 ....................................................................................31 圖 4-1-4 拋物線的等分線描點作圖 ......................................................................................32 圖 4-1-5 直線 AP 與直線 A′Q 的交點 R ................................................................................33 圖 4-1-6 R 的軌跡實驗（橢圓） ............................................................................................33 圖 4-1-7 R 的軌跡為一橢圓的證明 ........................................................................................34 圖 4-1-8 橢圓的等分線描點作圖 ..........................................................................................35 圖 4-1-9 直線 AP 與直線 A′Q 的交點 R ................................................................................35 圖 4-1-10 R 的軌跡實驗（雙曲線） ......................................................................................36 圖 4-1-11 R 的軌跡為一雙曲線的證明 ..................................................................................36. vi.

(9) 圖 4-1-12 雙曲線的等分線描點作圖 ....................................................................................37 圖 4-2-1 橢圓的參數式作圖 ..................................................................................................39 圖 4-2-2 雙曲線的參數式作圖 ..............................................................................................41 圖 4-2-3 曲線. a 2 b2 + = 1 的參數式作圖 ...............................................................................42 x2 y 2. a 2 b2 − = 1 的參數式作圖 ...............................................................................43 x2 y 2 圖 4-2-5 橢圓（GSP 畫面） ..................................................................................................45. 圖 4-2-4 曲線. 圖 4-2-6 雙曲線（GSP 畫面） ..............................................................................................45 圖 4-2-7 曲線. a 2 b2 + = 1 （GSP 畫面） ...............................................................................45 x2 y 2. a 2 b2 − = 1 （GSP 畫面） ...............................................................................45 x2 y 2 圖 4-3-1 通過三個定點且次數不超過兩次的多項函數圖形 ..............................................47. 圖 4-2-8 曲線. 圖 4-3-2 圖 4-3-3 圖 4-3-4 圖 4-3-5 圖 4-3-6. 通過四個定點且次數不超過三次的多項函數圖形 ..............................................48 通過五個定點且次數不超過四次的多項函數圖形 ..............................................49 三個定點的情形（GSP 畫面） ..............................................................................50 四個定點的情形（GSP 畫面） ..............................................................................50 五個定點的情形（GSP 畫面） ..............................................................................50. 圖 5-1-1 複數的幾何表示 ......................................................................................................52 圖 5-1-2 複數的絕對值 ..........................................................................................................53 圖 5-1-3 共軛複數 ..................................................................................................................53 圖 5-1-4 複數的極式 ..............................................................................................................54 圖 5-1-5 複數平面實驗 ..........................................................................................................54 圖 5-2-1 複數的加法 ..............................................................................................................55 圖 5-2-2 複數的減法 ..............................................................................................................56 圖 5-2-3 複數的乘法 ..............................................................................................................56 圖 5-2-4 複數的除法 ..............................................................................................................57 圖 5-2-5 複數的四則運算實驗 ..............................................................................................57 圖 5-3-1 複數的 n 次方根 ......................................................................................................59 圖 5-3-2 1 的 n 次方根（ n = 2, 3, 4, 5, 6 ） ............................................................................59 圖 5-3-3 圖 5-4-1 圖 5-4-2 圖 5-4-3. 複數的 n 次方根實驗 ..............................................................................................60 平行四邊形 ..............................................................................................................61 不動點 ......................................................................................................................62 凸六邊形 ABCDEF .................................................................................................64. vii.

(10) 第一章緒論本章主要在說明研究的背景、研究動機與目的，並概略說明整個論文的結構。. 1-1 研究背景資訊科技的發展日新月異，電腦設備的使用也日益普及，加上教育心理學的發展由行為學派逐漸轉向認知觀點，這些變遷對教學型態產生重大的影響。過去電腦科技的使用是希望能取代老師傳授知識的角色，現在則是強調將資訊科技融入教學，以創造一個優質的教學環境，提升老師的教學品質，並增進學生的學習效果。資訊科技融入教學早已是世界各先進國家教學的趨勢，我國教育部於民國九十年提出「中小學資訊教育總藍圖」，也正積極從事資訊科技融入教學的推展工作。在數學教育方面，運用資訊科技協助老師呈現過去傳統教材難以呈現的教學內容，或提供環境引導學生進行數學問題的探索，有助於引發學生的學習動機及理解數學概念的形成過程，這都是資訊科技融入數學教學所希望達成的目標。美國數學教師協會（NCTM）建議各階段的老師在教導數學技能與概念時，為了讓學生達到有效的學習，都應該使用科技的工具。現今高中數學課程，幾乎停留在紙筆的抽象推理與研究，難以實際理解或進行更複雜的操作，利用電腦軟體對數學加以重新詮釋，已經是不可或缺的課程。九十八學年普通高級中學數學科課程綱要草案中，針對對數學有興趣的學生規畫一門 2 個學分的「數學軟體」選修課程，希望藉著各種數學軟體，進一步對高中數學加以驗證，並提供學生進行專題研究時的另一種絕佳輔助途徑。. 1-2 研究動機與目的科學哲學家萊茵巴赫將科學的求知活動分成前後兩個階段：發現的過程與驗證的過程。應用到數學來，數學的求知活動是由問題出發，先有探索的發現過程，然後才有邏輯證明與整理成嚴謹的知識系統，兩個階段兼備才算完美。然而，一般數學教科書、教學或文章，往往只展示冰冷且抽象的後半段，而忽略掉最精彩且最能啟迪思想的前半段。這是造成許多學生不喜歡數學，甚至討厭數學的主因（蔡聰明，2000）。傳統的講述教學法是教師最常採用的教學方法，不但操作簡單，而且能以最經濟的方式產生一定的學習成果。然而，這種教師主導整個教學過程的教學法，容易養成學生被動學習及懶惰思考的習慣，不適用於深層或具創意的思考。教師應針對不同的教學內. 1.

(11) 容，採用適當的教學方法，特別是注重概念的理解及思考訓練的數學，如此才能達到最高的教學效能。在數學學習的領域上，面對資訊科技的結合，教與學的方法孕育出動態學習的教學理念。過去的學習方式著重於「認知的獲得」，由完善的證明與推理、循序漸進的邏輯組織，結構出數學嚴謹的全貌，卻忽略了經由觀察、實驗、操作、猜想、測試等歸納方式獲得的數形理念。由於網際網路的發展，快速的傳輸使得圖形檔案與文字資料得以完整、清晰、迅速地呈現在使用者的眼前，使得動態學習能順利進行。有了電腦作為動態學習的輔助教學工具，加上優良的互動式軟體，不僅能夠簡單地呈現數學的動態圖形，或以編序教學為理論基礎之傳統電腦輔助教學，它也提供動態模擬、圖形變換的功能，同時誘發學生主動學習、操作、嘗試及實驗的興趣，如此我們才能兼顧數學「認知的發展」（李政豐，2003）。藉由數學軟體所提供的教學或學習環境，讓學生透過操作與實驗的方式進行數學探究，以達成數學學習及體驗數學概念建構的過程，是資訊科技融入數學教學的可行方案。本研究從高中數學豐富的題材中挑選一些主題，運用動態幾何軟體有強大的計算與繪圖能力、可操作、互動性高及可模擬問題情境的特性，具體呈現傳統教材不易呈現的內容，並設計可供學生進行數學探究的實驗，希望能激發學生對數學的學習興趣，增進學習效果，並培養主動學習與積極探索的態度。. 1-3 論文結構本研究主要是透過動態幾何軟體 GSP 所提供的環境，引導學生從事數學探究的活動，讓學生有機會體驗數學的求知活動中，由問題出發到實驗、觀察、猜測與驗證的完整過程。除第一章緒論及第二章文獻探討外，各章的內容概略說明如下。第三章探索極值問題。首先，探討平面上，如何找直線上一點到線外兩定點的最小距離和，並推廣到兩相交直線的情形。另外，我們從探討圓內接三角形的最大面積出發，進而解決橢圓內接三角形的最大面積問題。最後，我們探討正餘弦函數的疊合問題，主要是藉由兩個動態「圖說證明」的例子，以視覺化的方式同時呈現證明過程及結果，達到將抽象化的數學概念具體化的目的。第四章探索軌跡問題。首先，探討如何由兩直線的交點形成圓錐曲線，進而得到利用矩形各邊的等分線交點描繪圓錐曲線圖形的作法。另外，我們針對圓錐曲線中參數式與三角函數有關的橢圓及雙曲線，從參數式的幾何意義方面著手，探討其圖形的作法，而類似的作法也可以應用在其它參數式與三角函數有關的曲線上。最後，我們探討通過坐標平面上已知定點的多項函數圖形的作法，可藉此觀察各種不同形狀的多項函數圖形。. 2.

(12) 第五章就高中數學所介紹複數的相關內容為題材，從幾何的觀點探索複數的幾何性質，並舉出幾個例子，說明這些幾何性質如何應用在解決平面幾何的問題上，希望讓學生對複數的概念有更清楚的認識，同時也能感受到其實複數是有用的。. 3.

(13) 第二章文獻探討本章主要在探討資訊科技融入教學、數學探究、動態幾何及動態幾何軟體 GSP 的相關文獻。. 2-1 資訊科技融入教學資訊科技融入教學是將資訊科技融入於教學目標、課程設計與教學活動中，使資訊科技成為一項不可或缺的教學工具，並成為教學的一部分，使教學活動更有意義且多元，不僅能增加教學的深度與廣度，更可提升學生的學習興趣，增進自主學習與創新的機會。資訊科技融入教學亦是教師藉助電腦、媒體與網路等資訊科技，製作教材教具，進行輔助教學或補救教學，或是引導學生透過資訊科技，來協助學習、主動探索，以及解決問題，並於學習歷程中獲得資訊科技的相關知識（湯誌龍等，2005）。 Jonassen 等學者（2000）曾在所著的書中說明學習資訊科技有三階段的發展，分別是「從電腦學（Learning from Computer）」、「學電腦（Learning about Computer）」、「用電腦學（Learning with Computer）」（引自張國恩，2002）。由於學習科技理論的發展，加上電腦與網路科技的進步，未來人類學習的模式朝向「用電腦學」的方向。因此，在九年一貫課程中，資訊融入教學成為相當重要的議題。九年一貫課程中，學生應培養十大基本能力，其中多種能力與電腦融入教學有關，張國恩認為電腦融入教學的意義，係指老師運用電腦科技於課堂教學上和課後活動上，以培養學生「運用科技與資訊」的能力和「主動探索與研究」的精神，讓學生能「獨立思考與解決問題」，並完成「生涯規劃與終身學習」。各國資訊科技融入教學的實施現況，美國強調電腦與網路資源共享的特性，以擴大學習的範圍，從以往單機式的電腦輔助教學，至今日網際網路無遠弗屆的教學。英國強調資訊科技統整於各學科，融入於課程之中。歐盟則將中、小學連結區域網路、訓練教師及開發教學軟體等，視為資訊科技融入教學發展的重點。日本強調全體教師必須會操作電腦，且確認「資訊化教育立國」的目標，同時全力發展學生的資訊素養，並將資訊科技融入於中學階段的課程中。新加坡則特別強調資訊科技融入各學科的教學，並鼓勵教師運用電腦多媒體進行教學，學生則能使用網際網路，蒐集資料，並進行相關的學習活動（湯誌龍等，2005）。我國為了推動中、小學資訊科技融入教學，教育部於民國九十年完成「中小學資訊教育總藍圖」，強調「資訊隨手得，主動學習樂；合作創新意，知識伴終生」。除將透過各項培訓，讓所有教師具有資訊科技融入教學的專業能力，同時要求教師於教學活動中，應用資訊科技占其教學總時數應達 20%以上，以使學生體驗不同的學習方法，有效提高學習興趣和教學品質（湯誌龍等，2005）。 4.

(14) 2-2 數學探究探究是指由學生主動去尋找知識及尋求問題解決的過程。探究教學法是誘發學生自行思考去探索問題及發現答案的一種教學策略或計劃。許多社會科學學者均認為杜威為探究教學法的始祖，他在 1909 年的著作中，指出當時的美國教育制度過份強調知識之攝取，而忽略思考技能，故提倡一種類似問題解決方法的教學法，其主要元素為：(1) 問題的確定與定義；(2)建立假設；(3)搜集資料，並加以組織與分析；(4)結論的陳述； (5)驗證假設，將假設予以證實、拒絕或修正。就是透過重組或結合這五個步驟，學生能自我作出通則，了解事物背後意義。而布魯納之探究導向式學習理論也對探究教學法有很大的影響，他指出我們教導學生某學科時，我們的目的不在增加學生某學科的知識，而是鼓勵他們好像科學家或歷史學者一樣思考，共同參與獲得知識的過程，故此求知是一個過程，而非成果。探究教學法要求學生利用教師或教材提供的材料，主動地進行學習，強調學生自我思考、探究和發現事物，而不是消極地接受知識（霍秉坤，2004）。中華人民共和國教育部制訂的普通高中數學課程標準中，課程的基本理念之一，是倡導積極主動、勇於探索的學習方式。學生的數學學習活動不應只限於接受、記憶、模仿和練習，高中數學課程還應倡導自主探索、動手實驗、合作學習、閱讀自學等學習數學的方式。這些方式有助於發揮學生學習的主動性，使學生的學習過程成為在教師引導下的「再創造」過程。因此，高中數學課程要求將數學探究的思想以不同的形式滲透在各模組和考題內容之中，並在高中階段至少安排一次較為完整的數學探究活動（中華人民共和國教育部，2003）。數學探究即數學探究性課題學習，是指學生圍繞某個數學問題，自主探究、學習的過程。這個過程包括：觀察分析數學事實，提出有意義的數學問題，猜測、探求適當的數學結論或規律，給出解釋或證明。數學探究有助於學生初步了解數學概念和結論產生的過程，初步理解直觀和嚴謹的關係，初步嘗試數學研究的過程，體驗創造的激情，建立嚴謹的科學態度和不怕困難的科學精神；有助於培養學生勇於質疑和善於反思的習慣，培養學生發現、提出、解決數學問題的能力；有助於發展學生的創新意識和實踐能力（中華人民共和國教育部，2003）。數學教育家波利亞指出，數學的創造過程是與任何其它知識的創造過程一樣的，在證明一個數學定理之前，你先得猜測這個定理的內容，在你完全做出詳細證明之前，你先得推測證明的思路。數學家高斯曾提到，他的許多定理都是靠實驗和歸納發現的。數學家歐拉也認為，數學這門科學需要觀察，也需要實驗。不少數學家都有共識：用來發現數學新思想的方法之一是進行實驗（蔡政樺，2006）。布置數學實驗環境，基本上是希望如同工程、物理、化學等自然科學的方式，讓學生在此環境中做數學實驗。在實驗中，學生能有適當的工具，可輕鬆、愉快、簡易地作圖，並建構相關的動態數學。學生能親自操作、觀察、度量圖形的動態變化，以建立學習單元中的數學概念。實驗過程中，教師以暗示、鼓勵學生猜測一些數學性質或特徵， 5.

(15) 進而引導學生說明與驗證他所發現或猜測的數學性質。即使是錯誤的猜測，也能給予學生作為反例驗證的實驗或說明，並由此進入較高層次的探討，發展此概念的各種性質。教師配合學習單元的主題及綜合學生的結論，引導學生進入理論層次的研究，以數學邏輯推理作嚴密的證明並建立應用層面的模擬（左台益，2002）。. 2-3 動態幾何清華大學全任重教授指出，動態幾何是指 1990 年代發展成的電腦環境，在這個環境下，使用者得以建立點、線、圓等幾何物件，並且定義它們彼此之間的幾何關係。對於設定好的圖形，使用者得以透過滑鼠操縱幾何物件的位置，整幅幾何圖像即依循幾何關係作瞬間的改變。動態幾何環境適合平面幾何、射影幾何、幾何作圖、解析幾何等學科裡數學實驗之進行。根據維基百科的解釋，動態幾何軟體是一種可以讓使用者製作並且操作一些幾何物件的軟體。一般來說，這裡的幾何物件都是在歐氏幾何中的物件。我們可以說動態幾何軟體基本上是一個可以在電腦上作尺規作圖的軟體，不過還提供了更多的彈性、互動性，還有一些動態的展示。動態幾何軟體有以下的優點（King & Schattschneider, 1997）： 1.. 作圖精確：任何歐氏幾何的尺規作圖、歐氏幾何作圖的變換所產生的圖形、或當部分圖形沿著一定路徑移動時所產生物件的軌跡，動態幾何軟體都提供了精確的作圖工具。. 2.. 視覺化：動態幾何軟體有助於所有數學課上的視覺化處理過程，並非只有幾何上的學習而已。. 3.. 探索與發現：在傳統的幾何課程中，總是老師告訴學生定義及定理，並且指定問題及證明，學生都沒有體驗發現幾何關係，也沒有發明任何數學。動態幾何軟體非常適合不論是引導式或完全開放式的探索與發現。. 4.. 證明：儘管動態幾何軟體無法實際產生證明，但它所提供的實驗性證據更確定了學生想要證明的動機。. 5.. 變換：動態幾何軟體可以在使用者面前現場展示圖形的變換。. 6.. 軌跡：動態幾何軟體內建追蹤物件軌跡的功能，非常適合用來展示軌跡如何生成，以及顯示軌跡的形狀。. 7.. 模擬：動態幾何軟體中拖曳、動態模擬、追蹤軌跡及產生自由點的功能，提供許多模擬多種情境變化的機會。. 6.

(16) 8.. 微世界：動態幾何軟體提供一個可以探索歐氏幾何的環境，也可以創造新的環境。. 動態相對於靜態，意味著可操作及互動性，動態幾何軟體確實提供了學生一個探索及學習幾何的良好學習環境。顏貽隆（2003）指出，目前國內已有多所大學開設動態幾何課程，如台灣師範大學、清華大學、彰化師範大學、高雄師範大學、台北市立教育大學等，其重要性由此可見。. 2-4 動態幾何軟體 GSP 動態幾何軟體 GSP（The Geometer’s Sketchpad 的簡稱）是美國 Swarthmore College 及 Key Curriculum Press 在 NSF 之下產官學合作視覺幾何研究計畫的產品。它是一套架構在視窗下，物件導向動態連結的幾何繪圖軟體，可作為幾何學研究與教學的輔助工具。尤其在中學幾何的學習上，深受中學教師與學生的喜愛（國立台灣師範大學數學系網路小組，1999）。 GSP 是在視窗環境內幾何構圖的電腦輔助教學軟體，可以當作尺規作圖的電腦版，在教學上能節省繪圖時間，並簡易地構造動態幾何。經由動態幾何圖形的變換及度量來描述我們可以發現的一些幾何關係，有助於增強開放式的猜測與研究。GSP 不僅可由簡易尺規作圖構造出複雜幾何圖形，更可對固定結構圖形作連續的變化。它也提供動態模擬、圖形變換及圖形改換時，長度、角度、比例、面積等度量的功能。它更可對結構性作圖作巨集建構、文字說明，形成簡易操作鈕，提供使用者幾何學習的良好環境（學習加油站高中數學軟體資源）。 GSP 提供了基本幾何作圖工具，具有尺規作圖、圖形可作動態連續變換、保持結構、特殊即一般、記錄作圖過程等特質，新版的軟體，甚至可以將檔案存成 html 檔案，直接放置於網頁上展示。這些功能及特質，不只能提供精確的幾何圖形，而且能協助教師針對教學單元，設計方便操作、易於探討圖形性質的教學及學習環境（林保平，2004）。. 7.

(17) 第三章探索極值問題與幾何相關的極值問題，是要在滿足一定條件的情況下，求某個幾何量的最大值或最小值，並求發生最大值或最小值的條件，如長度、面積、體積、角度、…等。幾何問題當然最好有圖形配合，然而如果只是靜態的呈現，單靠紙筆的模擬或憑空想像，很難達到預期的效果。運用電腦的輔助使靜態的幾何變成動態，讓學生透過動手操作的過程探索極值問題，這種經由實驗、觀察、猜測及驗證的過程去發現進而理解的數學概念，往往讓學生留下深刻的印象，達到最佳的學習效果。正餘弦函數疊合的概念，經常應用在與三角函數有關的極值問題上，其純代數運算的證明過程固然嚴謹，但缺乏幾何的直觀性，如果能用具體的圖形甚至動態的方式呈現，相信被接受的程度會更高。在數學中，一個公式或定理的證明有各種方式，其中的「圖說證明」（proof without words）具有直觀、輕巧、雅緻之趣（蔡聰明，2000）。幾何圖形具有直觀易明的優點，「一個圖勝過千言萬語」正是圖說證明的最佳寫照。本章透過動態幾何軟體 GSP 探索極值問題，共分為三節，分別說明如下。 3-1 直線上一點到線外兩定點的最小距離和透過動態幾何軟體 GSP 所設計的實驗，探討平面上如何在一直線 L 上找一點 P, 使其到線外兩定點 A, B 的距離和 AP + PB 為最小。此外，如何在兩相交直線 L1 及 L2 上各找一點 P 及 Q, 使其距離 PQ 與其到線外兩定點 A, B 的距離 PA , QB 之和. AP + PQ + QB 為最小，也是本節進一步要探討的另一個問題。 3-2 圓及橢圓內接三角形的最大面積從探討圓內接三角形的最大面積出發，進而解決橢圓內接三角形的最大面積問題。我們透過動態幾何軟體 GSP 所設計的實驗，分別觀察當圓及橢圓內接三角形的三頂點位置改變時，其三內角及面積的變化情形，進而猜測面積的最大值及面積達到最大時三角形的形狀，最後用綜合幾何及解析幾何的方法加以驗證。 3-3 正餘弦函數疊合的極值對於由 y = sin x 與 y = cos x 的線性組合所形成的函數 y = a sin x + b cos x , 首先，用一般純代數運算的推導方法，將其化成 y = r sin( x + φ ) 或 y = r cos( x + φ ) 的形式，而求得其最大值與最小值。接著，透過動態幾何軟體 GSP 設計兩個動態「圖說證明」的例子，藉由圖形直觀地說明 a sin θ + b cos θ 化成 r sin(θ + φ ) 或 r cos(θ + φ ) 形式的結果，並進一步探索其極值問題。最後，我們再透過動態幾何軟體 GSP, 將函數 y = a sin x + b cos x 的圖形以動態的方式呈現出來。 8.

(18) 3-1 直線上一點到線外兩定點的最小距離和本節透過動態幾何軟體 GSP 所設計的實驗，探討平面上如何在一直線 L 上找一點 P, 使其到線外兩定點 A, B 的距離和 AP + PB 為最小。此外，如何在兩相交直線 L1 及 L2 上各找一點 P 及 Q, 使其距離 PQ 與其到線外兩定點 A, B 的距離 PA , QB 之和 AP + PQ + QB 為最小，也是本節進一步要探討的另一個問題。. 3-1-1 一直線及線外兩定點在平面上，給定一直線 L 及線外兩定點 A, B, 如果 A, B 兩點在直線 L 的異側，由於平面上兩點之間以直線距離為最短，且線段 AB 與直線 L 相交。因此，連接 A, B 兩點，那麼線段 AB 與直線 L 的交點 P, 就是直線 L 上使 AP + PB 為最小的點 P, 且. AP + PB = AB 為最小距離和，如圖 3-1-1。但是，如果 A, B 兩點在直線 L 的同側呢？ B. L P. A. 圖 3-1-1 一直線及線外兩定點（異側）問題一：在平面上，給定一直線 L 及線外兩定點 A, B, 其中 A, B 兩點在直線 L 的同側，如圖 3-1-2。如何在直線 L 上找一點 P, 使 AP + PB 為最小？. 9.

(19) B A. L P. 圖 3-1-2 一直線及線外兩定點（同側）我們透過動態幾何軟體 GSP 設計一個實驗來探討這個問題，如圖 3-1-3。. 圖 3-1-3 最小距離和實驗在 GSP 的操作畫面中，給定一直線 L 及在直線 L 同側的兩定點 A, B, 且 P 為直線 L 上的動點。畫面上除了顯示線段 AP 及線段 PB 的長度，以及 AP + PB 的值之外，為了方便使用者觀察 AP + PB 達到最小的條件，我們同時顯示線段 AP 及線段 PB 與直線 L 的夾角大小。當 P 的位置改變時，畫面上會即時顯示最新的數據，由於電腦採數值運算的結果，所以數據是近似值（本實驗設定取至小數點後五位）而非精確值。實驗操作的方法，使用者可以任意調整 P 在直線 L 上的位置，目的是使 AP + PB 的值盡可能達到最小。. 從實際操作的過程中，我們發現隨著 AP + PB 的值逐漸減小的同時，線段 AP 及線段 PB 與直線 L 的夾角有慢慢接近的趨勢，且當 AP + PB 的值達到最小時，兩夾角幾乎是相等的，如圖 3-1-4。. 10.

(20) 圖 3-1-4 最小距離和為了討論的方便，我們將線段 AP 及線段 PB 與直線 L 的夾角分別以 α 及 β 表示。如圖 3-1-5，當直線 L 上某個點 P 滿足 α = β 時，延長線段 AP , 則由兩直線相交其對頂角相等的原理知 α = γ , 故 β = γ . 過 B 作直線 L 的垂直線，分別與直線 L 及直線 AP 交於 H 及 B′ , 由三角形 ASA 全等性質知 ∆BHP ≅ ∆B′HP , 即 B′ 是 B 對直線 L 的對稱點。因此，如果要在直線 L 上找到滿足 α = β 的點 P, 首先作 B 對直線 L 的對稱點 B′ , 然後連接 A, B′ 兩點，那麼線段 AB′ 與直線 L 的交點即為所求。 B A. α. β P γ. H. L. B'. 圖 3-1-5 B′ 是 B 對直線 L 的對稱點猜測一：直線 L 上滿足 α = β 的點 P, 就是直線 L 上使 AP + PB 為最小的點 P. 接下來，我們證明上面的猜測一是正確的。證明：設 P 是直線 L 上滿足 α = β 的點，且 P′ 是直線 L 上異於 P 的任一點，如圖 3-1-6。. 11.

(21) B A. L P. P'. B'. 圖 3-1-6 最小距離和的證明由 B′ 是 B 對直線 L 的對稱點知 PB = PB′ 及 P′B = P′B′ , 故 AP′ + P′B = AP′ + P′B′. > AB′ = AP + PB′ = AP + PB . ▓ 有了上面的分析及證明，我們得到下面的結論一。結論一：在平面上，給定一直線 L 及線外兩定點 A, B, 其中 A, B 兩點在直線 L 的同側。首先作 B 對直線 L 的對稱點 B′ , 然後連接 A, B′ 兩點，那麼線段 AB′ 與直線 L 的交點 P, 就是直線 L 上使 AP + PB 為最小的點 P, 且 AP + PB = AB′ 為最小距離和，如圖 3-1-7。 B A. L P. B'. 圖 3-1-7 最小距離和的作法（一直線）在問題一的討論中，我們發現對稱的觀念扮演著關鍵的角色，一點對一直線作對稱時，其與此直線上任一點的距離保持不變。因此，當 A, B 兩點在直線 L 的同側時，只要作其中一點對直線 L 的對稱點，將兩點在直線 L 的同側轉換成兩點在直線 L 的異側，這個問題便迎刃而解了。. 12.

(22) 3-1-2 兩相交直線及線外兩定點我們將前一小節的問題，由一直線推廣為兩相交直線，繼續做進一步的探討。問題二：在平面上，給定兩相交直線 L1 , L2 及線外兩定點 A, B, 其中 A, B 兩點在 L1 與 L2 所分割成四個區域中的同一個區域內，如圖 3-1-8。如何在直線 L1 及 L2 上各找一點. P 及 Q, 使 AP + PQ + QB 為最小？. L1 A B. P. L2 Q. 圖 3-1-8 兩相交直線及線外兩定點根據前一小節的結論，我們不難推出問題二的答案。首先，在直線 L1 上任選一點. P, 使 P, A 兩點在直線 L2 的同側，此時線段 AP 的長度是固定的，如果要在直線 L2 上找一點 Q, 使 AP + PQ + QB 為最小，先作 B 對直線 L2 的對稱點 B1 , 再連接 P, B1 兩點，那麼線段 PB1 與直線 L2 的交點即為所求，且此時 AP + PQ + QB = AP + PB1 為最小距離和，如圖 3-1-9。因此，對直線 L1 上任意選定的一點 P, 直線 L2 上使 AP + PQ + QB 為最小的點 Q 是由 P 所決定的，即線段 PB1 與直線 L2 的交點，且此時最小距離和為 AP + PB1 。 L1 A B. P. L2 Q. B1. 圖 3-1-9 B1 是 B 對直線 L2 的對稱點 13.

(23) 接著，對在直線 L1 同側的兩定點 A, B1 , 如果要在直線 L1 上找一點 P, 使 AP + PB1 為最小，先作 B1 對直線 L1 的對稱點 B2 , 再連接 A, B2 兩點，那麼線段 AB2 與直線 L1 的交點即為所求，且此時 AP + PB1 = AB2 為最小距離和，如圖 3-1-10。 L1 A B P. L2. B2. B1. 圖 3-1-10 B2 是 B1 對直線 L1 的對稱點綜合上面的推論，我們得到下面的結論二。結論二：在平面上，給定兩相交直線 L1 , L2 及線外兩定點 A, B, 其中 A, B 兩點在 L1 與 L2 所分割成四個區域中的同一個區域內。首先作 B 對直線 L2 的對稱點 B1 , 再作 B1 對直線 L1 的對稱點 B2 , 然後連接 A, B2 兩點，線段 AB2 與直線 L1 交於 P, 再連接 P, B1 兩點，線段 PB1 與直線 L2 交於 Q, 那麼 P 及 Q 分別就是直線 L1 及 L2 上使. AP + PQ + QB 為最小的點 P 及點 Q, 且 AP + PQ + QB = AB2 為最小距離和，如圖 3-1-11。 L1 A B. P. L2 Q. B2. B1. 圖 3-1-11 最小距離和的作法（兩相交直線）. 14.

(24) 3-2 圓及橢圓內接三角形的最大面積本節從探討圓內接三角形的最大面積出發，進而解決橢圓內接三角形的最大面積問題。我們透過動態幾何軟體 GSP 所設計的實驗，分別觀察當圓及橢圓內接三角形的三頂點位置改變時，其三內角及面積的變化情形，進而猜測面積的最大值及面積達到最大時三角形的形狀，最後用綜合幾何及解析幾何的方法加以驗證。. 3-2-1 圓內接三角形我們先透過動態幾何軟體 GSP 探討圓內接三角形的情形，如圖 3-2-1。. 圖 3-2-1 圓內接三角形實驗在 GSP 的操作畫面中，P, Q, R 為圓 C 上的三個動點，畫面的左上角除了顯示 ∆PQR 的面積之外，為了方便使用者觀察使面積達到最大的條件，我們同時列出 ∆PQR 的三內角大小。當 P, Q, R 的位置改變時，畫面上會即時顯示最新的數據，由於電腦採數值運算的結果，所以數據是近似值（本實驗設定取至小數點後五位）而非精確值。實驗操作的方法，首先任意給定 P, Q, R 的位置，記錄第一筆資料，內容包括 ∠P , ∠Q , ∠R 的大小及 ∆PQR 的面積；然後調整 P 的位置使 ∆PQR 的面積盡可能達到最大，此時約 ∠Q = ∠R , 記錄第二筆資料；再調整 Q 的位置使 ∆PQR 的面積盡可能達到最大，此時約 ∠R = ∠P , 記錄第三筆資料；再調整 R 的位置使 ∆PQR 的面積盡可能達到最大，此時約 ∠P = ∠Q , 記錄第四筆資料；接著依照 P, Q, R 的順序繼續調整其位置，均使 ∆PQR 的面積盡可能達到最大，總共記錄 10 筆資料，如表 3-2-1 所示。. 15.

(25) 表 3-2-1 圓內接三角形的三內角及面積. ∠Q. ∆PQR 的面積( cm 2 ). 32.69321°. ∠R 62.73727°. 84.56952°. 47.66507°. 47.76541°. 37.55911. 66.18997°. 47.66507°. 66.14496°. 42.63726. 56.94337°. 56.91168°. 66.14496°. 44.27056. 56.94337°. 61.53495°. 61.52168°. 44.64484. 59.26017°. 61.53495°. 59.20488°. 44.74151. 60.39611°. 60.39901°. 59.20488°. 44.76484. 60.39611°. 59.75386°. 59.85003°. 44.77131. 60.12314°. 59.75386°. 60.12300°. 44.77266. 59.91823°. 59.95877°. 60.12300°. 44.77328. ∠P 84.56952°. 32.94903. 從以上實驗操作的過程，我們發現 ∆PQR 的面積呈現遞增的情形，且當面積達到最大時， ∠P , ∠Q , ∠R 均接近 60° , 即 ∆PQR 近乎正三角形，如圖 3-2-2。. 圖 3-2-2 圓內接三角形的最大面積上面的觀察結果可歸納成為下面的猜測一。猜測一：當圓內接三角形為一正三角形時，其面積為最大。接下來，我們藉由下面的引理一及引理二，證明上面的猜測一是正確的。引理一：當圓內接三角形的一邊固定時，以另兩邊等長的銳角等腰三角形之面積為最大。證明： q 上異於 A, B, 設 ∆ABC 為圓 O 的內接銳角等腰三角形，其中 AB = AC , 且 A′ 為 BAC HJJG C 的一點，作 AH 及 A′H ′ 分別垂直 BC 於 H 及 H ′ , 如圖 3-2-3。 16.

(26) A. A'. O. B. H. H'. C. 圖 3-2-3 一邊固定的圓內接三角形. 1 1 ∆ABC 的面積為 BC ⋅ AH , ∆A′BC 的面積為 BC ⋅ A′H ′ , 因為 AH = AO + OH 2 2 = A′O + OH > A′H > A′H ′ , 所以 ∆ABC 面積 > ∆A′BC 面積。因此，當圓內接三角形. 的一邊 BC 固定時，以 AB = AC 的銳角等腰 ∆ABC 之面積為最大。 ▓ 引理二：圓內接銳角等腰三角形中，以正三角形的面積為最大。證明：設圓 O 的半徑為 a, 且 ∆ABC 為圓 O 的內接銳角等腰三角形，其中 AB = AC , 作 AH 垂直 BC 於 H, 如圖 3-2-4。. A. a O a. B. x H. C. 圖 3-2-4 圓內接銳角等腰三角形令 OH = x （ 0 < x < a ）, 則底 BC = 2 a 2 − x 2 , 高 AH = a + x , 故 ∆ABC 面積 =. 1 1 BC ⋅ AH = ⋅ 2 a 2 − x 2 ⋅ (a + x) = (a + x) a 2 − x 2 = (a + x)3 (a − x ) . 2 2 17.

(27) a+x a+x a+x + + + (a − x) 3 3 由算幾不等式，得 3 ≥ 4. 式可化簡為 (a + x)3 (a − x) ≤. 4. a+x a+x a+x ⋅ ⋅ ⋅ (a − x) , 此 3 3 3. 27 4 3 3 2 a , 故 ∆ABC 面積 ≤ a . 等號成立時， 16 4. a+x 1 = a − x , 得 x = a , 此時 ∠BAC = 60° , 即 ∆ABC 為正三角形。因此，半徑為 3 2 a 的圓，其內接銳角等腰三角形中，以正三角形的面積. 3 3 2 a 為最大。 ▓ 4. 綜合引理一及引理二，我們得到下面的定理一。定理一：半徑為 a 的圓，其內接三角形中，以正三角形的面積. 3 3 2 a 為最大。 4. 3-2-2 橢圓內接三角形現在，我們透過動態幾何軟體 GSP 探討橢圓內接三角形的情形，如圖 3-2-5。. 圖 3-2-5 橢圓內接三角形實驗在 GSP 的操作畫面中，P, Q, R 為橢圓 Γ 上的三個動點，圓 C 為以橢圓中心為圓心，橢圓長軸長為直徑所作的圓，過 P, Q, R 作長軸的垂直線，分別與圓 C 交於 P′ , Q′ , R′ , 其中 P 和 P′ , Q 和 Q′ , R 和 R′ 分別在長軸的同側。畫面的左上角除了顯示 ∆PQR 的面積之外，為了方便使用者觀察使面積達到最大的條件，我們同時列出 ∆PQR 及 ∆P′Q′R′ 的三內角大小。當 P, Q, R 的位置改變時，畫面上會即時顯示最新的數據，本實驗仍然設定取至小數點後五位的近似值。實驗操作的方法，首先任意給定 P, Q, R 的位置，記錄第一筆資料，內容包括 ∠P , ∠Q , ∠R 的大小， ∠P′ , ∠Q′ , ∠R′ 的大小及 ∆PQR 的面積；然後調整 P 的位置使 ∆PQR 的面積盡可能達到最大，此時約 ∠Q′ = ∠R′ , 記錄第二. 18.

(28) 筆資料；再調整 Q 的位置使 ∆PQR 的面積盡可能達到最大，此時約 ∠R′ = ∠P′ , 記錄第三筆資料；再調整 R 的位置使 ∆PQR 的面積盡可能達到最大，此時約 ∠P′ = ∠Q′ , 記錄第四筆資料；接著依照 P, Q, R 的順序繼續調整其位置，均使 ∆PQR 的面積盡可能達到最大，總共記錄 10 筆資料，如表 3-2-2 所示。表 3-2-2 橢圓內接三角形的三內角及面積 ∆PQR 的面積. ∠P. ∠Q. ∠R. ∠P ′. ∠Q ′. ∠R ′. 99.62568°. 42.67761°. 37.69672°. 86.24887°. 63.00000°. 30.75113°. ( cm 2 ) 18.80243. 82.97654°. 32.81183°. 64.21163°. 86.24887°. 46.80000°. 46.95113°. 21.98566. 70.91866°. 29.23274°. 79.84860°. 66.60000°. 46.80000°. 66.60000°. 25.39465. 55.22405°. 36.56617°. 88.20977°. 56.70000°. 56.70000°. 66.60000°. 26.51699. 59.63949°. 39.81363°. 80.54688°. 56.70000°. 61.65000°. 61.65000°. 26.77406. 61.26547°. 40.16023°. 78.57430°. 59.15304°. 61.65000°. 59.19696°. 26.84194. 63.42594°. 39.06589°. 77.50817°. 60.50304°. 60.30000°. 59.19696°. 26.85869. 62.99749°. 38.77130°. 78.23122°. 60.50304°. 59.85000°. 59.64696°. 26.86191. 62.76315°. 38.71899°. 78.51786°. 60.14495°. 59.85000°. 60.00505°. 26.86386. 62.54891°. 38.82582°. 78.62527°. 60.01128°. 59.98367°. 60.00505°. 26.86409. 從以上實驗操作的過程，我們發現 ∆PQR 的面積呈現遞增的情形，且當面積達到最大時， ∠P′ , ∠Q′ , ∠R′ 均接近 60° , 即 ∆P′Q′R′ 近乎正三角形，如圖 3-2-6。. 圖 3-2-6 橢圓內接三角形的最大面積上面的觀察結果可歸納成為下面的猜測二。猜測二：設 P, Q, R 為橢圓 Γ 上的相異三點，圓 C 為以橢圓中心為圓心，橢圓長軸長為直徑所作的圓，過 P, Q, R 作長軸的垂直線，分別與圓 C 交於 P′ , Q′ , R′ , 其中 P 和 P′ , Q 和 Q′ , R 和 R′ 分別在長軸的同側。當圓 C 的內接 ∆P′Q′R′ 為一正三角形時，橢圓 Γ 的內接 ∆PQR 之面積為最大。. 19.

(29) 接下來，我們利用前一小節的定理一，證明上面的猜測二是正確的。證明：設橢圓 Γ 的長軸半長為 a, 短軸半長為 b, 以橢圓 Γ 的長軸所在直線為 x 軸，短軸所在直線為 y 軸，建立直角坐標系。令 P, Q, R 的坐標分別為 P (a cos α , b sin α ) , Q(a cos β , b sin β ) , R(a cos γ , b sin γ ) , 則 P′ , Q′ , R′ 的坐標分別為 P′(a cos α , a sin α ) , Q′(a cos β , a sin β ) , R′(a cos γ , a sin γ ) , 如圖 3-2-7。 y P '( a cosα , a sin α ) Q '( a cosβ , a sin β ). P( a cosα , b sin α ). b. C. Q( a cosβ , b sin β ). x. a. O. R( a cosγ , b sin γ ) R'( a cosγ , a sin γ ). 圖 3-2-7 橢圓內接 ∆PQR 及圓內接 ∆P′Q′R′ a cos α 1 ∆PQR面積 = | a cos β 2 a cos γ. b sin α 1 a cos α b 1 b sin β 1 | = ⋅ | a cos β a 2 b sin γ 1 a cos γ. a sin α 1 b a sin β 1 | = ⋅ ∆P′Q′R′面積， a a sin γ 1. 根據定理一，當圓 C 的內接 ∆P′Q′R′ 為一正三角形時，其面積時，橢圓 Γ 的內接 ∆PQR 之面積. 3 3 2 a 為最大，此 4. 3 3 ab 為最大。 ▓ 4. 有了上面的證明，我們得到下面的定理二。定理二： x2 y2 + = 1 , 其中 a > b > 0 , 圓 C : x 2 + y 2 = a 2 , 且 P, Q, R 為橢圓 Γ 上的 a 2 b2 相異三點，過 P, Q, R 作長軸的垂直線，分別與圓 C 交於 P′ , Q′ , R′ , 其中 P 和 P′ , Q 和 Q′ , R 和 R′ 分別在長軸的同側。當圓 C 的內接 ∆P′Q′R′ 為一正三角形時，橢設橢圓 Γ :. 圓 Γ 的內接 ∆PQR 之面積. 3 3 ab 為最大。 4 20.

(30) 數學傳播季刊八卷一期的「問題徵答」中，第 8102 題為「求橢圓內接三角形最大面積」，八卷二期刊出三個獲得特優的解答，分別用解析幾何及綜合幾何的方法，非常值得參考。. 21.

(31) 3-3 正餘弦函數疊合的極值本節對於由 y = sin x 與 y = cos x 的線性組合所形成的函數 y = a sin x + b cos x , 首先，用一般純代數運算的推導方法，將其化成 y = r sin( x + φ ) 或 y = r cos( x + φ ) 的形式，而求得其最大值與最小值。接著，透過動態幾何軟體 GSP 設計兩個動態「圖說證明」的例子，藉由圖形直觀地說明 a sin θ + b cos θ 化成 r sin(θ + φ ) 或 r cos(θ + φ ) 形式的結果，並進一步探索其極值問題。最後，我們再透過動態幾何軟體 GSP, 將函數 y = a sin x + b cos x 的圖形以動態的方式呈現出來。. 3-3-1 疊合法設有兩函數 y = f ( x) 與 y = g ( x) , 其定義域相同，則 y = f ( x) + g ( x) 也是一個函數，且其圖形可由 y = f ( x) 與 y = g ( x) 的圖形疊合而得。疊合的方式是藉由兩函數 y = f ( x) 與 y = g ( x) 原有的圖形，將同一變數 x 所對應的函數值 f ( x) 與 g ( x) 相加，得到一個新函數值 f ( x) + g ( x) , 便可描出新函數 y = f ( x) + g ( x) 圖形上的一點。仿此作法，可描出其它的點，而整個新函數 y = f ( x) + g ( x) 的圖形便可描繪出來。雖然疊合法容易產生誤差，尤其是圖形上某些特殊位置的點容易被忽略，但是它具有直觀的特點，從初步得到的圖形，只須配合原函數的相關性質，便能精確地掌握新函數的圖形。正弦函數 y = sin x 與餘弦函數 y = cos x 的圖形是三角函數的基本圖形。利用疊合法，我們可以畫出函數 y = sin x + cos x 的圖形，並且發現 y = sin x + cos x 的圖形與 y = sin x 或 y = cos x 的圖形，基本上形狀是相同的，都是以 2π 為週期的波狀圖形，只是振幅變大，且波峰與波谷的位置左右稍有不同，如圖 3-3-1。 y. y = si n x y = cos x y = si n x + cos x. 2. 1. x -2π. -. 3π 2. -π. -. π 2. π 2. π. 3π 2. -1. -2. 圖 3-3-1 函數 y = sin x + cos x 的圖形. 22. 2π.

(32) 如果再根據兩原函數 y = sin x 與 y = cos x 的關係，我們可以猜測函數 y = sin x + cos x 的圖形是將 y = sin x 的圖形上下伸長為 2 倍，再向左平移的圖形上下伸長為 2 倍，再向右平移. π. π 4. 單位而得，或是將 y = cos x. 單位而得。這個結果可透過和角公式驗證如下：. 4. (1) y = sin x + cos x = 2(. 1 1 π π π sin x + cos x) = 2(sin x cos + cos x sin ) = 2 sin( x + ) ; 4 4 4 2 2. (2) y = sin x + cos x = 2(. 1 1 π π π sin x + cos x) = 2(cos x cos + sin x sin ) = 2 cos( x − ) . 4 4 4 2 2. 3-3-2 正餘弦函數疊合的證明對於一般由 y = sin x 與 y = cos x 的線性組合所形成的函數 y = a sin x + b cos x（a, b 是不皆為 0 的常數），是否也具有 y = r sin( x + φ ) 或 y = r cos( x + φ ) 的形式，使其圖形可由 y = sin x 或 y = cos x 的圖形上下伸縮，再左右平移而得呢？隨著係數 a, b 的不同，如果直接將 y = a sin x 的圖形與 y = b cos x 的圖形疊合，似乎不容易觀察出 y = a sin x + b cos x 的圖形形狀，即使它具有 y = r sin( x + φ ) 或 y = r cos( x + φ ) 的形式，也很難從疊合後的圖形找出真正的 r, φ 與 a, b 之間的關係。因此，我們仿照 y = sin x + cos x 的推導方法，來探討 y = a sin x + b cos x 的情形。 (1) 將 y = a sin x + b cos x 化成 y = r sin( x + φ ) 的形式： y = a sin x + b cos x = a 2 + b 2 ( (. a a +b 2. 2. b. )2 + (. a +b 2. 2. a a +b 2. 2. sin x +. ) 2 = 1 , 所以點 P (. b. a a +b 2. cos x) , 因為. a + b2 2. 2. ,. b a + b2 2. ) 在以原點 O 為圓心的. 單位圓上。設有向角 α 以 OP 為終邊（ α 不是唯一的），則 cos α = sin α =. b a +b 2. 2. a a + b2 2. ,. , 此時， y = a 2 + b 2 (sin x cos α + cos x sin α ) = a 2 + b 2 sin( x + α ) .. 因此，函數 y = a sin x + b cos x 的圖形可由 y = sin x 的圖形上下伸縮為 a 2 + b 2 倍，再左右平移 | α | 單位（ α < 0 為向右平移， α > 0 為向左平移）而得，且當 x 為任意實數時，其最大值 a 2 + b 2 與最小值 − a 2 + b 2 分別發生在. π 3π x = ( − α ) + 2nπ 與 x = ( − α ) + 2nπ , 其中 n 為整數。 2 2. 23.

(33) (2) 將 y = a sin x + b cos x 化成 y = r cos( x + φ ) 的形式： y = a sin x + b cos x = a 2 + b 2 (. (. b a +b 2. 2. a. )2 + (. a +b 2. 2. a a +b 2. 2. sin x +. ) 2 = 1 , 所以點 Q(. b. b a +b 2. cos x) , 因為. a + b2 2. 2. ,. a a + b2 2. ) 在以原點 O 為圓心的. 單位圓上。設有向角 β 以 OQ 為終邊（ β 不是唯一的），則 cos β =. sin β =. a a +b 2. 2. b a + b2 2. ,. , 此時， y = a 2 + b 2 (cos x cos β + sin x sin β ) = a 2 + b 2 cos( x − β ) .. 因此，函數 y = a sin x + b cos x 的圖形可由 y = cos x 的圖形上下伸縮為 a 2 + b 2 倍，再左右平移 | β | 單位（ β > 0 為向右平移， β < 0 為向左平移）而得，且當 x 為任意實數時，其最大值 a 2 + b 2 與最小值 − a 2 + b 2 分別發生在 x = β + 2nπ 與. x = (π + β ) + 2nπ , 其中 n 為整數。上面利用三角函數的和角公式所推導的方法屬於純代數的運算，缺乏幾何的直觀性。雖然初學者對於給定 a, b 的函數 y = a sin x + b cos x , 經過多次的練習之後，都能正確地將其化成 y = r sin( x + φ ) 或 y = r cos( x + φ ) 的形式，即使變數 x 有範圍限制時，也都能進一步求得其最大值與最小值，但是如果能透過圖形來說明，相信會讓初學者對正餘弦函數的疊合有更深刻的理解。. 3-3-3 正餘弦函數疊合的圖說證明接下來，我們透過動態幾何軟體 GSP 設計兩個動態「圖說證明」的例子，圖 3-3-2 展示 a sin θ + b cos θ 化成 r sin(θ + φ ) 的形式，圖 3-3-3 展示 a sin θ + b cos θ 化成 r cos(θ + φ ) 的形式。. 圖 3-3-2 正餘弦函數疊合的圖說證明（ sin ）圖 3-3-3 正餘弦函數疊合的圖說證明（ cos ）. 24.

(34) 在 GSP 的操作畫面中，使用者可以在畫面的左上角任意調整 a, b 的大小，以觀察在不同條件下的情形。另外，在 a, b 固定的條件下，使用者也可以透過手動調整或按下「動態展示」按鈕由電腦自動調整圖中「動點」的位置，以改變角 θ , 而進一步探索 a sin θ + b cos θ 的最大值與最小值，並觀察何時發生最大值與最小值。由於利用線段長度表示 a, b 的值，所以我們在「a, b 皆為正數」的限制下進行討論。以下我們就兩個「圖說證明」的例子分別詳細加以說明。. (1) a sin θ + b cos θ 化成 r sin(θ + φ ) 形式的說明：設 P 是以原點 O 為圓心，a 為半徑的圓 C 上一動點，且有向角 θ 以 OP 為終邊，. PQ ⊥ OP 且 PQ = b , 如圖 3-3-4。. y. a2+b2. Q. a si n θ + b cos θ. b. C. a2+b2 α. P. a. θ. O. x. - a2+b2. 圖 3-3-4 a sin θ + b cos θ 化成 r sin(θ + φ ) 形式的說明. `. 不論 P 在圓 C 上的位置如何改變， OP = (a cos θ , a sin θ ) ,. π π ` PQ = (b cos(θ + ), b sin(θ + )) = (−b sin θ , b cos θ ) , 2. 2. ` ` `. OQ = OP + PQ = (a cos θ − b sin θ , a sin θ + b cos θ ) , Q 的 y 坐標即為 a sin θ + b cos θ .. 另一方面， OQ = a 2 + b 2 , 令 ∠POQ = α , 則. `. OQ = ( a 2 + b 2 cos(θ + α ), a 2 + b 2 sin(θ + α )) , Q 的 y 坐標為 a 2 + b 2 sin(θ + α ) . 25.

(35) 因此， a sin θ + b cos θ = a 2 + b 2 sin(θ + α ) 恆成立，其中銳角 α 滿足. a. cos α =. a 2 + b2. 及 sin α =. b a 2 + b2. a. , 即 α = cos −1. a 2 + b2. （ = sin −1. b a 2 + b2. ）. 當. P 在圓 C 上移動時，Q 的軌跡形成以 O 為圓心， a 2 + b 2 為半徑的圓，其 y 坐標的值介於 − a 2 + b 2 與 a 2 + b 2 之間，即 − a 2 + b 2 ≤ a sin θ + b cos θ ≤ a 2 + b 2 . 當 Q 落在 y 軸正向上時，其 y 坐標 a sin θ + b cos θ 達到最大值 a 2 + b 2 , 此時 P 在有向角. π 2. − α 的終邊上，即 θ =. π 2. − α ; 當 Q 落在 y 軸負向上時，其 y 坐標. a sin θ + b cos θ 達到最小值 − a 2 + b 2 , 此時 P 在有向角. θ=. 3π − α 的終邊上，即 2. 3π −α . 2. (2) a sin θ + b cos θ 化成 r cos(θ + φ ) 形式的說明：設 P 是以原點 O 為圓心，a 為半徑的圓 C 上一動點，且有向角 θ 以 OP 為終邊，. OQ ⊥ OP 且 OQ = a , QR ⊥ OQ 且 QR = b , 如圖 3-3-5。. y. P. C. - a2+b2. a2+b2. θ. O. x. a si n θ + b cos θ a2+b2 a. β b. R. Q. 圖 3-3-5 a sin θ + b cos θ 化成 r cos(θ + φ ) 形式的說明. 26.

(36) 不論 P 在圓 C 上的位置如何改變，. `. π. `. π. OQ = (a cos(θ − ), a sin(θ − )) = (a sin θ , − a cos θ ) , QR = (b cos θ , b sin θ ) , 2 2. ` ` ` OR = OQ + QR = (a sin θ + b cos θ , − a cos θ + b sin θ ) , R 的 x 坐標即為 a sin θ + b cos θ . 另一方面， OR = a 2 + b 2 , 令 ∠POR = ∠ORQ = β , 則. ` OR = (. a 2 + b 2 cos(θ − β ), a 2 + b 2 sin(θ − β )) , R 的 x 坐標為 a 2 + b 2 cos(θ − β ) .. 因此， a sin θ + b cos θ = a 2 + b 2 cos(θ − β ) 恆成立，其中銳角 β 滿足. cos β =. b a +b 2. 2. 及 sin β =. a a +b 2. 2. , 即 β = cos −1. b a +b 2. （ = sin −1. 2. a a + b2 2. ）. 當. P 在圓 C 上移動時，R 的軌跡形成以 O 為圓心， a 2 + b 2 為半徑的圓，其 x 坐標的值介於 − a 2 + b 2 與 a 2 + b 2 之間，即 − a 2 + b 2 ≤ a sin θ + b cos θ ≤ a 2 + b 2 . 當 R 落在 x 軸正向上時，其 x 坐標 a sin θ + b cos θ 達到最大值 a 2 + b 2 , 此時 P 在有向角 β 的終邊上，即 θ = β ; 當 R 落在 x 軸負向上時，其 x 坐標 a sin θ + b cos θ 達到最小值 − a 2 + b 2 , 此時 P 在有向角 π + β 的終邊上，即 θ = π + β .. 3-3-4 函數 y = a sin x + b cos x 的圖形最後，我們利用 3-3-3 小節的觀念，透過動態幾何軟體 GSP, 將函數 y = a sin x + b cos x 的圖形以動態的方式呈現出來，如圖 3-3-6。. 圖 3-3-6 函數 y = a sin x + b cos x 的圖形 27.

(37) 在 GSP 的操作畫面中，使用者可以在畫面的正上方任意調整 a, b 的大小，向右為正，向左為負，並配合按下「Show（或 Hide） y = a sin x + b cos x 的圖形」按鈕，以顯示（或隱藏）函數 y = a sin x + b cos x 的圖形。另外，在 a, b 固定的條件下，使用者也可以透過手動或按下「畫 y = a sin x + b cos x 的圖形」按鈕由電腦自動畫出函數 y = a sin x + b cos x 的圖形，藉此觀察圖形形成的過程。. 28.

(38) 第四章探索軌跡問題傳統的數學活動主要以紙筆為工具，對於幾何學中軌跡的探索並不適合，縱使可利用幾何性質或代數運算直接求得軌跡方程式，但這通常不是一件容易的事，況且缺乏幾何的直觀性，不容易引起學生的興趣。如果以描點的方法想找出軌跡的形狀，又往往受限於精確性的不足及圖形中有些特性不容易掌握，而無法得到正確或完整的結果。利用電腦設計實驗，讓學生透過動手操作的過程探索軌跡問題，想必能達到較佳的學習效果。在處理圓錐曲線的相關問題時，參數式經常扮演著重要的角色。然而許多學生只知道如何用參數式表示圓錐曲線上點的坐標，卻沒有真正瞭解其中參數所代表的幾何意義，特別是參數式與三角函數有關的橢圓及雙曲線，導致有時會有誤用的情形，實在有必要從幾何的觀點讓學生認識參數式。多項函數是數學中最基本且最重要的函數，而圖形最能表現出函數的性質。在沒有電腦輔助的情況下，要畫出一般多項函數的圖形是相當困難的，學生也往往因為沒有具體的圖形概念，而無法對多項函數的性質做全面性的理解。因此，探討多項函數圖形的作法是有必要的。本章透過動態幾何軟體 GSP 探索軌跡問題，共分為三節，分別說明如下。. 4-1 圓錐曲線的等分線描點作圖兩相交直線上各有一動點，我們探討分別過這兩點的某兩直線之交點軌跡問題，透過動態幾何軟體 GSP 所設計的實驗，我們發現產生拋物線、橢圓及雙曲線等圓錐曲線的作法，接著用解析幾何的方法加以驗證，進而得到利用矩形各邊的等分線交點，分別描繪出拋物線、橢圓及雙曲線等圓錐曲線部分圖形的作法。. 4-2 圓錐曲線的參數式作圖探討如何利用橢圓及雙曲線的參數式作出其圖形，同時作出過曲線上一點的切線，並且仿照橢圓及雙曲線的作法，探討另外兩個參數式與三角函數有關的曲線，其方 a 2 b2 a 2 b2 程式分別為 2 + 2 = 1 及 2 − 2 = 1 . 此外，我們透過動態幾何軟體 GSP, 就這四 x y x y 種曲線分別設計一個畫面，以顯示其參數式作圖的結果。. 4-3 通過已知定點的多項函數圖形探討在坐標平面上給定若干個定點，其中任兩點不在同一鉛直線上，如何作出通過這些點且次數最低的多項函數圖形。我們依序就三個定點、四個定點及五個定點的情形，利用 Aitken’s Lemma 分別作出通過這些點且次數不超過兩次、三次及四次的多項函數圖形。此外，我們透過動態幾何軟體 GSP, 就這三種情形分別設計一個畫面，以顯示其作圖的結果，同時使用者也可藉此觀察各種不同形狀的多項函數圖形。. 29.

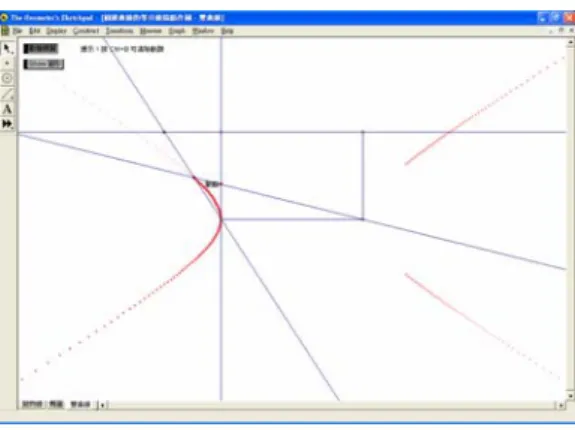
(39) 4-1 圓錐曲線的等分線描點作圖兩相交直線上各有一動點，我們探討分別過這兩點的某兩直線之交點軌跡問題，透過動態幾何軟體 GSP 所設計的實驗，我們發現產生拋物線、橢圓及雙曲線等圓錐曲線的作法，接著用解析幾何的方法加以驗證，進而得到利用矩形各邊的等分線交點，分別描繪出拋物線、橢圓及雙曲線等圓錐曲線部分圖形的作法。在此，我們就拋物線、橢圓及雙曲線三種情形分別加以討論。. 4-1-1 拋物線問題一：如圖 4-1-1，直線 OB 與直線 BA 垂直於 B, 動點 P 與動點 Q 分別在直線 OB 與直線 BA 上作等速直線運動，當 P 移動到 O 的位置時，Q 移動到 B 的位置，且當 P 移動到 B 的位置時，Q 移動到 A 的位置。假設過 P 且平行於直線 BA 的直線與直線 OQ 相交於 R, 則 R 所形成的軌跡為何？ B. P. A. Q. R. O. 圖 4-1-1 過 P 且平行於直線 BA 的直線與直線 OQ 的交點 R 透過動態幾何軟體 GSP 的實驗結果，如圖 4-1-2，我們觀察到 R 所形成的軌跡似乎是一拋物線。因此，我們有了下面的猜測一。. 30.

(40) 圖 4-1-2 R 的軌跡實驗（拋物線）猜測一：當 P 與 Q 分別在直線 OB 與直線 BA 上移動時，R 必落在以 O 為頂點，過 O 且平行於直線 BA 的直線為對稱軸，且通過 A 的拋物線上。上面的猜測一是否成立？接下來，我們用解析幾何的方法加以檢驗。證明：以過 O 且平行於直線 BA 的直線為 x 軸，直線 OB 為 y 軸，建立直角坐標系，且令 A, B 兩點的坐標分別為 (a, b) , (0, b) , 如圖 4-1-3。 y B(0,b). A(a,b). Q. P(0,t) R O. x. 圖 4-1-3 R 的軌跡為一拋物線的證明設 P 的坐標為 (0, t ) , 由於動點 P 與動點 Q 移動的速度比為 b : a , 於是 Q 的坐標為. a ( t , b) , 此時，過 P 且平行於直線 BA 的直線方程式為 y = t , 且直線 OQ 的方程式 b ⎧ y0 = t b2 b2 ⎪ 2 2 為 ty = x . 設 R 的坐標為 ( x0 , y0 ) , 則 ⎨ , 消去 t, 得 y0 = x0 , 故 R 落 b a a ⎪ty0 = x0 a ⎩. 31.

(41) 在拋物線 y 2 =. b2 x 上。 ▓ a. 以上的證明，使猜測一成了下面的定理一。定理一：直線 OB 與直線 BA 垂直於 B, 動點 P 與動點 Q 分別在直線 OB 與直線 BA 上作等速直線運動，當 P 移動到 O 的位置時，Q 移動到 B 的位置，且當 P 移動到 B 的位置時，Q 移動到 A 的位置。假設過 P 且平行於直線 BA 的直線與直線 OQ 相交於 R, 則 R 必落在以 O 為頂點，過 O 且平行於直線 BA 的直線為對稱軸，且通過 A 的拋物線上。根據以上討論的結果，我們可以利用一個矩形各邊的等分線交點畫出一拋物線的部分圖形，如圖 4-1-4。將一矩形的一組對邊作 n 等分，另一組對邊作 2n 等分，分別予以編號，從 0, 1, 2, …到 n（圖中以 n = 16 為例），接著取各編號相同的直線之交點，用平滑的曲線將各點連接起來，便形成一拋物線的部分圖形。 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16. 圖 4-1-4 拋物線的等分線描點作圖. 4-1-2 橢圓問題二：如圖 4-1-5，矩形 ABB′A′ , 動點 P 與動點 Q 分別在直線 A′B′ 與直線 B′B 上作等速直線運動，當 P 移動到 A′ 的位置時，Q 移動到 B′ 的位置，且當 P 移動到 B′ 的位置時，Q 移動到 B 的位置。假設直線 AP 與直線 A′Q 相交於 R, 則 R 所形成的軌跡為何？. 32.

(42) B'. B. Q. P R A'. A. 圖 4-1-5 直線 AP 與直線 A′Q 的交點 R 透過動態幾何軟體 GSP 的實驗結果，如圖 4-1-6，我們觀察到 R 所形成的軌跡似乎是一橢圓。因此，我們有了下面的猜測二。. 圖 4-1-6 R 的軌跡實驗（橢圓）猜測二：當 P 與 Q 分別在直線 A′B′ 與直線 B′B 上移動時，R 必落在以直線 A′A 及線段 A′A 的中垂線為兩對稱軸，線段 A′A 長及線段 AB 長為長、短軸長，且 A, A′ 為兩頂點的橢圓上。上面的猜測二是否成立？接下來，我們用解析幾何的方法加以檢驗。證明：以直線 A′A 為 x 軸，線段 A′A 的中垂線為 y 軸，建立直角坐標系，且令 A, A′ , B, B′ 四點的坐標分別為 (a, 0) , (−a, 0) , (a, 2b) , (−a, 2b) , 如圖 4-1-7。. 33.