無人螺旋航空載具的軌跡控制

(1)

國

立

交

通

大

學

電機與控制工程學系

碩

士

論

文

無人螺旋航空載具的軌跡控制

The Trajectory Tracking of Rotorcraft-Based

Unmanned Aerial Vehicles

研究生：張紹興

指導教授：林心宇博士

(2)

無人螺旋航空載具的軌跡控制

The Trajectory Tracking of Rotorcraft-Based

Unmanned Aerial Vehicles

研究生：張紹興 Student：Shao-Hsiang Chang

指導教授：林心宇 Advisor：Dr. Shin-Yeu Lin

國立交通大學

電機與控制工程學系

碩士論文

A Thesis

Submitted to Department of Electrical and Control Engineering College of Electrical Engineering and Computer Science

National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master

in

Electrical and Control Engineering June 2004

HsinChu, Taiwan, Republic of China

(3)

無人螺旋航空載具的軌跡控制

學生：張紹興

指導教授

：

林心宇博士

國立交通大學電機與控制工程學系碩士班

摘　　要

在近十年間控制技術快速的發展使得自動航空載具變的較小且功

能較強；在很多的領域上需要減少實際的參與人力與避免危險，由於

這個原因，自動航空載具即將成為很多應用的一部份。

演算法應用在離散化的最佳控制問題上，可作平行且簡單的運

算，演算法在運算的步驟上具有簡單且規律的流程。因此，具有二次

效益評估值與最終時間固定的非線性最佳控制問題最適合運用此一演

算法。

在本論文中，我們的研究適合非線性模型在無人螺旋載具上的軌

跡控制；利用 RQPD ( recursive quadratic programming with dual method )

演算法在限制輸入與限制狀態下做位置軌跡與機鼻姿態的追蹤，比較

最低能量控制與軌跡控制的差別。　

(4)

The Trajectory Tracking of Rotorcraft-Based

Unmanned Aerial Vehicles

Student：Shao-Hsiang Chang

Advisors：Dr. Shin-Yeu Lin

Department of Electrical and Control Engineering

National Chiao Tung University

ABSTRACT

The rapid development of control technology in the last few decades

has made autonomous vehicles smaller and more powerful. And the need to

alleviate the actual human participation in order to save human efforts and

avoid hazards has been ever increasing in numerous fields. As a result,

autonomous vehicles are about to become part of reality in many

applications.

The algorithm is applied to discretized optimal control problems, a

simple and parallel computation and a simple and regular data flow patter

between consecutive computational steps results. Therefore, this technique

is best suited to obtain the discrete solution of fixed final-time constrainted

nonlinear optimal control problems with quadratic performance index.

In this thesis, we investigate the feasibility of a nonlinear model

tracking control for unmanned aerial vehicle. We use a RQPD algorithm

for planning path under input and state constraints and tracking position

and heading trajectories, and compare minimum-control-effort with

(5)

論文貢獻

本論文應用 Lin[13]提出的方法用在無人直昇機的軌跡控制上，在 6.5 節中分 別討論最佳控制與低耗能控制兩種，預先規劃出三種飛行路徑與姿態，所得到的 狀態歷程與控制歷程加以比較與分析。提供 behavior model 的模擬分析資訊，對於 想以 cell-base 方法實現[13]硬體設計之研究者一個先期的模擬與討論。

(6)

誌　　謝

首先，必需感謝我的父母與家人，一直不曾對你們說聲謝謝，由於你們的關心與支持，才能讓我無後顧之憂的度過這兩年，順利完成學業，在此致上由衷的感謝，僅將此榮耀與你們共享。本論文得以順利完成，首要衷心感謝指導教授林心宇博士在這兩年的研究過程中，所給予的悉心指導與教誨，使學生得以在學術研究方面有所啟迪，且對於為人處世的方法態度上，也獲益匪淺。同時也要向李福進老師、鄭木火老師致謝，感謝您們在口試期間的寶貴意見與指導。另外，要感謝士程學長、榮壽學長，謝謝您們在論文寫作期間給予我許多寶貴意見與股勵。

(7)

目　錄

中文摘要　 i 英文摘要 ii 論文貢獻 iii 誌謝 iv 目錄 v 表目錄 viii 圖目錄 viii 符號說明 ix 第一章　緒論 1 第二章　直昇機之非線性模型簡介 3 2.1 直昇機模型的架構 ...3 2.2 剛體動力學 ...4 2.2.1 角速度移動座標系統下的尤拉延伸式 ...4 2.2.2 考慮旋轉運動下的牛頓定律 ...5 2.3 座標轉換與尤拉角 ...6 2.4 角速度 ...8 2.5 系統方程式 ...8 第三章　最佳化理論 11 3.1 受限制的最佳化問題 ... 11 3.2 拉格朗基乘子( Lagrange Multipliers )... 11 3.3 肯恩˙塔克條件( Kuhn-Tucker Conditions )...12 3.3.1 肯恩˙塔克必要定理 ...13 3.3.2 肯恩˙塔克充分定理 ...13

(8)

3.4 二階最佳化條件 ...14 3.4.1 二階必要條件 ...14 3.4.2 二階充分條件 ...15 3.5 解限制性問題的線性化方法 ...15 3.5.1 線性限制式問題 ...16 3.5.2 一般性的非線性規劃問題 ...16 3.6 可分離規劃（Separable Programming） ...17 3.6.1 單變數可分離函數 ...18 3.6.2 多變數可分離函數 ...19 3.7 線性規劃（Linear Programming）...20 3.8 二次規劃（Quadratic Programming） ...20 3.9 對偶性理論 ...21 第四章　最佳控制理論 24 4.1 考慮的系統 ...24 4.2 實際的限制 ...25 4.3 效益評量 ...26 第五章　遞迴二次對偶規劃(RQPD) 29 5.1 問題的公式化 ...29 5.2 Runge-Kutta Method ...29 5.3 二次規劃遞迴法 ...30 5.4 對偶法 ...31 5.5 RQPD 演算法...32 5.6 RQPD 在最佳控制上的應用...34 第六章　利用遞迴二次對偶規劃解最佳控制問題 41 6.1 簡介 ...41

(9)

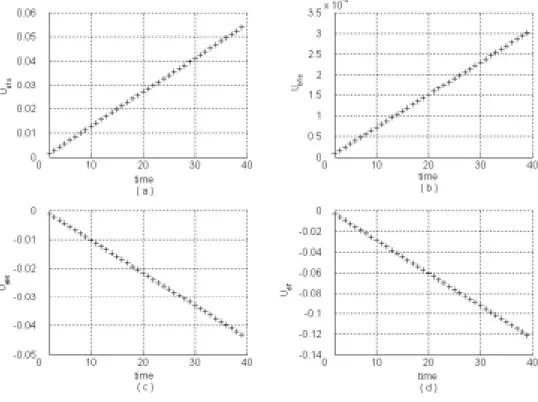
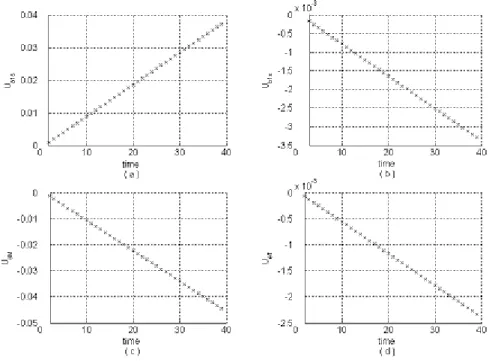
6.3 模擬追蹤問題 ...44 6.4 模擬範例程式流程圖 ...47 6.5 模擬結果與討論 ...48 第七章　結論 69 參考文獻 70 附錄 72

(10)

表目錄

表 2.1 定義座標符號 ... 6

圖目錄

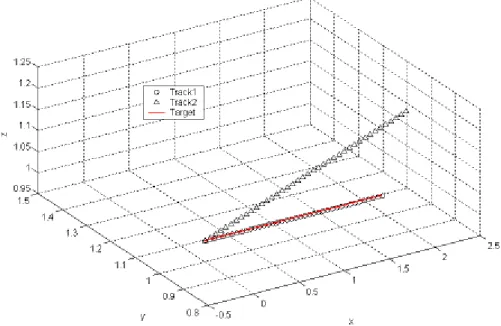
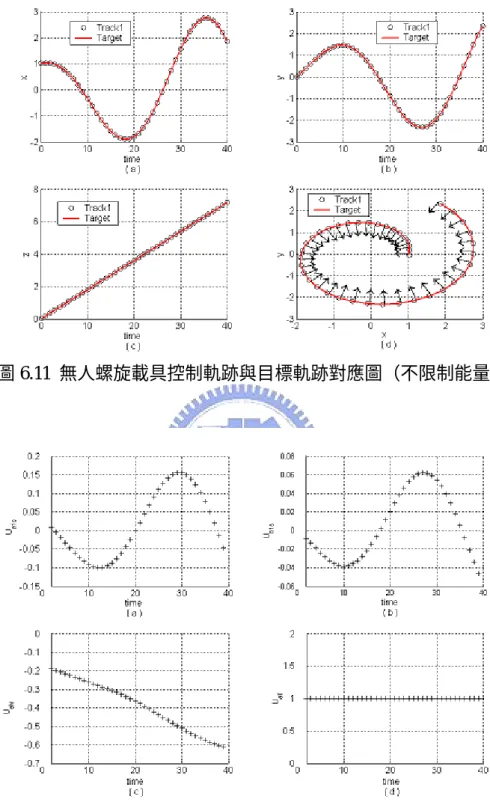
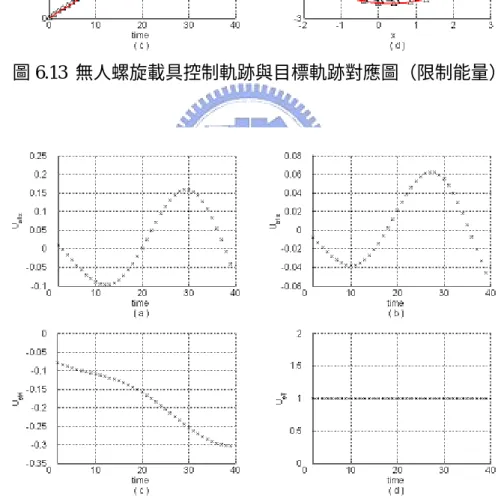
圖 2.1 直昇機飛行時的自由度 ... 3 圖 2.2 直昇機的動力系統 ... 4 圖 2.3 直昇機的座標軸 ... 6 圖 2.4 球體座標系統與機體座標系統 ... 7 圖 2.5 旋翼葉轂平面與主翼尖端平面的縱向傾角 ... 9 圖 2.6 旋翼葉轂平面與主翼尖端平面的橫向傾角 ... 9 圖 2.7 無人螺旋載具動力系統方塊圖 ... 10 圖 3.1 片段線性曲………..………18 圖 5.1 RQPD 演算法的整體架構... 33 圖 5.3 RQPD 終值限制式之最佳控制問題演算法的整體架構... 40 圖 5.2 RQPD 無終值限制式之最低耗能制問題演算法的整體架構... 47 圖 6.1 無人螺旋載具控制軌跡與目標軌跡對應圖（不限制能量） ... 51 圖 6.2 無人螺旋載具控制訊號（不限制能量） ... 52 圖 6.3 無人螺旋載具控制軌跡與目標軌跡對應圖（限制能量） ... 53 圖 6.4 無人螺旋載具控制訊號（限制能量） ... 54 圖 6.5 低耗能控制（Track2）與軌跡控制（Track1）... 55 圖 6.6 無人螺旋載具控制軌跡與目標軌跡對應圖（不限制能量） ... 57 圖 6.7 無人螺旋載具控制訊號（不限制能量） ... 57 圖 6.8 無人螺旋載具控制軌跡與目標軌跡對應圖（限制能量） ... 59 圖 6.9 無人螺旋載具控制訊號（限制能量） ... 59 圖 6.10 低耗能控制（Track2）與軌跡控制（Track1）... 61 圖 6.12 無人螺旋載具控制訊號（不限制能量） ... 63 圖 6.13 無人螺旋載具控制軌跡與目標軌跡對應圖（限制能量） ... 65 圖 6.14 無人螺旋載具控制訊號（限制能量） ... 65 圖 6.15 低耗能控制（Track2）與軌跡控制（Track1）... 67 圖 6.16 低耗能控制（Track2）與軌跡控制（Track1）... 67

(11)

符號說明

m 無人載具的質量 F 對質量為 m 的物體所施的力。 Vc 質量中心的速度。 τ c 質量中心的轉矩。 Hc 質量中心的角動量（H = lω）。 ω 角速度。 Ixx、Iyy、Izz 螺旋載具相對各軸的質量慣性矩。 p、q、r 機身的三軸角速度分量。 u、v，w 機身的三軸速度分量。 φ、θ、ψ 機身姿態角。 x p 、p 、_y p _z 表示球座標系統的位置 1s a 、b ₁_s 分別表示為主螺旋槳縱向與橫向的傾斜角度。 fb r 為陀螺儀表示的機體方向。 M u_θ 為控制主旋翼集合傾角，所謂集合傾角即同時改變所有翼片的傾角來達到不同升力效果。主要的升力控制並達到控制螺旋載具的升降或加速。 T u_θ 則為控制尾旋翼之槳距，可以克服力矩及調整機身行進之方向。 1 a s u 、u_{b s}₁ 為控制循環傾角，u_{a s}₁ 可以操控螺旋載具前後之飛行姿態，u_{b s}₁ 可以操控螺旋載具左右之飛行姿態。 f t 最終時間。 N 取樣次數。

(12)

α 、β 、ξ 跨步長度。 max j 拉格朗基最大遞迴次數。 max l 二次遞迴規劃最大遞迴次數。 1 ε 拉格朗基終止參數。 2 ε 二次遞迴規劃終止參數。 Q、M、R 權重矩陣。

( )

, 0, , r i i= … N 軌跡函數。 λ、μ(≧0) 拉格朗基乘子。 ( )L i x 、 ( )U i x 變數 xi給定或假設的下界與上界。

( )

i x f l 函數 f 對 x 作偏微分。

( )

i u f l 函數 f 對 u 作偏微分。

(13)

第一章　緒論

由於製程技術與 IC 設計技術的成熟，對於整合性控制晶片的實現不再是個難 題，將原本循序執行的程式，藉由硬體轉變成平行方式的執行，且硬體實現的方法可以大幅增加執行效率。目前在無人航空載具的應用領域上，偵察與搜救是較常被使用到，如何使無人航空載具依循規劃的軌跡飛行，並且達到即時的軌跡與飛行姿態控制，無人直昇機航空載具模型[1]，[5]-[7]，利用此一非現性動態模型作為控制的基礎。本論文針對可分解的非凸集（non-convex）最佳化問題，應用一個可完全解構的平行演算法快速計算出控制解，解決運算量大的問題達到即時控制。此一演算法結合遞迴二次規劃（recursive quadratic programming）與對偶方法（dual method） [13]-[15]。 論文中以 Matlab 來做演算法的模擬，雖然在程式中是以循序的方式完成，但 其演算法本身是以平行方式運算，演算法完全是由硬體的觀點來計算；在 VLSI 陣 列處理器的技術上，Lin [15]有完整演算法在硬體計機架構的實現；以目前 cell-base design 的流程在行為模式驗證後即可利用 ASIC 來做硬體的實現。由於飛行控制需 要考量即時的效果，此一演算法用硬體實現後可增加計算效率，可彌補計算時間長的問題，有機會可用在無人直昇機系統的控制。

在第六章中利用遞迴二次對偶規劃法(recursive quadratic programming with dual method)解最佳控制問題，針對無人直昇機的控制，我們考慮低耗能問題與追蹤問題，並以三種不同的飛行姿態與軌跡作為目標函數，對於低耗能問題與追蹤問題的控制歷程分別作討論。本論文的架構大致如下，而第二章中，我們介紹小型無人直昇機的控制模型與動態方程式。在第三章中，討論所需的最佳化基礎理論；在第四章中，討論如何完成最佳控制的效益評估函數；第五章說明如何將遞迴二次對偶規劃法運用在

(14)

解最佳控制問題上；第六章運用 RQPD 解低耗能問題與追蹤問題；最後在第七章 中做一結論。

(15)

第二章　直昇機之非線性模型簡介

2.1 直昇機模型的架構

直昇機的系統可以分解成四個主要的子系統，如促動機動力系統（actuator dynamics）、螺旋翼動力系統（rotary wing dynamics）、力與力矩的產生過程（force & moment generation process）、剛體動力系統（rigid body dynamics）。直昇機飛行自由度如圖 2.1 所示，子系統之間的連結與控制變數關係如圖 2.2 所示。對於次系統而言，我們描述其動態模式的自由度各為 (1) 主旋翼及尾旋翼：旋翼葉片的擺動角度。 (2) 機身及尾翼：速度、角速度、姿態角、描述剛體運動的自由度。 (3) 發動機：主旋翼的轉速和發動機的輸出轉矩。圖 2.1 直昇機飛行時的自由度資料來源[1]

(16)

Actuator Dynamics Rotary Wing Dynamics Force & Moment Generation Process Rigid Body Dynamics uM uT uB uA θ_M θ_T B A TM TT a1s b1s f b τb P vp ωb Actuator Dynamics Rotary Wing Dynamics Force & Moment Generation Process Rigid Body Dynamics uM uT uB uA θ_M θ_T B A TM TT a1s b1s f b τb P vp Θ ωb Actuator Dynamics Rotary Wing Dynamics Force & Moment Generation Process Rigid Body Dynamics uM uT uB uA θ_M θ_T B A TM TT a1s b1s f b τb P vp ωb Actuator Dynamics Rotary Wing Dynamics Force & Moment Generation Process Rigid Body Dynamics uM uT uB uA θ_M θ_T B A TM TT a1s b1s f b τb P vp Θ ωb 圖 2.2 直昇機的動力系統根據[1]中的直昇機剛體模型，可以利用牛頓-尤拉方程式[2]，[3]表示直昇機的動力方程式。

2.2 剛體動力學

運用直昇機的質量中心為體框架座標（body coordinate frame）的圓心，可以寫出直昇機的移動方程式。動力學上表示線性動量用牛頓定律（Newton’s law），而角動量用尤拉延伸公式（Euler’s extension）。將兩個數學式合起來表示為牛頓-尤拉（Newton-Euler）方程式： . V F d c m dt = （2.1） . τ_c d H_c dt = （2.2） F : 對質量為m的物體所施的力。 Vc：質量中心的速度。 τ c：質量中心的轉矩。 Hc：質量中心的角動量。（H = lω） 由於上式（2.2）是對固定點 O 或質心 G 而言。

2.2.1 角速度移動座標系統下的尤拉延伸式

如果我們以相對於一具有角速度ω的移動座標系統來表示 H 的話，轉矩關係

(17)

(

)

(

)

(

)

(

)

.

H

τ

ω

H

i

j

k

ω

H

i

j

k

x y z x y z x y z z y y z x x z z x y y x

d

d t

H

ω





=

_

_

+

×





=

+

×

=

−

+

−

+

−

+

∑

（2.3） 對任意物體及原點 O，至少可以找到一個座標系使該物體的慣性積為零，則 該座標系的座標軸即為主慣性軸，如果將體座標系軸與主慣性軸重合，且體座標 原點落在質量中心的話，則 Ixy，Iyz，Izx皆為零，公式（2.3）便可寫成：

(

)

(

)

(

)

(

)

.

c c c

H

τ

ω

H

i

j

k

ω

H

i

j

k

x y z x y z x x x y y y z z z y z y y y z z z x x x z x z z z x x x y y y x y

d

d t

H

I

ω

ω ω

ω

ω ω

ω

ω ω





=

_

_

+

×





=

+

×

=

−

+

−

+

−

+

∑

（2.4）

2.2.2 考慮旋轉運動下的牛頓定律

一般線性動量方程式(2.1)不考慮旋轉運動，現在將旋轉運動考慮進去(右式第二項的向心力)，線性動力方程式可寫成： . V F c ω V c d m m dt = + × （2.5）剛體動力方程式中以 b _∈_ℜ3 f (force)與τb∈ℜ3(torque)分別表示加在質量中心上力與力距。可以寫出體座標下的牛頓-尤拉（Newton-Euler）方程式： 0 . 0 I b b b b b b b b m v ω mv f ω ω ω τ    ×      + =         _×  Ι    I    （2.6）這裡的 b∈ℜ3 v 為體速度向量，ωb ∈ℜ3 為體角速度向量，m∈ℜ為質量， 33 I∈ℜ × 為

(18)

單位矩陣，而且I ∈ℜ3×3 是慣性矩陣。

2.3 座標轉換與尤拉角

飛行姿態可以用尤拉角度來表示，傳統上旋轉矩陣R

( )

Θ 是由三個尤拉角旋轉矩陣相乘所形成；我們將其解構成三個部分，直昇機機頭的俯仰角( x 在 X-Z 平面的投影向量與 X 軸的夾角)為θ ，機身的滾動角( y 在 Y-Z 平面的投影向量與 Y 軸的夾角)為φ，機頭的指向角( x 在 X-Y 平面的投影向量與 X 軸的夾角)為ψ 。圖 2.3 直昇機的座標軸直昇機的移動方程式以機頭的方向為 x 座標，右邊機身方向為 y 座標，機腹方向為 z 座標。表 2.1 定義座標符號

OXYZ：球座標系統（Earth-fixed coordinate system ） oxyz：體座標軸系統（Body axes coordinate system）

φ,θ,ψ：體座標對球座標的旋轉尤拉角（Euler angles for rotation from Earth-fixed to body axes coordinate system）

(19)

( )

1 0 0 0 cos sin . 0 sin cos x R φ φ φ φ φ     ≡    −    （2.7）

( )

cos 0 sin 0 1 0 . sin 0 cos y R

θ

−     ≡       （2.8）

( )

cossin cossin 00 .

0 0 1 z R

ψ

    ≡ −_ _     （2.9）旋轉矩陣R

( )

Θ B→S的通式可以寫成R

( )

Θ B→S =R R R_{φ θ ψ}

( )

. B S R R R R c c c s s s s c c s s s s c c s c c s c s s c s s s c c c φ θ ψ

θ ψ

θ

φ θ ψ φ ψ

φ θ

φ θ ψ φ ψ

φ θ

→ Θ = −     =_ − + _  + −    （2.10）

( )

[

]

, , T B S , , T . S S S x y z R → u v w   = Θ   （2.11）圖 2.4 球體座標系統與機體座標系統這裡的

[

]

T x = 1 0 0 ,y =

[

0 1 0

]

T ,z=

[

0 0 1

]

T ； s θ , c θ 分別為 sin( θ ) 與

(20)

cos(θ)，其它符號表示與前者相似。

2.4 角速度

機體的角速度由（2.10）式得知角速度向量可寫成 . ω=ψ k+θ j+φ i （2.12）進一步將（2.12）式展開為

(

)

(

)

(

)

(

) (

)

. ω i j k i j k i j k i j k x y z c s s s c c c s c s c s c c ω ω ω φ θ φ φ ψ θ φ θ φ θ φ ψ θ θ φ ψ φ θ θ φ ψ φ θ = + + = + − + − + + = − + + + − + （2.13）可以得到體角速度ωx,ωy與ωz相對於角度 φ, θ, ψ 的關係式為 1 0 0 . 0 x y z s c s c s c c ω θ φ ω φ φ θ θ ω φ φ θ ψ   −         ₌             −     _{  } （2.14）

( )

1 sin tan cos tan

0 cos sin

0 sin sec cos sec 1 sin tan cos tan

0 cos sin .

0 sin sec cos sec

b x y z p q r φ θ ω ψ φ θ φ θ ω φ φ ω φ θ φ θ ω φ θ φ θ φ φ φ θ φ θ     = Ψ Θ               =_ − _{  }                 =_ − _{  }         （2.15）

2.5 系統方程式

多輸入多輸出（MIMO）系統的非線性方程式如下：

( )

( ) ( )

. x t = f x +g x u 15 , . K D x=_x x _∈

(21)

1 1 , , , , , , , , . D S S f b x =u v p q a b w r r _

[

a s1 , b s1 , M, T

]

. u= u u u_θ u_θ （2.16） 這裡的 S 為球座標符號。而r 為陀螺儀的迴授狀態。在這個模型中縱向葉片傾角_fb 與橫向葉片傾角 a1s , b1s動態方程式可表示為 1 1 1 1 1 1 _{a s} 1 _{b s} 1 . s s b s s u a s u b s f b b p B a B u B u τ = − − + + + （2.17） 1 1 1 1 1 1 _{a s} 1 _{b s} 1 . s s b s s u a s u b s f a a q A b A u A u τ = − − + + + （2.18） a1s z_HP z_TPP

Tip Path Plane

Hub Plane x_TPP xHP a1s z_HP z_TPP

Tip Path Plane

Hub Plane x_TPP xHP 圖 2.5 旋翼葉轂平面與主翼尖端平面的縱向傾角 b1s zHP zTPP

Tip Path Plane

Hub Plane yTPP yHP b1s zHP zTPP

Tip Path Plane

Hub Plane

yTPP

yHP

圖2.6旋翼葉轂平面與主翼尖端平面的橫向傾角

(22)

1 1 1 1 1 1 1 sin sin M s M T s M yy xx M M M M M M T T s s xx xx xx xx zz xx M M M M M M T s s yy yy yy yy M M M T s zz T g a vr wq m T T g b ur wp m m u T v _g _{uq vp} m w I I Q T h dR T y T h p _a _b _qr I I I I q I I T h dM Q T l Q r a b pr I I I I T l Q T l b I θ φ − − + − − − − +     − + −     =   ₋ ₋ + ₋ + ₊ −       ₊ ₋ ₋   − + +   − + + T xx yy zz zz I I pq I I                               −  ₊        （2.19）對於T_M,T 與_T Q_M,Q 可以由_T u_θ_M, , , , ,u v w r r_fb所組成。直昇機的動力系統可以表示為圖 2.7，下圖的uθM、uθT、ua s1 與ub s1 為系統的輸入控制訊號，Px、Px、Px、φ、θ、 ψ無人直昇機系統的輸出訊號[5]−[8]。

Servomotor Main Rotor Thrust Dynamics Vertical Dynamics Servomotor Servomotor Servorotor Dynamics Attitude Dynamics

Servomotor _{Thrust Dynamics}Tail Rotor Yaw Dynamics

Horizontal Velocity Dynamics Euler Angle Integration Euler Angle Transform Integration u_a1s u_b1s u_θΜ u_θΤ q_θΜ q_θΤ u v p A1 B1 q TM TT v u a1s b1s a1s p q r p q r u v w _Vx Vy Vz Px Py Pz θ φ ψ 圖2.7 無人螺旋載具動力系統方塊圖

(23)

第三章　最佳化理論

在進入第四章之前，先介紹一些基礎的最佳化理論[9]；一般而言最佳化方法是用數學上的結果及數值方法，從一大堆可用的事物中尋找出最好的，卻不必將所有可用事物都加以評估才挑選出來。

3.1 受限制的最佳化問題

考慮包含有數個等式限制的最佳化問題：

(

1, 2, , N

)

. Minimize f x x … x

(

1, ,

)

0 , 1, , . k N Subject to h x … x = k= … K （3.1） 基本上，這問題可用等式限制式消去 K 個獨立變數，而視為是無限制的最佳 化問題。等式限制式的出現使得問題的維度從原本的 N 減少成 N-K。一旦問題轉 化成無限制性的最佳化問題，針對單變數函數（functions of a single variable）與多變數函數（functions of several variables）分別利用各自的方法尋找最佳點，如：牛頓-雷佛森法（Newton-Raphson Method）、柯契法（Cauchy’s Method）…等。

只要能從等式限制式解出一組外顯形式的獨立變數，就可以使用變數消去法（variable-elimination method）。若出現好幾個等式現制式，消去的過程就會變的很不容易。而且在某些情況可能根本無法從限制式中解出外顯形式的解，而利用變數消去法。因此，問題包含有數個複雜的等式限制式，最好是用拉格朗基乘子法[10] （Lagrange multipliers）來處理限制式。

3.2 拉格朗基乘子( Lagrange Multipliers )

拉格朗基乘子法基本上是供給一組必要條件，用來辨明受等式限制最佳化問題的候選最佳點。這是運用稱為拉格朗基乘子的非確定參數，將受限制問題轉換

(24)

為對等的無限制問題。 考慮受限於一個等式限制式的 N 變數函數之最小化問題：

(

1, 2, , N

)

. Minimize f x x … x

(

)

1 1, , N 0 . Subject to h x … x = （3.2）拉格朗基乘子法將這問題轉化成下列的無限制最佳化問題：

(

,

)

( )

1

( )

. T Minimize L x λ = f x +λ h x （3.3）無限制函數L x

(

,λ

)

稱為拉格朗基函數，而λ是一個未確定的常數稱為拉格朗基乘子，λ的值沒有正負號的限制。利用數值搜尋法可以用來求出所有可能解，對於每一個解

(

x,λ

)

，可以算出相

對於 x 的 L 之赫遜矩陣（Hessian matrix），以判斷它為正定（positive definite）區 域最小值或者為負定（negative definite）區域最大值。

3.3 肯恩˙塔克條件( Kuhn-Tucker Conditions )

拉格朗基乘子可以用來發展具有等式限制的最佳化問題，肯恩˙塔克[11]擴展了這個理論，包含等式與不等式限制的一般非線性規劃（NPL），考慮一般非線性規劃的問題：

( )

. Minimize f x

( )

0 , 1, 2, , . j Subject to g x ≤ for j= … J

( )

0 , 1, 2, , . k h x = for k= … K

(

1, 2, , N

)

. x= x x … x （3.4）

(25)

3.3.1 肯恩˙塔克必要定理

考慮（3.4）式所提供的 NLP 問題，令 f、g 和 h 是可微分的函數，而 x*_{是 NLP} 的一個可用解（feasible solution），令I =

{

j g_j

( )

x∗ = 。而且對於 j I0

}

∈ ，∇g_j

( )

x∗ 和對於 1,k = …,K，∇h_k

( )

x∗ 是線性獨立的。若 x*_{是 NLP 的一個最佳解，則存在}

(

λ µ∗, ∗

)

，使得

(

x∗,λ µ∗, ∗

)

為（3.5）至（3.9）式肯恩˙塔克問題的解。

( )

T

( )

T

( )

0. k j f x λ h x µ g x ∇ + ∇ + ∇ = （3.5）

( )

0 , 1, 2, , . j g x ≤ for j= … J （3.6）

( )

0 , 1, 2, , . k h x = for k= … K （3.7）

( )

0 , 1, 2, , . T j g x for j J µ = = … （3.8） 0 , 1, 2, , . T for j J µ ≥ = … （3.9）一般很難去驗證限制資格，因為這必須事先知道最佳解才行。而對某些特別 的 NLP 問題，限制資格是可以滿足的： (1) 當所有的等式和不等式限制式都是線性的。 (2) 當所有的不等式限制式都是凹函數（concave function），等式限制式是線性 的，而且至少存在一個可用的 x，它是必須存在於不等式限制的可用區域之 內部。換句話就是存在 x*_{使得對於} 1, , j= … J ， g_j

( )

x∗ <0，且對於 1, , k= … K，h_k

( )

x∗ =0。當最佳點不符合限制資格之時，肯恩˙塔克問題的解可能不存在。

3.3.2 肯恩˙塔克充分定理

考慮方程式（3.4）式所提供的 NLP 問題。令目標函數 f x

( )

是凸函數（convex

(26)

function），對於 j= …1, ,J，不等式限制式gj

( )

x 皆為凹函數（concave function），而且對於k = …1, ,K ，等式限制式hk

( )

x 是線性的。若存在一解

(

x ,λ µ,

)

∗ ∗ ∗ _滿足 （3.5）至（3.9）式肯恩˙塔克條件，則 x*_{是這個 NLP 問題的最佳解。}

3.4 二階最佳化條件

在第 3.3 節中討論受限制最佳化問題的必要與充分定理，稱為肯恩˙塔克條件，採用目標函數與限制式的梯度。應用到二次可微分函數的二階必要和充分最佳化條件。

3.4.1 二階必要條件

考慮（3.4）式所提供的 NLP 問題，令 f、g 和 h 是二階可微分的函數，並使得

x*在非線性規劃中是可用點（feasible point）。令在 x*_{的活躍限制（active constraint）}

之集合是 I

{

j gj

( )

x 0

}

∗ = = 。更進一步假設對於 j∈ ，I gj

( )

x ∗ ∇ 和對於 1,k = …,K， hk

( )

x ∗ ∇ 是互相線性獨立的。則 x*_{的 NLP 問題區域最小點的必要} 條件是 (1) 存在

(

λ µ∗, ∗

)

使得

(

x∗,λ µ∗, ∗

)

是一個肯恩˙塔克點。 (2) 對於每一個向量y_{( )}₁_×_n 滿足

( )

0 , . j g x∗ y for j I ∇ = ∈ （3.10）

( )

0 , 1, 2, , . k h x∗ y for k K ∇ = = … （3.11）必須是

(

, ,

)

0 . T L y H x∗ λ µ∗ ∗ y≥ （3.12）

(27)

(

, ,

)

( )

T

( )

T

( )

. k j L x λ µ = ∇f x + ∇λ h x +µ ∇g x （3.13）而且HL

(

x ,λ µ,

)

∗ ∗ ∗ _{是 L 對於 x 的二階偏微分赫遜矩陣在}

(

)

, , x∗ λ µ∗ ∗ 處計算所得之矩陣。

3.4.2 二階充分條件

NPL 問題中 f、g 和 h 是二階可微分的函數。點 x*的 NLP 問題之嚴格區域最小 點的充分條件是 (1) 存在

(

λ µ∗, ∗

)

使得

(

x∗,λ µ∗, ∗

)

是一個肯恩˙塔克點。 (2) 對於每一個非零向量y_{( )}₁_×_n 滿足

( )

0 , 1

{

( )

0, 0 .

}

j j g x∗ y j I j g x∗ µ∗ ∇ = ∈ = = > （3.14）

( )

0 , 2

{

( )

0, 0 .

}

j j g x∗ y j I j g x∗ µ∗ ∇ ≤ ∈ = = = （3.15）

( )

0 , 1, 2, , . k h x∗ y k K ∇ = = … （3.16） 0 . y≠ 必須要

(

, ,

)

0 . T L y H x∗ λ µ∗ ∗ y> （3.17）

3.5 解限制性問題的線性化方法

一般的非線性函數 f x

( )

再點x 的附近可以用泰勒展開是來逼近。 0

( )

( )(

)

(

)

2 0 0 0 0 f x = f x + ∇f x x−x +O x−x （3.18）忽略掉較高階項

(

0

)

2 O x−x ，因此函數f x

( )

被 f 在 0 x 的線性化函數所近似，將其 記為

(28)

(

0

) ( )

0

( )(

0 0

)

; . f x x = f x + ∇f x x−x （3.19）

3.5.1 線性限制式問題

線性限制式的非線性規劃（NLP）形式為

( )

. Minimize f x , 0 . Subject to Ax b x ≤ ≥ （3.20）因為 f x

( )

是非線性，最佳點不在侷限於可用區域的頂點或角落點，而可能是區域中的任何點。若 f x

( )

是非凸形的，線性限制 NPL 問題可能出現多重區域最小點。 線性化建構最簡單和最直接的運用是在某個選定的預估解，把所有問題函數線性化，取代一般性非線性問題。知道此一特性之後，考慮線性限制問題建構在某可用點 0 x 的線性化

(

0

)

; . Minimize f x x , 0 . Subject to Ax b x ≤ ≥ （3.21） 問題變成一個 LP 的問題，如果假設可用區域是有界的，最佳點將出現在可用區的 角落。近似問題的解 x∗要和那一個 NLP 的區域最小點最接近，完全決定於所選擇 的線性化點。因此在非凸形的情況下無法保證可得到全域最小解。因 x∗必定是角 落點，x*_{可能在任何位置也可能是內部點，即使}

( )

f x 是凸形的， x∗仍然需要做進 一步的調整，使它確定能夠較接近 x*_。

3.5.2 一般性的非線性規劃問題

一般非線性規劃（NLP）的形式為

(29)

( )

. Minimize f x

( )

0 , 1, 2, , . j Subject to g x ≤ for j= … J

( )

0 , 1, 2, , . k h x = for k= … K ( ) ( ) , 1, 2, , . U L i i i x ≥ ≥x x for i= … N （3.22）給定一個估計值 ( )t x ，在x 可以建構一個直接的線性近似問題 ( )t ( )

( )

(

( )

)

. t t t Minimize f x + ∇f x x−x ( )

( )

(

( )

)

0 , 1, 2, , . t t t j j Subject to g x + ∇g x x−x ≤ for j= … J ( )

( )

(

( )

)

0 , 1, 2, , . t t t k k h x + ∇h x x−x = for k = … K ( ) ( ) , 1, 2, , . U L i i i x ≥ ≥x x for i= … N （3.23） 非線性規劃問題已經轉變成線性規劃問題，可以運用 LP 方法去解，而得到新點 ( )t+1 x 。即使 ( )t x 是原非線性問題的可用解，卻不能保證x( )t+1 將是可用點，實際上若限制函數是非線性的，點 ( )t+1 x 在大部分情形是不可用的。若 ( )t+1 x 是不可用的，由目標函數的線性近似值所獲得的改善，即是 ( ) ( )

(

1

)

(

( ) ( )

)

; ; . t t t t f x + x < f x x （3.24）並不保證得到的是真正有改善的估計點。為了要能收斂到真正的最佳解，充分條件是對於每一點 ( )t x ，皆可在目標函數值和限制的不可用性上得到改善。若x 是( )t 一連續的點，每一點都是由前一 LP 問題的解當成線性化點，所得 LP 的問題的解 即為最佳點。

3.6 可分離規劃（Separable Programming）

這種技巧可將某些形式的非線性受限制最佳化問題重新推導成只包含線性函數的對等問題。這技巧產生的動機是：對於一般涵蓋大區間的非線性函數，改善

(30)

線性近似的一種好方法，把區間分割成多個子區間，然後對各個區間建立個別的線性近似。

3.6.1 單變數可分離函數

考慮定義在區間0≤ ≤x a

的

連續性單變數函數 f x

( )

，假設在區間中任意選定 K 個分割點，標記為x( )k ，k = …1, ,K。對於每一個 ( )k x 求出 ( )k

( )

( )k f = f x ，並在每相鄰分割點 ( )k x 與 (k 1) x + 間畫出一條線，連接點

(

x( )k , f( )k

)

和

(

( 1) ( 1)

)

, k k x + f + 。一個片段線性近似函數 f x （圖 3.1）

( )

。連接兩點

(

x( )k , f( )k

)

和

(

x(k+1) , f(k+1)

)

的直線為，

( )

( ) ( ) ( ) ( ) ( )

(

( )

)

1 1 . k k k k k k f f f x f x x x x + + − = + − − （3.25）方程式將與每一個子區間 ( )k (k 1) x ≤ ≤x x + 相對應。因此 f x

( )

由 K-1 個線性方程式所 構成，每個方程式在各自的限制區間中有效。 任何 x 在 ( )k (k 1) x ≤ ≤x x + 的範圍中可以寫成 A B C D E F G 0 x(1) x(2) x(3) x(4) x(5) x(6) x(7) 圖 3.1 片段線性曲線 a

(31)

( ) ( ) ( 1) ( 1) . k k k k x=λ x +λ + x + （3.26） 把 x 的表示式代入（3.25）式中：

( )

( ) ( ) ( ) ( ) ( )

(

( ) ( )

(

( )

)

( )

)

1 1 1 1 1 . k k k k k k k k k f f f x f x x x x λ λ + + + + − = + − − − （3.27）

( )

( ) ( 1)

(

( 1) ( )

)

( ) ( ) ( 1) ( 1) . k k k k k k k k f x = f x +λ + f + − f =λ f +λ + f + （3.28）

3.6.2 多變數可分離函數

一個具有 N 個分量的向量變數 x 的函數是可分離的，則它可以表示成單變數 函數的和，而每一個單變數函數都只含 N 個變數之中的一個。 在多變數函數 f x

( )

是可分離且為連續的限制下，f x

( )

的片段線性近似得建構 進行如下：用 ki個分割點把每一個變數 xi的區間劃分出來。因此每一變數將會對應於一點序列 ( ) ( )1 ( )2 ( ) ( ) ( ) . i K L j U i i i i i i x =x <x < <x < <x =x （3.29）（3.23）式中 ( )L i x 與xi( )U 是變數 xi給定或假設的上界與下界。 ( )k

( )

( )k i i i f = f x 為縮寫表示，近似函數 f x 變成

( )

1 ( ) ( ) 2 ( ) ( ) ( ) ( ) 1 1 2 2 1 2 1 . N K K K k k k k k k N N k k k f x λ f λ f λ f = = = =

∑

+

∑

+ +

∑

（3.30）式中 ( ) ( ) 1 , 1, , . i K k k i i i k x λ x i N = =

∑

= … （3.31） (1) ( ) 1 1. i K k i k λ = =

∑

(2) λi( )k ≥0 , k= …1, ,Ki. (3) λ λi( ) ( )k ij =0 , if j> +i 1 ;i=1,…,Ki−1. 符合上述 3 項條件，任何非線性函數 f x

( )

可用線性的函數 f x 來取代。若需要非

( )

(32)

常近似 f x

( )

，則分割點以及變數λ的數目將變的相當大，線性化要付出增加相當維度的代價。

3.7 線性規劃（Linear Programming）

考慮一非線性最佳化問題：

( )

. Minimize f x

( )

0 , 1, 2, , . j Subject to g x ≤ for j= … J （3.32） 將目標函數與限制條件在起始設計點 x0以一階泰勒級數線性化，展開成如下形式：

( )

(

)

0 0 0 1 . n i i i i _x f Minimize f x x x x = ∂  + − _ _ ∂  

∑

( )

(

)

0 0 0 1 0 , 1, 2, , . n j j i i i i _x g Subject to g x x x for j J x = ∂   + − _ _ ≤ = ∂  

∑

… 0 . li i i ui a ≤ −x x ≤a （3.33）此一問題變成線性規劃子問題，可以用線性規劃中的方法，得到下一次迭代的設計點。（3.33）式的限制條件稱為移動限制(move limit)，主要是因為利用線性規劃解非線性最佳化問題時，函數是以一階泰勒級數方式近似展開，只有在設計點附近才會較近似於原來的非線性曲線，超過一定範圍線性近似便相當不準確。每次迭代過程中設計變數改變量必須以移動限制加以侷限，否則會發生振盪及發散的情況。

3.8 二次規劃（Quadratic Programming）

線性規劃法中移動限制形式ali ≤ −xi x0i ≤aui，是給每一次迭代的設計點一個「方形」的移動區域，另一種可能的移動限制式則是給每次迭代的設計點一個「圓

(33)

(

) (

)

0 2 0.5 0 0 . T x−x ≤ ξ ⇒ x−x x−x ≤ξ （3.34）改用圓形的移動區域後，線性規劃法中的線性規劃子問題成為

( )

(

)

0 0 0 1 . n i i i i x f Minimize f x x x x = ∂  + − _ _ ∂  

∑

( )

(

)

0 0 0 1 0 , 1, 2, , . n j j i i i i x g Subject to g x x x for j J x = ∂   + − _ _ ≤ = ∂  

∑

…

(

0

) (

0

)

0.5 x−x T x−x ≤ξ. （3.35）上述的問題已經不再是線性規劃問題，改成圓形區域定義移動限制，依舊有移動步長ξ設定大小的問題。然而這個數學模型可進一步變形，把移動步長的限制條件併入目標函數中如（3.34）、(3.35）式，便無需實際訂定移動步長ξ

( )

(

)

(

)

0 2 0 0 0 1 1 0.5 . n n i i i i i i _x i f Minimize f x x x x x x = = ∂  + − _ _ + − ∂  

∑

( )

(

)

0 0 0 1 0 , 1, 2, , . n j j i i i i _x g Subject to g x x x for j J x = ∂   + − _ _ ≤ = ∂  

∑

… （3.36）上式是一個二次規劃（quadratic programming）問題，也就是其目標函數為二次函數，而所有的限制條件均為線性。二次規劃法是一個頗為強健的演算法，也是目前解大型非線性最佳化問題相當流行且重要的演算法。

3.9 對偶性理論

對偶性理論[11]的基本概念：每一個線性規劃都有一個相對應的線性規劃，稱為對偶，使得其中一個線性規劃的解一定是另一個的解。原始和其對偶的解之間有很多重要的關係。考慮一非線性最佳化問題

( )

. Minimize f x

(34)

( )

0 . Subject to h x = （3.37） 也可將上述的限制式擴張成為包含不等式與等式。假設 x*_{為上述問題的區域最小} 值，可對應到拉格朗基乘子λ*_使得

( ) ( ) ( )

0 . T f x∗ λ∗ h x∗ ∇ + ∇ = （3.38）而且拉格朗基乘子的赫遜矩陣（Hessian matrix）為

( ) ( ) ( ) ( )

. T L x∗ =F x∗ + λ∗ H x∗ （3.39）必須保證為正半定（positive semidefinite）。由上述的觀點發展區域對偶理論導入區域凸集的假設，特別假設赫遜矩陣

( )

L x∗ 在所有的空間中皆為正定。這樣的假設可以保證拉格朗基乘子

( )

T

( )

l x = f x + λ∗ h x 在 x*點是區域凸集。 進一步假設 x*_{點不是只是限制問題（3.37）的唯一區域解，也同時是非限制問} 題的唯一區域解

( )

. T Minimize f x + λ∗ h x （3.40）且對於區域最小點滿足一階與二階充分條件，對於任何趨近λ∗的λ皆對應一個區 域最小點 x 趨近 x*_滿足

( )

T

( )

f x +λ h x 。上述的函數隱含了

( )

T

( )

0 . f x λ h x ∇ + ∇ = （3.41）當λ趨近λ∗即有一解 x 趨近 x*，在解為 x*點時赫遜矩陣

( )

T

( )

F x +λ H x 為正定。因 此在區域中有為一相對應於非限制問題解的 x 與λ

( )

T

( )

. Minimize f x +λ h x （3.42）將對偶函數φ定義趨近λ∗

( )

T

( )

φ λ =  +λ  （3.43）

(35)

這是一個針對 x 趨近 x*_{的區域最小點。我們可以知道限制問題（3-37）是相等於針}

(36)

第四章　最佳控制理論

軌跡追蹤問題[12]是一個很典型的最佳控制問題。假設有個系統其模式可由下列的動態方程式及輸出方程式來描述

( )

(

( ) ( )

)

( )

0 0 , , , . . x t f x t u t t x t x y t h x t = = = （4.1）我們希望能找到一組控制解u∗

( )

t ，使系統的輸出軌跡y t

( )

能遵循一個期望的輸出軌跡r t

( )

。任何一組控制解u t

( )

皆能得到一個輸出軌跡，但是任意的輸出軌跡並非我們所期望的，達到我們目標真正的輸出軌跡與期望的輸出軌跡的差距最小的控制解，即為我們所謂的最佳控制解。最佳控制問題的基本要素 (1) 考慮的系統 (2) 實際的限制 (3) 效益的評估

4.1 考慮的系統

將任何控制問題作模型化處理的工作是重要一環。目的是為的獲得一個簡單的數學描述方程式，它可以將所有實際輸入系統的訊號，反應在對應於實際系統 的輸出端。我們所討論系統的狀態變數是由微分方程描述而成，假設在時間為 t 的狀態變數表示為 x t₁

( ) ( )

,x t₂ ,…,x t_n

( )

，在時間為 t 的輸入控制訊號為

( ) ( )

( )

1 , 2 , , n u t u t … u t ，則系統可由 n 個一階微分方成所描述

(37)

( )

(

( ) ( )

( ) ( ) ( )

( )

)

( )

(

( ) ( )

( ) ( ) ( )

( )

)

( )

(

( ) ( )

( ) ( ) ( )

( )

)

1 1 1 2 1 2 2 2 1 2 1 2 1 2 1 2 , , , , , , , , , , , , , , , , , , , , , , , , , , . n m n m n n n m x t a x t x t x t u t u t u t t x t a x t x t x t u t u t u t t x t a x t x t x t u t u t u t t = = = … … … … … … （4.2）我們定義系統的狀態向量為

( )

1 2 . n x t x t x t x t               控制向量為

( )

1 2 . m u t u t u t u t               可將（4.2）的狀態方程式改寫成

( )

(

( ) ( )

, ,

)

. x t =a x t u t t 在時間_t₀,_{t f}_間的控制輸入訊號可以表示為 u 或稱做控制歷程，在時間_t₀,_{t f}_間的 狀態值可以表示為 x 或稱做狀態軌跡。

4.2 實際的限制

在我們選定數學模型之後，下一步將要定義控制值與狀態值的實際限制。假設狀態向量限制有兩個變數，狀態變數x1在 t0時為 0 且 tf時達到 e，表示如下

( )

1 0 1 0 , . f x t x t e = = （4.3）狀態變數x₂在 t0時為 0 且 tf時為 0，表示如下

( )

2 0 2 0 , 0 . f x t x t = = （4.4）

(38)

狀態變數的限制條件矩陣為

( )

1 2 0 0 , . 0 ₀ ₀ 0 , 0 . e x t x t f x t e x t   _ _   =_{ }= _ _=_{ }       ≤ ≤ ≤ （4.5）控制向量輸入限制有兩個變數，控制變數u₁在 t0時為 0 且 tf時達到 M1，控制變數u2 在 t0時為−M2且 tf時為 0，表示如下

( )

1 1 2 2 0 , 0 . u t M M u t ≤ ≤ − ≤ ≤ （4.6）有限制條件的基本概念後，將這樣的概念再進一步描述 (1) 可行的控制向量變數(admissible control)滿足控制向量變數限制如

( )

1 0 , 0, f q u t ≤ t∈ t t _{ 或} q₂

(

x t

( ) ( )

,u t

)

≤0 , t∈ t t₀, _f_ 的控制向量變數。

(2) 可行的狀態軌跡(admissible state trajectories)滿足狀態向量變數限制如

( )

1 0 , 0, f p x t ≤ t∈ t t _{ 或} p₂

(

x t

( ) ( )

,u t

)

≤0 , t∈ t t₀, _f_ 的狀態軌跡。 (3) 目標區(target set)：系統最後的狀態x t

( )

f 必須落腳的區域，滿足

( )

(

f , f

)

0 S x t t = 的限制式。

4.3 效益評量

一個評估系統效益的量化指標，一般而言它可以用下式來表示

( )

(

)

(

( ) ( )

)

0 , tf , , . f f t J =h x t t +

∫

g x t u t t dt （4.7）其中 1 : n h + → 為最終狀態的成本函數，g: n m+ +1→ 為在時間t∈ t t0, f

)

之軌跡 成本函數；n 是

( )

的維數，m 是

( )

的維數。

(39)

效益評量依問題所要的目的不同，而有不同的選擇 (1) 最短時間控制問題(Minimum-time control) 0 f J = − 或 t t 0 1 f t t J =

∫

dt . （4.8）

(2) 最終狀態控制問題(Terminal state control)

( ) ( )

_f _f T

( ) ( )

_f _f . J =_x t −r t _ H x t_ −r t _ （4.9）其中r t

( )

_f 代表期望的最終狀態，H 是正定(positive definite)的權重矩陣。 (3) 最少的控制耗力問題(Minimum-control-effort)

( )

0 ₁ . f p t i i t i J β u t dt = =

∫

∑

（4.10）其中u t_i

( )

是第 i 個控制變數；βi是 ui的權重係數。 (4) 最低耗能問題(Minimum energy)

( ) ( )

0 . f t _T t J =

∫

u t Ru t dt （4.11）

其中 R 是一個實正定(real positive definite)的權重矩陣。 (5) 追蹤問題(Tracking)

( ) ( )

( ) ( ) ( )

0 . f t T t J =

∫

_x t −r t _ Q t _x t −r t dt_ （4.12）

( )

r t ：期望的狀態軌跡。

( )

Q t ：實半正定對稱(real positive semi-definite symmetric)的權重矩陣。 (6) 調節問題(Regulation)

( ) ( ) ( )

0 . f t _T t J =

∫

x t Q t x t dt （4.13）這是當r t

( )

=0,t∈ t t0, f 的追蹤問題。

利用效益評量來轉換硬限制(hard constraints)成軟限制(soft constraints)，如：

(1) 我們可以在原本的效益評量中加上一項

( ) ( )

T f f f f x t r t H x t r t  −   −     亦

(40)

即 J =…+_x t

( ) ( )

_f −r t_f _T H x t_

( ) ( )

_f −r t_f _ 以取代終端狀態的硬限制

( ) ( )

f f 0 x t −r t = 。 (2) 為了防止控制輸入太大，我們可以用

{

( ) ( )

}

0 f t T t J =

∫

…+u t Ru t dt 取代

( )

max max , 0, f u u t u t t t  − ≤ ≤ _{∈ } _{ 。}

(41)

第五章　遞迴二次對偶規劃(RQPD)

利用二次規劃的特性將目標函數與限制式分別作二次近似與一次近似目標函數的，目標函數的赫遜矩陣（Hessian matrix）對角線為正數，如果不為正數的則令它為一個小的正數。再利用對偶法解二次規劃的目標函數，對偶法的目標函數為λ的含數，由於原赫遜矩陣（Hessian matrix）為正定，所以保證對偶法的目標函數對λ為非凸集型。合併二次規劃與對偶法解非線性的最佳控制問題[13]-[15]。

5.1 問題的公式化

本章中討論的非凸集可分離最佳化問題如下

( )

1 min k i i y i z y =

∑

.

s.t

.

( )

1 0 k i i i h y = =

∑

,

( )

1 0 k i i i c y = ≤

∑

. （5.1）在這裡討論的

(

₁, ,

)

n, nj k i y= y … y ∈ y ∈ 而且

∑

k_i₌₁n_i =n ；限制式方程式 : ni m, : ni q i i h → c → 與目標函數 : ni , 1, 2, , i z → i= … ，皆為二次可微分的k i y 函數。

5.2 Runge-Kutta Method

系統為非線性動態方程式，利用用 Runge-Kutta Method[16]將系統的非線性動 態方程式離散化，first-order Runge-Kutta 法如下

(

)

1 , n n n n x₊ =x +hf x u . （5.2） second-order Runge-Kutta 如下

(42)

(

)

1 , , 2 2 n n n n n n h h x₊ =x +hf x_ + f x u u + _  . （5.3） 在此一問題中我們使用的是 first-order Runge-Kutta，一階與二階或是四階近似的差 別在於對非線性動態方程式離散後的近似度，使用一階近似時可以選用較小的 step- size，同樣可以達到較精準得離散動態方程式。

5.3 二次規劃遞迴法

由於在 3.8 節中已經大略的介紹過二次規劃法，所以在此節將不再贅述，直接運用二次規劃法重寫（5.1）式為

( )

(

)

(

( )

)

1 1 min 2 i k T y i i i i i i i d i z y l d d B y l d = ∇ +

∑

.

s.t.

(

( )

)

(

( )

)

1 0 i k i i y i i i i h y l h y l d = + ∇ =

∑

,

( )

(

)

(

( )

)

1 0 i k i i y i i i i c y l c y l d = + ∇ ≤

∑

. （5.5）上式中的 ni i d ∈ ，

( )

i yhi ∇ i 為m n× 的矩陣，_i

( )

i yci ∇ i 為q n× 的矩陣，而_i

( )

i yzi ∇ i 為 ni維度的列向量，B y li

(

i

( )

)

是個ni× 的正定對角矩陣，例如第 j 個對角元素 ni ( ) ( ) 2 2 2 , 2 0 ; , . i i ij ij ij _{y l} _{y l} if y y b otherwise γ  ∂ ∂ _> _∂ _∂ =    這裡的γ為大於零的純量，向量 yi的第 j 個元素表示為 yij，且

( )

T i 表示為

( )

i 的轉置矩陣。利用遞迴二次規劃法求解（5.1）式，遞迴更新的程序如（5.6）式

(

1

)

( )

, 1, , i i i y l+ = y l +αd∗ i= … k. （5.6）這裡的d_i∗為（5.5）式的最佳解，也是（5.1）式的搜尋方向。對偶法是最適合解（5.5）

(43)

用一維線性搜尋法，沿di

(

d1, ,dk

)

∗ ₌ ∗ _… ∗ 方向搜尋的最小值。

5.4 對偶法

利用對偶法求解（5.5）式描述如下：

(

)

, , Maximize λ µ Φ λ µ . 0 µ ≥ . （5.7）對偶函數Φ

(

λ µ,

)

是拉格朗基乘子

(

λ µ,

)

的函數，λ∈ m ，µ∈ q ，如下：

(

)

(

( )

)

(

( )

)

( )

(

)

(

( )

)

1 1 1 1 , min 2 , , . i k T y i i i i i i i d i T T k k i i i i i i i i z y l d d B y l d H y l d C y l d λ µ λ µ = = =    Φ = _ _∇ + _          +_ _ +_ _ _     _

∑

（5.8）上式的H_i

(

y l_i

( )

,d 與_i

)

C y l_i

(

_i

( )

,d 分別表示為： _i

)

( )

(

,

)

(

( )

)

(

( )

)

i i i i i i y i i i H y l d =h y l + ∇ h y l d ,

( )

(

,

)

(

( )

)

(

( )

)

i i i i i i y i i i C y l d =c y l + ∇ c y l d .

利用對偶法來解（5.5）式，再利用梯度法（gradient ascent method）解（5.7）式，遞迴的過程如下：

(

1

)

( )

t

( )

, 1, , t t j j _λ j t m λ + =λ + ∇ Φβ = … .

(

1

)

( )

v

( )

, 1, , v v j j _µ j v q µ + =µ + ∇ Φβ = … . （5.9） 這裡的 j 代表遞迴的次數，Φ

(

λ µ,

)

用Φ

( )

j 來表示第 j 次的遞迴，而且λt_與_μv_分別表示λ與μ的第 t 個與第 v 個元素。利用一維線性搜尋法求得參數β 的值，並使

( )

( ) ( )

( )

(

)

{

}

arg max_β j _λ j , j _µ j β = _∈Ω Φ λ + ∇ Φβ µ + ∇ Φβ ，這裡的

( )

{

β µ j β _µ j 0

}

Ω = ∈ + ∇ Φ ≥ ；對於所有的

(

∇ Φ_λ

( )

j ,∇ Φ_µ

( )

j

)

可以根據下列公

(44)

式求得：

( )

(

( )

)

1 ˆ , t k t i i i i j H y l d λ = ∇ Φ =

∑

,

( )

(

( )

)

1 ˆ , v k v i i i i j C y l d µ = ∇ Φ =

∑

. （5.10）由於（5.8）式中最小解dˆ為

(

λ µ,

)

=

(

λ

( ) ( )

j ,µ j

)

的函數，因此求得λ與μ收斂解的同時也求出最小解dˆ。在（5.10）式的H_it

(

y l_i

( )

,dˆ_i

)

與C_it

(

y l_i

( )

,dˆ_i

)

分別代表

( )

(

_, ˆ

)

i i i H y l d 與C y l_i

(

_i

( )

,dˆ_i

)

的第 t 個與第 v 個元素。 由於（5.5）式是可分離的，所以可以針對λ值將（5.8）解構成 k 個獨立的最 小化子問題，每個子問題 I 可以由下列方程式求得：

( )

(

)

(

( )

)

( )

(

)

( )

(

( )

)

( )

1 ˆ i i i T i i i y i i T T y i i y i i d B y l z y l h y l λ j c y l µ j − _ = _∇  +∇ + ∇ _ （5.11）因為B y li

(

i

( )

)

1 − 為對角矩陣，所以可以平行的計算 k 個dˆi。所有的∇ Φλ

( )

j 與

( )

j µ ∇ Φ 也可以根據（5.10）式作平行計算。

5.5 RQPD 演算法

根據上面的推演，對於非凸集可分離得最佳化問題，我們已經有了最適的的求解方式：演算法I. 步驟 0：設定初始值γ、y

( )

0 和i=0 。步驟 1：設定初值λ

( )

0 與µ

( )(

0 µ ≥0

)

， j= 。 0 步驟 2：利用（5.11）式平行計算dˆ。

(45)

步驟 4：假如

{

_λ

( )

j _∞, _µ

( )

j

}

ε₁ ∞ ∇ Φ ∇ Φ < ，執行步驟 6.，其它情況執行步驟 5.。步驟 5：利用（5.9）式平行的處理與更新

(

λ

(

j+1 ,

) (

µ j+1

)

，返回步驟 2.。步驟 6：假如 dˆ _∞< 結束，且輸出ε₂ y l

( )

得解；其它則利用（5-6）式作平行的更新y l

(

+1

)

，並返回步驟 1。（注意：ε1與ε2表示解的準確度，而

( )

i _∞為

( )

i 的無限-範數。）　　　　　　　　計算設定初值設定

( )

{

∇ Φλ j _∞,∇ Φµ j _∞

}

<ε1 2 ˆ d _∞<ε Y ˆ d 計算

( )

(

∇ Φ_λ j ,∇ Φ_µ l

)

平行運算

( ) ( )(

0 , 0 0

)

λ µ µ≥

(

) (

)

(

λ j+1 ,µ j+1

)

N

(

1

)

y l+ N Y 停止輸出系統的解圖 5.1 RQPD 演算法的整體架構

無人螺旋航空載具的軌跡控制

國

立

交

通

大

學

電機與控制工程學系

碩

士

論

文