數位式直流轉直流切換降壓控制器設計

國 立 交 通 大 學

電機學院 IC設計產業研發碩士班

碩 士 論 文

數位式直流轉直流切換降壓控制器設計

Design of Digital DC-DC Switching buck Controller

研 究 生：蕭吉隆 Student：Chi-Lung Hsaio

指導教授：林進燈 博士 Advisor：Dr. Chin-Teng Lin

數位式直流轉直流切換降壓控制器設計

Design of Digital DC-DC Switching buck Controller

研 究 生：蕭吉隆 Student：Chi-Lung -Hsaio

指導教授：林進燈 博士 Advisor：Dr. Chin –Teng Lin

國 立 交 通 大 學

電機學院

IC 設計產業研發碩士班

碩 士 論 文

A Thesis

Submitted to College of Electrical and Computer

Engineering

National Chiao Tung University

in partial Fulfillment of the Requirements

for the Degree of

Master

in

Industrial Technology R & D Master Program on

IC Design

August 2007

Hsinchu, Taiwan, Republic of China

中華民國九十六年八月

數位式直流轉直流切換降壓控制器設計

學生：蕭吉隆 指導教授：林進燈 博士

國立交通大學電機學院

IC 設計產業研發碩士班

摘 要

近年來，由於可攜式電子產品的輕薄短小，除了電池使用外，定電壓 和低漣波的穩壓晶片在電源電路設計上是必然的趨勢。對於傳統的類比穩 壓晶片，當其電源電路的規格有所變動時，需要根據新的參數改變整個晶 片的設計。然而，對數位式穩壓晶片，運用數位式控制調變技術，可用來 提昇系統電路之性能。這種數位式控制調變技術使用比例積分微分補償器 (PID)之原理為設計基礎，主要特點是系統的輸出電壓經過類比數位轉換 器(ADC)成為迴授訊號，並與參考電壓的差值作為數位控制器的調變訊 號，以獲得電力電子之高效率直流切換電壓轉換。 在本論文中，數位控制器的設計以可程式化邏輯閘陣列(FPGA)作為電 路實現的架構，並透過電壓轉換器之系統電路來驗證所設計數位控制器之 功能與效能。此控制器的設計有較大的動態輸入電壓範圍，輸出電壓固定 在3.3V，最大輸出負載電流為1A，和最大功率轉換效率可達到85.7%。 關鍵字: 比例積分微分補償器、類比數位轉換器、可程式化邏輯閘陣列、 功率轉換效率、調變。

Design of Digital DC-DC Switching Buck Controller

Student: Chi-Lung Hsaio Advisor: Dr. Chin –Teng Lin Industrial Technology R&D Master Program of

Electrical and Computer Engineering College National Chiao Tung University

Abstract

In recent years, due to development of frivolous and small portable electronic products quickly, except use of the battery, a fixed-voltage and low-ripple voltage regulator in the power circuit design has already been the essential tendency. For a traditional analog voltage regulator, when the power circuit specification has been changed, it needs to redesign according to new parameters. For a digital voltage regulator, it is realized by the digital control modulation technique to promote the performance of the system circuit. This technique makes use of the proportion integral differential (PID) compensator as the basic foundation of system design.To obtain transformation of high-efficiency DC voltages, this thesis proposes a novel digital DC-DC switching buck controller. The controller output voltage is transferred to feedback signals via an analog to digital converter (ADC), and then the difference between the feedback signal and the reference voltage is regarded as a major modulation signal.

In this thesis, design of the digital controller is implemented and verified by using the filed programmable gate array (FPGA). We demonstrate a system circuit which uses the penetration voltage drop called the buck voltage converter in order to verify the digital controller. The input voltage of the controller has wider ranges volts, and the output is fixed as 3.3 volts. Finally, the proposed design can achieve the maximum output load current of 1A and the power transformation rate of 85.7%.

Keywords: Proportion integral differential, PID, ADC, buck, FPGA, power transformation rate, modulation.

誌謝

在交大研究所高唱青青校樹的日子裡，回想在交大裡頭充滿許多挑戰，在許多驚 濤骇浪的學習中有很多值得個人一再省思的，也有很多人是要感謝的卻不知從何說起 好。首先，先要感謝我的指導教授 林進燈老師，老師在我碩士生涯時光中給予我無限 廣闊的學習空間發展與光陰悉心指導與啟蒙鼓勵使我在課業和論文上得以順利完成並 在處世上受益良多。另外也感謝口試委員們的許多建議與指教，將使本篇論文更加完 整。 個人原是學識相當淺薄的人今日能有尺寸躍進之效，都有賴在這期間從范倫達老 師身上學到不少實事求是做研究的道理及研究方法，從鍾仁峰博士 感受到學長他個人 對我許多期許及在很多方面觀念啟發指導及精益求精的做事態度，使我成長不少讓我 可以在日後將來的學習道路上有更加長足的進步，就我個人而言是彌足珍貴的人生砥 礪經驗。而我要感激在心頭的人也少不了幫助我解決諸多疑難雜症問題提供不同意見 的實驗室的每位同學經翔、 紹航、靜瑩、智文、德瑋、煒忠、孟哲、蘇愷和許多學弟 妹，大家給我許多架構過程上的指導以及實作上的諸多建議。 其次就是要感謝給我很多無私無我友情支援陪伴我一起渡過碩士班學習的伙伴大 B、小燕子、男哥和工研院的小智及在當兵的阿彰學長、李小杰還有在業界工作的聖智 鐵哥和成大呂同學在許多方面給我的討論與交流，使我對數位power ic的整個架構有 更進一步理解領會。其實要感謝的人很多無法一一提及如同陪伴我在校園中渡過的每 位師友們謝謝您們大家對我這些日子來關心與愛護，讓大家煩心擔憂，真的很過意不 去。 最後，個人謹向最摯愛的長上父母親雙親謝謝您們對我的多年栽培教育，雖然爸 媽未能讓我足夠有力的經濟支援，但讓我背後有了一切無限的精神支拄，使我能安心 完成碩士學業，僅以本論文獻給我的家人和所有關心我的師長和老同學朋友們，願大 家共享這份榮耀。

目錄

摘 要... i Abstract ... ii 誌謝... iii 目錄... iv 圖目錄... vi 表目錄... viii 第一章 概論... 1 1.1 研究背景... 1 1.2 研究動機與目的... 1 1.3 論文內容大綱架構... 4 第二章 控制器設計原理... 5 2.1 類比控制電源與數位控制電源整體結構的比較... 5 2.2 控制電路轉換介紹... 8 2.3 輸出電壓取樣電路... 10 2.4 ADC0820 的特性 ... 11 2.4.1 ADC0820 的工作原理 ... 11 2.5 數位補償器電路... 14 2.6 數位脈波寬度調變器... 16 2.6.1 量化效應... 16 2.6.2 數位脈波寬度調變器之架構... 18 2.7 低壓差架構... 21 第三章 數位控制設計與類比調整電路... 23 3.1 數位控制器方法介紹... 23 3.2 數位控制結合智慧控制的操作... 23 3.2.1 PID 數位穩定控制理論推導設計 ... 25 3.3 LDO 附屬調整電路 ... 40 3.3.1 壓降電壓... 41 3.3.2 靜態電流或接地電流... 42 3.3.3 線性穩壓... 43 3.3.4 負載穩壓... 44 3.3.5 電源拒斥比... 45 3.4.6 精確度... 46 第四章 控制電路FPGA 實現 ... 48 4.1 硬體描述語言簡介... 49 4.2 A/D 轉換器... 50 4.3 數位補償器... 53

4.4 數位脈波寬度調變器... 55 4.4.1 Deadtime 產生器 ... 55 4.4.2 工作週期暫存器... 57 4.5 LDO 穩壓的設計考量 ... 58 4.6 功率效率... 59 第五章 實驗模擬及量測結果... 60 5.1 模擬結果... 60 5.2 量測結果... 64 第六章 結論及未來工作... 69 6.1 結論... 69 6.2 未來工作... 69 REFERENCES... 70

圖目錄

圖 1 台灣與美國就POWER IC 領域各方優勢比較方塊圖... 2 圖 2 數位式降壓型直流電源轉換器... 3 圖 3 類比控制電源方塊圖... 6 圖 4 數位化控制電源方塊圖... 7 圖 5 類比降壓直流電源轉換器基本公式方塊圖... 8 圖 6 數位降壓直流電源轉換器方塊圖... 9 圖 7 數位降壓直流電源轉換器架構圖... 9 圖 8 ADC0820 接腳圖 ...11 圖 9 ADC0820 讀取模式時序圖 ... 12 圖 10 ADC0820 寫入-讀取模式時序圖（trd > tI）... 13 圖 11 ADC0820 寫入-讀取模式時序圖（trd < tI）... 14 圖 12 ADC0820 寫入-讀取模式下 Stand-Alone 時序圖... 14 圖 13 PID 電路結構圖 ... 16 圖 14 Limit Cycling 圖 ... 18 圖 15 Four-Phase 電路結構圖 ... 20 圖 16 Four-Phase DPWM 輸出波形圖示意圖 ... 20 圖 17 基本的LDO 低壓差穩壓架構 ... 21 圖 18 數位控制結合智慧控制示意圖... 24 圖 19 類比降壓DC 電源轉移線性等效圖 ... 25 圖 20 Q-ON 並且 D-OFF 狀態圖 ... 26 圖 21 Q-OＦＦ並且 D-OＮ 狀態圖 ... 28 圖 22 轉移方程矩陣的說明圖 ... 33 圖 23 補償迴圈圖 ... 34 圖 24 系統回授網路架構... 38 圖 25 根軌跡的MATLAB CODE... 39 圖 26 根軌跡圖... 40

圖 27 kp、ki、kd 的 MATLAB CODE... 40

圖 28 Vin 與 Vout 的關係圖 ... 42 圖 29 LDO 穩壓的靜態電流圖 ... 42 圖 30 PMOS 的 LDO 穩壓圖 ... 43 圖 31 LDO 穩壓的 PSRR 圖 ... 45 圖 32 Xilinx 發展介面 ... 48 圖 33 Xilinx 系統發展實驗板 ... 49 圖 34 ADC0820 取樣電路方塊圖 ... 51 圖 35 時序控制電路方塊圖... 51 圖 36 產生誤差值電路方塊圖(1)... 52

圖 37 產生誤差值電路方塊圖(2) ... 52 圖 38 PID 與誤差值產生電路連接方式方塊圖 ... 54 圖 39 SHIFT 方式乘法電路... 54 圖 40 四相位 DPWM 計數器分時切割電路 ... 55 圖 41 Deadtime 波形圖 ... 56 圖 42 Deadtime 產生器方塊圖 ... 56 圖 43 工作週期暫存器寫入圖... 57 圖 44 LDO 典型運用電路方塊圖 ... 58

圖 45 MATLAB 模擬切換電壓狀態圖分別在 Vin =5V ,Vin=10V ... 61

圖 46 MATLAB 模擬切換電壓狀態圖分別在 Vin =10V、Vin=20V ... 61

圖 47 DEADTIME (死區)切換電路簡易模擬波形 ... 61

圖 48 MODELSIM 模擬 DUTY ... 62

圖 49 MODELSIM 模擬四相位 DPWM... 63

圖 50 HSPICE 模擬開關 power stage 充放電穩定現象... 63

圖 51 整體電路的板上連接電路圖... 64

圖 52 工作實驗平台... 65

圖 53 Deadtime 經由示波器量測 ... 66

圖 54 示波器量測輸入電壓 Vo≅ 3.3V , 開關頻率=250K... 66

表目錄

表 1 PID 控制函數在時域和頻域的比較表 ... 35

表 2 轉移函數表... 35

表 3 轉移係數方法表... 37

第一章 概論

1.1 研究背景

近年來，由於可攜式電子產品的輕薄短小，除了電池使用外，定電壓 和低漣波的穩壓晶片在電源電路設計上是必然的趨勢。對於傳統的類比穩 壓晶片，當其電源電路的規格有所變動時，需要根據新的參數改變整個晶 片的設計。然而，對數位穩壓晶片，運用數位式控制調變技術，可用來提 昇系統電路之性能。這種數位式控制調變技術使用比例積分微分補償器 (PID)之原理補償為設計基礎，主要特點是系統的輸出電壓經過類比數位 轉換器(ADC)成為迴授訊號，並與參考電壓的差值當做數位控制器的調變 訊號，以獲得電力電子之高效率直流切換電壓轉換。

1.2 研究動機與目的

一般的直流轉直流的穩壓器(DC-DC Regulator)大概分成交換式穩壓 器(Switching Regulator) 及 電 荷 幫 浦 穩 壓 器 (Charge-Pump Regulator) 。 DC-DC 轉換器廣泛被應用在直流供應器以及直流馬達驅動器。因此，對 於切換直流轉直流轉換器的控制使其在輸入電壓與輸出負載變動的情況 下，能夠調整輸出電壓為所設定的位準，實為一項重要的研究。 數位控制器的觀念，在許多的研究報告以及實驗結果也都有實例來證 明數位控制器的確相較於類比控制器方式，數位控制的方式不止在成本上 具較佳的優勢，它所具有的優異特性，例如可與外界溝通的能力以及可程

式化的彈性操作，這些因素都將使得數位控制有可能會在最短的時間內去 取代整個電源的控制方式。 從市場的角度來看，數位電路在成本的控制上會比類比電路更具競爭 性，以類比電路所設計的 IC 要達到縮小晶片尺寸的機會並不大，除非有 部份功能數位化才有可能完成這項工作。成本的高低一向視晶片的大小考 量而決定，假使傳統類比電源控制方式能夠一併數位化，將使晶片尺寸縮 小的速度也將會追隨著Moore's law 的準則而得到合理的解釋，相對地對 於降低成本也有所幫助。由圖 1 闡明整體 Power IC 的市場及台灣與美國 就各方面優勢比較。 圖 1 台灣與美國在POWER IC領域各方優勢比較圖

然而控制分為類比控制系統與數位控制系統，我們所採用的是數位控 制系統，因為數位式控制器可以提供下列優點[1]： 1. 降低成本，系統積體電路化，提高靜態與動態系統的特性。 2. 減小對製程參數、溫度參數變化的靈敏度。 3. 設計所需時間較短，有許多現成工具（EDA）可以使用。 4. 可程式化，一個控制器可以經過修改而再去控制其他的轉換器 減少類比元件的使用。 5. 控制器的差異性可藉由程式的設定達成，而不需硬體的更換。 圖 2 數位降壓直流電源轉換器 舉例說明如圖2 的一個數位降壓直流電源轉換器的設計中，圖下方的 DC-DC 控制器部份用來送出一個週期性的方波。這一個方波可以控制功 率電晶體(Power MOS)的開與關。當其中一個功率電晶體導通，另一個電 DC-DC controller (Digital control system)

NMos PMos L C _R RLC Duty DC + _ LDO _Vo

晶體就會完全關起來。造成電流流過電感或是不通過電感。因方波訊號的 週期是固定的，所以功率電晶體開關的比率 (Duty Ratio) 可以決定輸出 電壓的大小。

數位的控制器可以分作控制電壓穩定度補償 (Proportional Integral Derivative Compensator; PID) 外，也可用以控制電壓高低位階的脈波寬度 調變(Digital Pulse Width Modulator，DPWM)。因為控制器根據電壓來調 變輸出方波的開關比率(Duty Ratio)，這種型式的控制器就稱作電壓控制 型電源轉換器。 電感(L)與電容(C)還有負載電阻(R)可以稱為 RLC Power Stage。這個 儲能轉移網路所導出的轉移函數就是控制器要補償的受控體。如果控制器 只根據電源轉換器的輸出電壓(Vo)來決定方波的開關比率。可以稱這種形 式的電源轉換器為電壓控制型電源轉換器。

1.3 論文內容大綱架構

本論文共分五個章節說明 各章節的標題與內容簡述如下: 第一章 概論: 說明本論文之研究背景、動機及電源轉換器簡介。 第二章 控制器設計原理 第三章 數位控制器設計與附屬類比調整電路 第四章 控制電路FPGA實現 第五章 實驗模擬及量測結果 第六章 結論及未來工作: 對整體的研究做總結並討論未來可能的研究方 向。

第二章 控制器設計原理

2.1 類比控制電源與數位控制電源整體結構的比較

在類比控制的方式上，輸出電壓會被取樣而與參考電壓作比較，其所 產生的誤差電壓，會被放大後以提供類比PWM調變器作參考以調整適當 的脈波寬度去產生所要求的輸出電壓，在功率MOSFET開關中被放大的電 流及電壓會經由輸出濾波器過濾後，以得到所設計的直流輸出電壓。 在類比控制電源閉迴路系統(如圖3)內，控制電路必需滿足整個迴路 增益在任何工作頻率下要＜1 （此時相位延遲等於360度）。除了閉迴路 系統內含的180度反向器之外，外部元件所造成的相位延遲（例如：電容 及電感）以及放大器、調變器和驅動開關線路也提供了額外但較少的相位 延遲。 在電路中，針對相位以及回授放大倍率，所作之調整稱之為補償，是 在誤差放大器上，針對迴路增益以及相位延遲所採取的一種補償方式，使 電路不會產生震盪，並且能夠快速的達到我們的預設狀態，以確保整個電 路能在預期的條件下正常且穩定工作，針對隔離式的輸入／輸出設計，亦 可套用如圖3的做法，其觀念上是一樣的。 因此，如何以數位化方式來取代原先的類比控制，特別是針對PWM 的功能在誤差訊號的處理以及補償方式的數位化處理。

圖 3 類比控制電源方塊圖 使用數位化來控制，其中不同在於類比補償控制改換成PID補償控制穩定 度。從圖3基礎所衍生出來圖4的架構，欲瞭解其動作原理，首先從電源 MOSFET開關的部份開始，數位化的脈波寬度調變器去驅動控制電源 MOSFET開關部份以放大電壓及電流，但此時所控制電源MOSFET開關的 On和Off的時間是經過了計算而得到的結果，若以類比控制的方式，其開 (On)與關(Off)的時間決定是以正反器的CLK觸發點為On，而以上升的速 度及設定最大電壓的觸發點為Off，作為其時間長短的判斷。如此的差異 性決定了數位控制電源的優異特性，這在稍後再加以說明。

在PWM之前是稱之為PID（Proportional Integral Derivative）或「控制

裁決補償處理器」的系統，它是將數位化的輸出電壓轉換成內含Duty Cycle控制的資訊給PWM作參考之用，更清楚解釋是PID的工作是去調整 脈波寬度以即時的方式將輸出電壓鎖定在預設的範圍之內，就如同類比控 SCALE PWM ANALOG COMPENSATER NETWORK DC ERROR VOLTAGE REF ANALOG CONTROL CHIP CLOCKED VOLTAGE RAMP POWER SWITCHING FILTER DC INPUT POWER DC OUTPUT POWER Analog Pulse Train

制方式一樣，PID也必須去補償迴路增益及相位延遲去穩定整個迴路控 制，在數位系統內，還有其他的相位延遲因素，例如資料處理器的計算延 遲時間。所以在類比控制電源內影響到迴路增益與相位延遲的因素（例如 輸出電容及電感濾波器）也會在數位控制電源的設計上出現，只是多了額 外的資料處理器的計算時間以及A/D的傳輸延遲時間。 再往前一步看到A/D轉換器，它會將輸出電壓轉換成數位資料以高速 的脈波頻率提供PID作參考，其資料格式為2進位資料，而A/D的比較參考 電壓及字元的長度會決定輸出電壓的精密度。在數位世界裡，被量化後的 類比資料會以一整串連續的資料值表示，介於資料值與資料值之間的間隔 （解析度）會取決於資料的位元長度以及A/D轉換器所取樣的電壓範圍大 小。 圖 4 數位化控制電源方塊圖 SCALE (H) DPWM PID PROCESSOR COMPENSATER Scaled DC Voltage A/D Converter POWER SWITCHING FILTER DC INPUT POWER DC OUTPUT POWER Analog Pulse Train

2.2 控制電路轉換介紹

C

L

D

i

v

o

v

+

+

_

_

_ ˆ ( ) 1 ˆo_{( )} i _{( )} c1s ₁ o o v s r C V s d s w w Q + = + + 1 ,w_o , LC = 1 1 ( ) o L c Q L w r r C R = + + 圖 5 類比降壓直流電源轉換器基本公式方塊圖 在本論文中，我們將介紹由圖5早期全類比式降壓電路轉換成數位式 可程式調變控制積體電路來控制降壓直流轉直流轉換器電路。數位調變控 制電路中包含了三主要元件：類比至數位轉換器ADC（A/D Converter）、 數位補償器PID（Digital Compensator ）、數位脈波寬度調變器DPWM

（ Digital Pulse-Width Modulator）。整個直流轉直流轉換器的方塊圖，如

圖 6 數位降壓直流電源轉換器方塊圖[3] 由圖6知，數位調變控制電路與切換降壓直流轉直流轉換器形成閉迴 路回授（Closed-loop Feedback）的系統，而控制電路的主要功能就是調整 直流轉直流轉換器的輸出電壓（Vo）。當切換降壓直流轉直流轉換器的輸 出電壓因為輸入電壓（Vi）或負載電流（IL）的變動而改變時，此時，控 制電路所送出的訊號（Duty Ratio）便會對轉換器做調整的動作，使得轉 換器的輸出電壓又能夠穩定地保持在我們所要的參考電壓（Ｖref）設定， 其數位調變控制電路內部架構如圖7所示。 圖 7 數位降壓直流電源轉換器架構圖

Switching power converter

Target voltage setting and other Specification definitions A/D Vout Vg Digital controller DPWM D E[n] D[n] Vsense

當數位調變電路開始啟動時，切換降壓直流轉直流轉換器會將輸入電 壓（Vg）降壓而輸出（Vo）。其輸出電壓與輸入電壓的關係式如式（2-1） [4]。 Vo = DVg, （2-1） 其中 D 為責任週期（duty ratio），其值為0 < D < 1。首先，控制電路中 的類比至數位轉換器（A/D）會對直流轉直流轉換器的輸出電壓做取樣而 得到一個取樣電壓（Vsense），一般的情況下，Vsense = Vout。接著類比至數

位轉換器將取樣電壓與送至類比至數位轉換器的參考電壓（Vref）做比較， 其比較後的誤差值即是誤差訊號（E[n]）。這個誤差訊號被送至數位補償 器做運算，其運算的結果為訊號（D[n]），這就是數位脈波寬度調變器的 輸入，調變器會根據訊號D[n]的值，而送出一個頻率固定的脈波訊號（Duty Ratio），脈波寬度即是由D[n]值所決定的。最後，這個新產生的脈波寬度 訊號會再送至切換降壓直流轉直流轉換器的開關元件而做切換，使轉換器 轉換不同的輸出電壓。經由這樣不斷的取樣、比較、補償，所以會使切換 降壓直流轉直流轉換器的輸出電壓穩定。

2.3 輸出電壓取樣電路

若要對切換直流轉直流轉換器做電壓的調整，由圖6 所示得知，第一 步就是要對轉換器的輸出電壓取樣，這步驟算是在整個控制積體電路中最 重要的一個電路。如果取樣電壓不準確的話，接下來的補償就沒意義了。 舉例說明，若系統操作頻率為250KHz，則切換直流轉直流轉換器的 輸出電壓的頻率亦為250KHz，所以要對這樣頻率的電壓取樣，我們就得

選擇一顆轉換速度至少達250KHz，即轉換時間至少要在4 us 以內的類比 至數位轉換器。所以基於上述的分析，必須要先知道所設計系統的需求， 再去選擇一顆適合的類比至數位轉換器。因此，在本論文的設計中，選擇 了ADC0820 這顆類比至數位轉換器[10]。

2.4 ADC0820 的特性

ADC0820 是一顆8位元的CMOS 類比至數位轉換器，共有20隻接 腳，其接腳圖如圖8所示。ADC0820 的主要特性如下說明： z 解析度為：8 Bits。 z 轉換時間： RD 模式最大2.5 us。WR-RD 模式最大1.5 us。 z 功率消耗：最大75 mW。 z 最大誤差： ± 1/2 LSB 至± 1LSB。 圖 8 ADC0820接腳圖[11]

2.4.1 ADC0820 的工作原理

ADC0820 類比至數位轉換器有兩種操作模式，讀取模式(RD-Mode)

與寫入-讀取模式（WR-RD Mode）。模式的選擇由第七支腳（MODE） 來決定，當MODE腳輸入為〝0〞時，執行在RD模式，MODE腳輸入為〝1〞 時，執行在WR-RD 模式。兩種模式將說明如下： z RD 模式 ADC0820 的寫入模式時序如圖9所示。當ADC0820 的第七支腳 MODE輸入為〝0〞時，ADC0820 即進入讀取模式。先將第13腳（CS） 設為〝0〞，致能ADC0820。在讀取模式下，一個完整的轉換是當第8 腳 （RD）輸入為〝0〞時開始，直到輸出有資料送出為止。當轉換結束後， 第9支腳（INT）會由1 變0 以表示轉換器正在忙碌中或是可以讀取資料。 圖 9 ADC0820 讀取模式時序圖[11] z WR-RD 模式 ADC0820 的寫入模式時序如圖10 所示。當ADC0820 的第七支腳 MODE輸入為〝1〞時，ADC0820 即進入寫入-讀取模式。將第13腳（CS） 設為〝0〞，致能ADC0820。ADC0820 的寫入-讀取模式是由第6 腳 CS RD RDY INT DB0-DB7 tp

WITH EXTERNAL PULL-UP tRDY tCRO t1H toH tACCO tINTH tACC3

（/WR&RDY ）所控制的，然而在此種模式下又有兩種讀取操作。一種 為先等INT 腳 1 變0 時，再去讀取資料，通常INT 會在WR腳上升後800 ns 才由1 變0，如圖10所示。如果需要快一點的轉換時間，另一種做法為 不需要等待800 ns，大約在WR 腳上升後600 ns就可以直接去讀資料，如 圖11所示。 圖 10 ADC0820 寫入-讀取模式時序圖（trd > tI）[11] CS WR RD INT DB0-DB7 tP tWR t1H toH tACC2 tINTH tRD tINTL CS WR RD INT DB0-DB7 tP tWR t1H toH tACC1 tINTH tRD tINTL tR1

圖 11 ADC0820 寫入-讀取模式時序圖（trd < tI）[11] z Stand-Alone 模式 在寫入-讀取模式下使用Stand-Alone 操作時，CS腳跟RD 腳可以同 時為〝0〞，當WR 腳 1 變0 時，ADC0820 開始轉換，大約800ns後資料 就會送至輸出。Stand-Alone 模式時序圖如圖12所示。 圖 12 ADC0820 寫入-讀取模式下Stand-Alone 時序圖[11]

2.5 數位補償器電路

數位補償器電路是數位脈波寬度調變控制電路中負責做運算的部 份，其角色像是中樞控制的部份。當類比至數位轉換器取樣到直流轉直流

轉換器的輸出電壓（Vo）並與Vref 比較得到一個誤差訊號（Error Signal）

值e[n]後，A/D轉換器會把這誤差值送到此補償器。 補償器其實是一個控制理論的一種實現，本論文的補償器所要實現 的控制理論是根據PID 控制器的觀念所設計，PID控制器的電路結構如圖 CS LOW WR RD LOW INT DB0-DB7 tP tWR tID DATA tI tINT

13所示，其所實現的關係式如下列式子所表示： dp(n) = Gpe(n) (2-2) di(n) = Gi e(n) + di(n-1) (2-3) dd(n) = Gd [ e(n) – e(n-1) ] (2-4) d(n) = dp(n) + di(n) + dd(n) (2-5) 由上式，d[n]代表的是補償器目前的責任週期（Duty Ratio）輸出值，

e[n]則是代表A/D 轉換器目前的誤差訊號（Error Signal）輸出值。e[n-1]

則為該訊號前一次週期的誤差訊號（Error Signal）輸出值，di[n-1]則為上 一週期的積分值，Gp、Gi、Gd 為比例積分微分各部份的增益常數。 由上式(2-2) (2-3) (2-4) (2-5)可知，要設計一個補償器需要使用到數 個加法器與乘法器，然而對於一個積體電路設計者而言，乘法器的使用是 非常佔用晶片面積又有速度上的考量，所以勢必要改用另一種設計的方 式，因此我們使用移位再相加的方式實現乘法電路，其方法描述將在4.3 加以說明。 sh ift s h ift + sh ift + e (n ) ID S a m p le G p G i G d d i d (n ) d p d d re g iste r re g is te r d ( n )

圖 13 PID 電路結構圖 [2]

2.6 數位脈波寬度調變器

在整個系統中，由外部連接到內部做運算時須將訊號由類比轉至數 位，因此我們需要有AD轉換器；反之也同樣的，若運算完畢後需將內部 的數位資料轉換到外部的類比電路，一般的方式有DA轉換器，或者是利 用高速開關的方式達成的PWM方式，而數位脈波寬度調變器所提供的功 能其實就是一個數位至類比的轉換器（D/A Converter）。因為它所輸出的 是一個頻率固定寬度可依據d[n]值而調變的訊號（Duty Ratio）。這個訊 號將輸出至切換直流轉直流轉換器的開關元件，利用不同的寬度調變，開 關元件也會以不同時間的導通與截止，如此一來就可以調整我們所要的輸 出電壓。PWM 訊號，利用數位脈波寬度調變方式達到電路預期特性，主 要有以下 5 大 優點[7]： (1) 可產生可程式化的驅動波形訊號輸出。 (2) 不受元件誤差，特性漂移以及老化的影響。 (3) 隨時可因應不同環境變化而改變其設定參數。 (4) 可記錄操作情況以作為參考除錯之用。 (5) 與早就數位化的外界溝通。

2.6.1 量化效應

類比控制可調整出非常精準的輸出電壓，原則上，在類比控制的世 界中，輸出電壓可以調整至任何所需要的電壓，僅受限於迴路增益，熱效

應以及雜訊的影響。從數位控制來看，其連續有限的取樣點是量化元件所 造成的結果，此量化元件乃指“A/D轉換器＂以及“DPWM（Digital Pulse Width Modulator）。所以解析的程度就以取樣點的多少作決定，以二進制 控制系統而言，n位元的控制字元代表可產生2n的取樣點狀態，若以一個 電源開關系統為例，以2n的資料量控制脈波寬度，其輸出電壓的解析度可 以VIN/2n_來代表。 這些一連串連續的量化輸出，必須符合輸出電壓的規格要求，其中

也包括了誤差範圍，例如輸出電壓VOUT= 3.3 Volts， 其容忍誤差 ∆VOUT =

0.033Volts。 A/D轉換器所需要的位元數 n = int (log2 (VOUT/∆VOUT)) = int

(log2(100)) = 7 這說明，A/D轉換器至少必須有7個位元的資料量才可以 達到所要輸出的電壓值以及其所設定的誤差範圍。因A/D轉換器的解析度 及比例因素H(由圖4)的作用，配合A/D的轉換以達到所設計的輸出電壓， 所以A/D轉換器的解析度與比例因素便決定了輸出電壓的精密範圍。 若在下一階段的量化元件DPWM的解析度比A/D轉換器還要少的 話，則A/D轉換器將無法找到其合適的輸出電壓以供DPWM參考使用，也 就是說，A/D轉換器的LSB（Least Significant Bit）會因為DPWM所調整出 的輸出電壓無法配合A/D的解析度而一直改變，這結果會使得系統無法鎖 住輸出電壓，而產生輸出電壓彈跳的現象，這種現象我們稱之為“限制性 循環(Limit Cycling)＂，圖14可解釋此現象的形成[9] 。 由於Duty Ratio 可以調整直流轉直流轉換器的輸出電壓，因此數位 脈波寬度調變器的解析度就格外顯得重要。假如數位脈波寬度調變器的解 析度不夠高時，直流轉直流轉換器的輸出電壓便會振盪。這是因為數位脈 波寬度調變器所調整的輸出電壓增量值沒有落在相對應於前端A/D 轉換 器參考電壓（Vref）的輸出電壓改變量（∆ Vo）的範圍內，因此就會造成

輸 出 電 壓 值 的 振 盪 。 解 決 的 方 式 就 是 對 應 於d[n]值最小位元（Least significant bit, LSB）的Vo 增量值必須小於∆Vo，即resolution（DPWM）> resolution（A/D）。 DPWM必須具有比ADC更高的精確度，否則ADC輸出的1-LSB變化 就可能導致DPWM使輸出電壓變化大於1-LSB。其結果是，輸出電壓穩 定地在兩個數值之間轉換，這個狀態被稱之為“限制性循環＂。 圖 14 Limit Cycling [9]

2.6.2 數位脈波寬度調變器之架構

要提供DPWM更高的精度就意謂必須拉高脈波串列的速率，脈波速 率決定了在任一給定時間內能夠產生多少bit。 然而，DPWM脈波速率 限制了它對所有來自控制器的資料處理時間。Erickson [24]的例子介紹 +2 LSB +1 LSB -2 LSB -3 LSB -4 LSB -2LSB ADJUSTMENT -1LSB ADJUSTMENT ZERO ADJUSTMENT +1LSB ADJUSTMENT +2LSB ADJUSTMENT +3LSB ADJUSTMENT A/D Action

Avg DPWM output levels

-2LSB ADJUSTMENT -1LSB ADJUSTMENT ZERO ADJUSTMENT +1LSB ADJUSTMENT +2LSB ADJUSTMENT +3LSB ADJUSTMENT +2 LSB +1 LSB -1 LSB Vout Vout Lower DPWM Reolution Higher DPWM Reolution 3..300V 3..300V Vout -5 LSB

了一個假設的具有1MHz開關速率和10位元ADC的DPWM。其調變器要 求超過1GHz的脈波速率。 如此的高速度是不切實際的，因此數位控制器的設計者必須找到另 一種替代解決方案。 其中著名方案是引入一些DPWM dither。穩壓器輸 出濾波器對輸入的任一脈波串列進行平均，這使對每一個輸出脈波的寬 度進行相當於1-LSB的調整成為可能。 Dither可將脈波串列的平均值增加或降低了1-LSB精度的1/m倍，如 果在控制器輸入端的1-LSB使輸出脈波串列平均變化10mV，這將使每四 脈波縮短相應於10mV的時間，那麼通過濾波器的平均輸出電壓將降低 10mV/4也就是2.5mV。 一個高解析度、高頻率的數位脈波寬度調變器的架構可以由快速計 數器和數位比較器所建構成。假設要設計一個8-bit 且操作在fs 切換頻率 的數位脈波寬度調變器時，我們所需要的計時頻率為2n fs。例如，要完成 一個8-bit 且操作頻率為1 MHz 的數位脈波寬度調變器時，就需要64 MHz 的計數頻率。本論文我們使用四相位(Four-Phase)方式，每相位的開關週 期需要fs =250KHz。四相位(Four-Phase) 數位脈波寬度調變器輸出端的架 構，如圖15所示。

圖 15 Four-Phase 電路結構圖[8] 在四相位(Four-Phase)電路中，DPWM Controller的輸出方式輸出的 波形訊號大致如圖16所示，波形工作週期寬度為15%，每個波形間隔為1/4 週期。 圖 16 Four-Phase DPWM輸出波形圖示意圖[8] V in L 1 L 2 L 3 L 4 C RL D P W M V o C o n tro l L a w P ID A D C D ig it a l c o n t r o lle r

2.7 低壓差架構

圖17 說明了 LDO 低壓差之穩壓架構，包含一個參考電壓(Reference

Voltage) 以 及 起 動 電 路 (Start-Up Circuit) 、 一 個 傳 輸 電 晶 體 (Pass Transistor) 、一個誤差放大器(Error Amplifier) 、一個回授網路(Feedback Network)和一些限制溫度，電流及防電池逆向的保護電路(Protection Circuit) [13]。 S t a r t - u p C i r c u i t R e f e r e n c e V o l t a g e E r r o r A m p . P a s s T r a n s i s t o r C u r r e n t S e n s e E l e m e n t F e e d b a c k N e t w o r k P r o t e c t i o n C i r c u i t s V o u t V i n V f b V r e f V i n 圖 17 基本的LDO 低壓差穩壓架構 [12] 整個 LDO 低壓差之穩壓器可看成一個串聯輸入，並聯輸出負回授 系統，輸出電壓經負回授系統的調節下，可以保持在一個穩定的電位。理 想上，參考電壓(Reference Voltage)是一個不被溫度及輸入電源影響電壓 源(Vref)，提供給誤差放大器當作參考。當負載電流突然變大時，輸出電 壓會瞬間下降，經由回授網路產生回授電壓(Vfb) ，再由誤差放大器(Error Amplifier)根據參考電壓來比較，進而控制傳輸電晶體(Pass Transistor)供 給更多的電流給負載， 而當負載電流突然變小時，則反之。

LDO 的輸出電壓可由以下公式決定[17]: 1 2 1 F F O U T ref F

R

R

V

V

R

+

=

×

_{, (2-6)}

Vref是參考電壓(Reference Voltage) ，RF1及RF2是回授網路的分壓電阻，

為了確保LDO 在一定條件下工作，因此需要一些保護電路，而這些額外

的保護電路在正常工作下，並不會影響 LDO 低漣波穩壓作用的輸出電壓

第三章 數位控制設計與類比調整電路

3.1 數位控制器方法介紹

在一個PID 控制器中， ADC 輸入要執行一系列係數的演算法包含 比例係數、整數係數和誘導係數。 而比例係數是與靈敏度相關的增益因 數；整數係數按照錯誤出現的時間長短來調節 PWM 的寬度；誘導係數 補償迴路的時間延遲。綜合起來，PID 演算法的各個係數決定了系統的 頻率響應。 控制器隨後將ADC 的輸出電壓表示轉換成維持期望的輸出電壓所 需的脈衝持續時間(寬度)訊號。然後，該訊號被傳送至 PID，經過運算 後送至 DPWM，它行為模式與 PWM 模擬的驅動訊號產生功能一樣，但 以提高其輸出電壓精準度。

3.2 數位控制結合智慧控制的操作

以數位所設計的電路，理所當然的可以與外面的數位世界透過BUS 作指令溝通，資料交換以及偵測外界狀態的功能。如圖18 的架構透過 BUS 結合了一些重要資訊的提供，例如外界 MOSFET 的溫度，輸入電壓、輸 出電流或者更複雜的外界資訊給數位控制電源系統作為參考，如此可更有 效的運用數位控制電源。

圖 18 數位控制結合智慧控制示意圖 嚴格說起來，送至DPWM的資料流量並非直接從A/D轉換器提供，其 中還經過一個控制裁決補償處理器，也就是PID處理過後才送至DPWM。 此過程會將A/D轉換器的輸出加以修正，但並不會影響其原有的解析度。 輸出電壓經由A/D轉換器所形成二進制輸出經由式子(2-2) (2-3) (2-4) (2-5) 方程式轉換後再送至DPWM。

控 制PWM 脈 波 寬 度 的 控 制 者 稱 為 PID （ Proportional Integral Derivative）或「控制補償處理器」的系統，它是將數位化的輸出電壓轉 換成內含Duty Cycle控制的資訊給PWM作參考之用，更清楚解釋PID的工 作是調整脈波寬度以即時的方式將輸出電壓鎖定在預設的範圍之內，就如 同類比控制方式一樣，PID也必須去補償迴路增益及相位延遲去穩定整個 迴路控制。在數位系統內，還有其他的相位延遲因素，例如資料處理器的 計算延遲時間。所以在類比控制電源內影響到迴路增益與相位延遲的因素 MEMORY DPWM MCU PID PROCESSOR (Compensator) COMM I2C DIGITAL CONTROL IC FILTER POWER SWITCHING SCALE H USER Hardware ADC DC INPUT POWER DC OUTPUT POWER

（例如輸出電容及電感濾波器）也會在數位控制電源的設計上出現，只是 多了額外的資料處理器的計算時間以及A/D的傳輸延遲時間。

3.2.1 PID 數位穩定控制理論推導設計

首先我們必須將整體推導過程劃分成五個步驟和兩種情況推演。第

一種是情況是 Q-ON 並且 D-OFF 的狀態，另一種則是 Q-OFF 並且

D-ON 的狀態。我們將 DC 直流分析和 AC 交流分析放入兩種情況中，接

著我們做Laplace 轉換 S-Domain。最後我們在從 Z-Domain 轉換中去找到

轉移函數( ^ ^ Vo d )的最終數值[24]。以下描述產生轉移函數過程: Q D C

C

C L

L

L i i i

i

i

_i 2 y 1

u

v

_i i

v

o

v

o

v

o v

i

R R i R i c

v

c

v

c

v

c

i

c i c i c

r

c r c

r

L

r

L r L

r

L

i

L

i

L

i

i

_o o

i

o

i

d

i

d

i

d

i

2 u

R

R

R

1

x

2

x

y

1 +

+

+

+ +

+

− −

−

− −

v

i 圖 19 類比降壓DC電源轉移線性等效圖 [24]

步驟1.

先描繪出切換降壓轉換器的線性等效電路如圖19所示。 然後選擇電感電流

i

L 和電容電壓

v

C狀態的變量如下式。 1 2 L c x i x v

x

=

⎡

_⎣

⎤

_⎦

=

⎡

_⎣

⎤

_⎦

選出輸入直流電壓

v

i和輸出擾動電流

i

d 當成輸入變量後整理如下式。 1 2 i d v u u i

u

=

⎡

_⎣

⎤

_⎦

=

⎡

_⎣

⎤

_⎦

最後選出輸出直流電壓

v

d 和輸入電流

i

i 當成輸出變量如下式。 1 2 d i v y y i y = ⎡_⎣ ⎤_⎦ = ⎡_⎣ ⎤_⎦

步驟2.

寫出電流方程式對於每個等效電路的其中一種狀態變量的形式。 (1)狀態一（situation 1）: Q-ON 並且 D-OFF 狀態

C L i

i

v

_o R i c v c i c r L r i_L i_o i_d R + + − i

v

圖 20 Q-ON 並且 D-OFF 狀態圖 [24]

由圖20我們可以計算其中等效電路輸入電壓(v_i )。 i c L L L c c d v d i v L i r r c v d t d t = + + + (3-1) 從式(3-1)移項整理可得式(3-2) ( ) c c c L C d d v r c v i i i R d t + = − + ( c ) L d d v i c i R d t = − + c L d d v i R R c i R d t = − + ( ) c c L c d d v r R C i R v i R d t + = − + (3-2) 從式(3-2)得到一個對電容電壓的微分方程式如式(3-3)。 ( ) ( ) ( ) c L c d c c c d v i R v i R d t = r + R C − r + R C + r + R C (3-3) 因此等效輸入電流(ii)等同於通過電感(iL)電流，即ii = iL 。 從圖20中 我們分析輸出電壓節點網路得到下面方程式。 ( ) o L c d v = i − +i i R = i _L R − i_c R + i_d R { } ( ) ( ) ( ) c d L L d c c c v i R i R i R R C i R r R C r R C r R C = − − + + + + + L c c c d c c c i R r R v R r i r R r R r R = + + + + + 我們得到等效輸出電壓如式(3-4) L c c c d o c c c i R r R v R r i v r R r R r R = + + + + + (3-4) 利用式(3-4)在Q-OFF 並且 D-ON 狀態下做矩陣轉換，寫出的矩陣方程式 如下：

1 1 1 1 1 1 1 1 0 c c L c c c i L L c c d c c c i v R r R R r r L R r L R r L R r i v v _{R R} i C R r C R r C R r L ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ − + − − + + + − + + + −

⎡

⎤

⎡

⎤

⎢

⎥

⎢

_{⎥ ⎡ ⎤}

⎡ ⎤

⎡ ⎤

⎣ ⎦

_⎢

_⎥

⎣ ⎦

_⎢

_⎥

⎣ ⎦

⎣

⎦

⎣

⎦

=

+

0 1 0 0 0 c c o c c L c i i c d R r R R r v R r R r i R r v i v i + + +

⎡

⎤

⎡

⎤

⎡ ⎤

=

⎢

⎥

⎡ ⎤

+

⎢

⎥

⎡ ⎤

⎣ ⎦

_⎢

_⎥

⎣ ⎦

_⎢

_⎥

⎣ ⎦

⎣

⎦

⎣

⎦

(2) 狀態二（situation 2）: Q-OFF並且 D-ON 狀態

C L i

v

o v R i c

v

c i c r L r iL o i

i

d R

+

+ − − i

i

圖 21 Q-OFF並且 D-OＮ 狀態圖 [24] 由圖21，分析輸出電容和電感節點網路 ( ) ( ) c c c c L c d L d c L d d v d v r C v i i i R i C i R d t d t d v R i R C i R d t + = − + = − + = − + (3-5) 對式(3-5)進行移項整理，可以得到式(3-6)。 0 L c L L c c d v d i L i r r C v d t d t = + + + (3-6)

再對式(3-6)進行移項整理得到下式: ( ) ( ) ( ) ( ) c c L c d c L c d c c c d v R r C i R v i R d t d v i R v i R d t R r C R r C R r C + = − + = − + + + + (3-7) 由 式(3-7) 得 到 電 感 電 流 的 微 分 表 示 式 。 分 別 對 (3-1) 及 (3-5) 式 子 以 ( ) ( ) ( ) c d L c c c v i R i R R + r C − R + r C + R +r C 項置換 c d v C d t 項 我們可以獲得 0 ( ) ( ) ( ) c d L L L L c c c c c v i R d i i R L i r r v d t R r R r R r ⎛ ⎞ = + + _⎜ − + _⎟ + + + + ⎝ ⎠ 從上面公式中再做移項得到下式： ( ) ( ) ( ) c d L L L L c c c c c v i R d i i R L i r r v d t R r R r R r ⎛ ⎞ = − − _⎜ − + _⎟ − + + + ⎝ ⎠ c c L L c i d c c c R r R R r r i v i R r R r R r ⎛ ⎞ ⎛ ⎞ = − _⎜ + _⎟ − _{⎜ ⎟} − + + + ⎝ ⎠ ⎝ ⎠ 從上式電感電流中得到微分表示式如下： 1 _c 1 1 _c L L L C i d c c c R r R r d i R r i v i d t L R r L R r L R r ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = − _⎜ + _⎟ − _{⎜ ⎟} − _{⎜ ⎟} + + + ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ 由圖21 我們知道其中等效輸入電流 (ii)為零，即ii = 0 。再以相同方式 去分析圖21 輸出電壓節點網路。 ( ) o L c d v = i − i + i R = i R_L − i R_c + i R_d ( ) ( ) ( ) c d L L d c c c v i R i R i R R C i R C R r C R r C R r ⎛ ⎞ = − _⎜ − + _⎟ + + + + ⎝ ⎠ ( ) ( ) ( ) c c L c d c c c R r R R r i v i R r R r R r = + + + + + 得到其中等效輸出電壓如下: ( ) ( ) ( ) c c o L c d c c c R r R R r v i v i R r R r R r = + + + + + 因此我們將從上式結果做矩陣轉換得到如下式子。

Q-ON 並且 D-OFF 矩陣狀態方程式如下: 1 1 1 0 0 1 1 1 1 c c L c c c i L L c c d c c c R r R R r r L R r L R r L R r v i i v _R v _R i C R r C R r C R r ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ − _⎜ + _⎟− _{⎜ ⎟} − _{⎜ ⎟} + + + ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ − ⎜ ₊ ⎟ ⎜ ₊ ⎟ ⎜ ₊ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠

⎡

⎤

⎡

⎤

⎢

⎥

⎢

⎥

⎡ ⎤

=

⎡ ⎤

+

⎡ ⎤

⎣ ⎦

_⎢

_⎥

⎣ ⎦

_⎢

_⎥

⎣ ⎦

⎣

⎦

⎣

⎦

0 0 0 0 0 c c o c c L c i i c d R r R R r v R r R r i R r v i v i + + +

⎡

⎤

⎡

⎤

⎡ ⎤

=

⎢

⎥

⎡ ⎤

+

⎢

⎥

⎡ ⎤

⎣ ⎦

_⎢

_⎥

⎣ ⎦

_⎢

_⎥

⎣ ⎦

⎣

⎦

⎣

⎦

步驟3

. 由使用Duty Ratio當成為額外因子去平均每一個狀態並且將上面兩式結合 成單一式。 Q: 1 1 1 1 x A x B u y C x E u = + = + * d 1 + D: 2 2 2 2 x A x B u y C x E u = + = + * d 2 使用Duty Ratio額外因子去平均每一個狀態得到下式。 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 ( ) ( ) ( ) ( ) x A d A d x B d B d u y C d C d x E d E d u = + + + = + + + (3-8)

步驟4.

擾動(3-8)上式的平均方程式子去產生直流DC和小訊號項並且排除掉產生 非線性項替代成下式。 x = X + xˆ : y = Y + yˆ : u = U + uˆ 1 1 ˆ d = D + d : d₂ = D₂ + dˆ 接著做平均方程式(從步驟3中) 。 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 ( ) ( ) ( ) ( ) x A d A d x B d B d u y C d C d x E d E d u = + + + = + + +

由(3-8)中我們從x = X + xˆ 得到一個微分表示式。 1 1 ˆ 2 2 ˆ 1 1 ˆ 2 2 ˆ ˆ ˆ ˆ ( ) ( ( ) ( ))( ) ( ( ) ( ))( ) d X x A D d A D d X x B D d B D d U u d t + = + + − + + + + − + 1 1 1 1 1 1 2 2 2 2 2 2 2 1 1 1 1 1 1 2 2 2 2 2 2 ˆ _ˆ ˆ_ˆ ˆ ˆ _ˆ ˆ_ˆ ˆ _ˆ ˆ_ˆ ˆ _ˆ ˆ_ˆ A D X A dX A D x A dx A D X A dX A dX A D x A dx B D U B dU B D u B du B D U B dU B D u B du = + + + + − + + − + + + + + − + − (3-9) 擾動狀態方程式由上面(3-9)結果得到下面式子。 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 2 1 2 1 2 1 2 ˆ ˆ ˆ ( ) ( ) ( ) ( ) ( ) ˆ ˆ_ˆ ˆ_ˆ [( ) ( ) ] ( ) ( ) d X x A D A D X B D B D U A D A D x B D B D u d t A A X B B U d A A d x B B d u + = + + + + + + + + − + − + − + − 1 1 ˆ 2 2 ˆ 1 1 ˆ 2 2 ˆ ˆ ( ( ) ( ))( ˆ) ( ( ) ( )( ˆ) Y + y = C D + d + C D − d X + x + E D + d + E D − d U + u 1 1 2 2 1 1 2 2 1 1 2 2 1 2 1 2 1 1 2 2 1 2 1 2 ˆ ( ) ( ) ( ) ˆ _{ˆ ˆ} ˆ ˆ_ˆ [ ( ) ( ) ] ( ) ( ) ( ) C D C D X E D E D U C D C D x C C X E E U d E D E D u C C x d E E d u = + + + + + + − + − + + + − + − 直流分析: 使用上面擾動狀態方程式結果。設定所有變數項為零，我們可以得到下式 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 0 ( ) ( ) ( ) ( ) A D A D X B D B D U A X B U Y C D C D X E D E D U C X E D = + + + = + = + + + = + 因此 1 1 ( ) X A B U Y C A B E U − − = − = − + 排除掉直流項次，讓 d x 0 d t = 0 AX +BU = 並且 Y =CX +EU 我們可以得到D.C.模式方程式: D.C. 分析 0 [ _L ( _c) ] _{L c i} c R r R r I V V D R r ⎛ ⎞ = − + − _{⎜ ⎟} + + ⎝ ⎠ 1 0 _{L c} c c R I V R r R r ⎛ ⎞ ⎛ ⎞ =_{⎜ ⎟} −_{⎜ ⎟} + + ⎝ ⎠ ⎝ ⎠

( ) 0 c L c c R V R r I V R r ⎛ ⎞ = _{− ⎜ ⎟} + ⎝ ⎠ s L I =DI

1. 電路學(Fundamentals of Electric Circuits)作者Matthew N.O.Sadika在其

著作中線性電路章節中的分析提到DC 模式給了 DC 固定的穩定狀態 (Steady-State Behavior)要忽略掉非線性產生項次 dˆ ⋅ xˆ 和

d u

ˆ ˆ

⋅

。 我們可以得到AC 模式的小訊號(Small-Signal) 方程式: ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ d x A x B u F d d t y C x E u G d = + + = + + 接著得到 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 2 1 2 1 2 1 2 ( ) ( ) ( ) ( ) A A D A D B B D B D C C D C D E E D E D F A A X B B U G C C X E E U = + = + = + = + = − + − = − + − A. C. 分析 對電感電流和電容電壓微分，分別得到輸出電壓和輸入電流。 1 _ˆ ˆ _{ˆ ˆ} 1 _ˆ 1 1 _ˆ ˆ ˆ ˆ ˆ ( ) ˆ L c i L L C i c c L c c c o c L c s L L c r R r V d i R D i v v d d t L L R r L L d v R i v d t c R r L R r R v R r i v i D i I d R r ⎛ ⎞ + ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = − _{⎜ ⎟} + _{⎜ ⎟} + _{⎜ ⎟} + _{⎜ ⎟} + ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ = − _{⎜ ⎟} − _{⎜ ⎟} + + ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ = + _{⎜ ⎟} = + + ⎝ ⎠ ， AC 模式給的小訊號的資訊是由直流工作點得到。

步驟5.

轉換交流（AC）State-Space模式在頻域中（Frequency Domain）用Laplace Transforms 轉換成 S-Domain。

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ d x A x B u F d d t y C x E u G d = + + = + + 在此之後, ˆx ˆy ˆu ˆd 變數將因簡易化被忽略不看。小訊號的變數將被表 示使用以小寫方式(ac項) 。PWM DC-DC轉換器動態方程式被轉換如下： d x A x B u F d d t y C x E u G d = + + = + + 開始做 Laplace 轉換: 1 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) u d u d s x s A x s B u s F d s y s C x s E u s G d s x s s I A B u s s I A F d s H s u s H s d s H s s I A B H s s I A F d s − − − − = + + = + + = − + − = + = − = − 1 1 1 2 2 1 2 2 1 1 1 1 ( ) ( ) 1 ( ) ( ) ( ) [ ( ) ] [ ( ) ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) u u u u u d u d G s G s u G s G s y s C s I A B E C s I A F G d s G s u s G s d s G s C s I A B E G s C s I A F G G s C s I A B E − − − − − = − + + − + = + = − + = − + ⎡ ⎤ = − + _{= ⎣ ⎦} 將上面係數代換進入圖22，我們得到轉移方程矩陣。 11 12 21 22 ( ) ( ) ₁ ( ) ( ) 2

( )

( )

o u u i i u u d v G s G s v _d i G s G s i d

G

s

G

s

⎡

⎤

⎡ ⎤ ⎡

=

⎤ ⎡ ⎤

_{+ ⎢}

_⎥

⎣ ⎦ ⎣

⎦ ⎣ ⎦

_⎣

_⎦

圖 22 轉移方程矩陣的說明圖 [24]

Control to input current gain Load to line current gain

Input Admittance Input to output voltage gain

Output impedance Control to output Voltage gain

從圖22中的轉移矩陣所得到的結果，我們再將其中所得參數代入圖23做補 償運算。

圖 23 補償迴圈圖 [24]

由表1，我們可以明白基本對於時域( Time Domain)及頻域( Frequency

Domain)轉移關係。然後做

D

uty的三個變數加總形成了頻域上的PID。 Results

ˆ

i

i

ˆ

_o

v

ˆ

ˆ

ˆ

::

_ˆ

::

_ˆ

ˆ

i i i i o

i

i

i

v

i

d

ˆ

ˆ

ˆ

::

_ˆ

::

_ˆ

ˆ

o o o i o

v

v

v

v

i

d

Disturbances

ˆ

o

i

ˆ

_i

v

Loop compensator A(s)

v

ˆ

o

KPWM Control action

ˆ

d

表 1 PID 控制函數在時域和頻域的比較表[24]

Time Domain

Frequency Domain

Proportional Control

Integral Control

Derivative Control

由表2 中， 知道轉移函數 ( ^ ^ V o d )可以被推廣使用於 Z-Domain。 表 2 轉移函數表 [24]

Transfer Function

Transfer Function

1 2 ˆ ( ) 1 ˆ ( )o i c D o v s r C s F v s d s w + = = ∆ 2 2 ˆ ( ) 1 ˆ ( ) i L L D L o V i s r C s F s r d s w + = _∆ = 1 1 2 ˆ ( ) 1 ˆ ( ) o c U i o v s r C s F D s v s w + = _∆ = 2 1 2 ˆ ( ) 1 ˆ ( ) U L i o F i s D R C s s v s R w + = _∆ = 2 12 1 1 1 2 1 ( ) ˆ ( ) ˆ ( )o eq U d o s S v s w Q w F R s i s w + + = _∆ = 2 2 2 ˆ _{( ) 1} ˆ ( )_dL C U o r C s F i s s i s w + = − _∆ = 在從以下的降壓轉換器的基本類比公式使用在轉移函數其中。 ( ) ( ) u t = K e t 0 ( ) t ( ) I K u t e d T

η η

=

∫

( ) _D ( ) u t = K T e t&

K

I K T s D

K T s

( ) 1 ( ) 1 ( ) D I u s D s K T s e s T s ⎛ ⎞ = = _⎜ + + _⎟ ⎝ ⎠

2 o 2 o w s s s w Q = + + ：ｓ-domain 二階公式 e q L R = r ：等效電阻＝電感上電阻 1 1 ( ) o L c Q L w _{r r C} R = + + ：品質因子 1 1 1 1 L c Q L w _{r C} r = + ：第一品質因子 1 o w L C = ：諧振頻率 1 1 L c r w r L C = ：第一諧振頻率 ˆ ˆ 0 , 0 ˆ ( ) ˆ o o v i d i v G s v = = = ：由輸入到輸出的開迴路增益 ˆ ( ) ˆ c o v A s v = ：補償器增益 1 p w m p K V = ：PWM 直流增益 ˆ ˆ p w m c d k v = ：PWM 調變器增益 ˆ ˆ 0 , 0 ˆ ˆ i o p v d o v Z i = = = ：開迴路輸出阻抗 ˆ ˆ 0 , 0 ˆ ˆ i o o d v i v G d = = = ：控制輸出轉移函數 在最多情況下，因為 R>>

(

r r

L

+

c

)

，上面公式方程式會被逼近近似到 只使用如下的值： 1 o w L C = 2 o 2 o w s s s w Q = + + 1 1 ( ) o L c Q L w _{r r C} R = + + 2 ˆ ( ) 1 ˆ ( ) o c i o v s r C s v s d s w + = _∆ 2 ˆ ( ) 1 ˆ ( ) _{1 ( )} o c i c L v s s r C D L v s s r r C s L C R + = ⎛ ⎞ + _⎜ + + _⎟ + ⎝ ⎠

2 ˆ ( ) 1 ˆ ( )o i _{1 (} c ₎ c L v s s r C V L d s _{s r r C s L C} R + = ⎛ ⎞ + _⎜ + + _⎟ + ⎝ ⎠ (3-10) 由下面的表3中，轉移係數方法表中從S-Domain 到 Z-Domain區塊 中，是由高等工程數學的離散方程中個別數種最常用的轉移係數方法，選 取最合適簡易的轉移逼近近似值來做係數轉換工作。 表 3 轉移係數方法表

Transformation Methods S-Domain Z-Domain

Backward Euler

_S

₁

1 s

Z

T

−

−

Bilinear

S

1 1 2 1 1 s Z T Z − − + − Step Invariant G_C ( )S ₁ ( ( ) s ) T s C e Z G S S − − Pole/Zero Match S a S a j b + + ± 1 1 2 1 1 2 cos dTs dTs dTs Z e Z e bTs Z e − − − − − − − − + 經由 (3-10)式我們使用表3中Backward Euler法去逼近近似獲得z-domain 轉移方程式。 2 ^ ^ 2 2 ( ) ( ) ( 2 ) ( 1 ) T s V g V o _{L C} G v d Z T s T s T s d Z Z R C L C R C = = − − + + − (3-11) 當諧振電容 （XC）=諧振電感（XL）去計算出諧振頻率

2 2 1 1 2 1 2 2 1 ( 2 ) X L L fL X C C fC X L X C fL fC C f L ω π ω π π π π = = = = = = > = = > = 目標值定為 L=100µH，C=4µF 依據電力電子對降壓電路的經驗法則得知目標設定電容與諧振電容 有 10 倍大小差距，故求出諧振電容 C=40µF 再經由圖 24 整體系統的回 授網路架構。 圖 24 系統回授網路架構[5] 2 ^ ^ 2 2 ( ) ( ) ( 2 ) (1 ) T s V g V o _{L C} G v d Z T s T s T s d _{Z Z} R C L C R C = = − − + + − (3-12) 接著我們整合整體回授網路，得到轉移函數 (3-13)： +

Control to output transfer function of the CCM buck converter Vref

DPWM gain

10-bit to 8-bit

conversion PID compensator

Delay A/D gain 1 4 1_z 1 Vq Vo + -1 1 0 2 3 2 2 2 ( ) (2 ) (1 ) Ts Vg LC Ts Ts Ts Z Z RC LC RC − − + + − K

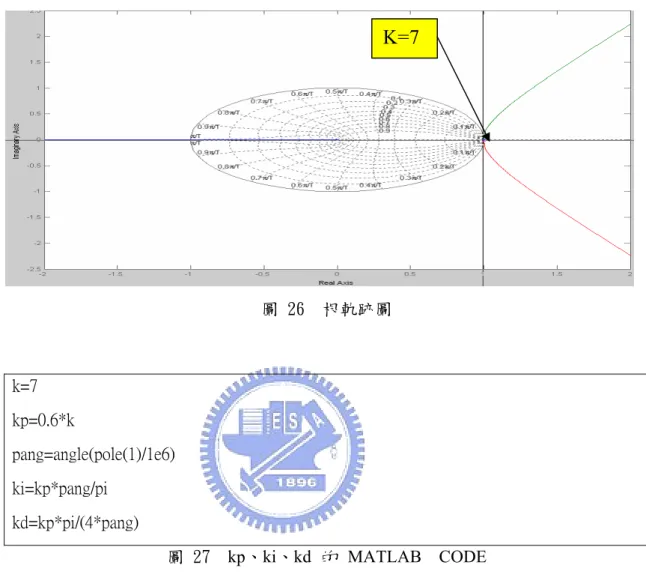
2 2 2 ( ) 1 1 1 1 ( ) 4 1023 _{(2 ) (1 )} T s V g L C T Z K T s T s T s V q Z Z Z R C L C R C = ⋅ ⋅ ⋅ ⋅ ⋅ − − + + − (3-13) 以電感和電容數值代入 (3-12)，獲得下列轉移函數: 2 ^ ^ 2 2 2 2 2 2 ( ) ( ) (2 ) (1 ) (1 ) ( ) 1 2 1 0 0 4 0 1 (1 ) 1 (2 ) (1 ) 3 .3 4 0 1 0 0 4 0 3 .3 4 0 0 .0 0 3 1 .9 9 2 4 2 0 .9 9 2 6 7 T s V g V o _{L C} G v d Z T s T s T s d _{Z Z} R C L C R C V H F Z Z F H F F Z Z µ µ µ µ µ µ µ µ µ µ = = − − + + − ⋅ ⋅ = − − + + − Ω ⋅ ⋅ Ω ⋅ = − ⋅ + 把上面方程式計算所得函數代入(3-13)式， 就整體系統轉移函數而 言，可以獲得下列結果: 2 3 3 2 1 1 1 1 ( ) ( ) 4 1023 1 1 0.003 1 1 4 1023 1.99242 0.99267 19.5 12.5322 10 1.99242 0.99267 T Z K Gvd Z Vq Z K Z Z mV Z K Z Z Z − = ⋅ ⋅ ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ ⋅ − ⋅ + ⋅ = ⋅ − ⋅ + ⋅ 將上面方程式最後的係數代入 MATLAB 中計算。執行以下命令，則出 現圖26的圖形，我們點選橢圓點與拋物線交點，接著可以求出K值和第1 極點。 a=[12.5322e-3] b=[1 -1.99242 0.99267 0] g=tf(a,b,-1) rlocus(g) [k,pole]=rlocfind(g) 圖 25 根軌跡的MATLAB CODE

圖 26 根軌跡圖 k=7 kp=0.6*k pang=angle(pole(1)/1e6) ki=kp*pang/pi kd=kp*pi/(4*pang)

圖 27 kp、ki、kd 的 MATLAB CODE

從圖26獲得K值後，再執行圖27 MATLAB 程式，計算最後得到所

需的kp=4.2、ki=0.02、kd=209。

3.3 LDO 附屬調整電路

在附屬電路 LDO 的架構之中，必須對 LDO 更多瞭解，包含:低壓

降(Dropout Voltage)，靜態電流或接地電流(Quiescent Current or Ground K=7