Performance Analysis of Noncoherent Digital
Delay Locked Loops for Direct Sequence
Spread Spectrum Systems With Doppler
Shift and Quantized Adaptation
Wern-Ho Sheen, Ming-Jou Chang, and Cheng-Shong Wu
Abstract—The noncoherent second-order digital delay locked loop (DLL) with the presence of Doppler shift is investigated. The loop performance such as lock-in range, transient response, mean time-to-lose lock (MTLL), and mean square tracking error (MSE) are analyzed. The analysis is unique in two respects. First, MTLL and MSE are evaluated more accurately than by previous methods. Second, the impact of quantized adaptation on the loop performance is examined for digital DLL that was neglected pre-viously. Numerical results show that: 1) the quantized adaptation may significantly alter the loop behaviors, including the lock-in range, transient responses, MTLL, and MSE; and 2) the tradi-tional analysis based on Gaussian approximation may result in a large error in performance evaluation when quantized adaptation is taken into account.
Index Terms—Direct sequence spread spectrum, doppler shift, noncoherent digital delay locked loops (DLLs), quantized adap-taion.
I. INTRODUCTION
P
SEUDONOISE (PN) code synchronization is essential for direct-sequence spread spectrum (DSSS) systems to work effectively. PN code synchronization is achieved in two steps—code acquisition followed by code tracking [1], [2]. Code acquisition is a coarse alignment that aligns the received and local PN codes to a range that is suitable for code tracking. Code tracking, on the other hand, attempts to maintain fine synchronism of the two codes at all times. For global posi-tioning systems (GPS’s) and/or other broadcast applications, PN code synchronization follows a procedure of combined tracking/reacquisition/tracking, etc., after an initial acquisition. Both code acquisition and tracking have been active areas of research [1]–[18]. In this paper, we are only concerned with the code tracking part.Manuscript received July 3, 2002; revised June 25, 2003; accepted September 19, 2003. The editor coordinating the review of this paper and approving it for publication is M. Sawahashi.
W.-H. Sheen is with the Department of Communication Engineering, National Chiao Tung University, Hsinchu 300, Taiwan, R.O.C. (e-mail: whsheen@cm.nctu.edu.tw).
M.-J. Chang is with the Computer and Communications Research Laborato-ries, ITRI, Hsinchu 310, Taiwan, R.O.C. (e-mail: mjchang@itri.org.tw).
C.-S. Wu is with the Department of Electrical Engineering, National Chung Cheng University, Chia Yi 621, Taiwan, R.O.C.
Digital Object Identifier 10.1109/TWC.2004.837662
Code tracking is mostly achieved with a delay locked loop (DLL). Extensive research has been devoted to the design, analysis, and implementation of DLLs. For example, different types of multipath resistant DLLs were proposed in [3]–[6] for the multipath environment, effective DLLs were proposed for GPS code tracking in [7]–[9], and efficient implementation was discussed in [10] for different types of DLLs. As to the performance analysis, the first-order analog DLL was analyzed thoroughly in [11], [12] for the additive white Gaussian noise (AWGN) channel. Specifically, in [12], mean square error (MSE) and mean time-to-lose lock (MTLL) are obtained by applying the renewal theory approach. This approach was extended in [13] to include the effects of multipath fading and multiuser access interference. The second-order analog DLL was analyzed in [16], where approximate MSE and MTLL were obtained for high signal-to-noise ratios (SNRs), under the presence of Doppler shift. On the other hand, digital DLLs were analyzed in [14]–[17]. In particular, in [14], MSE and MTLL of the first-order loop were evaluated for a band-limited system, and in [15] emphasis was on the effect of carrier frequency uncertainty on the MSE performance. In [17], MSE of the first- and second-order loops were obtained particularly for the GPS applications, and finally in [18], MSE is obtained for a low-complexity DLL with 1-b noncommensurate sampling. Digital code tracking becomes very popular because of the evolution toward all digital modem implementation of DSSS systems.
In this paper, accurate nonlinear analysis for the noncoherent second-order digital code tracking loops is investigated over AWGN channels with the presence of Doppler shift. This modeling of channel finds applications in GPS [17] and other civilian or military satellite-based DSSS systems, where Doppler shift is due to the relative movement between the satellite and the receiver. In the analysis, based on a regenerative Markov chain modeling of the code tracking process, the lock-in range, transient response, MSE, and MTLL are evaluated more accurately than the traditional analysis. Furthermore, in a digital DLL, the adaptation of code tracking can only be done in discrete steps, i.e., quantized adaptation and that will result in significant changes in the loop performance. In this analysis, the effect of quantized adaptation is evaluated as well.
The rest of this paper is organized as follows. Section II describes the noncoherent second-order digital DLL. In
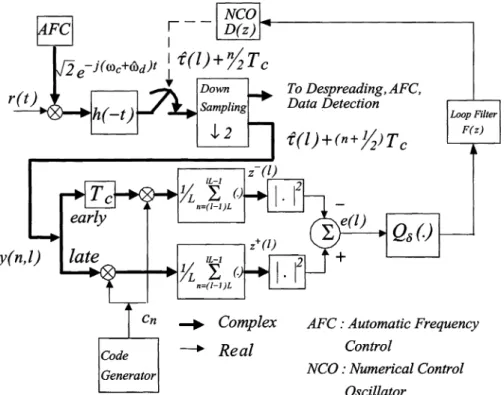
Fig. 1. Noncoherent digital DLL.
tion III, an accurate nonlinear analyzes is given to obtain the lock-in range, transient response, MSE, and MTLL, with em-phasis on the effects of code Doppler and quantized adaptation. In Section IV, some numerical results are given and discussed. Finally, conclusions are given in Section V.
II. NONCOHERENTDLL
A typical digital code tracking system for DS spread spec-trum signals is shown in Fig. 1. After frequency translation, chip matched filtering, and down sampling, the code phase of the received signal is tracked by a noncoherent digital DLL. In Fig. 1, is the estimated carrier shift obtained in the code ac-quisition stage. The sampling could also be done in front of chip matched filter. In any case, at least two times of over-sampling is needed for proper operation of DLL. In this study, the two-times over-sampling is employed. After down-sampling, as shown in Fig. 1, the sampled signal is directed to two different routes. The integer–chip samples are directed to a despreading unit for the subsequent carrier recovery, data detection and other signal pro-cessing, and the half-chip samples (early and late samples) are directed to a digital DLL for fine code tracking.
The correlation in the early or late branches of the digital DLL can be of passive types (moving average) or active (integrate and dump). For passive correlation, the code phase estimate is adjusted once per chip time and, hence, the digital DLL can track times code Doppler than by using active correlation, where the code phase estimate is adjusted once per . is the number of chips involved in the correlation. Nevertheless, passive correlation has a complexity of times larger than that of active correlation. Since there is no difference between these two types of correlations from the performance analysis point of view, only active correlation will be considered in this paper.
Let the received signal be denoted as . Then, for an AWGN channel with the presence of Doppler shift, we have
(1) where is the chip energy, is the spreading sequence, and
is a shaping function with
(2)
where and are the time-varying code-phase shift and carrier-frequency shift due to Doppler effect, respectively. In addition, is the initial phase uncertainty, and is AWGN with two-sided power spectral density watts/hertz. In this paper, instead of considering a specific system, we do the anal-ysis over an AWGN channel with the presence of Doppler shift. As mentioned, the channel model finds application in GPS and other satellite-based DSSS systems.
Without considering the acceleration which is small in practice, the time-varying code-phase shift is obtained as , where is the time-varying distance between the satellite and receiver, is the initial delay at , and and are the speed of the satellite and light,
respectively. Define , . In practice,
10 and is called as the normalized code Doppler factor [19].
Let and be the in- and quadrature-phase compo-nents at the matched filter output. Then
(3) and
(4)
where , denotes convolution, and and
are the baseband in- and quadrature-phase white Gaussian noise, respectively. After sampling at , it can be shown that for the case , the half-chip samples are give by
(5) and
(6) where is the code phase estimated at the instant of ,
is the chip index, , and
are independent Gaussian noises with variance equal to , and
(7)
is the auto-correlation function of the chip-matched filter. Furthermore, after correlation, the complex-valued early and late correlator outputs are defined as
(8) Writing and as the sum of their DC and noise terms, we have, for the case of
(9) and (10) where (11) (12) (13) (14)
and denotes the expectation operation. The first term in (13) and (14) is the code-self noise and can be neglected for a mod-erate to large , although it can also be incorporated in the anal-ysis as in [14], [17]. As a result, and are independently and identically distributed (i.i.d.) Gaussian vari-ables with zero mean and variance .
From Fig. 1, the error signal is given by
(15) Again, writing the error signal into the sum of DC and noise terms, (15) becomes
where
(17) is the actually the -curve of the loop, the useful term for tracking the code phase through the quantizer, loop filter, and numerical control oscillator (NCO). The total noise is defined as (18) where (19) and (20) Clearly, are non-Gaussian i.i.d. random variables, al-though they have been approximated as Gaussian in previous analysis [14]–[16].
For , the case of practical interest, then , , and hence, (11) and (12) become
(21) and
(22)
where , is the normalized tracking error at the instant of , and
(23) with
(24)
In (23), is the -curve of
the noncoherent DLL with no Doppler shift, and is the well-known SNR loss due to the carrier frequency discrepancy
.
As is mentioned, in digital DLLs, the adaptation of code tracking can only be done in discrete steps. In Fig. 1, the quan-tizer which quantizes the error signal is employed
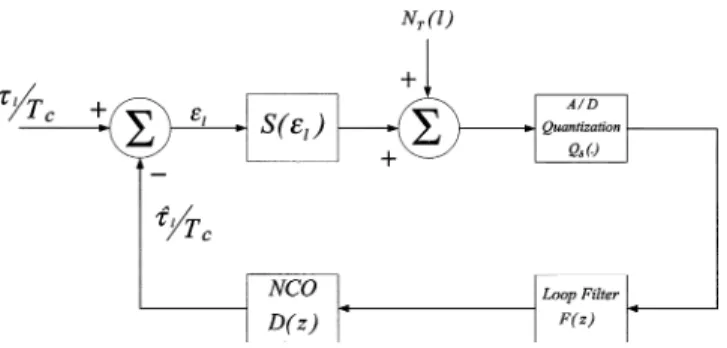
Fig. 2. Nonlinear baseband equivalent model for digital DLL.
to investigate this effect. The quantizer has the following input and output characteristics:
; ,
(25) where is the quantization limit, is the unit quantiza-tion level and is the total number of quantization levels. In addition, since we consider the second-order loop, , the transfer function of the loop filter, is given by
, where and are constants, and, as usual,
NCO is modeled as . If , the loop
becomes a first order. By using (15) and Fig. 1, the nonlinear model for the digital DLL is obtained as in Fig. 2.
III. PERFORMANCEANALYSIS
As discussed, for GPS and/or other satellite based broad-casting DSSS systems, PN code synchronization follows a pro-cedure of combined tracking/reacquisition/trackin, etc., after an initial acquisition. That is, during tracking whenever
, a new acquisition will be initiated and a new tracking follows. Hence, for a stationary channel as we considered here, the tracking process will restart itself after each code reacquisi-tion and, hence, can be modeled as a regenerative process [20]. In the following, the independent tracking process after each reacquisition will be named as an element process of the regen-erative process, and MTLL and MSE will be analyzed based on this regenerative process modeling of the tracking process.
Starting from Fig. 2 and following a procedure similar to that in [17], [21], it can be shown that for an element process of the regenerative tracking process
(26) and for (27) Define (28) and (29)
Then, from (27), we have
(30) with the initial conditions , , and determined by
(31) and
(32)
Furthermore, let and , the element
tracking process can be described by the following state equa-tions:
(33) and
(34) Since are stationary white noises, it is evident that (33) and (34) describe a homogeneous two-dimensional Markov chain.
Define , where is a positive integer, and let and be quantized to the values of and , respectively. Then, from (30)–(34), and, hence, and , will take on the values of multiples of , if is a rational number1and , , and in (31) and (32) are properly selected. Note that from (34), is the unit adaptation step of the loop and is a parameter relevant to the resolution of analysis. For example, from (29), the tracking error can only take the values of mul-tiple , if is a positive integer. ( has been known to give the best transient response for the case with no quantiza-tion [17], [21].)
A. Mean Time-to-Lose Lock
Define be the number of steps from the start of an (element) Markov chain to reach the absorbing state. The absorbing state
is the state with . By definition,
the MTLL of an element process is given by
(35) Since is the probability that the loop still remains in lock at the step, i.e.,
(36)
1This will practically place no restriction on the applicability of this method.
where and is the set of
pos-sible defined in (29), (35) can be rewritten as
(37)
where . Furthermore,
de-fine and
, then from (29), (33), and (34), we also have
(38)
In Appendix A, it is shown that for , , for some positive integer . In addition,
for some of the states in the set
, i.e., not all the states are legitimate states. (The legitimate states are actually the transient states of the (el-ement) Markov chain.) For simplicity of notation, however, the illegitimate states are also included in (38). The same practice will be employed in (39)–(45).
According to the homogeneous Markovian property, it can be shown that
(39)
where is the transition probability from the state
( , ) to the state ( ,
). Since , , if
. (39) can also be written in matrix form as follows: (40) and (41) where (42) (43) (44) and (45), located at the bottom of the page. Thus, the problem of finding MTLL reduces to solving the system of linear equa-tions in (41). Before to proceed further, three observaequa-tions are in order. First, the equations associated with in (41)
should be removed, i.e., ( , ) is an unal-lowed state. Second, is a sparse matrix and, after removing the rows and columns corresponding to the illegitimate states, is ac-tually the transition matrix for the transient states of the Markov chain. Third, the system of linear equations (41) might have a very large dimension, depending the numbers and . As an example, is a 2113 2113 matrix for the numerical exam-ples in Section IV. Hence, the direct solution methods such as Gaussian elimination or matrix factorization may be too com-plex to be used. On the other hand, however, since is a sparse matrix, iterative methods is expected to provide a solution more efficiently [22].
From (34), the transition probability is given by
(46) or equivalently,
for ,
for ,
and
for . Clearly, the transition probability can be evaluated if the cumulative probability density (CDF) or complementary CDF of the random variable is known. In Appendix B, the method of saddle point integration is employed to evaluate complementary CDF of . This evaluation is more accurate than the previous analysis, where
is assumed to be a Gaussian variable.
Let , (41) becomes
(47) where the equations associated with in (41) have been removed implicitly. In Appendix B, it is shown that is an -matrix and, hence, the iterative successive relaxation method (SOR) can be used to solve (47) in a way that is much more efficient than the direct solution method [22]. As in [22], let
(48) where is the diagonal matrix consisting of the main diagonal elements of , and and are the lower and upper block ma-trix triangular parts of , respectively. Then, the SOR iterative algorithm is given by
(49) where is the approximate solution at the stage , and is the algorithm parameter, called relaxation parameter that needs to be determined for the fastest convergent rate.
B. MSE
As discussed, the operation of code tracking can be modeled as a regenerative Markov chain. Hence, from Theorem 3.7.1 of [20], the stationary state probability at the state (of the regenerative Markov chain) is given by (50),2located at bottom of the following page. In (50), can be evaluated by using (29), after is solved in (47). Hence, the MSE can be evaluated easily as follows:
(51)
IV. NUMERICALRESULTS
For the numerical results that follow, the following set of system parameters are employed: , ,
, , and , and ,
otherwise. Here, means that the analysis resolution is . Basically, the selection of and is a tradeoff between the tracking error due to noise and the ability to track the dynamics of the input code phase. Here, we are mainly con-cerned with the effect of discrete adaptation, and hence the fixed values of and are used throughout.
Two extreme cases will be employed to examine the effects of discrete adaptation on the loop behaviors, including the transient response, lock-in range, MSE and MTLL. The first (Case I) is to fix the quantization limit to , the maximum value of -curve, and (hence, ) is varied to see the effects. Recall that , and is the unit adaptation step. The other (Case II) is to fix equal to 1/64, i.e., , and is then changed according to . In practice, however, the selection and is often a tradeoff between performance and complexity.
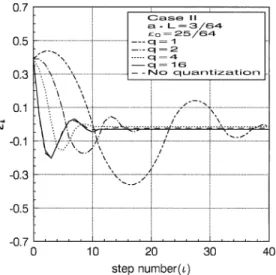
Figs. 3 and 4 show example effects of quantized adaptation on the transient response of the loop. For Case I, 16 behaves almost the same as the continuous adaptation (no quantization) case. However, a large tracking error is observed for 4 due to large quantization error. On the other hand, for Case II, the convergence of the loop is slowed significantly for 2 because of the limitation on the value of . That is the useful signal for error correction has been cut off. The tracking error is not much different for different after convergence, though. In Figs. 3 and 4, the residual tracking error for the case of no quantization is due to the distortion in -curve incurred by a large code Doppler shift [5].
2Note that for an element process,P ("(m)) = 0 8 m because eventually
the process will lose lock.
Fig. 3. Effects of quantized adaptation on the transient response.
Fig. 4. Effects of quantized adaptation on the transient response.
Figs. 5 and 6 are the loop lock-in ranges with different quan-tization levels. The lock-in rage is defined as the range of initial conditions such that the tracking error will never exceed during the subsequent tracking process, i.e., no reacquisi-tion. For case I, the lock-in range varies slightly for 2. (For , the lock-in range is very irregular because of very large quantization error.) For Case II, on the other hand, the lock-in range is significantly reduced for a small , again because of the incurred limitation on the value of . Note that the lock-in
Fig. 5. Effects of quantized adaptation on the lock-in range.
Fig. 6. Effects of quantized adaptation on the lock-in range.
range is odd-symmetric with respect to because of the very same property associated with the -curve [5].
Fig. 7 shows the effects of quantized adaptation on MSE and MTLL for case I. As is evident, for a large code Doppler, too small a will result in a significant performance loss; 4 is a necessity in this case. Fig. 8 shows the same effects for Case II. As seen, unlike Case I an optimal exists, depending on SNR; a large not necessarily gives a better performance. This is especially true at low SNRs, where the tail ends of impose a significant adverse effect on the loop performance.
Fig. 7. Effects of quantized adaptation on MSE and MTLL.
Fig. 8. Effects of quantized adaptation on MSE and MTLL.
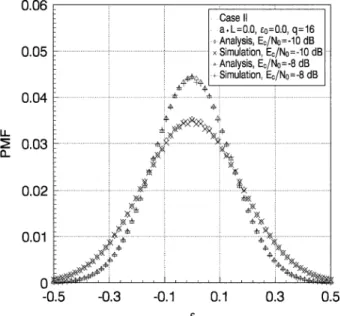
Fig. 9 compares the MSE and MTLL with those obtained by using Gaussian approximation for Case II. It is clear in the figure that the analysis based on the Gaussian approximation may result in a large error for a small . Nevertheless, it becomes more accurate for a large , as already discussed in previous analysis where quantization is not taken into account [14]–[16]. Fig. 9, simulation results are also given and that agree very well with the analysis. The simulations are Fig. 11 gives example probability mass functions. Again, the simulations agree very well with the analysis.
V. CONCLUSION
The noncoherent second-order digital delay lock loops for direct sequence spread spectrum systems is analyzed with the presence of Doppler shift. A new analysis based on a regenera-tive Markov chain modeling of the tracking process is proposed with the loop quantized adaptation being taken into account that has been neglected in previous analysis. For second order loops,
Fig. 9. Comparisons of MSE and MTLL with those obtained with Gaussian approximation.
Fig. 10. Example probability mass functions.
it is shown that the transition matrix of the transient states of the Markov chain is a sparse matrix with a very nice property, called -matrix, that leads to an efficient analysis. Numerical results show that quantized adaptation has a significant impact on the loop performance, including transient responses, lock-in range, MSE, and MTLL. In addition, without imposing a Gaussian ap-proximation in the analysis, MTLL and MSE are evaluated more accurately than previous methods.
APPENDIX A
In this Appendix, we discuss the range of and for the tracking loop to remain in lock. From (34), it can be shown that
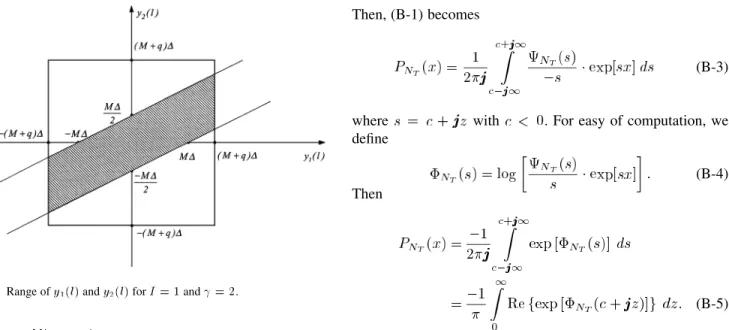
Fig. 11. Range ofy (l) and y (l) for I = 1 and = 2.
Since , we have
(A-2) where , is the largest integer less than , and for the tracking loop to remain in lock. On the other hand, since , we also have
(A-3) Finally, by definition
(A-4) and, hence, and has the same range. From (A-2)–(A-4), it is clear that ,
for some positive integer . As an example, Fig. 11 shows the range of and for the cases of and , where . In addition, from Fig. 11, we note that not all the states within the range of , are legitimate states, due to the constraint in (A-2)–(A-4), where for is one of such examples.
APPENDIX B
In this Appendix, the saddle-point integration is used for cal-culating the probability of
(B-1)
where is the probability density function (pdf) of . Recall that are i.i.d. random variables. Let
be the moment generating function of . That is
(B-2)
Then, (B-1) becomes
(B-3)
where with . For easy of computation, we define
(B-4) Then
(B-5)
In (B-5), we have used the property that
is an even function of [23]. The integration (B-5) would be most efficient if carried along the path of steepest descent of the integrand. For simplicity, however, the integration path is usually deformed to a straight line that passes through the saddle point of the integrand [23]. This method of integration is the so called saddle-point integration. The saddle point is the negative root of the equation
(B-6) where is the first derivative of . Since for , is a convex function, there is only one negative root in the (B-6) [23]. After obtaining the saddle point, then the in-tegration (B-5) can be evaluated by using the trapezoidal rule as follows [23].
(B-7) for a positive integer . The approximation (B-7) can be made as accurate as desired by using a large and a small enough and , respectively. As in [23], the step size can be initially taken as
(B-8) and then halved successively until the desired precision is ob-tained.
From (18)–(20), can be written as the following quadratic form:
(B-9) where
and with , ,
, and . Note that , and
(B-11)
From [24], the moment generating function for this quadratic form is given by
(B-12) With this , the probability (B-1) can be evaluated by using (B-7).
APPENDIX C
In this Appendix, we prove that in (47) is an -matrix, so that the successive over relaxation (SOR) iterative method is convergent and can be employed to solve (47) very efficiently. Before to proceed, the following definitions and theorem are useful.
Definition 1 [22]: A matrix is said to be
nonneg-ative, denoted , if .
Definition 2 [22]: A real-square matrix is called
a nonsingular -matrix if for , and if it is monotone, i.e., .
Theorem 1 (Lemma 5.2 in [22]): For a arbitrary square
ma-trix .
1) , iff , where , called
spectral radius, is the maximum absolute value of any eigenvalues of .
2) If , then is
convergent.
Theorem 2: The matrix is an -matrix.
Proof: First, since is the transition matrix of the tran-sients states of a Markov chain, , and
, , for . Second, from Theorem 1,
is convergent and . From the defini-tion 1, the theorem follows.
REFERENCES
[1] M. K. Simon, J. K. Omura, R. A. Scholtz, and B. K. Levitt, Spread
Spectrum Communications. Rockville, MD: Computer Science Press, 1985, vol. III.
[2] R. L. Peterson, R. E. Ziemer, and D. E. Borth, Introduction to Spread
Spectrum Communications. Englewood Cliffs, NJ: Prentice-Hall, 1995.
[3] M. El-Tarhuni and A. Ghrayeb, “A multipath resistant PN code tracking algorithm,” in Proc. IEEE Int. Symp. Personal, Indoor, and Mobile Radio
Communications (PIMRC), Sept. 2002, pp. 1834–1838.
[4] P. Schulz-Rittich, G. Fock, J. Baltersee, and H. Meyr, “Low-com-plexity adaptive code tracking with improved multipath resolution for DS-CDMA communication over fading channels,” in Proc. IEEE Int.
Symp. Spread Spectrum Techniques Applicat. (ISSSTA) , Sept. 2000,
pp. 30–34.
[5] W.-H. Sheen and C.-H. Tai, “A noncoherent tracking loop with diver-sity and multipath interference cancellation for direct sequence spread spectrum systems,” IEEE Trans. Commun., vol. 46, pp. 1516–1524, Nov. 1998.
[6] W.-H. Sheen and G. L. Stüber, “A new tracking loop for spread-spec-trum systems on frequency-selective fading channels,” IEEE Trans.
Commun., vol. 43, pp. 3063–3072, Dec. 1995.
[7] S. J. Kim and R. A. Iltis, “GPS code tracking with adaptive beamforming and jammer nulling,” in Proc. IEEE 36th Asilomar Conf. Signals,
Sys-tems Computers, Mar. 2000, pp. 118–124.
[8] D. Gustafson, J. Dowdle, and K. Flueckiger, “A deeply integrated adap-tive GPS-based navigator with extended rang code tarcking,” in Proc.
IEEE Position Location and Navigation, Nov. 2002, pp. 975–979.
[9] M. C. Laxton and S. L. DeVilbiss, “GPS multipath mitigation during code tracking,” in Proc. IEEE American Control Conf., June 1997, pp. 1429–1433.
[10] J. Scheim and B. Z. Bobrovsky, “Computationally efficient discrimi-nator for code tracking loops,” IEEE Trans. Veh. Technol., vol. 52, pp. 727–732, May 2003.
[11] M. K. Simon, “Noncoherent pseudonoise code tracking performance of spread spectrum receivers,” IEEE Trans. Commun., vol. COM-25, pp. 327–345, Mar. 1977.
[12] A. Polydoros and C. L. Weber, “Analysis and optimization of correl-ative code-tracking loops in spread-spectrum systems,” IEEE Trans.
Commun., vol. COM-33, pp. 30–43, Jan. 1985.
[13] J. Caffery Jr. and G. L. Stuber, “Effects of multiple-access interference on the noncoherent delay lock loop,” IEEE Trans. Commun., vol. 48, pp. 2109–2119, Dec. 2000.
[14] R. D. Gaudenzi, M. Luise, and R. Viola, “A digital chip timing recovery loop for band-limited direct-sequence spread spectrum signals,” IEEE
Trans. Commun., vol. 41, pp. 1760–1769, Nov. 1993.
[15] K. Kallaman and G. Davis, “Jitter performance of a baseband sampled code tracking loop,” IEEE Trans. Commun., vol. 42, pp. 2919–2925, Nov. 1994.
[16] N.-Y. Yen, S.-L. Su, and S.-C. Hsieh, “Performance analysis of dig-ital delay lock loops in the presence of Doppler shift,” IEEE Trans.
Commun., vol. 44, pp. 668–673, June 1996.
[17] W. Zhuang and J. Tranquilla, “Modeling and analysis for the GPS pseu-dorange observable,” IEEE Trans. Aerosp. Electron. Syst., vol. 31, pp. 739–751, Apr. 1995.
[18] K. J. Quirk and M. Srinivasan, “Analysis of sampling and quantization effects on the performance of PN code tracking loops,” in Proc. IEEE
Int. Communications Conf., May 2002, pp. 1480–1484.
[19] M. Katayama, A. Ogawa, and N. Morinaga, “Carrier synchronization under Doppler shift of the nongeosataionary satellite communication systems,” in Proc. IEEE Int. Symp. Information Theory Applicat.
(ICCS/ISITA), 1992, pp. 466–470.
[20] S. M. Ross, Stochastic Processes, 2nd ed. New York: Wiley, 1996. [21] C. A. Pomalaza-Raez and C. D. McGillem, “Digital phase-locked loop
behavior with clock and sampler quantization,” IEEE Trans. Commun., vol. COM-33, pp. 753–759, Aug. 1985.
[22] O. Axelsson, Iterative Solution Methods. Cambridge, U.K.: Cam-bridge Univ. Press, 1994, ch. 5,6.
[23] C. W. Helstrom, Elements of Signal Detection and Estimation. Engle-wood Cliffs, NJ: Prentice-Hall, 1995.
[24] J. Omura and T. Kailath, “Some useful probability distributions,” Stan-ford Univ., StanStan-ford, CA, Tech. Rep. 7050-6, Sept. 1965.
Wern-Ho Sheen (M’91) received the B.S. degree
from the National Taiwan University of Science and Technology, Taipei, Taiwan, R.O.C., in 1982, the M.S. degree from the National Chiao Tung University, Hsinchu, Taiwan, in 1984, and the Ph.D. degree from the Georgia Institute of Technology, Atlanta, in 1991.
From 1993 to 2001, he was with the National Chung Cheng University, Chia Yi, Taiwan, where he held positions as a Professor in the Department of Electrical Engineering and the Managing Director of the Center for Telecommunication Research. Since 2001, he has become a Professor in the Department of Communication Engineering, National Chiao Tung University. His research interests include general areas of communication theory, cellular mobile and personal radio systems, adaptive signal processing for wireless communications, spread spectrum communications, and VLSI design for wireless communications systems.
Ming-Jou Chang received the B.S. degree from
the National Taiwan University of Science and Technology, Taipei, Taiwan, R.O.C., in 1991, and the M.S.E.E. and Ph.D. degrees from the National Chung Cheng University, Chia-Yi, Taiwan, in 1994 and 2000, respectively.
Since September 2000, he has been with the Computer and Communications Laboratories, In-dustrial Technology Research Institute, Hsinchu, Taiwan, where he is mainly involved in the projects of wireless communications. His research interests include spread-spectrum communications, mobile communications, VOIP, and network security.
Cheng-Shong Wu was born in Taoyuan, Taiwan,
R.O.C., in 1961. He received the B.S. and M.S. de-grees in electrical engineering from National Taiwan University, Taipei, Taiwan, in 1983 and 1985, and Ph.D. degree in electrical engineering from Univer-sity of Southern California, Los Angeles, in 1990.
In 1991, he was a Visiting Assistant Professor in the Center for Advanced Computer Studies, Univer-sity of Southwestern Louisiana, Lafayette. He joined the Department of Electrical Engineering, National Chung-Cheng University, Chia Yi, Taiwan, in fall of 1991, and is currently a Professor there. His research interests include broadband networks, wireless networks, queuing theory, and mathematical programming.