Registration Area Planning for PCS
Networks Using Genetic Algorithms
Tsan-Pin Wang, Shu-Yuen Hwang, and Chien-Chao Tseng
Abstract— In a personal communication services (PCS’s)
net-work, the signaling traffic required to support user mobility is extremely high due to the huge numbers of users and the small sizes of cells. The requirement to minimize this traffic increases the importance of registration area (RA) planning in the PCS network design. In the literature, several heuristic algorithms have been proposed for RA planning, however, they may get trapped into local minimums and may lack robustness. In this paper, we reformulate the problem of RA planning as a cost-optimization problem and propose genetic algorithms for RA planning in PCS networks. Simulation results show that genetic algorithms are robust for RA planning.
Index Terms— Personal communication services, registration
area planning.
I. INTRODUCTION
A
PERSONAL communication services (PCS’s) network [2], [3] is a digital communication system that enables subscribers to initiate or receive calls at any time from any location. To do this, the system must support the mobility of users and be able to find users as they move from cell to cell (roaming). Thus, a called portable must be located before a connection can be established [4], [5]. There are two alternatives to this task: paging and registration. Paging is impractical since a PCS network may cover an extremely large area. In the registration scheme [6], the system area is divided into several RA’s (or location areas in cellular networks). In general, an RA consists of an aggregation of cells forming a contiguous geographical region.When a portable enters a cell which belongs to a different RA, a location update (LU) procedure that informs the network about the portable’s new location is performed. When a portable is called, first the RA being traversed by it is determined and then a paging procedure is applied within that RA to identify the specific base station servicing its connection. During the paging process, every base station in the RA broadcasts a specific message to inform the portable this connection request. Both LU and paging generate network traffic overhead in PCS networks and consume the scarce radio resource. Moreover, LU also increases the load of distributed location databases and thus increases the implementation com-plexity of the databases [7], [8].
Manuscript received March 4, 1995; revised November 13, 1995. This work was supported by the National Science Council, Taiwan, R.O.C., under NSC Grants 85-2213-E-009-063 and 86-2213-E-009-076.
The authors are with the Department of Computer Science and Information Engineering, National Chiao Tung University, Hsinchu 300, Taiwan, R.O.C. (e-mail: tpwang@csie.nctu.edu.tw).
Publisher Item Identifier S 0018-9545(98)05867-8.
Due to the huge numbers of users and the small sizes of cells in PCS networks, the signaling required to support user mobility, e.g., paging and location updating, is significant. RA planning has therefore been playing an increasingly important role in improving the PCS network performance. In general, RA dimensioning [9], [10] is based on the tradeoff between the amount of signaling caused by paging and location updating. As the sizes of the RA’s increase (decrease), the paging cost increases (decreases) and the LU cost decreases (increases). An RA planning algorithm during the design of a PCS network should be able to minimize the overall network location updating and paging cost.
In the literature, there has been little research on RA planning for PCS networks [9]–[12]. RA planning decomposes a group of cells into RA’s in which LU traffic is mini-mized without violating the paging bound. It can be mapped into a graph-partition problem, which is a well-known NP-complete problem [13]. Consequently, an exact search for optimal solutions is impractical due to exponential growth in execution time. Previous researchers have used graph models to represent RA planning and utilized greedy approaches to solutions. Gamst [9] proposed a graph theoretical model and presented a greedy method for RA planning. Markoulidakis et al. [10], [11] proposed two heuristic algorithms to obtain better results by adjusting the border weights in future mobile telecommunication networks. Plehn [12] proposed a weighted greedy algorithm that consists of two phases—the merge and exchange phases. According to their experience, the algorithm performed superior to previously used methods. Although heuristics has been proposed to obtain better results, RA planning was generally based on the hill-climbing algorithm.
However, hill-climbing [14] approaches may get trapped into local minimums and lack robustness. In addition, the graph theoretical models have the following drawbacks.
1) A tradeoff between LU traffic and preset configurations (soft preset) is impossible. A preset is a given in an RA configuration that might have been planned in a previous state of expansion of the network or might have been fixed by the planning engineer. In practice, presets are generally required in PCS network design due to the existing network configuration. The advantage of presets is that they provide a network designer a way to state his/her preference during the planning stage to reduce the cost of network installation. In this paper, we consider two types of presets: soft and hard presets. A soft preset is a preset configuration that can be violated. For example, some neighboring cells may be preset to 0018–9545/98$10.00 1998 IEEE
2) They cannot support soft constraints. A soft constraint allows some violation, for example, the paging bound can be broken if it greatly reduces LU traffic.
The graph theoretical approach aims only to minimize network cost. It does not quite hit the actual problem. Moreover, some paging bandwidth may be locally reserved for network growth, e.g., cell splitting in heavy-load areas.
To overcome these drawbacks, formulating RA planning as a cost-optimization problem is obviously superior to conven-tional graph theoretical models. Genetic algorithms [15], [16] have been considered as robust stochastic search algorithms for various optimization problems. In this paper, we propose genetic algorithms for RA planning in PCS networks.
The organization of this paper is shown as follows. In Section II, we formally define the RA planning problem. In Section III, we present a brief introduction to genetic algorithms and propose a genetic approach for RA planning. In Section IV, we provide details on customizing RA planning. The simulation results are presented in Section V. Finally, a conclusion is given in Section VI.
II. RA PLANNING
Proper design of RA’s is based on a tradeoff between paging traffic and LU traffic. Generally, paging traffic is less critical than LU traffic [9] since LU affects not only the radio resource, but the load of distributed location databases as well, so the optimization goal is to minimize LU cost without violating the paging bound of each RA. In this paper, a general definition of RA planning will be examined. Our RA planning objective is to minimize LU traffic on the network subject to the constraints such as the paging bound of each RA, preset configurations, and other specific constraints.
In general, paging traffic is proportional to the number of calls to all portables in the RA while LU traffic is proportional to the number of portables crossing RA borders. Prior to the RA planning procedure, PCS network designers must collect these data as input parameters. Although obtaining these data may present considerable difficulty in practice, it can be accomplished in the following ways. Markoulidakis and Sykas [17] proposed a model to estimate location update and handover rate for mobile communication, and practical PCS networks such as the global system for mobile communications (GSM) may provide data that enable an approximation of this information. Without loss of generality, we may assume then that these data are already available. The basic assumptions used in this paper are shown as follows.
1) Cell planning has been done. In each cell, LU and paging traffic have been estimated.
2) Each RA contains a disjoint set of cells—RA overlap-ping is not allowed in this paper.
3) The bandwidth available for paging in each RA, i.e., the paging bound, is limited.
Based on these assumptions, we first describe the graph models and relevant algorithms and then derive a general
Fig. 1. A hill-climbing algorithm for RA planning.
model for optimization. In graph models, a PCS network configuration is defined by a weighted (undirected) graph , where is the set of vertices, is the set of edges, is a function whose domain is , and is a function whose domain is Each vertex represents a cell, and each edge denotes a border between cells. The function assigns weights called paging cost to the vertices in , and the function assigns weights called LU cost to the edges in
In this model, the hill-climbing algorithm shown in Fig. 1 is performed to explore the solution. Edges in graph are removed only when the removal would not violate the paging bound for any RA. Hill-climbing algorithms ensure the correctness of solutions by preventing searches that lead to illegal nodes, however, they do not ensure optimal or even near-optimal solutions. Moreover, supporting soft presets and constraints is nontrivial in this model.
In this paper, we formulate RA planning as a cost-optimization problem in which solutions are described by a cost function and techniques for minimizing (or maximizing) the cost function. We also remove constraints by means of a weighted penalty function that assigns weights according to constraint importance. Thus, RA planning is reduced to the cost-optimization problem.
Consequently, let denote the set of objectives and represent the set of constraints, where the goal of RA planning is to minimize a cost function , which is defined as follows:
(1)
where and are weights for the objective and constraint , respectively. The objective function is a function that maps from objectives to costs and contributes to the RA planning goal. The penalty function is a function that maps from constraints to costs and punishes violation of constraints such as paging bounds, soft presets, and others. The objective and penalty functions are calculated using the configuration graph making this model a general form of RA planning. For special cases, let X contain only the total LU cost and Y contain only the paging bound constraint, where our goal is to minimize the LU cost without violating the paging bound constraint as previous work.
Fig. 2. An example of the H-mesh configuration with dimension 2.
Fig. 3. An RA planning result for Fig. 2.
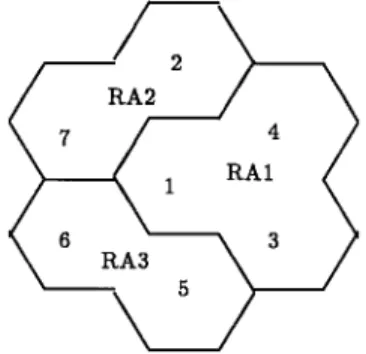
We use a simple example of the H-mesh configuration [18] with dimension 2 to illustrate RA planning as shown in Fig. 2. In this example, denotes the paging cost of the th cell and denotes the LU cost of the th border. Assume that the
paging bound for each RA is 30 for all and and
and , otherwise, Fig. 3
shows the optimal result for this example: consists of cells 1, 3, and 4, consists of cells 2 and 7, and consists of cells 5 and 6.
III. GENETIC APPROACH TO RA PLANNING
Genetic algorithms have been applied to various optimiza-tion problems. In general, they use a penalty funcoptimiza-tion to encode constraints and allow a search for illegal nodes, e.g., a node may violate the paging bound. Allowing a search for illegal nodes may prevent falling down into a local minimum and generate a better solution. It is well suited to the cost-optimization model we propose for RA planning. In this section, we first review the fundamentals of genetic algorithms and then describe the representation and fitness function for RA planning.
A. Fundamentals of Genetic Algorithms
In principle, genetic algorithms [15], [16] are adaptive procedures that find solutions to problems by an evolution-ary process based on natural selection. In practice, genetic algorithms are iterative search algorithms with various
applica-Fig. 4. A chromosome.
tions. They combine survival of the fittest, genetic operations, random, but structured searches, and parallel evaluation of nodes in the search space.
In general, genetic algorithms maintain a population of individual candidate solutions to specific domain challenges. An individual can be represented by a string (chromosome) as shown in Fig. 4. During each iteration, or called generation, the individuals in the current population are rated for their fitness as domain solutions. The fitness function evaluates the “goodness” of each individual. As a result of this evaluation, a new population of candidate solutions is generated using specific genetic operators. Generally, genetic algorithms make use of three primary operators called selection, crossover, and mutation, which are described below.
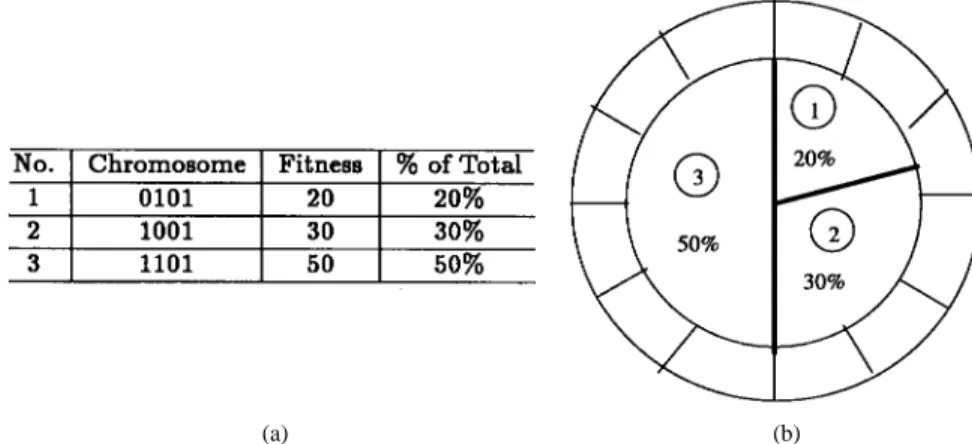
1) Selection (or Reproduction): Individuals in the popula-tion can be heuristically or randomly initialized. The population of the next generation reproduces using a probabilistic selection process. Practically, reproduction allocates offspring strings using a roulette wheel [15] with slots sized according to fitness as shown in Fig. 5. In this example, the fitness of chromosomes 1, 2, and 3 are 20, 30, and 50, respectively, and the percentage of chromosomes 1, 2, and 3 are 20% (20/20 30 50),
30% (30/20 30 50), and 50% (50/20 30 50)
in the offsprings, respectively. Thus, individuals with higher fitness have more chances to reproduce. In order to guarantee the convergence [19] of genetic algorithms, the best individuals from the previous population along with a fixed percentage, called the clonation percentage, is retained in the new one. This also assures a more efficient search of the solution space.
2) Crossover: After reproduction, crossover proceeds with a probability This operator takes two randomly chosen parent individuals as input and combines them to generate two children. This combination is performed by choosing two crossing points in the strings of the parents and then exchanging the allelic values between these two points as shown in Fig. 6. The crossover operator provides a powerful exploration capacity by exchanging the information from two parents.
3) Mutation: The crossover operator may lead to falling into a local minimum of the fitness function because gen-erated children tend to be very similar to their parents. In order to reduce this phenomenon, mutation operates with a probability and creates new individuals by modifying one or more of the gene values of an existing individual, as shown in Fig. 7. It provides a random search in the problem space and prevents complete loss of genetic features through selection and elimination. Thus, the mutation operator reduces the probability of falling into a local minimum of the fitness function.
(a) (b)
Fig. 5. Simple selection allocates offspring chromosomes using a roulette wheel with slots sized according to fitness.
Fig. 6. Two-point crossover (j denotes a crossing point).
Fig. 7. Mutation.
Following reproduction, crossover, and mutation, the new population is ready for testing. Genetic algorithms decode new strings, calculate fitness, and then generate a new population. Fig. 8 depicts the outline of a genetic algorithm. The recom-bination process invokes a set of genetic operators, such as crossover and mutation.
The construction of a genetic algorithm for any problem can be separated into the following tasks.
1) Choose the representation of the genetic chromosome. 2) Design a set of genetic operators.
3) Define the fitness function.
4) Determine the probabilities controlling the genetic op-erators.
Each of the tasks above may greatly affect the quality of obtained solutions as well as the performance of the genetic algorithm. In the following sections, we examine how each of them applies to the problem of RA planning.
B. Representation
In our study, two representation schemes were used to encode the RA planning problem—cell- and border-oriented.
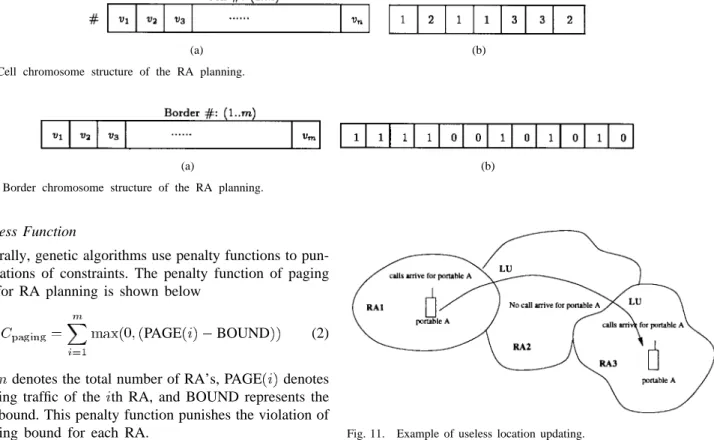
1) Cell-Oriented Representation: Cells are labeled from one to the total number of the cells and RA’s are labeled from one to the total number of RA’s. The cell representation of chromosome structure is shown in Fig. 9(a), where the th cell belongs to the th RA. For example, the chromosome of the example shown in Fig. 3 is shown in Fig. 9(b).
Fig. 8. A genetic algorithm.
2) Border-Oriented Representation: Borders are labeled from one to the total number of borders. The border representation of chromosome structure is shown in Fig. 10(a), where , and is the border , which exists in RA planning, otherwise, For example, the chromosome of the example shown in Fig. 3 is shown in Fig. 10(b).
Choosing cell- and border-oriented representation is a trade-off. Cell-oriented representation is excellent for evaluating paging cost, but poor at evaluating LU cost. On the other hand, border-oriented representation is superior to cell-oriented representation at evaluating LU cost, but inferior at evaluating paging cost. Without loss of generality, we concentrate mainly on border-oriented representation hereafter.
C. Genetic Operators
There is no special genetic operator designed for RA plan-ning. Three general operators discussed in previous sections are used to explore the state space.
1) The selection operator produces individuals with higher potential to be optimal solutions.
2) The crossover operator explores the solution space by exchanging the information from two parents.
3) The mutation operator provides opportunities for long jumps from local minima.
(a) (b) Fig. 9. Cell chromosome structure of the RA planning.
(a) (b)
Fig. 10. Border chromosome structure of the RA planning.
D. Fitness Function
Generally, genetic algorithms use penalty functions to pun-ish violations of constraints. The penalty function of paging bound for RA planning is shown below
PAGE BOUND (2)
where denotes the total number of RA’s, PAGE denotes the paging traffic of the th RA, and BOUND represents the paging bound. This penalty function punishes the violation of the paging bound for each RA.
Thus, the cost function is equal to the total cost generated by LU traffic plus the paging penalty as shown in the following:
Cost (3)
where denotes the total number of , denotes the
LU traffic of the th RA, and parameters and are used to balance the relative importance of the penalty function and the objective function.
In border-oriented representation, let be the total number of borders, represent the crossing intensity of the th border, and be the value of the th chromosome (either zero or one). For the sake of convenient computation, the cost function for border-oriented representation could be rewritten as follows:
Cost (4)
Since the selection operator will try to maximize the fitness function, we need to convert the cost function into maximiza-tion form. This can be done by defining the fitness funcmaximiza-tion as follows:
Fitness Cost (5)
where denotes the maximum value observed so far of the cost function in the population. Let cost be the value of the cost function for the chromosome, and can be calculated by the following iterative equation:
cost (6)
where is initialized to zero.
Fig. 11. Example of useless location updating.
E. Initial Population
Individuals in the population can be initialized randomly or heuristically. We use the result of hill climbing as one individual and randomly generate other individuals to con-struct the initial population. Moreover, the preset of the cell configuration (either soft or hard presets) also provides the information of constructing the initial population.
IV. CUSTOMIZING RA PLANNING
In this section, we discuss some details of applying genetic algorithms to RA planning.
A. Useless Location Updating
Useless location updating [10] refers to the case of subse-quent LU’s without using the updated information as shown in Fig. 11. In this example, the LU in RA2 is a useless location updating since no calls arrive for portable A during the time period that the portable A was in RA2. As we mentioned in Section I, the reason for updating location information is to make the network be able to locate a portable whenever this portable is called. Thus, useless location updating indicates the waste of signaling and database access. It is not necessary for a portable to perform LU’s much more frequently than the portable receives calls. To improve the network perfor-mance, we should minimize the probability of useless location updating.
The probability of useless location updating can be defined as the probability of two subsequent LU’s caused by the same portable traversing an RA without the arrival of any
(7) where the notation used is listed as follows:
time interval between the previous phone call to a portable and the time when the portable moves out of the RA;
independent and identically distributed random variable which represents the time interval between two consecutive calls directed from an RA to a portable;
density function for the random variable ; density function for the random variable . The following equation is then added to the cost function and affects the fitness function:
(8) where is the parameter for adjusting the weight of the useless location updating. The fitness function handles the fitness of genetics such that reduces the impact of useless location updating.
B. Presets and Constraints
A preset or constraint can be defined by a string
, where is the number of cells: if
the th border is necessary to exist, if the th border is necessary to remove, otherwise, , which ignores the th border. For example, we preset assignment of cells 1 and 2 to the same RA, i.e., border 1 is not necessary to exist in the example shown in Fig. 2. The preset string is equal to The penalty function of the preset can be defined as the following:
(9) where
if or
otherwise.
In a similar manner, we can compute the penalty of con-straint The following equations are added to the cost function to deal with soft (hard) presets and constraints:
(10) (11) However, large parameters may outweigh the importance, on the other hand, small parameters may lead to generation of illegal solutions. Finding appropriate parameters is not a trivial job. A postprocessing stage is necessary to filter out illegal solutions in dealing with hard presets or constraints.
1Assumet
mandtcare i.i.d. with exponential distributions, so this equation can be greatly simplified [7].
and run-time efficiency.
1) Probability of Mutation: In the beginning of the algo-rithm, we may initialize a large mutation probability value to search a larger state space. However, this might not obtain better results as the algorithm near convergence. We resolve this problem by decreasing the probability of mutation by half after a predefined number of generations, for example, 100 generations.
2) Heuristics: It is easy to encode search heuristics in genetic algorithms using the mutation operator. In this paper, we propose two heuristics to improve the performance of genetic algorithms.
1) Large-Weight Preference: We prefer to remove borders with large weights, e.g., the probability of mutation from one to zero of large weights is also large as shown in the following:
(12)
On the other hand, we also prefer to add borders with lower weights in a similar manner.
2) Relatively Large-Weight Preference: We prefer to re-move borders with large weights relative to their neigh-bors. The weights are adjusted relative to the minimum weight in the same RA, called relative weights. These relative weights are then used to calculate the probability of mutation as follows:
(13) (14)
where represents the minimum weight of borders including the border , which constitutes a single RA. Note that these heuristics implies extra processing2that is proportional to the number of borders and the number of chromosomes in the generation because we need to know the RA which each border belongs to. To avoid this overhead, the authors suggest that these heuristics should not be frequently applied.
V. SIMULATION RESULTS
We simulated a hexagonal system in which the cells are configured as an H mesh [18]. The paging cost for each cell and the crossing intensity for each border were generated from a normal random number with mean 100 and variance 20. The paging bound per RA was 800 in our simulations. The parameters used by the genetic algorithm throughout the simulations are listed below.
1) Population size
2This overhead should not be the disadvantage of our approach since
TABLE I
COMPARISON OFHILLCLIMBING ANDGENETICALGORITHM INTERMS OF THELU COST
Fig. 12. A tradeoff between LU cost and execution time in a single run.
Fig. 13. H meshn = 3: Results of RA planning over 100 runs.
2) Clonation percentage 3) Crossover probability 4) Mutation probability
5) Maximum number of generations
The simulation was performed on a Sun Sparc10 worksta-tion. After 100 simulation runs, the mean and variance of the results in terms of the LU cost were collected. These results were compared to those of hill climbing as shown in Table I and found to be superior after 1000 generations.
Fig. 12 shows the behavior of the genetic algorithm and a tradeoff between solution quality and run-time efficiency. In the first 200 generations, the LU cost rapidly decreases. The genetic algorithm may get trapped in a local minimum from the 200th to 700th generation. After the 700th generation, the algorithm jumps from the local minimum and the LU cost continues decreasing. Generally, as the execution time increases, the LU cost decreases. That is, the longer the time of execution, the better the result we obtained.
Figs. 13–16 show the mean results of RA planning in 100 simulation runs. Genetic algorithms with a random initial
Fig. 14. H meshn = 4: Results of RA planning over 100 runs.
Fig. 15. H meshn = 5: Results of RA planning over 100 runs.
Fig. 16. H meshn = 6: Results of RA planning over 100 runs.
population prove to be superior to hill climbing in 100 generations (except in the case of Fig. 16). As the number of cells increases, it takes a longer execution time to obtain better results.
based on a genetic approach. Simulation results showed that genetic algorithms are robust for RA planning.
In our model, search nodes are represented as strings determining which borders exist between cells. Three general genetic operators—selection, crossover, and mutation—were employed. Additionally, defining the fitness function required neither a priori knowledge nor information on the possible form of the solution. The only task was to penalize the individual strings that might violate specific constraints. Control parameters for genetic algorithms can be determined either by a sophisticated technique [20] or by experience. Experiential parameters may not be optimal, but at least feasible for the RA planning.
In summary, the advantages and limitations of using genetic algorithms for the problem of RA planning are listed as follows.
1) Simplicity: Defining representation, operators, and fit-ness function requires neither a priori knowledge nor information on the possible form of the solution. 2) Flexibility: Genetic algorithms are flexible for
support-ing soft presets and soft constraints.
3) Convergence: Genetic algorithms are guaranteed to con-verge [19]. Illegal solutions can be filtered out in the postprocessing stage. By adjusting parameters of the penalty function, we will always be able to obtain a legal solution. Furthermore, the longer the time of execution, the better the result obtained.
4) Robustness: As a reviewer pointed out, heuristic ap-proaches will be much more efficient compared to the traditional genetic algorithms in extreme cases where the number of illegal solutions is a remarkable percentage of the total possible solutions. This drawback can be alleviated by using heuristics to avoid random search in the space of illegal solutions. Our approach has encoded some heuristics and by no means excludes heuristics proposed in other papers: it is robust for a diversity of cases. In general cases, it performs much better than heuristic approaches. On the other hand, our approach would be little less efficient compared to heuristic approaches in some special cases, but it has the potential to obtain better solutions. Unfortunately, heuristics imply extra processing which will be applied in the population of the generation. The limitation of our approach is that network designers should be able to estimate the cost of applying heuristics and decide the frequency of applying these heuristics.
5) Parallelism: Parallelism is inherent in genetic algo-rithms.
The time complexity of hill climbing, genetic algorithms,
and exhaustive searches is and ,
respectively, where denotes the total number of the borders, is the maximum number of generations, and is the popula-tion of the generapopula-tion. Practically, the populapopula-tion of the genera-tion is a small constant, e.g., in our simulations. Thus,
valuable approach to RA planning in designing PCS networks. ACKNOWLEDGMENT
The authors would like to thank Professor Y.-B. Lin and the reviewers for their valuable comments.
REFERENCES
[1] D. C. Cox, “Personal communications—A viewpoint,” IEEE Communi-cations Mag., vol. 128, no. 11, pp. 8–92, 1990.
[2] C. Y. Lee, Mobile Cellular Telecommunications Systems. New York: McGraw-Hill, 1990.
[3] , Mobile Communications Design Fundamentals. New York: Wiley, 1993.
[4] R. Jain, Y. B. Lin, C. Lo, and S. Mohan, “A caching strategy to reduce network impacts of PCS,” IEEE J. Select. Areas Commun., vol. 12, pp. 1434–1444, Oct. 1994.
[5] Y. B. Lin, “Determining the user locations for personal communications services networks,” IEEE Trans. Veh. Technol., vol. 43, pp. 466–473, Aug. 1994.
[6] S. Mohan and R. Jain, “Two user location strategies for personal communications services,” IEEE Personal Communications, vol. 1, no. 1, pp. 42–50, 1994.
[7] Y. B. Lin and S. Y. Hwang, “Comparing the PCS location tracking strategies,” IEEE Trans. Veh. Technol., vol. 45, pp. 114–121, Feb. 1996. [8] J. G. Markoulidakis, G. L. Lyberopoulos, D. F. Tsirkas, and E. D. Sykas, “Evaluation of location area planning scenarios in future mobile telecommunications systems,” ACM/Baltzer Wireless Networks, vol. 1, no. 1, pp. 17–29, 1995.
[9] A. Gamst, “Application of graph theoretical methods to GSM radio network planning,” in Proc. IEEE Symp. Circuits and Systems, pp. 1991, pp. 942–945.
[10] J. G. Markoulidakis and E. D. Sykas, “Method for efficient location area planning in mobile telecommunications,” Electron. Lett., vol. 29, pp. 2165–2166, Dec. 1993.
[11] J. G. Markoulidakis and J. Dost, “Heuristic algorithms for optimal plan-ning of location areas in future mobile telecommunication networks,” National Technical Univ. Athens Tech. Rep., 1994.
[12] J. Plehn, “The design of location areas in a GSM-network,” in Proc. IEEE 45th Veh. Technol. Conf., 1995, pp. 871–875.
[13] M. R. Garey and D. S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness. San Francisco, CA: Freeman, 1979. [14] E. Rich and K. Knight, Artificial Intelligence. New York:
McGraw-Hill, 1992.
[15] D. E. Goldberg, Genetic Algorithms in Search, Optimization & Machine Learning. Reading, MA: Addison-Wesley, 1989.
[16] Z. Michalewicz, Genetic Algorithms + Data Structures = Evolution Programs. New York: Springer-Verlag, 1992.
[17] J. G. Markoulidakis and E. D. Sykas, “Model for location updating and handover rate in mobile telecommunications,” Electron. Lett., vol. 29, pp. 1574–1575, Aug. 1993.
[18] Y. B. Lin and V. W. Mak, “Eliminating the boundary effect of a large-scale personal communication service network simulation,” ACM Trans. Modeling and Computer Simulation, vol. 4, no. 2, pp. 165–190, 1994. [19] G. Rudolph, “Convergence analysis of canonical genetic algorithms,”
IEEE Trans. Neural Networks, vol. 5, pp. 96–101, Jan. 1994. [20] J. J. Grefenstette, “Optimization of control parameters for genetic
algorithms,” IEEE Trans. Syst., Man, Cybern., vol. 16, no. 1, pp. 122–128, 1986.
Tsan-Pin Wang received the B.S. degree in ap-plied mathematics and the M.S. degree in com-puter science and information engineering, both from National Chiao Tung University, Hsinchu, Taiwan, R.O.C., in 1990 and 1992, respectively. He is currently working toward the Ph.D. degree at National Chiao Tung University.
From 1992 to 1993, he was a System Engineer in the R&D Division of Taiwan NEC Ltd. His research interests include PCS networks and mobile computing.
Shu-Yuen Hwang received the B.S. and M.S. de-grees in electrical engineering from National Taiwan University, Taiwan, R.O.C., in 1981 and 1983 and the Ph.D. degree in computer science from the University of Washington in 1989.
He is a Professor in the Department of Com-puter Science and Information Engineering, Na-tional Chiao Tung University, Hsinchu, Taiwan. His current research interests include artificial intelli-gence, computer simulation, and mobile computing.
Chien-Chao Tseng received the B.S. degree in in-dustrial engineering from National Tsing-Hua Uni-versity, Hsinchu, Taiwan, R.O.C., in 1981 and the M.S. and Ph.D. degrees in computer science from the Southern Methodist University, Dallas, TX, in 1986 and 1989, respectively.
He is currently a Professor in the Department of Computer Science and Information Engineer-ing, National Chiao-Tung University, Hsinchu. His research interests include mobile computing and parallel and distributed processing.