國立宜蘭大學土木工程學系 (研究所) 碩士論文 Department of Civil Engineering National Ilan University Master Thesis

(1)

國立宜蘭大學土木工程學系 (研究所) 碩士論文

Department of Civil Engineering National Ilan University

Master Thesis

河川潛板系統形狀變化對交互作用現象及系統最佳設置之影響

The effect of submerged vane shape on the interaction between vanes and optimal system configuration

指導教授：歐陽慧濤博士 Huei-Tau Ouyang Ph. D.

研究生：林政斌 Cheng-Pin Lin

中華民國九十六年十一月

(2)

(3)

(4)

(5)

謝誌

很快的兩年的研究所生活一下子就過去了，在兩年的研究所生活中要感謝歐陽慧濤老師對於論文的悉心指導，讓我獲得不少學識。感謝土木系游棫誠老師、李洋傑老師、曾浩璽老師，當我在低潮失落時給予我鼓勵。感謝學長志晃、元宏、偉謙、冠維，同學文宏、祥儀、

祺惟、芝岩、怡靜，有了你們的陪伴，讓我研究所的生活更加的多彩多姿。另外感謝系上的助教明惠、雅鈴、聿均，謝謝你們在行政方面的協助，以及一群在網路上的好友們猛男一家、塔哥、猪姐、玲姐、

榕樹、AFAR、KB，感謝你們一路上支持鼓勵我。最後要感謝我的父母二十幾年來的栽培，照顧我成長並在我身旁支持我、鼓勵我。要感謝的人很多，希望沒有遺漏，謝謝你們在這兩年來對我的幫助、支持以及鼓勵，讓我順利取得學位，感激在心。

(6)

摘要

潛沒式導流板為一穩定河岸的工法，對於穩定河川凹岸岸壁及河川底床泥沙運移有良好成效，潛板系統係指將一系列的潛板沿水流方向或徑向方向設置以提高潛板的影響範圍。過去研究指出潛板效能與潛板設置數量、設置位置、角度及潛板尺寸等有關，但關於潛板之形狀與最佳化位置相關的探討則較少有研究者觸及。本研究利用小板法可模擬不同板形潛板的特性進行分析，計算出潛板後方的河川底床徑向剪應力分布，並引入河川動量方程式與水流、沉滓之連續方程式計算河川彎道二次流對底床產生的剪應力，以求解河川底床受到彎道二次流以及潛板影響下的徑向床形，並應用前人的實驗資料加以驗證。最後並探討矩形板、前傾板及板頂束縮板三種板形所組成的潛板系統的最佳設置位置。

研究結果顯示各形之單片潛板於彎道中最佳位置近乎一致，以束縮板的效果為最佳。雙片潛板系統間的交互作用會隨攻角改變而增強，其中以束縮板各片潛板之交互作用的差異最大。潛板系統對凹岸底床抬升量隨潛板數量增加其效果也會增加，各形潛板系統又以束縮板對底床抬升的效果為最優良。

(7)

ABSTRACT

Submerged vane is a technique on stable the river bank. It has well performance on streambank protection and sediment control. Submerged vane system is a series of vanes installed follwoing the flow direction or parallel along a river cross-section to increase the performance. Previous researchers have shown that the performance of the submerged vane system is related to the number of the vanes ,the angle of attack ,the installing position ,and the size of the vane. However, not much for the optimal planform of the vane and optimal configuration of the submerged vane system are investigated. The study utilize the Lifting-Panel Method for the calculation of the flow field induced by the vane system. By adopting previous research’s bend flow model, the method is capable of calculating the transverse bed profile induced by vanes with various shapes and dimensions. The study investigated the following three types of submerged vane systems： 1.rectangle vanes;2.forward-swept vanes; 3.tapered vanes.

The results show that the optimal location of a single vane

(8)

for these three types of vanes are almost the same. Upon the others, the tapered vane has the best performance. The interaction among the vanes increased with increasing angle of attack of the vanes and the tapered vane has the most difference between vanes. By increasing the number of the vanes the function of the vanes on sediment control is improved. For the three types of vanes, the tapered vane has the best performance the sediment control.

(9)

目錄

摘要 ... I ABSTRACT ... II 目錄 ... IV 圖目錄 ... VI 符號表 ... X

第一章導論 ... 1

1-1 前言 ... 1

1-2 文獻回顧 ... 1

1-3 研究動機 ... 2

1-4 研究方法 ... 2

1-5 本文流程 ... 3

第二章潛板與床型模式之建立 ... 4

2-1 一渦流段所產生之速度向量 ... 4

2-2 小板法 ... 8

2-3 受潛板系統影響之床形 ... 10

2-4 邊界效應 ... 13

第三章數值模式建立與驗證 ... 14

3-1 網格密度與垂直鏡像數量分析 ... 15

3-2 網格密度與水平鏡像數量分析 ... 16

3-3 模式驗證 ... 17

3-3.1 直渠道單潛板 ... 17

3-3.2 直渠道單潛板 ... 18

3-3.3 直渠道潛板系統 ... 18

3-3.4 彎曲渠道無潛板 ... 19

3-3.5 彎曲渠道潛板系統 ... 19

第四章結果與討論 ... 21

4-1 潛板系統的交互作用現象 ... 21

(10)

4-1.1 二潛板系統的交互作用 ... 22

4-1.2 二潛板系統與垂直岸壁的交互作用 ... 25

4-1.3 三潛板系統的交互作用 ... 26

4-1.3.a A 板之交互作用因子 ... 26

4-1.3.b B 板之交互作用因子 ... 27

4-1.3.c C 板之交互作用因子 ... 28

4-2 潛板系統的最佳位置 ... 28

4-2.1 單片板各板形於彎道之最佳位置 ... 29

4-2.2 潛板系統於彎曲渠道中之最佳設置位置 ... 30

4-2.3 潛板系統最佳設置所產生之凹岸底床變化 ... 31

4-3 潛板系統之效果與效率分析 ... 31

第五章結論 ... 33

5-1 結論 ... 33

5-2 建議 ... 34

參考文獻 ... 35

附錄 A 彎道模式推導 ... 37

(11)

圖目錄

圖 1-1 研究流程圖 ... 47

圖 2-1 潛板所產生之渦流 ... 48

圖 2-2 受潛板尾跡渦流影響之徑向床形 ... 48

圖 2-4 三維單位渦流示意圖 ... 49

圖 2-5 小板法之渦流環系統 ... 50

圖 2-6 垂直鏡像示意圖 ... 51

圖 2-7 水平鏡像示意圖 ... 52

圖 2-8 潛板系統水平及垂直鏡像合成示意 ... 52

圖 3-1 矩形板示意圖 ... 53

圖 3-2 前傾板示意圖 ... 53

圖 3-3 束縮板示意圖 ... 54

圖 3-4 斷面最小水深示意 ... 54

圖 3-5 不同垂直鏡像與網格密度下之計算差量(矩形板) ... 55

圖 3-6 不同垂直鏡像與網格密度下之計算差量(前傾板) ... 55

圖 3-7 不同垂直鏡像與網格密度下之計算差量(束縮板) ... 56

圖 3-8 不同水平鏡像與網格密度下之計算差量(矩形板) ... 56

圖 3-9 不同水平鏡像與網格密度下之計算差量(前傾板) ... 57

圖 3-10 不同水平鏡像與網格密度下之計算差量(束縮板) ... 57

圖 3-11 Wang 之直渠道水槽試驗佈置 ... 58

圖 3-12 Wang 之彎曲渠道水槽試驗佈置 ... 58

圖 3-13 Odgaard and Spoljaric 之直渠道水槽試驗佈置 ... 59

圖 3-14 直渠道單潛板之計算床形與 Odgaard and Spoljaric(1986) 之試驗資料比較(a)

x d /

₀

= 3.3

(b)

x d /

₀

= 5.1

(c)

x d /

₀

= 6.9

.... 60

圖 3-15 直渠道單潛板之計算床形與 Wang(1991)之試驗資料比較 (a)

x d /

₀

= 0.962

(b)

x d /

₀

= 1.923

(c)

x d /

₀

= 3.846

... 61

圖 3-16 計算床形與 Wang(1991)之 MS4 試驗資料比較 ... 62

圖 3-17 計算床形與 Wang(1991)之 MB1 試驗資料比較 ... 62

圖 3-18 計算床形與 Wang(1991)之 MB2 試驗資料比較 ... 62

(12)

圖 4-1 二片潛板潛板系統佈置 ... 63

圖 4-2 矩形板於不同攻角時之效能 ... 63

圖 4-3 前傾板於不同攻角時之效能 ... 64

圖 4-4 束縮板於不同攻角時之效能 ... 64

圖 4-5 各板形之 1 號板的效能(

α

=10^D)... 65

α

=10^D)... 65

α

=20^D) ... 66

α

=20^D) ... 66

圖 4-9 矩形板不同攻角各板形二板效能之比 ... 67

圖 4-10 前傾板不同攻角各板形二板效能之比 ... 67

圖 4-11 束縮板不同攻角各板形二板效能之比 ... 68

圖 4-12 二潛板間距近時渦流影響示意圖 ... 68

圖 4-13 二潛板間距遠時渦流影響示意圖 ... 69

圖 4-14 攻角 10 度各板形

λ

₁與

λ

₂之比 ... 69

圖 4-15 攻角 20 度各板形

λ

₁與

λ

₂之比 ... 70

圖 4-16 潛板系統與岸壁配置示意圖 ... 71

圖 4-17 矩形板潛板系統 A 板與岸壁交互作用 ... 72

圖 4-18 矩形板潛板系統 B 板與岸壁交互作用 ... 72

圖 4-19 前傾板潛板系統 A 板與岸壁交互作用 ... 73

圖 4-20 前傾板潛板系統 B 板與岸壁交互作用 ... 73

圖 4-21 束縮板潛板系統 A 板與岸壁交互作用 ... 74

圖 4-22 束縮板潛板系統 B 板與岸壁交互作用 ... 74

圖 4-23 真實與鏡像範束渦流於岸壁示意圖 ... 75

圖 4-24 各板形 A 板受岸壁影響之效能(

δ

_B

/ d

₀

= 1.0

) ... 76

圖 4-25 各板形 B 板受岸壁影響之效能(

δ

_B

/ d

₀

= 1.0

) ... 76

δ

_B

/ d

₀

= 2.0

)... 77

δ

_B

/ d

₀

= 2.0

)... 77

δ / d = 3.0

) ... 78

(13)

δ

_B

/ d

₀

= 3.0

) ... 78

δ

_B

/ d

₀

= 4.0

)... 79

δ

_B

/ d

₀

= 4.0

)... 79

δ

_B

/ d

₀

= 5.0

) ... 80

δ

_B

/ d

₀

= 5.0

) ... 80

圖 4-34 三潛板配置示意圖 ... 81

圖 4-35 矩形板三片潛板系統 A 板之效能 ... 82

圖 4-36 前傾板三片潛板系統 A 板之效能 ... 82

圖 4-37 束縮板三片潛板系統 A 板之效能 ... 83

圖 4-38 各板形 A 板效能之比較(

δ

₁₃

/ d

₀

= 1.0

)... 83

δ

₁₃

/ d

₀

= 2.0

) ... 84

δ

₁₃

/ d

₀

= 3.0

) ... 84

δ

₁₃

/ d

₀

= 4.0

) ... 85

δ

₁₃

/ d

₀

= 5.0

) ... 85

圖 4-43 矩形板三片潛板系統 B 板之效能 ... 86

圖 4-44 前傾板三片潛板系統 B 板之效能 ... 86

圖 4-45 束縮板三片潛板系統 B 板之效能 ... 87

圖 4-46 各板形 B 板效能之比較(

δ

_BC

/ d

₀

= 1.0

) ... 87

δ

_BC

/ d

₀

= 2.0

) ... 88

δ

_BC

/ d

₀

= 3.0

) ... 88

δ

_BC

/ d

₀

= 4.0

) ... 89

δ

_BC

/ d

₀

= 5.0

) ... 89

圖 4-51 矩形板三片潛板系統 C 板之效能 ... 90

圖 4-52 前傾板三片潛板系統 C 板之效能 ... 90

圖 4-53 束縮板三片潛板系統 C 板之效能 ... 91

圖 4-54 各板形 C 板效能之比較(

δ

_CA

/ d

₀

= 1.0

) ... 91

δ

_CA

/ d

₀

= 2.0

) ... 92

δ

_CA

/ d

₀

= 3.0

) ... 92

(14)

δ

_CA

/ d

₀

= 4.0

) ... 93

δ

_CA

/ d

₀

= 5.0

) ... 93

圖 4-59 單片潛板於彎道凹岸所造成之水深變化(

r b

_c

/ = 10

，

α = 20

^D) ... 94

圖 4-60 不同曲率半徑矩形板單片潛板的最佳設置位置 ... 94

圖 4-61 不同曲率半徑前傾板單片潛板的最佳設置位置 ... 95

圖 4-62 不同曲率半徑束縮板單片潛板的最佳設置位置 ... 95

圖 4-63 不同曲率半徑各板形單片潛板的最佳設置位置 ... 96

圖 4-64 不同曲率半徑矩形板雙片潛板的最佳設置位置 ... 96

圖 4-65 不同曲率半徑前傾板雙片潛板的最佳設置位置 ... 97

圖 4-66 不同曲率半徑束縮板雙片潛板的最佳設置位置 ... 97

圖 4-67 不同曲率半徑各板形雙片潛板的最佳設置位置(A 板) ... 98

圖 4-68 不同曲率半徑各板形雙片潛板的最佳設置位置(B 板) ... 98

圖 4-69 不同曲率半徑矩形板三片潛板的最佳設置位置 ... 99

圖 4-70 不同曲率半徑前傾板三片潛板的最佳設置位置 ... 99

圖 4-71 不同曲率半徑束縮板三片潛板的最佳設置位置 ... 100

圖 4-72 不同曲率半徑各板形三片潛板的最佳設置位置(A 板 ... 100

圖 4-73 不同曲率半徑各板形三片潛板的最佳設置位置(B 板) .. 101

圖 4-74 不同曲率半徑各板形三片潛板的最佳設置位置(C 板) .. 101

圖 4-75 矩形板潛板系統潛板數量與抬升量關係(

r b

_c

/ = 10

) .... 102

圖 4-76 前傾板潛板系統潛板數量與抬升量關係(

r b

_c

/ = 10

) .... 102

圖 4-77 束縮板潛板系統潛板數量與抬升量關係(

r b

_c

/ = 10

) .... 103

圖 4-78 各板形潛板系統潛板數量與抬升量關係(

r b

_c

/ = 10

) .... 103

圖 4-79 各形潛板系統效果與效率比較(

r b

_c

/ = 5

)... 104

r b

_c

/ = 10

) ... 104

r b

_c

/ = 20

)... 105

r b

_c

/ = 100

) ... 105

圖 A-1 彎道正交曲線座標系統示意 ... 106

(15)

符號表

iA 潛板面積

( m

²

)

a

_ni,mj 第

m 片潛板的第 j 個渦流環於第 n 片潛板上的第i 個小

板上中點法向量之影響係數分量

B Coulomb

摩擦因子，通常

B

=

4 b

河川寬度

( m )

C Chezy

係數

D

沉滓中值粒徑

( m ) d

河川水深

( m ) dv G

微小渦流段的長度

( m ) d

_b 河川凹岸水深

( m )

d

_v 渦流段至計算點

p 之距離 ( m ) d

_w 河川未設置潛板之凹岸水深

( m ) d

₀ 河川平均水深

( m )

(d

_h

)

_M 於

M 組垂直鏡像計算量下之河川凹岸水深 ( m )

E

尺度因子

F Darcy-Weisbach

摩擦係數

F

p 沉滓福祿數， _p

u

F

=

gD

f

ij

JG 影響係數向量

, ni mj

JG

f

影響係數向量

(16)

F

s

、 F

n

、 F

z

分別為 s 、 n 、 z 三方向之應力項 ( N

2

m ) g

重力加速度

( m

2

s )

g

s

、 g

n 分別為

s、n 方向上單位寬度之河川宰體積流率 ( m

³

s )

K

s 沉滓特性係數

k

近底床流速與平均流速之比

L

潛板板長

( m )

L

t 束縮板板頂長度

( m ) L

b 束縮板板底長度

( m )

l

v 渦流段之長度

( m )

m

流速剖面指數

M

垂直鏡像數量

N

潛板系統中的潛板數量

n G

ni

各片潛板小板作用點之單位法向量

P

壓力

( N )

, ni mj

q

G 潛板系統中第

m 片潛板上的第 j 個渦流環於第 n 片潛

板上的第

i 個小板中心所產生的速度場

q

_θ

Δ

渦流段於計算點

p 所產生的切線速度 ( ^m _s ) R

彎道中斷面上任一點之曲率半徑

( m )

r

_c 彎道斷面中心點之曲率半徑

( m ) r

G

微小渦流段之中點指向計算點

p 的向量

(17)

r

微小渦流段之中點指向計算點

p 的長度 ( m ) r

1

G 、 r G

2

分別為計算點

p 指向渦流的向量

r

0

G

渦流兩端依右手定則之渦流向量

r

d 距渦流中心的長度

( m ) S

s

、 S

r 分別為縱向及徑向水面坡降

U

∞ 入流平均流速

( ^m _s )

u 、 v 、 w 分別為 s 、 n 、 z 三方向之流速項 ( ^m _s ) u

距底床高度

z 之流速 ( ^m _s )

u

* 為剪力速度

( ^m _s )

u 、 v

分別為

s 及 n 方向之平均流速 ( ^m _s ) u

b

、 v

b 分別為

s 及 n 方向之底床流速 ( ^m _s )

u' 、 v’

分別為

s 及 n 方向之流速與平均流速之差 ( ^m _s ) V

i 第

i 片潛板所產生的最大徑向流速 ( ^m _s )

V

w 無設置潛板時之最大徑向流速

( ^m _s ) V JG

m

第

m 片潛板對下游計算點 p 所產生之合成速度場

V JG

ind

潛板系統對計算點

p 所產生之合成速度場 v'

b 為近底床處

n 方向流速與平均流速之差 ( ^m _s )

v

θ 受粘性擴散影響之渦流切線速度

( ^m _s )

W

1

、 W

2 分別為

1

號板及

2

號板鎖產生的範束渦流

(18)

W

m 為鏡像潛板所產生的範束渦流

w

12

W

1對

2

號板所產生的速度向量

( ^m _s ) w

21

W

2對

1

號板所產生的速度向量

( ^m _s )

w

12s

、 w 分別為

_12n

w

₁₂延水流方向及垂直水流方向的分量

( ^m _s ) w

21s

、 w 分別為

_21n

w

₂₁延水流方向及垂直水流方向的分量

( ^m _s ) w

mA 為鏡像潛板的範束渦流對

A

潛板所產生的速度向量

( ^m _s )

w

mAs

、 w

_mAn

分別為 w 延水流方向及垂直水流方向的分量

_m₁

( ^m _s ) x

v 計算點與渦流中心沿水流方向之長度

( m )

z

_s

、 z

_g 分別為水面高程及底床高程

( m )

α

^{潛板之攻角}

β

0 沉滓運移係數，值介於

2

到

4

之間

β

計算點

p 與微小渦流段的夾角

β 、

1

β

₂ 分別為計算點至點

1

及點

2

的夾角 Δ 沉滓浸沒比重

δ

t 前傾板板頂前傾長度

( m )

δ 、

A

δ

_B 分別為

A

板及

B

板與岸壁的距離

( m )

ε

^{渦流黏滯係數}

Γ 渦流之環流量

Γ 第

j 個渦流環的強度

(19)

Γ mj 第

m 片潛板對第 j 個渦流環的強度

η

束縮板板頂與板底之比值

κ ^{von Karman}

^係數

Λ 前傾板板頂前傾長度與板長之比值

λ

i 第

i 片潛板的交互作用因子

θ

臨界

Shield

參數

ρ

s 沉滓密度

( kg

3

m ) ρ

_流體密度

₍ ^kg

₃

m )

τ 、

vs

τ

_vn 分別為潛板產生之

s

及

n

方向之底床剪應力

( N

2

m ) τ 、

bs

τ

_bn 分別為

s

及

n

方向之底床剪應力

( N

2

m ) τ 、

s

τ

_n 分別為

s

及

n

方向之剪應力

( N

2

m )

(20)

第一章導論

1-1 前言

天然河川因地形高低起伏的變化大多呈現蜿蜒曲折的彎曲河道，水流通過彎道時由於離心力的作用與上下層水體間的速度差，產生河川彎道中特殊的二次流現象，此二次流現象目前已知是造成彎道凹岸淘蝕與凸岸淤積的主要原因，對於河道的穩定有嚴重影響。

針對此一造成河岸侵蝕的成因，美國愛荷華大學水力工程研究所

(Iowa Institnte of Hydraulic Research,IIHR)

的

Odgaard

教授等人提出以潛沒式導流板

(

簡稱潛板

)

的水工設施來改變彎道中的流場進而達到保護河岸的效果。潛板係一系列垂直設置於渠道底床上且與水流方向呈一夾角之薄板，利用水流通過時於潛板的兩側所產生的速度差，於下游流場中捲合成衣與河川二次流方向相反之尾跡渦流以產生抵消或減小彎道二次流的效果，進而達到保護河岸的目的。

本研究的目的係針對矩形、板頂前傾、板頂束縮等三種板形所組成的潛板系統，探討各形潛板間的交互作用現象，同時分析在交互作用的影響下各形潛板於河川彎道中的最佳位置，期能使潛板系統發揮最大的效能。

1-2 文獻回顧

關於潛板的研究首推美國愛荷華大學水工試驗所近二十年來的一系列理論推導與實驗分析，研究結果並已進入實用階段，應用範圍包含河川取水口泥沙排除、河岸保護、渠道疏濬等，茲略舉相關研究如下：

Odgaard and Mosconi(1987)

將潛板設置於美國

East

Nishnabotna

河以防止河岸彎道受二次流影響而改變，於沒有

(21)

Odgaard(1991)

以彎道理論推導受潛板影響之底床側向剪應力及徑向底床剖面，並進行單片潛板以及潛板系統之水槽實驗驗證。

Wang(1996)

分別於美國

Cedar River

及

Rock River

以潛板系統改變渠道底床高程以利河川取水口之取水效率，結果發現潛板可有效降低取水口之渠道底床高程以利河川的取水效率。

Johnson

及

Hey (2001)

等人，將潛板緊貼於岸壁並與水流方向呈一攻角，進行以潛板控制渠道中橋墩基腳淘刷的試驗，實驗結果發現潛板對於保護橋墩基腳有非常優良的效能，試驗最後並找出最佳的板高及攻角，最佳效果之潛板數量，以及於橋墩上游設置潛板之位置。盧

(2006)

以彎道凹岸處的水深為最佳化目標，進行潛板系統配置的最佳化。發現當潛板系統設置位置皆於最佳位置時，潛板數量增加，其效果上升而效率下降，其效率下降程度與渠道渠寬比、寬深比及沉滓福祿數有關。羅

(2006)

嘗試以小板法找出單一潛板的最佳設計尺寸及形狀，模擬結果顯示出潛板設計最佳高度約為

0.58

至

0.7

倍水深，且在潛板面積固定下，板高固定板長改變的板頂束縮及板頂前傾兩種形狀可以加強潛板的效能。 1-3 研究動機

在前人的研究中

(Wang, 1991

；盧，

2006)

曾指出潛板間有交互作用的現象產生，此一交互作用現象不但影響每一潛板所產生的渦流強度，同時對該潛板系統於底床上所產生的泥沙運移效果也有直接的關連。然而，由於前人的研究大多採用簡化的渦流理論探討此一交互作用現象，因此研究效果多僅適用於矩形潛板系統，對於其他形狀的潛板系統間的交互作用現象，則較少有研究者觸及。

1-4 研究方法

本研究應用機翼理論中的小板法

(Lifting-surface method)

將潛板系統中各潛板切分為數個小板，分別計算各小板所產

(22)

生之環流量，並推算各潛板在後方河川底床所產生的徑向剪應力，分別疊加後計算整體潛板系統所產生的底床徑向剪應力，配合

Odgaard

與

Wang(1991)

推導之床形公式，計算在潛板系統作用下的床形變化。同時並引用

Wang(1991)

及

Odgaard and Spoljaric(1986)

之水槽試驗進行模式的驗證。最後並嘗試找出在不同潛板尺寸及形狀下，潛板系統於渠道中的最佳排列位置。

1-5 本文流程

本研究共分為五個章節，各章節內容如下，流程圖如圖

1-1

所示。

第一章：回顧前人對潛沒式導流板所進行之研究以及結論，並簡介本研究之動機及方法。

第二章：對本研究所採用潛板系統之數學模式進行推導。

第三章：對本模式所採用的網格密度及鏡像數量進行探討，並以實驗資料對數值計算的結果進行驗證。

第四章：討論各種板形潛板系統的交互作用現象及潛板系統的最佳設置位置。

第五章：將本研究之成果整理歸納並條列說明。

(23)

第二章潛板與床型模式之建立

當水流通過與流向呈一夾角之潛板時，因潛板兩側的流速差而產生一環繞於潛板之渦流，此渦流一般稱為範束渦流

(bound vortex)

。範束渦流到達潛板頂端時，受到水流的帶動而轉變成一向下游之渦流，

此渦流一般稱為尾跡渦流

(wake vortex)

或翼尖渦流

(tip vortex)

，如圖

2-1

所示。因受到流體黏滯性的影響，尾跡渦流離開潛板後隨距離的增加而逐漸衰減直到完全消散。潛板即是利用此尾跡渦流改變下游的流場及底床剪應力分布，達到控制底床沉滓運移進而改變渠道床形的目的，如圖

2-2

所示。

本研究應用小板法以密佈於一潛板系統中各潛板上的渦流系統模擬該潛板系統所產生的流場，以探討潛板系統中各潛板間的交互作用，並分析渠道底床在潛板系統作用下的床形變化，理論說明如下。

2-1 一渦流段所產生之速度向量

一微小的渦流段如圖

2-3

所示，此渦流段所產生的切線速度向量可由

Biot-Savart Law

表示如下

4

3

d v r q π r

Γ × Δ =

G G

(2-1)

式中

(24)

Γ 為微小渦流段之環流量；

r

G

為微小渦流段之中點指向計算點

p

之向量；

r 為微小渦流段之中點指向計算點 p

之長度純量；

d v G

為微小渦流段之長度。

由圖

2-3

之幾何關係，將上式改寫為切線速度的純量式。

2

sin

4

^v

q dl

θ

r

γ π

Δ = Γ (2-2)

式中

q

_θ

Δ 為該渦流段於計算點

p

所產生之切線速度；

β

為計算點

p

與微小渦流段之夾角；

l

v為渦流中心至計算點沿水流方向之距離；

又因以下幾何關係

v

cos

d = r β

_(2-3)

v v

tan

l = d β

_(2-4)

cos2 v v

dl d d β

=

β

(2-5)

其中

d

_v為渦流段中心至計算點

p

之垂直距離。

可將式

(2-2)

改寫為下式

(25)

4

_v

sin

q d

θ

d β β

π

Δ = Γ (2-6)

由圖

2-4

中考慮一段自點

1

至點

2

之渦流所產生之切線速度，將

(2-6)

式對

β

進行積分後得到下式。

1,2 1 2

( ) (cos cos )

4

_v

q

^θ

d β β

π

= Γ − (2-7)

式中

β

₁及

β

₂分別為計算點至點

1

及點

2

之夾角。

如圖

2-4

所示，由三維向量之幾何關係可得下列關係式。

0 2 1

r = − r r

G G G

(2-8)

2 1

0

r r dv r

= ×

G G

G (2-9)

0 1

1

0 1

cos r r

β

=

r r

^⋅ G G

G G (2-10)

0 2

2

0 2

cos r r

β

=

r r

^⋅ G G

G G (2-11)

上述式中

r

1

G

、

r G

2

分別為計算點

p

至點

1

及點

2

之向量；

r

0

G

為點

1

至點

2

之向量。

該渦流段於計算點

p

所產生之速度的方向可由下式表示

(26)

1 2

r r r r

×

× G G

G G (2-12)

分別將式

(2-8)

至式

(2-12)

代入式

(2-7)

中並整理如下

1 2 1 2

2 0 1,2

1 2

4 r r r r

q r

r r r r

π

⎛ ⎞

Γ ×

= ⋅⎜ − ⎟

× ⎝ ⎠

G G G G

G G

G G (2-13)

由於受到流體黏滯度的影響，潛板下游之尾跡渦流隨距離增加而逐漸衰減直至消散，其切線速度的衰減可由下式表示

(Lamb,1932)

2/ 4

(1

^ur^d ^x^v

)

v

_θ

= Γ − e

⁻ ^ε (2-14)

式中

u

為水流速度；

r

d為渦流中心至目標點之垂直距離；

x

v為潛板後緣至計算目標點之水流方向距離；

ε

為紊流黏滯係數可由下式進行推算

(Odgaard and Spoljaric,1986)

0

1 1 1

6 (1 )(1 )(1 )

2 3

ud

m m m m

ε = κ

+ − −

^(2-15)

式中

m

為縱向流速剖面指數；

(27)

κ

為

von Karman

係數。

2-2 小板法

小板法是將潛板切分為數個密佈於潛板上的小板，並以一矩形之環狀渦流模擬每片小板周圍之流場如圖

2-5

所示。應用

(2-13)

式之渦流速度計算公式，單一潛板上第

j 個渦流環於第i 個小板中心所產生

之速度場為

1,2 2,3 3,4 4,1

( )

ij ij j ij

q

K =

q

K +

q

K +

q

K +

q

K = Γ JK

f

(2-16)

式中

Γ

j為第

j

個渦流環的強度；

f

ij

JK

為影響係數向量可由下式推算

1 2 1 2 2 3 2 3

2 01 2 02

1 2 2 3

3 4 3 4 4 1 4 1

2 03 2 04

3 4 4 1

1

ij

4

ij

r r r r r r r r

r r

r r r r

f r r r r r r r r

r r

r r r r

π

⎡ × ⋅ ⎛ − ⎞ + × ⋅ ⎛ − ⎞ ⎤

⎢ ⎜ ⎟ ⎜ ⎟ ⎥

× ⎝ ⎠ × ⎝ ⎠

⎢ ⎥

= ⎢ ⎥

⎛ ⎞ ⎛ ⎞

× ×

⎢ + ⋅ ⎜ − ⎟ + ⋅ ⎜ − ⎟ ⎥

⎢ × ⎝ ⎠ × ⎝ ⎠ ⎥

⎢ ⎥

⎣ ⎦

K K K K K K K K

JJK JJK

K K K K

JK K K K K K K K K

JJK JJK

K K K K

(2-17)

(2-16)

式可推廣至多片潛板之潛板系統之模式，如下式所示

, ( 1,2 2,3 3,4 4,1) , ,

ni mj ni mj mj ni mj

q

K =

q

K +

q

K +

q

K +

q

K = Γ JK

f

(2-18)

式中

, ni mj

q K

為潛板系統中第

m

片潛板上的第

j 個渦流環於第 n

片潛板上

(28)

的第

i 個小板中心所產生之速度場。

Γ

mj為第

m

片潛板上第

j

個渦流環的強度。

, ni mj

JK f

為影響係數向量。

潛板系統中各片潛板上之渦流系統與水流的合成流場必須要滿足法線方向上速度為零的條件，如下式所示

(

q

ni mj,

U

∞)

n

ni 0

∇ K + JG ⋅G =

(2-19) 其中

U

∞

JG

為入流之深度平均流速。

n G

ni

第

n

片潛板上第

i

個小板之單位法線方向向量。

對一含有

M

片潛板且每片潛板上切分為

N

個小板的潛板系統，

將式

(2-19)

整理後可得如下之線性方程式系統

11,11 11,12 21,11 1,

12,11 12,12 2,

21,11 22,11

,11 ,12 ,

... ... ...

... ... ... ...

... ... ... ... ... ... ...

... ... ... ... ...

... ... ... ... ... ... ...

... ... ... ...

M MN

M MN

MN MN MN MN

a a a a

a a a

a a

a a a

⎛ ⎞

⎜ ⎟

⎜⎜

⎜⎝ ⎠

11 11 12 12

21 21

... ...

MN MN

U n U n

U n

∞

Γ ⎛ ⎞

⎛ ⎞ ⋅

⎜ ⎟

⎜ Γ ⎟ ⎜ ⋅ ⎟

⎜ ⎟

⎜ Γ ⎟ = −⎜ ⋅ ⎟

⎟⎜ ⎟

⎜ ⎟

⎟⎜ ⎟

⎜ ⎟

⎟⎜ ⎟

⎜ ⎟

⎟⎜ ⎟

⎜ ⎟ ⎜ ⎟

⎟ Γ⎝ ⎠ ⎝ ⋅ ⎠ JK K JK K JK K

JK K

(2-20)

其中

a

_{ni mj}_. 為第

m 片潛板的第 j 個渦流環於第 n 片潛板上的第 i 個小板

上中點法向量之影響係數分量，如下式所示。

, ni mj, ni

ni mj

a

=

∑

^JK

f

⋅

n

^K ^(2-21)

(29)

解出(2-20)式後即可得到各小板上渦流環Γ 之強度。 _mj

解出Γ 後，第 m 片潛板及水流對下游計算點 p 所產生之合成速_mj 度場可用下式計算

1

2

, 1 , 2

...

,

...

m

m p m p m p mn m

mn

V f f f U

∞

⎡ Γ ⎤

⎢ Γ ⎥

⎢ ⎥

⎡ ⎤

= ⎣ ⎦ ⎢ ⎥ +

⎢ Γ ⎥

⎣ ⎦

JK JK JK JK JK

(2-22)

而整體潛板系統對計算點

p

的速度場則為

11 12

,11 ,12 ,21 ,

21

... ... ...

...

ind p p p p MN

MN

V f f f f U

∞

⎡ Γ ⎤

⎢ Γ ⎥

⎢ ⎥

⎡ ⎤

= ⎣ ⎦ Γ ⎢ ⎢ ⎥ ⎥ +

⎢ ⎥

⎢ Γ ⎥

⎣ ⎦

JK JK JK JK JK JK

(2-23)

其中

JK f

_{p mj}_,

為第

m

片潛板的第

j 個渦流環對計算點 p

所產生之影響係數向量。

在上述渦流環強度的計算中，由於各渦流環對合成流場的影響皆已考慮在內，因此

(2-20)

式的解已包含各板間的交互作用現象，可由各板單獨產生之床形側向速度變化加以分析。

2-3 受潛板系統影響之床形

本研究引用

Odgaard and Wang(1991)

的彎道床形模式進行渠道床

(30)

形形狀變化的計算，該模式的推導過程詳見附錄

A

，其中水深在徑向的變化如下式所示

( )

bn

d d m

dn kuB gD τ

ρ θ

= − Δ

^(2-24)

式中

( ) /

d d dn

為受到彎道二次流影響下徑向水深變化率；

m

為縱向流速剖面指數；

ρ

為流體密度；

u

為渠道中平均流速；

B

為

Coulomb

摩擦因子；

θ

為臨界

Shields

剪力；

Δ

為沉滓浸沒比重；

g

為重力加速度；

D

為底床沉滓中值粒徑；

τ

bn為

n

方向之底床剪應力，彎道二次流所產生之

τ

_bn可由下式推估

(Odgaard and wang,1991)

2

2 2

(2 1)( 1)

[2 ( 1)]

bn

k m m u

m m k m d R

τ = − ⁺ ⁺ ρ

+ +

^(2-25)

其中

k

為近底床流速與平均流速之比值，

Odgaard and Wang(1991)

建議

(31)

以

1

進行計算。

R

為渠道逕向上各點之曲率半徑。

應用小板法求得潛板系統所產生的流場後，依據

Rozoskii(1957)

的假設，底床上徑向剪應力與縱向剪應力的比值約略與徑向流速與縱向流速的比值成正比，如下式所示

vn vb

bs b

v u τ

τ ⁼

^(2-26)

上式中

τ

vn為潛板引致之底床剪應力。

v

vb為潛板所引致之底床徑向流速。

u

b為近底床縱向流速，以

u

_b

= u k /

求得。

τ

bs為底床縱向剪應力，可由

Darcy-Weisbach

公式計算如下

2 2 bs 2

u m

τ = ρκ

^(2-27)

彎道中設置潛板系統後的底床徑向剪應力為彎道二次流所產生之底床徑向剪應力

( τ

_bn

)

及潛板系統所產生之底床徑向剪應力

( τ

_vn

)

二者的疊加，同時

(2-24)

則可改寫如下

( ) (

_bn _vn

)

d d m

dn kuB gD τ τ

ρ θ

= − +

Δ

^(2-28)

(32)

此式即為受彎道二次流及潛板系統影響下之徑向床形變化。

2-4 邊界效應

由於河川流場同時受到自由水面與底床之水平方向邊界及兩側岸壁之垂直邊界的影響，本研究採用鏡像法

(method of images)

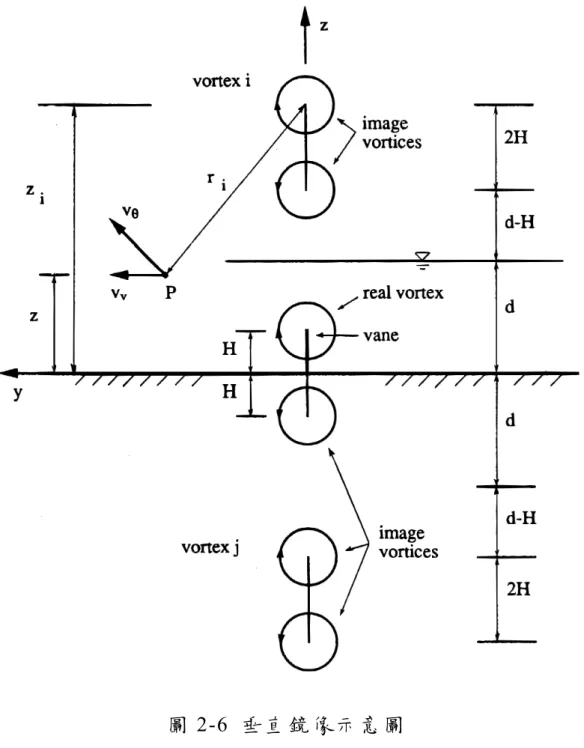
加以模擬這些邊界的效應。自由水面與底床的邊界效應係利用在水面上方及底床下方的垂直對應位置處設置潛板系統的虛擬鏡像加以模擬，如圖

2-6

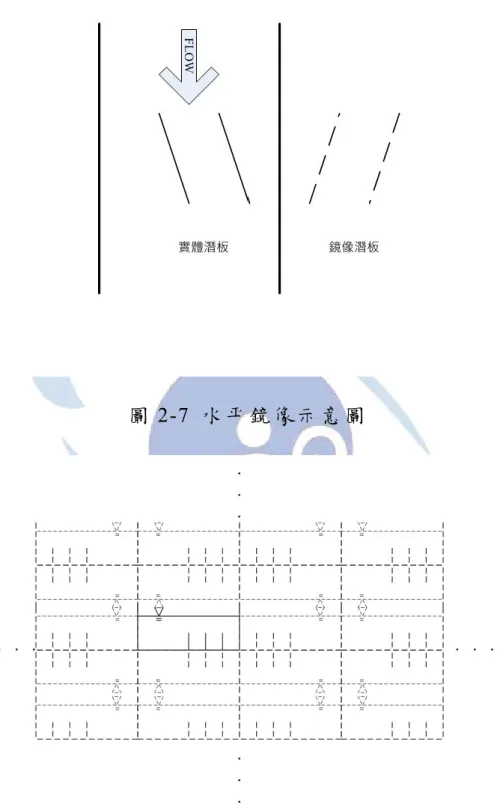
所示，虛擬板上的渦流系統強度與實體板完全相同，但方向相反。

同理兩側岸壁的邊界效應則利用在岸壁外的水平對應位置設置的潛板系統虛擬鏡像加以模擬如圖

2-7

所示。渠道中的流場則由所有渦流系統

(

包含實體潛板系統及虛擬潛板系統

)

的總和效應疊加而得，如圖

2-8

。理論上水平及垂直鏡像皆須設立無限多組方能完整模擬各個邊界對流場所產生的影響，然而實際計算上並不可行，確切的鏡像數量將再下一章加以分析。

(33)

第三章數值模式建立與驗證

本研究以潛板的垂直鏡像模擬水面及河川底床的邊界效應，理論上須無限多組垂直鏡像方能完整模擬流場的變化，但實際計算上並不可行，故必須決定合理的鏡像組數，才可正確反映水面及底床的邊界效應。

此外，由於小板法係以密佈於潛板上之渦流系統模擬該潛板所產生的流場，計算結果的精確度與渦流系統的密度有關，為提高模擬的精確度，潛板網格密度必須提高，但相對的計算時間也會延長。考慮計算精度及合理的計算時間，必須決定適當的網格密度。

由於網格密度及鏡像組數皆會影響本模式的模擬結果，故將此二者合併討論以決定適當的網格密度及鏡像組數。

本研究主要針對三種不同形狀的潛板進行分析，分別為矩形板、

前傾板及束縮板。各種板形分別定義如下：

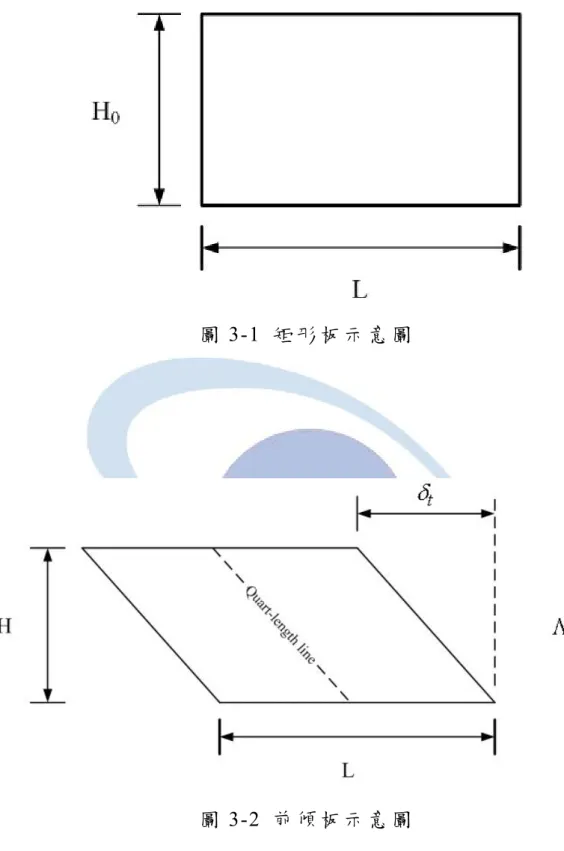
矩形板係一外形為矩形之平板，其長度與高度分別為

L

與

H

如圖

3-1

所示。

前傾板係板頂逆水流方向位移一

δ

_t長度，高度為

H

之平行四邊形板，如圖

3-2

所示，並定義其前傾程度為板頂前傾之長度與板長之比如下式所示

t

L

Λ =

δ (3-1)

(34)

其中

δ

_t為板頂前傾之長度。

束縮板係板頂自板底收縮一長度之梯形板，由機翼理論的定義束縮板四分之ㄧ板長之連線為一垂直線，其束縮程度則以板頂長度與板底長度之比值加以定義，如下式所示

t b

L

η = L (3-2)

由羅

(2006)

的研究指出矩形板在底邊與高的比為

0.65

時會有最

佳的底床抬生量，故便以此面積作為基準，在不改變板高及面積的條件下改變前傾板的前傾比以及束縮板的束縮比。依據前述各種板形的定義，針對矩形板

(H/L=0.65)

、前傾板

( Λ = 0.5 )

及束縮板

( η

=0.5

)

三種板形，進行網格密度及鏡像組數的數值試驗分析。

3-1 網格密度與垂直鏡像數量分析

垂直鏡像主要模擬水面及底床之邊界，因水面與底床間之範圍與潛板系統所能影響之範圍相當接近，故需較多的垂直鏡像進行模擬，

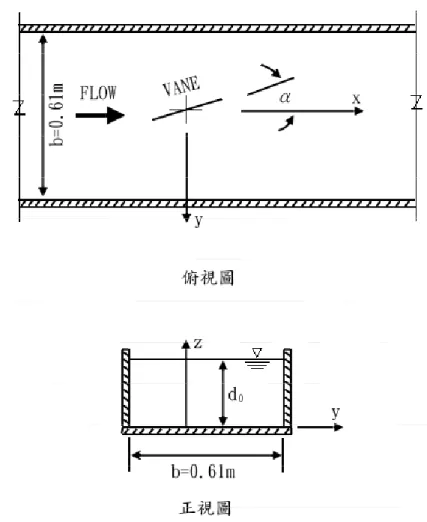
本研究模擬 0 至 50 組垂直鏡像與網格密度之關係進行比較，以找出最佳的垂直鏡像數量與網格密度。數值試驗的佈置條件如下水深

d

₀為 0.152

m

；流速u 為 0.259 /

m s

；底床中質粒徑為0.0017

m

；潛板設置角度

α

為 20 度。網格密度分別以 N=5×2、10×5、14×7、20×10、30×

15 格，鏡像數量則由 1 組變化至 50 組，分別計算上述情況下三種板

(35)

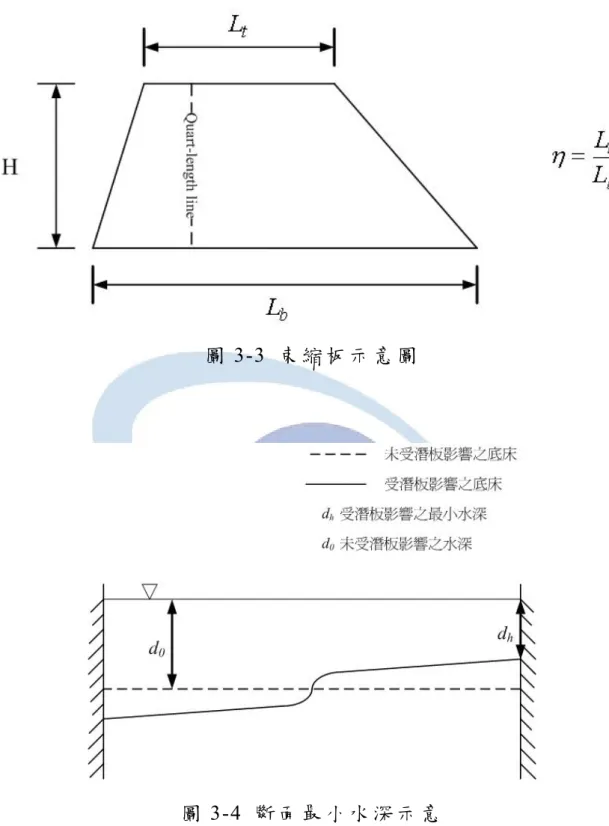
形之斷面最小水深如圖3-4 所示，並以前後兩組鏡像計算結果之差量評估結果的收斂性，如下式所示

( ) 1 ( ) ( ) 100

h M h M

h M

d d

d

+ − × ％ (3-3)

上式中

M

為垂直鏡像組數。

( )

d

_{h M}₊1為

M + 1

組垂直鏡像組數計算斷面之最小水深。

( )

d

_{h M} 為

M

組垂直鏡像組數計算斷面之最小水深。

圖 3-5、圖 3-6 及圖 3-7 分別為矩形板、前傾板及束縮板在不同垂直鏡像與網格密度之差量下的計算收斂情形，圖中顯示在各種網格佈置下的計算結果於鏡像組數低於10 組時的計算差量變化較大，於 20 組以上鏡像後變化趨於平緩，故本研究選定 20 組垂直鏡像於後續的計算分析中。網格點密度除 N=5×2 外其餘各組於鏡像數量達 20 組後均維持穩定變化，在 N=20×10 的網格密度下，以 20 組鏡像及 21 組鏡像進行計算的結果差量已低於萬分之ㄧ，考慮合理的計算時間與計算精確度，本研究選定網格點密度為N=20×10 進行後續分析模擬。

3-2 網格密度與水平鏡像數量分析

水平鏡像主要用於模擬渠道岸壁的邊界效應，由於渠道寬度遠大於潛板系統所能夠影響之範圍，故並不需要過多的水平鏡像，本研究

(36)

針對矩形板、前傾板、束縮板分別以0 至 2 組鏡像進行計算並分析其結果。

圖3-8、圖 3-9 及圖 3-10 分別為矩形板、前傾板及束縮板於不同水平鏡像與網格密度之模擬結果，其中受潛板影響之斷面最小水深

d h

以無潛板之斷面水深

d _w

無因次化。圖中顯示各板形於各種不同網格配置下，水平鏡像數量 1 組與 2 組之計算結果趨近一致，故本研究選定以1 組水平鏡像於後續計算中。

3-3 模式驗證

本研究採用 Spoljaric and Odgaard(1986)及 Wang(1991)所進行之水槽試驗進行模式的驗證。Wang 的水槽試驗分為直渠道及彎曲渠道配置，分別如圖 3-11 及圖 3-12 所示。Spoljaric and Odgaard(1986)進行之直渠道水槽試驗佈置如圖3-13 所示。

3-3.1 直渠道單潛板

本驗證採Spoljaric and Odgaard(1986)進行之直渠道試驗資料，相關試驗佈置參數如下：渠道寬2

ft

；初始水深0.17

m

；沉滓中值粒徑 0.3

mm

；沉滓臨界剪力為 0.034；渠道平均流速為 0.304745 /

m s

；縱向流速剖面指數

m

= 。於渠道中設置一矩形潛板，其中板高及板長3 分別為 0.085

m

及 0.21

m

；設置攻角為 15 度；設置位置為渠道中央，

(37)

分別取位於潛板後方3.3 倍水深、5.1 倍水深及 6.9 倍水深三處斷面床形資料進行模式的驗證，並將模擬結果與驗證資料繪製於圖 3-14(a) 至圖 3-14(c)。圖 3-14(a)中模擬結果因該斷面與潛板距離較近，流場較不穩定，故驗證結果較不理想。圖 3-14(b)及圖 3-14(c)則趨勢大多與試驗資料相符，驗證成果尚可接受。

3-3.2 直渠道單潛板

此驗證採用Wang(1991)之 MR1 水槽試驗資料，試驗佈置參數如下：渠道寬 2 英尺；初始水深 0.52

ft

mm

ft s

5.2

m

= ，於渠道中設置一矩形潛板，其中板高為 0.25

ft

；板長為 0.5

ft

；設置攻角為 20 度；設置位置為渠道中央。分別取位於潛板後方0.962 倍水深、1.923 倍水深及 3.846 倍水深三處斷面床形資料進行模式的驗證，驗證結果如圖 3-15(a)至圖 3-15(c)所示。圖 3-15(a)及圖 3-15(b)中模擬結果與試驗資料趨勢一致，結果良好，圖 3-15(c)因與潛板距離較遠，二次流因流體黏滯的關係衰減，故模擬結果較差。

3-3.3 直渠道潛板系統

此驗證採用Wang(1991)之 MS4 試驗資料，相關試驗佈置如下：

渠道寬2.44

m

；初始水深0.1615

m

mm

；沉滓臨

(38)

界剪力為 0.034；渠道平均流速為 0.3383 /

m s

；縱向流速剖面指數 4.7

m

= ，於徑向設置四矩形潛板，其中板高為 0.0762

m

；板長為 0.1524

m

；設置攻角為 20 度；設置位置分別為距凹岸 0.59

m

、0.74

m

、 0.89

m

及1.09

m

。模擬驗證結果如圖3-16 所示，模擬成果大致與試驗結果接近。

3-3.4 彎曲渠道無潛板

此驗證採用Wang(1991)之 MB1 試驗資料，試驗佈置如下：彎道中心曲率半徑

r

_c =12.68

m

；渠道寬度1.94

m

；初始水深 0.1524

m

；沉滓中值粒徑為 0.41

mm

m s

m

=4.8。本試驗因無潛板影響，主要是試驗底床受二次流影響下之床形，經與模擬結果比對展繪於圖3-17 中，驗證結果相當良好，由圖可知本模式可正確反映出河川底床於二次流影響下之徑向床形。

3-3.5 彎曲渠道潛板系統

此驗證採用 Wang(1991)之 MB2 試驗資料，彎道中心曲率半徑 12.68

r

c =

m

；渠道寬度1.94

m

；初始水深 0.1524

m

；沉滓中值粒徑為 0.41

mm

；沉滓臨界剪力為0.034；渠道平均流速為 0.4023 /

m s

m

=4.8 ，於徑向設置二矩形潛板，其中板高為

(39)

0.0762

m

；板長為 0.1524

m

；設置攻角為 15 度，設置位置非別為距凹岸 0.27

m

及 0.45

m

，模擬結果與是驗資料套疊展繪於圖 3-18 中，

驗證結果尚稱滿意。

(40)

第四章結果與討論

本章針對矩形板、前傾板及束縮板三種板形所組成的潛板系統進行分析，探討方向分為三部份：

1.各形潛板系統間的交互作用現象 2.各形潛板系統的最佳設置位置 3.各形潛板系統的效果與效率分析

探討的三種板形分別如第三章所定義，依據羅(2006)的研究，板長與水深比為 1 時矩形板之最佳板高與板長之比約為 0.65，本研究採用此種比例為矩形潛板之基準板形。同時，為比較三種板形的分析結果前傾板及束縮板之板高與矩形板相同，並改變前傾板及束縮板之板長，使各板形的面積一致。在三種板形的面積與高度相同的條件下，針對潛板形狀變化對其效能的影響進行比較分析。

4-1 潛板系統的交互作用現象

Wang(1991)及盧 (2006)的研究曾指出，潛板系統中各潛板之間有交互作用的現象，各板由於受到其他潛板的影響而導致效能減弱，且此一交互作用對徑向床形的變化有直接的影響。

(41)

本研究以小板法計算出各潛板上的渦流環強度後，應用 (2-22)式計算各潛板所產生之底床側向流速分佈，並定義潛板的效能如下

i i

w

V

λ

=

V

(4-1)

式中

λ _i

為第

i 片潛板之效能；

V i

為第

i 片潛板所產生之最大徑向流速； V w

為單一潛板所產生之最大徑向流速；

λ i

越大表示該板所受交互作用影響小，效能損失小；

λ _i

越小表示該板所受交互作用影響大，效能損失大。

以下分別探討各種板形所組成之二潛板系統的交互作用、二潛板系統與岸壁的交互作用及三潛板系統的交互作用。

4-1.1 二潛板系統的交互作用

本節主要討論由二片潛板所組成的二潛板系統間的交互作用現象，各板編號由板尾指向的方向開始依序編號，模擬佈置如圖 4-1 所示。圖 4-2 至圖 4-4 分別為矩形板、前傾板、束縮板的二潛板系統的效能在

α

=10^。及 20^。時，隨二板間距

δ

/

d

₀ 的變化情形，由圖中顯示三種各板形於攻角 20 度時二板間效能的差量皆大於攻角 10 度時二板間效能的差量，顯示攻角越

(42)

大二潛板間的交互作用越劇烈。圖 4-5 為三種板形之 1 號板於

α

=10^。時之效能變化情形的比較，圖中顯示各板形的 1 號板於二潛板接近時矩形板所受之交互作用最為強烈，前傾板及束縮板所受交互作用後的效能幾乎一致，隨二潛板間距逐漸增加，各板形交互作用也逐漸降低使效能趨近於 1。圖 4-6 則為

α

=10^。時三種板形之 2 號板的效能變化情形，圖中顯示二潛板接近時於 2 號板束縮板所受之交互作用最為強烈，前傾板次之，而矩形板則最輕微。隨間距增加各板形潛板交互作用也逐漸減小，使效能趨近於 1。將攻角 20 度各板形 1 號板之效能繪製於圖 4-7 中，結果顯示於 1 號板之交互影響作用也以矩形板為最強烈，前傾板與束縮板也近乎一致，隨潛板間間距越大其交互作用也越小，使其效能趨近於 1。將攻角 20 度各板形 2 號板之效能繪製於圖 4-8 中，結果顯示潛板間距接近時束縮板之交互作用最為強烈，矩形板交互作用較小。

圖 4-9 至圖 4-11 分別為矩形板、前傾板、束縮板於 =10

α

^D 及20^D時二板之效能的比值

λ λ

₂/ ₁隨二板間距

δ

/

d

₀的變化情形，圖中顯示各板形潛板間的效能比於攻角20 度隨

δ

/

d

₀的變化較攻角 10 度的更為明顯，說明攻角越大則潛板間的交互作用也越強烈；圖中顯示潛板間距較近時

λ λ

₂/ ₁小於 1 即 1 號板的效

(43)

能大於 2 號板的效能，而潛板間距大時

λ λ

₂/ ₁大於 1 為 2 號板的效能大於 1 號板的效能，此現象可由機翼理論加以說明。如圖 4-12 及圖 4-13 所示，圖中

W 1

、

W ₂

分別為 1 號板及 2 號板所產生之範束渦流；

w 12

為

W ₁

對 2 號板所產生的速度向量；

w 21

為

W ₂

對 1 號板所產生的速度向量；

w 12s

、

w _12n

分別為沿水流方向及垂直水流方向之

w ₁₂

分量；

w 21s

、

w _21n

分別為沿水流方向及垂直水流方向之

w ₂₁

分量；

由於

w _12n

與

w _21n

的影響，使得各板的入流攻角減少，而造成各板效能的減弱，此即為潛板間交互作用現象的成因，當二板間距較小時，如圖 4-12 所示，由於

w _12n

大於

w _21n

使得 2 號板的有效攻角小於 1 號板的有效攻角，造成 2 號板的效能小於 1 號板的效能。反之、當二潛板遠離時，如圖 4-13 所示，由於

w _21n

大於

w _12n

使得 1 號板的有效攻角小於 2 號板的有效攻角，造成 1 號板的效能小於 2 號板的效能。

比較各板形之

λ λ

₂/ ₁在

α

=10^D及 20^D時的變化，如圖 4-14 及圖 4-15 所示。圖中顯示二潛板間的效能差異在

δ

/

d

₀小於 1.4 時，以矩形板最小，束縮板則差異最大，二板的效能差異隨間距增大而逐漸接近，當

δ

/

d

₀大於 1.4 後，二板的效能已大

(44)

致相同，比較圖 4-14 及圖 4-15 可看出當攻角增大時，前述現象也越明顯。

4-1.2 二潛板系統與垂直岸壁的交互作用

本節主要討論在垂直岸壁與潛板系統間的交互作用，當潛板系統的設置接近岸壁時，因受到岸壁邊界效應的影響，使得潛板系統的交互作用產生不同的結果。圖 4-16 為潛板系統的設置示意圖，圖中

δ A

為岸壁與 A 板的間距；

δ B

為岸壁與 B 板的間距；

圖 4-17 至圖 4-22 分別為矩形板、前傾板及束縮板的二潛板系統之效能隨

δ

_A/

d

₀與

δ

_B/

d

₀的變化情形。結果顯示各板形於潛板的位置接近岸壁時該板的效能皆出現大於 1 的情況，此現象類似於機翼裡論中的地面效應(Ground Effect)，其原因可由圖 4-23 加以說明，圖中

W A

為 A 潛板產生之範束渦流；

W m

為鏡像潛板產生之範束渦流；

w mA

為鏡像潛板的範束渦流對 1 號潛板所產生的速度向量；

國立宜蘭大學土木工程學系 (研究所) 碩士論文 Department of Civil Engineering National Ilan University Master Thesis