臺灣生育率變遷對於人口成長的慣性作用

No. 40, June 2010, pp. 1-39

臺灣生育率變遷對於

人口成長的慣性作用

†

陳信木

*

_林佳瑩

** † 感謝兩位匿名審查者提供寶貴意見，長庚大學醫務管理學系陳寬政教授對於初稿多所 指正建議，在此特予致謝。另外，作者必須感謝研究助理張巧旻、黃俞樺、和陳雅琪 協助處理資料分析與論文編排。 * 國立政治大學社會學系專任副教授，E-mail: hsinmu@nccu.edu.tw ** 國立政治大學社會學系專任副教授，E-mail: cylin@nccu.edu.tw 收稿日期：2010.06.18；接受刊登：2010.07.25

中文摘要

對於一個封閉人口而言，自然增加乃是決定其人口繁衍之規模與 速度的動力來源。但是，自然增加率固然是測量人口成長的良好指 標，卻是無法反映人口之年齡結構，因而不能正確掌握該人口特定年 齡群體的生育與死亡風險，相對地，Lotka 的穩定人口理論，改以淨 繁殖率測量人口繁衍的水準。具體而言，穩定人口模型在固定年齡結 構的假定之下，將人口成長的水準透過複合式年輪的繁殖函數而反 映，所以，透過 Lotka 的人口再生方程式可以瞭解人口動力變遷之下 的年齡結構變化。不過，正因穩定人口理論假定「穩定人口」條件， 用以測量實際人口成長時，特別是劇烈轉型的人口而言，亦將相當程 度失真偏誤。因此，擴展古典的穩定人口理論，針對非穩定人口測量 其人口繁衍水準，已經成為近來的人口研究熱門課題。本研究即以 NIR、古典 Lotka 模型、與 variable-r 模型三個途徑，分別比較臺灣人 口成長，藉以獲得更佳的人口估計和瞭解臺灣的人口發展潛在問題。 除此之外，即使完成生育轉型的社會，低度生育率對於稍後人口成長 仍將產生相當程度的影響作用，此即所謂的「人口慣性效應」。所 以，本文亦將特別著重於探討臺灣在生育率轉型變遷過程，其所產生 的人口成長慣性效應與其後果。 關鍵詞：繁衍、淨繁殖率、穩定人口、定常人口、人口慣性

對於一個封閉人口而言，自然增加（natural increase）乃是決定其 人口繁衍之規模與速度的動力來源。自然增加率（natural increase rate;

NIR）係指一個人口在特定時期中的生育率與死亡率落差，反映人口 成長的數量、速度、與方向：1 NIR

=

CBR CDR

=

B_P D_P 等式(1) NIR 固然是測量人口成長的良好指標，由於屬於粗率（crude rate）測量，無法反映人口之年齡結構，因而不能正確掌握此一人口 的生育與死亡風險，導致結果，以 NIR 測量人口繁衍將會失真或是偏 誤。 有鑑於此，人口分析經常運用複合式年輪（synthetic cohort）途徑 以反映人口的生育與死亡水準，例如，總生育率（total fertility rate;

TFR）與平均餘命（life expectancy）即是最為經常應用者。2 _另一途

徑，則是採用 Lotka 的穩定人口（stable population）理論，以淨繁殖 率（net reproduction rate; NRR）測量人口繁衍的水準（Lotka 1907, 1922）。由於每一個特定人口隱含一個 stable equivalent population， 所以，NRR 在固定年齡結構的假定之下，將人口成長的水準透過複合 式年輪的繁殖函數（maternity functions）而反映，亦即，應用 Lotka

1 CBR和 CDR 分別代表粗出生率（crude birth rate）和粗死亡率（crude death rate），以 人口數（P）和出生數（B）與死亡數（D）計算生育和死亡發生率。 2 總生育率和平均餘命，分別反映一個假設的複合性年輪，倘若經歷當前盛行之時期性 年齡別生育率或年齡別死亡率，其終生生育水準或是存活壽命。總生育率為育齡階段 [ ， ]之年齡別生育率 f x 的總和： TFR= f x dx 平均餘命 e° x則是 x 歲時存活人口在年齡別死力 x 作用下，至壽命極限 前的平均存 活時間： e°x= xl x+a da l x = x l x e x x+a x+y dy_da l x = xe x x+a x+y dy_da （由於死力為 x =lim n 0[ l x l x+n n l x ]= d l x dx ，將等號左右分別從年齡 x 積 分至 x+a，最後可得 l x+a =l x e x x+a x+y dy_。）

的人口再生方程式，可以知道：3 l

=

e r x m x p x dx 等式(2) 由此可見，NIR 與 NRR 的落差係源自年齡結構效應，此即穩定人 口模型的用處。不過，正因為 NRR 建立在穩定人口的假定之上，且為 一個複合式年論的測量指標，用以測量實際人口成長時，特別是劇烈 轉型的人口而言，亦將相當程度失真偏誤。 因此，擴展古典的穩定人口理論，針對非穩定人口測量其人口繁 衍水準，已經成為近來的人口研究熱門課題。本研究即以 NIR、NRR， 與 variable-r 三個途徑，分別比較人口成長，藉以獲得更佳的人口估計 和瞭解臺灣的人口發展潛在問題。除此之外，即使完成生育轉型的社 會，低度生育率對於稍後人口成長仍將產生相當程度的影響作用，此 即所謂的「人口慣性效應」（population momentum）。4_{所以，本文} 亦將特別著重於探討臺灣在生育率轉型變遷過程，其所產生的人口成 長慣性效應與其後果。

壹、臺灣人口成長與年齡結構

1906年時臺灣人口為 314 萬人，1941 年臺灣人口超過六百萬， 至 1989 年達到兩千萬，迄今，人口數為兩千三百餘萬人。過去一個 世紀以來，臺灣人口巨幅成長，出現「人口爆炸危機」，近年來，臺 灣人口成長已趨緩和，甚至，未來十年內即將出現人口負成長衰退的 3 Lotka的人口再生方程式說明繁殖函數 m x 、存活率 p x 、與人口內在固有成長率三 者關係。此一特徵方程式（characteristic equation）中，m x 反映一個穩定人口在年齡 時的繁殖水準（通常透過年齡別生育率測量之），p x 則是新生兒存活至年齡的機 率，至於則是穩定人口在不受年齡結構與人口規模影響下，生育繁殖水準與存活水準 平衡下的人口成長率，所以稱之為內在固有於其生育與死亡動力的成長率。 4 根據 Lotka 的人口再生方程式 B t = 0 t B t x p x m x dx（Keyfitz 1977; Land

et al. 2005; Pretson et al. 2001），上一代的出生數和盛行的生育率對於次一代的出生數 將會具有加乘影響，所以，低度生育率（低於替代水準）將會進一步促成次代人口規 模不斷衰減，終將出現人口負成長現象。

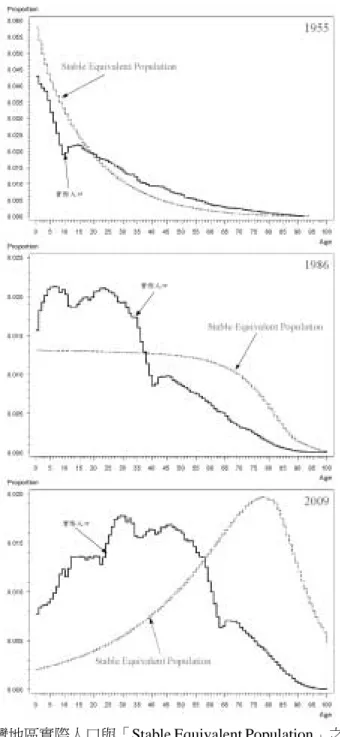
現象。在這一個世紀內，臺灣人口成長曾經幾度受到人口遷徙的重大 影響，也相當程度改變人口結構的面貌；不過，整體而言，自然增加 乃是左右臺灣人口成長的主要動力。 特別是在過去六十年裡，臺灣的人口自然增加從傳統高峰幾近千 分之四十的水準而持續下降，至今，僅有千分之二。毫無疑問，人口 成長的趨勢正是反映臺灣在二十世紀的人口轉型歷程。然而，人口成 長的動力固然來自生育率死亡率，生育和死亡動力的後果與成因，卻 是在於人口結構本身。相應於人口成長率的急速變遷，臺灣的人口結 構也在過去世紀發生劇變—特別是對於人口成長具有顯著影響力的 育齡人口，在過去六十年裡，不論人口規模和年齡組成都徹底改變， 圖 1 比較臺灣在 1947-2009 年間育齡婦女人數變遷，可以明顯看到規 模擴張與週期性演化趨勢。 每一時間點的人口年齡組成，乃是過去人口動力發展的歷史產 物，同時，亦將影響未來人口動力的發展。傳統上，人口分析典型運 圖 1 臺灣地區育齡婦女人數變遷按五歲年齡組分，1947-2009 資料來源：歷年〈台閩地區人口統計〉。

用穩定人口理論探討人口動力後果與未來變遷。不過，穩定人口理 論，雖然具有極高應用價值，其長處優點正也是本身的限制。本研究 將從古典的穩定人口理論出發，然後擴展納入考量人口年齡結構，藉 此分析探討臺灣過去的人口成長變遷以及未來發展。

貳、人口繁殖與 Lotka 的

古典穩定人口理論

替代（replacement）乃是人口的基本生物本能，更是物種存在的 目 的 和 動 機。人 口 或 是 任 何 物 種 的 替 代 機 制，乃 是 透 過 繁 殖 （reproduction）或是再生而兌現，當然將會受到死亡風險抑制。圖 2 呈 現 兩 個 暴 露 於 不 同 死 亡 風 險 水 準 的 人 口，理 論 上 的 育 齡 人 口 （EFGH）在生存風險差異下，實際存活至育齡而能產生替代功能的 數量並補相等（即 IJGH 和 KLGH），不過，實際的替代效應則又將 取決其繁殖水準而有差異。 圖 2 生命表人口、育齡人口、生育率、與淨繁殖率之關係

人類繁衍的表現—生育，將會決定一個人口的替代能力，因 此，在圖 2 裡，透過生育（ASFR）的機制，一個人口將能產生子代 （NRR），以替代親代（IJGH）。所以，在圖 2 中的 NRR 與育齡人口 （IJGH）之相對關係將會展現一個人口的繁殖結果。 任何一個現存人口，都是先前出生人口存活的結果，亦即 N x，t

=

B t x p x 等式(3) 在 t 時間點上年齡為的人口 N x，t 乃是先前 t x 時出生者 B t x 存活（p x 為存活率）的結果。從另一個角度來看，現在的 所有新生人口 B t ，乃是過去出生者（上代）存活至育齡階段（即 B t x p x ），再透過繁殖作用（即 m x ）所衍生的子代。因 此，出現人口再生現象（Coale 1972; Keyfitz 1977; Keyfitz and Caswell 2005; Land et al. 2005; Pretson et al. 2001）：

B t

=

0 t B t x p x m x dx 等式(4) Alfred Lotka早在百年前（1907）即發現—倘若一個人口一直維 持固定生育率與死亡率水準，那麼，這個人口將會「遺忘過去的歷 史」，最終發展成為一個年齡結構固定、永恆的人口。例如，在圖 3 裡，假定臺灣的 2000 年人口若是從此維持不變的生育率和死亡率水 準，一段時間（大約 70 年）之後，年齡結構將會永恆固定。

根據這個現象，Lotka 提出穩定人口（stable population）的理論， 成為人口分析的重要工具之一（Caselli et al. 2006; Coale 1957; Coale and Trussell 1996; Hinde 1998; Keyfitz 1968, 1970; Keytfitz and Caswell 2005; Land et al. 2005; Preston and Coale 1982; Preson et al. 2001; Véron 2009）。基本上，穩定人口理論以上述等式(4)的所謂人口再生方程式 做為基礎，並據此建立 Lotka 的穩定人口特徵方程式（characteristic equation）：5

其中，m x 為繁殖函數（maternity functions），通常以實際觀測 的年齡別生育率測量，p x 乃是存活率（即一個新生兒活存至年齡的 機 率，通 常 以 nLx

n l0 測 量），至 於 r 則 是 所 謂 的 內 在 固 有 成 長 率

（intrinsic growth rate），反映該穩定人口的成長速率。

根據這個方程式，只要一個人口穩定化發展，最終其年齡結構將 會固定不變，亦即 c x，t

=

B t_{N t} e r x p x

=

b e r x p x

=

c x 等式(6) 換言之，如果一個人口開始穩定化發展（也就是年齡別生育率和 年齡別死亡率維持固定水準），未來任何時間 t 點上年齡的人口所 圖 3 人口年齡結構穩定化過程 5 等式(5)亦可改寫為 l= e r x p x m x dx= 0 e r x p x m x dx，在此方程式 積分的上下限雖然不同（ 為育齡下限、 為育齡上限、0 為新生年齡、 或為∞壽命 極限），由於育齡階段以外的繁殖函數皆為零（亦即 m x =0，for x < and x > ）， 因此，積分結果相等。

佔比例（c x，t ）皆是相同，等於一個固定的數值 c x 。而且，由 於年齡別生育率和年齡別死亡率固定，年齡別人口比例又恆常，粗出 生率和粗死亡率也會維持固定。6 而且，這個穩定人口在任何時間點上的特定年齡組的人口規模， 可以由以下等式得知： N x，t

=

B er t x p x

=

B er t e r x p x

=

B x e r x p x 等式(7) 等式(7)當中，B 為基期的出生數，B t 是 t 年的出生數，p x 則 是新生兒存活至 x 年齡的機率。 上述穩定人口理論的價值，不僅只是在於描述人口成長與人口結 構，更 可 以 運 用 這 個 模 型 分 析 年 齡 別 死 亡 率 及 生 育 率 系 列 時 程 （fertility schedule and mortality schedule）對於其他人口測量的影響。 例如，某一既定的年齡別生育率和死亡率，將會隱含特定水準的淨繁 殖率（NRR）：

NRR

=

er T 等式(8) 等式(8)中的 T 為所謂的平均代距（average length of generation）， 即上下兩代之間的平均距離年數。進一步來說，淨繁殖率（NRR）、 人口成長的內在固有成長率（r）與平均代距（T）將會呈現如下關 係： r

=

NRR_T 等式(9) 此外，人口的內在固有成長率（r）也與總生育（TFR）關連如 6 由於年齡別生育率、年齡別死亡率、和年齡別人口比例皆是固定，任何時間點上的粗 出生率 b t 和粗死亡率 d t 將是常數： b t = 0c x，t m x，t dx= 0c x m x dx=b d t = 0c x，t m x，t dx= 0c x m x dx=d

下： r

=

TFR

+

S_T

+

p AM 等式(10) 等式中(10)的 S 成分代表新生兒中女嬰比例，p AM 則是出生女 嬰可以存活至「平均生育年齡」的存活機率。所以，如果兩個人口的 出生性別比例、存活機率、和平均代距相等，則在不同總生育率水準 下其內在固有成長率的差距為 r

=

TFR₂ TFR₁ T 等式(11) 上述穩定人口模型的數學等式，其實可以解釋為許多實質的人口 學意涵。舉例言之，根據等式(11)，如果平均生育年齡固定，那麼， 兩個人口的成長率差異，將會取決於其生育率水準（TFR）的相對比 率。由此推演，當生育水準（TFR）較高時，相對於低 TFR 水準，相 等數量的 TFR 增減，其對於人口成長的作用較少，也就是說，當 TFR 由 2 下降至 1，相對於 TFR 由 4 下降到 3，其對人口成長的作用更為 顯著。因此，在低生育率時代，「些微」的生育水準變化，將會巨大 影響人口成長。 其次，根據等式(8)，在固定生育水準（NRR）之下，平均代距 （或是平均生育年齡）與人口成長成反比關係，所以，固定生育水準 下，生育步調（fertility tempo）的改變，將會影響人口成長率。 在穩定人口理論中，核心的概念就是 r—所謂的內在固有成長 率。之所以稱之為內在固有（intrinsic），乃是因為穩定人口的成長 率，完全取決於生育率（m x ）與死亡率（p x ），不受原始人口 的年齡結構影響。換言之，「穩定人口」乃是一個『遺忘歷史』的特 殊人口，不論過去人口動力如何波動影響，其所遺留的現今年齡結 構，將在「人口穩定化」過程隱沒，終將發展成為一個固定年齡結構

的人口。7

參、穩定人口模型的限制與擴展

穩定人口模型已經成為人口分析的重要工具，可以用來了解死亡 率與生育率對於人口繁殖成長的影響作用。然而，若干的限制卻也影 響其效用。具體來說，在穩定人口模型當中，核心的內在固有成長率 （r）乃是衍生自淨繁殖率，定義為： NRR

=

p x m x dx 等式(12) 從 定 義 上 可 以 知 道，NRR 是 個 標 準 的 時 期 性 測 量（period measure），所以反映一個假設的複合性年輪，因此存在一般時期性測 量的限制。具體來說，在複合年輪中，每一個特定年齡人口（N x，t ） 對於 NRR 的加值權相等，就長期而言，一旦成為穩定人口之後，這個 預設為真，8_{然而，在穩定化之前，可能就會造成相當程度偏誤。例} 如，在圖 4 裡，NRR 與實際出生數以及存活至育齡的子代（女兒）之 間差距頗大，換言之，此一穩定人口（或是 stable-equivalent）所反映 的繁殖率，不能真正等同未穩定化的人口成長率。正是因為如此，穩 定人口模型應用於人口推計時，將會出現相當程度誤差。 析言之，淨繁殖率係假定育齡階段各年齡組女性人口規模相等， 7 當然，人類歷史上未曾出現「穩定人口」，畢竟任何內在與外在力量都可能改變一個 人口的年齡別生育率與年齡別死亡率，不過，理論上，每一個實際人口皆隱含背後的 所謂「等同的穩定人口（stable equivalent population）」，亦即該人口在穩定化條件下 最 終 將 會 演 變 的 後 果。與 穩 定 人 口 相 關 的 概 念，則 是「定 常 人 口」（stationary population）或是生命表人口，亦即，一個穩定人口如果不只維持固定的年齡別生育率 與年齡別死亡率，其出生數和死亡數也都固定不變（就像是慣用的生命表），則此人 口的年齡結構永恆固定（每一年齡組人口比重為_{n l}nLx 0 ），人口規模永遠維持在 T0，粗 死亡率與粗出生率相等為l0 T0 = 1 e0 ，因為每年出生數與死亡數皆是 l₀，即生命表的基數 （radix）。 8 正確地說，即使是在穩定人口當中，每一年齡組 對於生育水準或是人口繁衍程度的貢獻 加權值，不隨時間變化而改變，亦即 N x，t =N x ，不過，不同年齡組的加權值取決 於其人口規模，所以，除非存活機率相等（即 p x1 =p x2 ），否則 N x1 N x2 。

亦即： NRR

=

p x [m x L_x] dx

=

p x [m x 1.0] dx

=

p x m x dx 等式(13) 在當代低死亡率社會裡，新生兒存活至育齡階段、甚至完成育齡 的存活率的確極高，然而，並非完全相等，更何況在死亡率轉型過程 裡，育齡階段的年齡別存活率（p x

=

1_lLx 0 ）差異很大，n L_x不僅歷 時變異，更重要是在同一時間點上不同 x 年齡的定常人口數也可能出 現顯著差異。因此，固然穩定人口模型係假定封閉人口、人口動力穩 定發展、以及複合性年輪等條件，若是漠視實際人口年齡結構事實， 應用穩定人口模型進行人口估計時，將會導致某一程度的偏誤後果。 總之，穩定人口模型提供人口分析絕佳、有利工具，不過，根源 於時期性測量的限制，近年來，若干學者試圖擴展古典模型，納入動態 發展的因素。舉例言之，傳統的生命表設定ex t

=

x e x x+a x+y，t dy_da， 圖 4 淨繁殖率與實際人口替代水準之比較

這是測量一個複合性假設年輪的死亡率水準。在 t 年時年齡為的 x 群 體，雖然在 t 年將會經歷 x，t 的死亡風險，他們到了次年 x

+

1歲 時，不會經歷 x

+

1，t 的死亡風險，而是 x

+

1，t

+

1 。當代社 會裡， x

+

1，t 與 x

+

1，t

+

1 是不斷地在變動，因此 ex t 不僅 無法反映某一特定年次的人口，即使針對年的全體人口來說，也是無 法捕捉總體的死亡風險。許多學者針對傳統生命表測量的限制，提出 若干替代途徑，試圖調整 tempo distortion 的問題，或是捕捉年輪變遷 的效應。例如，Bongaarts（2005）、Bongaarts and Feeney（2002,2006）、 Canudas-Romo and Schoen（2005）、Goldstein（2006）、Goldstein and Wachter（2006）、Guillot（2003）、Rodrigues（2006）、Schoen（2006）。 古典的穩定人口模型，一方面建立在時期性測量，另一方面預設 生育率與死亡率固定不變，在當代的人口發展環境中偏離事實，因 此，近年來，若干的研究試圖克服這些限制。Bennett and Horiuch 在 1981 年首先提出變動性成長率的穩定人口模型（variable-r stable population），藉以擴展 Lotka 古典穩定人口模型。由於此一嶄新途徑 不僅考量個別年輪人口的差異成長率，更是適用於非封閉性人口，也 就是可以納入遷移對於人口成長的作用效應，因此，也被稱為非穩定 人口模型（non-stable population model）。

首先，我們定義年齡組 [x，x

+

n 人口在[0，T]期間的人口成長率 為nrx[0，T]： nrx[0，T]

=

lnnNx T nNx 0 T 等式(14) 那麼，以前進或倒推存活率的人口估計（forward-reverse survival rate method of population estimation）方法，我們可以知道在 0 或 T 時 間點上 [x，x

+

n 年齡組的人口數量為：

nNx 0

=

nNx T e T nrx0，T nNx T

=

nNx T T N nLx nLx T nNx 0

=

nNx T e T nrx0，T

=

nNx T T N nLx nLx T e T nrx0，T 等式(15) 因此，透過年齡 別人口 成長率與 存活率 的想法，Bennett and Horiuchi（1981）指出，在某一時間點 t 的特定年齡組人口 N x，t ， 可以從同一時間點上其他年齡組人口得知： N x，t

=

N y，t e y x r a，t da lx l_y 等式(16) 上述等式(16)說明，某一時間點上 x 年齡的人口數量，可以藉由 y 年齡的人口數量及其累積年齡別人口成長率（即 e y x r a，t da_）和存活 率lx ly計算而得（lx和 ly分別為 x 與 y 年齡的生存數）。

稍後，Preston and Coale（1982）隨即指出，Bennett and Horiuchi 所發現年齡組別之間人口數量的關係，不僅成立於封閉人口，更是可 以納入年齡別人口遷移率（i a，t ）： N x，t

=

N y，t e y x r a，t i a，t da lx l_y 等式(17) 或者，我們直接以該時間點上 0 歲的人口數量 N 0，t 可以得知 任一年齡組的人口數量為： N x，t

=

N 0，t e y x r a，t i a，t da _{p x，t 等式(18)} 其中，p x，t 為新生兒存活至歲的存活機率。由於 0 歲的人口 數即為出生數（N 0，x

=

B t ）所以， N x，t

=

B t e y x r a，t i a，t da _{p x，t 等式(19)}

為了簡化等式，以下討論將省略等式中的時間t和遷移率 i a，t 。 Preston and Coale（1982）計算年齡組人口所佔比例為：

N x N

=

B N e 0 x r a da _{p x，t}

₌

_{c x}

₌

_{b e 0}xr a da _{p x} 等式(20) 等式(20)中，c x 為 x 年齡人口所佔比重，N 為全體人口數，B 為出生數，p x 為存活至 x 歲的機率，b 則為粗出生率。由於累計全 部年齡組人口所佔比例即是全體人口，因此： 0 c x

=

1

=

0 b e 0 x r a da _{p x dx 等式(21)}

Preston and Coale（1982）從等式(21)中發現，出生率為：

b

=

1 0 e 0r a da p x dx 等式(22) 而且，粗出生率又是人口數量 c x 與繁殖函數 m x 之乘積的總 和，9_{即 b}

₌

_{c x m x dx，另外等式(20)得知} c x

=

b e 0 x r a da _{p x ，所以，} b

=

b e 0 x r a da _{p x m x dx 等式(23)} 進一步將等式(23)化簡為： l

=

e 0 x r a da _{p x m x dx 等式(24)} 等式(24)事實上就是古典的 Lotka 特徵方程式（參見上文等式 9 粗出生率（b）乃是全部出生數（B）相對全體人口（N），所以推演可得： b=B_N= N x _Nm x dx= N x_N m x dx= c x m x dx

(5)），現在將會適用於非封閉人口。如果以 v x 代表生母年齡分布 比例，那麼，我們也可以定義淨繁殖率（NRR）為： v x

=

B x_B

=

B e 0 x r a da _{p x m x} B

=

e 0 x r a da _{p x m x dx 等式(25)} NRR

=

p x m x dx

=

v x e 0 x r a da _{dx 等式(26)} 所以，從等式(26)可以得知，一個人口的淨繁殖率，只要根據其 生母年齡分布比例、以及年齡別人口成長率即可計算得知。

Preston and Wang（2007）進一步發現，在開放的人口體系裡，x 年齡的人口數量 N x 為： N x

=

N 0 e 0 x r a da _e 0 x i a da _{p x 等式(27)} 若 p* _{x 以代替人口遷移率，那麼變動成長率之人口再生方程式} 可以轉換為： l

=

e 0 x r a da _{e 0}xi a da _{p x m x dx}

=

e 0 x r a da _p* _{x p x m x dx}

=

e 0 x r a da _{v x e 0}xr a da_{dx 等式(28)} 由此可見，等式(28)證明，人口遷移的效應將會反映在生母年齡 分布比例和年齡別人口成長率之上，換言之，v x e 0 x r a da_將能捕

捉開放人口的作用效應。最後，Preston and Wang（2007）將等式(28) 轉換為：

l

=

0

=

0 e r* x v x e 0 x r a da_{dx 等式(29)} 其中，r*_{就是非穩定人口的內在固有成長率，此一成長率與古典} Lotka's r之間的差異，就是反應人口成長過程效應以及人口遷移作用。 以上這個變動性成長率的穩定人口模型，直到最近幾年開始受到 重視（例如：Cai 2008; Goldstein et al. 2003; Guillot 2009; Horiuchi and Preston 1988; Preston and Wang 2007; Schoen 2005, 2006, 2009; Schoen and Kim 1994; Sparks 2009; Vallin and Caselli 2006a, 2006b）。除此之 外，Horiuchi and Preston（1988）、Preston（1986）、Preston and Coale （1982）、Schoen and Kim（1994）等人也對於變動性成長率之穩定人 口模型的各個成分，以及該穩定人口與實際人口之間連結關係，已經 深入探討分析，可以做為實證運用的依據。 本文以下就分別運用 Lotka 的古典理論和變動性成長率之穩定人 口模型，探討臺灣的人口成長。雖然人口模型分析經常以「兩性」 （two-sex）做為分析對象，基於模型檢視與函數定義簡化考量，在 此，我們採用目前人口研究中慣用的單性途徑（one-sex approach）， 也就是完全以女性人口為主，分析過程排除探討男性人口部份—當 然，男性人口的繁衍過程也是與女性相同，只是其繁殖函數與存活函 數有所差異。至於本文所使用的臺灣人口資料、以及資料插補相關問 題，詳細敘述於附錄。基本上，本文分析資料取自歷年〈中華民國人 口統計年刊〉（包含先前年代的〈臺閩地區人口統計〉、〈臺灣人口 統計〉、〈臺灣省人口統計〉、與〈臺灣省戶籍統計要覽〉等），不 過，當中 1951-1973 年期間的年齡別人口數與生命統計數，由於軍民 分籍造成涵蓋誤差，所以，我們採用行政院經濟設計委員會綜合計畫 處與內政部戶政司合編（1976）之〈臺灣地區戶籍人口統計之調整 （民國四十年至六十二年）〉的人口數據。

肆、臺灣的人口繁衍與穩定人口

二十世紀裡，臺灣的人口發展，不論內在與外在環境皆是動盪激 烈—首先，1910-1920 期間流行性疾病肆虐，接下來則是中日戰爭 與國共內戰，然後則是數量龐大的內戰移民潮，1970 年代以後的工業 化與經社變遷更是前所未見。這些人口外部環境因素，造成人口結構 與人口動力必須調整回應。正是因為如此，跨越不同年輪（cohort） 的人口行為（特別是人口繁衍行為），也就呈現截然不同的面貌。 首先，以生育年齡來看，圖 5 呈現歷年的平均生育年齡變遷，過 去六十年裡，平均生育年齡的變遷趨勢呈現 V 型，由高到低再回昇， 其谷底為 1975-1985 年間。至於圖 5 當中生母平均年齡與生育時程 （fertility schedule）平均數的差異，正是反映育齡婦女的組成年輪之 規模效應： 生育時程平均數

=

x m x dx m x dx 等式(30) 嬰兒出生時母親平均年齡

=

x m x c x dx m x c x dx 等式(31) 因此，圖 5 意涵，在 1950 年代，年輕年輪的育齡女性規模較為 龐大，而且處於生育水準高峰，到了 1960 年代以後年輪規模對於平 均年齡的效應就縮減（1970 年代的規模效應，乃是反映 1950 年代較 高生育數量的慣性效用）。整體而言，1990 年以後，生母平均年齡與 生育時程平均數幾乎相同，顯示年輪的規模效應已經消失。 上述生育平均年齡的變遷，其實也在每一個人口所隱含的 stable

equivalent population當中完全反映，所以，圖 5 另外也比較親子上下 兩代的平均長度。至於平均代距與穩定人口之平均生育年齡（AB）、 及生育時程的平均數（ ）之間關係為： T

=

ln p x m x dx r 等式(32) A_B

=

e r x p x x m x dx 等式(33)

=

p x x m x dx p x m x dx 等式(34) T AB

+

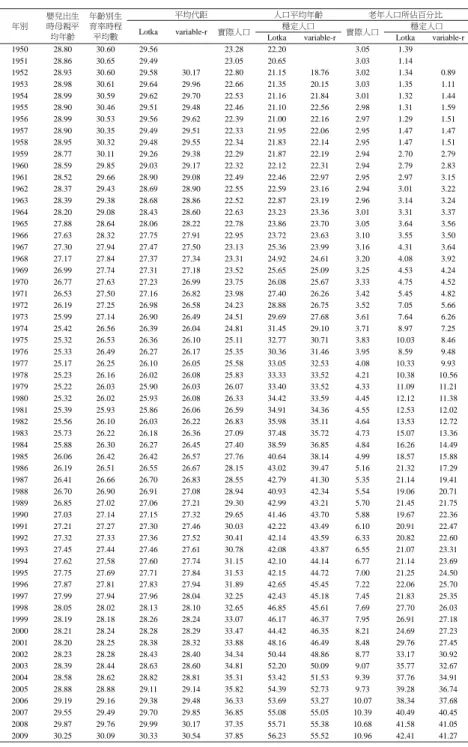
2 等式(35) 整體而言，圖 5 當中，不論從那一角度測量生育年齡，都可以看 到共同呈現 V 字型現象—究其緣故，人口繁衍的育齡期間雖然長達 圖 5 臺灣地區生育年齡相關統計的變遷

達三十五年，在傳統自然生育狀態時期，婦女可能在育齡全程都是處 生於生育、養育身份，然而，在生育轉型過程，我們首先看到，高齡 （三十歲以上）階段的生育率下降，到了一九八○年代之後，年輕階 段的生育率則大幅下降。 接下來，我們以穩定人口模型為基礎，比較人口成長率變遷— 圖 6 呈現人口自然增加率（NIR）與其所應對之內在固有成長率 （分 別以傳統之 Lotka 模型和變動率模型測量）。圖 6 的結構相當令人訝 異—在 1970 年代以前，臺灣的人口自然增加率與穩定人口內在成 長率居然完全吻合，代表實際人口不論年齡組成，抑或生育與死亡水 準，其實就是一個穩定人口，當然，以高於 2%的成長率發展（甚至 在 1960 年以前超過 3%），人口將在短於三十年內倍增。 臺灣的死亡率轉型在 1920 年代開始發生，到了 1950 年代已經下 降到低水準，尤其是育齡階段的存活率已經很高，所以，對於人口繁 圖 6 臺灣地區實際人口與穩定人口成長率以及人口慣性效應， 1950-2009

衍的效應極小。相對地，生育率轉型明顯從 1960 年代後期發酵，其 對人口結構與人口繁衍的作用也明顯產生。自 1970 年開始，臺灣的 人口自然增加雖已趨緩，仍是維持在 1%以上，直到 1990 年代後期， 自然增加率才下降至 1%以下，不過，截至目前仍處於正成長階段。 但是，如果檢視穩定人口成長率，似乎前景並不樂觀—穩定人 口成長率在 1980 年代初期即已下降為負成長，現在更是超過 -2% ， 表示長期結果，即使維持目前生育水準，未來每三十年人口將會減 半。最後，值得一提者，圖 6 所呈現兩種穩定人口成長率之間的差 異，顯示人口遷徙與年輪結構的歷史痕跡，對於人口未來發展仍將發 揮某一程度作用。 接下來，我們探討臺灣地區人口穩定化發展的結果。圖 7 分別以 1955、1986 和 2009 年做為基礎，比較實際人口的年輪組成與其所對 應的穩定人口結局。顯然地，回應上述討論，1950 年代的臺灣人口， 就當時所盛行的生育水準與生育時間模型而言，穩定化之後的人口結 構，不僅貌似、其實幾乎等同實際人口，只是展現高成長率（每年以 3-4%的速度增長規模），這正是二十世紀前半時期人口緩慢成長的後 果。至於圖中所顯示 1950 年代 20 歲以上人口較之穩定人口更為龐大 的原因，乃是實際人口當中相當部份成年女性係因內戰移民來臺，換 言之，封閉人口的特性為之破壞，所以，一些出入實際人口與穩定人 口之間出現差距。 1984年乃是臺灣人口發展的里程碑—生育率維持在替代水準。 然而，此一替代水準的卻是意涵實際人口的年齡結構將會完全改變面 貌，當然，最終演變成為人口學家眼中「理想的」替代水準人口（由 於內在固有成長率已為負成長，所以，人口規模似將逐年微幅縮 減）。最後，2009 年的人口穩定化發展，毫無疑問地，將是我們不願 期待—維持目前生育水準發展，臺灣人口終將成長倒金塔型，人口 高度老化，而且每年超過 2%的速度衰減。

圖 7 臺灣地區實際人口與「Stable Equivalent Population」之年齡結構 比較

伍、臺灣的人口慣性效應與老化趨勢

古典的穩定人口理論，係假定在封閉人口當中，一旦人口動力 （生育率與死亡率）固定不變，發展結果，終將「遺忘歷史」—原 有年齡結構痕跡遲早（大約現存人口全部替換的時間，約為七十至八 十年左右）將會消失。此一「遺忘歷史」效應的特色，致使穩定人口 理論忽視人口變遷歷程。所以 Keyfitz 在 1971 年時，專文探討穩定人 口理論與人口規模之間的關係，將重心從人口動力和年齡結構關係轉 移，進而提出人口慣性（population momentum）的概念。事實上，我們 必須特別指出，Lotka 所謂穩定人口發展「終將」遺忘歷史，乃是在 「既存人口」為次代新生人口完全取代之後才會發生，而且，穩定化 只是發生在「人口的年齡結構」之上；因此，人口慣性的觀點，從相 反的角度來看，強調一個人口即使從此維持固定的年齡別生育率和年 齡別死亡率水準而發展，既存的年齡結構與人口規模，仍將持續「烙 印」在未來的人口發展路途上，尤其是對於人口規模將會顯著作用。 所謂的人口慣性，就是現有人口如果瞬間發生生育率下降，轉型 進入替代水準（所以，淨繁殖率為 1）並持續固定穩定發展，最終此 一人口將會演化成為一個定常人口（stationary population），屆時， 不僅人口年齡結構將會固定不變，人口規模亦將固定不增不減。因 此，定義人口慣性為 M

=

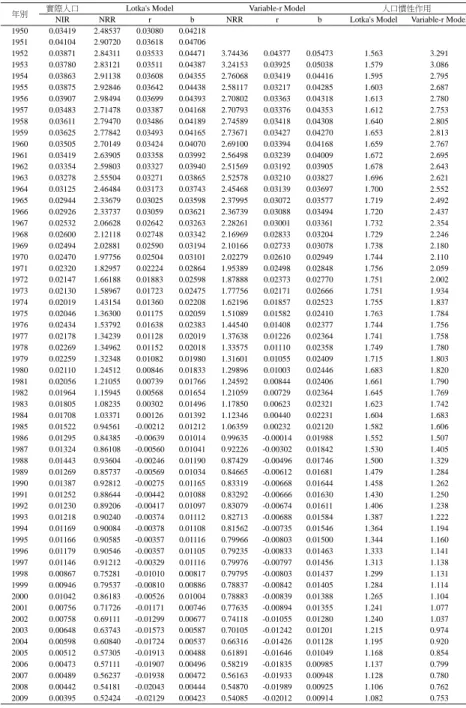
P_PS 0 等式(36) 其 P0代表現存人口規模，PS則是定常人口的規模。換言之，人口 慣性係指現存人口發展成為定常化之後，人口規模增長的效應。 Keyfitz 的人口慣性概念，的確相當程度擴大穩定人口理論的價 值，有助於瞭解人口動力對於人口成長的作用。不過，由於 Keyfitz 對

於人口慣性效應（係數）的界定過於繁複，致使應用於人口分析時相 當困難，嗣後，許多人口學家紛紛探討如何測量人口慣性效應（例 如：Goldstein 2002; Kim and Schoen 1993, 1997; Kim et al.1991; Li and Tuljapurkar 1999; Schoen and Jonsson 2003; Schoen and Kim 1991, 1998）。其中，Preston and Guillot 在 1997 年提出一個相當簡易途徑， 可以快速測量人口慣性作用： M

=

0 c x cS x w x dx 等式(37) 其中 c x 為既存人口的年齡組比例，cS x 則是該年齡組人口在 定常人口中的比例，至於 w x 的數值是 w x

=

p y m y dx A* 等式(38) 反映定常人口中，x 年齡以上的生育水準。實證經驗顯示，w x 函數在不同生育水準的人口之其間差異甚微。Preston and Guillot 上述 對於人口慣性的測量，雖然係以古典 Lotka 的穩定人口模型做為依據， 我們可以擴展應用至 variable-r 模型。在變動人口成長率狀態下， c x cS x

=

b e 0 x r y dy _{p x} p x e°₀

=

b e ° 0 e 0 x r y dy _等式(39) 進一步來說，b e° 0 b為內在固有粗出生率，為定常人口出生時平 均餘命）可以反映人口慣性作用，代表從今爾後每年出生數固定於目 前的數值（b e° 0），最終產生的慣性成長效應。 根據上述討論，我們針對臺灣過去歷年人口，分別測量各項慣性 效應指標，結果呈現於表一至表三以及圖 6。首先，人口研究早已不 斷指出，生育率下降與人口老化兩者如影隨形，而且，快速的生育率 水準的危機下，政府處心積慮研擬應對人口老化的對策。然而，事實 上，臺灣人口老化的隱憂早已成形，過去的一些研究更是力陳這些危

機的嚴重後果（例如：陳寬政 1987, 1995, 1997；魯慧中 1999），但 是，一直未曾受到重視，進而關注應對。 事實上，連結表一與表二數據可以發現，即便早在 1970 年代初 期，雖然生育率仍居於高水準（NRR 在 1.5 以上），政府努力推動控 制生育政策，當時的實際人口的確處於年輕化階段（平均年齡僅 24 歲），可是，其生育率水準所意涵的穩定人口已經開始老化（平均年 齡進入 30 歲，而老年人口比例則超過 10%）。到了 1984 年，臺灣進 入替代水準，其所對應的穩定人口則是相當老化—平均年齡近 40 歲，老年人口將近比重為五分之一。當然，毋庸多言，現今所面對的 老化嚴重危機—穩定人口的平均年齡超過 55 歲，老化人口更是高 於四成。 至於生育率下降對於人口成長的慣性作用，在表三和圖 6 中可以 明顯看出，若以傳統 Lotka 的穩定人口理論做為依據，臺灣在過去六 十年裡，生育率下降過程（即使至今依然），由於過往高生育率的歷 史記憶，終將獲得正向成長的定常人口—定常人口的規模仍將大於 目前人口數量。 圖 6 當中，Lotka 模型所帶來的樂觀遠景，的確相當令人欣慰— 臺灣在過去二十餘年裡，雖然生育率低於替代水準，甚至處於超低生 育率，如果，能夠「及時」促使生育率回昇，人口慣性效應仍將促使 未來定常人口的規模高於目前水準。這樣理想的遠景，的確正是當前 政府人口政策的樂觀信心來源。可是，如果我們檢視圖 6 的另一資 訊，亦即變動成長率模型，考量年齡結構與生育率變遷力量，人口的 慣性效應其實已經處於負向。具體來說，2009 年生育動力背景下， Lotka模型所呈現的慣性效應為 1.082，代表定常人口的規模仍將高於 目前人口數量的 8%，可是，在變動成長率模型之下的慣性作用卻是 相當令人沮喪—定常人口規模的慣性效應為 0.753，亦即，縱使臺 灣的生育率可以從現今 NRR

=

0.52回升至替代水準，臺灣的人口規模 仍將減少 25%。

上述的人口慣性發展效應，我們必須非常重視，事實上，近年 來，人口研究開始關注慣性對於人口成長的作用—例如，Bonggarts （1994, 1999）即發現，二十一世紀，多數國家的人口成長動力來源 中，人口慣性具有最為關鍵的地位，甚至，就是未來人口成長量的一 半來源。相反地，現今處於超低生育率的國家，即便可以瞬間促使生 育率回升至替代水準，人口衰減仍是必然的後果，其負成長規模端視 回升的速度而有嚴重與否的差別。

陸、結語

穩定人口模型可以提供做為一個形式工具，分析人口動力與人口 結構之間的互動關係。Lotka 的古典穩定人口模型係以封閉人口做為 基礎，考量「即時」的人口動力對於外來人口繁衍的效應。近年來， 變動性成長率的穩定人口模型已在 Lotka 理論基礎上擴展，不僅可以 適用於任何人口，除了納入考量遷徙效應，更能捕捉人口變遷的影響 力。因此，這個擴展模型將會更為有助於各種人口估計分析。不過， 目前仍有許多議題必須在方法論上突破，才能真正發揮其價值： 1.人口發展過程，各種人口動力產生變遷之下，其對人口結構的 影響結果，必須建立明確的模型關係，藉此預測變遷效應或是 進行人口政策評估規劃。 2.人口穩定化過程中，人口結構如何變遷，特別是不同的生育時 程（fertility schedule ）在穩定化歷程將會產生的效應如何？ 3.長期歷史發展中，人口成長率與人口繁衍之間的動態關係如 何？特別是在存活曲線矩形化下，非育齡階段人口比重改變， 是否對於人口成長率發生互動影響？

表 1 臺灣地區人口成長率指標

年別

實際人口 穩定人口

CBR CDR NIR 年增率 _NRR Lotka's Model_{r b NRR} Variable-r Model_{r b} 1950 0.04524 0.01105 0.03419 0.04623 2.48537 0.03080 0.04218 1951 0.05206 0.01102 0.04104 0.03127 2.90720 0.03618 0.04706 1952 0.04862 0.00991 0.03871 0.03706 2.84311 0.03533 0.04471 3.74436 0.04377 0.05473 1953 0.04723 0.00943 0.03780 0.03264 2.83121 0.03511 0.04387 3.24153 0.03925 0.05038 1954 0.04686 0.00823 0.03863 0.03489 2.91138 0.03608 0.04355 2.76068 0.03419 0.04416 1955 0.04750 0.00875 0.03875 0.03752 2.92846 0.03642 0.04438 2.58117 0.03217 0.04285 1956 0.04680 0.00773 0.03907 0.03767 2.98494 0.03699 0.04393 2.70802 0.03363 0.04318 1957 0.04317 0.00834 0.03483 0.03489 2.71478 0.03387 0.04168 2.70793 0.03376 0.04353 1958 0.04352 0.00741 0.03611 0.03462 2.79470 0.03486 0.04189 2.74589 0.03418 0.04308 1959 0.04307 0.00682 0.03625 0.03536 2.77842 0.03493 0.04165 2.73671 0.03427 0.04270 1960 0.04157 0.00652 0.03505 0.03403 2.70149 0.03424 0.04070 2.69100 0.03394 0.04168 1961 0.04036 0.00617 0.03419 0.03231 2.63905 0.03358 0.03992 2.56498 0.03239 0.04009 1962 0.03943 0.00589 0.03354 0.03121 2.59803 0.03327 0.03940 2.51569 0.03192 0.03905 1963 0.03830 0.00552 0.03278 0.03091 2.55504 0.03271 0.03865 2.52578 0.03210 0.03827 1964 0.03649 0.00524 0.03125 0.03035 2.46484 0.03173 0.03743 2.45468 0.03139 0.03697 1965 0.03445 0.00500 0.02944 0.02918 2.33679 0.03025 0.03598 2.37995 0.03072 0.03577 1966 0.03420 0.00494 0.02926 0.02794 2.33737 0.03059 0.03621 2.36739 0.03088 0.03494 1967 0.03015 0.00483 0.02532 0.02528 2.06628 0.02642 0.03263 2.28261 0.03001 0.03361 1968 0.03078 0.00478 0.02600 0.02456 2.12118 0.02748 0.03342 2.16969 0.02833 0.03204 1969 0.02950 0.00456 0.02494 0.02492 2.02881 0.02590 0.03194 2.10166 0.02733 0.03078 1970 0.02902 0.00432 0.02470 0.02345 1.97756 0.02504 0.03101 2.02279 0.02610 0.02949 1971 0.02733 0.00412 0.02320 0.02319 1.82957 0.02224 0.02864 1.95389 0.02498 0.02848 1972 0.02563 0.00416 0.02147 0.02211 1.66188 0.01883 0.02598 1.87888 0.02373 0.02770 1973 0.02540 0.00410 0.02130 0.01943 1.58967 0.01723 0.02475 1.77756 0.02171 0.02666 1974 0.02424 0.00405 0.02019 0.01762 1.43154 0.01360 0.02208 1.62196 0.01857 0.02523 1975 0.02420 0.00374 0.02046 0.01825 1.36300 0.01175 0.02059 1.51089 0.01582 0.02410 1976 0.02817 0.00383 0.02434 0.02144 1.53792 0.01638 0.02383 1.44540 0.01408 0.02377 1977 0.02555 0.00377 0.02178 0.02118 1.34239 0.01128 0.02019 1.37638 0.01226 0.02364 1978 0.02631 0.00362 0.02269 0.01945 1.34962 0.01152 0.02018 1.33575 0.01110 0.02358 1979 0.02637 0.00378 0.02259 0.02036 1.32348 0.01082 0.01980 1.31601 0.01055 0.02409 1980 0.02511 0.00400 0.02110 0.02022 1.24512 0.00846 0.01833 1.29896 0.01003 0.02446 1981 0.02472 0.00417 0.02056 0.01962 1.21055 0.00739 0.01766 1.24592 0.00844 0.02406 1982 0.02366 0.00402 0.01964 0.01928 1.15945 0.00568 0.01654 1.21059 0.00729 0.02364 1983 0.02207 0.00402 0.01805 0.01734 1.08235 0.00302 0.01496 1.17850 0.00623 0.02321 1984 0.02105 0.00397 0.01708 0.01586 1.03371 0.00126 0.01392 1.12346 0.00440 0.02231 1985 0.01919 0.00397 0.01522 0.01480 0.94561 -0.00212 0.01212 1.06359 0.00232 0.02120 1986 0.01703 0.00408 0.01295 0.01248 0.84385 -0.00639 0.01014 0.99635 -0.00014 0.01988 1987 0.01726 0.00402 0.01324 0.01167 0.86108 -0.00560 0.01041 0.92226 -0.00302 0.01842 1988 0.01862 0.00419 0.01443 0.01233 0.93604 -0.00246 0.01190 0.87429 -0.00496 0.01746 1989 0.01687 0.00418 0.01269 0.01179 0.85737 -0.00569 0.01034 0.84665 -0.00612 0.01681 1990 0.01805 0.00417 0.01387 0.01211 0.92812 -0.00275 0.01165 0.83319 -0.00668 0.01644 1991 0.01696 0.00444 0.01252 0.01187 0.88644 -0.00442 0.01088 0.83292 -0.00666 0.01630 1992 0.01683 0.00453 0.01230 0.01040 0.89206 -0.00417 0.01097 0.83079 -0.00674 0.01611 1993 0.01679 0.00461 0.01218 0.01020 0.90240 -0.00374 0.01112 0.82713 -0.00688 0.01584 1994 0.01654 0.00486 0.01169 0.00996 0.90084 -0.00378 0.01108 0.81562 -0.00735 0.01546 1995 0.01645 0.00479 0.01166 0.00950 0.90585 -0.00357 0.01116 0.79966 -0.00803 0.01500 1996 0.01623 0.00444 0.01179 0.00909 0.90546 -0.00357 0.01105 0.79235 -0.00833 0.01463 1997 0.01613 0.00467 0.01146 0.01002 0.91212 -0.00329 0.01116 0.79976 -0.00797 0.01456 1998 0.01318 0.00451 0.00867 0.01059 0.75281 -0.01010 0.00817 0.79795 -0.00803 0.01437 1999 0.01382 0.00436 0.00946 0.00943 0.79537 -0.00810 0.00886 0.78837 -0.00842 0.01405 2000 0.01484 0.00442 0.01042 0.00921 0.86183 -0.00526 0.01004 0.78883 -0.00839 0.01388 2001 0.01228 0.00472 0.00756 0.00835 0.71726 -0.01171 0.00746 0.77635 -0.00894 0.01355 2002 0.01176 0.00418 0.00758 0.00675 0.69111 -0.01299 0.00677 0.74118 -0.01055 0.01280 2003 0.01079 0.00431 0.00648 0.00563 0.63743 -0.01573 0.00587 0.70105 -0.01242 0.01201 2004 0.01027 0.00429 0.00598 0.00496 0.60840 -0.01724 0.00537 0.66316 -0.01426 0.01128 2005 0.00962 0.00450 0.00512 0.00511 0.57305 -0.01913 0.00488 0.61891 -0.01646 0.01049 2006 0.00956 0.00483 0.00473 0.00589 0.57111 -0.01907 0.00496 0.58219 -0.01835 0.00985 2007 0.00939 0.00451 0.00489 0.00609 0.56237 -0.01938 0.00472 0.56163 -0.01933 0.00948 2008 0.00902 0.00460 0.00442 0.00539 0.54181 -0.02043 0.00444 0.54870 -0.01989 0.00925 2009 0.00872 0.00478 0.00395 0.00555 0.52424 -0.02129 0.00423 0.54085 -0.02012 0.00914

表 2 臺灣地區人口結構年齡指標 年別 嬰兒出生 時母親平 均年齡 年齡別生 育率時程 平均數 平均代距 人口平均年齡 老年人口所佔百分比

Lotka variable-r 實際人口 _Lotka穩定人口_variable-r 實際人口 _Lotka穩定人口_variable-r

1950 28.80 30.60 29.56 23.28 22.20 3.05 1.39 1951 28.86 30.65 29.49 23.05 20.65 3.03 1.14 1952 28.93 30.60 29.58 30.17 22.80 21.15 18.76 3.02 1.34 0.89 1953 28.98 30.61 29.64 29.96 22.66 21.35 20.15 3.03 1.35 1.11 1954 28.99 30.59 29.62 29.70 22.53 21.16 21.84 3.01 1.32 1.44 1955 28.90 30.46 29.51 29.48 22.46 21.10 22.56 2.98 1.31 1.59 1956 28.99 30.53 29.56 29.62 22.39 21.00 22.16 2.97 1.29 1.51 1957 28.90 30.35 29.49 29.51 22.33 21.95 22.06 2.95 1.47 1.47 1958 28.95 30.32 29.48 29.55 22.34 21.83 22.14 2.95 1.47 1.51 1959 28.77 30.11 29.26 29.38 22.29 21.87 22.19 2.94 2.70 2.79 1960 28.59 29.85 29.03 29.17 22.32 22.12 22.31 2.94 2.79 2.83 1961 28.52 29.66 28.90 29.08 22.49 22.46 22.97 2.95 2.97 3.15 1962 28.37 29.43 28.69 28.90 22.55 22.59 23.16 2.94 3.01 3.22 1963 28.39 29.38 28.68 28.86 22.52 22.87 23.19 2.96 3.14 3.24 1964 28.20 29.08 28.43 28.60 22.63 23.23 23.36 3.01 3.31 3.37 1965 27.88 28.64 28.06 28.22 22.78 23.86 23.70 3.05 3.64 3.56 1966 27.63 28.32 27.75 27.91 22.95 23.72 23.63 3.10 3.55 3.50 1967 27.30 27.94 27.47 27.50 23.13 25.36 23.99 3.16 4.31 3.64 1968 27.17 27.84 27.37 27.34 23.31 24.92 24.61 3.20 4.08 3.92 1969 26.99 27.74 27.31 27.18 23.52 25.65 25.09 3.25 4.53 4.24 1970 26.77 27.63 27.23 26.99 23.75 26.08 25.67 3.33 4.75 4.52 1971 26.53 27.50 27.16 26.82 23.98 27.40 26.26 3.42 5.45 4.82 1972 26.19 27.25 26.98 26.58 24.23 28.88 26.75 3.52 7.05 5.66 1973 25.99 27.14 26.90 26.49 24.51 29.69 27.68 3.61 7.64 6.26 1974 25.42 26.56 26.39 26.04 24.81 31.45 29.10 3.71 8.97 7.25 1975 25.32 26.53 26.36 26.10 25.11 32.77 30.71 3.83 10.03 8.46 1976 25.33 26.49 26.27 26.17 25.35 30.36 31.46 3.95 8.59 9.48 1977 25.17 26.25 26.10 26.05 25.58 33.05 32.53 4.08 10.33 9.93 1978 25.23 26.16 26.02 26.08 25.83 33.33 33.52 4.21 10.38 10.56 1979 25.22 26.03 25.90 26.03 26.07 33.40 33.52 4.33 11.09 11.21 1980 25.32 26.02 25.93 26.08 26.33 34.42 33.59 4.45 12.12 11.38 1981 25.39 25.93 25.86 26.06 26.59 34.91 34.36 4.55 12.53 12.02 1982 25.56 26.10 26.03 26.22 26.83 35.98 35.11 4.64 13.53 12.72 1983 25.73 26.22 26.18 26.36 27.09 37.48 35.72 4.73 15.07 13.36 1984 25.88 26.30 26.27 26.45 27.40 38.59 36.85 4.84 16.26 14.49 1985 26.06 26.42 26.42 26.57 27.76 40.64 38.14 4.99 18.57 15.88 1986 26.19 26.51 26.55 26.67 28.15 43.02 39.47 5.16 21.32 17.29 1987 26.41 26.66 26.70 26.83 28.55 42.79 41.30 5.35 21.14 19.41 1988 26.70 26.90 26.91 27.08 28.94 40.93 42.34 5.54 19.06 20.71 1989 26.85 27.02 27.06 27.21 29.30 42.99 43.21 5.70 21.45 21.75 1990 27.03 27.14 27.15 27.32 29.65 41.46 43.70 5.88 19.67 22.36 1991 27.21 27.27 27.30 27.46 30.03 42.22 43.49 6.10 20.91 22.47 1992 27.32 27.33 27.36 27.52 30.41 42.14 43.59 6.33 20.82 22.60 1993 27.45 27.44 27.46 27.61 30.78 42.08 43.87 6.55 21.07 23.31 1994 27.62 27.58 27.60 27.74 31.15 42.10 44.14 6.77 21.14 23.69 1995 27.75 27.69 27.71 27.84 31.53 42.15 44.72 7.00 21.25 24.50 1996 27.87 27.81 27.83 27.94 31.89 42.65 45.45 7.22 22.06 25.70 1997 27.99 27.94 27.96 28.04 32.25 42.43 45.18 7.45 21.83 25.35 1998 28.05 28.02 28.13 28.10 32.65 46.85 45.61 7.69 27.70 26.03 1999 28.19 28.18 28.26 28.24 33.07 46.17 46.37 7.95 26.91 27.18 2000 28.21 28.24 28.28 28.29 33.47 44.42 46.35 8.21 24.69 27.23 2001 28.20 28.25 28.38 28.32 33.88 48.16 46.49 8.48 29.76 27.45 2002 28.23 28.28 28.43 28.40 34.34 50.44 48.86 8.77 33.17 30.92 2003 28.39 28.44 28.63 28.60 34.81 52.20 50.09 9.07 35.77 32.67 2004 28.58 28.62 28.82 28.81 35.31 53.42 51.53 9.39 37.76 34.91 2005 28.88 28.88 29.11 29.14 35.82 54.39 52.73 9.73 39.28 36.74 2006 29.19 29.16 29.38 29.48 36.33 53.69 53.27 10.07 38.34 37.68 2007 29.55 29.49 29.70 29.85 36.85 55.08 55.05 10.39 40.49 40.45 2008 29.87 29.76 29.99 30.17 37.35 55.71 55.38 10.68 41.58 41.05 2009 30.25 30.09 30.33 30.54 37.85 56.23 55.52 10.96 42.41 41.27

表 3 臺灣地區人口成長慣性作用指標

年別 實際人口_{NIR NRR} Lotka's Model_{r b NRR} Variable-r Model_{r b Lotka's Model}人口慣性作用_{Variable-r Model} 1950 0.03419 2.48537 0.03080 0.04218 1951 0.04104 2.90720 0.03618 0.04706 1952 0.03871 2.84311 0.03533 0.04471 3.74436 0.04377 0.05473 1.563 3.291 1953 0.03780 2.83121 0.03511 0.04387 3.24153 0.03925 0.05038 1.579 3.086 1954 0.03863 2.91138 0.03608 0.04355 2.76068 0.03419 0.04416 1.595 2.795 1955 0.03875 2.92846 0.03642 0.04438 2.58117 0.03217 0.04285 1.603 2.687 1956 0.03907 2.98494 0.03699 0.04393 2.70802 0.03363 0.04318 1.613 2.780 1957 0.03483 2.71478 0.03387 0.04168 2.70793 0.03376 0.04353 1.612 2.753 1958 0.03611 2.79470 0.03486 0.04189 2.74589 0.03418 0.04308 1.640 2.805 1959 0.03625 2.77842 0.03493 0.04165 2.73671 0.03427 0.04270 1.653 2.813 1960 0.03505 2.70149 0.03424 0.04070 2.69100 0.03394 0.04168 1.659 2.767 1961 0.03419 2.63905 0.03358 0.03992 2.56498 0.03239 0.04009 1.672 2.695 1962 0.03354 2.59803 0.03327 0.03940 2.51569 0.03192 0.03905 1.678 2.643 1963 0.03278 2.55504 0.03271 0.03865 2.52578 0.03210 0.03827 1.696 2.621 1964 0.03125 2.46484 0.03173 0.03743 2.45468 0.03139 0.03697 1.700 2.552 1965 0.02944 2.33679 0.03025 0.03598 2.37995 0.03072 0.03577 1.719 2.492 1966 0.02926 2.33737 0.03059 0.03621 2.36739 0.03088 0.03494 1.720 2.437 1967 0.02532 2.06628 0.02642 0.03263 2.28261 0.03001 0.03361 1.732 2.354 1968 0.02600 2.12118 0.02748 0.03342 2.16969 0.02833 0.03204 1.729 2.246 1969 0.02494 2.02881 0.02590 0.03194 2.10166 0.02733 0.03078 1.738 2.180 1970 0.02470 1.97756 0.02504 0.03101 2.02279 0.02610 0.02949 1.744 2.110 1971 0.02320 1.82957 0.02224 0.02864 1.95389 0.02498 0.02848 1.756 2.059 1972 0.02147 1.66188 0.01883 0.02598 1.87888 0.02373 0.02770 1.751 2.002 1973 0.02130 1.58967 0.01723 0.02475 1.77756 0.02171 0.02666 1.751 1.934 1974 0.02019 1.43154 0.01360 0.02208 1.62196 0.01857 0.02523 1.755 1.837 1975 0.02046 1.36300 0.01175 0.02059 1.51089 0.01582 0.02410 1.763 1.784 1976 0.02434 1.53792 0.01638 0.02383 1.44540 0.01408 0.02377 1.744 1.756 1977 0.02178 1.34239 0.01128 0.02019 1.37638 0.01226 0.02364 1.741 1.758 1978 0.02269 1.34962 0.01152 0.02018 1.33575 0.01110 0.02358 1.749 1.780 1979 0.02259 1.32348 0.01082 0.01980 1.31601 0.01055 0.02409 1.715 1.803 1980 0.02110 1.24512 0.00846 0.01833 1.29896 0.01003 0.02446 1.683 1.820 1981 0.02056 1.21055 0.00739 0.01766 1.24592 0.00844 0.02406 1.661 1.790 1982 0.01964 1.15945 0.00568 0.01654 1.21059 0.00729 0.02364 1.645 1.769 1983 0.01805 1.08235 0.00302 0.01496 1.17850 0.00623 0.02321 1.623 1.742 1984 0.01708 1.03371 0.00126 0.01392 1.12346 0.00440 0.02231 1.604 1.683 1985 0.01522 0.94561 -0.00212 0.01212 1.06359 0.00232 0.02120 1.582 1.606 1986 0.01295 0.84385 -0.00639 0.01014 0.99635 -0.00014 0.01988 1.552 1.507 1987 0.01324 0.86108 -0.00560 0.01041 0.92226 -0.00302 0.01842 1.530 1.405 1988 0.01443 0.93604 -0.00246 0.01190 0.87429 -0.00496 0.01746 1.500 1.329 1989 0.01269 0.85737 -0.00569 0.01034 0.84665 -0.00612 0.01681 1.479 1.284 1990 0.01387 0.92812 -0.00275 0.01165 0.83319 -0.00668 0.01644 1.458 1.262 1991 0.01252 0.88644 -0.00442 0.01088 0.83292 -0.00666 0.01630 1.430 1.250 1992 0.01230 0.89206 -0.00417 0.01097 0.83079 -0.00674 0.01611 1.406 1.238 1993 0.01218 0.90240 -0.00374 0.01112 0.82713 -0.00688 0.01584 1.387 1.222 1994 0.01169 0.90084 -0.00378 0.01108 0.81562 -0.00735 0.01546 1.364 1.194 1995 0.01166 0.90585 -0.00357 0.01116 0.79966 -0.00803 0.01500 1.344 1.160 1996 0.01179 0.90546 -0.00357 0.01105 0.79235 -0.00833 0.01463 1.333 1.141 1997 0.01146 0.91212 -0.00329 0.01116 0.79976 -0.00797 0.01456 1.313 1.138 1998 0.00867 0.75281 -0.01010 0.00817 0.79795 -0.00803 0.01437 1.299 1.131 1999 0.00946 0.79537 -0.00810 0.00886 0.78837 -0.00842 0.01405 1.284 1.114 2000 0.01042 0.86183 -0.00526 0.01004 0.78883 -0.00839 0.01388 1.265 1.104 2001 0.00756 0.71726 -0.01171 0.00746 0.77635 -0.00894 0.01355 1.241 1.077 2002 0.00758 0.69111 -0.01299 0.00677 0.74118 -0.01055 0.01280 1.240 1.037 2003 0.00648 0.63743 -0.01573 0.00587 0.70105 -0.01242 0.01201 1.215 0.974 2004 0.00598 0.60840 -0.01724 0.00537 0.66316 -0.01426 0.01128 1.195 0.920 2005 0.00512 0.57305 -0.01913 0.00488 0.61891 -0.01646 0.01049 1.168 0.854 2006 0.00473 0.57111 -0.01907 0.00496 0.58219 -0.01835 0.00985 1.137 0.799 2007 0.00489 0.56237 -0.01938 0.00472 0.56163 -0.01933 0.00948 1.128 0.780 2008 0.00442 0.54181 -0.02043 0.00444 0.54870 -0.01989 0.00925 1.106 0.762 2009 0.00395 0.52424 -0.02129 0.00423 0.54085 -0.02012 0.00914 1.082 0.753

參考文獻

中文部份

陳寬政（1987）人口週期研究上的一些問題，人口學刊，10：15-28。 陳寬政（1995）因應我國人口高齡化之對策，行政院研究發展考核委 員會報告。 陳寬政（1997）臺灣地區人口出生數量的動態模擬，人口學刊，18： 1-18。 魯慧中（1999）人口老化—從最適人口成長的觀點重新詮釋，人口 學刊，20：139-165。

英文部份

Baili, P., A. Micheli, A. Montanari, and R. Capocaccia. 2005. "Comparison of Four Methods for Estimating Complete Life Tables from Abridged Life Tables Using Mortality Data Supplied to EUROCARE-3."

Mathematical Population Studies 12(4):183-198.

Beaujot, R. 2003. "Projecting the Future of Canada's Population: Assump-tions, ImplicaAssump-tions, and Policy." Canadian Studies in Population 30(1):1-28.

Bennett, N. G. and S. Horiuchi. 1981. "Estimating the Completeness of De-ath Registration in a Closed Population." Population Index 47(2):207-221. Bongaarts, J. 1994. "Population Policy Options in the Developing World."

Science 263(5148):771-776.

Bongaarts, J. 1999. "Population Momentum." Pp. 3-15 in Population

Econ-omics, Demographic Transition, and Development: Research and Policy Implications, edited by Mason, A., T. Merrick, and R. P. Shaw.

Washing-ton, D.C.: IBRD/World Bank.

Bongaarts, J. and G. Feeney. 2002. "How Long Do We Live?" Population

and Development Review 28(1):13-29.

Bongaarts, J. and G. Feeney. 2006. "The Quantum and Tempo of Life-Cycle Events." Vienna Yearbook of Population Research 2006:115-151. Bongaarts, J. 2005. "Five Period Measures of Longevity." Demographic

Re-search 13(21):547 - 558.

Cai, Y. 2008. "An Assessment of China's Fertility Level Using The Vari-able-r Method." Demography 45(2):271-281.

Canudas-Romo, V. and R. Schoen. 2005. "Age-Specific Contributions to Changes in the Period and Cohort Life Expectancy." Demographic

Research 13:63-82.

Caselli, G., J. Vallin, and G. Wunsch. 2006. "Population Models." Pp. 249-267 in Demography: Analysis and Synthesis. A Treatise in Population, vol. I, edited by Caselli, G., J. Vallin, and G. Wunsch. Burlington, Massachusetts: Elsevier Academic Press.

Chandola, T., D. A. Coleman, and R. W. Hiorns. 1999. "Recent European Fertility Patterns: Fitting Curves to "Distorted" Distributions." Population

Studies 53(3):317-329.

Chandola, T., D. A. Coleman, and R. W. Hiorns. 2002. "Distinctive Features of Age-Specific Fertility Profiles in the English-Speaking World: Com-mon Patterns in Australia, Canada, New Zealand and the United States, 1970-98." Population Studies 56(2):181-200.

Coale, A. J. 1957. "A New Method for Calculating Lotka's r: The Intrinsic Rate of Growth in a Stable Population." Population Studies 11(1):92-94. Coale, A. J. 1972. The Growth and Structure of Human Populations: A

Mathematical Investigation. Princeton, N.J.: Princeton University Press.

the Age Structure of Childbearing in Human Populations." Population

Index 40(2):185-258.

Coale, A. and J. Trussell. 1996. "The Development and Use of Demogra-phic Models." Population Studies 50(3):469-484.

Elandt-Johnson, R. C. and N. L. Johnson. 1999. Survival Models and Data

Analysis. New Ed edition. New York: Wiley-Interscience.

Goldstein, J. and K. Wachter. 2006. "Relationships between Period and Co-hort Life Expectancy: Gaps and Lags." Population Studies 60(3): 257-269.

Goldstein, J. R. 2002. "Population Momentum for Gradual Demographic Transitions: An Alternative Approach." Demography 39(1):65-73. Goldstein, J. R. 2006. "Found in Translation? A Cohort Perspective on

Tem-po-Adjusted Life Expectancy." Demographic Research 14:71-84. Goldstein, J., W. Lutz, and S. Scherbov. 2003. "Long-Term Population

De-cline in Europe: The Relative Importance of Tempo Effects and Genera-tional Length." Population and Development Review 29(4):699-707. Guillot, M. 2003. "The Life Table: Modeling Survival and Death."

Population Studies 57(3):380-382.

Guillot, M. 2009. "The Effect of Changes in Fertility on the Age Distri-bution of Stable Populations." Demographic Research 20(24):595-598. Hinde, A. 1998. Demographic Methods. London: Arnold a member of the

Hodder Headline Group.

Hoem, J. M., D. Madsen, J. L. Nielsen, E. M. Ohlsen, H. O. Hangsen, and B. Rennermalm. 1981. "Experiments in Modeling Recent Danish Fer-tility Curves." Demography 18(2):231-244.

Horiuchi, S. and S. H. Preston. 1988. "Age-Specific Growth Rates: The Legacy of Past Population Dynamics." Demography 25(3):429-441.

Studies 22(2): 235-252.

Keyfitz, N. 1970. "The Demographic Significance of Age and Sex."

Demografiay Economia 4(2):11, 165-191.

Keyfitz, N. 1977. Applied Mathematical Demography. New York: John Wiley & Sons, Inc.

Keyfitz, N. and H. Caswell. 2005. Applied Mathematical Demography. Third Edition. New York: Springer-Verlag.

Keyfitz, N. and H. Caswell. 2005. Applied Mathematical Demography. Third Edition. New York: Springer Science+Business Media, Inc.

Kim, Y. J. and R. Schoen. 1993. "On the Intrinsic Force of Convergence to Stability." Mathematical Population Studies 4(2):89-102.

Kim, Y. J., Robert Schoen, and P. Sankara Sarma. 1991. "Momentum and the Growth-Free Segment of a Population." Demography 28(1):159-173. Land, K. C., Y. Yang, and Y. Zeng. 2005. "Mathematical Demography." Pp. 659-717 in Handbook of Population, edited by Poston, D. L. and M. Micklin. New York: Spinger Science+Business Media, LLC.

Li, N. and S. Tuljapurkar. 1999. "Population Momentum for Gradual De-mographic Transitions." Population Studies 53(2):255-262.

Lotka, A. J. 1907. "Relations Between Birth Rates and Death Rates." Science New Series 26(653):21-22.

Lotka, A. J. 1922. "The Stability of the Normal Age Distribution." Proceedings

of the National Academy of Sciences 8:339-345.

Peristera, P. and A. Kostaki. 2007. "Modeling Fertility in Modern Popula-tions." Demographic Research 16(6):141-194.

Preston, S. H. 1986. "The Relation between Actual and Intrinsic Growth Rates." Population Studies 40(3):343-351.

Preston, S. H. and A. J. Coale. 1982. "Age Structure, Growth, Attrition and Accession: A New Synthesis." Population Index 48(2):217-259.

Preston, S. H. and H. Wang. 2007. "Intrinsic Growth Rates and Net Reproduction Rates in the Presence of Migration." Population and

Development Review 33(4):657-666.

Preston, S. H., P. Heuveline, and M. Guillot. 2001. Demography: Measuring

and Modeling Population Processes. Malden, Massachusetts: Blackwell

Publishing.

Rodriguez, G. 2006. "Demographic Translation and Tempo Effects: An Accelerated Failure Time Perspective." Demographic Research 14(6): 85-110.

Schoen, R. 2005. "Intrinsically Dynamic Population Models." Demographic

Research 12:51-76.

Schoen, R. 2006. Dynamic Population Models. Dordrecht, The Netherlands: Springer.

Schoen, R. 2009. "The Metastable Birth Trajectory." Demographic Research 21(25):759-764.

Schoen, R. and S. H. Jonsson. 2003. "Modeling Momentum in Gradual Demographic Transitions." Demography 40(4):621-635.

Schoen, R. and Y. J. Kim. 1991. "Movement Toward Stability as a Funda-mental Principle of Population Dynamics." Demography 28(3):455-466. Schoen, R. and Y. J. Kim. 1994. "Cyclically Stable Populations." Mathematical

Population Studies 4(4):283-295.

Schoen, R. and Y. J. Kim. 1998. "Momentum under a Gradual Approach to Zero Growth." Population Studies 52(3):295-299.

Sparks, C. 2009. "An Application of the Variable-r Method to Subpopula-tion Growth Rates in a 19th Century Agricultural PopulaSubpopula-tion." Demographic

Research 21(2):23-64.

Thompson, Patric A., William R. Bell, John F. Long, and Robert B. Miller. 1989. "Multivariate Time Series Projections of Parameterized

Age-Spe-cific Fertility Rates." Journal of the American Statistical Association 84 (407):689-699.

Vallin, Jacques and Graziella Caselli. 2006a. "Population Replacement." Pp. 239-247 in Demography: Analysis and Synthesis. A Treatise in

Popu-lation, vol. I, edited by G. Caselli, J. Vallin, and G. Wunsch. Burlington,

Massachusetts: Elsevier Academic Press.

Vallin, J. and G. Caselli. 2006b. "The Future of Mankind: Looking Ahead after the Transition." Pp. 235-257 in Demography: Analysis and

Syn-thesis. A Treatise in Population, vol. III, edited by Caselli, G., J. Vallin,

and G. Wunsch. Burlington, Massachusetts: Elsevier Academic Press. Verma, R. B. P., S. Loh, S. Y. Dai, and D. Ford. 1996. "Fertility Projections

for Canada, Provinces and Territories, 1993-2016." Demography Division, Statistics Canada.

Véron, J. 2009. "The French Response to the Demographic Works of Alfred Lotka." Population 64(2):319-340.

附錄

人口數、生育率、

死亡率資料來源與插補

1.資料來源 本研究使用之臺灣地區年齡別人口數和生育數資料，主要是以內 政部戶籍統計為主，取自歷年「臺灣省戶籍統計要覽」、「臺灣省人 口統計」、「臺灣人口統計」、「臺閩地區人口統計」、以及「中華 民國人口統計年刊」。至於死亡率資料則是以內政部統計處編製之臺 灣地區生命表做為基礎。 2.單齡別生育率估計 臺灣的生育測量統計，可以溯及 1947 年，不過，在 1975 年以前， 生育率統計係以五歲年齡組方式計算，所以，我們以人口估計方式， 建立單齡別年齡別生育率。傳統上，人口學發展許多插補方法，可以 從分組資訊（grouped data）中重建細部（例如，單一年齡別）資訊。 例如，可以援引Sprague乘數進行密切插補（osculatory interpolation）， 而將五歲組的年齡別生育率分解為單一年齡組生育率（Judson and Popoff 2004）。是類的密切插補方法，不僅由來已久，而且用途廣 泛；可是仍舊存在限制—尤其，經常可能產生負數的插補結果，並 不符合人口事件的事實。除此之外，密切插補方法也不適用於推計不 完整資料（incomplete data）。 所以，在此我們提出一種新式的策略，可以估計單齡別生育率， 其具體途徑如下： 假定單一年齡別生育率的參數模型為10

f x

=

F1 2 2₁ 1 x 3 2 exp 2 1 2 2₁ 1 x

+

x 1 2

+

F2 2 2₂ 2 x 3 2 exp 2 2 2 2₂ 2 x

+

x 2 2 五歲組生育率為單一年齡別生育率之累計： 5 < f_x

=

1₅ 4 i=01 < f_x+i 以預測之五歲生育率估計實際觀察之生育率： 5fx

=

5 < f_x 在此，我們的 loss function 為誤差最小平方和，即 5fx 5 < fx 2 最小判準。 藉由上述三個步驟，可以得到參數模型之參數估計值，然後計 算預測之單一年齡別生育率，即1 < f_x。 3.單齡別死亡率率估計 內政部統計處所編製的生命表，係從 1950 年開始發佈，唯在 1950-1969年期間只有五歲年齡組的簡易生命表，在 1970 年以後則一 併發佈單齡的完全生命表。此外，生命表最高年齡組目前仍為 85 歲。 參 考 Baili et al.（2005）的 研 究 結 果，我 們 以 Elandt-Johnson and

10 人口學家曾經援引若干參數，藉此描述年齡別生育率模式（Coale and Trussell 1974; Keilman and Van Imhoff 1995; Hoem et al. 1981）。例如，加拿大人口普查局曾經使用 Pearson TypeⅠ函數（目前偏好 Pearson Type Ⅲ函數）進行生育率推計（Beaujot 2003; Verma et al. 1996），Thompson et al.（1989）使用 Gamma 函數推計生育率。當然， Coale and Trussell（1974）的模型則是最負盛名。基本上，各種參數模型在描述年齡別 生育率模式時，其適配程度（goodness-of-fit）差異不大。不過，基於考量參數模型必 須具有人口學意義，在此，我們援用 Hadwiger 函數（Chandola et al. 1999, 2002; Hoem et al. 1981; Peristera and Kostaki 2007）做為基礎，並且考量人口異質，以 Mixture Hadwiger 函數分佈配適臺灣的實證資料。

Johnson（1999）所建議的乘數，將五歲組簡易生命表進行密切插補， 以取得單齡別生存數（lx）。至於高齡人口的死亡率外插，則是採用

Brass的 relational model 策略，援用鄰近年度的國民生命表做為標準， 以人口轉譯（demographic translation）的作法取得高齡組死亡率。在 此，我們進一步採用 Namboodiri（1991）的發現，改以五參數模型而 非原始 Brass 的兩參數模型進行轉譯： lx

= +

1 ec lSx ₁ c if l S x < 0

= +

2 ec lSx ₁ d if l S x > 0

Momentum Effect of Changing Fertility

on Population Growth in Taiwan

Hsinmu Chen

*

_{Chia-Ying Lin}

**

Abstract

Taiwan has been experiencing radical fertility transition over the past several decades. Initially, Taiwan struggled against the population explosion caused by high fertility level. However, depopulation nightmare is currently suffered by Taiwan's demographic regime. Classical Lotka's stable population model has extensively employed to study the relationship between vital dynamics and age structure. Keyfits suggested the population momentum approach by relating stable population model to population size rather than to age structure or vital dynamics. In this study, we adopt Keyfit's new formulation and apply it to the non-stable, or variable-r, demographic conditions in Taiwan. Based on the findings from non-stable population model, the momentum effect of population growth in Taiwan is more pessimistic than any image suggested by previous studies. Were we able to raising Taiwan's lowest-low fertility to the replacement level, it is going to losing the population size more than 25% in the future.

Keywords: net reproduction rate; stable population model; variable-r approach; non-stable population model; population momentum

* Associate Professor, Department of Sociology, National ChengChi University. E-mail: hsinmu@nccu.edu.tw

** Associate Professor, Department of Sociology, National ChengChi University. E-mail: cylin@nccu.edu.tw