國立交通大學
土木工程研究所
碩士論文
應用希伯特黃轉換於結構物損壞判斷之研究
Application of Hilbert-Hung transform on
structural damage detection
研 究 生:羅振剛
指導教授:洪士林 博士
應用希伯特黃轉換於結構物損壞判斷之研究
Application of Hilbert-Hung transform on structural damage detection
研 究 生:羅振剛 Student: Zhen-Gang Luo 指導教授:洪士林 Advisor: Dr. Shih-Lin Hung
國立交通大學 土木工程研究所
碩士論文
A Thesis
Submitted to Department of Civil Engineering College of Engineering
National Chiao Tung University
In Partial Fulfillment of the Requirements for the Degree of
Master of Science in
Civil Engineering August 2007
HsinChu, Taiwan, Republic of China 中華民國九十六年八月
應用希伯特黃轉換於結構物損壞判斷之研究 學生:羅振剛 指導教授:洪士林 博士 國立交通大學土木工程學系 摘 要 結構損壞判斷是結構健康監測領域一個重要問題。基於結構動力學的損 壞判斷方法,不僅涉及到結構動力學理論,還涉及到對信號測式、數據處 理方法的相關研究。希爾伯特-黃轉換的重要應用價值在於提供了描述信號 即時變化特性的方法,因而適用於處理非線性非平穩等具有的明顯隨時間 變化特性的信號。 本論文探討應用希伯特-黃轉換邊際譜的結構物損壞判斷方法,研究了 如何從結構物的加速度記錄,通過比對損壞前後 HHT 邊際譜的相對變化來 判斷損傷位置。本文分析了三層樓數值模型,結果表明應用帶通濾波器的 加速度記錄,經過經驗模態分解法與 Hilbert 轉換後,繪製出正規化邊際 譜,對照無損傷結構物的正規化邊際譜,可以判斷出結構物損壞的位置。 而後實際應用在溫俊明博士於國立交通大學結構實驗大樓縮小尺寸之剪力 屋結構模型上,並驗證此方法的可行性。 關鍵字:希伯特黃轉換、邊際譜、損傷診斷
Application of Hilbert-Hung transform on structural damage detection
Student : Zhen-gang Luo Advisor : Dr. Shih-Lin Hung
Department of Civil Engineering College of Engineering National Chiao Tung University
ABSTRACT
The structural damage detection is the key of the structural health monitoring techniques. Damage detection methods based on the structural dynamics are involving new methods research on signal testing and data processing techniques, not only including the deep research on the theory of structural dynamics . The Hilbert-Hung Transform(HHT) is suited to be used in the nolinear and unstable signal processing for it offers a approach to describe the signal's instantaneous characters.
This work attempts to discuss a new approach to diagnose the structural damage application Hilbert Huang transform , analyzes the method of extracting modal responses detecting damage location. The numerical results of a three 3 story frame show that the model responses can be extracted by Bandpass Filters , and the damage location can be detected by comparing the Hilbert marginal spectrums of the undamaged structures with those of the damaged ones.
誌 謝
在研究所兩年的學習過程,隨著論文的完稿即將劃上句點,這段時間以 來的點點滴滴,有回憶與不捨;回憶之情將在我的懷中日漸晶瑩光耀,不 捨之心將使我的人生成就勇氣。 本文承蒙洪士林教授之悉心指導,始能順利完成,謹此致上最誠摯的 謝意。感謝黃炯憲、林昌佑、陳振華口試委員,均熱心提供許多寶貴的意 見,在此一併致謝。 在研究所修業期間,感謝同窗伙伴瀞云與巍贏兩年來的切磋討論與鼓 勵,詹君治大師兄在旁的建議獲益良多,與學長忠錦、心農、學弟怡廷、 世賢、承禹一起玩樂,永難忘懷。 最後,將本文給我敬愛的父母,感謝您們無怨無悔的養育與無時無刻的 關懷照顧,以及經濟上與精神上的支持,讓我能無憂無慮的專注於課業研 究中,願以此與家人共享。目 錄
目 錄
中文摘要 ... i 英文摘要 ...ii 目 錄 ... iv 第一章 緒論 ... 1 1.1研究動機與目的... 1 1.2研究背景... 2 1.3文獻回顧... 4 1.4本文內容... 5 第二章 希伯特-黃轉換(HHT)的基本介紹... 8 2.1 希伯特黃轉換... 8 2.2 即時頻率的概念... 92.3 內建模態函數(Intrinsic Mode Function , IMF)... 10
2.4 經驗模態分解法(Empirical Mode Decomposition ,EMD)... 12
2.6.1 邊際譜(marginal spectrum)的物理意義... 19
2.6.2 邊際頻譜與傅立葉頻譜 ... 19
2.7 邊際譜(marginal spectrum)在損傷部位判斷上的應用... 20
2.8 本章小結... 21
3.1 引言... 23
3.2HHT 結合 RDT 識別模態參數... 24
3.2.1 模態參數識別的基本介紹 ... 24
3.2.2 頻率域識別方法概述 ... 26
3.2.3 時間域識別方法概述 ... 26
3.2.4 隨機遞減法(Random Decrement Technique) ... 28
3.3HHT+RDT 真實案例應用... 29 3.4 裝設補強肢之效應... 31 3.5 數值模擬結構損壞部位判斷... 32 3.5.1 數值模擬的結構參數與地震反應... 32 3.5.2 Fourier 頻譜分析 ... 33 3.5.3 損傷部位判斷流程 ... 34 3.5.4 數值案例一 ... 35 3.5.5 數值案例二 ... 36 3.5.6 數值案例三 ... 37 3.5.7 數值案例四 ... 38 3.6 數值結構損傷程度判別... 39 3.6.1 結構參數及其地震反應 ... 39 3.6.2 數值案例五 ... 39
3.6.3 數值案例六 ... 40 3.6.4 數值案例七 ... 41 3.7多樓層損壞判斷... 42 3.7.1 數值案例八 ... 43 3.7.2 數值案例九 ... 43 3.7.3 數值案例十 ... 44 3.8 本章小結... 45 第四章 真實案例應用... 47 4.1 應用對像簡介... 47 4.2 各真實案例結構參數... 48 4.3 Fourier 頻譜分析... 49 4.4 損傷部位判斷流程... 50 4.5 損傷位置判斷... 51 4.5.1 真實案例一 ... 51 4.5.2 真實案例二 ... 52 4.5.3 真實案例三 ... 52 4.5.4 真實案例四 ... 53 4.5.5 真實案例五 ... 54 4.5.6 真實案例六 ... 55
4.5.7 真實案例七 ... 55 4.6 本章小結... 56 第五章 結論與建議... 58 5.1結論... 58 5.2 建議... 58 參考文獻 ... 59
表 目 錄
表 3.1 編號 Kobe008_dk123 地震力,第一模態識別成果比較表... 62 表 3.2 編號 Kobe008_dk123 地震力,第二模態識別成果比較... 62 表 3.3 編號 Kobe008_dk123 地震力,第三模態識別成果比較表... 63 表 3.4 編號 Kobe008_dk123 地震力,第四模態識別成果比較表... 63 表 3.5 Kobe008_nnn 無加勁肢與 Kobe008_aaa 有加勁肢,頻率識別結果.. 64 表 3.6 數值案例一~四參數... 64 表 3.7 數值案例五~七參數... 65 表 3.8 各數值案例各層樓正規化邊際譜增減量... 65 表 4.1 國立交通大學地震模擬振動臺規格... 66 表 4.2 四層鋼骨構架模型之設計參數... 66 表 4.3 真實案例一~真實案例四類神經識別頻率 ... 66 表 4.3 真實案例一~真實案例四類神經識別頻率 ... 67 表 4.4 真實案例一正規化邊際譜振幅與振態... 67 表 4.5 真實案例二正規化邊際譜振幅與振態... 67 表 4.6 真實案例三正規化邊際譜振幅與振態... 68 表 4.7 真實案例四正規化邊際譜振幅與振態... 68 表 4.8 真實案例五正規化邊際譜振幅與振態... 69 表 4.9 真實案例六正規化邊際譜振幅與振態... 69圖 目 錄
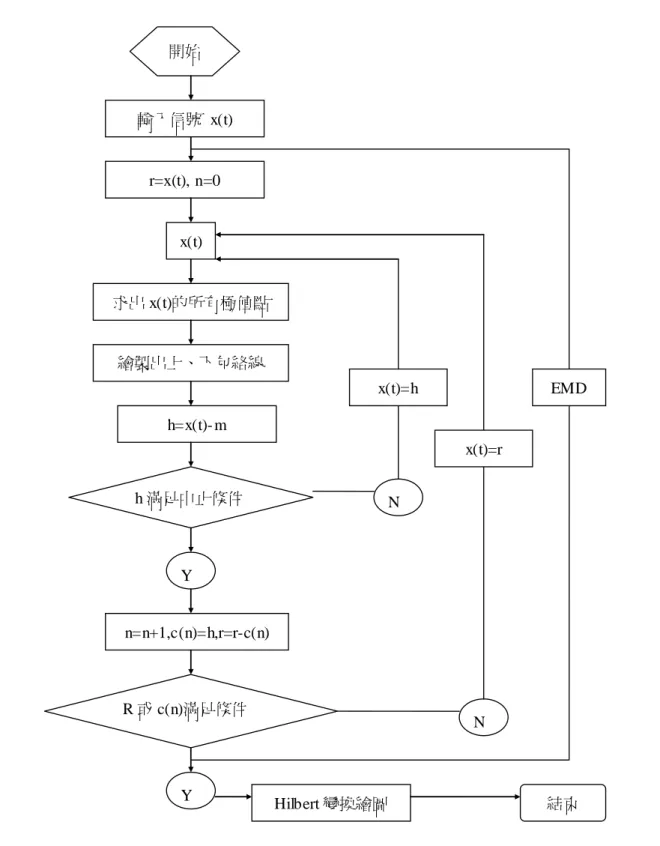
圖 2.1 希伯特理論架構流程圖... 70
圖 2.2 EI Centro 地震波 ... 71
圖 2.3 (a)EI Centro 地震波、(b) EI Centro 地震波局部放大 ... 72
圖 2.4 (a)分量 h1(t)、(b)分量 h1(t)局部放大 ... 72 圖 2.5 (a)原始信號與平均包絡線之差 (b)差值的局部放大 ... 72 圖 2.6 (a)分量 h2(t)、(b)分量 h2(t)局部放大 ... 73 圖 2.7 (a)分量 h3(t)、(b)分量 h3(t)局部放大 ... 73 圖 2.8 (a)第一個內建模態函數 (b)局部放大第一個內建模態函數 ... 74 圖 2.9 (a)第二個內建模態函數 (b)局部放大第二個內建模態函數 ... 75 圖 2.10 EI Centro 地震波所有的內建模態函數 ... 76 圖 2.11 EMD 流程圖 ... 77 圖 2.12 邊界譜的物理意義示意圖... 78 圖 2.14 IMF01 與 IMF02 的即時振幅 ... 79 圖 2.15 傅立葉譜... 80
圖 3.1 Using HHT and RDT to identify modal parameters ... 81
圖 3.2 編號 Kobe008_dk123 感測器反應,左邊每層樓加速度反應、右圖為 其傅立葉轉換……….83
圖 3.4 經過 EMD 後所得第一個 IMF... 82 圖 3.5 所有的內建模態函數及餘數... 83 圖 3.6 最小平方法近似... 83 圖 3.7 Analyzed model... 84 圖 3.8 EI Centro 地震波地表加速度曲線 ... 84 圖 3.9 數值案例一各樓層的加速度與位移反應... 85 圖 3.10 數值案例二各樓層的加速度與位移反應... 85 圖 3.11 數值案例三各樓層的加速度與位移反應... 86 圖 3.12 數值案例四各樓層的加速度與位移反應... 86 圖 3.13 數值案例一各樓層加速度反應與傅立葉譜... 87 圖 3.14 數值案例二各樓層加速度反應與傅立葉譜... 87 圖 3.15 數值案例三各樓層加速度反應與傅立葉譜... 88 圖 3.16 數值案例四各樓層加速度反應與傅立葉譜... 88 圖 3.17 左為數值案例一各層加速度記錄,右為其第一個內建模態函數 .. 89 圖 3.18 數值案例一正規化邊際譜... 89 圖 3.19 左為數值案例二各層加速度記錄,右為其第一個內建模態函數 .. 90 圖 3.20 數值案例二正規化邊際譜... 90 圖 3.21 左為數值案例三各層加速度記錄,右為其第一個內建模態 ... 91 圖 3.22 數值案例三正規化邊際譜... 91
圖 3.23 左為數值案例四各層加速度記錄,右為其第一個內建模態函數 .. 92 圖 3.24 數值案例四相對邊際... 92 圖 3.25 數值案例五各樓層的加速度與位移反應... 93 圖 3.26 數值案例六各樓層的加速度與位移反應... 93 圖 3.27 數值案例七各樓層的加速度與位移反應... 93 圖 3.28 左為數值案例五各層加速度記錄,右為其第一個內建模態 ... 94 圖 3.29 數值案例五正規化邊際譜... 94 圖 3.30 左為數值案例六各層加速度記錄,右為其第一個內建模態 ... 95 圖 3.31 數值案例六正規化邊際譜... 95 圖 3.32 左為數值案例七各層加速度記錄,右為其第一個內建模態 ... 96 圖 3.33 數值案例七正規化邊際譜... 96 圖 3.34 數值案例八各樓層的加速度與位移反應... 97 圖 3.35 數值案例九各樓層的加速度與位移反應... 97 圖 3.36 數值案例十各樓層的加速度與位移反應... 97 圖 3.37 左為數值案例八各層加速度記錄,右為其第一個內建模態函數 .. 98 圖 3.38 數值案例八正規化邊際譜... 98 圖 3.39 左為數值案例九各層加速度記錄,右為其第一個內建模態函數 .. 99 圖 3.40 數值案例九正規化邊際譜... 99 圖 3.41 左為數值案例九各層加速度記錄,右為其第一個內建模態函數 100
圖 3.42 數值案例十正規化邊際譜... 100 圖 3.43 數值模擬案例一相對振幅與振態比較圖... 101 圖 3.44 數值模擬案例二相對振幅與振態比較圖... 101 圖 3.45 數值模擬案例三相對振幅與振態比較... 102 圖 3.46 數值模擬案例四相對振幅與振態比較圖... 102 圖 4.1 國立交通大學地震模擬振動台... 105 圖 4.2 縮尺四層鋼骨構架模型:(a)強軸(x)方向設計尺寸;(b)弱軸(y) 方向設計尺寸;(c)各樓層平面(俯視圖)設計尺寸 ... 105 圖 4.3 四層鋼構模型(未裝設補強肢) ... 106 圖 4.4 四層鋼構模型(裝設補強肢) ... 106 圖 4.5 真實案例一各樓層加速度反應與傅立葉譜... 107 圖 4.6 真實案例二各樓層加速度反應與傅立葉譜... 107 圖 4.7 真實案例三各樓層加速度反應與傅立葉譜... 108 圖 4.8 真實案例四各樓層加速度反應與傅立葉譜………111 圖 4.9 真實案例五各樓層加速度反應與傅立葉譜... 109 圖 4.10 真實案例六各樓層加速度反應與傅立葉譜... 109 圖 4.11 真實案例七各樓層加速度反應與傅立葉譜... 110 圖 4.12 左為真實案例一各層加速度記錄,右為其第一個內建模態 ... 111 圖 4.13 真實案例一正規化邊際譜... 112
圖 4.14 真實案例一相對振幅與振態比較圖... 112 圖 4.15 左為真實案例二各層加速度記錄,右為其第一個內建模態 ... 113 圖 4.16 真實案例二正規化邊際譜... 114 圖 4.17 真實案例二相對振幅與振態比較圖... 114 圖 4.18 左為真實案例三各層加速度記錄,右為其第一個內建模態 ... 115 圖 4.19 真實案例三正規化邊際譜... 116 圖 4.20 真實案例三相對振幅與振態比較圖... 116 圖 4.21 左為真實案例四各層加速度記錄,右為其第一個內建模態 ... 117 圖 4.22 真實案例四正規化邊際譜... 118 圖 4.23 真實案例四相對振幅與振態比較... 118 圖 4.24 左為真實案例五各層加速度記錄,右為其第一個內建模態 ... 119 圖 4.25 真實案例五正規化邊際譜... 120 圖 4.26 真實案例五相對振幅與振態比較... 120 圖 4.27 左為真實案例六各層加速度記錄,右為其第一個內建模態 ... 121 圖 4.28 真實案例六正規化邊際譜... 122 圖 4.29 真實案例六相對振幅與振態... 122 圖 4.30 左為真實案例七各層加速度記錄,右為其第一個內建模態……...125 圖 4.31 真實案例七正規化邊際譜... 124 圖 4.32 真實案例七相對振幅與振態... 124
第一章 緒論 1.1 研究動機與目的 結構物在強烈地震作用下,其內部某些結構或構件產生損壞,勁度、強 度等力學性能之降低,進而導致結構的頻率、阻尼比等結構動力特性發生 變化。因此,通過分析結構動力特性的變化來識別結構健康診斷成為當前 工程界研究的熱門課題之一。傳統損壞識別是基於傅立葉變換的頻譜分析 法,傅立葉變換是信號在時間域上的統計平均值,不能反應信號的局部特 性,且要求分析信號是穩態的、線性的。然而,在土木工程領域,大部份 量測的振動反應訊號是非穩態的,或是非線性的,傅立葉譜分析法既不能 捕捉這些振動過程中的非線性和非穩態特性[15],也不能識別結構損壞發 生過程。為此,在土木工程領域的系統識別和健康診斷中,應用小波變換 的時間域分析法受到了廣泛關注[1]。然而,小波分析法仍然以傅立葉變換 為基礎,是對傅立葉變換的改進,在識別振動信號包含的非線性、非平穩 特性上仍存在局限性[2]。 Hilbert-Huang Transform(HHT)是由美籍華人博士提出的一種全新的數 據處理方法,具有方法簡單有效、自適應性強、高解析度、多解析度等優 點[3]。該方法提出後,在大氣、海洋、醫學等各個工程領域迅速推廣和應 用,而土木工程領域林宏宇應用 HHT 在結構物系統識別進行了研究[4]。本
文則將採用此 HHT 方法中的邊際譜(marginal spectrum)進行結構損傷判 斷,邊際譜的物理含義是不同頻率成份在整個時間域內的能量貢獻。因此 可以通過對比每個測量點損壞前後邊際譜的相對變化來確定損壞位置。 通過二種三層樓模型地震反應的數值模擬分析,證明了比對正規化邊際 譜可顯現在結構物的損壞樓層位置。最後將此方法實際應用在溫俊明博士 在國立交通大學結構實驗大樓縮小尺寸之剪力屋結構模型上,以無裝設補 強肢模擬該層受損,亦可從比對正規化邊際譜中得知損壞樓層的位置。 1.2 研究背景 近年來,信號的分解與重構在通信、圖像處理、故障診斷等領域中受到 專家學者的極大重視,常用的信號分解與重構的方法有傅立葉變換法和小 波分析方法等。本質上傅立葉變換是將是任意信號分解成正弦信號的加權 和,而每一個正弦信號對應著一個固定的頻率(傅立葉頻率)與固定的振 幅,因此用傅立葉變換分析頻率不隨時間變化的平穩信號是十分有效的, 但對於頻率隨時間變化的非平穩信號,傅立葉就顯得無能為力了。此類分 解方法在數學上構造完善但缺乏實際物理意義,在應用中存在著難以進行 模型解釋的難題[12]。在許多問題如廣播電視、通信、雷達以及地震資料 分析中,即時參數的求取與研究具有不可取代的作用。人們提出了很多方 法,其中包含解析信號法(Hilbert 變換方法),對於任意指定的時間,通過
Hilbert 變換運算後的結果只能存在一個頻率值,即只能處理單一頻率的信 號,那麼對於實際中多頻率成份的信號這種分析顯然是不合理的。對於非 平穩信號(例如地震信號),想要獲得某一時間的頻率成份或者某一頻率的 分佈情況,時間域分析就變得重要,但對目前的時間域方法來說,想得到 精確的時頻分佈圖或確定頻率與時間的變化關係,還有待更進一步的研究。 直到 1998 年,美國華裔科學家黃鍔等人才提出了一種真正基於即時頻 率的信號處理方法-經驗模態分解法(EMD) ,並在此基礎上提出了希伯特-黃變換,從直觀上解決了上述問題。黃鍔博士(N.E.Huang) 提出來了一種 稱為(Hilbert-Huang Transformation, HHT)新的信號處理方法,該方法的 主要創新是內建模態函式(Intrinsic Mode Function,簡稱 IMF)概念的提 出和經驗模態分解法(Empirical Mode Decomposition,簡稱 EMD)的引入。 通過 EMD 將一個時間序列信號分解成有限個不同時間尺度的 IMF,對每個 IMF 進行 Hilbert 變換解析信號,得出信號的即時頻率和即時振幅,進而得 到能量分佈譜圖(Hilbert Spectrum)[2]。HHT 是基於信號局部特性的與自 適應的,因而是高效的。它特別適用於分析生活中普遍存在大量頻率隨時 間變化的非線性、非穩態信號。然而地震記錄一般是非線性、非穩態數據, 用 HHT 方法來處理地震記錄,可以很好的識別結構自然頻率的時變特性。 與傅立葉變換和小波分析相比,HHT 方法在客觀性上和解析度上方法都具有 明顯的優越性,能有效提取結構的損壞特性。
1.3 文獻回顧 希伯特-黃轉換(Hilbert-Huang Transformation, HHT)是上世紀未美國 航空太空總署(NASA)的黃鍔博士(Norden E Huang)等人首次提出了一種新 的信號分析理論[2]。其 HHT 重大發明,在美國獲得八項專利。2006 年榮獲 「美國服務貢獻獎」殊榮,2000 年當選美國國家工程研究院院士、2003 年 NASA 年度發明家、2004 年中央研究院院士。實際中,HHT 得到了相當廣泛 的應用,也表現出一些特有的優點。Huang 本人主要建立了 HHT 的基本框架, 分析了 HHT 的基本依據,引入了內建模態函數(IMF)的概念,提出了經驗模 態分解法(EMD),定義了 Hilbert 譜和邊際譜概念,討論了 HHT 正交性的問 題,比較了 HHT 與小波及其他信號分析方法的區別,並研究了 HHT 在非線 性系統分析、水波分析、風速分析、潮汐和海嘯分析、海洋環流分析和地 震信號分析等應用。在生物醫學信號研究領域,用 HHT 分析肺部血壓信號 [6]、應用 EMD 方法分離胃電信號中的人工干擾[7]、應用 EMD 方法分解猴 子視覺神經信號[8]等;在地球物理學領域,各種信號(如海洋波動信號、 潮汐信號、溫度信號、地震信號等)由於受到自然因素影響而變得十分複 雜,都是一些非線性非平穩信號。Huang N E 等應用 HHT 分析一些典型的地 球物理數據[2]、WuML 等應用 HHT 分析南亞夏季季節性降雨數據[9]、 Gloerson P 等應用 EMD 方法分析南北極海冰面數據[10]等;在振動工程領 域,HHT 變換被廣泛應用於故障檢測、參數識別等方面。Leisk G 等[11]指
出由於機械加工過程是動態的,包含了工件、切具和機器本身之間複雜的 相互作用,並應用 HHT 變換分析其複雜振動信號的時間序列,證明瞭將此 方法應用於狀態檢測系統的可行性。在土木工程領域中,林宏宇 [4]分析 了國科會 Benchmark 加速度記錄,研究 HHT 變換在結構模態參數識別中的 應用,並與類神經識別成果進行比較,對比表明 HHT+RDT 識別方法有很好 的識別效果,適用於土木工程結構的模態參數識別。而在國內國立中央大 學於 2006/12/18 成立數據方法研究中心,發明人黃鍔院士擔任中心主任, 可望快速提升台灣在國際學術界的能見度。黃鍔表示,當今的數據分析, 都是數學家提出的,他們基於嚴謹、理想化的假設,並以一成不變的基方 程來分析。但「現實的世界是多變的」,自然界的訊號,必須要用更客觀、 近似值的分析方法,因此中心的成立,目的就在於依循自適性方法,推展 有關 HHT 理論的建立及其在各領域的應用。其組識成員包含其他各種不同 學術領域,如應用力學、物理、統計、土木等,其中成員包含有張建中 Dr. Chang, Chien-Chung,吳明佳 Dr. Ming-Chya Wu,吳天堯 Dr. Tian-Yau Wu, 張玉媚 Dr. Yumei Chan…等。
1.4 本文內容
本論文研究的主要內容是對 HHT 邊際譜進行損壞判斷應用,首先採用二 種不同三層樓數值模型,改變勁度以模擬樓層受損,接著比對前後正規化 邊際譜來判斷損壞位置。在真實案例方面,利用在博班俊明學長於國立交
通大學結構實驗大樓縮小尺寸之剪力屋結構模型量測到的加速度資料,根 據損壞部位振動集中的特點[15],通過比對損傷前後的 HHT 邊際譜相對變 化來判斷損壞樓層位置。具體抱含以下內容。 1. 對近年來出現對非線性非平穩信號處理新方法希伯特-黃轉換 (Hilbert-Huang Transform)的基本理論進行簡述。 2. 在應用 HHT 邊際譜來判斷損壞樓層位置時,會應用到帶通濾波器, 而帶通濾波器中的阻帶衰減量設定對系統識別成果影響很大[4],為 了得知那種設定值對識別成果最佳,這裡採用林宏宇論文裡的程式 來識別國立交通大學結構實驗大樓縮小尺寸之剪力屋結構模型的自 然頻率,並與俊明學長類神經識別成果做比較,進而決定帶通濾波 器相關設定值。 3. 利用 HHT 邊際譜可以呈現不同頻率成份在整個時間域內的能量貢 獻,根據損壞部位振動集中的特點,因此分析通過比對每個測點損 傷前後邊際譜來確定損壞樓層的位置。本文這部份先以數值模擬做 驗證,以勁度 2.7*107 N/m 做為健康無受損結構,而受損樓層以勁度 2.1*107 、1.5*107 N/m 模擬。用九個數值案例來模擬損壞樓層位置與 程度,進而比對損壞前後 HHT 邊際譜中的層間增減量來判斷損壞位 置是否如預期。 4. 在真實案例中採用溫俊明博士實驗數據,關於結構損傷之模擬以結
構層間勁度之折減為之,將以層間補強肢抽離以模擬損傷情況。由 於結構在遭受地震力侵害下其損壞位置通常位於較低之樓層,因此 在應用上採用一至三層樓之層間無補強肢情況下數據,接著一樣繪 出受損的 HHT 正規化邊際譜,接著比對完整無損壞的正規化邊際譜 來判斷損壞的樓層位置。 5. 最後提出對本文結論與未來展望。
第二章 希伯特-黃轉換(HHT)的基本介紹 2.1 希伯特黃轉換 對任何訊號而言若能提供保持原始訊號的基底,並作其頻譜轉換則函數 解析才有物理意義,在傅立葉轉換中,訊號被分解成許多固定頻率之諧和 函數作線性疊加組合,各諧和函數的大小也能代表該函數在某一頻率所具 有的能量大小,若訊號是穩態分佈且不隨時變化的時間序列,即能有效透 過頻譜轉換呈現訊號之特性。但是,對於非線性、非穩態之訊號而言,傅 立葉轉換只能代表訊號能量的平均分佈,無法呈現隨時間變化的訊息。再 者,若原訊號不是諧和函數,則必須額外疊加相當多的高頻諧和函數來模 擬被扭曲的變形波,但這些額外的高頻並原始訊號所包含,也因此,能量 散佈到較大的頻寬,造成判讀上的錯誤。 1998 年美國華裔黃鍔博士發表經驗模態分解法(Empirical Mode Decomposition)EMD,利用資料變化的內部時間尺度來做能量的直接析出, 將原來訊號資料展開多個內建模態函數(Intrinsic mode function,IMF), 把 IMF 當作展開的基底,再利用 Hilbert-Transform 來求出 IMF 的瞬時頻 率及振幅,為頻率加權的正規化同時結合時間、振幅、頻率之分佈,使訊 號能表現瞬時變化的訊息與特性,稱為希伯特黃轉換[2],圖(2.1)所示為 希伯特轉換 Y(t)架構之流程圖。
1 ( ) ( ) X Y t PV d t τ τ π τ ∞ −∞ = −
∫
(2-1) 其中 Y(t):希伯特轉換;X(t):對任意的時間序列 PV:柯西主值(Cauchy Principal Value)因 X(t)和 Y(t)組合成一共軛複數函數,得到一解析的訊號 Z(t): ( ) ( ) ( ) ( ) ( ) i t Z t = X t +iY t = a t eθ (2-2) 其中 a(t)=[X2 (t)+Y2 (t)]1/2 (2-3) θ(t)=tan-1 Y(t)/X(t) (2-4) 希伯特黃轉換提供了一個方法來定義虛部,簡單來說,希伯特黃轉換即 定義為 X(t)與 1/t 的迴旋積分(Convolution);因此希伯特黃轉換的物理意 義在於強調 X(t)局部特性。在(2-5)式中,極座標的表示式更進一步闡明了 它的局部性:它是振幅及相位角的最佳近似方法,使用改變的三角調和函數 來近似 X(t)。
( )
d
t
dt
θ
ω
=
(2-5) 2.2 即時頻率的概念 內建模態函數中,即時頻率為不可缺少的因素,它指引分量函數所要的 限制條件,在定義即時頻率之後,符合這些限制條件的函數,這就是內建分量。 即時頻率(Instantaneous Frequency)的意義卻一直廣受討論,這促使 Cohen[16],提出了一個特殊單一分量訊號的概念,才使即時頻率有了一個 具體的概念。在傅統的傅立葉分析中對於即時頻率的定義以正弦及餘弦調 和函數來作為基底,並且振幅是固定不變,即時頻率表示每一瞬間的頻率 值。就傅立葉分析而言,因為取樣的訊號必須大於一個完整的震盪周期, 因此最少要有一個完整的正弦或餘弦波震盪周期來定義局部的頻率值。 對於頻率值隨著時間改變的非穩態訊號而言是不正確的,故為了得到有 意義的即時頻率,而採用 Gabor 與 Bedrosian[17],所討論而得的嚴格條件: 對於任一函數要得到其有意義的即時頻率,它的傅立葉轉換的實部必須只 有正的頻率,對於資料分析而言,必須要使這個條件變成具體可以實行而 發展出一個簡單的方法可以加以應用。由於這個目的,必須修正這個限制 條件將從原本是全面性的變成局部性的。 傅立葉頻率與即時頻率的差異如下: 1.傅立葉頻率是一個獨立的量,而即時頻率是時間的函數。 2.傅立葉頻率是一個全局性的量,它是信號在整個時間區間內的體現, 而即時頻率是信號在特定時間上的局部體現,理論上它應該是信號在 該時刻所具有的頻率。
雖然 Hilbert 變換具有優良的特性,但不幸的是,大多數信號或數據不 是單一頻率。任何時刻,數據中可能包含不止一個單一頻率,這就是為什 麼簡單的 Hilbert 變換不能給出一個一般信號的完全頻率內容的原因 [13]。因此必須把數據分解成基本模式分量;在物理上定義一個有意義的 即時頻率的必要條件是:函數相對於局部零均值(local zero mean)是對稱 的,並且有相等的跨零點(zero-crossings)個數和極值點(extrema)個數。 因此,黃鍔提出滿足下面條件的一種函數-內建模態函數(Intrinsic Mode Function , IMF),對其條件如下:
內建模態函數(Intrinsic Mode Function , IMF)滿足兩個條件: (1)在整個數據集中,極值的數目和跨零點個數相等或最多相差 1 個; (2)在任何時間點上,由極大值包絡線(maxima envelope)及極小值包絡線
(minima envelope)所定義的均值包絡線(mean envelope)必須是零。其 中這裡的極大值包絡線是由局部極大值所定義的,極小值包絡線是由局 部極小值所定義的。
第一個條件,與傳統平穩高斯過程(Stationary Gaussian Process)中 窄頻寬的要求很類似。第二個條件是一個新的建議,目的在將整體性要求 改變成局部性的要求,這樣的好處在於對處理不對稱的波形時即時頻率也 將不會產生不必要的晃動;理想中,要處理訊號的局部均值(local mean) 應該要是零,但是對於非平穩性的訊號而言,局部均值是需要一個局部的
時間尺度(local time scale)來計算,這是非常不容易的。因此為了完成 這個動作,將利用局部極大值定義的極大值包絡線及由局部極小值定義的 極小值包絡線來強迫局部的對稱,這是為了避免局部平均時間尺度而必要 近似的定義。內建模態函數(IMF)它表達了深藏在訊號內部振盪模態,在每 一個循環中由跨零點所定義的內建模態函數只包含一個模態的振動,不會 有很複雜的載波亦不會被限制到是一個窄頻寬的訊號,它的振幅及頻率是 可以變動的,頻率或振幅完全變動的函數皆可以為內建模態函數,因此內 建模態函數將可以是非平穩性的。綜觀之前的論述,若要得到即時頻率, 需要解析一個任意的資料成為內建模態函數分量,即時頻率才可以應用到 每一個內建模態函數分量裡去,對於複雜的資料來說,在同一時刻可能會 得到超過一個以上的即時頻率。 為了使用即時頻率這個特殊定義,必須把一個隨意數據集分解成 IMF 分 量,這樣一個即時頻率值可以被賦予各個 IMF 分量。然而對於複雜數據, 在一個局部時間可以有多個即時頻率,下一節將引入經驗模態分解法來將 數據分解成為所需要的 IMF。
2.4 經驗模態分解法(Empirical Mode Decomposition ,EMD)
如前所述,對 IMF 分量進行 Hilbert 變換得到的即時頻率能夠提供信號 所描述現象合理的物理解釋。但是,大部份自然信號都不能滿足 IMF 分量
的條件。在任意時刻,一般信號不只包含一個振動模態,因此使得簡單的 Hilbert 變換無法為一般信號的頻率含量提供全面描述[2]。因此,必須先 將一般信號分解成若干 IMF 分量,然後再對 IMF 分量進行 Hilbert 變換。 提出了 IMF 分量的概念後,根據 IMF 定義,黃鍔發展了一種將任意信號 分解成 IMF 分量的方法,即經驗模態分解法(Empirical Mode
Decomposition ,EMD)。與其他信號處理方法相比,EMD 方法是直觀的、直 接的、後驗後、以及自適應的,其分解所用的訊號是源自於原始訊號[2]。 該方法的實質是通過特徵時間尺度 (characteristic time scale)來識別 信號中所內涵的振動模態,然後對其進行分解。在這一過程中,特徵時間 尺度及 IMF 的定義都具有一定的經驗性和近似性,因此如前所述,這種方 法是一種物理上的方法。僅管如此,前面也提到過,經過黃鍔博士的驗證, EMD 方法分解信號所得到的 IMF 分量即使在最壞的情況下,對其進行 Hilbert 變換所得到的即時頻率也能夠與所研究系統的物理機制相一致。 由於分解的基底是從原來訊號推導而來的,因此有下列三項假設條件: (1) 欲分析之訊號至少有兩個極值,其中包括一個極大值和一個極小值; (2) 訊號特徵時間尺度定義為兩個極值之間的時間差; (3) 若資料全無極值,若只包含反曲點,將訊號微分一次或多次,把極值 找出來。 本節將以如圖(2.2)所示的 EI Centro 地震波為例詳細介紹EMD方法分
解複雜信號時的具體過程如下。根據經驗利用訊號中特徵時間尺度來定義 其振動模態,然後依據它來分解訊號,這是一個有系統的方法用來解析出 內建模態函數,又可稱為轉移過程(Shifting Process)。首先,將圖(2.2) 所示波形中所有局部極大值點和局部極小值點取出來;然後用立方弧線 (cubic spline)[18]將所有局部極大點連接起來構成原始波形的上包絡 線,同樣用立方弧線將所有局部極小值點連接起來構成原始波形的下包絡 線,上下包絡線應將原始波形包在中間;最後求出上下包絡線的平均值 m0(t),用原始信號 X(t)減去 m0(t)就得到分量 h1(t),即; h0(t)=X(t), h0(t)-m0(t)=h1(t) (2-6) 上述過程即稱為一次轉移過程(Shifting Process)。該過程可以用圖 (2.3)、圖(2.4)、圖(2.5)說明:圖(2.3) 繪出原始 EI Centro 地震波波形, 總共 20250 採樣點,取樣頻率 250,共記錄 81 秒;圖(2.4)中實線表示原始 EI Centro 地震波波形,兩條虛線分別表示極大點上包絡線與極小點下包絡 線,而中間的點則表示上、下包絡線的平均值;圖(2.5)則給出了原始波形 與包絡線均值之差,即 h1(t)。 在理想條件下,h1(t)應該為 IMF。但是在一般情況下,由於立方弧線中 的突起和凹陷以及原始波形中的 h1(t)並不滿足 IMF 條件:在 h1(t)的波形 中仍然存在局部極大值點位於零線下方和局部極小值點位於零線上方的情 況,即畸行波。為此上述轉移過程應重復多次以最終獲得 IMF 分量。在第
二次轉移過程中,將 h1(t)作為原始波形,求出其平均包絡線 m1(t),然後 得到: h1(t)-m1=h2(t) (2-7) h2(t)的波形如圖(2.6)所示,相比 h1(t),該波形有了一定的改進;但是, 該波形仍然存在著關於零線不對稱的波。再進行一次轉移過程後所得到的 h3(t)如圖(2.7)所示。經過這次轉移過程後,波形有了更好的改進,但是到 然不能滿足 IMF 條件。因此,我們到需要重復轉移過程處理,經過 k 次轉 移次數之後就可以得到了 hk(t): hk-1(t)-mk-1=hk(t) (2-8) 上述轉移過程重復多次後達到一定標準後,hk(t)就成為原始信號的第 一個 IMF 分量,即: C1(t)=hk(t) (2-9) 如圖(2.8),歷來,黃鍔博士等人曾提出兩種不同的收斂停止條件: (1) 前後轉移函數間的標準差小於我們預先設定的值,標準偏差(standard deviation, SD)公式定義如下:
( )
( )
2 1 0 2 1 0 T k k t k T k t h t h t SD h − = − = − =∑
∑
(2-10) (2)選定一個轉移次數值 S,使得跨零點數量和局部極值總數量(局部極大值 數量加上局部極小值數量)要相等或差一個。Rilling 等提出的終止條件,定義函數
( )
min max min max e e e e t a − + = (emax,emin分別為上下包絡線) (2-11) 作為判定是否終止轉移過程的依據。設定三個門限值θ1、θ2、α,規定 當a( )
t 裡面小於θ1的比率達到 α,且不存在大於θ2的值時,終止轉移過 程。Rilling 博士建議為,θ1=0.05,θ2=0.5,α=0.95,本文也將照此預 設值。 按照此標準,我們就可以從式(2.9)給出的原始信號第一個 IMF 分量, 該分量為原始信號中最高頻的分量。從原始信號中分離出 C1(t)後,我們就 可以得到如下殘餘信號: X(t)-C1(t)=r1(t) (2-12) 然後 r1(t)作為新的信號,對 r1(t)進行上述轉移過程處理後可以得到第 二個 IMF 分量 C2(t),如圖(2.9)然後將 r1(t)減去 C2(t)後以得到 r2(t),如 此重複下去,就可以得到一系列的 IMF 分量: r1(t)-C2(t)=r2(t)……rn-1-Cn(t)=rn(t) (2-13) 上述過程結束的標準為: (1)最後得到的 IMF 分量 Cn(t),或殘餘信號 rn(t)的振幅非常低,低於預先 設定好的值 (2)最後的殘餘信號 rn(t)為時間的單調函數就可以分解成了數個 IMF 分量。則: ( ) ( ) ( ) n i n i n X t C t r t = =
∑
+ (2-14) 至此,將信號分解成 n 個經驗模態和一個殘餘信號 rn(t),它就是一個平均的趨勢或是一個常數。EI Centro 地震波的所有 IMF 分量如圖(2.10) 所示。該地震加速度記錄分解一共得到了 20 個 IMF 分量和 1 個殘餘分量。 其整個程式過程如圖(2.11)所示。
2.5 希伯特黃頻譜(Hilbert Huang Spectrum)
將原訊號藉由內部模態函數分解 IMF 分量,藉由希伯特黃轉換而得到希 伯特黃頻譜。對每一個 IMF 分量做希伯特黃轉換之後,將資料表達成下列 的形式: ( ) 1 ( ) ( ) j n i t dt j j X t a t e ω = ∫ =
∑
(2-15) 由式(2-2)知 ( )( )
( )
( )
( )
i tZ t
=
X t
+
iY t
=
a t e
θ 設原始函式 X(t)=Z(t), 則 X(t)=a(t)eiθ(t) , 因 d ( )t dt θ ω =∫
ω
( )
t dt
=
∫
d
θ θ
=
所以 ( )( )
( )
i t dtX t
=
a t e
∫
ωn 個 IMF 分量得 ( ) 1 ( ) ( ) n i j t dt j j X t a t e ω = ∫ =
∑
希伯特黃轉換可以當作一個很長週期振盪的單調趨勢,考慮長趨勢的不 確定性,以及低頻和高頻分量,原函數提供每一個分量,隨時間函數的振 幅與頻率函數。 若是相同的資料以傅立葉展開則為 1 ( ) i jt j j X t a eω ∞ = =∑
(2-16) (2-16)式中 aj與ωj皆為常數。比較(2-15)式和(2-16)式,可知 IMF 變 化的振幅與即時頻率不只是改進展開的效率,而且還能應用到非平穩性資 料。使用 IMF 展開式,振幅及頻率的變異也能很清楚地分離,打破了從前 只能用常數振幅及固定頻率的傅立葉展開的限制。以希伯特頻譜分析也將 隨時間變化的振幅及即時頻率表示成頻譜,此類振幅-頻率-時間分佈圖命 名為希伯特振幅頻譜(Hilbert Amplitude Spectrum)H(ω,t),簡稱希伯特 頻譜而希伯特能量頻譜(Hilbert Energy Spectrum)為希伯特振幅的平方 H(ω,t)2表示。
2.6 邊際頻譜(marginal spectrum)
由希伯特振幅頻譜對時間進行積分,可定義邊際頻譜(marginal spectrum),即:h(ω):邊際頻譜
0
( )
T( , )
h
ω
=
∫
H
ω
t dt
(2.17) 在整個時間長度裡累積的能量,邊際譜提供了對於每個頻率的總振幅 (或能量)量測,但因解析方式不同,所得到的頻率都跟傅立葉分析有不同 的意義:在傅立葉分析中,在某個頻率所存在的能量即是指通過整個資料 長度中一個正弦或餘弦的分量,當傅立葉會使得其低頻及高頻能量密度改 變,故能量散佈到很大的頻寬,但是希伯特邊際譜則可以得到一個能量集 中的頻譜。希伯特頻譜是一個加權的非正規化的結合振幅-頻率-時間分佈 (join amplitude-frequency-time distribution)。2.6.1 邊際譜(marginal spectrum)的物理意義 由圖(2.12)裡的 fi (t)來表示即時頻率,根據式(2.17),邊際譜是 Hilbert 譜 H(fi ,t)對時間的積分,由圖(2.12)可以直接看出 H(fi ,t)對任意 固定頻率 fi 的時間積分就是對頻率為 fi =fi (t)的所有時刻 t 所對應的振幅 a(t)求和,因此即時頻率 fi 的邊際譜含義是:信號中即時頻率 fi (t)的總振 振幅(總能量)大小。可以這樣認為,即時頻率表示信號交換快慢的物理量, 任一即時頻率都有一定的能量,將所有時刻某一即時頻率的能量(振幅)加 起來就是信號中該頻率的總能量(總振幅),即邊際譜線的高度。 2.6.2 邊際頻譜與傅立葉頻譜
假定y1=2*sin(60*pi*t)與y2=5*sin(90*pi*t);與均零值組成內建模態 函數集,圖(2.13)為前兩個IMF的Hilbert即時頻率,圖(2.14)為前兩個IMF 的Hilbert即時振幅,圖(2.15)為傅立葉振幅譜。經由HHT方法解析y1及y2 可以從圖(2.13)與圖(2.14)中清楚地看出,即時頻率由30Hz、45Hz組成, 即時振幅由2、5組成,顯示了HHT方法的正確性,而從傅立葉振幅譜圖(2.15) 就不能得出如此詳細訊息了。 Zhong You-ming 等人在文獻[14]中對邊際譜的物理意義作了說明。他 們指出,無論 Hilbert spectrum H(fi ,t)中的頻率還是邊際譜 h(fi )中的頻 率(即時頻率),其意義都與 Fourier 分析中的頻率(即 Fourier 頻率)完全 不同,在 Fourier 分析中,某一處頻率 f 處能量的存在,代表一個正弦或 餘弦波在整個時間軸上的存在,而邊際譜 h(fi )中某一頻率 f 處能量的存在 僅代表在整個時間軸上可能有這樣一個頻率的振動波在局部出現過,h(fi ) 越大,代表頻率 fi 出現的可能性就越大。HHT 中的即時頻率與 Fourier 頻率 確實有本質區別的,Fourier 頻率是用整個正弦或餘弦信號定義的,而即時 頻率一個局域性概念,它可以隨時出現,也可以隨時消失,當 H(fi ,t)或 h(fi ) 中有某一頻率的能量出現時就表示一定有該頻率振動波出現。事實上這正 是邊際譜的優越性及邊際譜與 Fourier 譜的本質區別。 2.7 邊際譜(marginal spectrum)在損傷部位判斷上的應用
當結構在振動中發生損傷時,其瞬時頻率必然發生變化,同時振態和結 構內部能量分佈產生相應的變化。因此通過分析反應結構振動能量分佈的 HHT 邊際譜可以判斷損壞位置。 結構振動時,其損傷具有局域性和集中性,即結構損傷通常集中於結構 的某一個局部範圍內,其他部位的結構和構件的損傷明顯小於該受損部 位,如地震中建築物的破壞通常集中於某個樓層。根據損傷部位振動集中 的特點[15],分析各部位損傷前後相對振動能量的變化,即可以判斷出具 體損傷部位。 HHT 譜是對信號振幅在時間-頻域上的描述,因此能夠反應振動信號在 不同時刻、不同頻率範圍內的能量分佈。再根據 HHT 進一步定義 HHT 邊際 譜,邊際譜的物理含義:不同頻率成份在整個時間域內的能量貢獻。因此, 可以通過對比每個測量點損壞前後邊際譜的相對變化來確定損傷位置。 2.8 本章小結 本章主要工作有 1.對黃鍔等人提出的希伯特-黃轉換、內建模態函數(IMF)的概念,經驗模 態分解法的過程進行簡要的歸納。 2.給出即時頻率的概念,並討論了即時頻率與傅立葉頻率的區別。
3.介紹了 HHT 譜與 HHT 邊際譜的物理意義,並說明如何應用 HHT 邊際譜在 判斷結構物損壞位置方法。
第三章 希伯特-黃轉換在數值模態中損壞判斷應用 3.1 引言 希伯特-黃轉換(HHT)的重要應用價值在於提供了描述信號即時變化特 性的手段。經驗模態分解法(EMD)能夠對非平穩,非線性過程中的數據進行 平穩化和線性處理,並在分解的過程中保留數據的本身特性。當結構發生 微小損傷時,微弱的損傷信號夾雜在結構的整體信息中,難以體現出來。 通過經驗模態分解法對結構的振動響應信號進行預處理,可以把非平穩的 原始響應信號分解成一系列具有不同特徵尺度的平穩信號,把原信號的能 量分配到了各個內建模態函數(IMF)分量上,而且這種分解是自適應的,因 而更能反應損傷的本質資訊。再通過希伯特轉換,得到每個內建模態函數 分量的即時頻率、即時振幅以及邊際譜等資訊,把損傷的訊息體現出來。 對於頻率成份複雜的信號,一般採用濾波器進行帶通濾波器,將濾波後 得到的歷時資訊近似看做成單一成份的信號,為了得到單一結構模態反應 信號,在進行結構損傷診斷時將應用到帶通濾波器。在應用帶通濾器的過 程當中尚有幾個參數設定還沒決定,例如:濾波器的形式、階數、阻帶衰 減量(Stopband Attenuation)。由上屆學長的研究成果得知[4],阻帶衰減 量對於識別的成果影響很大。利用 HHT 邊際譜進行損傷診斷時,為了提取 第一模態將應用帶通濾波器。因此本章將引用上屆學長的研究成果來識別
國立交通大學結構實驗大樓縮小尺寸之剪力屋結構模型的頻率與阻尼,再 與俊明學長採用類神經的識別成果互相比較,進而決定何種阻帶衰減量設 定值對於此結構模型有較佳的識別,而後本文所有的帶通濾波器設定值也 將以此為準。 工程結構在複雜的服務環境中,由於受到自然環境的侵蝕,材料老化和 其他災害的作用下,必然會產生不同形式的損傷。因此健康診斷領域所關 注的三個主要問題為損傷位置、損傷程度、損傷發生時間。為此本文為瞭 解損傷位置,安排數個三層樓數值模擬,當中改變各樓層勁度大小來模擬 損壞情況,最後利用邊際譜來前判別受損位置。 3.2 HHT 結合 RDT 識別模態參數 3.2.1 模態參數識別的基本介紹 我們如把結構物視為一個系統,則可利用結構矩陣與結構動力等概念建 立出其等效的數學模型,當此系統接收到一個外部的輸入訊號時,如地震 力、風力…等,將可從結構物的實際量測或數值模型的推導對應得到此一 結構物反應的輸出訊號,如:樓層的位移、速度、加速度。而所謂的系統 識別就是利用輸入訊號與輸出訊號之間的關係反推出其等效的數學模型進 而得到此結構物系統的各項參數。所求得的參數可用來檢驗結構的建造是 否如同我們設計時所預期,亦可以用來評估建築物經歷過地震、強風或材
料的老化後的強度及其安全性,可做為補強的依據,來確保結構物的安全。 一般的結構系統識別依據描述系統的方式,可分為參數模式與非參數模 式識別。若從識別時所用的資料,可分為時間域與頻率域識別。又依量測 數據之處理程式,則系統識別技巧可再概分成兩類,線上模式(on-line model)及離線模式(off-linemodel)。所謂參數識別是指識別代表該結 構物系統的數學模式中,具有物理意義之參數,像是一般在結構動力分析 裡的自然頻率ω及阻尼比ξ等。至於非參數的識別乃對系統不作任何物理 或數學模型之假設,僅對已知的輸入和輸出資料之間以一組相關的數學函 數來連結,而此函數的係數,即為識別的對象,是沒有明確的物理意義。 時間域的系統識別是直接將所量測的時間域反應來做系統識別的資料,而 頻率域系統識別法則是先將時間域反應的資料轉換到頻率域再進行系統識 別,頻率域識別若在時變或非線性系統,可以移動視窗方式找尋等值線性 系統參數,優點為計算快速,缺點則是精確度受限於所收集資料長短和取 樣頻率大小。時間域識別,需選擇適當數學模式和合理的誤差準則(Error Criterion),再運用數值方法識別出相關參數。線上模式為數據進來一筆; 即進行系統識別一次,其分析技巧架構於遞迴公式(Recursive Formula)。 而離線模式,則是將所有量測到的數據記錄完成後,再進行系統識別。線 上分析模式,雖有減少數據儲存時間、計算快速及可分析時變系統之優點, 但於分析線性非時變系統,則其精度一般不如離線分析模式。
3.2.2 頻率域識別方法概述 模態參數的頻率域識別方法是指在頻率域內識別模態參數的方法。頻率 域識別方法的研究與應用時間相對久遠一些,是由傅立葉變換的問世後而 發展起來的。最早頻率域識別方法是圖解法。從實測數據經傅立葉變換得 到的粗略地識別模態頻率、阻尼比和振態。隨之,又陸續發展了線性參數 或非線性參數最小二乘法進行曲線擬合的多種模態參數的頻率域識別方 法,例如頻率域最小二乘法、頻域加權最小二乘法、有理分式多項式法和 正交多項式法等。 頻率域識別法的最大優點的是直觀,從實測可直接觀測到模態的分佈以 及及模態參數的粗略估計值以作為有些頻率域識別法需要輸入的初值。其 次是雜訊影響小,由於在處理實測數據過程中用頻域平均技術,抑制了雜 訊影響,使模態定階問題易於解決。 模態參數的頻域識別方法是經典的模態參識別方法。由於頻域識別的輸 入數據是直觀的,容易掌握模態參教分佈情況,因此普遍為人們所接受。 用頻域方法識別模態參數,最關鍵的問題是實測數據的好壞,優質的實測 數據無論用什麼方法去識別都可以獲得精度較高的模態參數。反之,實測 不良數據,選用再好的識別方法,所求出的模態參數誤差也不小。 3.2.3 時間域識別方法概述
模態參數的時間域識別方法是指在時間域識別試驗結構模態參數的方 法。時間域識別方法的研究與應用相對的比頻域率方法來的晚,是近十幾 年隨著電腦運算能力增強而發展起來的一種新技術。時間域方法可以克服 頻域法的一些缺陷。特別是對大型複雜結構,如大壩、橋梁、高層建築物、 飛機、船舶受到如風、大浪、及地震的作用時,它們在工作中承受的荷重 很難測量,但輸出信號容易測得,因此直接利用輸出的時間域信號進行參 數識別無疑是很有意義的。目前時間域的參數系統識別方法主要有時間域 最小二乘法、ITD 法、STD 法、複指數法(Prony 法)、ARMA 模型時序分析等。
近年來,直接用環境激勵下的輸出(反應)數據識別結構的模態參數,無 需對結構施加激勵,激勵是未知的,例如無需對大橋、海洋結構、高層建 築等大型結構進行激勵,僅需直接測量結構在風力、交通、地震等環境下 引起的輸出反應數據就可以識別出結構物的模態參數。用環境激勵下的振 動反應數據進行模態參數識別,一般需要對這些振動輸出數據進行預處 理,使之成為符合時間所需要的形式,例如可通過隨機遞減法從振動反應 信號中提取自由指動信號的訊據,作為模態參數時間域識別的輸入數據。 模態參數時間域識別方法的主要優點是可以使用實際量測到的反應信 號,無需經過傅立葉變換處理,因而可以避免由於信號裁斷而引起的洩露、 出現旁瓣,解析度降低等因素對參數識別精度所造成的影響。同時利用時 間域方法還可以對連續運行的設備,例如發電機組、大型壓縮機組、大型
化工設備進行線上參數識別。這種在實際運行情況下識別的參數直接反應 了結構的實際動態特性。由於時間域的參數識別技術只需要反應的時間域 信號,從而減少了激勵設備,大大節少了測試時間與費用,這些都是頻率 域方法所不具有的優點。當不然用激勵響應信號時,缺點也很明顯。由於 沒有使用平均技術,因而分析信號中包含雜訊干擾,所識別的模態中除系 統模態外,還包含雜訊模態,合理地選擇識別方法、和一些參數,一直都 是時間域法研究中的重要課題。
3.2.4 隨機遞減法(Random Decrement Technique)
隨機遞減法是從結構的隨機振動響應信提取該結構的自由衰減振動信 號的一種處理方法,是為試驗模態參數時間域識別提供輸入數據所進行的 預處理。例如在環境激勵下大型結構如大壩、橋梁、海洋平臺、高層建築 的動力特性測試分析。對於這些大型結構,為了測試其動力特性而進行激 振,不是花費昂貴就是難以實現,而且還能可測試結構造成損傷。解決的 辦法是採用環境激勵,例如地震力、交通、風力等。環境激勵具有很多優 點, 例如不需要激振設備,並能真實地反應結構在工作狀態下的動力特 性。但是直接使用由此獲取的數據來進行結構模態參數識別往往精度較 差。若能提高環境激勵下結構模態參數,識別精度,無疑在大型結構動力 特性測試中將有良好的工程應用前景。隨機遞減技術正是基於這一種目的
而提出來的,用平均和數理統計方法,從環境激勵的反應中提取自由衰減 振動反應。隨機遞減法是從線性振動系統的一個或多個平穩隨機反應樣本 中,消除或減少隨機成份從而獲得一定初始激勵下的自由反應信號。該方 法主要的想法是利用平穩隨機振動信號的平均值為零的性質,將包含有確 定性振動信號和隨機信號兩種成為的實測振動響應信進行辨別,將確性信 號從隨機信號中分離出來,得到自衰減動反應信號,而後可以用時間域識 別方法進模態參數識別。 對於受強迫振動的MDOF系統,根據模態疊加原理,可以應用EMD法將結 構總反應分解為各個模態反之之和,為提高分解精度,避免模態混疊,在 應用EMD之前先進行帶通濾波處理。每個模態反應由強迫反應和自由振動反 應組成,應用RDT法可得到每個模態的自由振動反應,然後就可以應用單自 由度方法進行各自的模態參數識別,其完整的流程圖如圖(3.1)。 3.3 HHT+RDT真實案例應用 本小節將引用上屆學長的研究成果來識別國立交通大學結構實驗大樓 縮小尺寸之剪力屋結構模型的頻率與阻尼。首先將編號 Kobe_008_dk123 感 測器記錄的資料進行傅立業轉換,再來約略決定帶通濾波器的剪切頻寬, 通過帶通濾波器所得到的加速度反應,接著使用經驗模態分解法得到第一 個內建模態函數,經過多次的轉移後,再搭配隨機遞減法來得到自由振動,
此後將可以希伯特轉換求得即時頻率與振幅,在以最小平方法近似,經由 推出的公式計算將可得到自然頻率與阻尼比。過程見圖(3.2)到圖(3.6)。 圖(3.2) Kobe008_dk123 地震力作用下各感測器的反應,左圖為 y 方向 弱軸量測到的加速度反應,右圖為其快速傅立業轉換的結果,之後往上的 Floor1、Floor2、Floor3、Floor4 依序為一二三四層樓的反應,圖(3.3) 將圖(3.2)第四樓之加速度反應經過 10 階通帶 1~1.5(Hz),阻帶衰減 80(dB) 之帶通濾波器後所得到第一個模態的加速度反應歷時圖。圖(3.4)將圖(3.3) 所得到第一個模態反應經過數次轉移後所得到第一個內建模態函數,圖 (3.5)為所有的內建模態函數及餘數。圖(3.6)的自由振動衰減訊號經過希 伯特轉換後得到的即時振幅取自然對數後對時間的關係圖,直線段為最小 平方法近似之直線。 為了得知何種阻帶衰減量對識別成果較佳,接下來重復上述步驟,並改 變阻帶衰減量設定值,進行識別每個模態以觀察識別的結果,依續由第一 模態至第四模態識別成果見表(3.1)~表(3.4)。表(3.1)為四層樓之交通大 學架設縮尺模型於振動臺上,Kobe_008g 地震力作用。固定 10 階濾波器, 通帶 1~1.5(Hz),改變阻帶衰量減從 20~120(dB),得到第一個模態自然 頻率與阻尼比的識別結果。表(3.2)則為第二模識別成果比較,其帶通濾波 器設定值為,10 階、通帶 3.4~4.0(Hz)、改變阻帶衰量減從 20~120(dB)。 表(3.3)則為第三模識別成果比較,其帶通濾波器設定值為,10 階、通帶
5.5~6.1(Hz)、改變阻帶衰減量從 20~120(dB)。表(3.4)則為第四模識別 成果比較,其帶通濾波器設定值為,10 階、通帶 7.1~7.4(Hz)、改變阻帶 衰量減從 20~120(dB)。將表(3.1)~表(3.4)中的阻帶衰減量設為 X 軸、識 別成果設為 Y 軸繪製成圖(3.47)~圖(3.50),從表可以得知當阻帶衰減量為 80dB 時,對識別成果較準確,唯獨識別第四模態的成果與類神經方法相差 較大,可能是圖(3.2)第四樓層 FFT 圖不明顯之故。 3.4 裝設補強肢之效應 本論文在第四章真實案例應用中,藉由無裝設補強肢來模態該樓層受 損,進而判斷損傷樓層位置 。因此本小結為瞭解結構在裝設補強肢後,是 否發揮其預期之效果。取試驗 Kobe_0.08_aaa 與 Kobe_0.08_nnn 分別為有 加勁肢與無加勁肢兩組加速度記錄,識別結果表(3.9)來看,在裝設補強肢 後,各自然振動頻率皆相對提高,顯示裝設補強肢確實可達到增加層間勁 度,進而改變其系統參數之目的。應用類神經進行系統識別,在未裝設補 強肢時的振動頻率為 1.5106 Hz、4.6107 Hz、7.3021 Hz、9.214Hz,而裝 設補強肢後的振動頻率則變為 1.6384Hz、5.0798 Hz、8.1122 Hz、10.1870 Hz,其頻率變化各為 11.18%、8.62%、10.77%、10.73%。而採用 HHT+RDT 未 裝設補強肢時,識別出的頻率為 1.5106 Hz、4.6107 Hz、7.3021 Hz、9.214 Hz,而裝設後的振動頻率則提高至 1.6384 Hz、5.0798 Hz、8.1122 Hz、10.1870
Hz,其實際頻率變化為 8.46%、10.174%、11.094%、10.56%。從表(3.9)得 知,有裝設補強肢時,無論採用 ANN 或 HHT 頻率約提高 10%左右,顯示出裝 設補強肢確實可以提高勁度。而後在第四章真實案例應用中將以裝設補強 肢來模態健康無損壞結構物,以抽離補強肢來模擬該層受損。 3.5 數值模擬結構損壞部位判斷 3.5.1 數值模擬的結構參數與地震反應 圖(3.7)為一個三層剪切型框架結構數值模型,各層樓質量設定為 m=105 kg,健康樓層的勁度設定為 2.7*105 N/m,受損的樓層勁度設定為 1.5*105 N/m。安排四種案例,案例一假定三層樓完全無受損,層間勁度全以 2.7*105 N/m 設定,頻率依續為 1.16、3.26、4.71Hz。案例二假定一層樓受 損時,其層間勁度以 1.5*105 N/m 設定,其餘勁度以 2.7*105 N/m 設定,頻率 依續為 0.9671、2.9868、4.6152。案例三假定二層樓受損時,其層間勁度 以 1.5*105 N/m 設定,其餘勁度以 2.7*105 N/m 設定,頻率依續為 1.0254、 3.1270、4.1578。案例四假定三層樓受損時,其層間勁度以 1.5*105 N/m 設 定,其餘勁度以 2.7*105 N/m 設定,頻率依續為 1.1133、2.7091、4.4202。 具體各案例條件和數值模型參數見表(3.10)。輸入地震波為 EI centro,總 共 20250 採樣點,取樣頻率 250,共記錄 81 秒,圖(3.8)為此輸入地震波加 速度曲線。
計算四種案例的結構動力反應,圖(3.9)為案例一所有樓層的加速度與 位移反應。圖(3.10)為案例二所有樓層的加速度與位移反應。圖(3.11)為 案例三所有樓層的加速度與位移反應。圖(3.12)為案例四所有樓層的加速 度與位移反應。由圖(3.9)~圖(3.12)得知在有損傷的案例時,薄弱層所在 樓層的層間變形反應較大,其他樓層變形減小,且損傷層位置不同時,結 構地震反應也都不相同。 3.5.2 Fourier 頻譜分析 圖(3.13)為案例一各樓層加速度反應的傅立葉譜,圖(3.14)為案例二各 樓層加速度反應的傅立葉譜,圖(3.15)為案例三各樓層加速度反應的傅立 葉譜,圖(3.16)為案例四各樓層加速度反應的傅立葉譜。從圖(3.13)~圖 (3.14)Fourier 譜中,可以看出: (1) 結構勁度大,自然頻率越高。 (2) 案例二、三、四的模態頻率低於案例一,且薄弱層位置越靠近地面,結 構頻率越低,說明薄弱層消弱了結構的整體勁度,其位置越低,結構剛 度損失越大。 (3) Fourier 譜中的峰值與表(3.10)中計算的理論頻率不完全對應,高頻附 近有多峰值現象,因此不能直接通過 Fourier 譜準確判斷出結構的模態 頻率,由其是高頻部份。
上述分析說明,直接通過結構地震反應與 Fourier 譜不能準確識別出頻 率,更不能判斷損傷部位及其發展規律。但是 Fourier 譜可以讓我們大 概掌握頻率範圍,如案例一的第一頻率約 1.0~1.4Hz 之間,第二頻率約 3.0~3.5Hz。 3.5.3 損傷部位判斷流程 從 2.9 節得知,結構受損時通常集中於結構的某一個局部範圍內,其他 部位的結構的損傷明顯小於該受損部位,同時振態和結構內部能量分佈產 生相應的變化,根據損傷部位振動集中的特點[15],分析各部位損傷前後 相對振動能量的變化,即可以判斷出具體損傷部位。邊際譜表示不同頻率 成份在整個時間域內的能量貢獻。因此,可以通過對比每個測量點損傷前 後邊際譜的相對變化來確定損傷位置。 為了得到各個模態的振動反應將使用帶通濾波器,剪切頻率為該頻率加 上±0.15Hz。採用 ChebyshevⅡ濾波器型式 10 階,從 3.3 節得到阻帶衰減量 為 80dB 時,因此往後帶通濾波器皆照上述參數設定。 應用希爾伯特-黃轉換(HHT)進行數值模擬結構損傷診斷具體過程如下: (1) 結構處於完好無受損狀態時,採用 EI centro 地表地震力當做輸入力, 求得各層加速度反應,再應用帶通濾波器截取所需模態反應。 (2) 對每層加速度反應信號進行經驗模態分解法,得到每個內建模態函數 (IMF),將每個內建模態函數經 Hilbert 變換得到即時頻率和即時振幅,
接著沿時間積分得到每個反應信號的邊際譜。 (3) 繪出完好無損傷結構(每層勁度 2.7*105 N/m)的每層樓邊際譜,將每層邊 際譜振幅除以第三層邊際譜峰值,繪製成正規化邊際譜作為結構完好狀 態的參考。 (4) 當結構發生損生時(例如某層勁度 1.5*105 N/m),重復第 2 步驟求得損傷 狀態下每層邊際譜,並繪製出正規化邊際譜。 (5) 與數值案例一結構完好無受損正規化邊際譜比較,計算改變量 (受損 未受損- *100% 未受損 ),判斷結構是否存在損傷。 3.5.4 數值案例一 數值模擬中案例一模擬成無受損健康結構,其中 k1=k2=k3=2.7*105N/m 圖 3.17(a)為各層經過帶通濾波器後所得之加速度記錄,圖 3.17(b)為經過 經過模態分解法後所得到第一個內建模態函數。圖(3.18)為數值案例一正 規化邊際譜,說明出一階模態中上部結構振動能量高於下部各層,相鄰層 正規化邊際譜之間的差值可以解釋為該層所消秏的振動能量,其值越大, 表示該層的振動越強。因此從各層正規化邊際譜之間的差值可以判斷各層 的振動強度。假設數值案例一為無損傷結果,其它受損數值案例正規化邊
[ ]
5 5 5 10 0 0 0 10 0 * 0 0 10 M kg ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦[ ]
1 2 2 2 2 3 3 3 3 0 0 k k k k k k k k k k + − ⎡ ⎤ ⎢ ⎥ = −⎢ + − ⎥ ⎢ − ⎥ ⎣ ⎦際譜與數值案例一正規化邊際譜進行比較,可以發現薄弱層或損傷層的層 間正規化邊際譜明顯高於數值案例一的相對應層,而無損傷層間正規化邊 際譜下降。因此可以很容易判斷損傷發生的具體部位。觀察數值案例一正 規化邊際譜的峰值之間的比例 1、0.7856、0.4356,再觀察與表(3.10)數值 案例一的一階振態 1、0.802、0.445 相接近,這說明數值案例一邊際譜真 實反應結構物振動中的實際能量分佈。 3.5.5 數值案例二 數值案例二模擬受傷樓層於第一層,其中 k1=1.5*105N/m, k2=k3=2.7*105N/m, 圖 3.19(a)為各層經過帶通濾波器後所得之加速度記錄,圖 3.19(b)為經過 經過模態分解法後所得到第一個內建模態函數。圖(3.20)為數值案例二正 規化邊際譜,各層峰值為 1、0.8708、0.6005,比對數值案例一正規化邊際 譜的峰值 1、0.7856、0.4356,計算得到第一層峰值增加 37.856%,而無損 傷層間正規化邊際譜下降,第二層減少-22.771%,第三層減少-39.739%, 得知一樓層間正規化邊際譜明顯高於數值案例一的相對應層,而無損傷層 間正規化邊際譜下降。因此可以判斷出損傷發生在第一樓層。觀察數值案
[ ]
5 5 5 10 0 0 0 10 0 * 0 0 10 M kg ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦[ ]
1 2 2 2 2 3 3 3 3 0 0 k k k k k k k k k k + − ⎡ ⎤ ⎢ ⎥ = −⎢ + − ⎥ ⎢ − ⎥ ⎣ ⎦例二正規化邊際譜的峰值之間的比例 1、0.8708、0.6005,再關察與表(3.10) 數值案例二的一階振態 1、0.863、0.608 相接近,說明案例二邊際譜反應 了結構物振動中的能量分佈。 3.5.6 數值案例三 數值案例三模擬受傷樓層於第二層,其中 k2=1.5*105N/m, k1=k3=2.7*105N/m, 圖 3.21(a)為各層經過帶通濾波器後所得之加速度記錄,圖 3.21(b)為經過 經過模態分解法後所得到第一個內建模態函數。圖(3.22)為數值案例三正 規化邊際譜,各層峰值為 1、0.8614、0.3434,比對數值案例一正規化邊際 譜的峰值 1、0.7856、0.4356,計算得到第二層峰值增加 48.00%,而無損 傷層間正規化邊際譜下降,第一層減少-21.166%,第三層減少-35.354%, 得知二樓層間正規化邊際譜明顯高於數值案例一的相對應層,而無損傷層 間正規化邊際譜下降。因此可以判斷出損傷發生在第二樓層。觀察數值案 例三正規化邊際譜的峰值之間的比例 1、0.8614、0.3434,再關察與表(3.10) 數值案例三的一階振態 1、0.846、0.335 相接近,說明數值案例三邊際譜
[ ]
5 5 5 10 0 0 0 10 0 * 0 0 10 M kg ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦[ ]
1 2 2 2 2 3 3 3 3 0 0 k k k k k k k k k k + − ⎡ ⎤ ⎢ ⎥ = −⎢ + − ⎥ ⎢ − ⎥ ⎣ ⎦反應了結構物振動中的能量分佈。 3.5.7 數值案例四 數值案例四模擬受傷樓層於第三層,其中 k3=1.5*105N/m, k2=k3=2.7*105N/m, 圖 3.23(a)為各層經過帶通濾波器後所得之加速度記錄,圖 3.23(b)為經過 經過模態分解法後所得到第一個內建模態函數。圖(3.24)為數值案例四正 規化邊際譜,各層峰值為 1、0.6761、0.3936,比對數值案例一正規化邊際 譜的峰值 1、0.7856、0.4356,計算得到第三層峰值增加 51.073%,而無損 傷層間正規化邊際譜下降,第一層減少-9.642%,第二層減少-19.286%,得 知三樓層間正規化邊際譜明顯高於數值案例一的相對應層,而無損傷層間 正規化邊際譜下降。因此可以判斷出損傷發生在第二樓層。觀察數值案例 三正規化邊際譜的峰值之間的比例 1、0.6761、0.3936,再關察與表(3.10) 數值案例四的一階振態 1、0.674、0.371 相接近,說明數值案例四邊際譜 反應了結構物振動中的能量分佈。
[ ]
5 5 5 10 0 0 0 10 0 * 0 0 10 M kg ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦[ ]
1 2 2 2 2 3 3 3 3 0 0 k k k k k k k k k k + − ⎡ ⎤ ⎢ ⎥ = −⎢ + − ⎥ ⎢ − ⎥ ⎣ ⎦3.6 數值結構損傷程度判別 3.6.1 結構參數及其地震反應 本小節為瞭解邊際譜是否能體現損傷程度上的差異,這裡將受損樓層的 勁度改變為 2.1*105 N/m。質量設定與輸入地震波與 3.5 節相同。加上安排 三種數值案例以瞭解受損程度上差異,數值案例五假定一層樓受損時,其 層間勁度以 2.1*105 N/m 設定,其餘勁度以 2.7*105 N/m 設定,頻率依續為 1.081、3.128、4.660。數值案例六假定二層樓受損時,其層間勁度以 2.1*105 N/m 設定,其餘勁度以 2.7*105 N/m 設定,頻率依續為 1.1091、 3.2111、4.4288。數值案例七假定三層樓受損時,其層間勁度以 2.1*105 N/m 設定,其餘勁度以 2.7*105 N/m 設定,頻率依續為 1.1458、3.0269、4.5475。 具體數值案例條件和數值模型參數見表(3.11)。 計算數值案例條件的結構動力反應。圖(3.25)為數值案例五所有樓層的 加速度與位移反應。圖(3.26)為數值案例六所有樓層的加速度與位移反 應。圖(3.27)為數值案例七所有樓層的加速度與位移反應。由圖(3.25)~圖 (3.27)得知與在有損傷的情況時,薄弱層所在樓層的層間變形反應較大, 其他樓層變形減小,且損傷層位置不同時,結構地震反應也都不相同。 3.6.2 數值案例五 數值案例五模擬受傷樓層於第一層,其中 k1=2.1*105N/m,
k2=k3=2.7*105N/m, 圖 3.28(a)為各層經過帶通濾波器後所得之加速度記錄,圖 3.28(b)為經過 經過模態分解法後所得到第一個內建模態函數。圖(3.29)為數值案例五正 規化邊際譜,各層峰值為 1、0.8315、0.5075,比對數值案例一正規化邊際 譜的峰值 1、0.7856、0.4356,計算得到第一層峰值增加 16.5%,而無損傷 層間正規化邊際譜下降,第二層減少 7.423%,第三層減少 21.41%,得知一 樓層間正規化邊際譜明顯高於數值案例一的相對應層,而無損傷層間正規 化邊際譜下降。因此可以判斷出損傷發生在第一樓層。比對 3.5.5 小節數 值案例二第一樓層的邊際譜相對振幅增減量 37.856%,大於本小節的 16.5%,驗證正規化邊際譜可以體現損傷程度。 3.6.3 數值案例六 數值案例六模擬受傷樓層於第二層,其中 k2=2.1*105N/m, k1=k3=2.7*105N/m,