權重克利金模式之發展與應用

國

立

交

通

大

學

土木工程學系

碩

士

論

文

權重克利金模式之發展與應用

Development and Application of

Weighted Kriging Models

研 究 生：陳柏宏

指導教授：楊錦釧 博士

權重克利金模式之發展與應用

Development and Application of

Weighted Kriging Models

研 究 生：陳柏宏 Student：Bo-Hung Chen 指導教授：楊錦釧 Advisor：Jinn-Chuang Yang 吳祥禎 Shiang-Jen Wu 國 立 交 通 大 學 土 木 工 程 研 究 所 碩 士 論 文

A Thesis Submitted to Civil Engineering College of Engineering

National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master in

Civil Engineering

June 2007

Hsinchu, Taiwan, Republic of China

謝 誌

本論文承蒙恩師 楊錦釧教授與吳祥禎博士在攻讀碩士學位研究期間 的悉心指導，使得本論文研究得以順利完成。研究期間，感謝 湯有光教授 給予諸多寶貴的意見與方向，並感謝口試委員 虞國興教授與 童慶斌教授 的不吝指正與提供寶貴的意見，使的學生受益良多，在此由衷的致上萬分 感謝與敬意。 在學期間，感謝東霖學長、德勇學長、夢祺學長、胤隆學長、世偉學 長、昇學學長、曉萍學姊、浩榮學長、欣瑜學姐、宣汝學姐、仲達學長、 力瑋學長...等學長姐在生活及學業上的照顧與提攜；在此亦感謝同窗 好友們與學弟妹們在這段期間的陪伴與大力的幫忙協助。 另外，還要感謝新竹的大學同學與認識的朋友們，在剛開始來到這個 新環境的時候所給予的鼓勵與在新竹這段期間的幫忙，能讓我在新竹這兩 年的時間裡過得多采多姿。 最後，最重要的是感謝我所敬愛的父母親的養育與栽培之恩，與兄姊 們的關心支持，沒有你們的付出與打氣我無法無後顧之憂的完成至今的一 切。最後，將此論文獻給我從小至今，於在學期間過世的最疼愛與支持我 的奶奶，與她一起分享這份喜悅。

權重克利金模式之發展與應用

研究生：陳柏宏 指導教授：楊錦釧

吳祥禎

國立交通大學土木工程學系

摘 要

本研究主要為了提高常用理論半變異數模式對於空間變數特性套配之 準確性，以各模式之誤差值倒數之加權因子為基礎，建構而得一權重克利 金模式(Weighted Kriging model)，藉由該模式解決過去傳統應用克利金法推 估空間變數時，需先套配選用出一誤差最小之理論半變異數模式之要求。 在模式驗證方面，主要分別以假設案例與實際集水區降雨事件作為空 間模擬與推估對象。其中設計案例主要是以二維平面空間變數為分析對 象，並假設該變數分別為球型、指數、高斯、冪次、碎塊(Nugget)空間分佈 特性，再以上述理論半變異數模式，分別考慮碎塊與非碎塊效應模式及本 研究所發展之權重克利金模式，進行未知點位的模擬推估。由結果可知， 權重克利金模式在各種設計案例下，皆可以得到較其他理論半變異數模式 為佳的推估結果。 在實際案例之應用方面，本研究主要是以淡水河流域之 20 個雨量站所 測得之時雨量資料作為模式的推估與分析對象，同樣也採用常用理論半變 異數模式，分別考慮碎塊與非碎塊效應模式及權重克利金模式，進行空間 變數的推估，最後再以實際測站所量測之雨量資料和模式所推估結果進行 比較，由驗證結果可以得知權重克利金模式應用於實際案例也有不錯之成 效。 綜合假設案例與淡水河流域實際案例的驗證結果得知，權重克利金模

配效果，提高空間變數推估結果之可靠度及準確性，亦可省去傳統克利金 法在推估空間變數前需套配一合適之半變異數模式之限制。

關鍵詞：克利金法、半變異數模式、雨量資料、區域化變數理論、淡水河

流域

Development and Application of

Weighted Kriging Models

Student：Bo-Hung Chen Advisors：Dr. Jinn-Chuang Yang

Dr. Shiang-Jen Wu

Department of Civil Engineering

National Chiao-Tung University

ABSTRACT

This study proposed a weighted kriging model (WKM) to circumvent the heed of traditional kriging models which require a best-fit theoretical semi-variograms model being specified in advance. The basic idea of the proposed WKM is to calculate the weighted average of spatial variables estimated by using theoretical semi-variogram models (Spherical, Exponential, Gaussian and Power models). In this study, estimation of the spatial variables by the proposed WKM can be made in two ways; one is to use weighted semi-variogram (denoted as WKM_I); and the other is to weighted spatial variables obtained by using individual variogram, (WKM_II).

To verify the proposed WKM, spatial data are generated under a specified semi-variogram model which, in turn, are used for the basis of verification. The proposed WKM is validated through the visual and numerical comparisons of the spatial data fields estimated by the conventional and proposed kriging procedures with the generated baseline data. Referring to both the graphical comparison and performance indices, the assigned semi-variogram model used in the generation of the baseline data has the best-fit result. Moreover, the estimated spatial variables match the baseline data closer than those by the conventional semi-variogram models, except for the assigned semi-variogram

model. Also, the similar conclusion can be drawn from the numerical performance indices. For example, the mean square error (MSE) and mean square weighting error (MSWE) for WKM are smaller and the indices (KG and KS) associated with the WKM closer to 1 than those by the conventional single semi-variogram models.

In addition to the numerical experiment based on the generated spatial data, this study also compares the proposed weighted kriging models with the conventional single model approach based on real observed rainfall data. In general, rainfall data are possibly affected by the geographical locations of the rainfall gauges. Therefore, spatial rainfall dist’n hardly satisfies with the second-order stationary, that is, the assumption mean of rainfall data is constant in space and the covariance of rainfall data between different gauges is only related to their distance. Hence, rainfall data are standardized before conducting model validation. According to numerical results, similar conclusion to the numerical experiment can be drawn, that is, the proposed weighted kriging models are also more appropriate than the conventional single variogram model approach for estimating the rainfall field.

Based on the above results, the proposed weighted kriging models not only avoid the possibility of using inappropriate theoretical semi-variogram model as the best-fit model, but also enhance the accuracy of estimating spatial by distributed rainfall, especially when the study area has few gauges.

目 錄

謝誌 ...i 摘要 ...ii Abstract ...iv 目錄 ...vi 表目錄 ...viii 圖目錄 ...xi 符號說明 ...xiv 第一章、 緒論 ... 1 1.1 研究動機與目的... 1 1.2 文獻回顧... 2 1.3 研究分析架構與方法 ... 3 第二章、 應用理論基礎簡介... 5 2.1 區域化變數理論... 5 2.2 半變異數分析... 7 2.3 常用理論半變異數模式 ... 10 2.3.1 模式簡介... 10 2.3.2 模式參數率定... 11 2.4 克利金空間推估法 ... 11 2.4.1 基本特性... 11 2.4.2 克利金系統方程式 ... 12 2.4.3 克利金變異數 ... 14 2.5 模式驗證... 14 第三章、 權重半變異數模式之發展... 20 3.1 基本概念說明... 20

第四章、 模式應用於設計案例之檢定與比較 ... 25 4.1 設計案例基本資料概述 ... 25 4.2 驗證流程... 25 4.3 模擬推估結果之比較與驗證分析 ... 28 第五章、 模式應用於實際案例之驗證與比較 ... 57 5.1 資料收集與分析... 57 5.1.1 淡水河流域概況 ... 57 5.1.2 雨量站資料整理 ... 58 5.1.3 雨量資料選取與分析 ... 58 5.2 雨量資料之無因次化 ... 59 5.3 模式的推估及驗證 ... 60 5.3.1 驗證目標之選取 ... 60 5.3.2 推估結果之比較與驗證分析 ... 60 第六章、 結論與建議... 133 6.1 結論... 133 6.2 建議... 133 第七章、 參考文獻... 135

表 目 錄

表 4.1 已知點位... 31 表 4.2 未知點位... 31 表 4.3 理論半變異數各模式之參數設定與所對應距離之變異元 ... 32 表 4.4 試驗半變異數之套配... 33 表 4.5 各設計案例之空間點位變數值... 34 表 4.6 各選用理論半變異數模式之權重比例... 35 表 4.7 球型模式設計案例下各模式推估結果... 36 表 4.8 指數型模式設計案例下各模式推估結果... 37 表 4.9 高斯型模式設計案例下各模式推估結果... 38 表 4.10 冪次型模式設計案例下各模式推估結果... 39 表 4.11 碎塊模式設計案例下各模式推估結果... 40 表 4.12 球型模式設計案例各模式驗證指標計算結果... 41 表 4.13 指數型模式設計案例各模式驗證指標計算結果... 42 表 4.14 高斯型模式設計案例各模式驗證指標計算結果... 43 表 4.15 冪次型模式設計案例各模式驗證指標計算結果... 44 表 4.16 碎塊型模式設計案例各模式驗證指標計算結果... 45 表 5.1 淡水河流域雨量站資料... 65 表 5.2 各降雨場雨量資料... 66 表 5.2 各降雨場雨量資料(續) ... 67 表 5.3 降雨場各座標軸回歸參數值... 68 表 5.4 各降雨事件之理論半變異數模式之權重因子... 69 表 5.4 各降雨事件之理論半變異數模式之權重因子(續)... 70 表 5.5 第一場降雨事件各未知測站推估值... 71 表 5.6 第二場降雨事件各未知測站推估值... 71

表 5.8 第四場降雨事件各未知測站推估值... 72 表 5.9 第五場降雨事件各未知測站推估值... 73 表 5.10 第六場降雨事件各未知測站推估值... 73 表 5.11 第七場降雨事件各未知測站推估值... 74 表 5.12 第八場降雨事件各未知測站推估值... 74 表 5.13 第九場降雨事件各未知測站推估值... 75 表 5.14 第十場降雨事件各未知測站推估值... 75 表 5.15 第十一場降雨事件各未知測站推估值... 76 表 5.16 第十二場降雨事件各未知測站推估值... 76 表 5.17 第十三場降雨事件各未知測站推估值... 77 表 5.18 第十四場降雨事件各未知測站推估值... 77 表 5.19 第十五場降雨事件各未知測站推估值... 78 表 5.20 第十六場降雨事件各未知測站推估值... 78 表 5.21 第十七場降雨事件各未知測站推估值... 79 表 5.22 第十八場降雨事件各未知測站推估值... 79 表 5.23 第十九場降雨事件各未知測站推估值... 80 表 5.24 第二十場降雨事件各未知測站推估值... 80 表 5.25 第二十一場降雨事件各未知測站推估值... 81 表 5.26 第二十二場降雨事件各未知測站推估值... 81 表 5.27 第二十三場降雨事件各未知測站推估值... 82 表 5.28 各降雨場目標值與推估值均方誤差... 83 表 5.29 第一場降雨各模式指標排序... 84

表 5.33 第五場降雨各模式指標排序... 88 表 5.34 第六場降雨各模式指標排序... 89 表 5.35 第七場降雨各模式指標排序... 90 表 5.36 第八場降雨各模式指標排序... 91 表 5.37 第九場降雨各模式指標排序... 92 表 5.38 第十場降雨各模式指標排序... 93 表 5.39 第十一場降雨各模式指標排序... 94 表 5.40 第十二場降雨各模式指標排序... 95 表 5.41 第十三場降雨各模式指標排序... 96 表 5.42 第十四場降雨各模式指標排序... 97 表 5.43 第十五場降雨各模式指標排序... 98 表 5.44 第十六場降雨各模式指標排序... 99 表 5.45 第十七場降雨各模式指標排序... 100 表 5.46 第十八場降雨各模式指標排序... 101 表 5.47 第十九場降雨各模式指標排序... 102 表 5.48 第二十場降雨各模式指標排序... 103 表 5.49 第二十一場降雨各模式指標排序... 104 表 5.50 第二十二場降雨各模式指標排序... 105 表 5.51 第二十三場降雨各模式指標排序... 106 表 5.52 權重克利金模式 I 各指標排序出現次數 ... 107 表 5.53 權重克利金模式 II 各指標排序出現次數 ... 107

圖 目 錄

圖 2.1 半變異數函數、共變異數關係示意圖... 17 圖 2.2 碎塊效應示意圖... 17 圖 2.3 半變異數函數特性說明圖... 18 圖 2.4 試驗半變異數函數示意圖... 18 圖 2.5 常用之理論半變異數模式套配示意圖... 19 圖 3.1 (a)權重模式 I 概念示意圖 ... 23 圖 3.1 (b)權重模式 II 概念示意圖 ... 23 圖 3.2 權重克利金模式推估流程圖... 24 圖 4.1 設計案例中各座標點位分佈圖... 46 圖 4.2 球型模式試驗半變異數圖... 47 圖 4.3 指數型模式試驗半變異數圖... 47 圖 4.4 高斯型模式試驗半變異數圖... 48 圖 4.5 冪次型模式試驗半變異數圖... 48 圖 4.6 碎塊型模式試驗半變異數圖... 49 圖 4.7 球型模式設計案例之降雨分佈圖... 50 圖 4.8 指數型模式設計案例之降雨分佈圖... 50 圖 4.9 高斯型模式設計案例之降雨分佈圖... 51 圖 4.10 冪次型模式設計案例之降雨分佈圖... 51 圖 4.11 碎塊型模式設計案例之降雨分佈圖... 52 圖 4.12 球型模式設計案例下各模式推估結果... 53 圖 4.13 指數型模式設計案例下各模式推估結果... 53

圖 4.17 模式驗證流程圖... 56 圖 5.1 淡水河流域雨量站位置圖... 108 圖 5.2 第一場降雨雨量分佈圖... 109 圖 5.3 第二場降雨雨量分佈圖... 109 圖 5.4 第三場降雨雨量分佈圖... 110 圖 5.5 第四場降雨雨量分佈圖... 110 圖 5.6 第五場降雨雨量分佈圖... 111 圖 5.7 第六場降雨雨量分佈圖... 111 圖 5.8 第七場降雨雨量分佈圖... 112 圖 5.9 第八場降雨雨量分佈圖... 112 圖 5.10 第九場降雨雨量分佈圖... 113 圖 5.11 第十場降雨雨量分佈圖... 113 圖 5.12 第十一場降雨雨量分佈圖... 114 圖 5.13 第十二場降雨雨量分佈圖... 114 圖 5.14 第十三場降雨雨量分佈圖... 115 圖 5.15 第十四場降雨雨量分佈圖... 115 圖 5.16 第十五場降雨雨量分佈圖... 116 圖 5.17 第十六場降雨雨量分佈圖... 116 圖 5.18 第十七場降雨雨量分佈圖... 117 圖 5.19 第十八場降雨雨量分佈圖... 117 圖 5.20 第十九場降雨雨量分佈圖... 118 圖 5.21 第二十場降雨雨量分佈圖... 118 圖 5.22 第二十一場降雨雨量分佈圖... 119 圖 5.23 第二十二場降雨雨量分佈圖... 119 圖 5.24 第二十三場降雨雨量分佈圖... 120

圖 5.25 淡水河流域地形分佈圖... 120 圖 5.26 第一場降雨事件各目標測站推估值... 121 圖 5.27 第二場降雨事件各目標測站推估值... 121 圖 5.28 第三場降雨事件各目標測站推估值... 122 圖 5.29 第四場降雨事件各目標測站推估值... 122 圖 5.30 第五場降雨事件各目標測站推估值... 123 圖 5.31 第六場降雨事件各目標測站推估值... 123 圖 5.32 第七場降雨事件各目標測站推估值... 124 圖 5.33 第八場降雨事件各目標測站推估值... 124 圖 5.34 第九場降雨事件各目標測站推估值... 125 圖 5.35 第十場降雨事件各目標測站推估值... 125 圖 5.36 第十一場降雨事件各目標測站推估值... 126 圖 5.37 第十二場降雨事件各目標測站推估值... 126 圖 5.38 第十三場降雨事件各目標測站推估值... 127 圖 5.39 第十四場降雨事件各目標測站推估值... 127 圖 5.40 第十五場降雨事件各目標測站推估值... 128 圖 5.41 第十六場降雨事件各目標測站推估值... 128 圖 5.42 第十七場降雨事件各目標測站推估值... 129 圖 5.43 第十八場降雨事件各目標測站推估值... 129 圖 5.44 第十九場降雨事件各目標測站推估值... 130 圖 5.45 第二十場降雨事件各目標測站推估值... 130 圖 5.46 第二十一場降雨事件各目標測站推估值... 131

符號表

a =影響範圍； C =常數值； Cov =共變異數； o C =碎塊效應； CE =效率係數； EST =推估值； E =期望值； h =相對距離； KG =幾何信賴指標； KS =統計信賴指標； MSE =均方誤差； MSWE =

均方權重誤差；

OBS =目標值； PPCC =機率點繪相關係數； Var =變異函數； W =權重因子； WKM =權重克利金模式； Z =觀測値；

( )

x Z =任一位置 x 之隨機變數； * Z =推估值； μ =平均值； 2 σ =變異數；

( )

h γ =半變異數函數；

ν =拉格蘭茲乘常數；

ε =誤差項；

第一章、 緒論

1.1 研究動機與目的

水資源調配、水工結構物及治洪、排水設施的設計等水利相關措施， 均需以可靠且準確的氣象資料為背景來做為一切系統設計之依據。然而氣 象資料多數為集水區裡固定之水文測站所量測蒐集而得，其所收集獲得之 資料，嚴格而言僅能代表該地點或是其附近小範圍區域內之特性，對於範 圍外之地區則可能呈現不具代表關係之現象。因此，如果想以單獨各別之 水文測站所收集之資料來做為參考依據，則可能會無法適切的應用於大範 圍的水資源設計和調配，因此必須藉由鄰近區域之其他測站所結合形成的 測站網，分析出測站間氣象資料在其空間分佈之特性，進而推估出具有可 靠性且全面性的水文資訊，才能較為準確的掌握該區域水文現象之分佈情 況，以應用於各項決策之參考。 然而在進行氣象資料空間分佈的推估，常常因為許多空間上的不確定 性與分佈的不均勻性或是資料量測誤差等種種因素的效果，造成空間推估 上的偏差，進而對依據其所設計的水工構造物造成了安全上的風險。為減 少此類型因空間分佈不均勻所造成的不確定性，最有效的方式則是增加區 域內測站的數目，然而在設站經費有限及可設站的地點少的條件下，站網 的分佈區域及數量有一定的限制，為解決上述問題一般常應用地理統計方 法(Geostatistics Method)。例如克利金空間推估方法配合氣象資料空間分佈 特性，推估其他未設測站地之資料，以提高氣象資料之可用性。 在進行克利金空間推估法之前必須先得知欲推估區域內該氣象資料之 空間分佈特性，也就是推估各測站氣象資料差異程度與測站間距離之關 係，即區域內水文量之試驗半變異數(Experimental Semi-Variogram)，再以 不同的理論半變異數模式(Theoretical Semi-Variogram Model)套配之，並選

作為後來建置權重克利金模式的依據。然而氣象資料常因人為量測誤差或 儀器故障等因素而具有不確定性，連帶使得合適理論半變異數模式及其參 數之率定亦產生了不確定性。因此本研究將採用權重概念，整合常用理論 半變異數模式，發展出一權重克利金模式。以解決上述因選取不適當的理 論半變異數模式所帶來的不確定性並且提高推估值之可靠度，以獲得更準 確的推估結果。

1.2 文獻回顧

克利金法最早是起源於南非採礦工程上的應用，由南非礦冶工程師 Krige 於 1951 年為了探查礦脈分佈所發展，相隔 12 年之後經由法國數學及 地質學家 Matheron 於 1963 年研究 Krige 等人多年來對南非礦脈的採礦資料 及分析結果，以地理統計方式來估計南非礦區的黃金礦脈，於 1971 年提出 了區域化變數理論，為紀念 Krige 的貢獻，特稱此方法為克利金(Kriging)推 估法，近年來克利金推估法已經被廣泛應用於氣象、土壤物理、地下水、 礦冶、環境監測及水文等研究領域，例如 Creutin 與 Obled(1982)使用克利 金推估等方法，進行對於降雨場目標點的解析與繪製雨量圖、Vijay Kumar 與 Remadevi(2006)將 Kriging 應用於印度的 Rajasthan 地區地下水位的推估。 就克利金空間推估法應用於水文量之觀測方面而言，最大之目的則是 為了得知全面性氣象資料的空間分佈情況，以作為設計決策之參考依據， 又因為其為一種空間性的推估，故其在推估的過程當中仍然存在著許多空 間與時間上的不確定性與不均勻性，所以就推估的準確性來說則是一項值 得探討的議題。就水文量之收集而言，當欲推估點位鄰近測站數越多，其

年主持「台灣水文網先驅計畫」，並於會中建議台灣雨量站網設計站數應與 面積及人口數成正相關，在平原地區每 1000km2可設置 6~25 站可採用 15 站/1000km2_{。世界氣象組織(WMO)於 1965 年建議降雨站網最小密度，}

Bleasdale(1965)有更詳細的指出於一已知面積條件下，須設置最少雨量站個 數的限制，如 2 站/10mi2_{、6 站/100mi}2_{與 15 站/1000mi}2_{。Shaw(1989)指出於}

山 中 地 區 之 站 網 最 小 密 度 為 100~250km2 / 站 ， 而 較 乾 燥 地 區 則 設 定 為 1500~10000km2/站。 就水文測站數量與位置之研究，林金樹、陳峰盛(2004)以鄰點數量與分 佈型態對一般克利金模式雨量估計值誤差的影響作了以下之結論，以圓 型、球型、高斯及指數等四種模式作研究，考慮異向性結構的試驗模式均 顯然地優於等向性結構的試驗模型，就異向性而言以八方向性型態所推估 的值最為準確，且鄰近測站點數越多所推估出的誤差均值差異越小。 綜合上述，克利金空間推估法係一種空間的差值法，所以每當已知條 件點位數較多或是有較佳點位分佈設計過後之條件下，均會有較佳推估之 效果，而假設在滿足上述最佳情況條件下之後，所取得之水文量是否還有 改善其精確度的空間，則是另一項重要的研究方向。如 Delfiner 於 1975 年 提出的交叉驗證法(Cross-Validation)用於驗證半變異數模式之不偏性與最佳 化，以檢定各種理論半變異數模式之適用性，並擇其具最佳套配效果之模 式應用。

1.3 研究分析架構與方法

本研究乃以區域化變數理論所發展而得之克利金空間推估法為基礎， 整合常用理論半變異數模式如球型(Spherical)、指數(Exponential)、高斯 (Gaussian)、冪次(Power)與其分別考慮碎塊效應之理論半變異數模式所模擬 出來之結果，發展出一套權重克利金模式。最後以各種驗證指標，比較權

模式的分析之外，並採用淡水河流域之既有時雨量資料進行實際案例模擬 評估權重模式的適用性與精確性。本研究架構主要分為：第一章緒論，概 述研究動機與目的及前人研究；第二章理論基礎分析，主要介紹區域化變 數理論的原理與克利金法分析步驟，並介紹本研究所應用於參數之率定與 模式之計算與和驗證方式；第三章主要是介紹分析本研究之核心“權重克 利金模式＂之整體應用概念及模式特性；第四章採用設計案例應用於各模 式進行檢定與比較，主要是以球型、指數、高斯、冪次、碎塊分佈特性下 之ㄧ水文量假設條件，分別以各常用理論半變異數模式進行套配與模擬推 估後，最後再以各種驗證指標分析比較其準確性；第五章為實際案例之驗 證與比較，首先簡介所採用之實際研究地點淡水河流域之概況與降雨量之 收集與分析情況，之後再以各種常用理論半變異數模式與權重模式作實際 空間變數推估，並以各種驗證指標分析比較其個別之準確性；第六章彙整 本研究之研究結果並提出建議；第七章為參考文獻。

第二章、 應用理論基礎簡介

本章主要介紹克利金空間推估法之理論基礎及概念，依序的從各種模 式之特性分別作敘述之後再介紹到整體空間變數之推估。此外，亦介紹本 研究所應用之模式參數率定方法及驗證方式。

2.1 區域化變數理論

當自然界中的諸多現象，例如降雨、氣溫、地下水位等現象之某種特 定之隨機變數。分佈在一特定範圍之內，並且在時間和空間上的變異程度 存在著空間結構，則稱為區域化變數。也因為其存在著時間和空間的結構 特 性 ， 所 以 區 域 化 變 數 又 可 分 為 定 常 性 (Stationarity) 與 非 定 常 性 (Nonstationarity)。定常性意指在區域內的隨機變數其統計特性相似，且不會 因為時間和空間的不同而改變。而非定常性指的則是相反，其統計參數特 性隨著時間和空間之不同皆有不同之變化。 現將區域化變數理論之相關基本假設，說明如下： 1. 隨機函數（Random Function） 在自然界中諸多的變數，多在時間和空間上具有的變異性，如果是以 針對某一個空間或是時間的觀點來看，這些水文量多呈現一隨機變數之型 態而形成一隨機變域，而該隨機變域在不同考量觀點的情形下，皆為空間 或時間的函數。

2. 二階定常性（Second-Order Stationary Hypothesis）

二階定常性假設又稱為廣義定常性假設(Wide-Sense Stationarity)，一隨 機變域且同時符合下列三項特性者，則稱為滿足二階定常性假設。 (1) 隨機變數在不同位置的期望值(Expected Value)不會因為位置的不同 而改變，為一常數值。

( )

[

]

式中Z

( )

x 表任一位置 x 之隨機變數；E 表示取期望值；μ表平均值；

及 C 表任一常數值。

(2) 隨機變數在不同位置的變異數(Variance)不會因為位置的不同而改 變，為一常數值。

Var

[

Z

( )

x

]

=σz2 =C,of all x (2.2)

Z

( )

x 表任一位置 x 之隨機變數；Var表示變異函數；及 C 表任一常數

值。

(3) 在一空間中任一兩不同位置之隨機變數Z

( )

X1 、Z

( )

X2 其共變異數

(Covariance)只與兩位置之相對距離有關，與其個別所在位置無關。 Cov

(

Z

( ) ( )

x1,Z x2

)

=E

{

[

Z

( )

x1 −μ

]

[

Z

( )

x2 −μ

]

}

=Cov

( )

h ,of all x (2.3) Cov表共變異數；及h表相對距離。其中當兩點之間距離越大時，其共 變異數越小。 3. 本質假設（Intrinsic Hypothesis） 因在實際應用上，許多物理現象時常無法滿足二階定常性假設，所以 區域化變數理論又延伸出了本質假設。本質假設是一種較弱的限制假設， 當隨機變數符合下列兩項條件時，稱為符合本質假設。 (1) 區域中任意兩個不同位置的隨機變數，其之間差值的期望值為兩位置 點間距離的函數，且與其所在位置無關。如下式所示： E

[

Z

(

x+h

) ( )

−Z x

]

=C

( )

h ,of all x (2.4) E 表示取期望值；C 表任一常數值；及Z

( )

x 、Z

(

x+h

)

表任一位置 x 與 距離 h 位置之隨機變數。 (2) 區域中任意兩個不同位置的隨機變數，其之間的變異函數為兩位置點

函數；及Z

( )

x 、Z

(

x+h

)

表任一位置 x 與距離 h 位置之隨機變數。 4. 準定常性假設（Quasi-Stationary Hypothesis） 假設一隨機變數 Z(x)為非定常性，但 Z(x)在某一定距離內卻可滿足定 常性假設，即表示在該有限範圍內其隨機變數符合均一性，但如超出此範 圍外，則隨機變數不在滿足均一性。符合如此的假設條件，即稱為準定常 性假設。

2.2 半變異數分析

1. 半變異數基本定義 由(2.5)式可知，兩不同位置點隨機變數Z

(

x+h

)

與Z

( )

x 之變異數與其相對距離 之半變異數之關係，如下所示：

( )

Var

[

Z

(

x h

) ( )

Z x

]

2 1 h = + − γ

{

[

(

) ( )

]

[

(

) ( )

]

}

2 x Z h x Z E x Z h x Z E 2 1 _{+ − − + −} =

{

[

(

) ( )

]

[

(

(

)

)

(

( )

)

]

}

2 x Z E h x Z E x Z h x Z E 2 1 _{+ − − + −} = 若(2.4)式C

( )

h =0則表示E

[

Z

(

x+h

) ( )

−Z x

]

=0或E

[

Z

(

x+h

)

]

=E

[

Z

( )

x

]

=C(C 為一常 數)。則半變異數可表示成為下式：

( )

{

[

(

)

( )

]

2

}

x Z h x Z E 2 1 h = + − γ (2.6) 2. 半變異數特性

(1) 條件半正定（Conditional Semi-Positive Definite） 當任意一係數λi∈R，且在

∑

= = n 1 i i 1 λ 的條件下滿足下式，即可稱為 該半變異數函數γ(h)滿足條件半正定，半變異數函數γ

( )

h 必須滿足條 件半正定之特性。

∑∑

(

)

= = ≥ − − n 1 i n 1 j j i j iλ γ x x 0 λ (2.7)

因為半變異數函數必須滿足條件半正定的特性，所以當空間相對 距離 h 越遠趨近於無窮時，半變異數函數γ

( )

h 之變量應遠小於其相對 距離平方的增量。

( )

0 h h lim ₂ h→∞ = γ (2.8) 當半變異數無法滿足此特性時，表示其無法滿足本質假設，即該隨機 變域為非定常性，而在此特性下，其空間結構在相對距離很大時仍然 存在著某種空間趨勢。 (3) 半變異數與共變異數之相對關係： 由二階定常性假設之條件下，可將(2.2)式改寫成 Var

[

Z

( )

x

]

=σ_z2 =C =>

[

( )

]

[

(

)

]

2 z h x Z Var x Z Var = + =σ 將(2.3)式改寫成為 Cov

(

Z

( ) ( )

x1 ,Z x2

)

=E

{

[

Z

( )

x1 −μ

]

[

Z

( )

x2 −μ

]

}

=Cov

( )

h =>

( )

[

(

) ( )

2

]

x Z h x Z E h ov C = + −μ 之後再配合半變異數函數之表示式，最後可解得半變異數函數γ

( )

h 與 共變異數Cov

( )

h 間之關係，其關係式如下所示：

( )

{

[

(

) ( )

]

2

}

x Z h x Z E 2 1 h = + − γ

[

(

)

2

]

[

(

) ( )

]

[ ]

( )

2 x Z E 2 1 x Z h x Z E h x Z E 2 1 _{+ − + +} =

[

(

)

2 2

]

[

( )

2 2

]

[

(

) ( )

2

]

x Z h x Z E x Z E 2 1 h x Z E 2 1 _{+ −μ + −μ − + −μ} =

[

(

)

]

Var

[

Z

( )

x

]

Cov

( )

h 2 1 h x Z Var 2 1 _{+ + −} = =σz2 −Cov

( )

h

( )

( )

( )

表示半變異數函數於圖形座標上是由原點，依相對距離的關係而開始 作延伸，即稱之為半變異數函數γ

( )

h 的連續性。 (5) 碎塊效應（Nugget Effect） 半變異數因為具有連續性的性質，所以理論上當相對距離 h=0 時，其半變異數函數γ

( )

h 亦當為零。但在實際的應用上，往往由於量 測誤差或是在非常短的距離內量測值Z

( )

x 即產生相當大的變異，使得 半變異數函數γ

( )

h 在即小的距離之內無法表現出其變化之情形，而發 生非滿足連續性之情況，則稱之為碎塊效應，如圖(2.2)所示。 (6) 臨界變異元值（Sill） 理論上，當兩點間之相對距離 h 越大，則相互影響的關係越小而 半變異數值越大，如圖(2.3)所示。此外，在滿足定常性之假設條件下， 其半變異數函數γ

( )

h 之增值會隨著相對距離 h 的增加越漸趨緩，而當 相對距離 h 到達某一特定值後其所對應的γ

( )

h 則漸趨於一臨界值，此 一定值即稱之為臨界變異元值。 (7) 影響範圍（Influence Range） 當半變異數函數γ

( )

h 達到臨界變異元值時，其所對應之最小相對 距離即稱為影響範圍，如圖(2.3)所示。影響範圍顧名思義，表同一空 間裏各變量間相互影響的最大距離，在此一距離內各變數存在著某特 定之空間相依的特性；而在影響範圍之外，各變量間則相互獨立。 3. 試驗半變異數（Experimental Semi-Variogram） 由區域化變數理論可知，空間各不同位置之資料Z

( )

xi 相關變異情形可 以一連串之半變異函數γ

( )

h 來表示，如(2.6)式。因此採用實際觀測資料所求 出之半變異數函數γ

( )

h ，則稱之為試驗半變異數，如圖 2.4 所示。 其推求步驟如下所示： (1) 首先計算所有測站各別間之距離，並區分為若干個等距的區間。

(2) 計算點位之間的半變異數。

(3) 累計每個等級內的所有配對各數(Pairs) ，並求出每個等級內之距離 和變異圖的平均數，視為該等級距離與變異數的代表。

(4) 再將各代表點連接起來，便可得到其試驗半變異數。

2.3 常用理論半變異數模式（Theoretical Semi-Variogram Models）

2.3.1 模式簡介 因為試驗半變異數是由數個不連續點所連接，在實際應用上並無法直 接套用於克利金空間推估法，其仍需要以一連續性的模式套配完成後才能 予以應用，而此一連續性之模式便稱之為理論半變異數模式，常用之理論 半變異數模式有下列四種。 (1) 冪次模式(Power Model) γ

( )

h =ϖhε

(

ε <2

)

(2.10) (2) 球體模式(Spherical Model)

( )

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 3 a h 2 1 a h 2 3 h ϖ γ (2.11) (3) 指數模式(Exponential Model)

( )

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = a h exp 1 h ϖ γ ，影響範圍=3a (2.12) (4) 高斯模式(Gaussian Model)

( )

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = 2 a h exp 1 h ϖ γ ，影響範圍= 3a (2.13) 上些式中ω表臨界變異數；h 表距離；a 表影響範圍。

的 推 估 之 影 響 ， 於 該 模 式 下 臨 界 變 異 值 (Sill) 為 零 ， 且 影 響 範 圍 （Influence Range）a 也趨近於零。 γ

( )

h =C0 (2.14) 臨界變異數ω =0；影響範圍a≈0；Co =碎塊效應。 2.3.2 模式參數率定 本研究在決定各模式之碎塊效應Co、影響範圍 a 及臨界變異數ω(sill) 主要是採用黃金切割法，其步驟為，(1)設定其切割邊界為 0.00001 至 100， (2)依序分別固定各參數視其為控制變因，(3)將各階段之切割邊界值作為個 參數之定值分別套用於各模式內計算其理論半變異數之值，並計算其與試 驗半變異數之誤差值，(4)切割收斂條件為累積運算切割次數達 20 次或切割 邊界內之差值小於 0.0001，最後當達到收斂條件時，期間所計算出之所有 誤差值具有最小平均差之參數組，即為最佳理論變異圖之套配參數。

2.4 克利金空間推估法

克利金空間推估法係由區域化變數理論所推演而得，主要是應用自然 界中隨機變數的諸多現象之相關特性，如定常性或是非定常性，對於單一 點位或是區塊性之資料推估所發展出相對應的推估系統方程式。如一般最 常見的有，簡單克利金法(Simple Kriging)、一般克利金法(Ordinary Kriging) 及通用克利金法(Universal Kriging)，本研究乃以單一點位之ㄧ般克利金推 估法作為研究探討的對象，其特性如下所述。

2.4.1 基本特性

一般克利金推估法(Ordinary Kriging)主要應用於二階定常性假設之區 域化變數，以統計的觀點而言，其具有最佳線性不偏估(Best Linear Unbiased Estimator，又簡稱 BLUE)之特性，各特性說明如下：

∑

(

)

= = = n 1 i i oi * o Z ,i 1,2,...,n Z λ (2.15) Zi為Z

( )

x 在xi點位上之觀測値； * o Z 為Z

( )

x_o 之推估值；及λ_oi對應於Z_i 之權重因子。 2. 不偏估性（Unbiased）：估計值之期望值等於隨機變數之期望值 E

[ ]

Z_o* =E

[ ]

Z_o orE

[

Z_o* −Z_o

]

=0 (2.16) Zo為Z

( )

x 在xo點位上之觀測値；及 * o Z 為Z

( )

x_o 之推估值。 3. 最佳化（Optimal）：估計值與觀測值差之變異數為最小

{

[

]

[

(

o

)

2

]

}

* o o * o Z E Z Z Z Var min − = − (2.17) Zo為Z

( )

x 在xo點位上之觀測値；及 * o Z 為Z

( )

x_o 之推估值。 2.4.2 克利金系統方程式 一般克利金推估法(Ordinary Kriging)主要應用於二階定常性假設之區 域化變數，因此Z(x)之期望值皆為一定值，其值不隨位置的不同而改變即

( )

[

Z x

]

E

[

Z

(

x h

)

]

Const. E = + = ，且由線性式(2.15)和不偏估式(2.16)之特性可以推 求得下式：

∑

= = n 1 i oi 1 λ (2.18) 將(2.15)式帶入(2.17)式中可得知

[

( ) ( )

]

∑∑

[

(

)

(

)

]

= = − − = − n 1 i n 1 j o j o i oj oi 2 o o * Z Z Z Z E x Z x Z E λ λ

(

)

[

(

)

2

]

j i j i E Z Z 2 1 x x − = − γ 由上二式可得下式

[

( ) ( )

−

]

=−

∑∑

(

−

)

+

∑

(

−

)

n n n 2 * x x 2 x x x Z x Z E λ λ γ λ γ

示。

[

( ) ( )

]

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − =

∑

= n 1 i oi o o * 1 2 x Z x Z Var L ν λ

[

( ) ( )

]

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − =

∑

= n 1 i oi 2 o o * 1 2 x Z x Z E ν λ

(

)

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ − − + − − =

∑∑

∑

∑

= = = = n 1 i oi n 1 i n 1 j n 1 i o i oi j i oj oiλ γ x x 2 λ γ x x 2ν λ 1 λ 將上式分別對λoi及ν取偏微分，且令其微分式為 0，則可求得克利金系統方 程式及克利金變異數。 克利金系統方程式：

∑

(

)

(

)

= − = + − n 1 j i o j i ojγ x x ν γ x x λ

(

i=1,2,....,n

)

(2.19)

∑

= = n 1 i oi 1 λ 若以矩陣形式表示則克利金系統方程式可表示如下， (2.20) 其中

(

)

E

{

[

Z

( )

x Z

( )

x

]

}

,

(

i,j 1,2,....,n

)

2 1 x x_{i j i j} 2 ij =γ − = − = γ ，在克利金系統方程式當中 半變異數γij表示觀測點位彼此之間的相關特性。半變異數γio表示觀測點位 和推估點位間的相關特性，λi則為其各觀測點位所對應的權重因子。 若依傳統求解(2.20)式矩陣之作法來推求各λi，如果測點過多容易使得 克利金矩陣過於複雜而難以求解。因此本研究將採用可以率定多參數模式 之蒙地卡羅為基礎之最佳化方法(Simulation based optimization meathod)來 決定各測點之權重因子。其率定過程如下所示。 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 1 . . . . 0 1 ... 1 1 1 ... .... ... ... .... ... ... 1 ... 1 ... 0 n 20 10 n 2 1 nn 2 n 1 n n 2 22 21 n 1 12 11 γ γ γ ν λ λ λ γ γ γ γ γ γ γ γ γ

本研究在計算克利金系統方程式解係數λ值之方式主要是以下列步驟 計算之，(1)以蒙地卡羅法產生滿足

∑

= = n i oi 1 0 . 1 λ 之權重因子；(2)將各推估點之 權重因子模擬值代入

∑

= + = n j i j i j io 1 , , μ γ λ γ

(

i, j =1,2,3,...,n

)

之式子計算出γio 之 值；(3)代入理論半變異數模式計算求得各推估點之 io γ∧ ；(4)計算γio與

γ

_io ∧ 之 均方根誤差，即 0.5 n 1 i 2 io - _io n 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∑

∑

= ∧

γ

γ ，其中 n 為推估點數；(5)最後，取均 方根誤差差異最小者，則該組模擬值即為該模擬之推估權重因子λ最佳值。 2.4.3 克利金變異數 由克利金系統方程式所求得之點位的最佳估計係數λi,

(

i=1,2,....,n

)

帶回 (2.15)式即可求得最佳不偏估計値，而其所對應之克利金係數變異數，則如 下所示：

[

]

∑

(

)

= − + = − = n 1 i o i i o * o 2 k VarZ Z μ λγ x x σ (2.21) 當所推估之克利金變異數越接近於零時，則表示所選用的模式越佳。

2.5 模式驗證

從各點位推估結果當中可以大概看出各種理論半變異數模式與目標推 估值之差異，但其僅為該點位中所呈現之結果。就整體而言，並無法明顯 表示出各種理論半變異數模式推估之優劣程度。因此必須藉由下列所介紹 之各種驗證指標對於模式所作出之結果，進行驗證與分析，並且由各指標 值的大小對於其整體結果作出明確的歸納，本研究所使用之指標有下列六

之精確度越高。其關係表示式如下所示：

( )

( )

[

]

{

}

( )

[

]

{

}

∑

∑

= = − − − = _n 1 i 2 n 1 i 2 OBS i OBS i EST i OBS 1 CE (2.22)

( )

i

OBS 為點位觀測值；OBS為各觀測值之平均值；及EST

( )

i 為模式推估值。

2. 機率點繪相關係數(Probability plot correlation coefficient,PPCC)

當 PPCC 指數越接近於 1，則表示模式有較佳之推估成效，其推估值

( )

i EST 越趨近於觀測値OBS

( )

i

( )

[

]

[

( )

]

{

}

( )

[

]

{

}

{

[

( )

]

}

0.5 n 1 i n 1 i 2 2 n 1 i EST i EST OBS i OBS EST i EST OBS i OBS PPCC ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ _{− × −} − × − =

∑

∑

∑

= = = _(2.23)

( )

i

OBS 為點位觀測值；OBS為各觀測值之平均值；EST

( )

i 為模式推估值；及 EST 為模式推估值之平均值。 3. 均方誤差(Mean-Square error，MSE) 樣本之各點位推估值與觀測點位值之平均誤差，當 MSE 越趨近於 0 表 示模式推估值越符合觀測值，其定義如下所示：

( )

( )

[

]

{

}

N i OBS i EST MSE 5 . 0 n 1 i 2 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ₋ =

∑

= _(2.24)

( )

i OBS 為點位觀測值；及EST

( )

i 為模式推估值。

4.

均方權重誤差(Mean Square Weighted Error ,MSWE)

MSWE 指標如同 MSE 指標皆為計算模式推估值與觀測值，但 MSWE 更著重於高推估值之推估準確度。其關係式如下所示：

( )

[

( )

( )

]

{

}

0.5 n 1 i 2 N i EST i OBS i W MSWE ⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ _{× −} =

∑

= _(2.25)

( )

[

( )

]

(

)

OBS 2 OBS i OBS i W × + = OBS

( )

i ：為點位觀測值；OBS：為各觀測值之平均 EST

( )

i ：為模式推估值。

當

MSWE→0

則表示推估值接近於觀測值；此外，除了驗證整體模擬趨

勢與實測值誤差為最小之外，並著重於高於平均值之觀測值準確性。

5. 模式信賴指標(Model Reliability Indices)

由 Leggett 與 Williams(1981)提出兩種信賴指標，其分別為幾何信賴指 標(Statistical reliability index，KS)與統計信賴指標(Statistical reliability index，KS)兩種指標如下所示：

(1). 幾何信賴指標(Geometric reliability index，KG)

(

)

(

)

0.5 5 . 0 N SUM 1 N SUM 1 KG − + = (2.26) ( ) ( ) ( ) ( )

∑

= ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₋ = n 1 i 2 i OBS i EST 1 i OBS i EST 1 SUM

(2). 統計信賴指標(Statistical reliability index，KS)

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 5 . 0 N SUM EXP KS (2.27)

( )

( )

∑

= ⎭⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ _⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = n 1 i 2 i OBS i EST log SUM 當估計值 EST(i)與觀測值 OBS(i)完全吻合時，KG 與 KS 將趨近於下限 值 1.0；反之當估計值與觀測值差異大時，則 KG 與 KS 值亦會越大。

半變異元與共變異函數示意圖 0 0.2 0.4 0.6 0.8 1 1.2 1.4 0 2 4 6 8 10 12 14 16 相對距離 半變 異元 半變異元r(h) 共變異數C(h) 圖 2.1 半變異數函數、共變異數關係示意圖 圖 2.2 碎塊效應示意圖 碎塊效應示意圖 0 0.2 0.4 0.6 0.8 1 1.2 1.4 0 10 20 30 40 50 60 70 相對距離 半變 異元 _半變異元

圖 2.3 半變異數函數特性說明圖 圖 2.4 試驗半變異數函數示意圖 半變異元示意圖 0 0.2 0.4 0.6 0.8 1 1.2 1.4 0 10 20 30 40 50 60 70 相對距離 半變異元 半變異元 影響範圍 臨界變異 値 試驗半變異元函數示意圖 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 0 10 20 30 40 50 60 70 80 90 相對距離 h 半變異元 r (h ) 半變異元

常用理論半變異元模式示意圖 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 0 10 20 30 40 50 60 70 80 90 距離h 半變異元 試驗半變異元 r(h) 指數模式 r(h) 高斯模式 r(h) 球體模式 r(h) 次方模式r(h) 圖 2.5 常用之理論半變異數模式套配示意圖

第三章、 權重半變異數模式之發展

在應用克利金系統方程式推估未知點之值時，須經過一呈現連續性的 理論半變異數模式的套配，進而找出較為合適之模式。然而因水文資料本 身之不確定性常導致在決定合適的理論半變異數模式亦產生了不確定，進 而影響推估值之準確性，因此本研究將發展出一套使用權重概念之模式， 藉由各理論模式套配之準確度所產生的加權修正值而建構成的權重半變異 數模式，用以提升推估結果之準確性，以解決上述之問題。茲將權重半變 異數模式之發展過程說明如下。

3.1 基本概念說明

權重半變異數模式，主要的概念乃是經過傳統常用之理論變異數模式 套配之後，依照每一理論模式對於試驗變異圖的整體適合度之好壞，而產 生一相對性的加權值。當適合度越好，其所產生之加權值越大；當適合度 越差，其所產生之加權值越小。之後再依照每種理論模式所產生之加權值 及其半變異數或推估值，分別建構成權重克利金模式(Weighted Kriging model)。 權重半變異數模式依據加權對象可細分為兩種產生權重模式。兩種方 式主要加權概念方式皆相同，最大的差異處在於加權因子產生之後對於加 權的對象有所不同，下一小節會對於兩種權重模式之特性作更近一歩之介 紹。

model_1(WKM1))：加權對象為半變異數；(2)權重克利金模式 II(Weighted Kriging model_2(WKM2))：其加權對象為推估值。在進行權重模式介紹前， 先來了解如何計算各理論半變異數模式之權重比例。 於實際進行理論半變異數模式套配過程當中，不可能會有任何一試驗 半變異數與任一理論半變異數模式推估結果呈現吻合之狀態，因此試驗半 變異數與理論半變異數模式推估結果皆會產生誤差，在累積所有誤差值平 方開根號後取其平均值，即可獲得該理論模式之誤差εm，如(3.1)式所示。

( )

( )

(

)

(

)

0.5 p h 1 i 2 i o i m m h h p h 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − =

∑

= γ γ ε (3.1)

∑

= = _n m m m m W 1 1 1 ε ε (3.2) m ε 第 m 個理論半變異數模式之誤差；Wm第 m 個理論半變異數模式加權因 子；γ_m(h_i )由第 m 個理論半變異數模式於hi所推得之半變異數；γ_o(h_i )於hi 所推得之試驗半變異數；hp點位距離組數；n 理論半變異數模式之總數。 由(3.1)可知，當一理論半變異數模式所得之γ_m,i

( )

h −γ_o,i

( )

h 之值越大，其 誤差εm亦呈現正比增加。因此所有理論半變異數模式皆可計算其誤差εm， 最後累加所有理論半變異數模式之誤差之倒數

∑

= n m1 m 1 ε 後，帶入(3.2)式即可計 算出該理論半變異數模式之加權因子W_m。 因為在計算加權因子Wm的時候是以誤差函數εm之倒數概念，所以每當 誤差值εm越大則 m ε 1 之值則越小，因此所計算出之加權因子Wm也越小，其中 各理論半變異數模式所產生之加權因子其總和則為 1。 權重理論半變異數模式依其加權應用的對象不同又可分為下列兩種模式： 1. 權重克利金模式 I(Weighted Kriging model_1(WKM1)):

( )

_∑

= = n m m i m i WKM h W 1 , , 1 γ γ (3.3) m W 第 m 個理論半變異數模式加權因子；γ_m,i第 m 個理論半變異數模式半變 異數；及 n 採用理論半變異數模式之總數。 此一權重克利金模式，主要之概念是用各模式之權重因子Wm，以該相 對應理論半變異數模式之半變異數γm,i為對象，做相乘的動作並累加各種模 式相對應之乘績和後，進而計算出權重克利金模式 I 之各半變異數值

( )

h i WKM ,1 γ ，其表示式如(3.3)所示。之後，再以該計算結果之半變異數值γWKM ,1i

( )

h 帶入克利金方程式求解其係數值λ_oi,

(

i=1,2,....,n

)

，最後進而推求出空間未知點 位之推估值，其概念如圖(3.1a)所示。

2. 權重克利金模式 II(Weighted Kriging model_2(WKM2)):

( )

∑

= = n m m i m i WKM h Z W Z 1 , , 2 (3.4) m W 第 m 個理論半變異數模式加權因子；Z_m,i第 m 個理論半變異數模式所得 第 i 點位之推估值；及 n 採用理論半變異數模式之總數。 第二種權重克利金模式，主要之概念是以各模式之加權因子Wm與各理 論半變異數模式所推估空間推估值Zmi之乘績，且在累加之後而得之一權重 推估值ZWKM ,2i

( )

h ，其表示式如(3.4)所示。其所得之值ZWKM ,2i

( )

h 即為 WKM2 模式之推估結果。 權重克利金模式 I 與 II，其概念如圖(3.1b)所示。上述兩種權重模式其推估 流程整理如圖(3.2)所示。

權重模式I概念示意圖 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 0 10 20 30 40 50 60 70 80 90 距離h 半變異元 試驗半變異元 r(h) 指數模式 r(h) 高斯模式 r(h) 球體模式 r(h) 權重模式 r(h) 次方模式r(h) 圖 3.1(a)權重模式 I 概念示意圖 權重模式II概念示意圖 38 38.5 39 39.5 40 40.5 41 41.5 42 42.5 43 43.5 0 2 4 6 8 10 12 目標推估點位 推估 值 目標推估值 球型模式推估值 指數模式推估值 高斯模式推估值 次方模式推估值 權重模式II推估值 圖 3.1(b)權重模式 II 概念示意圖

圖 3.2 權重克利金模式推估流程圖 計算試驗半變異數 率定理論半變異數模式之參數並計算各模 式之半變異數值與其所佔權重因子W _m WKM1 WKM2 解各模式克利金方程 式之係數值 9 ~ 1 m=λ 推估各模式未知點 9 ~ 1 m=Z 之 數值 以各模式未知點推估值 9 ~ 1 m=Z 依權重比例Wm 計算Z_wkm2,i 以各模式半變異數值依 權重W 計算出_m γ_wkm1,i 解克利金方程式求出 wkm1 ∧ λ 求解未知點位推估 值Zwkm1,i

第四章、模式應用於設計案例之驗證與比較

本章主要重點在於測試權重半變異數模式(Weighted Kriging model)，與 傳統理論半變異數模式球型、指數、高斯、冪次、碎塊模式所設計之已知 空間分布條件下，進行未知點位的推估。並配合第二章所提過之 CE、PPCC、 MSE、KG、KS、MSWE，六種驗證指標計算結果進行分析與評估本研究所 發展的權重半變異數模式與傳統理論半變異數模式之差異性。

4.1 設計案例基本資料概述

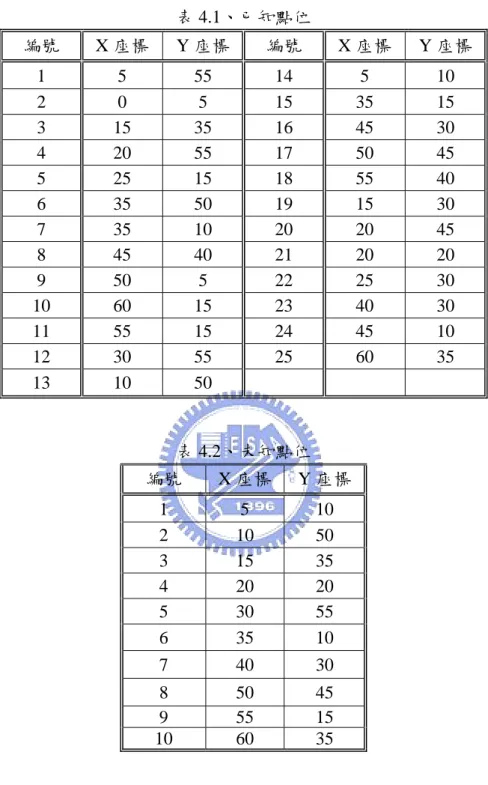
本設計案例範圍為ㄧ 60(km)×60(km)的正方形面積，於該面積上假設一 共有 25 個站，其 25 個站呈現均勻分部之狀態，各站之座標點位如表 4.1 所 示。本設計案例共分別假設五場具有不同型態空間分佈之降雨，並控制其 空間分佈型態分別呈現為球型、指數、高斯、冪次、碎塊五種不同之模式； 即表示由所設計之雨量資料所計算出之試驗半變異數圖，分別呈現球型、 指數、高斯、冪次、碎塊模式之分佈情況。 今以該五種設計雨型分佈作為已知設計雨量模擬之參考資料，分別以 各種常用理論半變異數模式與本研究之權重克利金模式，對於該十個未知 點位如表 4.2 所示，進行空間變異特性之推估與分析。各空間座標點位之分 布如圖 4.1 所示。

4.2 驗證流程

本案例之設計主要是為了驗證權重克利金模式，用於各種空間分佈情 形下對於未知點位推估之效果，並與其他常用理論半變異數模式推估效果 作比較，其驗證分析流程如下：

1. 衍生空間變數 本設計案例為驗證權重克利金模式是否適用於各種變數空間分佈之情 況，且其推估之結果也能優於其他常用理論半變異數模式，故須事先設計 半變異數空間分佈變數場，之後再以各常用理論半變異數模式和權重克利 金模式進行套配與推估，以便於判斷權重克利金模式之推估效果是否優於 其他理論半變異數模式。 首先在設計符合傳統理論半變異數模式之空間分佈變數場時，將已知 座標點位間距離分成 10 個等級，之後再以每個等級間之平均距離視為代表 距離，並以假設每一種模式之影響範圍、臨界變異數等參數，最後再衍生 出其每等級間之代表半變異數。其各模式之設計參數值及各模式等級間之 代表距離與所對應模式之半變異數值如表 4.3 所示。之後依序繪出各模式之 半變異數圖，並以該半變異數圖作為空間分佈特性之準則，製造出各種實 驗空間分佈變數場分佈，使其試驗半變異數圖能符合於該分佈特性(如表 4.4 與圖 4.2~4.6 所示)，其空間變數分佈之情況如圖 4.7~4.11 與表 4.5 所示。 2. 理論變異圖模式之套配及其權重因子之計算 衍生完上述五種實驗空間分佈變數場之後，與傳統克利金空間推估法 相同之步驟進行各種理論半變異數模式之套配，並進行各理論模式之權重 因子計算，如表 4.6 所示。 3. 計算未知點位之目標推估值 當空間變數分佈呈現某一個預設理論模式之分佈情況下，其未知點位

4. 各變異元模式參數之推估 以常用理論半變異數模式與權重克利金模式進行空間未知點位之推 估。因為本研究在計算克利金方程式求解係數之步驟，主要是以蒙地卡羅 方式求解，其求解過程可能產生些許差異，為解決其差異情況，故重複進 行 10 次的重複性模擬，以避免產生極端推估之影響產生，作為該空間未知 點位之推估值，其空間點位推估結果如表 4.7~4.11。最後推估值繪製如圖 4.12~4.16 所示。 5. 驗證指標之計算 由設計的各種模式之實驗空間分佈場情形下，每種理論半變異數模式 與權重克利金模式，皆會計算出一組推估值，然而每次重複模擬出之推估 值 與 目 標 推 估 值 之 差 異 大 小 主 要 是 以 CE(Coefficient of efficiency) 、 PPCC(Probability plot correlation coefficient)、 MSE(Mean-Square error) 、 KG(Geometric reliability index)、KS(Statistical reliability index)、MSWE(Mean square weighted error)，以上六種驗證指標作為實際判斷之依據。在每次進 行重複模擬之過程當中，每次的模擬皆會計算求得驗證指標，之後再將所 有所得驗證指標計算其平均值，最後以該平均值作為當次設計之空間分佈 場之驗證成果進行各理論半變異數及權重克利金模式準確度之排序。 上述驗證過程中，每一個設計案例之進行，為了消減蒙地卡羅法對於 克利金方程式之係數計算所產生些許之誤差，所以於每一次的設計案例模 擬流程當中，皆會重複上述步驟 3~5 共 10 次，以計算出整個設計案例之平 均推估值作為代表值，指標之檢定也是同樣的以各驗證指標平均值為其代 表值，上述驗證流程請參閱圖 4.17。

4.3 模擬推估結果之比較與驗證分析

1 推估值結果比較 於各個設計案例當中，在設計完其降雨空間分佈特性之後，藉由各種 傳統的克利金模式進行套配，依照第三章所介紹的權重克利金模式之概念 產生一權重比例，以構成為權重模式之最主要因子，如表 4.6 所示。由其權 重比例之大小分佈可以明顯得看出，當以某一特定理論半變異數模式設計 空間變數分佈情形，其該對應之模式所佔之權重比例值越大，即代表其試 驗變異圖之套配越佳，例如：在高斯型模式設計案例情況下，高斯模式與 高斯碎塊型模式分別佔有最大之權重 0.144。此外，也可觀察出於其他設計 案例下也有相同類似的套配結果，即於設計案例條件下其相對應模式皆有 明顯較佳的套配效果。以整體而言，其權重比例所呈現之結果與本案例設 計前欲達到之概念相同，也就是當選用與設計案例相同條件模式之下進行 模式之套配，其所佔的權重比例值越大，即表示該模式之套配效果越佳， 也表示其空間推估值也應呈現最佳之推估結果。 以推估結果表 4.7~4.11 對照圖 4.12~4.16 也可以看出，於某一設計案例 下，當使用理論半變異數圖模式進行未知點之推估時，除了原先所設定之 理 論 半 變 異 數 模 式 有 不 錯 之 推 估 結 果 以 外 ， 第 二 種 權 重 克 利 金 模 式 (Weighted Kriging model_2(WKM2))亦可以產生接近目標推估值之推估效 果，例如：於高斯模式設計案例條件下，於未知點位 1，高斯模式與目標推 估值差為 0.2524，WKM2 相差 0.0319；於未知點位 2，高斯模式與目標推 估值差為 0.6417，WKM2 相差 0.066；於未知點位 3，高斯模式與目標推估 值差為 0.4774，WKM2 相差 0.4151；於未知點位 4，高斯模式與目標推估

為 0.3018，WKM2 相差 0.0185；於未知點位 8，高斯模式與目標推估值差 為 0.5389，WKM2 相差 0.1372；於未知點位 9，高斯模式與目標推估值差 為 0.0949，WKM2 相差 0.2102；於未知點位 10，高斯模式與目標推估值差 為 0.0076，WKM2 相差 0.2378，由此可以明顯看出 WKM2 推估值與目標推 估值之差值幾乎皆小於高斯模式之推估結果，也就是 WKM2 明顯的有較佳 之推估效果。 2 驗證指標分析 若單純的以推估結果之分佈情況，僅可以看出各模式之推估趨勢及單 點間之誤差，但若欲分析精確度則需要應用各種驗證指標加以分析，本設 計案例主要使用第二章所述之下列六種驗證指標 CE、PPCC、MSE、KG、 KS、MSWE，以作為實際判斷之依據，當 CE、PPCC、KG、KS 越趨近於 1 即表示其模式推估結果越趨近於目標推估值，而當 MSE、MSWE 越趨近 於 0 也同樣表示其推估結果越符合目標推估值。 各設計案例之驗證指標計算結果及依次排序各模式準確度之結果，如 表 4.12~4.16 所示。就以上一小節之高斯型設計案例為例，當空間變數分佈 設定為高斯型模式分佈下，如表 4.6 權重因子一欄表中可知，球型、球型碎 塊、高斯、高斯碎塊模式皆有不錯套配結果。例如表 4.14 結果所示，其目 標推估值所採用的是高斯型模式對於未知點位所推估出之值，所以其結果 如同本案例設計之概念，於各種檢定模式之下，基本上高斯型模式做推估 可以得到最佳之套配與推估結果，但是在經由權重修正過後之 WKM2 所推 估 出 之 結 果 ， 不 論 是 CE=(0.6091) 、 PPCC=(0.8341) 、 MSE=(0.2354) 、 KG=(1.0186)、KS=(1.0186)、MSWE=(0.747)任一種驗證指標觀察可以發現 WKM2 皆呈現出比高斯模式 CE=(0.4523)、PPCC=(0.8042)、MSE=(0.2804)、 KG=(0.022)、KS=(1.022)、MSWE=(0.8886)顯示出有更好的推估效果。 然而由表 4.12~4.16 可以看出，於其他設計案例上的應用，WKM2 也都

可以得到比各設計案例相對應之模式有更好之推估效果，因此可以得到一 結論為：WKM2 的推估結果不但更勝於原本設計案例所對應之模式有更佳 的推估效果之外，甚至可以適用於各種設計案例當中，且其結果都優於其 他常用理論模式。以上結果證明權重克利金模式，不僅可以藉由加權的方 式優化空間推估的準確度，而且也可以適用於各種不同之空間分佈特性之 變數，以改善使用克利金空間推估法可能因選取不適合的理論半變異數模 式所造成之誤差。

表 4.1、已知點位 編號 X 座標 Y 座標 編號 X 座標 Y 座標 1 5 55 14 5 10 2 0 5 15 35 15 3 15 35 16 45 30 4 20 55 17 50 45 5 25 15 18 55 40 6 35 50 19 15 30 7 35 10 20 20 45 8 45 40 21 20 20 9 50 5 22 25 30 10 60 15 23 40 30 11 55 15 24 45 10 12 30 55 25 60 35 13 10 50 表 4.2、未知點位 編號 X 座標 Y 座標 1 5 10 2 10 50 3 15 35 4 20 20 5 30 55 6 35 10 7 40 30 8 50 45 9 55 15 10 60 35

表 4.3 理論半變異數各模式之參數設定與所對應距離之變異元

球型模式 指數模式 高斯模式 冪次模式

影響範圍(a) 臨界變異數(w) 影響範圍(a) 臨界變異數(w) 影響範圍(a) 臨界變異數(w) 冪次項(λ ) 臨界變異數(w)

距離(h) 32 1.12 9 1.1 14.49 1.14 0.25 0.45 碎塊模式 0 0 0 0 0 1.008 8.985 0.459 0.695 0.364 0.78 1.008 15.321 0.743 0.9 0.767 0.89 1.008 20.447 0.927 0.987 0.984 0.957 1.008 27.042 1.082 1.045 1.105 1.026 1.008 33.619 1.12 1.074 1.135 1.084 1.008 39.975 1.12 1.087 1.139 1.132 1.008 45.537 1.12 1.093 1.14 1.169 1.008 51.519 1.12 1.096 1.14 1.206 1.008 58.443 1.12 1.098 1.14 1.244 1.008 65.935 1.12 1.099 1.14 1.282 1.008

表 4.4 試驗半變異數之套配 球型模式 指數模式 高斯模式 冪次模式 碎塊模式 代表距離(h) 固定參數值 實際套配值 固定參數值 實際套配值 固定參數值 實際套配值 固定參數值 實際套配值 固定參數值 實際套配值 0 0 0 0 0 0 0 0 0 0 0 8.985 0.459 0.416 0.695 0.665 0.364 0.4 0.779 0.75 1.008 0.931 15.321 0.743 0.767 0.9 0.941 0.767 0.808 0.89 0.905 1.008 0.981 20.447 0.927 0.94 0.987 1.015 0.984 0.984 0.957 0.968 1.008 0.856 27.042 1.082 1.105 1.045 1.06 1.105 1.133 1.026 1.127 1.008 1.115 33.619 1.12 1.102 1.074 1.068 1.135 1.123 1.0836 1.047 1.008 1.042 39.975 1.12 1.196 1.087 0.999 1.139 1.114 1.132 1.132 1.008 1.066 45.537 1.12 1.377 1.093 1.201 1.14 1.321 1.169 1.15 1.008 0.937 51.519 1.12 1.463 1.096 1.374 1.14 1.42 1.206 1.198 1.008 1.076 58.443 1.12 1.111 1.098 1.543 1.14 1.148 1.244 1.162 1.008 1.725 65.935 1.12 0.617 1.099 0.128 1.14 0.634 1.282 0.799 1.008 0.97