數位式剪波器與類比式剪波器在正交分頻多工系統下之分析

(1)

Analysis of Digital Clipping and

Analog Clipping for OFDM

system

Student : Chun-Lin Yang

Advisor : Yuan-Pei Lin

Department of Electrical and Control Engineering

National Chiao Tung University

Abstract

In this thesis, we analyze digital and analog clipping in OFDM system. We derive the equations that show how digital and analog clipping affect the average autocorrelation of the transmitted signal. Earlier analysis of the clipped signals requires the assumption that input signal of the clipper is WSS. However, this assumption is not valid in the OFDM system in practice. We show that the clipper input should adequately be assumed to be WSCS. We will derive the power spectrum of the clipper output. Numerical simulation will be given to demonstrate the transmitted spectrum of the OFDM trans-mitter using analog clipping spreads more widely than the one using digital clipping. It will also be shown that transmitted spectrum is underestimated if we assume the clipper input signal is WSS.

(2)

List of Figures

1.1 Analog representation of the OFDM transmitter. . . 2

1.2 Commonly used DFT-Based implementation of the OFDM trans-mitter, where ω0 = 2π/M . . . 3

2.1 Schematic diagram of the clipper. . . 9

2.2 Digital-to-analog conversion scheme. . . 10

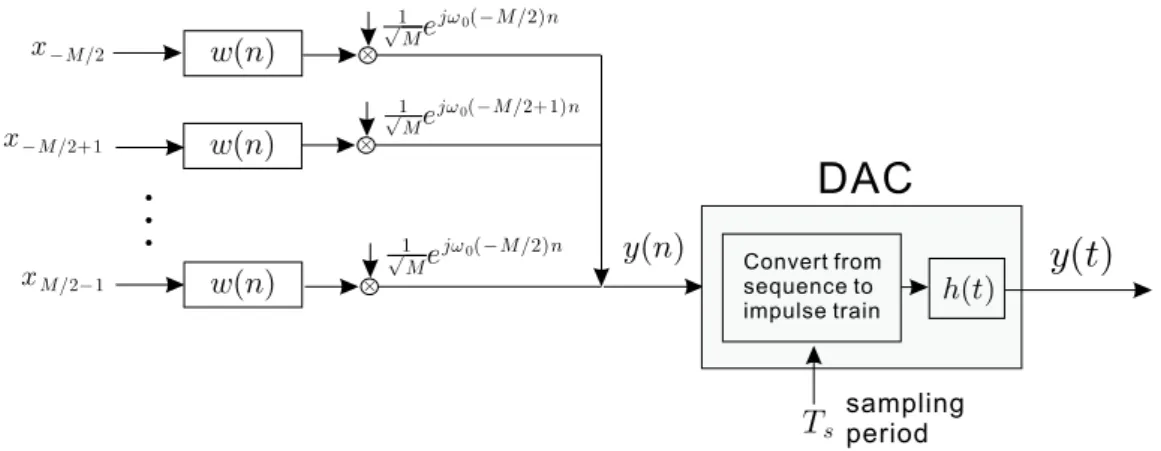
4.1 The OFDM transmitter with a digital clipper. . . 13

4.2 Equivalent model for digital clipping. . . 14

4.3 Digital modulator of the M subcarries for one-shot transmission. w(n) is the discrete window of lenth M and ω0 = 2π/M . . . . 15

4.4 digital-to-analog converter in the OFDM transmitter with digital clipper. . . 19

5.1 DFT-Based OFDM transmitter with analog clipper . . . 20

5.2 Equivalent model for DAC. . . 21

5.3 Equivalent model for analog clipping. . . 22

6.1 Frequency response of the pulse shaping filter p(t) in Fig. 1.1. . . 28

6.2 Frequency response of reconstruction filter h(t) in Fig. 1.2. . . . . 29

6.3 Average power spectral densities of the output of the two modu-lation models x(t) and y(t). . . . 29

6.4 Average power spectrum of the digital clipper output Sy,dc(ejω). . 31

6.5 Average power spectrum of the OFDM trasnmitter with digital clipper Sy,dc(ejΩ). The clipping ratio A/σyR = 0.1. . . . 32

(5)

6.6 Average power spectrum of the OFDM trasnmitter with digital clipper Sy,dc(ejΩ). The clipping ratio A/σyR = 0.5. . . . 32

6.7 Average power spectrum of the OFDM trasnmitter with digital clipper Sy,dc(ejΩ). The clipping ratio A/σyR = 1. . . 33

6.8 Average power spectrum of the OFDM trasnmitter with digital clipper Sy,dc(ejΩ). The clipping ratio A/σyR = 3. . . 33

6.9 Average power spectrum of the OFDM trasnmitter with analog clipper Sy,ac(jΩ). The clipping ratio A/σyR = 0.1. . . . 35

6.10 Average power spectrum of the OFDM trasnmitter with analog clipper Sy,ac(jΩ). The clipping ratio A/σyR = 0.5. . . . 36

6.11 Average power spectrum of the OFDM trasnmitter with analog clipper Sy,ac(jΩ). The clipping ratio A/σyR = 1. . . 36

6.12 Average power spectrum of the OFDM trasnmitter with analog clipper Sy,ac(jΩ). The clipping ratio A/σyR = 3. . . 37

6.13 Average power spectrum of the two OFDM trasnmitters with dig-ital and analog clipper, Sy,dc(jΩ) and Sy,ac(jΩ),respectively. The clipping ratio A/σyR = A/σyR = 1 . . . 37

6.16 Sy,ac(jΩ) with the clipper input under the WSS and WSCS as-sumption. The clipping ratio A/σ = A/σyR = 0.1. . . . 39

6.17 Sy,ac(jΩ) with the clipper input under the WSS and WSCS as-sumption. The clipping ratio A/σ = A/σyR = 0.5. . . . 40

6.18 Sy,ac(jΩ) with the clipper input under the WSS and WSCS as-sumption. The clipping ratio A/σ = A/σyR = 1. . . 40

(6)

as-Chapter 1

Introduciton

Orthogonal frequency-division multiplexing (OFDM) is an attractive transceiver scheme for its high transmission rate for the last several decades [1]-[3]. It has been well-adopted in many practical application, such as radio environment [4], mobile communications [5] and copper wired DSL application [6, 7]. In OFDM, large number of orthogonal subcarriers are used at the transmitter to transmit data, which can be achieved by inverse Discrete Fourier Transform (IDFT). In the similar way, Discrete Fourier Transform (DFT) demodulates the data at the receiver. The IDFT-DFT pair can be implemented by FFT algorithm which reduces the computational complexity. Easily achieved interblock interference (IBI) free is one of the major merits of the OFDM system. By inserting the guard interval, usually known for cyclic prefix (CP), at each block before transmitting, IBI can be removed if the channel order is not greater than the length of CP. Simple equalization is another advantage of the OFDM system. When coping with the frequency-selective channel, each subcarrier can be viewed as suffering a constant scaling if the subcarrier is enough narrow-banded, hence, the receiver needs only one-tap equalization.

One of the disadvantages in utilizing OFDM system is the large peak to aver-age power ratio (PAPR) of the OFDM signal. The large peak at the transmitter will cause the saturation in power amplifier and may suffer from poor power efficiency. Amounts of research have been presented to solve this problem. Sev-eral famous solutions such as selective mapping (SLM) [8], which multiplying the

(7)

specific sequence to the input signal, or partial transmit sequence (PTS) [9] that dividing the input signal into several subblocks then optimally joint them, they aim the target at how to reduce the probability of generating the large peaks. The drawbacks of these solutions are computational complicated and the side information is necessary.

One popular and convenient method is to clip or limit the peak amplitude of the OFDM signal to a maximum value, called clipping [10]. Clipping is widely used to reduce the large PAPR of the OFDM signals. Unfortunately, it brings the side effect called clipping noise, which is introduced additional out-of-band noise and degrades the performance of the system. Several schemes and investigations have been made to mitigate and analyze the clipping noise [11]-[16]. Though they are broadly adopted, several key problems take place on their modulation scheme and the assumption of the clipper input signal.

â â â x_{àM =2} x_{àM =2+1} x_M=2à1 p(t) p(t) p(t) M p1

e

jÒ0(àM=2)t M p1 ejÒ0(àM=2+1)t M p1

e

jÒ0(M=2à1)t

..

.

_x(t)

Figure 1.1: Analog representation of the OFDM transmitter.

The transmitter scheme applied in [11]-[14] is shown in Fig. 1.1 and the com-moly used digital communication of the OFDM transmitter is shown in Fig. 1.2.

p(t) in Fig. 1.1 is the pulse-shaping filter with length T0 = 2π/Ω0, and w(n) and h(t) are the transmitting window with M taps and reconstruction filter with natural frequency π/Ts, respectively. It is proved that these two kinds of schemes are equivalent only for special choices of p(t), w(n) and h(t) [17] and the spectral roll-off of x(t) and y(t) can be a significant difference. Hence, applying the analog

(8)

noise. â â â x_{àM =2} x_{àM =2+1} x_M=2à1 w(n) w(n) w(n) M p1 ej!0(àM=2)n M p1 ej!0(àM=2+1)n M p1 ej!0(àM=2)n

..

.

h(t) y(n)

_y(t)

DAC

Convert from sequence to impulse train Ts sampling period

Figure 1.2: Commonly used DFT-Based implementation of the OFDM transmit-ter, where ω0 = 2π/M

Another major problem is the inappropriate assumption of the clipper input signal. Under the assumption that clipper input is WSS, an analytical research of the clipping noise is given in [11, 16], however, is not appropriate for DFT-Based implementation and will underestimate the effect of the clipping noise.

In this thesis, we consider digital clipping and analog clipping in OFDM system. We begin from the model in Fig. 1.2, then digital or analog clipped are added, respectively. The clipper input y(t) is assumed to be a WSCS process now. In numerical simulation, the difference between the analog representation and DFT-Based implementation of the OFDM transmitter will be shown, especially in spectral roll-off. Also, we will demonstrate that the transmitted spectrum of the analog clipping spreads more widely than the digital clipping ones in different clipping ratio. We will show how that the clipping noise will be underestimated if we assume the clipper input signal is WSS.

1.1 Outline

• Chapter 2:A survey of previous works is given. Including showing the

(9)

of OFDM transmitter, and the analysis of clipping process under the as-sumption that clipper input signal is WSS, and illustration of the statistical property of DAC output signal when the DAC input is WSS.

• Chapter 3: Advanced analysis on DAC when DAC input is a WSCS process.

A similar result to the case that DAC input is WSS is derived.

• Chapter 4: Each block in the OFDM transmitter with digital clipper is

presented. The properties of the OFDM input signal is also introduced. Then, we make the discussions on the statistical properties of the modulator output signal, the digital clipper output signal and the output signal of the DAC. Thereafter, we focus on deriving their average autocorrelation.

• Chapter 5: The OFDM transmitter with analog clipper is shown, such

as transmitting window, DAC along with reconstruction filter and analog clipper. Next, the analysis on the statistical properties of the DAC output signal and the output signal of the analog clipper is given. Similarly, this average autocorrelation will be deduced.

• Chapter 6: The simulation will be given in this chapter, including that:

Showing the difference in spectral roll-off between the analog representation and DFT-Based implementation of the OFDM transmitter. Comparison of the average spectrum between analog clipping and digital clipping in different clipping ratio. How a different assumption of the clipper input signal affects the estimation of the clipping noise.

• Chapter 7: Conclusion.

1.2 Notation

1. <{·} denotes taking real part.

(10)

4. yR(n) represents that the real part of y(n), that is, <{y(n)}. 5. yI(n) represents that the imaginary part of y(n), that is, ={y(n)}. 6. δ(n) represents the kronecker delta function.

7. Q(x) is given by Q(x) =R_−∞x e−t2 dt.

8. The notation y(n) will be abbreviated as yn when applying mathematical deduction, especially the integration is applied.

1.3 Prerequisite [18]

1.3.1 Wide Sense Stationary Process

A random process x(n) is said to be wide sense stationary(WSS) if x(n) satisfies the following conditions:

1. E[x(n)] = mx,

2. E[x(n)x∗_{(n − k)] = R} x(k).

Mean function E[x(n)] is a constant independent of n and the autocorrelation function E[x(n)x∗_{(n − k)] depends on time difference k, not n. We define the} power spectrum of a WSS process as the Fourier transform of the autocorrelation function Rx(k), Sx(ejω) , ∞ X k=−∞ Rx(k)e−jωk.

For continuous time random processes, WSS property can be define in a similar manner. We say a continuous time random process y(t) is WSS if the mean function E[y(t)] is independent of t and the autocorrelation function E[y(t)y∗_(t−

τ )] only depends on τ . The power spectrum of a WSS process is defined as the

Fourier transform of the autocorrelation function,

Sy(jΩ) , Z _∞

−∞

(11)

1.3.2 Wide Sense Cyclostationary Process

A random process x(n) is said to be wide sense cyclostationary with period M (denoted by WSCS(M)) if it satisfies the following conditions:

1. E[x(n)] = E[x(n + M)],

2. E[x(n)x∗_{(n − k)] = E[x(n + M)x}∗_{(n + M − k)].}

These two properties represents that mean function E[x(n)] and the autocorre-lation function E[x(n)x∗_{(n − k)] is a periodic function of n with period M. We} define the average autocorrelation function as

Rx(k) , 1 M M −1_X n=0 E[x(n)x∗_{(n − k)].}

Also, we define the average power spectrum of a WSCS process as the Fourier transform of the average autocorrelation function,

Sx(ejω) , ∞ X k=−∞

Rx(k)e−jωk.

Similarly, we can define wide sense cyclostationary property for continuous time random process. We say a continuous time random process y(t) is wide sense cyclostationary with period T (denoted by WSCS(T )) if

1. E[y(t)] = E[y(t + T )],

2. E[y(t)y∗_{(t − τ )] = E[y(t + T )y}∗_{(t + T − τ )].}

Mean function E[y(t)] and the autocorrelation function E[y(t)y∗_{(t − τ )] is a} peri-odic function of t with period T . The average autocorrelation function is defined as Ry(τ ) , 1 Ts Z _T_s 0 E[y(t)y∗_{(t − τ )]dt.}

Then we define the average power spectrum of a WSCS process as the Fourier transform of the average autocorrelation function,

Sy(jΩ) , Z _∞

(12)

Chapter 2 A Survey of Previous Works

In this Chapter, we will introduce earlier analysis on analog and digital modula-tion process, clipping scheme and digital-to-analog conversion.

2.1 Analog Representation and DFT-Based

Im-plementation of OFDM Transmitter [17]

In this section, we reviewed the results relates to the analog and digital modulator, the explicit derivations are stated in [17].

Theorem 1 : Let the OFDM transmitter in Fig. 1.2 have a rectangular window

w(n)

w(n) =

½

1, 0 ≤ n ≤ M − 1 0, othewise

and an ideal lowpass reconstruction filter h(t) with H(jΩ) =

½

1, |Ω| < π Ts

0, othewise.

The outputs of the two systems, respectively, x(t) in Fig. 1.1 and y(t) in Fig. 1.2, are not the same for any choice of pulse shaping filter p(t).

Theorem 2 : The analog OFDM transmitter in Fig. 1.1 with a rectangular pulse

p(t) does not admit the DFT-based implementation in Fig. 1.2, regardless of the choices of w(n) and h(t).

(13)

Above two theorems state that for commonly used digital window, reconstruc-tion filter and pulse shaping filter, the analog representareconstruc-tion and DFT-based im-plementation of OFDM transmitter are not equivalent. The following theorem will show that these two transmitters are equivalent for only special cases. Theorem 3 : The OFDM transmitter in Fig. 1.1 can be implemented as in

Fig. 1.2, namely, the two systems are equivalent, if and only if the pulse shaping filter p(t), the digital window w(n), and the reconstruction filter h(t) satisfy

W (ejΩTs_{)H(j(Ω + kΩ}

0)) = G(jΩ), f or k = −M/2, −M/2 + 1, · · · , M/2 − 1.

2.2 Spectral Properties for a Clipped DMT ADSL

Signal [16]

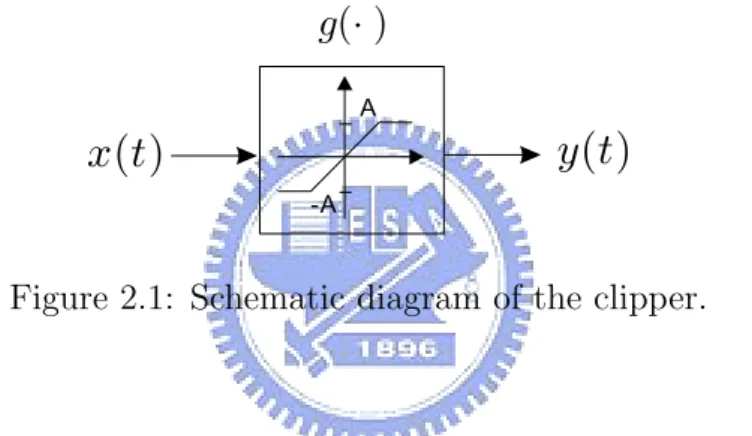
In this section, the analysis relates to the clipper is reviewed. The schematic diagram of the clipper is shown in Fig. 2.1. The clipper input signal x(t) is a DMT signal consists of a sum of modulated sinusoids which can be represented as a zero mean Gaussian random process. In addition, x(t) is assumed to be WSS with variance σ2_{. The clipping can be modeled by a clipping function g(·)} as follows y(t) = g(x(t)) =    A, x(t) ≥ A x(t), −A < x(t) < A −A, x(t) ≤ −A .

The statistics of the clipper output signal y(t) is developed in [16], which will be stated in the following theorem. The explicit derivations are also given in [16]. Theorem 4 : If the clipper input signal x(t) is a WSS, zero mean Gaussian

random process with variance σ2_{, and we suppose the autocorrelation function of}

x(t) is Rx(τ ), where Rx(0) = σ2, then the autocorrelation function of the clipper

output y(t) can be expressed as R (τ ) = R (0) · erf2 µ A √ ¶ r(τ ) + ∞ X C [r(τ )]n+1 ¸

(14)

where r(τ ) = Rx(τ )/Rx(0), erf(·) denotes the error function, the sum over the

index n is for even numbers only, and the distortion coefficients Cn is

Cn= 4H2 n−1(√A_2σ) π2n_{(n + 1)!} · exp ½ −A2 σ2 ¾

with Hn a Hermite polynomial of order n.

Notice that the first term of Ry(τ ) is usually called in-band signal which relates to the spectrum of the clipper input signal x(t), and the second term often named as clipping noise which comes from the clipping process and distorts the spectrum of clipper input signal.

x

(t)

y(t)

g

_{(á )}

-A A

Figure 2.1: Schematic diagram of the clipper.

2.3 DAC with WSS Input Signal [18, 19]

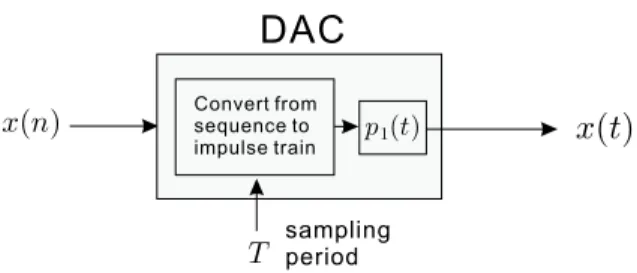
We will introduce previous investigations on a WSS signal passing through DAC in this section. The DAC scheme is shown in Fig. 2.2. The DAC input signal

x(n) is a WSS random process, p1(t) is the reconstruction filter and the sampling period of DAC is T . We will demonstrate that the DAC output signal x(t) becomes a WSCS process and give the expression of the average autocorrelation and average power spectrum of x(t). The explicit derivations have been shown in [18, 19].

Theorem 5 : Consider the DAC with a reconstruction filter p1(t) and sampling

period T as shown in Fig. 2.2. When the input signal x(n) is WSS, the output x(t) is a continuous time WSCS(T ) process, that is,

(15)

p1(t) x(n) _x(t)

DAC

Convert from sequence to impulse train T samplingperiod

Figure 2.2: Digital-to-analog conversion scheme.

Theorem 6 : When the input signal of DAC x(n) in Fig. 2.2 is WSS, the output

WSCS(T ) random process x(t) has an average autocorrelation Rx(τ ) = 1 T ∞ X k=−∞ Rx(k)f (τ − kT ) where Rx(τ ) , 1 T Z _T 0 E[x(t)x∗_{(t − τ )]dt} and Rx(k) = E[x(n)x∗(n − k)].

Then function f (τ ) is defined as

f (τ ) , p1(τ ) ∗ p1(−τ ) = R_−∞∞ p1(t)p1(t − τ )dt

where ∗ denotes convolution.

Taking the Fourier transform of the above conclusion, we obtain the average power spectrum of x(t) as Sx(jΩ) = 1 TSx(e jΩT_)|P 1(jΩ)|2,

(16)

Chapter 3 Advanced Analysis on DAC

In section 2.3, we demonstrate the autocorrelation of the output signal of DAC when the input signal is a WSS process. We now make an investigation on the DAC output signal x(t) in Fig. 2.2 while the input signal x(n) is a WSCS process. The following lemma will show that DAC output signal x(t) is still a WSCS process even the DAC input signal turns into a WSCS process.

Lemma 1 : If the DAC input x(n) in Fig. 2.2 is a WSCS(M) process, then the

DAC output x(t) in Fig. 2.2 is a WSCS(MT ) process, where T is the sampling period of DAC.

Proof: The explicit derivation will be given in Appendix A. 444

Next, we will demostrate the average autocorrelation of the DAC output signal

x(t), it can be seen that the expression is almost the same as the case that DAC

input signal is a WSS process.

Lemma 2 : When the input signal of DAC x(n) in Fig. 2.2 is WSCS(M), the

output WSCS(MT ) random process x(t) has an average autocorrelation Rx(τ ) = 1 T ∞ P k=−∞ Rx(k)f (τ − kT ), (3.1) where Rx(τ ) , _{M T}1 R_{M T} 0 E[x(t)x∗(t − τ )]dt (3.2) and Rx(k) = _M1 M −1_P k=0 E[x(n)x∗_{(n − k)].} _(3.3)

(17)

Then function f (τ ) in (3.1) is defined as

f (τ ) , p1(τ ) ∗ p1(−τ ) = R_−∞∞ p1(t)p1(t − τ )dt

(3.4)

(18)

Chapter 4 Transmitted Spectrum with

Digital Clipping

We aim our target at deriving Ry,dc(τ ) in this chapter. That is, we wish to derive the average autocorrelation of the signal ydc(t) in Fig. 4.1. Hence, the statistical properties of each output signal y(n), ydc(n), and ydc(t) in Fig. 4.1 should be discussed, and then the average autocorrelation Ry(k), Ry,dc(k), and Ry,dc(τ ) can be derived correspondingly.

4.1 System Model for Digital Clipping

â â â x_{àM =2} x_{àM =2+1} x_M=2à1 w(n) Ts w(n) w(n) M p1 ej!0(àM=2)n M p1 ej!0(àM=2+1)n M p1 ej!0(M=2à1)n

..

.

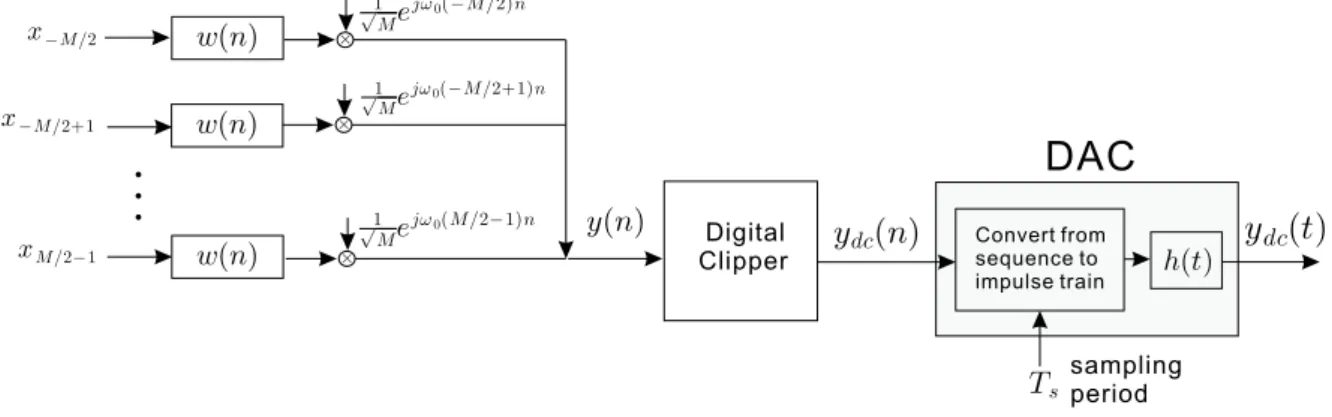
h(t) y(n) _Digital _y_dc_(n) _y_dc_(t) Clipper sampling period

DAC

Convert from sequence to impulse train

Figure 4.1: The OFDM transmitter with a digital clipper.

In this section, the system model used for digital clipping is presented. Fig. 4.1 is the commonly used DFT-Based OFDM transmitter with a digital clipper. The

(19)

first part performs the digital modulation of the M subcarriers with frequency spacing ω0 = 2π/M. The scalar √1_M is the normalized scaling. The input sequence of the OFDM system xk is a white, Gaussian distributed random process with zero mean and variance σ2

x. w(n) is a discrete window with real coefficients of length M. After digital modulating, y(n) is the modulator output as indicated in Fig. 4.1.

The second part carrying out the digital clipping. The digital clipper limits the real part of the clipper input sequence yR(n) and imaginary part of the clip-per input sequence yI(n) separately. The output signals of the limiting processes are ydc,R(n) and ydc,I(n), respectively. Combining both outputs sequence results in the digital clipper output sequence ydc(n). The clipping process can be equiv-alently modeled by two individual and identical clipping functions g(·) shown in Fig. 4.2. The clipping function g(·) is defined as

y = g(x) =    A, x ≥ A x, −A < x < A −A, x ≤ −A . (4.1) y(n) _y dc(n)

ñ

y(n) yR(n) g(á ) g(á ) ydc;R(n) yI(n) ydc;I(n) ydc(n) -A A -A A Digital Clipper

Figure 4.2: Equivalent model for digital clipping.

The last part of the OFDM transmitter with the digital clipper performs a digital-to-analog conversion, which converting the sequence to the impulse train, then passing through the reconstruction filter h(t) and the output signal ydc(t) is generated eventually . A reconstruction filter is usually a lowpass filter with real

(20)

4.2 Statistical Properties of the Modulator

Out-put Signal y(n)

In this section, we analyze the statistical properties of the modulator output signal y(n), including showing that y(n) is a WSCS process, and with jointly Gaussian distributed. â â â x_{àM =2} x_M=2à1

w(n)

M p1

e

j!0(àM=2)n M p1

e

j!0(àM=2+1)n M p1

e

j!0(M=2à1)n

..

.

_y(n)

x

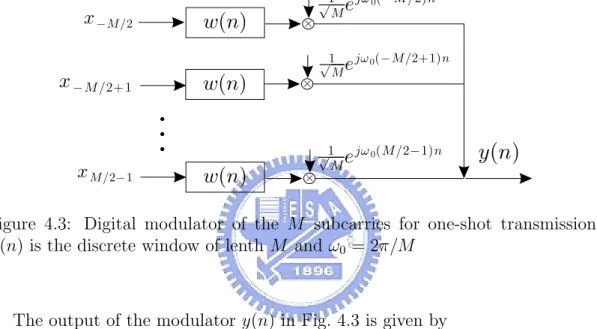
_{à M =2+ 1}

Figure 4.3: Digital modulator of the M subcarries for one-shot transmission.

w(n) is the discrete window of lenth M and ω0 = 2π/M

The output of the modulator y(n) in Fig. 4.3 is given by

y(n) = w(n) · _√1 M M 2P−1 k=−M 2 xk+B(n)M · ej 2π Mkn, ∀n ∈ Z (4.2)

where w(n) is the transmitting window with M coefficients, B(n) = bn

Mc is the block indicator. xkcan be expressed as ak+jbk, where akand bkcan be reasonably assumed that

E[alam] = E[blbm] = 1₂σx2δ(l − m)

E[albm] = 0 ∀l, m ∈ Z.

(4.3) Firstly, it can be shown that y(n) is a WSCS process under the assumption that xk is a white process.

Lemma 3 : If the input of the OFDM system xk is a white process, then the

(21)

is used, then y(n) is a WSCS process with period M, denoted as WSCS(M)

Proof: The explicit derivation will be given in Appendix C. 444

Secondly, we demonstrate the prrof that y(n) is a jointly Gaussian random process.

Lemma 4 : If xk is a jointly Gaussian random process, then y(n) in Fig. 4.3 is

also a jointly Gaussian random process.

Proof: Since y(n) = w(n) ·_√1 M M 2P−1 k=−M₂ xk+B(n)M· ej 2π

Mkn , which is a linear

com-bination of xk, therefore indeed a jointly Gaussian distributed random process.

444

4.3 Derivation of R

_y

(k)

We now derive Ry(k), which is the average autocorrelation of y(n) in Fig. 4.3. Lemma 5 : y(n) = w(n) · _√1 M M 2P−1 k=−M 2 xk+B(n)M · ej 2π Mkn , y_R(n) + jy_I(n), where

yR(n) = <{y(n)} and yI(n) = ={y(n)}. It can be shown that

1. yR(n) and yI(n) are uncorrelated, that is, E[yR(n)yI(m)] = 0, ∀n, m ∈ Z.

2. The joint pdf f (yR,n, yR,m, yI,n, yI,m) can be separated as

f (yR,n, yR,m, yI,n, yI,m) = f (yR,n, yR,m) · f (yI,n, yI,m)

3. E[yR(n)yR(m)] = E[yI(n)yI(m)] = 1₂σ2xw(n)w(m)δ(m − n).

4. Ry(k) = Ry,R(k) + Ry,I(k) = 1 M M −1_P n=0 σ2 xw(n)w(n − k)δ(k). where Ry(k) is defined as Ry(k) = 1 M M −1_X n=0 E[y(n)y∗(n − k)]

, which is a function independent of n.

(22)

4.4 Statistical Properties of the Digital Clipper

Output Signal y

dc

(n)

In this section, we discuss the statistical properties of the clipper output sig-nal ydc(n) in Fig. 4.2, including giving the proof that ydc,R(n) and ydc,I(n) are uncorrelated and showing that ydc(n) is also a WSCS process.

Lemma 6 : If the joint pdf f (yR,n, yR,n−k, yI,n, yI,n−k) = f (yR,n, yR,n−k)·f (yI,n, yI,n−k),

then the real and imaginary part in the output of the digital clipper, ydc,R(n) and

ydc,I(n) in Fig. 4.2, should be uncorrelated. Accordingly, we have

E[ydc(n)ydc∗ (n − k)] = E[ydc,R(n)ydc,R(n − k)] + E[ydc,I(n)ydc,I(n − k)].

Then obviously,

Ry,dc(k) = Ry,dc,R(k) + Ry,dc,I(k).

Notice that ydc,R(n) = g(yR(n)) ydc,I(n) = g(yI(n)) Ry,dc(k) = 1 M M −1_P n=0 E[ydc(n)y∗ dc(n − k)] Ry,dc,R(k) = _M1 M −1_P n=0 E[ydc,R(n)ydc,R(n − k)]. Ry,dc,I(k) = _M1 M −1_P n=0

E[ydc,I(n)ydc,I(n − k)].

Proof: The derivation will be given in Appendix E. 444

Lemma 7 : If the input sequence of the digital clipper y(n) is a Gaussian

dis-tributed WSCS(M) process, then the output sequence of the digital clipper ydc(n)

is also WSCS(M).

(23)

4.5 Derivation of R

y,dc

(k)

We then focus on the relationship between the input and the output of the digital clipper, i.e., y(n) and ydc(n) in Fig. 4.2, especially the relationship of the average autocorrelation. We then give the explicit derivation of Ry,dc(k).

Lemma 8 : If the digital clipper input signal y(n) is WSCS, then Ry,dc(k), the

average autocorrelation of clipper output signal ydc(n), can be expressed as

Ry,dc(k) = _M2 M −1_P n=0 erf (_√ A 2σ_yR,n)erf ( A √ 2σ_yR,n−k)E[yR,nyR,n−k] +2 M M −1_P n=0 ∞ P m=2,4,··· DmEm+1[yR,nyR,n−k] where Dm = 4Hm−1(√ A 2σyR,n)Hm−1( A √ 2σyR,n−k) π·2m_·(m+1)!·σm

yR,n·σyR,nm exp(−

A2 2σ2 yR,n) exp(− A2 2σ2 yR,n−k).

Proof: The explicit derivation will be given in Appendix G. 444

4.6 Statistical Properties of the DAC Output

Signal y

dc

(t)

We have shown the equation of Ry,dc(k), which is the average autocorrelation of the input singal of DAC ydc(n). In this section, we are going to make an analysis on the statistical properties of the DAC output signal ydc(t). We are going to show that the output of DAC ydc(t) is also a WSCS process, then the derivation average autocorrelation of the DAC output Ry,dc(τ ) would be stated in next section.

Lemma 9 : If the DAC input ydc(n) in Fig. 4.4 is a WSCS(M) sequence, then

the DAC output ydc(t) in Fig. 4.4 is a WSCS(MTs) process, where Ts is the

sam-pling period of DAC.

(24)

T

s h(t)

y

dc

(n)

y

dc

(t)

sampling period

DAC

Convert from sequence to impulse train

Figure 4.4: digital-to-analog converter in the OFDM transmitter with digital clipper.

4.7 Derivation of R

y,dc

(τ )

We then derive Ry,dc(τ ), the average autocorrelation of ydc(t) in Fig. 4.4.

Lemma 10 : If ydc(n) in Fig. 4.4 is a WSCS(M) sequence and ydc(t) is the

output signal that ydc(n) passing throug the DAC in Fig. 4.4, then

Ry,dc(τ ) = _T1_s ∞ P k=−∞ Ry,dc(k)f (τ − kTs), (4.4) where Ry,dc(τ ) , _{M T}1_s R_{M T}_s 0 E[ydc(t)ydc∗ (t − τ )]dt (4.5) and Ry,dc(k) = _M1 M −1_P k=0 E[ydc(n)y∗dc(n − k)]. (4.6) f (τ ) is defined as f (τ ) , h(τ ) ∗ h(−τ ) = R_−∞∞ h(t)h(t − τ )dt (4.7)

(25)

Chapter 5 Transmitted Spectrum with

Analog Clipping

In this chapter, our focus is to derive Ry,ac(τ ), i.e., to derive the average au-tocorrelation of the signal yac(t) in Fig. 5.1. Hence, the statistical properties of the each output signal y(n), y(t) and yac(t) in Fig. 5.1 should be discussed, then the average autocorrelation Ry(k), Ry(τ ) and Ry,ac(τ ) are able to be derived correspondingly. However, we have investigated the properties y(n) and derived the representation of Ry(k) in chapter 4, therefore, the following paragraph will be concentrated on the statistical properties of y(t), yac(t) and the derivation of

Ry(τ ) and Ry,ac(τ ). y(n) _y ac(t) y(t)

DAC

Ts sampling period Analog Clipper â â â x_{àM =2} x_{àM =2+1} x_M=2à1 w(n) w(n) w(n) M p1 ej!0(àM=2)n M p1 ej!0(àM=2+1)n M p1 ej!0(M=2à1)n

..

.

(26)

5.1 System Model for Analog Clipping

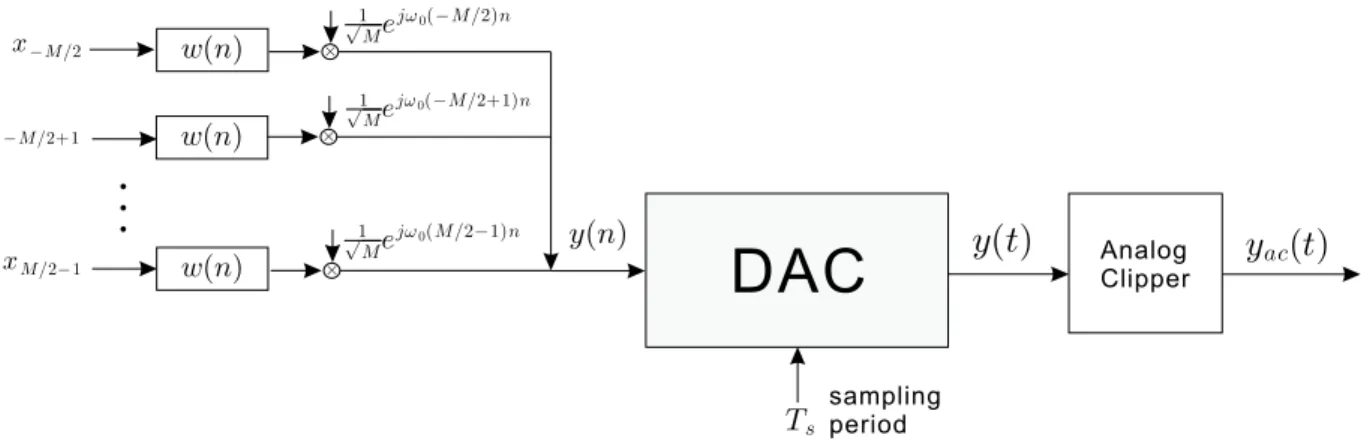
In this section, the system model used for analog clipping is presented. Fig. 5.1 is the commonly used DFT-Based OFDM transmitter with analog clipper. Similar to the structure in Fig. 4.1, the first part performs the digital modulation of the

M subcarriers with frequency spacing ω0 = 2π/M. The assumption of xk and the parameters of w(n) are the same as those in Fig. 4.1. y(n) is also the modulator output as indicated in Fig. 5.1.

ñ

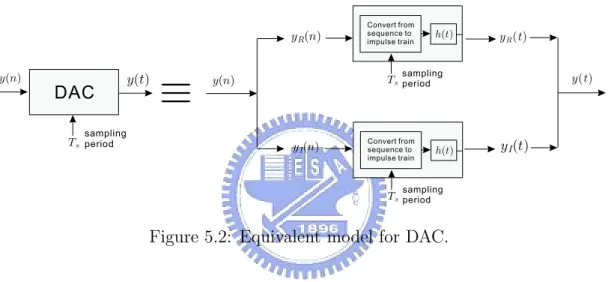
h(t) h(t) Convert from sequence to impulse train Convert from sequence to impulse train Ts Ts sampling period sampling period y(n) y(t) DAC Ts sampling period y(n) yR(n) yR(t) yI(n) yI(t) y(t)

Figure 5.2: Equivalent model for DAC.

The second part carrying out the digital-to-analog converting now. The struc-ture of the DAC is shown in Fig. 5.2, which applying digital-to-analog conversion individually on both the real part and imaginary part of the input signal, yR(n) and yI(n). And the output signal of the DAC y(t) is the combination of the output of the converted signal yR(t) and yI(t). The reconstruction filter h(t)and the sampling period Ts is the same as what we presented in section 4.1.

The last part is the analog clipper. It is similar that analog clipper limits the real part of the clipper input signal yR(t) and imaginary part of the clipper input sequence yI(t) separately. The output signal of the process are yac,R(t) and

yac,I(t), respectively. The output of the analog clipper yac(t) is the combination of yac,R(t) and yac,I(t). The clipping process can also be equivalently modeled by two individual and identical clipping functions g(·) shown in Fig. 5.3. The clipping function g(·) is defined in (4.1).

(27)

y(t) yac(t) y(t) yac(t)

ñ

yR(t) yac;R(t) yI(t) yac;I(t) Analog Clipper g(á ) g(á ) -A -A A A

Figure 5.3: Equivalent model for analog clipping.

5.2 Statistical Properties of the DAC Output

Signal y(t) and the Derivation of R

y

(τ )

In this section, the analysis on the statistical properties of the DAC output signal

y(t) in Fig. 5.2 is given. We are going to show that: yR(t) and yI(t) are uncor-rlated, y(t) is a Gaussian WSCS process, the joint pdf f (yR,t, yR,t−τ, yI,t, yI,t−τ) =

f (yR,t, yR,t−τ) · f (yI,t, yI,t−τ). Then, the derivation on the average autocorrelation of the DAC output Ry(τ ) are also to be shown in this section.

Lemma 11 : The real part and the imaginary part of the DAC output in Fig. 5.2,

yR(t) and yI(t), are uncorrelated. Thus,

E[y(t)y∗_{(t − τ )] = E[y}

R(t)yR(t − τ )] + E[yI(t)yI(t − τ )].

Proof: From Fig. 5.2, we have

yR(t) = ∞ P n=−∞ yR(n)h(t − nTs) yI(t − τ ) = ∞ P m=−∞ yI(m)h(t − τ − mTs). (5.1)

And their cross correlation will be

E[yR(t)yI(t − τ )] = ∞ P n=−∞ ∞ P m=−∞ E[yR(n)yI(m)]h(t − nTs)h(t − τ − mTs).

(28)

From Lemma 5, we know that E[yR(n)yI(m)] = 0, therefore, we have the first conclusion that E[yR(t)yI(t − τ )] = 0, ∀τ ∈ R.

Therefore, the autocorrelation of y(t) becomes

E[y(t)y∗_{(t − τ )] = E[} µ yR(t) + jyI(t) ¶µ yR(t − τ ) − jyI(t − τ ) ¶ ] = E[yR(t)yR(t − τ )] + E[yI(t)yI(t − τ )].

(5.3)

We have given the proof of all the statement. 444

We are going to demonstrate the proof that y(t) is a jointly Gaussian process and independence of the joint pdf.

Lemma 12 : The DAC output y(t) in Fig. 5.2 is a jointly Gaussian process and

the joint pdf

f (yR,t, yR,t−τ, yI,t, yI,t−τ) = f (yR,t, yR,t−τ) · f (yI,t, yI,t−τ).

Proof: From Fig. 5.2, we have

y(t) = yR(t) + jyI(t) = P∞ n=−∞ µ yR(n) + jyI(n) ¶ h(t − nTs). (5.4)

Since yR(n) and yI(n) are both jointly Gaussian distributed, therefore, y(t) is a linear combination of yR(n) and yI(n), which is a jointly Gaussian process. This is the demonstration of the first statement. And from Lemma 11, we know that

E[yR(t)yI(t − τ )] = 0, ∀τ ∈ R. (5.5) Hence, the joint pdf f (yR,t, yR,t−τ, yI,t, yI,t−τ) apparently turns into

f (yR,t, yR,t−τ, yI,t, yI,t−τ) = f (yR,t, yR,t−τ) · f (yI,t, yI,t−τ). (5.6)

444

Next, the proof the y(t) is a WSCS process is given. In fact, the following proof is based on the former deduction results.

(29)

Lemma 13 : The DAC output y(t) in Fig. 5.2 is a WSCS process with period

MTs.

Proof: This result is a direct conclusion from Lemma 1. 444

Now, the final paragraph of this section is to show the average autocorrealtion

Ry(τ ). The derivation is also based on the results in Chapter 3.

Lemma 14 : If y(n) is a WSCS(M) process and y(t) is the output signal that

y(n) passing throug the DAC in Fig. 5.2, then Ry(τ ) = _T1_s ∞ P k=−∞ Ry(k)f (τ − kTs), (5.7) where Ry(τ ) , _{M T}1_s R_MT_s 0 E[y(t)y∗(t − τ )]dt, (5.8) Ry(k) = _M1 M −1_P k=0 E[y(n)y∗_{(n − k)],} _(5.9) and f (τ ) is defined as f (τ ) , h(τ ) ∗ h(−τ ) = R_−∞∞ h(t)h(t − τ )dt, (5.10)

Proof: It is an apparent conclusion can be made from Lemma 2. 444

5.3 Statistical Properties of the Analog Clipper

Output Signal y

ac

(t) and the Derivation of

R

y,ac

(τ )

In this section, firstly we will show the statistical properties of the analog clipper output signal yac(t), more explicitly, to prove that E[yac,R(t)yac,I(t)] = 0, ∀t ∈ R. Then, the derivation of Ry,ac(τ ) will be given.

(30)

yac,I(t) in Fig. 5.3, should be uncorrelated. Accordingly, we have

E[yac(t)yac∗ (t − τ )] = E[yac,R(t)yac,R(t − τ )] + E[yac,I(t)yac,I(t − τ )].

Then obviously,

Ry,ac(τ ) = Ry,ac,R(τ ) + Ry,ac,I(τ ).

Notice that yac,R(t) = g(yR(t)) yac,I(t) = g(yI(t)) Ry,ac(τ ) = _{M T}1_s R_{M T}_s 0 E[yac(t)yac∗ (t − τ )]dt Ry,ac,R(τ ) = _{M T}1_s R_{M T}_s

0 E[yac,R(t)yac,R(t − τ )]dt.

Ry,ac,I(τ ) = 1 M Ts

R_{M T}_s

0 E[yac,I(t)yac,I(t − τ )]dt.

Proof: Since the analog clipper in Fig. 5.3 can be also modeled by the two identical and individual clipping function g(·), which are the same as digital clipper, and f (yR,t, yR,t−τ, yI,t, yI,t−τ) = f (yR,t, yR,t−τ) · f (yI,t, yI,t−τ) has been given in Lemma 12, therefore, the first conclusion can directly made from Lemma 6. Next, since

E[yac(t)yac∗ (t − τ )] = E[yac,R(t)yac,R(t − τ )] + E[yac,I(t)yac,I(t − τ )], (5.11) integration on both side still remains the same, that is,

1 M Ts

R_{M T}_s

0 E[yac(t)yac∗ (t − τ )]dt = M T1s

R_{M T}_s

0 E[yac,R(t)yac,R(t − τ )]dt + 1

M Ts

R_{M T}_s

0 E[yac,I(t)yac,I(t − τ )]dt, (5.12) Hence, according to the definition, we have

Ry,ac(τ ) = Ry,ac,R(τ ) + Ry,ac,I(τ ). (5.13)

444

Now we put the focus on deriving the average autocorrelation of yac(t) in Fig. 5.3, that is, derivation of Ry,ac(τ ).

(31)

Lemma 16 : If the analog clipper input signal y(t) is WSCS, then Ry,ac(τ ), the

average autocorrelation of clipper output signal yac(t), can be expressed as

Ry,ac(τ ) = _{M T}2_s R_{M T}_s

0 erf (√2σA_yR,t)erf ( A √ 2σ_yR,t−τ)E[yR,ty ∗ R,t−τ]dt + 2 M Ts R_{M T}_s 0 ∞ P m=2,4,··· DmEm+1[yR,tyR,t−τ]dt where Dm = 4Hm−1(√ A 2σyR,t)Hm−1( A √ 2σyR,t−τ) π·2m_·(m+1)!·σm

yR,t·σyR,t−τm exp(−

A2 2σ2 yR,t) exp(− A2 2σ2 yR,t−τ).

(32)

Chapter 6 Numerical Simulation

6.1 Spectrums of Analog Representation and

DFT-Based Implementation of OFDM

Transmit-ters

Notice that we mentioned before that analog representation and commonly used DFT-Based implementation OFDM transmitter differs in spectral roll-off [17], and hence it is improper to use the analog representation modeling to analyze the clipping noise. To see how much the difference is, we then display both the spectrum of x(t) and y(t) in Fig. 1.1 and Fig. 1.2.

Consider the DFT size M = 64. The OFDM input signal xk is a white, Gaussian distributed random process with zero mean and variance σ2

x. In the analog representation of the OFDM transmitter, p(t) is a rectangular pulse given by

p(t) =

½

1, 0 ≤ t < T0

0, o.w. . (6.1)

where T0 = 2π/Ω0. The frequency response of p(t) is shown in Fig. 6.1.

As to the commonly used DFT-Based implementation, the window w(n) in OFDM system realization is a discrete rectangular window with coefficients

w(n) =

½

1, 0 ≤ n ≤ M − 1

0, othewise . (6.2)

The reconstruction filter h(t) of the DAC is chosen to be a zero-order hold followed by a second-order elliptical filter [22], that is, h(t) = hZOH(t) ∗ hellip(t), where the

(33)

zero-order hold hZOH(t) can be expressed as

hZOH(t) = ½

1, 0 ≤ t < Ts

0, o.w. , (6.3)

where Ts is the sampling period, and the parameters of the elliptical filter hellip(t) as follows: Passband ripple size = 1 dB, stopband attenuation = 20 dB, and natural frequency = 0.5Ωs, where Ωs = 2π/Ts. We plot the frequency response of the reconstruction filter h(t) in Fig. 6.2.

Now we are able to compare the average power spectrum of the output of these two transmitters in Fig. 6.3. The maximum value of these two spectrums has been normalized to one and we can see that the spectral roll-off are quite different. Hence, analog representation modeling is not suitable for analyzing the out-of-band noise for its spectral roll-off is way imprecise from the commonly used model. −0.3 −0.2 −0.1 0 0.1 0.2 0.3 −40 −35 −30 −25 −20 −15 −10 −5 0 5 10 Frequency normalized by Ω_s. Frquency response (dB)

(34)

−3 −2 −1 0 1 2 3 −60 −50 −40 −30 −20 −10 0 10 Frequency normalized by Ω_s. Frquency response (dB)

Figure 6.2: Frequency response of reconstruction filter h(t) in Fig. 1.2.

−2 −1 0 1 2 −60 −50 −40 −30 −20 −10 0 10 20 Frequency normalized by Ω_s.

Normalized average spectrum (dB)

average spectrum of x(t) average spectrum of y(t)

Figure 6.3: Average power spectral densities of the output of the two modulation models x(t) and y(t).

(35)

6.2 Digital Clipping in OFDM system

We will use results derived in earlier chapters to plot the average power spectrum of proposed conclusion on the digital clipped OFDM signal.

We will use the models of the OFDM transmitter with digital and analog clipper in Fig. 4.1. The parameters of w(n) and h(t) are the same as the previous section. According to the block diagram in Fig. 4.2, we know that a digital clipper can be modeled by two identical and separate clipping functions g(·) that clips the real and imaginary part of the clipper input signal individually. The clipping function g(·) is as defined in (4.1).

Firstly, consider the parameters M = 64, the clipping ratio A/σyR,n can be

reduced to A/σx from (G.37), which is independent of the variable n. Hence, the notation n can be dropped. The spectrum of ydc(n), which is the digital clipper output in Fig. 4.1, is shown in Fig. 6.4. The clipping ratio A/σyR = 1. Notice

that ydc(n) is the digitally clipped signal of y(n). From Lemma 5, we know that the average autocorrelation of y(n) stated in (D.11) is

Ry(k) = _M1 M −1_P

n=0

σ2

xw(n)w(n − k)δ(k), (6.4)

since w(n) is a rectangular window, Ry(k) becomes σ2xδ(k) and its spectrum

Sy(ejω) is white. Hence, from (G.36), we know that Sy,dc(ejω), the average spec-trum the digital clipper output ydc(n), is also white with only scaling difference from Sy(ejω_).

Next, The average spectrum of ydc(t) is considered. Since Ry,dc(k) is a single pulse, Ry,dc(τ ) in (B.10) becomes

Ry,dc(τ ) = C Tsf (τ )

= C

Tsh(τ ) ∗ h(−τ )

(6.5) where C is a known constant from the combination of Hermite polynomials and

(36)

where H(jΩ) is the frequency response of the reconstruction filter h(t). The figures given in Fig. 6.5 -6.8 are the figures for clipping ratio 0.1, 0.5, 1, 3, respectively. The spectrum of In-band Signal is the first term in (G.36) which relates to the spectrum of clipper input signal. The spectrums of D2, D4 and D6 are the second term in (G.36) with m = 2, m = 4 and m = 6, which consists in clipping noise. We can see that as the clipping ratio increases, the in-band signal is enlarged and the clipping noise is suppressed.

−1 −0.5 0 0.5 1 −10 −5 0 5 Frequency normalized by π. Average spectrum (dB)

(37)

−2 −1 0 1 2 −100 −90 −80 −70 −60 −50 −40 −30 −20 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D 2 D 4 D 6

Figure 6.5: Average power spectrum of the OFDM trasnmitter with digital clip-per Sy,dc(ejΩ_{). The clipping ratio A/σy}

R = 0.1. −2 −1 0 1 2 −100 −90 −80 −70 −60 −50 −40 −30 −20 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D 2 D₄ D 6

Figure 6.6: Average power spectrum of the OFDM trasnmitter with digital clip-per Sy,dc(ejΩ). The clipping ratio A/σyR = 0.5.

(38)

−2 −1 0 1 2 −100 −90 −80 −70 −60 −50 −40 −30 −20 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D 2 D 4 D 6

Figure 6.7: Average power spectrum of the OFDM trasnmitter with digital clip-per Sy,dc(ejΩ_{). The clipping ratio A/σy}

R = 1. −2 −1 0 1 2 −100 −90 −80 −70 −60 −50 −40 −30 −20 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D 2 D₄ D 6

Figure 6.8: Average power spectrum of the OFDM trasnmitter with digital clip-per Sy,dc(ejΩ). The clipping ratio A/σyR = 3.

(39)

6.3 Analog Clipping in OFDM system

We will plot the average power spectrum of proposed conclusion on the analog clipped OFDM signal.

We will use the models of the OFDM transmitter with digital and analog clipper in Fig. 5.1. The parameters of w(n) and h(t) are the same as the previous section. According to the block diagram in Fig. 5.3, we know that an analog clipper can also be modeled by two identical and separate clipping functions g(·) that clips the real and imaginary part of the clipper input signal individually.

As to Ry,dc(τ ) in (H.36), since Em+1[yR,tyR,t−τ] convolves itself for m + 1 times in frequency domain, it is predictable that the spectrum of the OFDM tansmitter with the analog clipper output yac(t) will spread much more broadly then that ydc(t). However, (H.36) is not a closed form solution, hence, numerical computation is used to resolve the equation. Consider the case DFT size M = 64. The clipping ratio A/σyR,t here is a function of time t, therefore, we take the time

average on σyR,t, where the average clipping ratio is defined as

A/σyR , A √ <σ_yR,t> = A r lim β→∞ 1 β Rβ/2 −β/2σ2yR,tdt (6.7)

The figures given in Fig. 6.9 - 6.12 are the figure for clipping ratio 0.1, 0.5, 1, 3, respectively. The spectrum of In-band Signal is the first term in (H.36) which relates to the spectrum of clipper input signal. The spectrums of D2, D4 and D6 are the second term in (H.36) with m = 2, m = 4 and m = 6, which consists in clipping noise. A similar result to the digital clipping, as the clipping ratio increases, the in-band signal is enlarged and the clipping noise is suppressed. Before the end of this section, the comparisons between the ODFM transmitter with two clippers are also shown in Fig. 6.13-6.15. The clipping ratio for the figure are 1, 3, 10. We can see that the spectrum of the system with the analog clipper indeed spreads more broadly than the one with the digital clipper. Furthermore, the increasing the value of clipping ratio, the more similar the two spectrums. The reason why they become so similar due to that larger clipping ratio means

(40)

Fig. 5.1 are simply reduced to the model in Fig. 1.2. −2 −1 0 1 2 −70 −65 −60 −55 −50 −45 −40 −35 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D 2 D₄ D 6

Figure 6.9: Average power spectrum of the OFDM trasnmitter with analog clip-per Sy,ac(jΩ). The clipping ratio A/σyR = 0.1.

(41)

−2 −1 0 1 2 −70 −65 −60 −55 −50 −45 −40 −35 −30 −25 −20 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D 2 D 4 D 6

Figure 6.10: Average power spectrum of the OFDM trasnmitter with analog clipper Sy,ac(jΩ). The clipping ratio A/σyR = 0.5.

−2 −1 0 1 2 −70 −60 −50 −40 −30 −20 −10 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D 2 D₄ D 6

Figure 6.11: Average power spectrum of the OFDM trasnmitter with analog clipper Sy,ac(jΩ). The clipping ratio A/σyR = 1.

(42)

−2 −1 0 1 2 −70 −60 −50 −40 −30 −20 −10 Frequency normalized by Ω_s. Average spectrum (dB) In−band Signal D₂ D 4 D 6

Figure 6.12: Average power spectrum of the OFDM trasnmitter with analog clipper Sy,ac(jΩ). The clipping ratio A/σyR = 3.

−3 −2 −1 0 1 2 3 −70 −60 −50 −40 −30 −20 −10 Frequency normalized by Ω_s.

Average spectrum Sy,dc(jΩ)

Average spectrum Sy,ac(jΩ)

Figure 6.13: Average power spectrum of the two OFDM trasnmitters with dig-ital and analog clipper, Sy,dc(jΩ) and Sy,ac(jΩ),respectively. The clipping ratio

(43)

A/σyR = A/σyR = 3 . −3 −2 −1 0 1 2 3 −70 −60 −50 −40 −30 −20 −10 Frequency normalized by Ω_s.

(44)

6.4 Different Assumption for the Clipper Input

Signal

We mentioned that the inappropriate assumption of the clipper input signal also results in a imprecise analysis. In earlier investigations [11, 16], the clipper input signal is assumed to be WSS. According to Lemma 13, the clipper input signal

y(t) in Fig. 5.1 is not a WSS process but a WSCS process. If we assume the

clipper input signal y(t) in Fig. 5.1 is WSS, then the parameters σyR,t and σyR,t−τ

in (H.36) becomes a constant and 1

M Ts

R_{M T}_s

0 E[yR,tyR,t−τ]dt = E[yR,tyR,t−τ] = h(τ ) ∗ h(−τ ). (6.8) We denote σyR,t = σyR,t−τ = σ. This inadequate assumption will underestimate

the out-of-band noise. This effect is shown in Fig. 6.16- 6.19. We can observe that the out-of-band noise for WSCS case is greater than the WSS case, hence, one wish to mitigate the clipping noise especially on suppressing the out-of-band noise should not use the WSS assumption for design.

Sy,ac(jΩ) with WSS assumption

Sy,ac(jΩ) with WSCS assumption

Figure 6.16: Sy,ac(jΩ) with the clipper input under the WSS and WSCS assump-tion. The clipping ratio A/σ = A/σyR = 0.1.

(45)

−3 −2 −1 0 1 2 3 −70 −65 −60 −55 −50 −45 −40 −35 −30 −25 −20 Frequency normalized by Ω_s.

Figure 6.17: Sy,ac(jΩ) with the clipper input under the WSS and WSCS assump-tion. The clipping ratio A/σ = A/σyR = 0.5.

Figure 6.18: Sy,ac(jΩ) with the clipper input under the WSS and WSCS assump-tion. The clipping ratio A/σ = A/σyR = 1.

(46)

−3 −2 −1 0 1 2 3 −70 −60 −50 −40 −30 −20 −10 Frequency normalized by Ω s.

Figure 6.19: Sy,ac(jΩ) with the clipper input under the WSS and WSCS assump-tion. The clipping ratio A/σ = A/σyR = 3.

(47)

Chapter 7 Conclusion

In this thesis, we proposed the analysis of digital and analog clipping in OFDM system. The proposed analysis derives the autocorrelation of the two transmit-ters under the assumption the clipper input signal is WSCS. Simulation shows the difference of spectral roll-off between the modulators that are of analog repre-sentation and DFT-Based implementation . The spectrums of the OFDM trans-mitter with the digital and analog clipping are shown. The comparison shows that the OFDM transmitter with the analog clipper spreads more widely than digital clipper one in the spectrum. It is shown that digital clipping is a preferred choice especially when clipping ratio is small. The simulation also demonstrates that the assumption that the input signal of the clipper is WSS is inadequate and the clipping noise will be underestimated.

(48)

Appendix A

Proof of Lemma 1

From the block diagram in Fig. 2.2, we know that

x(t) = P∞

n=−∞

x(n)p1(t − nT ). (A.1)

Hence, the mean of x(t) and x(t + MT ) are

E[x(t)] = P∞ n=−∞ E[x(n)]p1(t − nT ), (A.2) E[x(t + MT )] = P∞ n=−∞ E[x(n)]p1(t + MT − nT ) = P∞ n=−∞ E[x(n + M)]p1(t − nT ). (A.3)

Since x(n) is a WSCS(M) process, we have

E[x(n)] = E[x(n + M)]. (A.4)

Therefore, (A.2) and (A.3) are the same, that is, their means are the same. We then check the autocorrelation of x(t) and x(t + MT )

E[x(t)x∗_{(t − τ )] =} P∞ n=−∞ ∞ P m=−∞ E[x(n)x∗_(m)]p 1(t − nT )p1(t − τ − mT ) (A.5)

(49)

E[x(t + MT )x∗_{(t − τ + MT )] =} P∞ n=−∞ ∞ P m=−∞ E[x(n)x∗_(m)]· p1(t − nT + MT )p1(t − τ − mT + MT ) = P∞ n=−∞ ∞ P m=−∞ E[x(n + M)x∗_{(m + M)]·} p1(t − nT )p1(t − τ − mT ) (A.6) For x(n) is WSCS(M), we also have

E[x(n)x∗_{(m)] = E[x(n + M)x}∗_{(m + M)].} _(A.7)

Hence, we also know that (A.5) and (A.6) are the same. From above two conclu-sion, we know that x(t) is a WSCS process with period MT .

(50)

Appendix B

Proof of Lemma 2

Rx(τ ) = 1 M T R_{M T} 0 E[x(t)x∗(t − τ )]dt. (B.1)

According to (A.5), we have

Rx(τ ) = _{M T}1 ∞ P n=−∞ ∞ P m=−∞ E[x(n)x∗_(m)]RM T 0 p1(t − nT )p1(t − τ − mT )dt. (B.2) Let m = n − k, (B.2) becomes Rx(τ ) = _T1 ∞ P k=−∞ 1 M µ ∞ P n=−∞ E[x(n)x∗_{(n − k)]·} R_{M T} 0 p1(t − nT )p1(t − τ − nT + kT )dt ¶ . (B.3)

(51)

Gathering M terms of index n in a group, we have Rx(τ ) = _T1 ∞ P k=−∞ 1 M µ · · · + P−1 n=−M E[x(n)x∗_{(n − k)]}RM T 0 p1(t − nT )p1(t − τ − nT + kT )dt + M −1P n=0 E[x(n)x∗_{(n − k)]}RM T 0 p1(t − nT )p1(t − τ − nT + kT )dt + 2M −1P n=M E[x(n)x∗_{(n − k)]}RM T 0 p1(t − nT )p1(t − τ − nT + kT )dt + · · · ¶ (B.4) The index of n can be changed as

Rx(τ ) = _T1 ∞ P k=−∞ 1 M µ · · · + M −1P n=0 E[x(n − M)x∗_{(n − k − M)]·} R_{M T} 0 p1(t − nT + MT )p1(t − τ − nT + kT + MT s)dt + M −1P n=0 E[x(n)x∗_{(n − k)]}RM T 0 p1(t − nT )p1(t − τ − nT + kT )dt + M −1P n=0 E[x(n + M)x∗_{(n − k + M)]·} R_{M T} 0 p1(t − nT − MT )p1(t − τ − nT + kT − MT )dt + · · · ¶ , (B.5) we know that x(n) is a WSCS(M) process, therefore,

(52)

Then (B.5) is reduced as Rx(τ ) = _T1 ∞ P k=−∞ 1 M µ · · · + M −1P n=0 E[x(n)x∗_{(n − k)]·} R_{M T} 0 p1(t − nT + MT )p1(t − τ − nT + kT + MT s)dt + M −1P n=0 E[x(n)x∗_{(n − k)]}RM T 0 p1(t − nT )p1(t − τ − nT + kT )dt + M −1P n=0 E[x(n)x∗_{(n − k)]·} R_{M T} 0 p1(t − nT − MT )p1(t − τ − nT + kT − MT )dt + · · · ¶ . (B.7) Moreover, the intervals of the integrals can also be changed, then (B.7) becomes

Rx(τ ) = _T1 ∞ P k=−∞ 1 M µ · · · + M −1P n=0 E[x(n)x∗_{(n − k)]}R2M T M T p1(t − nT )p1(t − τ − nT + kT )dt + M −1P n=0 E[x(n)x∗_{(n − k)]}RM T 0 p1(t − nT )p1(t − τ − nT + kT )dt + M −1P n=0 E[x(n)x∗_{(n − k)]}R0 −M T p1(t − nT )p1(t − τ − nT + kT )dt + · · · ¶ , (B.8)

(53)

We collect all the other intervals of the integrals, (B.8) results in Rx(τ ) = _T1 ∞ P k=−∞ 1 M M −1_P n=0 E[x(n)x∗_{(n − k)]} µ · · · + R_{M T}2M T p1(t − nT )p1(t − τ − nT + kT )dt + R₀M Tp1(t − nT )p1(t − τ − nT + kT )dt + R_{−M T}0 p1(t − nT )p1(t − τ − nT + kT )dt + · · · ¶ , (B.9)

then the conclusion can derived as

Rx(τ ) = _T1 ∞ P k=−∞ µ 1 M M −1_P n=0 E[x(n)x∗_{(n − k)]} ¶ · µ R_∞ −∞p1(t − nT )p1(t − τ − nT + kT )dt ¶ = 1 T ∞ P k=−∞ µ 1 M M −1_P n=0 E[x(n)x∗_{(n − k)]} ¶ · µ R_∞ −∞p1(t)p1(t − τ + kT )dt ¶ = 1 T ∞ P k=−∞ Rx(k) · R_∞ −∞p1(t)p1(t − (τ − kT ))dt = 1 T ∞ P k=−∞ Rx(k)f (τ − kT ) (B.10)

(54)

Appendix C

Proof of Lemma 3

At the beginning, we wish to show that E[y(n)] = E[y(n + m)].

E[y(n)] = w(n) · _√1 M M 2P−1 k=−M₂ E[xk+B(n)M]ej 2π Mkn = 0 E[y(n + M)] = w(n) · _√1 M M 2P−1 k=−M 2 E[xk+B(n+M )M]ej 2π Mk(n+M ) = 0 (C.1)

Next, we are going to show that E[y(n)y∗_{(m)] = E[y(n + M)y}∗_{(m + M)].}

E[y(n)y∗_{(m)] = E[} µ w(n) ·_√1 M M 2P−1 k=−M 2 xk+B(n)Mej 2π Mkn ¶ · µ w∗_{(m) ·} _√1 M M 2P−1 l=−M 2 x∗ l+B(m)Me−j 2π Mlm ¶ ] = 1 Mw(n)w∗(m) M 2P−1 k=−M₂ M 2P−1 l=−M₂ E[xk+B(n)Mx∗_l+B(m)M] · ej 2π M(kn−lm) (C.2) We know that xk is a white sequence and possesses the property that

(55)

therefore, (C.2) becomes E[y(n)y∗_{(m)] =} 1 Mσx2w(n)w∗(m) M 2P−1 k=−M 2 M 2P−1 l=−M 2 δ(k − l + (B(n) − B(m))M)· ej2π M(kn−lm). (C.4) Now we make an observation on E[y(n + M)y∗_{(m + M)].}

E[y(n + M)y∗_{(m + M)]} = E[ µ w(n + M) ·_√1 M M 2P−1 k=−M₂ xk+B(n+M )Mej 2π Mk(n+M ) ¶ · µ w∗_{(m + M) ·} _√1 M M 2P−1 l=−M₂ x∗ l+B(m+M )Me−j 2π Ml(m+M ) ¶ ] = 1 Mσ2xw(n + M)w∗(m + M) M 2P−1 k=−M 2 M 2P−1 l=−M 2 δ(k − l + (B(n + M) − B(m + M))M)· ej2π M(k(n+M )−l(m+M ) (C.5) Since B(n) = bn

Mc, it is evident that B(n + M) = B(n) + 1, hence, (C.5) results in E[y(n + M)y∗_{(m + M)]} = 1 Mσ2xw(n + M)w∗(m + M) M 2P−1 k=−M 2 M 2P−1 l=−M 2 δ(k − l + (B(n) + 1 − (B(m) + 1))M)· ej2π M(kn−lm+(k−l)M ) = 1 Mσ2xw(n + M)w∗(m + M) M 2P−1 k=−M 2 M 2P−1 l=−M 2 δ(k − l + (B(n) − B(m))M)· ej2π M(kn−lm). (C.6) Since the same window is used in each block, that is, w(n) = w(n + M), ∀n, therefore in (C.4) and (C.6), we have E[y(n)y∗_{(m)] = E[y(n + M)y}∗_{(m + M)],} and from (C.1), we know E[y(n)] = E[y(n + M)], thus the conclusion is made.

(56)

Appendix D

Proof of Lemma 5

Define α(k, n) as α(k, n) , w(n)xk+B(n)M = αR(k, n) + jαI(k, n) (D.1) where αR(k, n) = w(n)ak+B(n)M , αI(l, m) = w(m)bl+B(m)M. (D.2) Then from (4.3), we can derive that

E[αR(k, n)αI(l, m)] = w(n)w(m)E[ak+B(n)Mbl+B(m)M] = 0 E[αR(k, n)αR(l, m)] = E[αI(k, n)αI(l, m)] = 1 2σ2xw(n)w(m)δ(k − l + (B(n) − B(m))M). (D.3)

Now, we focus on yR(n) and yI(n),

yR(n) = √1_M M 2P−1 k=−M 2 αR(k, n) cos2π_Mkn − αI(k, n) sin2π_Mkn yI(m) = √1_M M 2P−1 l=−M 2 αR(l, m) sin2π_Mlm + αI(l, m) cos2π_Mlm (D.4)

And the cross correlation between yR(n) and yI(n) would be

E[yR(n)yI(m)] = _2M1 σx2w(n)w(m) M 2P−1 k=−M₂ M 2P−1 l=−M₂ δ(k − l + (B(n) − B(m))M)· (cos2π

Mkn sin2πMlm − sin 2πMkn cos2πMlm).

(57)

Since −M + 1 ≤ k − l ≤ M − 1, it is obvious that delta function takes value with only k = l and B(n) = B(m), consequently, (D.5) becomes

E[yR(n)yI(m)] = _2M1 σx2w(n)w(m) M 2P−1 k=−M₂ sin2π Mk(m − n) = 1 2Mσx2w(n)w(m) M −1_P k=0 sin2π Mk(m − n) = 1 2Mσx2w(n)w(m)={ M −1_P k=0 ej2π Mk(m−n)} = 1 2Mσx2w(n)w(m)={1−e j2π(m−n) 1−ej 2πM (m−n)}. (D.6)

Under the condition B(n) = B(m), we have −M + 1 ≤ m − n ≤ M − 1, for this reason, ={1−ej2π(m−n)

1−ej 2πM (m−n)} = ={Mδ(m − n)} = 0. Thus, the first conclusion

E[yR(n)yI(m)] = 0, ∀n, m ∈ Z is made.

Secondly, From Lemma 4 and the previous conclusion, we know that y(n) is jointly Gaussian distributed and E[yR(n)yI(m)] = 0, ∀n, m ∈ Z, therefore, the joint pdf f (yR,n, yR,m, yI,n, yI,m) evidently turns into

f (yR,n, yR,m, yI,n, yI,m) = f (yR,n, yR,m) · f (yI,n, yI,m) (D.7) This is the conclusion of the second statement.

Next, we concentrate on both the autocorrelations of yR(n) and yI(n).

E[yR(n)yR(m)] = _2M1 σx2w(n)w(m) M 2P−1 k=−M₂ M 2P−1 l=−M₂ δ(k − l + (B(n) − B(m))M)· (cos 2π

Mkn cos2πMlm + sin2πMkn sin2πMlm)

= 1 2Mσx2w(n)w(m) M 2P−1 k=−M₂ cos2π Mk(n − m) = 1 2Mσx2w(n)w(m)<{Mδ[m − n]} = 1 2σx2w(n)w(m)δ[m − n]

數位式剪波器與類比式剪波器在正交分頻多工系統下之分析

Analysis of Digital Clipping and

Analog Clipping for OFDM

system

Student : Chun-Lin Yang

Advisor : Yuan-Pei Lin

Department of Electrical and Control Engineering

National Chiao Tung University

Contents

List of Figures

as-Chapter 1

Introduciton

e

e

..

.

x(t)

..

.

y(t)

DAC

1.1

Outline

1.2

Notation

1.3

Prerequisite [18]

1.3.1

Wide Sense Stationary Process

1.3.2

Wide Sense Cyclostationary Process

Chapter 2

A Survey of Previous Works

2.1

Analog Representation and DFT-Based

Im-plementation of OFDM Transmitter [17]

2.2

Spectral Properties for a Clipped DMT ADSL

Signal [16]

x

(t)

y(t)

g

(á )

2.3

DAC with WSS Input Signal [18, 19]

DAC

Chapter 3

Advanced Analysis on DAC

Chapter 4

Transmitted Spectrum with

Digital Clipping

4.1

System Model for Digital Clipping

..

.

DAC

ñ

4.2

Statistical Properties of the Modulator

Out-put Signal y(n)

w(n)

w(n)

w(n)

e

e

e

..

.

y(n)

x

4.3

Derivation of R

(k)

4.4

Statistical Properties of the Digital Clipper

Output Signal y

(n)

4.5

Derivation of R

_x(t)

_y(t)

_{(á )}

_y(n)