應用ARIMA與GARCH模式於台灣運輸產業股價之預測

國

立

交

通

大

學

運 輸 科 技 與 管 理 學 系

碩 士 論 文

應用

ARIMA 與 GARCH 模式於台灣運輸產業股價之預測

The Stock Price Forecasting of Transportation Industry in

Taiwan with ARIMA and GARCH Models

研

究 生：蔡 明 翰

指導教授：高 凱 博士

應用

ARIMA 與 GARCH 模式於台灣運輸產業股價之預測

研究生：蔡明翰 指導教授：高凱 博士

論文摘要

藉由預測可以得知未來可能變化，提供決策者資訊上的參考。本研究使用定量分 析，應用時間序列中ARIMA (Autoregressive Integrated Moving Average； Box & Jenkins， 1976)模式分析法，以及實證上最常使用的 ARCH (Autoregressive Conditional

Heteroscedasticity；Engle，1982)模式與 GARCH (Generalized Autoregressive Conditional Heteroscedasticity；Bollerslev，1986)模式於台灣運輸產業的股票價格，期能達到良好預 測績效，並做不同模式預測能力的比較。 傳統上一般線性迴歸之基本假設，為殘差具有白噪音(White noise)的統計性質，但 實證研究已發現許多總體經濟與財務的變數資料，皆與自身前幾期變數或與殘差項有 關，且呈現非定態(Non-Stationary)時間序列的特性，因而有了 ARIMA(p,d,q)模式，且過 去的文獻也發現許多財務與經濟的時間序列，具有高狹峰分配(Leptokurtic)與波動叢聚 (Volatility Clustering)的現象，這與一般常態分配和變異數不隨時間變化的性質不同，因 而有了GARCH 模式。 本研究將就 1999~2006 共八年間，既有的台灣加權指數運輸類股股價的公開資訊日 資料，依據不同類股的股價，將其取對數之差呈股價報酬率，若非定態則以差分方式平 穩化時間序列後，建構出預測模式，再將模式的預測值與2007 年間的觀測值做比較， 預測績效的指標由相關統計指標驗證，且做運輸類四家個股，在不同模式的股價預測能 力比較。 研究發現考量異質變異數的 AR(1)-GARCH(1,1)模式，在該類股具有異質變異的特 性時，較原先的AR(1)模式能提高預測能力，且當預測期間引入 2008 年，研究建構的 模式仍然有很好的預測能力。 關鍵字：時間序列、ARIMA、GARCH、股價預測

The Stock Price Forecasting of Transportation Industry in Taiwan with

ARIMA and GARCH Models

Student: Ming-Han Tsai Advisor: Dr. Kai Kao

Abstract

From forecast we may know the possible changes in the future, providing information references for policy-makers. This research use quantitative analysis, applying time series models to stock price forecasting of transportation industry in Taiwan.

We apply the Autoregressive Integrated Moving Average models proposed by Box& Jenkins(1976) and various volatility models, namely, the Autoregressive Conditional Heteroscedasticity(ARCH) models proposed by Engle(1982) and Generalized ARCH proposed by Bollerslev(1986). We expect to achieve good forecast results and compare the predictive ability of different models.

The traditional linear regressions assume that residuals have the white noise statistical nature. But the empirical studies have discovered that many financial and economic data, are not independent among returns of nearby days. These data have the non-stationary time series characteristic and leptokurtic and volatility clustering. The property can be explained by changes through time in volatility. The non-normal distribution assumption of GARCH model can successfully capture these general properties of returns.

We found that AR(1) model and AR(1)-GARCH(1,1) model are appropriate to

investigate empirically the statistical attributes of daily stock price changes from 1999 to 2006 in Taiwan’s transportation industries. And the latter has the good predictive ability, but

different models on different stocks do not have uniform result. When out-of-sample change, the models still to have good predictability.

致謝辭

想不到研究所兩年這麼快就過去了，時間的飛逝令人不勝唏噓，儘管

當中遭遇了些許波折，我的碩班生活與論文，終究是在這鳳凰花開的時節，

平靜的結束了，而我能夠求學至今並拿到碩士學位，首先要感謝的，就是

栽培我、養育我的父母，還有姊姊、哥哥，我親愛的家人們，是我做任何

事的動力與依靠的對象，希望我們家能夠一直像現在這樣，健康、幸福的

生活。

我在碩士班的這段期間，感謝指導教授高凱老師的辛勤指導，不敢說

從老師的寶庫中得到很多知識，但學習過程中的成長與面對事情獨立思考

的態度，是我人生不可或缺也是無可替代的經驗，再次感謝老師的指導，

也很高興成為老師碩士班的閉門弟子，即使再唸碩班一次，我也仍會選擇

高凱實驗室，因為這是正確的決定。

感謝實驗室唯一的夥伴，也一直幫助我的家銘學長，是個人很有耐性

的好好先生，感謝你幫助我這個學弟，解決許多問題，也預祝你拿到博士

學位，早日成為大學教授，實現自己的理想。另外碩士班的交大同學們與

我清大的大學時期朋友們，感謝你們陪我度過這段時間，有高興也有不愉

快，有學習也有玩樂，這最後的學生生涯，是值得的，希望畢業後各奔前

程，也能有所聯絡，十數年後，今日生活的點滴，仍是不可忘卻的記憶，

在腦海中迴盪不已。

最後，希望自己能夠繼續努力，碩士班的學習，只是人生中的一個過

程，還是要朝自己的目標前進，能夠將遇到的問題，妥善的解決，與人相

處間的圓融，都是我要改進的方向。

感謝大家!明翰會期許自己再加油，圓滿並有意義的過每一天，也祝福

我們都能平安喜樂!謝謝!

蔡明翰 於新竹交大綜合一館 十樓研究室 民國九十八年 六月

目錄

圖目錄... Ⅵ 表目錄... Ⅷ 第一章 緒論... 1 1.1 研究背景與動機 ...1 1.2 研究目的 ... 1 1.3 研究架構與建模流程 ... 2 第二章 文獻回顧... 7 2.1 效率市場與隨機漫步國內外相關之研究 ... 7 2.1.1 國外相關文獻... 7 2.1.2 國內相關文獻... 9 2.2 股價報酬率與條件異質變異數相關之研究 ... 9 2.2.1 國外相關文獻... 9 2.2.2 國內相關文獻... 10 第三章 研究方法 ... 13 3.1 ARIMA 模型推導... 13 3.1.1 定態型隨機過程... 13 3.1.2 離散型線性隨機過程... 14 3.1.3 自我迴歸過程... 14 3.1.4 移動平均過程... 15 3.1.5 混合自我迴歸移動平均過程... 15 3.1.6 自我迴歸整合移動平均模型... 15 3.2 ARIMA 模型階次與差分次數... 16 3.2.1 自我共變異數與自我相關函數... 16 3.2.2 單位根檢定... 17 3.3 ARMA 模型檢定與估計 ... 18 3.3.1 Q 統計量... 18 3.3.2 JB 統計量... 18 3.3.3 DW 統計量 ... 19

3.4 ARMA 模型的選擇 ... 19 3.5 ARCH 模型與 GARCH 模型 ... 20 3.6 ARCH 模型的推導 ... 21 3.7 ARCH 模型檢定與估計 ... 22 3.7.1 ARCH-LM 檢定 ... 22 3.7.2 2 Q 檢定 ... 22 第四章 實證分析... 23 4.1 長榮海運 ... 23 4.2 中華航空 ... 42 4.3 萬海航運 ... 48 4.4 長榮航空 ... 52 4.4 研究結果分析 ... 57 第五章 結論與建議... 60 5.1 研究結論 ... 60 5.2 後續研究建議 ... 61 參考文獻... 63

圖目錄

圖1. 1 研究架構圖 ... 3 圖1. 2 研究建模圖 ... 4 圖4. 1 長榮海運股價原始序列Z 趨勢圖 ... 23 _t 圖4. 2 長榮海運股價對數序列Y 趨勢圖 ... 24 t 圖4. 3 長榮海運股價原始與對數序列趨勢比較圖 ... 24 圖4. 4 長榮海運時間序列Y 之自我相關圖 ... 25 _t 圖4. 5 長榮海運時間序列W 之自我相關圖 ... 27 _t 圖4. 6 長榮海運 AR(1)無截距項模式預測結果圖... 28 圖4. 7 長榮海運 AR(1)有截距項模式預測結果圖... 29 圖4. 8 長榮海運 AR(2)無截距項模式預測結果圖... 30 圖4. 9 長榮海運 AR(2)有截距項模式預測結果圖... 31 圖4. 10 長榮海運股價報酬率變動圖 ... 34 圖4. 11 長榮海運時間序列W 殘差之自我相關圖 ... 34 t 圖4. 12 長榮海運時間序列W 殘差之統計分配圖 ... 35 t 圖4. 13 長榮海運 AR(1)-GARCH(1,1)無截距項模式殘差之自我相關圖... 36 圖4. 14 長榮海運 AR(1)-GARCH(1,1)無截距項模式殘差平方之自我相關圖.. 36 圖4. 15 長榮海運 AR(1)-GARCH(1,1)無截距項模式預測結果圖... 37 圖4. 16 長榮海運 AR(1)-GARCH(1,1)有截距項模式預測結果圖... 38 圖4. 17 長榮海運 AR(2)-GARCH(1,1)無截距項模式預測結果圖... 39 圖4. 18 長榮海運 AR(2)-GARCH(1,1)有截距項模式預測結果圖... 40 圖4. 19 中華航空股價原始序列Z 趨勢圖 ... 42_t 圖4. 20 中華航空股價對數序列Y 趨勢圖 ... 42t 圖4. 21 中華航空股價原始與對數序列趨勢比較圖 ... 43 圖4. 22 中華航空時間序列Y 之自我相關圖 ... 43_t 圖4. 23 中華航空 AR(1)無截距項模式預測結果圖... 46 圖4. 24 中華航空 AR(1)-GARCH(1,1)無截距項模式預測結果圖... 47 圖4. 25 萬海航運 AR(1)無截距項模式 2007 年預測結果圖... 48 圖4. 26 萬海航運 AR(1)無截距項模式 2007~2008 年預測結果圖... 49 圖4. 27 萬海航運 AR(1)-GARCH(1,1)無截距項模式 2007 年預測結果圖... 50

圖4. 28 萬海航運 AR(1)-GARCH(1,1)無截距項模式 2007~2008 預測結果圖.. 51 圖4. 29 長榮航空 AR(1)無截距項模式 2007 年預測結果圖... 52 圖4. 30 長榮航空 AR(1)無截距項模式 2007~2008 年預測結果圖... 53 圖4. 31 長榮航空 AR(1)-GARCH(1,1)無截距項模式 2007 年預測結果圖... 54 圖4. 32 長榮航空 AR(1)-GARCH(1,1)無截距項模式 2007~2008 預測結果圖.. 55

表目錄

表4. 1 長榮海運時間序列Y 單位根檢定表 ... 26 t 表4. 2 長榮海運時間序列W 單位根檢定表 ... 26 _t 表4. 3 長榮海運 AR(1)無截距項模式估計結果表... 28 表4. 4 長榮海運 AR(1)有截距項模式估計結果表... 29 表4. 5 長榮海運 AR(2)無截距項模式估計結果表... 30 表4. 6 長榮海運 AR(2)有截距項模式估計結果表... 31 表4. 7 長榮海運 AR 模式不同階次與有無截距項之對數股價預測比較表... 32 表4. 8 長榮海運樣本內資料不同年度區間原始股價資料表 ... 33 表4. 9 長榮海運股價、對數股價、股價報酬率基本資料分析表 ... 33 表4. 10 長榮海運 AR(1)-GARCH(1,1)無截距項模式估計結果表... 35 表4. 11 長榮海運 AR(1)-GARCH(1,1)有截距項模式估計結果表 ... 37 表4. 12 長榮海運 AR(2)-GARCH(1,1)無截距項模式估計結果表... 38 表4. 13 長榮海運 AR(2)-GARCH(1,1)有截距項模式估計結果表... 39 表4. 14 長榮海運 GARCH 模式不同階次與有無截距項預測能力比較表 ... 41 表4. 15 中華航空時間序列Y 單位根檢定表 ... 44 _t 表4. 16 中華航空時間序列W 單位根檢定表 ... 45 _t 表4. 17 中華航空 AR(1)無截距項模式估計結果表... 45 表4. 18 中華航空 AR(1)-GARCH(1,1)無截距項模式估計結果表... 46 表4. 19 萬海航運 AR(1)無截距項模式估計結果表... 48 表4. 20 萬海航運 AR(1)-GARCH(1,1)無截距項模式估計結果表... 49 表4. 21 長榮航空 AR(1)無截距項模式估計結果表... 52 表4. 22 長榮航空 AR(1)-GARCH(1,1)無截距項模式估計結果表... 53 表4. 23 萬海航運 AR(1)模式不同預測期間下預測能力比較表... 56 表4. 24 長榮航空 AR(1)模式不同預測期間下預測能力比較表... 56 表4. 25 萬海航運 AR(1)-GARCH(1,1)模式不同預測期間下預測能力比較表.. 57 表4. 26 長榮航空 AR(1)-GARCH(1,1)模式不同預測期間下預測能力比較表.. 57 表4. 27 AR(1)模式不同公司預測能力比較表... 58 表4. 28 AR(1)-GARCH(1,1)模式不同公司預測能力比較表... 58

第一章 緒論

1.1 研究背景與動機

台灣加權股價指數一般受到很多因素影響，包含國內各項總體經濟因素，如景氣循 環、物價膨脹、貨幣供給、利率、匯率及投資等，也受國外如中國、印度新興市場需求、 美國次級房貸風暴等而有所變動，此外也受政治、人為等非經濟因素所干擾，且近年來 國際原油價格波動幅度甚大，對依賴能源的國內運輸產業影響很大，使營運成本大幅增 加，運輸類股價波動幅度甚大，造成公司與投資人獲利或損失。 運輸類股的股價，相較於其他類股遽動幅度較小，股票價格與類股的數目也較少， 故類股的特性能夠具有運輸產業的代表性，過去國內僅針對運輸產業做探討的研究，相 較於電子類股與金融類股較少，且海運類股具有貨櫃與散裝的特性，國內主要的航空類 股數目也不多，恰為中華航空與長榮航空，本研究期望能就數家個股的特性，找出運輸 產業股價的特性，是否具有異質變異的現象，以利股價預測。 若能藉由研究相關的時間序列理論，建構有效的模式，找出最適的階次，並探討在 模式建構期間與預測期間改變時，對預測能力的影響，以準確的預測股價，了解其個股 變動情形，相信是所有投資者與公司經營者所渴望的，能夠預期到未來的升降幅度，將 能提早做出因應，減少風險所帶來不確定因素的影響，投機、套利、避險等市場操作都 將有新的局面，人們或將把時間、心力放至更實質面的考量，做出相關的最適決策。

1.2 研究目的

由於財務管理的目標，有極大化公司價值或股東權益或股價，因此過去已有很多對 股價的相關研究，Markowitz 投資組合理論，考量風險與報酬間的關係，與系統風險與 非系統風險所引發的波動程度；Fama 效率市場假說對基本分析、技術分析、內線消息， 具有充份、效率、即時的資訊對股價預測可行性之影響；總體變數對股價波動性的實證 研究等，股票市場在不同國家、時點、產業、個股的實證分析，市場是否具有效率性與 股價行為是否呈隨機漫步，學者們的研究各有其論點與解釋條件。 針對過去既有價格做預測，除股價屬公開資訊取得方便外，亦能探討股價報酬率與 殘差項的時間序列，是否呈常態分配、前後期是否線性或獨立、是否為白噪音過程、波 動性為同質或異質、該序列為定態或非定態、長期市場整合關係是否具共整合現象等，

都是實證上令人感興趣的議題，也能與相關理論做比較，檢驗後依其不同結果，有其後 續程序做資料處理，何種方法較準確、較有效率，與最終股價預測成效，有著密不可分 的關係。

自從 Box and Jenkins (1976)發展時間序列分析法以來，各種經濟與財務資料的實證 分析，因而有了重大突破，而本研究正是以時間序列分析法中，ARIMA 模式與 ARCH 模式應用到台灣運輸產業股價上，利用歷史資料預測未來股價趨勢，且藉由統計軟體 Eviews 的使用，將模式估計、檢定後應用在實務，提供參考。

1.3 研究架構與建模流程

本論文除本章緒論的基本介紹外；第二章文獻回顧，將過去國內外學者相關研究成 果，予以精要說明；第三章研究方法，就應用到之理論、預測模式、檢定方法、成效評 估，做適足論述；第四章實證分析，從資料取得、序列性質處理到統計軟體的模擬檢定、 數據解釋等，具體呈現研究結果；第五章結論與建議，總結研究成效與相關後續研究方 向。

第一章、緒論 股價影響因素、實證探討議題、 時間序列分析、Engle(ARCH) 應用至台灣運輸產業股價預測 第二章、文獻回顧 效率市場與隨機漫步研究 股價報酬率與異質變異數研究 第三章、研究方法 自我相關圖、ARIMA 與 ARCH 模式推導、估計與檢定、單位根 第四章、實證分析 台灣運輸產業海運類與航空類 AR 與 GARCH 模式預測結果 第五章、結論與建議 研究架構圖

研究建模流程(前) 取對數後股價之差 股價報酬率 其機率分配 呈常態分配 其時間序列 前後期獨立 其時間序列 符合白噪音 傳統財務理論 模型假設條件 傳統隨機變數 統計性質假設 傳統迴歸理論 模型假設條件 單位根 檢定 台灣運輸類股價 非定態 定態 差分 模式建構 否 否 假性迴歸 是 是 否 是

研究建模流程(後) 模式建構 由自我相關圖 判讀落後期數 一階自我迴歸模式 最小平方法 估計模式 檢視二階自我迴歸模式 依模型簡約 性原則 股價報酬 率預測 估計模式之殘差 是否自 我相關 是否常 態分配 模式估計良好 模式估計良好 最大概似估 計法估計模 式 一階自我迴歸條件異 質變異數模式 是否異 質變異 模式估計良好 是 是 模式估計後標準化殘差 降低殘差自我相關 使其近似常態分配 股價報酬 率預測 廣義自我相關條件異 質變異數模式 自我相關係數 偏自我相關係數 否 否 是 否

由公開的台灣加權股價指數取得研究資料，利用每交易日收盤股價取對數後的比值 表示日報酬率，彙整後形成股價報酬率之時間序列，探討能否支持傳統上統計性質的基 本假設，包括該時間序列之機率分配是否為常態分配、前後期間是否相關、該機率分配 之變異數是否固定不變、是否符合白噪音過程等，之後藉由自我相關圖(Correlogram) 簡易觀察後根據模型簡約性原則(parsimony)，建構一階自我迴歸模式，但前提是該時間 序列須為定態型時間序列，故以單位根檢定確認時間序列型態後，以差分方式平穩化時 間序列，才將樣本內資料使用最小平方法估計後的一階自我迴歸模式，預測樣本外的資 料。 考慮模式建構後殘差項的自我相關性、機率分配型態，並將殘差前後期相關性予以 消除後才使用最大概似估計法，使條件異質變異數模式具有良好的預測能力，最後考量 台灣運輸產業在海運類股與航空類股間，模式的股價報酬率預測能力比較，本研究建模 流程，在第四章實證分析，有其循序的觀察、估計、檢定、預測等內容介紹。

第二章 文獻回顧

自從Fama(1970)提出效率市場假說以來，學者們開始研究各種證劵市場，是否為效 率市場、股價行為是否為隨機漫步、股價是否可藉由預測而獲得超額報酬，這些想法與 問題，雖然至今仍沒有一定論，但卻開啟了實證研究的先河。 隨後Box 與 Jenkins(1976)發展時間序列分析法，提供了不同以往的預測方法，說明 隨機變數隨時間變化的特性，而ARIMA 模式能夠考量變數本身，與過去數期觀測值或 干擾值間的關係，以自我相關圖的自我相關係數、偏自我相關係數，來判別落後的階數 與特性，找出模式良好的配適度。 Granger 與 Newbold(1974)認為應先判別時間序列的定態性，以避免非定態時間序列 可能造成的假性迴歸現象，Dickey 與 Fuller(1979)依此發表了單位根檢定法，能夠檢定 時間序列的特性，成了建構時間序列模式前的重要檢定步驟。 其次，後續實証分析的發展，使過去傳統上的統計基本假設，包括白噪音的性質、 變數前後期獨立、常態分配等，紛紛遭到質疑，而其中股價報酬率，實証上出現傳統理 論所無法解釋的波動群聚現象，股價報酬率的機率分配也呈尖峰厚尾的特性。 Engle(1982)將自我相關的概念應用至條件異質變異數，使用的 ARCH 模式，能夠適 切的解釋上述的現象，並針對傳統迴歸模型估計時，殘差變異數固定不變的假設，提出 變異數異質的情形，對經濟與財務資料的實證研究，有相當大的貢獻，而Bollerslev (1986)的 GARCH 模式，更是實証上被使用最頻繁的模式，說明能夠好的預測效果。

2.1 效率市場與隨機漫步之研究

2.1.1 國外相關文獻

股價之預測方法可以分為基本分析與技術分析。基本分析是根據總體經濟變數建構 其與股價間之關係，從此關係來預測股價(Basu, 1977；Fama and French, 1992）。技術分 析則是利用股票市場成交量、成交價過去的資料，來判斷股價未來的趨勢。

Robert Brown(1827)觀察到分子間的碰撞移動是不具規則性、隨機的變化，無法由 過去的行為來預測未來的行為的隨機漫步(Random Walk)現象，Kendall(1953)的研究指出 股價變化符合隨機漫步，而股價是不可預測的。

Fama(1970)效率市場假說(Efficient Market Hypothesis)，是指在一個資訊傳遞無障礙 的市場中，所有的證劵價格皆能正確、即時及充分地反映所有相關訊息，投資人無論進

行何種交易策略皆無法獲得超額報酬(Abnormal Return)，即市場永遠處於均衡的狀態， 無人能以特殊的交易策略擊敗市場。 若以弱勢效率市場而言，意指證券的價格皆已充分地反應過去證券價格的資訊，亦 即證券價格的波動是呈隨機漫步行為，是無法預測的，投資者無法從過去歷史所提供的 資訊中找出一定的趨勢型態，進而作為獲取超額之報酬的依據，如Fama（1965）、Fama and Blume(1966)皆認為美國的證券市場存在弱勢效率性。 但 1980 年代起，實證上陸續發現了一些市場異常(Market Anomalies)的現象，不為 效率市場理論所認同，例如Gultekin(1983)的元月效應(January Effect)發現股票在元月份

報酬率往往高於其他月份；Lustig and Leinbach(1983)的規模效應(Size Effect)，經風險調 整後的小型股報酬率顯著優於大型股。

Kahnemann and Tversky(1979)應用心理學實驗，探討投資人實際上的決策行為，發 現投資人具有損失趨避的特性，也使行為財務學(Behavioral Finance)受到重視，例如以 價值函數取代傳統效用函數的展望理論(Prospect Theory)。

後續學者提出不同的觀點，認為仍可從過去證券價格的歷史軌跡，以技術分析的方 式來預測未來趨勢，從中獲得超額利潤（Brown and Jennings, 1989；Brock；Lakonishok and LeBaron, 1992）。

因此證券市場是否具有弱勢效率性，依不同研究方法、不同期間、不同市場的實證 分析而有所不同，股票市場效率性的問題尚未有一定論(Brealey；Myers and Marcus, 2004)。

檢驗弱勢效率市場與檢驗股票市場價格是否具隨機漫步，在某種程度上意義相符， 若拒絕則代表價格具有序列相關，因此在長期下價格將具有可預測性。

而透過檢定股票價格是否具有自我相關及白噪音現象，亦即股票價格是否符合隨機 漫步之假說時，即可進一步探討市場的效率性。

Fama and French (1988)研究美國紐約證交所的股票市場，得到3到5年的股票持有期

間之報酬率呈現負自我相關。Lo and Mackinlay(1989)以整體紐約證券交易所的週報酬率

做研究，結果發現價格取對數的週報酬率呈現正自我相關，長期則是呈現負自我相關。 Greene and Fielitz (1977)則以紐約證券交易所上市之200家公司股價報酬率為研究 對象、Eldridge and Bernhardt (1993)以S&P500指數，檢定美國資本市場之效率性，他們 的實證結果皆顯示出美國股票市場報酬率，在長期具有自我相關性，也因而拒絕了弱勢 效率市場假說。

2.1.2 國內相關文獻

林良炤(1997)進行 KD 技術指標應用在台灣股市之實證研究，研究結果發現，在買 長策略下可獲得超額報酬，技術分析能夠擊敗市場，因此台灣股票市場不符合弱式效率 市場假說。 陳健全(1998)進行台灣股市技術分析之實證研究，透過模擬交易的方式來探討台灣 股票市場之效率性，並評論各種技術指標之操作績效，在模擬交易過程中考慮了樣本類 型、股票屬性、技術指標及操作策略，研究獲得結論為技術分析之投資績效，未能優於 買入持有策略，因此未能推翻台灣股市符合弱式效率市場之假說。 徐正錦(2003)應用技術分析於台灣股市之實證研究，以 10 種技術指標包含大盤指 數、6 種類股指數及 60 家個股指數，實證結果說明，對有效的指標而言，表現愈差的公 司愈適合技術分析。 王殷盛(2003)研究財務預測資訊的市場效率性，研究範圍為1999年至2003年，樣本 627家公司，研究採事件研究法並建構市場模型，實證結果發現市場對於財務預測資訊， 存在著無法及時反應的現象，無法支持效率市場充份、即時資訊流通的假設。 賴素鈴、楊靜琪(2004)說明台灣股市雜訊交易因素及其對股價影響性之研究， 指出市場上有許多無法由效率市場假說加以合理解釋的異常現象，因此股價資料可能存 有時間序列相關，並應用變異數比率法進行台灣股市雜訊交易之存在驗證。 楊踐為、李家豪、類惠貞(2007)以30家台灣上市公司為研究對象，應用時間序列分 析法建構台灣證券市場之預測交易模型，實證結果顯示應用時間序列分析工具所建構的 交易系統，在扣除手續費與證券交易稅後其投資報酬率顯著的超過了買入持有交易策 略，顯示應用時間序列分析股價所建構的交易系統確實可以獲得超額報酬。

2.2 股價報酬率與條件異質變異數之研究

2.2.1 國外相關文獻

Mandelbrot(1963)實證發現股票報酬率的機率分配，呈現高狹峰與偏態的現象，此 與傳統上常態分配的假設不符，Fama(1965)、Akgiray(1989)的研究也發現股票報酬率具 有波動群聚的現象。 過去有許多的研究將 ARCH 以及 GARCH 模式運用在預測股價的波動上， Akgiray(1989)應用條件異質變異數在股票報酬率的實證與預測，研究發現日報酬時間序

列具有一階自我迴歸的現象，絕對值與平方的日報酬時間序列，在落遲多期時，仍很明

顯，但殘差項的時間序列前後期無自我相關性，而GARCH(1,1)被證明能更準確預測股

價波動性。

French,Schwert and Stambaugh(1987)檢視紐約證券交易所，有關股票報酬率與市場 波動性之關係，發現預期市場風險貼水與股票報酬的波動性，呈正向變動關係；預期股 票市場報酬率與預期股票報酬的波動性，則呈反向變動，而這些變數廣泛受過去幾年所 影響。 Engle(1982)發現英國的通貨膨脹率有波動性的存在，以 ARCH 模式的條件變異數會 隨時間而改變，且受其模式建構後殘差項前後其相關的影響，而Bollerslev（1986）發 現將股價報酬率以GARCH 模型來表示，其條件殘差仍呈現非常態分配，即模型仍無法 完全解釋股價報酬高峰、厚尾的特性。

因而後續許多研究，如 Engle、Lilien and Robins(1987)的 ARCH-M 模型，將 ARCH

概念擴展至估計報酬與風險的關係，Nelson(1991)提出 EGARCH 模型，藉由指數化反應 市場中有關財務的槓桿效果，即股價出現負報酬時會比正報酬時，產生更大的波動程 度，而對ARCH 或 GARCH 的修正與延伸模式，並以不同模型加以配適的相關文獻，一 般稱為GARCH-Family。

2.2.2 國內相關文獻

陳裴紋(1995)將台灣加權股價指數及10家上市公司為標的，以1991年4月至1994年8 月31日為研究期間，使用ARIMA模式與GARCH模式，進行臺灣股票市場報酬率及波動 性的預測，研究發現GARCH(1,1)-MA(1)模型具有較好的預測效果，且GARCH 模型對 短期波動性有相當的預測能力，較傳統的ARIMA時間序列模型更接近真實股價波動的 過程，也說明過去歷史資訊對預測期間條件變異數的影響，是會隨時間而有所改變的。 謝宗祐(1998)利用自我迴歸模型，來探討選擇權中波動率與實際股價波動率之間的 關連性，且將實證期間區分成崩盤前、崩盤後，發現股價波動性有序列相關，前後期彼 此會相互影響的特性，而在總體經濟變數上，股價波動性與實質生產風險、通貨膨脹風 險有正向關係。 呂文正(1999)利用ARCH-family模型與SWARCH(Markov-switching ARCH)模型，實 證研究台灣股票市場中，開發金、台塑及中環個股的波動性分析，實證結果發現SWARCH 的模型表現較好，但改變樣本外資料時，兩種模式在不同個股各有優劣，沒有一致性結 果，而ARCH-family模式在短期間的預測能力較好。

黃冠瑋(1999)使用蒙地卡羅模擬法，並加入GARCH(1,1)模型來預測波動性，考量波 動性會隨時間改變的情況，發現使用GARCH(1,1)模型估計參數所得到的預測之績效， 都較傳統上假設變異數固定不變的估計模型來的好。 陳煒朋(1999)比較GARCH模型與傳統模型的預測能力，企圖找出適合臺灣股票市場 的波動性模型，並將模型參數修正，研究結果發現台灣的股票市場，GARCH模式能提 供一個較好的估計與預測結果。 王淑君(1999)藉由GARCH模型探討各類股股價指數及報酬率，將前一期交易量、匯 率、前一期法人買賣超等變數，用以解釋GARCH模式，並分別將總體股價報酬率、各 類股指數報酬率、十八個股報酬率的MA(1)-GARCH(1,1)模型中，個別加入前一期交易 量、匯率及前一期法人買賣超三變數，發現在不同產業、類股，其解釋能力各有差異。 探討引入解釋變數的修正模型，和原先不加入外生變數的原始MA(1)-GARCH(1,1) 模型的GARCH效果，說明解釋變數是否成為股價波動的來源依據，研究結果發現在加 入前一期交易量及匯率的修正模型中，表示前一期交易量與匯率，能解釋部分GARCH 效果，而加入前一期法人變數的修正模型，無法解釋GARCH效果。 在各類股指數報酬率模型，其中紡織類股、機電類股、造紙類股，加入前一期交易 量、匯率、法人買賣超的修正模型，顯示這些解釋變數解釋了部分GARCH效果，而在 塑膠化工類股、水泥窯業、食品類股、營造建材類股及金融類股，加入前一期法人買賣 超的解釋變數，與營造建材類股在加入匯率變數的修正模型裡，這些變數則無法解釋 GARCH效果。 黃柏凱(2000)探討已開發國家與新興市場的市場規模、成交量等因素與股價報酬率 波動持續性之關連性，發現市場規模的不同，可用以解釋部份報酬率的波動持續性，在 GARCH(1,1)模型中，除考慮股價本身因素外，加入成交量因子後，能降低報酬率的波 動性，使模型的配適度更佳。

黃騰皓(2007)以NGARCH模型(nonlinear asymmetric GARCH)，探討在不同分配假設 下，對波動度與價格分配預測之表現，應用了NGARCH-常態模型、NGARCH-偏態t模 型及NGARCH-跳躍模型於S&P500指數、FTSE100指數，研究結果發現NGARCH-偏態t 模型與NGARCH-跳躍模型能提高模型配適度，而就波動性的預測而言，NGARCH-跳躍 模型的預測誤差在三種模型中為最小，且NGARCH-偏態t模型與NGARCH-跳躍模型都 能較NGARCH-常態模型，有更準確的估計與預測分配結果。

[註1]：弱勢效率性

Fama就股價反映訊息的程度，先後提出弱勢效率市場(Weak Form Efficient

Market)、半強勢效率市場(Semi-Strong Form Efficient Market)、強勢效率市場(Strong Form Efficient Market)，而當弱勢效率市場成立時，利用證劵價格、交易量、報酬率等歷史資 料進行預測的技術分析法，將會無效也不能獲得超額報酬，故一般實證上以檢視該市場 的弱勢效率性，即可驗證效率市場假說及隨機漫步行為是否成立。 [註 2]：白噪音 白噪音是滿足一些特定的統計定義的時間序列，若有一個時間序列的隨機變數，符 合期望值為零、變異數為一固定常數、自我共變異數為零此三個條件，則稱此數列符合 白噪音過程，且在此情況下，序列不存在自我相關。

第三章 研究方法

本章將先說明定態型隨機過程，並藉由離散型線性隨機過程，推導出自我迴歸過

程、移動平均過程與ARMA 模式、ARIMA 模式，以 Box＆Jenkins(1976)Time Series

Analysis：Forecasting and Control；Granger＆Newbold(1998) Forecasting Economic Time

Series 兩書為參考，而下述介紹可參見 Box＆Jenkins 書中首章介紹與總結(Introduction

and Summary)，模式推導主要以第三章線性定態模式(Linear Stationary Models)為依據，

而各型態隨機過程介紹則散佈各章節，亦可參閱Granger＆Newbold 該書。 時間序列是指以時間順序型態出現之一連串觀測值的集合，一離散型時間序列依等 長時間間隔l表示，如Z Z₁, ₂, , , ,_L Z_{t L} Z_N為t₀+l t, ₀+2 , ,l _L t₀+tl, ,_L t₀+Nl之觀測值，t 為₀ 時間之起始點，Nl在預測上稱為前置時間(Lead Time) ，Z 可稱為在時間 t 時的觀測值。 t 數列對未來結果無法確定，須以機率分配來表示者，稱為隨機性時間序列(Stochastic Time Series) ，大部分的時間序列皆屬於此型，若數列未來結果可用確定的數學式表示， 稱為確定性時間序列(Deterministic Time Series)，如Z_t =cos(2π ft)。

時間序列一般有三大重要的應用領域：

(1) 藉由過去或現在的時間序列，建構模式以預測未來值，也是本研究的主要方向。 (2) 研究二個以上時間序列，其投入數列與產出數列間的關係，藉由衝擊反應函數

(Impulse Response Function) ，建構系統之轉換函數模式(Transfer Function Models) 。 (3) 研究多個時間序列的聯合關係性，以建立控制系統，用來解釋多變數間之互饋關係

(Feed Forward And Feedback Control Schemes)。

有關時間序列之分析法，以時間定義域分析法(Analysis in Time Domain)中的自我相 關函數(Autocorrelation Function)做為分析之工具，建立隨機模式做預測分析，並將其繪 成圖形做基本觀察，以利後續研究。

3.1 ARIMA 模型推導

3.1.1 定態型隨機過程

所謂定態型時間數列(Stationary Time Series)，是指一個時間序列的統計特性不隨時 間變化而變化，而時間序列可視為隨機過程之實現值，故一個隨機過程在此種統計均衡 狀態，即稱為定態型隨機過程(Stationary Stochastic Process )。

的機率密度函數，f Z( )_t = f Z( _t+1)，同理f Z( )_t = f Z( _t+1)=_L= f Z( _{t n+} )，則可得其機率密 度函數在各時點皆相同，故其平均數μ=E Z( )t 與變異數 2 _{( )}2 Z E Zt σ = −μ 皆為固定。 而一組觀測值Z Z₁, ₂, ,L Zn的平均值與變異數之估計可以表示為： 1 1 n t t Z Z n = =

∑

與 2 2 1 1 ( ) n z t t Z n σ μ = =

∑

−

3.1.2 離散型線性隨機過程

所謂離散型線性隨機過程(Discrete Linear Stochastic Processes)，是假設隨機過程中 的每個觀測值，都可以表示為相同機率分配之隨機變數序列的線性組合。

若將其干擾項假設為期望值為零、變異數為固定的常態分配，即E X( ) 0= 、

2

( ) x

Var X =σ ，符合該統計特性，即稱為白噪音過程(White Noise)。

0 1 1 2 2 t t t t Z = +μ w X +w X ₋ +w X₋ +L (一般式/式 I) 0 t i t i i Z μ w X ∞ − = = +

∑

；μ為過程之平均值；一般設權數w =1 ₀ 即觀測值Z 可由當期干擾與所有過去干擾來表示。 _t 若BX_t = X_t−1 、B X2 _t =X_t−2、 B Xj _t = X_t−j 2 0 1 2 ( ) ( ) t t t Z = +μ w +w B+w B +_L X = +μ w B X

B 稱為線性濾波器(Linear Filter)，而由此推導而得的時間序列模式即為 Box-Jenkins

模式，可由線性濾波器的權數判定時間序列的型態。如權數{ }w 為有限或無限但收斂，_i 則為平穩型時間序列；權數{ }w 為無限且發散，則為非平穩型時間序列。 _i

3.1.3 自我迴歸過程

由 3.1.2 中(式 I)移項可得：X_t =Z_t − −μ w X_{1 t−1}−w X_{2 t−2}−L (式 II) t 用 t-1 代入：X_t−1 =Z_t−1− −μ w X_{1 t−2}−w X_{2 t−3}−L (式 III) 將(式 III) 代入(式 II) ： Xt =Zt− −μ w Z₁( t−₁− −μ w X₁ t−₂−w X₂ t−₃−L)−w X₂ t−₃−L ∴Z_t =μ(1−w₁)+w Z_{1 t−1}+X_t +(w₂−w2₁)X_t−2+(w₃−w w X_{1 2}) _t−3+L 同理可將X_t−2與X_t−3消去可得：

1 1 2 2 t t t p t p t Z = +C π Z₋ +π Z₋ + +_L π Z₋ +X … p 階自我迴歸過程 AR(p) 將權數 w 改成π 以區別一般式與自我迴歸式，即觀測值Z 可由當期干擾與所有過t 去觀測值X 來表示，故自我迴歸的當期觀測值Z 為同一數列諸個前期觀測值之迴歸。_t 例如AR(1)：Z_t = +C π₁Z_t−1+X_t ，即當期觀測值與前一期觀測值有關，又稱馬可夫過 程；AR(2)：Z_t = +C π₁Z_t−1+π₂Z_t−2+X_t。 若BZ_t =Z_t−1、B Z2 _t =Z_t−2、 j t t j B Z =Z₋ 2 1 2 ( p) t p t t Z = +C π B+π B + +_L π B Z +X 2 1 2 (1 p) p t t B B B Z C X π π π − − − −_L = + π_p( )B Z_t = +C X_t 可由多項式π_p( ) 0B = 之根落於單位圓之位置，判定時間序列的型態。

3.1.4 移動平均過程

將(式 I) Z_t = +μ X_t+w X_{1 t−1}+w X_{2 t−2}+ +_L w X_{q t q−} 中各項W 皆以_i − 代入： θ_i Zt = +μ Xt −θ₁Xt−₁−θ₂Xt−₂− −L θqXt q− 由後移運算子： 2 1 2 (1 q) ( ) t q t q t Z = + −μ θ B−θ B − −_L θ B X = +μ θ B X … q 階移動平均過程 MA(q) ， 例如MA(1)：Z_t = +μ X_t −θ₁X_t−1；MA(2)：Z_t = +μ X_t −θ₁X_t−1−θ₂X_t−2。

3.1.5 混合自我迴歸移動平均過程

自我迴歸與移動平均過程具有可逆性，可由數學轉換得知兩者互換的對應性質，即 一階自我迴歸等同於無窮階的移動平均過程AR(1)↔MA( )∞ ；一階移動平均等同於無窮 階的自我迴歸過程MA(1)↔ AR( )∞ 。 Zt = +C π₁Zt−₁+π₂Zt−₂+ +L πpZt p− +Xt −θ₁Xt−₁−θ₂Xt−₂− −L θqXt q− …混合 自我迴 歸移動平均過程ARMA(p,q)，例如 ARMA(1,1)：Z_t = +C π₁Z_t−1+X_t −θ₁X_t−1。

3.1.6 自我迴歸整合移動平均模型

一般假設原始的時間序列經由 d 次差分(d＞0) ，可將非平穩型資料轉成平穩型資 料，此模式即稱為自我迴歸整合移動平均模式ARIMA(p,d,q)，其中 p 表示為自我迴歸過

程的階數、d 為差分次數、q 表示為移動平均過程的階數。 ∇ =Zt Zt−Zt−₁=Zt−BZt = −(1 B Z) t 可得差分運算子∇與後移運算子 B 之關係為：∇ = −1 B，同理 d (1 )d B ∇ = − 。 一般化 ARIMA(p,d,q)模式之形式為： ( ) d( ) ( ) p B Zt C q B Xt π ∇ −μ = +θ 2 2 1 2 1 2 (1 p) d( ) (1 q) p t q t B B B Z C B B B X π π π μ θ θ θ − − − −_L ∇ − = + − − − −_L 舉例如下： ARIMA(0,1,1)：∇ =Zt Xt−θ₁Xt−₁ = −(1 θ₁B X) t ARIMA(0,2,2)： 2 2 1 1 2 2 (1 1 2 ) t t t t t Z X θ X₋ θ X₋ θ B θ B X ∇ = − − = − − ARIMA(1,1,1)：(1−π₁B)∇ Z_t = −(1 θ₁B X) _t

3.2 ARIMA 模型階次與差分次數

3.2.1 自我共變異數與自我相關函數

共變異數可解釋二變數間的線性關係，已由定態型的條件知，隨機變數Z 與_t Z_{t k+} 在 不同時點的機率結構皆相同，故在本身之隨機過程中，利用共變異數來探討任二個隨機 變數間的線性關係，即稱為自我共變異數(Autocovariance)，依此所形成的函數，稱為自 我相關函數(Autocorrelation Function)。 隨機變數Z 與_t Z_{t k+} ，相隔k 個時期之自我共變異數為 ( , ) [( )( )] k Cov Z Zt t k E Zt Zt k γ = ₊ = −μ ₊ −μ 其中μ =E Z( )_t 0 k = 時γ₀ =E Z( t −μ)2 =σ2Z 而為了解二個隨機變數間的線性關係程度，隨機變數Z 與t Zt k+ ，相隔k 個時期之自 我相關係數為 2 2 0 ( , ) [ ( ) ][ ( ) ] t t k k k t t k Cov Z Z E Z E Z γ ρ γ μ μ + + = = − − 若有 n 的觀測值之時間序列Z Z₁, ₂, ,L Zn則當k>0 時ρk之估計為 0 , 1, 2, k k c k c γ = = _L

其中 1 1 ( )( ), 1, 2, n k k t t k t c Z Z Z Z k n − + = =

∑

− − = _{L Z 為此數列的平均值} 2 0 1 1 ( ) n t t c Z Z n = =

∑

− 當時間序列變數具有AR或MA的特性時，其自我相關函數(autocorrelation

function，簡稱為ACF)和偏自我相關函數(partial autocorrelation function，簡稱為PACF) ， 將會有一些特性可用來判斷落後期數，做為ARMA模型之初步探討。

ACF 可以決定變數 DGP 的 MA 項之階次 q，PACF 則是能判斷變數的 DGP 之 AR

項之階次p，只要同時把變數的 ACF 和 PACF 畫出自我相關圖(Correlogram)，大致上就

可以看出其ARMA(p,q)的階次。

3.2.2 單位根檢定

Granger＆Newbord(1974)提出若對非定態之時間序列取迴歸，將會產生看似模型解 釋能力R 很高的假性迴歸現象(Spurious Regression)，故一時間序列若為非定態型之時間2 序列，存在單位根時，可藉由差分的方式消除變數趨勢，並將非定態之時間序列轉換成 定態之時間序列，如此定態的相關理論將仍可適用於非定態的情況，此即透過該序列的 整合階數(integrated of order)，以 I(d)表示，而一般經濟總體或財務資料，差分次數 d 不

會超過2。 Dickey＆Fuller(1976)發表用以檢定序列是否平穩的 DF 檢定法，考慮一階自我迴歸 方程式AR(1)如下： 1 1 t t t Y = ΦY₋ + ， e ~ (0, 2) iid t e N σ 其誤差項服從嚴格白噪音過程，單位根檢定即在檢定前一期變數之係數Φ 是否為₁ 1，但可能產生Φ 低估的偏誤，故可將上式兩邊同減₁ Yt−₁，則 Yt−Yt−₁ = Φ₁Yt−₁−Yt−₁+ ，et 2 ~ (0, ) iid t e N σ ∇ =Yt γYt−₁+ ，其中et γ = Φ − 1 1 此時差分後之方程式，其單位根檢定的虛無假設，是在檢定前一期變數之係數γ 是

否顯著為0，即H₀:γ = ，若不拒絕0 H ，表示₀ Y 序列存在單根，為非定態之時間序列。_t

若要適用於多階自我迴歸，可使用調整後之ADF 檢定法(Augmented Dickey-Fuller

Test)，或加以考量異質性，則有 Phillips-Perron 檢定法。

3.3 ARMA 模型檢定與估計

3.3.1 Q 統計量

在時間序列的實証研究中，如何判定該序列是否存在自我相關，須有適當的統計量 做為檢定的依據，即Q-test 之統計量。 針對所估計模型的殘差是否存在自我相關的檢定，所計算出來的統計量，又可分為 Box-Pierce Q 統計量與適用小樣本的 Ljung-Box Q 統計量，假設時間序列跑迴歸後所得 的殘差項為ε∧_t、樣本數N 個，則可求得殘差第 i 階的自我相關係數 ( )ρ i ： 1 2 1 ( ) N t t i n i N t n i ε ε ρ ε ∧ ∧ − = + ∧ = =

∑

∑

Box-Pierce Q 統計量計算式為 2 1 ( ) ( ) p i Q p N ρ i = =

∑

﹔p=1, 2,3_{L可藉此算出} (1), (2), (3) Q Q Q _L。 其虛無假設H ：該變數從第 1 階到第 p 階都不存在自我相關。 ₀ 對立假設H ：該變數從第 1 階到第 p 階至少有一階存在自我相關。 ₁ Ljung-Box Q 統計量計算式為 2 1 ( ) ( ) ( 2) p i i Q p N N N i ρ = = + −

∑

，依落遲n 項之 LB(n)可用 以判斷是否為嚴格白噪音。

3.3.2 JB 統計量

Jarque-Bera 統計量為針對所估計模型的殘差是否符合常態分配的檢定，所計算出來 的統計量，故又稱為常態性檢定(normality test) ，若迴歸殘差的偏態係數(skewness)為

S、峰態係數(kurtosis)為 K、殘差樣本數 N 個、模型中帶估計的參數個數為 n，則 JB 統 計量之計算式： 2 1_{( 3)}2 6 4 N n JB= − ⎛_⎜S + K− ⎞_⎟ ⎝ ⎠ 其虛無假設H ：該檢定的變數為常態分配。 ₀ 對立假設H ：該檢定的變數不為常態分配。 ₁

3.3.3 DW 統計量

檢驗時間序列迴歸模型AR(1)的誤差項，是否存在序列相關的統計量。 2 1 2 2 1 ( ) n t t t n t t u u DW u ∧ ∧ − = ∧ = − =

∑

∑

；DW 2(1 ρ) ∧ ≅ − 如果DW統計量大約為2，則拒絕序列相關，否則無法拒絕。

3.4 ARMA 模型的選擇

如何選擇適當的ARMA 模型，可由模型的配適度(goodness of fit)與模型的預測力

(forecastability)來看，如本研究就 1999~2006 共八年內，既有的台灣加權指數運輸類股 股價的公開資訊日資料，做為所謂的樣本內資料，用來建構模型是否能適當解釋該資

料；而2007 年則為樣本外資料，用以評估模型的預測能力。

在時間序列的實証研究中，常用 AIC(Akaike information criterion)與 SBC(Schwartz Bayesian information criterion ) ，做為模型配適度的指標，N 為樣本總數、SSE 為殘差 平方和、k 待估的參數個數，其計算式如下： ln( ) 2 AIC=N SSE + k。 ln( ) ln( ) SBC=N SSE +k N 。 由於SST =SSR+SSE，SSR 愈大代表模型樣本資料解釋能力愈好，故 SSE 愈小愈 好，即計算出之AIC 或 SBC 值較小，代表模型的配適度較佳。

文獻上有關AIC 與 SBC 的選取問題，Brooks(2002) & Enders(2004)有解釋如下： (1) 用 SBC 做選擇模型的準則時，待估參數個數較少者較有利、樣本數較大時較有一致

性。

(2) 使用不同樣本數時，用 SBC 做選擇模型的準則時，相較 AIC 不一致狀況更明顯。

要判斷AIC 與 SBC 是否有顯著性不同，利用模型估計所算出之最大概似值的檢定

統計量，即稱為概似比檢定(likelihood ratio test)，其計算式為：

2 2( R U) ~ ( ) LR= − L −L χ m

3.5 ARCH 模型與 GARCH 模型

財務的時間序列資料，常因資訊或外生變數影響而造成持續性波動，使正或負的離 群值會有群聚現象，過去的研究說明變異數並非固定不變的，而是會隨時間變化而變化 (time-varying)，Engle 於 1982 年研究總體資料發現，許多財務金融的時間序列具有大波 動跟隨著大波動、小波動之後出現小波動的波動群聚(volatility clustering)現象，據此提 出自我迴歸條件異質變異模式，以預測資料不同時期的變化，後續Bollerslev 於 1986 年 加入σ_t2的落後項數後，擴展成廣義的ARCH 模式。 典型的ARCH(q)模式為 y_t Ω_t~N X v( _t ,σ_t2) mean equation ：εt =yt −X vt variance equation ： 2 2 2 2 0 1 1 2 2 t t t q t q σ =α α ε+ ₋ +α ε₋ + +L α ε₋ t X ：迴歸式的自變量向量 v ：迴歸式的係數向量 t X v ：在資訊集合Ω 下 X 之線性組合 _t q ：落遲項階數 若X 代表單一時間序列的 ARMA，則可將均數方程式與變異數方程式表示為_t ARMA(m,n)-ARCH(q)： 0 1 1 m n t i t i t i t i i i y a a y₋ ε bε₋ = = = +

∑

+ +

∑

2 2 2 2 2 0 1 1 2 2 0 1 q t t t q t q i t i i σ α α ε₋ α ε₋ α ε₋ α α ε ₋ = = + + + +_L = +

∑

ARMA模型是受自我迴歸影響也受移動平均影響，使條件變異數不僅受前期預測誤 差平方項的影響，也受其條件變異數的影響，因而形成了較廣義之GARCH模型。故ARCH 是AR的概念應用在條件變異數之估計，而GARCH則是將AR和MA的概念應用在條件變 異數之估計。

典型的GARCH(q)模式為： t t y Ω ~N X v( t ,σt2) t yt X vt ε = − 2 2 2 0 1 1 q p t i t i i t i i i σ α α ε ₋ β σ ₋ = = = +

∑

+

∑

3.6 ARCH 模型推導

2 2 0 1 2 1 ~ (0, ) t t t q t j t j j t t t X F D μ ε σ α α ε ε σ − = − = + = +

∑

或 2 2 2 0 1 1~ (0,1) t t t t q t j t j t j j t t X F D μ σ ε σ α α σ ε ε − − = − = + = +

∑

假設σ_t為定態那麼X_t − 亦為定態，且μ_t X_t − 變異數的定態性即為μ_t σ_t2平均數的定 態性。 2 2 2 2 2 2 0 0 1 0 1 1 1 ( ) ( ) [ ( )] [ ] q q q t j t j t j j t j t j t j j t j j j j E σ α α E σ ₋ ε₋ α α Eσ ₋ E ε₋ F_{− −} α α Eσ ₋ = = = = +

∑

= +

∑

= +

∑

可將上述推導改成向量一階自我迴歸形式來表示：Q_t = AQ_t−1+ B 定態解存在表示A 的半徑要小於 1，當 1 1 q j j α = <

∑

時可找出變異數 2 0 1 1 t q j j α σ α = = −

∑

。 從前面推導式： 2 ₀ 2 1 ( ) [ ] q t j t j j E σ α α Eσ ₋ = = +

∑

，符合定態條件時E(σt2)=E(σt−j2)=σt2， 2 2 0 1 ( ) q t j t j j E σ α α σ ₋ = = +

∑

2 0 1 (1 ) q j t j α σ α = −

∑

= ∴ 2 0 1 (1 ) t q j j α σ α = = −

∑

3.7 ARCH 模型檢定與估計

實證上也因為變異數並非固定，造成估計出來的估計量不符合效率性(Efficiency)， 即不能同時滿足下列兩個條件： (1) ( )E θ θ ∧ = (2) Var( )θ Var( )θ1 ∧ ∧ ≤ 且所有θ1 ∧ 亦符合E( )θ1 θ ∧ = 因此找出模型中是否具有自我相關變異數不固定的情形是很重要的，以避免模型統 計量被低估，例如 1 1 t = ( ) SE β β ∧ ∧ 因所估計得到的標準誤不是最小，所以t 值被低估，造成錯 誤的推論。因此實證上常用ARCH-LM 檢定與 2 Q 檢定，來設法解決這樣的問題，分別 說明如下：

3.7.1 ARCH-LM 檢定

即為 Lagrange Multiplier Test，由變異數方程式

2 2 2 2 2 0 0 1 1 2 2 1 q t j t j t t q t q j σ α α ε ₋ α α ε₋ α ε₋ α ε₋ = = +

∑

= + + + +_L 若沒有ARCH(q)存在時，即 2 0 t σ =α 為一固定常數，因此可藉由檢定H₀:α α₁= ₂ =L=αq =0，來檢定殘差的變異 數，是否具有齊一性。

3.7.2

2 Q

檢定

此即 3.3.1 節所提到 Ljung-Box 的 Q 統計量，可藉由檢定H₀:α α₁= ₂ =_L=α_q =0， 來檢定殘差的變異數，是否具有齊一性。

第四章 實證分析

本研究蒐集台灣運輸產業中市佔率較高且具代表性的類股進行實證分析，以海運類 公司二家(長榮海運、萬海航運)與航空類公司二家(中華航空、長榮航空)為實例，藉由 1999 年 1 月至 2006 年 12 月共八年內，台灣加權股價指數的公開股價日資料做模式建 構，以此資料為「樣本內資料」，用以實證模型配適度。 資料來源由公開資訊觀測站、台灣經濟新報與聚財網等資料庫取得，以各交易日收 盤價共2023 筆資料，取對數後之比值定義為股價報酬率，做其時間序列分析與預測， 依2007 年 1 月至 2007 年 12 月共一年內的觀測值，共 247 筆資料，以此資料作為「樣 本外資料」，用以評估模式預測的準確程度，並使用相關統計軟體Eviews 加以探討。

另外Stephen A.DeLurigio Forecasting Principles and Applications ㄧ書，提到前置時

間與預測精準度的關係，有此原則：「降低預測時間長度會改善預測精準度、長的前置 時間會使目前增加了未來的不確定性」，且研究構想與數據蒐集時為2008 年期間，2008 整年的資料未齊，故本研究考慮2007 年的樣本外資料長度，對預測結果是否造成影響 加以探討，但萬海航運、長榮航空則引入2008 年資料，分別對 2007 年、2008 年與 2007~2008 年資料進行預測，且能驗證台灣股票市場是否為效率市場，因而在數據收集 與模式上有如此考量。 本章則為台灣運輸類股實證分析與預測，並以圖表與數據呈現研究結果。

4.1 長榮海運股價報酬率實證分析

圖4.1 長榮海運股價原始序列Z 趨勢圖 _t

共計 2023 個資料{ },Z_t t=1, 2,3 2022, 2023_L ，其股價隨時間變化之數列繪製如上 圖，第1 個資料為 1999 年 1 月 5 日；第 1000 個資料為 2002 年 7 月 2 日；第 2000 個資 料為2006 年 11 月 29 日，發現該數列趨勢為先向上漂浮後再下降漂浮，之後又再往上 攀升，可知為不具有固定趨勢、固定水準的非定態時間序列。 圖4.2 長榮海運股價對數序列Y 趨勢圖 _t 此時縱軸為取對數後的股價，數值明顯皆變小，但需放至相同的基準即相同 縱軸，才能進行趨勢比較。 圖4.3 長榮海運股價原始與對數序列趨勢比較圖 資料本身變異程度大，此時間序列的變異數是不穩定的，故取對數能降低原始序列

變異，且能求得其報酬率關係，令Y_t =ln( )Z_t ，{ },Y_t t=1, 2,3 2022, 2023_L ，由上圖可發 現在相同的縱軸座標下，取對數將使數值降低，減少序列的變異程度。 藉由計算時間序列Y ，其落後 p 階的自我相關係數(ACF)與落後 q 階的偏自我相關_t 係數(PACF)，呈現之自我相關圖(Correlogram)，可以協助初步判斷 ARMA 模型可能的 落後階數p、q，而 PACF 可以判斷變數 DGP 之 AR 項階次為何；ACF 則可以判斷變數 DGP 之 MA 項階次為何。 圖4.4 長榮海運時間序列Y 之自我相關圖 _t 從上圖可看出時間序列Y 的自我相關函數(ACF)非常大，隨落後期數增加而緩慢遞_t 減，且偏自我相關函數(PACF)於一階時特別顯著，符合一階自我迴歸模式 AR(1)的特性， 即時間序列Y 的 DGP 可能為_t y_t =0.996y_t−1+ 。 ε_t 但若原始股價時間序列Z ，再取對數後之時間序列_t Y ，仍為非定態型時間序列時，_t 直接將其取迴歸進行分析，將可能產生判定係數極大的假性迴歸現象，造成預測結果與 因果關係的誤判，故應先行測試是否存在單位根，若存在可藉由差分方式，將非定態型 時間序列轉為定態型時間序列，再進行模式之估計與檢定；若不存在單位根，則表示取 對數就能將原始時間序列轉成定態型時間序列，不需再進行差分。

表4.1 長榮海運時間序列Y 單位根檢定表 _t 單位根檢定形式選擇Augmented Dicky-Fuller 檢定法，選擇包含時間趨勢與截距 項，虛無假設為時間序列Y 存在單位根，檢定結果 ADF test 的值為-2.225417，皆大於各_t 顯著水準下(α =0.01,0.05,0.1)的值(-3.962589,-3.412033,-3.127926)，故無法拒絕單位根 存在的虛無假設，即該時間序列Y 為存在單位根的非定態型時間序列。 _t 表4.2 長榮海運時間序列W 單位根檢定表 _t

將取對數後的股價時間序列Y 進行一階差分，令為_t W ，此時亦為 ARIMA(0,1,0)模_t 式，再進行單位根檢定，選擇條件仍為包含時間趨勢與截距項，虛無假設為時間序列Y_t 存在單位根，檢定結果ADF test 的值為-40.71840，皆小於各顯著水準下(α =0.01,0.05,0.1) 的值(-3.962589,-3.412033,-3.127926)，故拒絕單根存在的虛無假設，該時間序列W 為不_t 存在單根的定態型時間序列，亦即一階差分確實能將該時間序列資料，由非定態型時間 序列轉為定態型時間序列，也因此可用ARMA 模式來估計該時間序列。 圖4.5 長榮海運時間序列W 之自我相關圖 _t 計算W 落後 p 階的自我相關函數(ACF)與落後 q 階的偏自我相關函數(PACF)，呈現t 之自我相關圖(Correlogram)具有些許震盪遞減的現象，但此時 PACF 的第一項較不突 出，意指一階條件較不明顯，為避免解讀時發生錯誤，並確保模式正確，仍考慮二階自 我迴歸模式AR(2)與有無截距項的情況，在後續統計分析與預測結果有相關解釋。 在此情況下自我相關圖的判斷較不嚴謹，故使用最小平方法(OLS)去估計W 真正的t

資料產生過程(Data Generating Process)，觀察估計的係數是否顯著，可依此刪去不必要

的落後變數，若暫定模式為AR(1)無截距項、AR(1)有截距項、AR(2)無截距項、AR(2)

有截距項共四種模式，其中AR(1)亦即 ARIMA(1,1,0)、AR(2)亦即 ARIMA(2,1,0)，將各

表4.3 長榮海運 AR(1)無截距項模式估計結果表 將時間序列第 249 個~第 2270 個資料，即 1999~2006 年共 2022 個樣本內資料，做 AR(1)無截距項模式的建構，並使用最小平方法進行參數估計，模式符合以下該式： 1 1.000015 t t t y = y₋ + 。 ε 圖4.6 長榮海運 AR(1)無截距項模式預測結果圖 將時間序列第 2 個~第 248 個資料，即 2007 年共 247 個樣本外資料，做為模式預測 能力的分析，上圖藍線為預測的趨勢圖，且評判指標RMSE 為 0.025948、MAE 為 0.018087、MAPE 為 0.571332(%)。

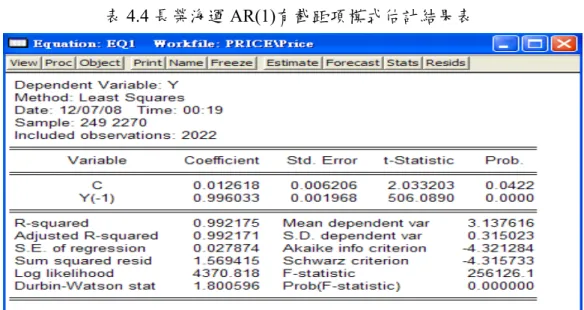
表4.4 長榮海運 AR(1)有截距項模式估計結果表 將時間序列第 249 個~第 2270 個資料，即 1999~2006 年共 2022 個樣本內資料，做 AR(1)有截距項模式的建構，並使用最小平方法進行參數估計，模式符合以下該式： 1 0.012618 0.996033 t t t y = + y₋ + 。 ε 圖4.7 長榮海運 AR(1)有截距項模式預測結果圖 將時間序列第 2 個~第 248 個資料，即 2007 年共 247 個樣本外資料，做為模式預測 能力的分析，上圖藍線為預測的趨勢圖，且評判指標RMSE 為 0.025907、MAE 為 0.018086、MAPE 為 0.571271(%)。

表4.5 長榮海運 AR(2)無截距項模式估計結果表 將時間序列第 249 個~第 2270 個資料，即 1999~2006 年共 2022 個樣本內資料，做 AR(2)無截距項模式的建構，並使用最小平方法進行參數估計，模式符合以下該式： 1 2 1.097837 0.097831 t t t t y = y₋ − y₋ + 。 ε 圖4.8 長榮海運 AR(2)無截距項模式預測結果圖 將時間序列第 2 個~第 248 個資料，調整為第 3 個~第 248 個資料，即 2007 年共 246 個樣本外資料，做為模式預測能力的分析，上圖藍線為預測的趨勢圖，且評判指標RMSE 為0.025643、MAE 為 0.018044、MAPE 為 0.570064(%)。

表4.6 長榮海運 AR(2)有截距項模式估計結果表 將時間序列第 249 個~第 2270 個資料，即 1999~2006 年共 2022 個樣本內資料，做 AR(2)無截距項模式的建構，並使用最小平方法進行參數估計，模式符合以下該式： 1 2 0.013825 1.095617 0.099974 t t t t y = + y₋ − y₋ + 。 ε 圖4.9 長榮海運 AR(2)有截距項模式預測結果圖 將時間序列第 2 個~第 248 個資料，調整為第 3 個~第 248 個資料，即 2007 年共 246 個樣本外資料，做為模式預測能力的分析，上圖藍線為預測的趨勢圖，且評判指標RMSE 為0.025596、MAE 為 0.018012、MAPE 為 0.569056(%)。

將上述 AR 模式在不同階次與有無截距項情況下，預測能力統計指標，整理如下表：

表4.7 長榮海運 AR 模式不同階次與有無截距項之對數股價預測比較表(本研究整理)

AR(1)無截距項 AR(1)有截距項 AR(2)無截距項 AR(2)有截距項

RMSE 0.025948 0.025907 0.025643 0.025596 MAE 0.018087 0.018086 0.018044 0.018012 MAPE 0.571332(%) 0.571271(%) 0.570064(%) 0.569056(%) 由上表研究整理，長榮海運對數股價的預測，在相同階數時有截距項的預測皆較無 截距項來的好，且相同截距情況時AR(2)的預測皆較 AR(1)來的好，而這是由 2007 年的 248 筆交易日資料進行模式驗證所得的預測結果，須注意的是本研究使用對數股價做為 預測數據，以避免報酬率過小造成不易觀察，而兩交易日之對數股價差距才為其股價日 報酬率。 藉由使用均方誤差、絕對平均誤差、絕對平均誤差率三項統計指標，做為模式預測 準確性的參考，以做數字大小的比較，愈小表示預測能力愈好，且研究結果發現，當自 我迴歸階數增加並考量截距項後，誤差值有些許下降，但不明顯，另外也由預測模型簡 約性(parsimony)的基本原則，即一階自我迴歸模型即具有充分的代表性，也說明每筆資 料皆受本身前一期很大的影響。 若以具截距項的一階自我迴歸模式來表示為Zt =a₀+a Z₁ t−₁+ ，即εt 1 0.0126 0.996 t t t Z = + Z₋ + ，用遞迴的概念推算一般化結果如下： ε 1 0.0126 0.996 2 1 t t t Z₋ = + Z₋ +ε₋ 代入上式 2 1 0.0126 0.996(0.0126 0.996 ) t t t t Z = + + Z₋ +ε ₋ + ε 同理Z_t−2 =0.0126 0.996+ Z_t−3+ε_t−2代入上式 3 2 1 0.0126 0.996[0.0126 0.996(0.0126 0.996 ) ] t t t t t Z = + + + Z₋ +ε₋ +ε₋ + ε 反覆代入整理後可得： 1 1 0 0 0 0.0126 (0.996) (0.996) (0.996) t t k t k t t k k k Z Z ε − − − = = =

∑

+ +

∑

兩邊取期望值： 1 ₀ 1 0 0 [ ] [0.0126 (0.996) ] [(0.996) ] [ (0.996) ] t t k t k t t k k k E Z E E Z E ε − − − = = =

∑

+ +

∑

1 0 0 [ ] 0.0126t (0.996)k (0.996)t t k E Z Z − = =

∑

+ ；Z 為時間序列起始值 ₀ 且因為a₁ =0.996 1< ，為收斂的情況，故此具截距項的一階自我迴歸模型時間序列， 其變數符合長期均衡存在的條件。

將長榮海運原始股價資料做基本觀察，看其平均數、標準差、偏態係數、峰態係數 等指標，且可由相關統計量測試其形成之機率分配，是否屬於常態分配或具有獨立性。 表4.8 長榮海運樣本內資料不同年度區間原始股價資料表(本研究整理) 時間間隔 1999~2002 2003~2006 1999~2006 樣本數 1027 996 2023 平均數 22.47 25.89 24.15 標準差 8.4370141 4.7913654 7.0993279 偏態係數 0.5992228 0.2651008 0.2048545 峰態係數 -0.4309919 -0.7437412 -0.2862502 表4.9 長榮海運股價、對數股價、股價報酬率基本資料分析表(本研究整理) 當統計量服從常態分配時 Skewness=0、Kurtosis=3，且 JB 統計量為 0，可由 Skewness 來判斷該機率分配的偏離程度，該值>0 時為右偏分配；<0 則為左偏分配，可由 Kurtosis 來判斷該機率分配的離峰程度，該值>3 時為高狹峰分配；<3 則為低狹峰分配，Pearson 實證也說明機率分配右偏時，平均數>中位數>眾數。 因此由上表可發現股價及股價報酬率皆大於 0，平均數也大於中位數，為右偏分配， 對數股價則為左偏分配，而只有股價報酬率Kurtosis 才大於 3，且非常明顯，形成非常 陡峭的高狹峰分配(leptokurtic)。 也由於上述性質和 JB 統計量異於 0，故傳統上常態分配的統計假設在實證上是值 得商確的，而一般結果顯示股價報酬率具有尖峰厚尾(heavy tails)的特性，不為常態分

配，本研究此實例符合此一般化結果。 圖4.10 長榮海運股價報酬率變動圖 觀察長榮海運股價報酬率發現有波動群聚(volatility clustering)的現象，即大波動通 常跟隨著大波動、小波動通常跟隨著小波動，而ARCH 模式能夠解釋並應用這樣的情形。 圖4.11 長榮海運時間序列W 殘差之自我相關圖 t 針對模型之殘差進行是否存在自我相關之 Q 檢定，發現 1 至 18 期的 p 值皆小於顯 著水準5%，1 至 12 期的 p 值皆小於顯著水準 1%，故無法拒絕各期間皆沒有自我相關