報告題名:
以大型顯示器為基礎之使用者行為研究
作者:張翔超、林琮琦、鄭鎧霆、丁瑞豪、文祥任、丘緒瀚、洪祺明 系級:工三乙 學號:D9667733、D9667598、D9667524、D9633529、D9667422、D9667393、 D9667483 指導教授:唐國豪 課程名稱:人因工程 開課系所:工業工程與系統管理學系 開課學年: 98 學年度 第 二 學期摘要
這是一個最黑暗的年代,也是一個最光明的年代。在現今這個高發展、高淘 汰率的社會下,發明者秉持著好,還要更好的理念,一再的嘗試與突破,希望能 滿足慾望深不見底的消費者,因此物品的變化是如此多元,然而在這變幻無窮的 環境下,物件不是變得比以往的大要不就是比之前小,當然電腦螢幕顯示器也不 例外。人在大螢幕下的使用行為是一門值得我們去探討的課程,然而在這嶄新的 課程中探討的內容為人在大螢幕(大螢幕分為曲面螢幕和平面螢幕)下的使用行 為,而主要研討方面為移動視窗的反應時間、螢幕中心點與視窗 X 軸之距離和 視窗 X 軸移動距離這些因子是否會因螢幕類型的不同而有差異。受測者以距離 正前方螢幕 75cm 進行測試,設受測者面對前方螢幕為 0 度,在受測者往左方偏 移 15 度、30 度及 45 度處放置 12 個視窗,受測時會先跳出 Message Box 告知受測 者要執行什麼動作,按確定鍵後指定的視窗會由工作列彈出讓受測者進行測試, 測試完畢關閉後又會跳出下一個 Message Box 讓受測者進行實驗,直到 12 種視窗 做完為止。由上述的測試方法中可以得知受測者在不同的螢幕類型下決定移動視 窗的反應時間是沒有差異的,然而螢幕中心點與視窗 X 軸之距離和視窗 X 軸移 動距離有明顯的差別。將螢幕不同類型的差異性運用至現今這創新的時期,使未 來的螢幕顯示器能更符合人的需求。關鍵字:
大螢幕致謝
此次實驗專題承蒙指導老師 唐國豪教授,感謝他在實驗過程中細心指導我 們做實驗的理論與步驟,以及對於實驗的分析方式,也給予許多強而有力的建 議,使我們在實驗的過程能更加順利,解開我們各種疑惑,讓本次實驗能順利進 行,並進而達到完成的目的;於此同時,亦特別感謝漂亮的岳樺學姐在這次專題 中,從剛開始討論專題到最後完成,岳樺學姐有耐心且不厭其煩的指點我們專題 的概念、步驟和實驗的設計及分析方法。雖然在實驗過程中一直遇到許多困難, 例如:儀器的架設、程式的問題等狀況,學姐都會盡心盡力的替我們找出適合的 建議給予我們參考,她常掛在嘴邊的一句話:『試試看嘛,你可以的』。讓我們理 解自己還有更大的進步空間與發展,多一點嘗試便有突破瓶頸的可能,也因為有 如此的鼓勵,我們才能不放棄任何希望,在不斷的嘗試及失敗中,找尋到正確的 目標,以不至於迷失方向,從而完成本次的專題。 除此之外,更要感謝資訊系鱉鱉學長等三人,因應我們的要求一改再改,將 實驗最不可或缺的程式完成。當然也要感謝組員間的相互配合,還有我們主要實 驗的受測者:宜貞、依玲、岳軒、尹瑋、思妤,感謝他們在百忙之中,抽出自己 那一點空閒時間,不辭勞苦的位我們的專題出一份力,讓我們的實驗能夠不受阻 礙如期完成。專題製作分工描述
張翔超:文獻、結論、上台報告、修改書面內容 林琮琦:分析數據、緒論 丁瑞豪:摘要、動機、目的 鄭鎧霆:分析數據、上台報告、修改書面內容 丘緒瀚:參考文獻、Power point 製作 文祥任:程式撰寫、分析數據 洪祺明:Power point 製作、致謝目 錄
摘要………1 致謝………2 專題製作分工描述………3 目錄………4 圖目錄………6 表目錄………9 第一章 緒論 ………10 第二章 文獻探討 ………12 2.1 大螢幕趨勢 ………12 2.2 使用者行為 ………13 2.3 與一個螢幕或雙螢幕比較 ………14 第三章 實驗方法設計與架構 ………17 3.0 前測實驗 ………17 3.1 實驗環境設定 ………20 3.1.1 曲面測試方式 ………21 3.1.2 平面側試方式 ………21 3.1.3 實驗程式設定流程 ………21 3.1.4 受測者選定 ………323.1.5 電腦工作站………32 3.1.6 電腦螢幕工作站條件………32 3.1.7 本專題實驗要求的環境因素………34 3.2 實驗設備………34 3.3 實驗流程………39 3.4 實驗作業及變數………43 第四章 分析與結果………44 第五章 結論………96 參考文獻………97
圖目錄
圖 2.0:螢幕解析度比較圖(Website Desigh & Screen Resolution)………12
圖 2.2:拼接螢幕與大螢幕滑鼠點擊比較圖(Bi and Balakrishnan, 2009) ………14
圖 2.3-1 作業內容(Bi and Balakrishnan, 2009) ………15
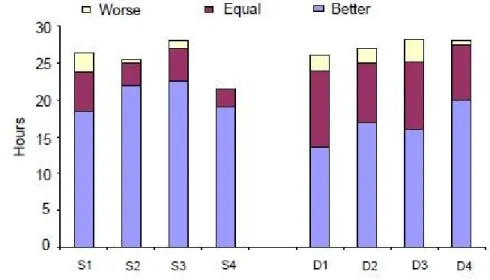
圖 2.3-2 單螢幕受測者(S1~S4)和雙螢幕受測者(D1~D4)使用感覺比較圖 (Bi and Balakrishnan, 2009)………15
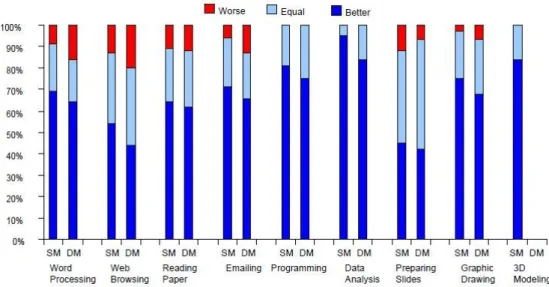
圖 2.3-3 各個作業內容受測者使用單一螢幕和雙螢幕感覺圖 (Bi and Balakrishnan, 2009) ………16
圖 2.3-4 單螢幕受測者(S1~S4)和雙螢幕受測者(D1~D4)視窗使用行為 …………16 圖 3.0 前測裝置圖 ………18 圖 3.1.2-1 Set 檔………21 圖 3.1.6 正確坐姿………33 圖 3.2-1 曲面螢幕………34 圖 3.2-2 曲面三台投影機………35 圖 3.2-3 曲面背投影………35 圖 3.2-4 曲面施測者量側受測者與螢幕之間的距離為 75 公分………36 圖 3.2-5 曲面受測者進行測試………36 圖 3.2-6 平面螢幕………37 圖 3.2-7 平面三台投影機………37
圖 3.2-8 平面背投影………38 圖 3.2-9 平面施測者量側受測者與螢幕之間的距離為 75 公分………38 圖 3.2-10 平面受測者進行測試………39 圖 3.1.2-1 BBWinLog 執行檔………40 圖 3.1.2-2 BBWinLog 執行檔執行後畫面………40 圖 3.1.2-3 訊息視窗………41 圖 3.1.2-4 最小化作業視窗………41 圖 3.1.2-5 作業視窗於 45°位置………41 圖 3.1.2-6 作業視窗於 15°位置………42 圖 3.1.2-7 作業視窗於 30°位置………42 圖 3.1.2-8 程式設定………42 圖 4.1 角度與決定移動時間之關係圖 ………48 圖 4.2 作業時間與決定移動時間之關係圖 ………50 圖 4.3 互動方式與決定移動時間之關係圖 ………51 圖 4.4 角度*作業時間的交互作用與決定移動時間之關係圖………52 圖 4.5 角度*互動方式的交互作用與決定移動時間之關係圖………53 圖 4.6 作業時間*互動方式的交互作用與決定移動時間關係圖………55 圖 4.7 平、曲面與 X 軸最大移動距離之關係圖 ………60 圖 4.8 角度與 X 軸最大移動距離之關係圖 ………61
圖 4.9 作業時間與 X 軸最大移動距離之關係圖………63 圖 4.10 互動方式與 X 軸最大移動距離之關係圖 ………64 圖 4.11 平曲面*角度的交互作用與 X 軸最大移動距離之關係圖 ………65 圖 4.12 角度*作業時間的交互作用與 X 軸最大移動距離之關係圖 ………66 圖 4.13 作業時間*互動方式的交互作用與 X 軸最大移動距離之關係圖…………68 圖 4.14 平曲面*互動方式的交互作用與 X 軸最大移動距離之關係圖 …………69 圖 4.15 角度*互動方式的交互作用與 X 軸最大移動距離之關係圖 ………70 圖 4.16 平曲面*角度*作業時間與 X 軸最大移動距離之三階關係圖 ………72 圖 4.17 角度*作業時間*互動方式與 X 軸最大移動距離之三階關係圖 …………75 圖 4.18 平曲面與視窗距螢幕中心距離之關係圖 ………81 圖 4.19 角度與視窗距螢幕中心距離之關係圖………82 圖 4.20 作業時間與視窗距螢幕中心距離之關係圖………84 圖 4.21 互動方式與視窗距螢幕中心距離之關係圖………85 圖 4.22 角度*作業時間與視窗距螢幕中心距離之關係圖 ………86 圖 4.23 角度*互動方式與視窗距螢幕中心距離之關係圖 ………87 圖 4.24 平曲面*互動方式與視窗距螢幕中心距離之關係圖 ………89 圖 4.25 作業時間*互動方式與視窗距螢幕中心距離之關係圖 ………90 圖 4.26 平曲面*角度*作業時間與視窗距螢幕中心距離之三階關係圖 …………92 圖 4.27 角度*作業時間*互動方式與視窗距螢幕中心距離之三階關係圖 ………94
表目錄
表 3.1.3-1 視窗初期大小………22 表 3.1.3-2 各角度視窗之中心點 ………26 表 3.1.3-3 以 15 度受測時各視窗的左上角端點位置 ………26 表 3.1.3-4 以 30 度受測時各視窗的左上角端點位置 ………26 表 3.1.3-5 以 45 度受測時各視窗的左上角端點位置 ………27 表 3.1.3-6 而各角度視窗之中心點 ………31 表 3.1.3-7 以 15 度受測時各視窗的左上角端點位置………31 表 3.1.3-8 以 30 度受測時各視窗的左上角端點位置………31 表 3.1.3-9 以 45 度受測時各視窗的左上角端點位置………32 表 4.1 決定移動的時間之重複量數分析………44 表 4.2 調整後決定移動時間的角度之成對比較………49 表 4.3 X 軸方向最大移動距離之重複量數分析 ………56 表 4.4 X 軸最大移動距離的角度之成對比較 ………62 表 4.5 距螢幕中心點距離之重複量數分析………77 表 4.6 距螢幕中心距離的角度之成對比較………83第一章 緒論
這是一個最黑暗的年代,也是一個最光明的年代。在現今這個高發展、高淘 汰率的社會下,發明者秉持著好,還要更好的理念,一再的嘗試與突破,希望能 滿足慾望深不見底的消費者,因此物品的變化是如此多元,然而在這變幻無窮的 環境下,物件不是變得比以往的大要不就是比之前小,當然電腦螢幕顯示器也不 例外。隨著大螢幕的趨勢 14 吋到 21 吋的螢幕似乎已成為過去,許多工作站(金 融業、房地產業、遊戲廠商…)已經開始運用多台顯示器和拼接螢幕,其原因不 乏是工作效率提升、更有臨場感… 等。順著大螢幕的潮流,為使人與電腦螢幕 的互動更加良好,故須探討人在大螢幕下的使用行為,使用者在平時開啟的視窗 量平均數為 10AP,這樣的行為是否是受限於螢幕的大小而將視窗縮至最小化? 但是在大視窗的效應下,視窗擺放不再受限於螢幕大小了,因為螢幕大到可以一 次擺放多個視窗,但使用行為會因此而改變嗎?由 Bi and Balakrishnan(2009)所撰寫的文獻-Comparing Usage of a Large High-Resolution Display to Single or Dual
Desktop Displays for Daily Work 可以得知:
受測者在 dual-monitor 與 large display 下鼠標的移動行為。
z single-monitor 與 dual-monitor 來操作日常使用的程式的喜好。
z single-monitor、dual-monitor 和 large display3 種情況下開啟視窗作視窗調 整的頻率。
然而這份文獻並沒有提到受測者在曲面螢幕的使用行為,被好奇心沖昏頭的我們 希望能窺探未來的雛形,因而決定探討人在大螢幕下的使用行為。 目前工研院以發展出可彎曲軟性顯示器,可彎曲軟性顯示器除了可彎曲、折 疊而且還很輕薄,還有一特點是亮度大幅提高,其反射率達到 25~30%,實物影 像呈現具相當真實性。在這個創新的時期,人們對於新事物的接受度也相對的提 升許多,況且現今資訊的接收量也比以往要來的快、要來的多,舉凡從電影情節 中可以想像、嚮往未來的雛形,在這些因子的推波助瀾下,想必軟性顯示器會成 為未來人們使用上的一個趨勢(在螢幕方面 NEC 和 CES 相繼推出曲型螢幕)。由 此現象更能確定曲面螢幕的趨勢,相信曲面螢幕將會運用至電腦螢幕上。順著時 代的洪流,和伴隨在腦中的求知慾,在這兩股交錯的氛圍下,明確的指出應前往 的方向-研究人在大螢幕下的使用行為。人在大螢幕下的使用行為(Resize、 move、maximize、minimize、destroy、activate、視窗擺放位置…)是一門值得我們 去探討的課程,然而在這嶄新的課程中探討的內容為人在大螢幕(大螢幕方面又 分為曲面螢幕和平面螢幕)下的使用行為,而主要研討方面為移動視窗的反應時 間、螢幕中心點與視窗 X 軸之距離和視窗 X 軸移動距離這些因子是否會因螢幕 類型的不同而有差異。
第二章 文獻探討
隨著 LCD 製造廠商的技術成熟及消費者對桌上型電腦螢幕顯示器尺寸的需
求漸增,電腦螢幕尺寸有逐年加大的趨勢,如圖 2.0 所示,高螢幕解析度的需求
逐年增加,截至 2010 年 1 月為止,超過 70%的電腦使用者,使用高於 1024*768
螢幕解析度
。
圖 2.0:螢幕解析度比較圖(Website Desigh & Screen Resolution)
2.1 大螢幕趨勢
隨著越來越多的使用者使用應用程式來處理不同類型的訊息,往往需要更多 的螢幕來進行工作。在過去的十年間,螢幕尺寸從 15 吋增加至 21 吋,更多的使 用者也開始依賴於多台顯示器。事實上,最近的研究舉出許多在個人工作站使用 更大螢幕的好處。當然,科技的發展一日千里,現在的技術使顯示器越做越大, 而許多的使用者對於其價格也都負擔得起。目前,其中一個最大的液晶顯示器是來使用者可以很容易地把整個牆壁變成螢幕。現在,我們可以很容易的做到這一 點,方法是利用多台投影機進行投影拼接成一個無縫的螢幕顯示器,在研究實驗 室進行研究,這種方法是可行的,但很可惜的是並沒有很廣泛使用。
2.2 使用者行為
不管是雙螢幕還是大螢幕都會讓受測者在心理上將畫面分割成主要作業區 和次要作業區。一般來說,主要作業區通常被用來編寫代碼、文字處理、編輯圖 形、圖像或繪圖,大多數的互動活動都會因為時間而行為有所改變,而次要作業 區通常被應用於次主要的作業,像是 E-mail 的收發、即時通訊和個人備忘錄。 使用兩個拼接螢幕,受測者在中心作業遠比放置於周邊來的多,根據 Bi and Balakrishnan(2009)的研究報告顯示,71%滑鼠點擊在單一螢幕,29%則在其他周 邊,如圖二所示。根據使用兩台螢幕的受測者的實驗報告,通常中心點的螢幕位 置為焦點作業地區,其他周邊區域則作為外設,由於顯示器的面板,跨越一個窗 口在兩個顯示器上會有視覺不連續,因此主要活動較局限於一台顯示器。然而, 當使用兩台拼接螢幕的受測者在大螢幕下工作時,81%的滑鼠點擊率在螢幕中 間,剩下的 19%則在其他區域並且呈現所謂的"倒 U 型" 所以該中心區域被用 來作為主要作業區,其他區域則為次要作業區。這樣分佈比較有可能的解釋是受 測者的坐姿,由於受測者坐在大螢幕的水平中心點位置,中心位置對於使用者來 說是最近的使用區域,並且容易且方便查看和互動。因此,使用者焦點工作的位 置在中心點區域,周圍的工作區域則較少被注意和使用。圖 2.2:拼接螢幕與大螢幕滑鼠點擊比較圖(Bi and Balakrishnan, 2009)
2.3 單螢幕或雙螢幕比較
根據 Bi and Balakrishnan(2009)的研究報告裡所配置的實驗,在單螢幕和雙螢
幕下都有讓 8 位受測者進行相同的一些作業內容,如圖 2.3-1,而我們實驗則擷
取前三項網頁瀏覽(Web Browsing)、文字編輯(Word Processing)、閱讀文章
(Reading Paper)做為我們的實驗的作業內容。而在 Bi and Balakrishnan(2009)所做
的統計圖表裡,如圖 2.3-2,顯示了每個受測者的主觀意見,原本使用單一螢幕 的受測者會比起雙螢幕更佳偏愛使用大螢幕,並且顯示出單一螢幕的受測者使用 大螢幕,有 81%認為一個小時的工作裡認為效果是好的,相較於使用雙螢幕只 有 61%,但相較於小螢幕,還是有些視窗受測者認為在單一螢幕上操作,比起 在雙螢幕或大螢幕上效果要來的好,如圖 2.3-3。受測者對於不同的訊息視窗有 不一樣的處理模式,如圖 2.3-4,有一個相同的特徵是所有受測者都有的,就是 有很高的比例在操作移動和縮放比起一般環境要來的頻繁。對於使用單一螢幕受 測者來說,在大螢幕下平均移動和縮放的比率是 51.5%(std.dev.= 2.4%),而 在單螢幕上則是 16.7%(std.dev.= 6.1%),對於雙螢幕受測者,在大螢幕下平 均移動和縮放的比率是 58.5%(std. dev.= 2.4%),而在雙螢幕上則是 29.5%
(std.dev。= 9.7%)。
圖 2.3-1 作業內容(Bi and Balakrishnan, 2009)
圖 2.3-2 單螢幕受測者(S1~S4)和雙螢幕受測者(D1~D4)使用感覺比較圖 (Bi and Balakrishnan, 2009)
圖 2.3-3 各個作業內容受測者使用單一螢幕和雙螢幕感覺圖 (Bi and Balakrishnan, 2009)
圖 2.3-4 單螢幕受測者(S1~S4)和雙螢幕受測者(D1~D4)視窗使用行為 (Bi and Balakrishnan, 2009)
第三章 實驗方法設計與架構
3.0 前測實驗
1. 時間:2010 年 5 月 22 日 2. 受測者:丁丁、緒瀚、琮琦 獨立變數:角度、作業型態、作業時間、專注力高低。 相依變數:反應時間、調整視窗大小、調整視窗位置。 測試方法:以背投影進行測試,將影像投影至壓克力板上,壓克力版左 上方及右上方有兩個小孔,將線來回穿過小孔,使壓克力板懸空,另一 段繫於天花板上,投影至壓克力板上的兩個視窗寬為 92 公分高為 35 公分。為避免受測者有學習效應故使用 Method of Constant Stimuli 進行測
試,此為施測者以隨機的角度進行測試,測試玩讓受測者休息 20 分鐘
後在進行下次測試(Ex:丁丁進行 25 度測試,緒瀚進行 15 度測試,琮
圖 3.0 前測裝置圖 3. 測試內容:受測者以距離正前方螢幕 75cm 進行測試,設受測者面對前 方螢幕為 0 度,在受測者往左方偏移 15 度、25 度及 36 度處放置 8 個視 窗,且視窗位於所限定度數之中央。視窗初期大小如下。 表 3.0 原始視窗大小 z 查看天氣 Wide:304 Hight:589 z 輸入生日 Wide:423 Hight:314 z 大家來找碴 Wide:477 Hight:408 z 輸入序號 Wide:423 Hight:314 z 釣魚遊戲 Wide:486 Hight:426 z 看影片找單字 Wide:615 Hight:428
z 皮卡丘打排球 Wide:438 Hight:357 z 欣賞影片 Wide:530 Hight:382 單位(像素) 一相數約為 1/19 公分 當受測者以偏移 15 度時,其正前方螢幕之中端距離左方螢幕的距離約為 20.97CM(tan15=x/75,其 x 為正前方螢幕之中端和左方螢幕的距離),偏移 25 度 時距離約為 34.97CM(tan25=x/75,其 x 為正前方螢幕之中端和左方螢幕的距離), 而當正前方螢幕距離左方螢幕 55CM 時其角度約為 36.254 度(tan^1(55/75)),茲 因壓克力板布夠大塊,故以壓克力板的長度作為調整。在受測者進行測試時以 SCREXES(錄影程式)記錄受測者多久會移動視窗,在以 PicPick 來記錄視窗移動的 位置、距離和縮放大小。
3.1 實驗環境設定
曲面設備配置:將受測者位置固定,以受測者眼睛的位置為圓心,畫出半徑 75 公分的圓弧,將壓克力(長:180 寬:60)板沿著畫出圓之軌跡擺放並以書本等 重物將其固定,避免壓克力板彈開。為加強曲面弧度固定在壓克力板四邊的孔以 線將上端兩點固定,下端兩孔如同上端做法將其固定(線長約 142cm)。 平面設備配置:將受測者為置固定,以受測者眼睛的位置前方 75 公分處垂 直桌面架設壓克力板,在壓克力左上及右上方鑽兩小孔,以線吊於天花板上,使 壓克力板垂直於桌面,桌面再以厚重書本固定壓克力板位置。 實驗以 3 台投影機進行背投影測試,為使 3 面投影看起來像 1 面螢幕進行矯 正(移動投影機、對焦…等工作)。為使實驗操作更加順暢,本次使用無線滑鼠和 鍵盤。在投影方面是利用 2 個 VE200(外接顯示擴充卡)使投影看起來像一體成型。 一台投影機投影出的螢幕寬約 52 公分其算法如下: 2πR×60/360×2=157cm(R=75cm ,2 邊度數相等) 157/3 約為 52cm(要投影成 3 個畫面故除以 3)3.1.1 曲面測試方法
受測者以距離正前方螢幕 75cm 進行測試,設受測者面對前方螢幕為 0 度,
在受測者往左方偏移 15 度、30 度及 45 度處放置 12 個視窗,(其視窗類型分為
Microsoft Word、Adobe Pdf、Microsoft IE、Flash 遊戲、Microsoft Media Player、
Microsoft 小畫家和 Microsoft 記事本等 7 種類型)而視窗的中心點會位於指定的 Pixel。
3.1.2 平面測試方法
同曲面的測試方法進行測試。3.1.3 實驗程式設定流程
將須使用的視窗路徑和大小設定好並將設定好的資訊打在 set 組態設定值上在設定時會看見 Path Name Command Message X Y W H|上述字串的
代表分別為指定開啟檔案的路徑、指定開啟的檔案、視窗彈出的位置、視窗大小。
表 3.1.3-1 視窗初期大小如下。 z 基本資料 Wide:408 Hight:412 z 圖片 Wide:434 Hight:434 z 問卷 Wide:544 Hight:572 z 無名 Wide:744 Hight:506 z 輸入序號 Wide:544 Hight:572 z 天氣 Wide:744 Hight:506 z 釣魚遊戲 Wide:606 Hight:472 z 文章 Wide:576 Hight:612 z 單字 Wide:744 Hight:506 z 統計圖 Wide:544 Hight:572 z IE 搜尋 Wide:744 Hight:506 z 影片 Wide:472 Hight:444 單位(像素) 一像素約為 1/19 公分 表 3.1.3-1 的視窗大小都是經過設計,根據不同類型和顯示不同的內容而 做調整,讓受測者可以清楚了解視窗裡的內容,以至於不會因為看不清楚內部字 串無法充分了解而馬上做出 Move、Resize 的動作。
曲面:
設受測者正前方為 0 度,當受測者以偏移 15 度時,Word 視窗中心位置 為 Wide:877,Hight:98其算法如下: 2πr × 15/360 = 19.635 公分 r = 75(公分) 1024(像素):52(公分) = X(像素):19.635(公分) X = 1024×19.635/52(像素) X = 386.462(像素) 1024+(512-386.462)=1149.538(像素) 先將曲面公分數算出後,在以比例關係算出 X。設一個螢幕的 Pixel(Picture element)為 1024 × 768,則 Wide 一半為 512。1024+512-386.462 = 1149.538(386.462 為 19.635 公分換成像素),故視窗中心點為 Wide:1149 Hight:384,因為需 求為視窗左上方的端點故 Wide = 1149.538-272 = 877.538 Hight = 384–286 =98(之前量出 Word 視窗右下方的點為 Wide:544 Hight:572,故將視窗中心點
設受測者正前方為 0 度,當受測者以偏移 30 度時,Word 視窗中心位置為 Wide:490,Hight:98其算法如下: 2πr × 30/360 = 39.270 公分 r = 75(公分) 1024(像素):52(公分) = X(像素):39.27(公分) X = 1024×39.27/52(像素) X = 773.317(像素) 1024+(512-773.317)=762.683(像素) 先將曲面公分數算出後,在以比例關係算出 X。設一個螢幕的 Pixel(Picture element)為 1024 × 768,則 Wide 一半為 512。1024+512-773.317= 762.683(773.317 為 39.27 公分換成像素),故視窗中心點為 Wide:762 Hight:384,因為需求視
窗左上方的端點故 Wide = 762-272= 490 Hight = 384–286 =98 (之前量出 Word 視
窗右下方的點為 Wide:544 Hight:572,故將視窗中心點-Word 視窗右下方
設受測者正前方為 0 度,當受測者以偏移 45 度時,Word 視窗中心位置為 Wide:104,Hight:98其算法如下: 2πr × 45/360 = 58.905 公分 r = 75(公分) 1024(像素):52(公分) = X(像素):58.905(公分) X = 1024×58.905/52(像素) X = 1159.975(像素) 1024+(512-1159.975)=376.025(像素) 先將曲面公分數算出後,在以比例關係算出 X。設一個螢幕的 Pixel(Picture element)為 1024 × 768,則 Wide 一半為 512。1024+512-1159.975= 376.025(1159.975 為 58.905 公分換成像素),故視窗中心點為 Wide:376 Hight:384,因為需求
為視窗左上方端點故 Wide = 376-272 = 104 Hight = 384–286 =98(之前量出 Word 視
窗右下方的點為 Wide:544 Hight:572,故將視窗中心點-Word 視窗右下方端
至於其他種類視窗中心位置算法如上(各角度視窗之中心點)-(視窗右下方邊 框之端點 Wide 和 Hight 的值除以 2(視窗初期大小)) 表 3.1.2-2 各角度視窗之中心點分別為: z 15 度 Wide:1149 Hight:384 z 30 度 Wide:762 Hight:384 z 45 度 Wide:376 Hight:384 表 3.1.3-3 以 15 度受測時各視窗的左上角端點位置如下 z 基本資料 Wide:945 Hight:178(記事本) z 圖片 Wide:932 Hight:167(小畫家) z 問卷 Wide:877 Hight:98(Word) z 無名 Wide:777 Hight:131(IE) z 輸入序號 Wide:877 Hight:98(Word) z 天氣 Wide:777 Hight:131(IE) z 釣魚遊戲 Wide:846 Hight:148 z 文章 Wide:861 Hight:78(Pdf) z 單字 Wide:777 Hight:131(IE) z 統計圖 Wide:877 Hight:98(Word) z IE 搜尋 Wide:777 Hight:131(IE) z 影片 Wide:913 Hight:162 表 3.1.3-4 以 30 度受測時各視窗的左上角端點位置如下 z 基本資料 Wide:558 Hight:178(記事本) z 圖片 Wide:545 Hight:167(小畫家) z 問卷 Wide:490 Hight:98(Word) z 無名 Wide:390 Hight:131(IE) z 輸入序號 Wide:490 Hight:98(Word) z 天氣 Wide:390 Hight:131(IE) z 釣魚遊戲 Wide:459 Hight:148 z 文章 Wide:474 Hight:78(Pdf) z 單字 Wide:390 Hight:131(IE) z 統計圖 Wide:490 Hight:98(Word) z IE 搜尋 Wide:390 Hight:131(IE) z 影片 Wide:526 Hight:162
表 3.1.3-5 以 45 度受測時各視窗的左上角端點位置如下 z 基本資料 Wide:172 Hight:178(記事本) z 圖片 Wide:545 Hight:167(小畫家) z 問卷 Wide:104 Hight:98(Word) z 無名 Wide:4 Hight:131(IE) z 輸入序號 Wide:104 Hight:98(Word) z 天氣 Wide:4 Hight:131(IE) z 釣魚遊戲 Wide:73 Hight:148 z 文章 Wide:88 Hight:78(Pdf) z 單字 Wide:4 Hight:131(IE) z 統計圖 Wide:104 Hight:98(Word) z IE 搜尋 Wide:4 Hight:131(IE) z 影片 Wide:140 Hight:162
平面:
設受測者正前方為 0 度,當受測者以偏移 15 度時,Word 視窗中心位置 為 Wide:877,Hight:98其算法如下: tan15=x/75 x=20.096cm 1024(像素):52(公分) = P(像素):20.096(公分) P = 1024×20.096/52(像素) P = 395.740(像素) 1024+(1024-396)=1652 (像素) 先將平面公分數算出後,在以比例關係算出 P。設一個螢幕的 Pixel(Picture element)為 1024 × 768。1024+(1024-395.740)=1652.26 (395.740 為 20.096 公分換成像 素),故視窗中心點為 Wide:1652 Hight:384,因為需求為視窗左上方的端點故 Wide = 1652-272 = 1380 Hight = 384–286 =98 (之前量出 Word 視窗右下方的點
為 Wide:544 Hight:572,故將視窗中心點-Word 視窗右下方端點的一半,
設受測者正前方為 0 度,當受測者以偏移 30 度時,Word 視窗中心位置為 Wide:1195,Hight:98其算法如下: tan30=x/75 x=43.302cm 1024(像素):52(公分) = P(像素):43.302(公分) P = 1024×43.302/52(像素) P = 852.705(像素) 1024+(1024-853)=1195(像素) 先將平面公分數算出後,在以比例關係算出 P。設一個螢幕的 Pixel(Picture element)為 1024 × 768。1024+(1024-852.705)=1195.295 (852.705 為 43.301 公分換成 像素),故視窗中心點為 Wide:1195 Hight:384,因為需求為視窗左上方的端
點故 Wide = 1195-272 = 923 Hight = 384–286 =98 (之前量出 Word 視窗右下方的
而得到兩點之間的 Pixel 的距離)。 設受測者正前方為 0 度,當受測者以偏移 45 度時,Word 視窗中心位置為 Wide:571,Hight:98其算法如下: tan45=x/75 x=75cm 1024(像素):52(公分) = P(像素):75(公分) P = 1024×75/52(像素) P = 1476.923(像素) 1024+(1024-1477)=571(像素) 先將平面公分數算出後,在以比例關係算出 P。設一個螢幕的 Pixel(Picture element)為 1024 × 768。1024+(1024-1476.923)=571.077 (1476.923 為 75 公分換成像 素),故視窗中心點為 Wide:571 Hight:384,因為需求為視窗左上方的端點故
Wide = 571-272 = 923 Hight = 384–286 =98 (之前量出 Word 視窗右下方的點為
到兩點之間的 Pixel 的距離)。 至於其他種類視窗中心位置算法如上(各角度視窗之中心點)-(視窗右下方邊 框之端點 Wide 和 Hight 的值除以 2(視窗初期大小)) 表 3.1.3-6 而各角度視窗之中心點分別為: z 15 度 Wide:1652 Hight:384 z 30 度 Wide:1195 Hight:384 z 45 度 Wide:571 Hight:384 表(二) 表 3.1.3-7 以 15 度受測時各視窗的左上角端點位置如下 z 基本資料 Wide:1148 Hight:178(記事本) z 圖片 Wide:1435 Hight:167(小畫家) z 問卷 Wide:1380 Hight:98(Word) z 無名 Wide:1280 Hight:131(IE) z 輸入序號 Wide:1380 Hight:98(Word) z 天氣 Wide:1280 Hight:131(IE) z 釣魚遊戲 Wide:1349 Hight:148(Flash) z 文章 Wide:1364 Hight:78(Pdf) z 單字 Wide:1280 Hight:131(IE) z 統計圖 Wide:1380 Hight:98(Word) z IE 搜尋 Wide:1280 Hight:131(IE)
z 影片 Wide:1416 Hight:162(Media Player) 表 3.1.3-8 以 30 度受測時各視窗的左上角端點位置如下 z 基本資料 Wide:991 Hight:178(記事本) z 圖片 Wide:978 Hight:167(小畫家) z 問卷 Wide:923 Hight:98(Word) z 無名 Wide:823 Hight:131(IE) z 輸入序號 Wide:923 Hight:98(Word) z 天氣 Wide:823 Hight:131(IE) z 釣魚遊戲 Wide:892 Hight:148(Flash) z 文章 Wide:907 Hight:78(Pdf) z 單字 Wide:823 Hight:131(IE) z 統計圖 Wide:923 Hight:98(Word) z IE 搜尋 Wide:823 Hight:131(IE)
表 3.1.3-9 以 45 度受測時各視窗的左上角端點位置如下 z 基本資料 Wide:367 Hight:178(記事本) z 圖片 Wide:354 Hight:167(小畫家) z 問卷 Wide:299 Hight:98(Word) z 無名 Wide:199 Hight:131(IE) z 輸入序號 Wide:299 Hight:98(Word) z 天氣 Wide:199 Hight:131(IE) z 釣魚遊戲 Wide:268 Hight:148(Flash) z 文章 Wide:283 Hight:78(Pdf) z 單字 Wide:199 Hight:131(IE) z 統計圖 Wide:299 Hight:98(Word) z IE 搜尋 Wide:199 Hight:131(IE)
z 影片 Wide:335 Hight:162(Media Player)
3.1.4 受測者選定
以逢甲大學工業工程與系統管理學系大學部三年級的學生為主,需具備人因 工程學科的基礎、清楚明白實驗程序並且可以客觀做判斷的大學部三年級學生為 主,前測 5 位、正式實驗 12 位受測者。3.1.5 電腦工作站
一個電腦工作站主要包括有工作桌、座椅、投影螢幕、無線鍵盤、無線滑鼠、 電腦主機、及相關電腦周邊設備。當然,作業人員也是不可缺少的主角。3.1.6 電腦螢幕工作站條件
(一)視距
操作電腦時,眼睛到螢幕中心的距離,稱為視距。正常工作站的視距建議為 60 到 80 公分,我們實驗視距訂定為 75 公分。(二)身體姿勢
1. 頭部:距離螢幕一個手臂長,螢幕在眼睛的正前方,使得雙眼能夠直視 或者微微的俯視。 2. 肩膀:輕鬆的放下,不要刻意的聳立,保持舒服姿勢。 3. 背部:直立著輕鬆客在椅背上,不呈現駝背姿勢。 4. 小手臂:與身體約呈 90 度角,並向身體內側微彎,保持輕鬆。手腕輕鬆 的握住滑鼠與手臂成一直線。 5. 膝蓋:略比屁股低。 6. 頸部:伸直,不可讓頸子向前或向後的姿勢保持太久。 7. 腳:平貼地面。 圖 3.1.6 正確坐姿3.1.7 本專題實驗要求的環境因素
(一)安靜
因為實驗的內容所需時間稍長,所以要保持受測環境之品質,避免干擾受測 者使受測者心煩氣躁。(二)時間
由於我們有平面、曲面和三種角度(15°、30°、45°)的交互作用下,避免讓受測 者受測時間過長,所以我們將實驗分成兩階段,也就是平面一個階段,曲面一個 階段,受測者一次只做一個階段,隔天再做另一階段。3.2 實驗設備
曲面:
圖 3.2-1 曲面螢幕圖 3.2-2 曲面三台投影機
圖 3.2-4 曲面施測者量側受測者與螢幕之間的距離為 75 公分
平面:
圖 3.2-6 平面螢幕
圖 3.2-8 平面背投影
圖 3.2-10 平面受測者進行測試
3.3 實驗流程
實驗分成曲面和平面兩個階段,每個階段各有三個角度水準。實驗一開始先 點選位於桌面 BBWinLog 程式執行檔,畫面上將會出現一個訊息視窗以及一個作 業視窗,看清楚訊息視窗中指定的作業後點擊確定鍵,作業視窗會縮小於視窗最 下方,再點擊縮小於下方的視窗,作業視窗會出現在指定的位置,測試完畢關閉 後又會跳出下一個訊息視窗讓受測者進行實驗,反覆操作 12 次,即完成一個實 驗角度。圖 3.1.2-1 BBWinLog 執行檔
圖 3.1.2-3 訊息視窗
圖 3.1.2-4 最小化作業視窗
圖 3.1.2-6 作業視窗於 15°位置
圖 3.1.2-7 作業視窗於 30°位置
3.4 實驗作業及變數
受測者為本組組員在加上其他五位受測者共十二人,在實驗過程中,受測者 皆以右手操作滑鼠。作業視窗以隨機方式出現在一角度,測量受測者在不同作業 型態下視窗縮放以及移動情形,一個角度測量完後再測其他兩個角度。 z 獨立變數:作業時間、作業型態、視窗角度、螢幕類型 因子:作業時間、作業型態、視窗角度、螢幕類型 作業時間分為兩水準:時間長、時間短 作業型態分為兩水準:單用眼睛操作、用眼睛鍵盤或滑鼠操作 視窗角度分為三個水準:15°、30°、45° 螢幕類型分為兩個水準:曲面、平面 z 相依變數:調整後決定移動時間、X 軸移動量最大距離、最終視窗中心點距 螢幕中心點距離 受測人數:12 名第四章 分析與結果
(一)調整後決定移動視窗的反應時間,利用SPSS做變異數分析 表4.1 決定移動的時間之重複量數分析 測量:MEASURE_1 來源 型 III 平方和 df 平均平方和 F 顯著性 平曲面 假設為球形 5.636 1 5.636 .945 .352 Greenhouse-Geisser 5.636 1.000 5.636 .945 .352 Huynh-Feldt 5.636 1.000 5.636 .945 .352 下限 5.636 1.000 5.636 .945 .352 誤差 (平曲面) 假設為球形 65.602 11 5.964 Greenhouse-Geisser 65.602 11.000 5.964 Huynh-Feldt 65.602 11.000 5.964 下限 65.602 11.000 5.964 角度 假設為球形 302.761 2 151.381 6.079 .008 Greenhouse-Geisser 302.761 1.165 259.776 6.079 .025 Huynh-Feldt 302.761 1.219 248.424 6.079 .023 下限 302.761 1.000 302.761 6.079 .031 誤差 (角度) 假設為球形 547.892 22 24.904 Greenhouse-Geisser 547.892 12.820 42.737 Huynh-Feldt 547.892 13.406 40.869 下限 547.892 11.000 49.808 作業時間 假設為球形 888.530 1 888.530 41.597 .000 Greenhouse-Geisser 888.530 1.000 888.530 41.597 .000 Huynh-Feldt 888.530 1.000 888.530 41.597 .000 下限 888.530 1.000 888.530 41.597 .000 誤差 (作業時間) 假設為球形 234.965 11 21.360 Greenhouse-Geisser 234.965 11.000 21.360 Huynh-Feldt 234.965 11.000 21.360 下限 234.965 11.000 21.360 互動方式 假設為球形 71.205 1 71.205 20.571 .001Greenhouse-Geisser 71.205 1.000 71.205 20.571 .001 Huynh-Feldt 71.205 1.000 71.205 20.571 .001 下限 71.205 1.000 71.205 20.571 .001 誤差 (互動方式) 假設為球形 38.076 11 3.461 Greenhouse-Geisser 38.076 11.000 3.461 Huynh-Feldt 38.076 11.000 3.461 下限 38.076 11.000 3.461 平曲面 * 角度 假設為球形 107.244 2 53.622 3.296 .056 Greenhouse-Geisser 107.244 1.042 102.956 3.296 .095 Huynh-Feldt 107.244 1.054 101.714 3.296 .094 下限 107.244 1.000 107.244 3.296 .097 誤差 (平曲面*角度) 假設為球形 357.925 22 16.269 Greenhouse-Geisser 357.925 11.458 31.238 Huynh-Feldt 357.925 11.598 30.861 下限 357.925 11.000 32.539 平曲面 * 作業時間 假設為球形 9.959 1 9.959 1.878 .198 Greenhouse-Geisser 9.959 1.000 9.959 1.878 .198 Huynh-Feldt 9.959 1.000 9.959 1.878 .198 下限 9.959 1.000 9.959 1.878 .198 誤差 (平曲面*作業時間) 假設為球形 58.327 11 5.302 Greenhouse-Geisser 58.327 11.000 5.302 Huynh-Feldt 58.327 11.000 5.302 下限 58.327 11.000 5.302 角度 * 作業時間 假設為球形 48.826 2 24.413 6.151 .008 Greenhouse-Geisser 48.826 1.613 30.268 6.151 .013 Huynh-Feldt 48.826 1.849 26.405 6.151 .009 下限 48.826 1.000 48.826 6.151 .031 誤差 (角度*作業時間) 假設為球形 87.323 22 3.969 Greenhouse-Geisser 87.323 17.744 4.921 Huynh-Feldt 87.323 20.340 4.293 下限 87.323 11.000 7.938
平曲面 * 角度 * 作業時間 假設為球形 13.247 2 6.624 1.120 .344 Greenhouse-Geisser 13.247 1.949 6.797 1.120 .343 Huynh-Feldt 13.247 2.000 6.624 1.120 .344 下限 13.247 1.000 13.247 1.120 .313 誤差 (平曲面*角度*作業時間) 假設為球形 130.166 22 5.917 Greenhouse-Geisser 130.166 21.441 6.071 Huynh-Feldt 130.166 22.000 5.917 下限 130.166 11.000 11.833 平曲面 * 互動方式 假設為球形 10.030 1 10.030 1.461 .252 Greenhouse-Geisser 10.030 1.000 10.030 1.461 .252 Huynh-Feldt 10.030 1.000 10.030 1.461 .252 下限 10.030 1.000 10.030 1.461 .252 誤差 (平曲面*互動方式) 假設為球形 75.524 11 6.866 Greenhouse-Geisser 75.524 11.000 6.866 Huynh-Feldt 75.524 11.000 6.866 下限 75.524 11.000 6.866 角度 * 互動方式 假設為球形 35.278 2 17.639 4.632 .021 Greenhouse-Geisser 35.278 1.524 23.141 4.632 .033 Huynh-Feldt 35.278 1.720 20.516 4.632 .027 下限 35.278 1.000 35.278 4.632 .054 誤差 (角度*互動方式) 假設為球形 83.785 22 3.808 Greenhouse-Geisser 83.785 16.769 4.996 Huynh-Feldt 83.785 18.915 4.430 下限 83.785 11.000 7.617 平曲面 * 角度 * 互動方式 假設為球形 2.486 2 1.243 .911 .417 Greenhouse-Geisser 2.486 1.992 1.248 .911 .417 Huynh-Feldt 2.486 2.000 1.243 .911 .417 下限 2.486 1.000 2.486 .911 .360 誤差 (平曲面*角度*互動方式) 假設為球形 30.027 22 1.365 Greenhouse-Geisser 30.027 21.909 1.371 Huynh-Feldt 30.027 22.000 1.365
下限 30.027 11.000 2.730 作業時間 * 互動方式 假設為球形 79.124 1 79.124 10.257 .008 Greenhouse-Geisser 79.124 1.000 79.124 10.257 .008 Huynh-Feldt 79.124 1.000 79.124 10.257 .008 下限 79.124 1.000 79.124 10.257 .008 誤差 (作業時間*互動方式) 假設為球形 84.856 11 7.714 Greenhouse-Geisser 84.856 11.000 7.714 Huynh-Feldt 84.856 11.000 7.714 下限 84.856 11.000 7.714 平曲面 * 作業時間 * 互動方 式 假設為球形 .250 1 .250 .035 .854 Greenhouse-Geisser .250 1.000 .250 .035 .854 Huynh-Feldt .250 1.000 .250 .035 .854 下限 .250 1.000 .250 .035 .854 誤差 (平曲面*作業時間*互動 方式) 假設為球形 77.731 11 7.066 Greenhouse-Geisser 77.731 11.000 7.066 Huynh-Feldt 77.731 11.000 7.066 下限 77.731 11.000 7.066 角度 * 作業時間 * 互動方式 假設為球形 7.486 2 3.743 .749 .485 Greenhouse-Geisser 7.486 1.565 4.783 .749 .457 Huynh-Feldt 7.486 1.778 4.209 .749 .471 下限 7.486 1.000 7.486 .749 .405 誤差 (角度*作業時間*互動方 式) 假設為球形 110.008 22 5.000 Greenhouse-Geisser 110.008 17.215 6.390 Huynh-Feldt 110.008 19.563 5.623 下限 110.008 11.000 10.001 平曲面 * 角度 * 作業時間 * 互動方式 假設為球形 8.158 2 4.079 1.524 .240 Greenhouse-Geisser 8.158 1.312 6.218 1.524 .245 Huynh-Feldt 8.158 1.419 5.750 1.524 .244 下限 8.158 1.000 8.158 1.524 .243 誤差 (平曲面*角度*作業時間 *互動方式) 假設為球形 58.891 22 2.677 Greenhouse-Geisser 58.891 14.432 4.081
Huynh-Feldt 58.891 15.605 3.774 下限 58.891 11.000 5.354 ※以下將針對呈現顯著的因子,進行作圖與分析。 (1) 不同角度下,決定移動的時間 由表 4.1 得知角度之 F(1,11) = 0.079,P-value = 0.008 < 0.01,呈現高度顯著, 表示決定移動的時間在不同角度下會有明顯的差異,並將其數據繪製成圖加以分 析,如圖 4.1。 圖 4.1 角度與決定移動時間之關係圖 從數據統計上得知調整後決定移動的時間在 15 度的平均值為 6.801(s),30 度的平均值為 5.369(s),45 度的平均值則為 4.298(s)。 另外從圖 4.1,可以看出隨著角度的增加,決定移動的時間有逐漸減少的趨 勢。
◎事後檢定 表4.2 調整後決定移動時間的角度之成對比較 測量:MEASURE_1 (I) 角度 (J) 角度 平均差異 (I-J) 標準誤差 顯著性a 差異的 95% 信賴區間a 下界 上界 15度 30度 1.432* .499 .015 .333 2.531 45度 2.503* .977 .026 .353 4.652 30度 15度 -1.432* .499 .015 -2.531 -.333 45度 1.071 .595 .099 -.238 2.379 45度 15度 -2.503* .977 .026 -4.652 -.353 30度 -1.071 .595 .099 -2.379 .238 根據估計的邊緣平均數而定 *. 平均差異在 .05 水準是顯著的。 a. 調整多重比較:最低顯著差異 (等於未調整值)。 由表 4.2 顯示,15 度與 30 度相比較,P = 0.015<α= 0.05,表示顯著;15 度 與 45 度相比較,P = 0.026<α= 0.05,表示顯著;30 度與 45 度相比較,P = 0.099 >α= 0.05,表示不顯著。三種角度的比較,15 度與 30 度之間是在這三組角度 中差異性最大。 (2) 不同作業時間下,決定移動的時間 由表 4.1 得知作業時間之 F(1,11) = 41.597,P-value < 0.01,呈現高度顯著,表 示決定移動的時間在不同作業時間下會有明顯的差異,並將其數據繪製成圖加以 分析,如圖 4.2。
圖 4.2 作業時間與決定移動時間之關係圖
從數據統計上得知調整後決定移動的時間在長時間作業的平均值為
3.733(s),短時間作業的平均值則為 7.246(s)。
另外從圖 4.2,可以看出在長時間作業上,其決定移動的時間要比在短時間
(3) 不同互動方式下,決定移動的時間 由表 4.1 得知互動方式之 F(1,11) = 20.571,P-value = 0.001< 0.01,呈現高度顯 著,表示決定移動的時間在不同互動方式下會有明顯的差異,並將其數據繪製成 圖加以分析,如圖 4.3。 圖 4.3 互動方式與決定移動時間之關係圖 從數據統計中顯示出調整後決定移動的時間在單用眼睛作業的平均值為 5.987(s),使用眼睛、鍵盤及滑鼠作業的平均值則為 4.992(s)。 另外從圖 4.3,可以看出不同互動方式下,需要使用到眼睛、鍵盤及滑鼠作 業時,其決定移動的時間要比單用眼睛作業下來得快。
(4) 不同角度與不同作業時間交互作用下,決定移動的時間 由表 4.1 得知角度*作業時間交互作用之 F(2,22) = 6.151,P-value = 0.008< 0.01,呈現高度顯著,表示決定移動的時間在角度*作業時間交互作用下會有明 顯的差異,並將其數據繪製成圖加以分析,如圖 4.4。 圖 4.4 角度*作業時間的交互作用與決定移動時間之關係圖 在數據統計中顯示出調整後決定移動的時間在長時間作業下,其 15 度的平 均值為 4.79(s),30 度的平均值為 3.286(s),45 度的平均值則為 3.123(s),另外在 短時間作業下,15 度的平均值為 8.812(s),30 度的平均值為 7.452(s),45 度的平 均值則為 5.474(s)。
另外從圖 4.4,可以看出在 15 度情形下,短時間的作業幾乎沒有做移動,長 時間作業平均則在 4.79 秒時做了移動,當角度從 15 度變成 30 度時,不論是長 時間作業或是短時間作業,在決定移動的時間方面都有減少的趨勢,而且趨勢的 差異性不大,不過在決定的時間上還是有明顯的差異,再當角度從 30 度變為 45 度時,長時間作業並沒有明顯的變化,短時間則依然呈現減少的趨勢,不過最終 在長時間作業下決定移動的時間,依舊比短時間作業下要來得快。 (5) 不同角度與不同互動方式交互作業下,決定移動的時間 由表 4.1 得知角度*互動方式交互作用之 F(2,22) = 4.632,P-value = 0.021 < α = 0.05,表示顯著,表示決定移動的時間在角度*互動方式交互作用下會有所差 異,並將其數據繪製成圖加以分析,如圖 4.5。 圖 4.5 角度*互動方式的交互作用與決定移動時間之關係圖
在數據統計中顯示出調整後決定移動的時間在單用眼睛作業的情況下,其 15 度的平均值為 6.933(s),30 度的平均值為 5.759(s),45 度的平均值為 5.268(s), 另外在使用眼睛、鍵盤及滑鼠作業的情況下,其 15 度的平均值 6.669(s),30 度 的平均值為 4.979(s),45 度的平均值為 3.329(s)。 另外從圖 4.5 的表示,可以看出在 15 度時,兩種互動方式的決定移動的時 間差異並不大,另外隨著角度的增加的情況下,兩種互動方式在決定移動的時間 上都有減少的趨勢,不過使用眼睛、鍵盤及滑鼠的作業下減少的趨勢要比單用眼 睛作業下來的明顯,在這樣的趨勢下,兩種互動方式在三種角度下的差異,會隨 著角度的增加,而逐漸變大。
(6)不同作業時間與不同互動方式交互作業下,決定移動的時間 由表 4.1 得知作業時間*互動方式交互作用之 F(1,11) = 10.257,P-value = 0.008 < 0.01,呈現高度顯著,表示決定移動的時間在作業時間*互動方式交互作用下會 有明顯差異,並將其數據繪製成圖加以分析,如圖 4.6。 圖 4.6 作業時間*互動方式的交互作用與決定移動時間關係圖 在數據統計中顯示出調整後決定移動的時間在單用眼睛的情形下,在長時間 作業的平均值為 3.706(s),在短時間作業的平均值為 8.267(s),當使用眼睛、鍵盤 及滑鼠時,在長時間的作業的平均值為 3.76(s),在短時間作業的平均值為 6.225(s)。
另外從圖 4.6 所示,在長時間作業的情況下,兩種互動方式其決定移動的時 間並沒有差異,不過隨著作業時間的縮短,兩種互動方式決定移動的時間都有增 加的趨勢,不過在單用眼睛作業方面,增加的趨勢要比使用眼睛、鍵盤及滑鼠作 業來得明顯,在這樣的趨勢下,兩種互動方式因作業時間的縮短,其決定移動的 時間的差異性會隨著增加。 (二)X軸方向最大移動距離,利用SPSS做變異數分析 表4.3 X軸方向最大移動距離之重複量數分析 測量:MEASURE_1 來源 型 III 平方和 df 平均平方和 F 顯著性 平曲面 假設為球形 273522.570 1 273522.570 5.236 .043 Greenhouse-Geisser 273522.570 1.000 273522.570 5.236 .043 Huynh-Feldt 273522.570 1.000 273522.570 5.236 .043 下限 273522.570 1.000 273522.570 5.236 .043 誤差 (平曲面) 假設為球形 574662.817 11 52242.074 Greenhouse-Geisser 574662.817 11.000 52242.074 Huynh-Feldt 574662.817 11.000 52242.074 下限 574662.817 11.000 52242.074 角度 假設為球形 2.625E7 2 1.312E7 286.564 .000
Greenhouse-Geisser 2.625E7 1.227 2.139E7 286.564 .000
Huynh-Feldt 2.625E7 1.302 2.015E7 286.564 .000
下限 2.625E7 1.000 2.625E7 286.564 .000 誤差 (角度) 假設為球形 1007567.324 22 45798.515 Greenhouse-Geisser 1007567.324 13.501 74630.507 Huynh-Feldt 1007567.324 14.327 70328.466 下限 1007567.324 11.000 91597.029 作業時間 假設為球形 1.408E7 1 1.408E7 90.184 .000
Huynh-Feldt 1.408E7 1.000 1.408E7 90.184 .000 下限 1.408E7 1.000 1.408E7 90.184 .000 誤差 (作業時間) 假設為球形 1717412.725 11 156128.430 Greenhouse-Geisser 1717412.725 11.000 156128.430 Huynh-Feldt 1717412.725 11.000 156128.430 下限 1717412.725 11.000 156128.430 互動方式 假設為球形 919801.218 1 919801.218 20.226 .001 Greenhouse-Geisser 919801.218 1.000 919801.218 20.226 .001 Huynh-Feldt 919801.218 1.000 919801.218 20.226 .001 下限 919801.218 1.000 919801.218 20.226 .001 誤差 (互動方式) 假設為球形 500235.517 11 45475.956 Greenhouse-Geisser 500235.517 11.000 45475.956 Huynh-Feldt 500235.517 11.000 45475.956 下限 500235.517 11.000 45475.956 平曲面 * 角度 假設為球形 572696.001 2 286348.001 8.460 .002 Greenhouse-Geisser 572696.001 1.552 368971.013 8.460 .005 Huynh-Feldt 572696.001 1.760 325444.460 8.460 .003 下限 572696.001 1.000 572696.001 8.460 .014 誤差 (平曲面*角度) 假設為球形 744661.538 22 33848.252 Greenhouse-Geisser 744661.538 17.074 43614.845 Huynh-Feldt 744661.538 19.357 38469.715 下限 744661.538 11.000 67696.503 平曲面 * 作業時間 假設為球形 2402.593 1 2402.593 .068 .799 Greenhouse-Geisser 2402.593 1.000 2402.593 .068 .799 Huynh-Feldt 2402.593 1.000 2402.593 .068 .799 下限 2402.593 1.000 2402.593 .068 .799 誤差 (平曲面*作業時間) 假設為球形 389328.702 11 35393.518 Greenhouse-Geisser 389328.702 11.000 35393.518 Huynh-Feldt 389328.702 11.000 35393.518 下限 389328.702 11.000 35393.518 角度 * 作業時間 假設為球形 2805266.949 2 1402633.474 28.326 .000
Greenhouse-Geisser 2805266.949 1.226 2289032.899 28.326 .000 Huynh-Feldt 2805266.949 1.300 2157985.633 28.326 .000 下限 2805266.949 1.000 2805266.949 28.326 .000 誤差 (角度*作業時間) 假設為球形 1089367.596 22 49516.709 Greenhouse-Geisser 1089367.596 13.481 80808.977 Huynh-Feldt 1089367.596 14.299 76182.658 下限 1089367.596 11.000 99033.418 平曲面 * 角度 * 作業時間 假設為球形 230599.925 2 115299.962 5.049 .016 Greenhouse-Geisser 230599.925 1.559 147957.396 5.049 .025 Huynh-Feldt 230599.925 1.769 130350.151 5.049 .020 下限 230599.925 1.000 230599.925 5.049 .046 誤差 (平曲面*角度*作業時 間) 假設為球形 502391.165 22 22835.962 Greenhouse-Geisser 502391.165 17.144 29303.995 Huynh-Feldt 502391.165 19.460 25816.757 下限 502391.165 11.000 45671.924 平曲面 * 互動方式 假設為球形 151486.898 1 151486.898 8.182 .016 Greenhouse-Geisser 151486.898 1.000 151486.898 8.182 .016 Huynh-Feldt 151486.898 1.000 151486.898 8.182 .016 下限 151486.898 1.000 151486.898 8.182 .016 誤差 (平曲面*互動方式) 假設為球形 203650.702 11 18513.700 Greenhouse-Geisser 203650.702 11.000 18513.700 Huynh-Feldt 203650.702 11.000 18513.700 下限 203650.702 11.000 18513.700 角度 * 互動方式 假設為球形 806014.086 2 403007.043 15.337 .000 Greenhouse-Geisser 806014.086 1.103 730953.663 15.337 .002 Huynh-Feldt 806014.086 1.135 710219.715 15.337 .001 下限 806014.086 1.000 806014.086 15.337 .002 誤差 (角度*互動方式) 假設為球形 578075.606 22 26276.164 Greenhouse-Geisser 578075.606 12.130 47658.369 Huynh-Feldt 578075.606 12.484 46306.510 下限 578075.606 11.000 52552.328
平曲面 * 角度 * 互動方式 假設為球形 65210.079 2 32605.039 3.057 .067 Greenhouse-Geisser 65210.079 1.950 33446.766 3.057 .069 Huynh-Feldt 65210.079 2.000 32605.039 3.057 .067 下限 65210.079 1.000 65210.079 3.057 .108 誤差 (平曲面*角度*互動方 式) 假設為球形 234656.234 22 10666.192 Greenhouse-Geisser 234656.234 21.446 10941.549 Huynh-Feldt 234656.234 22.000 10666.192 下限 234656.234 11.000 21332.385 作業時間 * 互動方式 假設為球形 1348424.105 1 1348424.105 31.360 .000 Greenhouse-Geisser 1348424.105 1.000 1348424.105 31.360 .000 Huynh-Feldt 1348424.105 1.000 1348424.105 31.360 .000 下限 1348424.105 1.000 1348424.105 31.360 .000 誤差 (作業時間*互動方式) 假設為球形 472973.352 11 42997.577 Greenhouse-Geisser 472973.352 11.000 42997.577 Huynh-Feldt 472973.352 11.000 42997.577 下限 472973.352 11.000 42997.577 平曲面 * 作業時間 * 互動方 式 假設為球形 31580.732 1 31580.732 3.066 .108 Greenhouse-Geisser 31580.732 1.000 31580.732 3.066 .108 Huynh-Feldt 31580.732 1.000 31580.732 3.066 .108 下限 31580.732 1.000 31580.732 3.066 .108 誤差 (平曲面*作業時間*互動 方式) 假設為球形 113291.508 11 10299.228 Greenhouse-Geisser 113291.508 11.000 10299.228 Huynh-Feldt 113291.508 11.000 10299.228 下限 113291.508 11.000 10299.228 角度 * 作業時間 * 互動方式 假設為球形 792629.327 2 396314.663 15.283 .000 Greenhouse-Geisser 792629.327 1.239 639752.858 15.283 .001 Huynh-Feldt 792629.327 1.318 601271.455 15.283 .001 下限 792629.327 1.000 792629.327 15.283 .002 誤差 (角度*作業時間*互動方 式) 假設為球形 570486.740 22 25931.215 Greenhouse-Geisser 570486.740 13.629 41859.590 Huynh-Feldt 570486.740 14.501 39341.718
下限 570486.740 11.000 51862.431 平曲面 * 角度 * 作業時間 * 互動方式 假設為球形 17916.372 2 8958.186 1.929 .169 Greenhouse-Geisser 17916.372 1.523 11762.029 1.929 .181 Huynh-Feldt 17916.372 1.718 10430.043 1.929 .176 下限 17916.372 1.000 17916.372 1.929 .192 誤差 (平曲面*角度*作業時間 *互動方式) 假設為球形 102185.205 22 4644.782 Greenhouse-Geisser 102185.205 16.756 6098.563 Huynh-Feldt 102185.205 18.895 5407.934 下限 102185.205 11.000 9289.564 ※以下將針對呈現顯著的因子,進行作圖與分析。 (1)平、曲面螢幕下,X 軸最大移動距離 由表 4.3 顯示出平曲面之 F(1,11) =5.236,P = 0.043 <α= 0.05,呈現顯著,表 示視窗在平面與曲面這兩種螢幕下,其 X 軸最大移動距離會有所差異,將其數 據繪製成圖,如圖 4.7。 圖 4.7 平、曲面與 X 軸最大移動距離之關係圖
由數據統計上得知,視窗在平面螢幕下,其 X 軸最大移動距離的平均值為 509.547(pixel),在曲面螢幕下,其 X 軸最大移動距離的平均值為 447.912(pixel)。 從圖 4.7 中可以看出,受測者在平面螢幕下,視窗的移動距離(X 軸)較大,而在 曲面下,受測者移動視窗的距離(X 軸)則有較小的趨勢。 (2) 不同角度下,X 軸最大移動距離 由表 4.3 顯示出角度之 F(2,22) =286.564,P<α= 0.01,呈現高度顯著,表示 視窗在不同角度(15°、30°、45°)下,其 X 軸最大移動距離會有所差異。將其數據 繪製成圖,如圖 4.8。 圖 4.8 角度與 X 軸最大移動距離之關係圖 由數據統計上得知,視窗在角度 15°時,其 X 軸最大移動距離的平均值為 129.003(pixel),視窗在 30°時,X 軸最大移動距離的平均值為 441.510(pixel),視窗
在 45°時,X 軸最大移動距離的平均值則為 865.675(pixel)。從圖 4.8 中可以看出, 當視窗出現在角度 15°時,其 X 軸方向的移動距離較小,或可能不移動,而視窗 若出現在 45°的地方時,受測者對視窗的移動距離(X 軸方向)較大所以,隨著角度 變大,視窗的移動距離(X 軸方向)有變大的趨勢。 ◎事後檢定 表4.4 X軸最大移動距離的角度之成對比較 測量:MEASURE_1 (I) 角度 (J) 角度 平均差異 (I-J) 標準誤差 顯著性a 差異的 95% 信賴區間a 下界 上界 15度 30度 -312.507* 16.127 .000 -348.003 -277.011 45度 -736.672* 39.535 .000 -823.688 -649.656 30度 15度 312.507* 16.127 .000 277.011 348.003 45度 -424.165* 32.238 .000 -495.121 -353.209 45度 15度 736.672* 39.535 .000 649.656 823.688 30度 424.165* 32.238 .000 353.209 495.121 根據估計的邊緣平均數而定 *. 平均差異在 .05 水準是顯著的。 a. 調整多重比較:最低顯著差異 (等於未調整值)。 由表 4.4 顯示,15 度與 30 度相比較,P<α= 0.01,表示高度顯著;15 度與 45 度相比較,P<α= 0.01,表示高度顯著;30 度與 45 度相比較,P<α= 0.01, 也表示高度顯著。三種角度的比較,彼此都有顯著性,我們從這可得知,彼此都 具有差異性。
(3)不同作業時間下,X 軸最大移動距離 由表 4.3 顯示出作業時間之 F(1,11) =90.184,P<α= 0.01,呈現高度顯著,表 示在不同作業時間(長時間、短時間)的情況下,其 X 軸方向的最大移動距離會有 差異。將其數據繪製成圖。如圖 4.9。 圖 4.9 作業時間與 X 軸最大移動距離之關係圖 由數據統計上得知,作業時間較長的視窗,其 X 軸方向最大移動距離的平 均值為 699.840(pixel),作業時間較短的視窗,其 X 軸方向最大移動距離的平均 值則為 257.619(pixel)。從圖 4.9 中可以看出,需長時間的的作業視窗,受測者將 其 X 軸方向的移動距離較大,而需短時間的作業視窗,受測者對其 X 軸方向的 移動距離較小,或可能不移動。
(4)不同互動方式下,X 軸最大移動距離 由表 4.3 顯示出互動方式之 F(1,11) =20.226,P = 0.01<α= 0.05,呈現顯著, 表示在不同的互動方式(單用眼睛、眼睛鍵盤滑鼠)下,其 x 軸方向的最大移動距 離有所差異。將其數據繪製成圖,如圖 4.10。 圖 4.10 互動方式與 X 軸最大移動距離之關係圖 由數據統計上得知,單用眼睛的視窗,受測者對其 x 軸方向的平均移動距離 為 422.216(pixel),需要運用眼睛、鍵盤及滑鼠的視窗,受測者對其 x 軸方向的平 均移動距離為 535.243(pixel)。從圖 4.10 中可以看出,只需單用眼睛即可完成作業 的視窗,受測者對其移動距離(x 軸方向)較小,或可能不移動,而需運用眼睛+鍵 盤+滑鼠的作業視窗,受測者對其移動距離(x 軸方向)則有較大的趨勢。
(5)平、曲面螢幕與不同角度交互作用下,X 軸最大移動距離 由表 4.3 顯示出在平曲面與角度交互作用下之 F(2,22) =8.460,平曲面*角度 P = 0.02<α= 0.05,呈現顯著。表示在平曲面與不同的角度交互作用下,其 x 軸方 向的最大移動距離有所差異。將其數據繪製成圖,如圖 4.11。 圖 4.11 平曲面*角度的交互作用與 X 軸最大移動距離之關係圖 由數據統計上得知,在平面螢幕下,視窗出現在 15°時,x 軸方向最大平均移 動距離為 111.177(pixel),視窗出現在 30°時,x 軸方向最大平均移動距離為 461.892(pixel),視窗出現在 45°時,x 軸方向最大平均移動距離為 955.573(pixel); 在曲面螢幕下,視窗出現在 15°時,x 軸方向最大平均移動距離為 146.830(pixel), 視窗出現在 30°時,x 軸方向最大平均移動距離為 421.128(pixel),視窗出現在 45°
時,x 軸方向最大平均移動距離為 775.778(pixel)。 從圖 4.11 中可以觀察出,角度越大,x 軸方向的平均移動距離有越大的趨勢, 視窗在 15°與 30°時,平曲面螢幕的移動距離(x 方向)較無明顯差別,而視窗在 45° 時,平曲面螢幕在 x 軸方向的移動距離較有明顯差異,在 45°角度下,平面螢幕 有較大的趨勢。 (6)不同角度與不同作業時間交互作用下,X 軸最大移動距離 由表 4.3 顯示出角度與作業時間的交互作用下之 F(2,22) =28.326,角度*作業 時間 P<α= 0.01,呈現高度顯著。表示在不同角度與不同作業時間的交互作用 下,其 x 軸方向的最大移動距離有所差異。將其數據繪製成圖,如圖 4.12。 圖 4.12 角度*作業時間的交互作用與 X 軸最大移動距離之關係圖
由數據統計上得知,長時間的作業視窗出現在 15°時,其 x 軸的平均移動距 離為 217.083(pixel),出現在 30°時,其 x 軸的平均移動距離為 692.559(pixel),出 現在 45°時,其 x 軸的平均移動距離為 1189.878(pixel);短時間的作業視窗出現在 15°時,其 x 軸的平均移動距離為 40.924(pixel),出現在 30°時,其 x 軸的平均移動 距離為 190.462(pixel),出現在 45°時,其 x 軸的平均移動距離為 541.472(pixel)。 從圖 4.12 中可以觀察出,需較長作業時間的視窗,其 x 軸最大移動距離有增 大的趨勢,也可看出,當角度越大,其 x 軸最大移動距離也有增大的趨勢,另外, 從圖中也可觀察出,角度 30 到 45,不管長時間或是短時間的視窗,其 x 軸方向 移動距離都有很明顯的增大趨勢,在角度 15 到 30 出現的視窗,長時間的部分依 然有明顯的增大趨勢,但在短時間的部分,變化趨勢較為不明顯。 (7)不同作業時間與不同互動方式交互作用下,X 軸最大移動距離 由表 4.3 顯示出作業時間與互動方式的交互作用下之 F(1,11) =31.360,作業時 間*互動方式 P<α= 0.01,呈現高度顯著。表示在不同不同作業時間與不同互動 方式的交互作用下,其 x 軸方向的最大移動距離有所差異。將其數據繪製成圖, 如圖 4.13。
圖 4.13 作業時間*互動方式的交互作用與 X 軸最大移動距離之關係圖 由數據統計上得知,單用眼睛、長時間的視窗,其 x 軸最大平均移動距離為 711.752(pixel) , 單 用 眼 睛 、 短 時 間 的 視 窗 , 其 x 軸 最 大 平 均 移 動 距 離 為 132.681(pixel),使用眼睛鍵盤滑鼠、長時間的視窗,其 x 軸最大平均移動距離為 687.928(pixel),使用眼睛鍵盤滑鼠、短時間的視窗,其 x 軸最大平均移動距離為 382.558(pixel)。 從圖 4.13 中可以觀察出,在長時間作業視窗下,兩種的互動方式彼此 x 軸方 向的移動距離並沒有明顯差異,但作業時間縮短,兩種的互動方式,其 x 軸方向 的移動距離都有明顯下降的趨勢,而單用眼睛的作業視窗,其下降的趨勢比用眼 睛+鍵盤滑鼠的作業來的明顯。
(8)平、曲面螢幕與不同互動方式交互作用下,X 軸最大移動距離 由表 4.3 顯示出平曲面與互動方式的交互作用下之 F(1,11) =8.182,平曲面*互 動方式 P = 0.016<α= 0.05,呈現顯著,表示在平曲面與不同作業時間的交互作 用下,其 x 軸方向的最大移動距離有所差異。將其數據繪製成圖,如圖 4.14。 圖 4.14 平曲面*互動方式的交互作用與 X 軸最大移動距離之關係圖 由數據統計上得知,在平面螢幕下,單用眼睛作業,其 x 軸最大平均移動距 離為 430.100(pixel),使用眼睛鍵盤滑鼠的作業,其 x 軸最大平均移動距離為 588.995(pixel);在曲面螢幕下,單用眼睛作業,其 x 軸最大平均移動距離為 414.333(pixel),若使用眼睛鍵盤滑鼠的作業,其 x 軸最大平均移動距離 為 481.491(pixel)。
從圖 4.14 中可以觀察出,單用眼睛的作業視窗,其平面與曲面的差異性不明 顯,但使用眼睛+鍵盤滑鼠的作業視窗,其平曲面就有明顯的差異性,平面到曲 面有明顯下降的趨勢。 (9)不同角度與不同互動方式交互作用下,X 軸最大移動距離 由表 4.3 顯示出角度與互動方式的交互作用下之 F(2,22) =15.337,角度*互動 方式 P<α= 0.01,呈現高度顯著。表示在不同角度與不同互動方式的交互作用 下,其 x 軸方向的最大移動距離有所差異。將其數據繪製成圖。如圖 4.15。 圖 4.15 角度*互動方式的交互作用與 X 軸最大移動距離之關係圖 由數據統計上得知,在角度 15°時,單用眼睛的作業,其 x 軸最大平均移動 距離為 124.493(pixel),眼睛+鍵盤滑鼠的作業,其 x 軸最大平均移動距離為 133.514(pixel);在角度 30°時,單用眼睛的作業,其 x 軸最大平均移動距離為
405.576(pixel) , 眼 睛 + 鍵 盤 滑 鼠 的 作 業 , 其 x 軸 最 大 平 均 移 動 距 離 為 477.444(pixel);在角度 45°時,單用眼睛的作業,其 x 軸最大平均移動距離為 736.580(pixel),眼睛+鍵盤滑鼠的作業,其 x 軸最大平均移動距離為 994.771(pixel)。 從圖 4.15 中可以觀察出,在角度 15°時,兩種互動方式沒有明顯差異,隨著 角度增加,兩種互動方式都呈現遞增的趨勢,而使用眼睛+滑鼠鍵盤的作業方式 遞增的趨勢比單用眼睛的作業方式來的明顯。 (10)平曲面螢幕、不同角度與不同作業間的三階交互作用 由表 4.3 顯示出平曲面、角度與作業時間三階的交互作用下之 F(2,22) =5.049, 平曲面*角度*作業時間 P = 0.016<α= 0.05,呈現顯著。表示在平曲面、不同角 度與不同作業時間的三階交互作用下,其 x 軸方向的最大移動距離有所差異。將 其數據繪製成圖,如圖 4.16 。
從數據統計上得知,長時間作業視窗在平面螢幕角度 15°的地方出現時,其 X 軸最大平均移動距離為 180.688(pixel),長時間作業視窗在曲面螢幕角度 15°的 地方出現時,其 X 軸最大平均移動距離為 253.479(pixel),長時間作業視窗在平面 螢幕角度 30°的地方出現時,其 X 軸最大平均移動距離為 697.306(pixel),長時間 作業視窗在曲面螢幕角度 30°的地方出現時,其 X 軸最大平均移動距離為 687.803(pixel),長時間作業視窗在平面螢幕角度 45°的地方出現時,其 X 軸最大 平均移動距離為 1322.646(pixel),長時間作業視窗在平面螢幕角度 45°的地方出現 時,其 X 軸最大平均移動距離為 1057.111(pixel)。 短時間作業視窗在平面螢幕角度 15°的地方出現時,其 X 軸最大平均移動距 離為 41.667(pixel),短時間作業視窗在曲面螢幕角度 15°的地方出現時,其 X 軸最 大平均移動距離為 40.181(pixel),短時間作業視窗在平面螢幕角度 30°的地方出現 時,其 X 軸最大平均移動距離為 226.479(pixel),短時間作業視窗在曲面螢幕角度 30°的地方出現時,其 X 軸最大平均移動距離為 154.444(pixel),短時間作業視窗 在平面螢幕角度 45°的地方出現時,其 X 軸最大平均移動距離為 588.500(pixel), 短時間作業視窗在曲面螢幕角度 45°的地方出現時,其 X 軸最大平均移動距離為 494.444(pixel)。 從上面圖 4.16 可以觀察出,在相同平曲面、相同角度下,需要長時間作業 的視窗,其 X 軸方向的移動距離,趨勢明顯大於短時間作業的視窗。而從圖中 也可看出,不管在長時間或是短時間的作業下,在角度 15°與 30°,其視窗從平面
到曲面的並沒有明顯的差異,但在角度 45°時,長時間或是短時間的作業視窗, 其 X 軸方向的移動距離從平面到曲面有較明顯的下降趨勢,而長時間的作業視 窗下降的趨勢比短時間的作業視窗來的更明顯。 (11)不同角度、不同作業間與不同互動方式的三階交互作用 由 表 4.3 顯 示 出 平 曲 面 、 角 度 與 作 業 時 間 三 階 的 交 互 作 用 下 之 F(2,22) =15.283,角度*作業時間*互動方式 P<α= 0.01,呈現高度顯著。表示在不同角 度、不同作業時間與不同互動方式的三階交互作用下,其 x 軸方向的最大移動距 離有所差異。將其數據繪製成圖,如圖 4.17 。