題組式適性診斷測驗系統之建置

(1)

國立台中教育大學教育測驗統計研究所理學碩士論文

指導教授：郭伯臣教授

題組式適性診斷測驗系統之建置

研究生：劉育隆撰

(2)

謝辭

時光匆匆！碩士班的生活一轉眼就結束，回想這七百多天日子，伴隨著考試、報告、計畫、研究和論文的壓力，一路走來，雖然辛苦，但充實了本身知識的深度和廣度，增加了自己的思考能力，也培養出積極的處事態度。本論文的完成，首先要感謝我生命中的貴人郭伯臣教授循循善誘的指導，感謝郭老師花時間且有耐心的指引我正確的方向，引導著我如何獨立的思索問題，不厭其煩的一字一句的修改著我生澀的文字，使我順利地走向論文完成之路。二年來對我的課業和生活亦照顧有加，其本身的為人處世、治學態度，亦是我所效法的對象，同時對學生的真誠相待與勉勵，是最令我難以忘懷的。另外，感謝兩位口試委員不辭辛勞地審查與提出寶貴意見，劉湘川校長和施淑娟教授，在口試時也給了我許多重要和良好的建議，讓我的論文品質更加提升，在此也特別感謝兩位老師。感謝台中教育大學測統所這二年來對我的照顧與付出，這兩年來，特別要感謝所上師長對學生的教導，恩師郭伯臣所長、劉湘川校長、許天維院長、林原宏教授、楊志堅教授等教師對學生二年來的教導與期勉，以及所辦施慶麟助教、賴聖尹院秘給予我的協助，僅在此致上最高的謝意。當然，跟我ㄧ起打拼，同甘共苦的好友們，你們也是我論文完成的一大功臣。感謝智為嚴謹而又認真的生活和求學態度，讓我鞭策自己說話要有邏輯，求學問不能苟且；感謝欣怡學姊、珮璇、建儒、惠謙、惟盛、凱怡、佳瑩跟我一起上健身房、一起打球運動，讓我的體力得以維持，也讓我的生活輕鬆許多，並且充滿歡笑；感謝彥鈞學長平常像大哥般扶持我，在計畫上給與很多協助與指導，讓我吸收不少經驗；感謝碩士班所有其他同學的幫忙和鼓勵，讓我這兩年的生活過的愉快，求學能夠順利。還有可愛的學弟妹們，感謝你們讓我覺得在研究所生活中是一項快樂的事。更要感謝婉星在我為了論文忙得不可開交之際，幫忙我許多計畫上的事情，以及典佑學長、暄博學長、佑軒、鈺卿、雅媛、亞君、曜翰、少祖、筱倩、宛婷、鈞翔、文俊、境蔚，具有革命情感的研究室朋友們，讓我覺得研究室像個溫暖的家，可以安心在這奮鬥。最後，我要感謝辛苦的爸爸、媽媽，您們讓我不用煩惱求學所需的種種經濟來源，也全力支持我決定的每一條路，您們的辛苦絕對比我完成這本薄薄的論文所付出的多出好幾倍，我會繼續認真負責地做好每一件事，努力不辜負您們對我的期待！二零零六年夏天劉育隆筆

(3)

摘要本研究旨在探討以題組結構為基礎之適性診斷測驗系統之建置，由於題組式題型被廣泛使用，大部分研究題組式適性選題策略都是在IRT的理論基礎下，但近年來適性診斷測驗日漸風行，由於以結構理論為基礎的適性診斷測驗能精確的指出學生的錯誤概念，在補救教學方面也能提供更多的訊息，但以題組結構為基礎的適性選題策略還未有學者進行研發。因此，本研究將評估及比較題組結構二元選題策略與題組結構多點選題策略之成效，應用於本研究所要建置「以結構理論為基礎的多點計分題組式適性診斷測驗系統」之中，並以「怎樣解題」單元針對現在國小學生1004進行電腦施測，研究結論如下：一、不論是二元或多點的適性測驗選題策略，皆可達到節省施測題數，與紙筆測驗相比，精準度為0.95時，約可節省一半以上的試題，精準度為0.9時，約可節省80％以上的試題，進而節省施測時間，效果很好。二、多點的適性測驗選題策略較二元的適性測驗選題策略有略好的效果。三、由精準度為0.95的多點計分題組結構作為選題策略，精準度由0.95降為0.92，平均施測題數為16.6題，與整份試卷都要作答共29題相比，約可節省四成以上的試題，因此，本研究所發展之多點計分題組選題策略及其適性診斷測驗系統有其一定的效果。關鍵字：適性診斷測驗、題組、選題策略、知識結構

(4)

Abstract

In recent years, adaptive diagnostic test has become a fashion trend as the day goes by. Since adaptive diagnostic testing system based on knowledge structure can clearly point out the student’s wrong concepts, it can also offer more information on Restoring Teaching. But the delivery strategy of item on testlet's structure has not yet been developed by scholars

Hence, this study compares the effects of the delivery strategy of item of binary testlet structure and polytomous testlet structure. In order to contribute in the construction of ' item structure based computerized adaptive testing system '. 1004 students of elementary school are tested with the unit ' how to solve a problem '. The results are as follow:

1. Both the delivery strategy of item of binary testlet structure and polytomous testlet structure can achieve the reduction of the number of questions. Compared with paper pen test, when the accurancy is 95%, the number of questions can be reduced by 50%, when accurancy is 90%, the number of questions can be reduced by 80%, when using this algorithm ,the result is very good in reducing the examination time.

2. 2.The the delivery strategy of item of polytomous testlet structure has slightly better effect then binary testlet structure.

3. 3.When using the 95% accuracte polytomous testlet structure the delivery strategy of item, the accurancy is lowered down between 92% and 95%, average questions been

administrated are 16.6. Comparing this result with the test paper which requires answering 29 questions, approximately it can reduce the number of questions by 40%. Therefore, the research unit’s adaptive diagnosis test system based on polytomous testlet structure can perform solid effect.

Keywords: computerized adaptive diagnostic test, testlet, ordering theory, knowledge

(5)

目錄

第一章緒論……… 1 第一節研究動機……… 1 第二節研究目的……… 2 第三節名詞解釋……… 3 第四節研究限制……… 4 第二章文獻探討……… 5 第一節電腦化適性測驗……… 5 第二節估計知識結構的方式……… 8 第三節以知識結構為基礎的多點計分模式……… 11 第四節題組題型……… 14 第五節系統開發方法……… 17 第三章研究方法與步驟……… 19 第一節研究方法……… 19 第二節研究流程……… 19 第三節研究範圍與對象……… 21 第四節研究工具……… 22 第五節選題策略實驗設計……… 29 第六節選題策略成效評估……… 33 第七節系統分析與設計……… 33 第八節系統成效評估……… 36 第四章研究結果……… 39 第一節多點計分題組式適性診斷測驗的最佳選題策略……… 39 第二節多點計分題組式適性診斷測驗系統之建置……… 41 第三節評估題組式適性診斷測驗系統之成效……… 45 第五章結論與建議……… 47 第一節研究結論……… 47 第二節未來研究方向……… 47

(6)

參考文獻……… 49

附錄一 94 年六年級怎樣解題專家結構……… 54

附錄二 94 年六年級怎樣解題施測試卷……… 55

附錄三 題組結構多點精準度……… 58

(7)

表目錄

表2-1 試題 j 與試題 k 之聯合邊界機率表……… 8 表2-1 OT、IRS 與 Diagnosys 順序性定義……… 10 表3-1 古典之試題參數、答題情形以及信度表……… 24 表3-2 IRT 之ａ、ｂ、ｃ值及 χ2 考驗 P-Value 表……… 25 表3-3 作答反應次數分配表……… 37 表4-1 題組結構二元選題策略各閾值預測精準度及平均施測題數表……… 40 表4-2 辨識率及平均施測題數……… 41 表4-3 電腦施測結果……… 45

(8)

圖目錄

圖2-1 三層式主從架構邏輯圖……… 17 圖3-1 研究流程圖……… 20 圖3-2 題組結構二元選題策略例圖……… 29 圖3-3 題組結構多點選題策略例圖……… 31 圖3-4 評估選題策略之成效圖……… 33 圖3-5 系統功能圖……… 34 圖_{3-6 施測流程圖……… 37} 圖_{4-1 二元計分題組結構……… 39} 圖4-2 建立結構介面……… 41 圖_{4-3 上傳試題介面……… 42} 圖4-4 參加測驗介面……… 43 圖4-5 帳號管理介面……… 43 圖4-6 學習診斷報告（上）……… 44 圖4-7 學習診斷報告（下）……… 45

(9)

第一章緒論

本研究主要目的在於建置以知識結構為基礎的多點計分題組式適性診斷測驗系統，本章包括研究動機、研究目的、名詞解釋及研究範圍與限制等四節，茲分述如下。第一節研究動機近年來，由於適性測驗理論的發展，電腦化測驗有了重大的突破，可以針對不同程度的受試者給予不同難易度的試題，且做答的題數減少很多即可測驗出學生能力，近年來與網路的結合，更將電腦在測驗上的功效發揮到最大(黃朝恭，2000)。電腦適性測驗(Computerized Adaptive Testing, CAT)可以有效的節省測驗題數，亦可縮短測驗時間，更能符合「因材施測」的原則。電腦化適性測驗依理論基礎大致可分為二大類（郭伯臣，2004 ）：一類是以試題反應理論 (Item Response Theory, IRT) 為基礎 (Wainer,2000)；另一類則是以知識或試題結構為基礎( Appleby, Samuels, Treasure -Jones,1997; Brown & Burton, 1978; Chang, Liu & Chen, 1998; VanLehn, 1988; Wenger,1987)。

以IRT 為基礎所進行的測驗，受試者成績為一「能力值」(ability)或「量尺分數」 (scale score)，較適合用於教育資源分配情境，例如：基本學力測驗、大學入學測驗等。根據郭伯臣(2003，2004，2005)的國科會專題研究「國小數學科電腦化適性診斷測驗 (I)(II)(III)」指出，將「順序理論」(Ordering Theory, OT) (Airasian & Bart, 1973)、「試題關聯結構分析法」(Item Relationship Structure analysis, IRS)(Takeya, 1991) 或 Diagnosys(Appleby, Samules, &Treasure-Jones, 1997)來分析學生知識結構，並依據學生知識結構建立電腦化適性測驗，可以提供學童一個適性測驗及立即的成績回饋，達到「因材施測」的效果。除此之外，並有相關研究顯示，這樣的電腦化適性測驗確實可以節省施測題數，並有不錯的預測精準度(蔡昆穎，2004；何政翰，2004；許志毅，2004；黃珮璇、王暄博、郭伯臣、劉湘川，2006；楊智為、張雅媛、郭伯臣、許天維，2006）。郭伯臣、謝友振、張峻豪、蔡坤穎(2005)指出使用良好的試題結構，可有效降低施測題數，該研究中比較了三種估計試題結構方法，美國學者所研發之 OT、日本學

(10)

者所研發之IRS 及英國學者所研發之 Diagnosys，研究結果顯示，使用 OT 所建立之結構應用在適性測驗選題策略上，所需訓練樣本較少與可節省較多施測題數，優於 IRS 與 Diagnosys，故本研究題組結構二元計分部份採用 OT 順序理論技術來估計學生結構，並用於適性測驗選題流程之建立。林文質(2005)的研究指出，比較二元計分試題結構與多點計分試題結構作為選題策略，得到下列結論：當預測精準度固定時，使用多點計分試題結構較 OT 估計之二元計分試題結構平均施測題數較少，顯見成效較佳，故本研究題組結構多點計分部份採用林文質(2005)所提出的多點計分技術來估計多點計分題組結構，並用於適性測驗選題流程之建立。從 60 年代開始選擇題或是非題的測驗題型，因其過度強調評量學生的記憶能力而飽受批評，之後的學校改革，便紛紛結合認知心理學觀點，以促進高層次思考的測量(王德蕙，2006)。Ebel(1951)曾提出以情境依賴的題組(context-dependent item set)，用來解決客觀式選擇題或是非題測驗最常被詬病的問題，就是只能測量受試者的記憶能力，而無法測量高層次的學習成果。Haladyna(1992)在檢視許多情境依賴題組的研究後，也認為此種題型，不僅適用在任何的測驗類型，如選擇題或實作題，還可以有效的測量到不同類型的高層次思考。一個情境依賴的題組必然包含一個刺激(stimulus)或題幹，和一組需以該刺激或題幹作為答題依據的試題。因題組在測驗上是很重要的題型，在目前市面上的適性診斷測驗系統還是以選擇題為主，因此本研究採選擇題型的題組為本研究的研究方向。本研究擬建立一個以結構理論為基礎的多點計分題組式適性診斷測驗系統，題組結構的多點計分部份採用林文質(2005)提出之理論技術來估計題組結構的上下位關係。並探討多點計分題組式最佳選題策略，以節省施測的時間，並提供個別學習診斷報告書，讓學生可以立即知道自己的錯誤觀念，也有利教師進行補救教學，達到因材施教的目標。第二節研究目的基於上述動機，本研究之研究目的分述如下：

(11)

壹、探討以結構理論為基礎的多點計分題組式適性診斷測驗的最佳選題策略。貳、建置以結構理論為基礎的多點計分題組式適性診斷測驗系統。參、以「怎樣解題」單元實作「以結構理論為基礎的多點計分題組式適性診斷測驗系統」並評估其成效。第三節名詞解釋針對本研究常見的重要名詞，詳細說明如下：壹、電腦化適性診斷測驗本研究的電腦化適性診斷測驗係採用網路介面的測驗方式，結合多點計分的知識結構理論加以施測。呈現給考生的試題順序，是根據考生先前的作答反應，呈現下一個要給考生作答的試題，選擇對考生估計錯誤概念最有貢獻的試題。如此一來，測驗的長度便可以縮短，並且也較不會犧牲測量精確性。因此，實施電腦化適性測驗，不僅可以做到因材施測的目的，也可精確估計考生的錯誤概念，節省許多施測時間和成本，可說是一舉數得。貳、結構理論本研究所稱之結構理論是由 Bart& Krus(1973)所提出順序理論(Ordering Theory, OT)，利用 OT 分析學生的作答反應，瞭解學生知識的上下位關係。參、專家知識結構專家知識結構是由學科專家根據學理以及教學經驗，分析施測範圍內所需具備的知識，再根據學生的學習歷程、概念發展順序及概念間上下位關係整理而成的一種結構關係。在專家知識結構中，最上層的概念為此單元的最難概念，下層則為各概念的下位概念。肆、多點計分題組結構以林文質(2005)提出的理論技術來估計題組與題組間的結構，和原本 OT 順序理論技術所估計的二元計分試題結構，這兩個結構結合在一起，使試題間的關係形成雙層結構，本研究稱為多點計分題組結構。

(12)

伍、錯誤概念「錯誤概念」指在數學解題歷程中所產生的系統性錯誤(system error)，這種錯誤與隨機錯誤(slips error)不同。其成因是來自於穩定的錯誤或因不完全、誤導的學習概念所造成，也可以說是錯誤概念所造成的結果。由於這種錯誤是由學生自己所建構而成，因此與專家知識有所不同，其特點是高度抗拒改變，經常會造成學習的障礙。陸、題組試題本研究所稱之題組試題，與王德蕙(2006)的研究定義相同：題組的試題結構可以分為二部分，一為訊息來源，而另外則為一組彼此之間有所關聯的試題(Allen & Sudweeks, 2001; Haladyna, 1992)；此訊息可以是一個段落文章、圖表、或其它的刺激(stimulus)材料，在訊息之後跟隨一些試題，這些試題的應答都必須依賴相同的訊息刺激(Lee, 2000)，這些試題本研究以子題稱之。第四節研究限制本研究由於時間、資源及人力限制的考量，所研擬探討的對象以國民小學六年級學生為範圍，研究題材訂為數學領域怎樣解題單元，因此，本研究結果的推論不可過度推論到其他教育層級的學生和其他學科。

(13)

第二章文獻探討

本研究主要目的為建置以結構理論為基礎的多點計分題組式適性診斷測驗系統，因此，本章將分成五節來加以闡述：第一節為電腦化適性測驗；第二節為估計知識結構的方式；第三節為以知識結構為基礎的多點計分模式；第四節為題組題型；第五節為系統開發方法。第一節電腦化適性測驗測驗與評量一直是教學過程中很重要的一環，透過測驗，可以反映出學生的學習狀況，供教師做後續補救教學的依據。早期測驗方式，多以紙筆測驗形式進行，並仰賴人工閱卷，近年來由於電腦科技的發達，許多測驗進行的方式已逐漸由傳統的紙筆測驗轉變成電腦化測驗，用來評估學生的學習成效或學習歷程(曾彥鈞，2007)。近年來，由於適性測驗理論的發展，電腦化測驗有了更重大的突破，可以針對不同程度的受試者給予不同難易度的試題，且做答的題數減少很多即可測驗出學生能力，近年來與網路的結合，更將電腦在測驗上的功效發揮到最大(黃朝恭，2000)。

一般的電腦化適性測驗可以分為以試題反應理論(Item Response Theory, IRT)為主的，以及利用知識或試題結構為主的兩種(郭伯臣，2004)，以下將分別介紹。壹、以試題反應理論為主的電腦適性測驗以試題反應理論為主的電腦適性測驗，是應用試題反應理論( Item Rsponse Theory, IRT)所發展出來之一種新的實施測驗方式。要實施適性測驗，也唯有在電腦誕生發明後，才有可能施行。電腦科技的發達，日新月異，它的超大容量可以貯存測驗訊息（如：測驗試題及其特徵指標）、編製、施測、和記錄測驗分數，因此使得推行適性測驗變得愈來愈可行(Bunderson, Inouye & Olsen, 1989; Wainer, 1990)。

以試題反應理論為主的電腦化適性測驗(computerized adaptive testing, CAT) 裡，呈現給考生的試題順序，是依據考生在前一個試題上的表現好壞來作決定的。在開始進行電腦化適性測驗之時，先由電腦終端機隨機呈現一組測驗試題（也

(14)

許是兩題或三題），在考生作出反應之後，電腦便根據這些反應資料，估計出考生的初步能力估計值(initial ability estimate)；然後，電腦會根據這些初步能力估計值，從現有的題庫(item bank)中挑選出最能對能力水準的估計發揮最大貢獻力量的試題，再呈現這些試題給考生作答，根據考生先前的表現好壞，呈現下一個要給考生作答的試題。換句話說，根據考生先前的表現情形，來決定下一階段將呈現給受試者作答的試題，而且這樣的試題是能對考生能力的估計精確性提供最大訊息量，循此原則，直到滿足一個預先設定的信賴水準或終止標準時，測驗即結束。透過這樣的機制，使得測驗的長度可以縮短，也不會犧牲測量精確性。換言之，對於高能力的受試者無需提供較為容易的試題作答，對於低能力的受試者，也不會有試題難度太高而造成心理上的打擊，因為這些試題是相對於他們的能力水準來選取的。因此就電腦化適性測驗來說，不僅可以做到精確估計考生能力來進行「因材施測」，更可節省許多施測時間和成本，優點相當明顯。此種施測方式是採機動的選題方式去配合受測者的表現，換言之，需要從題庫中根據試題的統計特質，即試題參數(item parameters)去選題，且受測者每完成一個反應，能力水準要再被估計，涉及的計算過程頗為複雜，因此需藉助電腦方能實施，所以此種測驗方式又稱為電腦化適性測驗。基於IRT 理論的電腦適性測驗，將根據受試者的作答情形，依照能力值的不同，給定不同的試題。換言之，一般以試題反應理論為基礎的電腦化適性測驗，施測結果為一能力值或量尺分數。由於學生的錯誤類型並不具順序性或線性排列，即並非所有學生皆會先出現錯誤類型1而後才出現錯誤類型2，因此無法單獨將錯誤類型與某一分數進行對應，只能根據受試者的作答情形，依照能力值的不同，給定不同試題。所以IRT 較適合用在成就測驗，如大學學力測驗。使用以估計能力值為目的之適性測驗來進行學習診斷，所提供的訊息相當有限；因此本研究將以國小數學領域為範例，發展以結構理論為基礎的多點計分題組式適性診斷測驗系統。

(15)

貳、以知識或試題結構為主的電腦適性測驗以知識結構為基礎之適性化診斷測驗系統，首先需建立知識結構，並依據此知識結構作為適性測驗的選題策略，能提供學生一個適性測驗立即的成績回饋，並於測驗後給予學生個別化、量身訂作的補救教學，讓學生知識的建構能有最好的效果。黃珮璇、王暄博、郭伯臣、劉湘川(2006)的研究證實了以知識結構為主的國小數學科電腦化適性診斷測驗具強韌性(robustness)，即電腦化適性診斷測驗系統之成效在廣泛應用於各單元或其它相關主題時，依然存有良好的表現。曾彥鈞、劉育隆、郭伯臣、楊智為(2006)實作開發出以知識結構為基礎的適性化診斷測驗系統，目前系統實際上已有94、95年康軒、南一版數學各單元教材上線，並由多位研究生進行實際使用、作為施測平台。許多研究（白曉珊、劉育隆、郭伯臣、施慶麟，2006；林立敏、白曉珊、郭伯臣、劉育隆，2006；莊惠萍、劉育隆、郭伯臣、曾彥鈞，2006；趙琬津，2006；盧炎成，2006）指出，以知識結構為基礎之適性化診斷測驗系統根據學生知識結構設計適性施測流程，可依不同受試者的作答情形而給予適當的試題，藉此節省大量的試題並可對學生的剖面圖得到精確的估計，確實可以有效節省施測題數，並有適性化的功能，且提供個別學習診斷報告書，讓學生可以立即知道自己的錯誤觀念，也有利教師進行補救教學。以知識結構為基礎之適性診斷測驗系統的特點如下所示（白曉珊、劉育隆、郭伯臣、施慶麟，2006；林立敏、白曉珊、郭伯臣、劉育隆，2006；莊惠萍、劉育隆、郭伯臣、曾彥鈞，2006；趙琬津，2006；盧炎成，2006）：一、「評量」、「診斷」與「補救教學」皆適性化、個別化，達到「因材施測」、「因材施教」的目的。二、與施測全部紙筆測驗試題情境比較，當預測精準度設定為0.95時，以知識結構為基礎之適性化診斷測驗系統平均可節省50%以上的施測題目(黃珮璇、王暄博、郭伯臣、劉湘川，2006；楊智為、張雅媛、郭伯臣、許天維，2006）。三、節省學生大量測驗時間，可把時間用於適性補救教學。

(16)

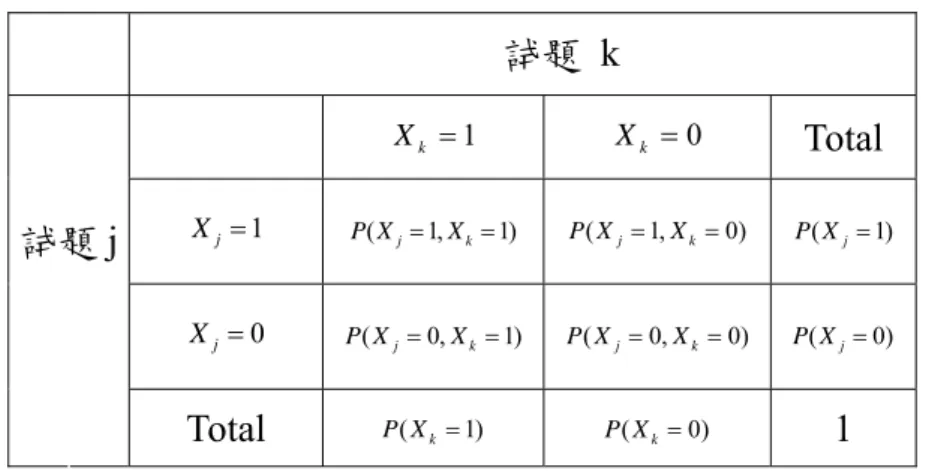
四、可診斷出同分不同錯誤類型之學生，便於因材施教。五、將知識結構為基礎之適性診斷測驗系統網路化，可達到隨時檢測的目的。六、可提供多媒體補救教材進行自主學習，以達事半功倍之效。第二節估計知識結構的方式 Diagnosys(Appleby et al., 1997)是一種基於知識結構為基礎的數學概念之電腦化診斷測驗，利用紙筆測驗預試所得到的資料，分析出題與題之間的關係，定義出屬於學生知識結構的試題概念表，將之應用於電腦測驗上。令X =(X₁,X₂,⋅⋅⋅,Xn)表示一個向量包含n 個二元試題成績變數，每一個受試者者作答n 題得到一個 0 與 1 的向量x=(x₁,x₂,⋅⋅⋅,xn)之後，試題 j 跟 k 的聯合及邊際機率 ( the joint and marginal probabilities)可以如表 2-1 表示。

表2-1 試題 j 與試題 k 之聯合邊界機率表 試題 k 1 = k X X_k =0 Total 1 j X = P X( _j=1,X_k=1) P X( _j=1,X_k=0) P X( _j=1) 試題j 0 j X = P X( j=0,Xk=1) P X( j=0,Xk=0) P X( j=0) Total P X( _k=1) P X( _k=0) 1 因原本的Diagnosys 試題結構定義不利於計算： 1. 若f

(

x_j =1,x_k=0

)

>> f

(

x_j=0,x_k=1

)

則X j → Xk。 2. 若f

(

x_j =1,x_k =1

) (

+f x_j =0,x_k =0

)

>> f

(

x_j =0,x_k =1

) (

+ f x_j =1,x_k =0

)

則Xj ↔ Xk( Appleby et al., 1997)。郭伯臣(2004)將其重新定義：

(17)

1. 若

(

₍

)

₎

<

β

= = = = 1 , 0 0 , 1 k j k j x x f x x f 則Xj → Xk。 2. 若

(

₍

) (

_{) (}

)

₎

<β = = + = = = = + = = 0 , 1 1 , 0 0 , 0 1 , 1 k j k j k j k j x x f x x f x x f x x f 則Xj ↔ Xk。只要

(

₍

)

₎

<β = = = = 1 , 0 0 , 1 k j k j x x f x x f ，即小於某個閾值( threshold)

β

，便確認試題X 為試題_j Xk 的下位試題。若

(

₍

) (

_{) (}

)

₎

<β = = + = = = = + = = 0 , 1 1 , 0 0 , 0 1 , 1 k j k j k j k j x x f x x f x x f x x f 成立時，我們確認試題X 與試題j Xk 兩者之間的關係是等價的。

Airasian & Bart(1973)順序理論的定義若是存在兩試題 j 與試題 k，若發生試題 j 做錯且試題k 做對機率很低時，定義如下所示： ε ε* = ( =0, =1) < k j jk P X X ，ε 代表閾值，且定義為0.02≤ε ≤0.04。因此當上式成立時，即試題 j 做錯且試題 k 做對的發生機率低於一定的值，代表兩者之間的關係可以被紀錄成Xj → Xk。

試題關聯結構法(Item Relationship Structure, IRS)是由 Takaya( 1991)發表的，使用另ㄧ種指示符號 * jk r ，也是用來定義試題 j 到試題 k 之間的順序關係，因此r 代表閾值 且被定義是為： _r X P X P X X P r k j k j jk ₌ ₌ ≥ = = − = ) 1 ( ) 0 ( ) 1 , 0 ( 1 * 若rjk ≥r * _{，則我們可以確認試題}_{j 為試題 k 的下位試題，兩者之間的關係可以被記} 錄成X_j → X_k。因此在OT 及 IRS 中，若X_j → X_k且X_k → X_j同時成立時，則兩者的關係可以表示成X_j ↔ X_k，這樣表示試題j 與試題 k 兩者是等價的。 OT 與 IRS 兩者是常用來定義試題間順序性的方法，早期這些方法常用於比較不同教學方法或不同版本教材，是否造成學生知識結構不同。主要是以紙筆測驗結果來進行知識結構推估，因此並非是針對電腦化測驗所設計的理論，但何政翰( 2004)將其

(18)

用來做為建立電腦測驗的依據，有很好的效果。為方便比較將OT、IRS 與 Diagnosys 三者之順序性定義表示於表 2-2。在該表中， IRS 裡的 γ 為閾值經常是被設定在 0.02≦γ≦0.04 的。至於在 OT 之中，利用 ε 來代表閾值，且建議大小為0.5(郭伯臣，2003)。表2-2 OT、IRS 與 Diagnosys 順序性定義 順序性定義 Xj→Xk Diagnosys

(

₍

)

₎

<β = = = = 1 , 0 0 , 1 k j k j x x f x x f IRS r X P X P X X P r k j k j jk ₌ ₌ ≥ = = − = ) 1 ( ) 0 ( ) 1 , 0 ( 1 * OT ε* = ( =0, =1)<ε k j jk P X X

(19)

第三節以知識結構為基礎的多點計分模式「態度問題關聯結構分析法」原稱「語意結構(semantic structure)分析法」，簡稱 SS 分析法，是日本心理計量學者竹谷誠於 1987 年所倡（胡豐榮，2001；竹谷誠，1987； Takeya，1999），此法利用圖形理論(graph theory)，將態度尺度資料分析出潛在之階層結構，然後再利用該階層結構來解釋態度資料間之關聯。竹谷誠將常見之選項數相等之非類別態度尺度資料，依計分方式之不同分為兩種，劉湘川( 2003)稱之為「等級計分資料」、「對稱計分資料」，竹谷誠( 1987)分別提出了前二者專有之「問題關聯順序係數」，惟兩種計分資料間，不能互相通用，且只適用於所有問題選項數均相等時。 令試題 j 與試題 k 之選項數分別為m 、_j m ，選項得分分別為k q ，r ，Njk( rq, )表 試題 j 得分 q 分，試題 k 得 r 分之受試人數且試題 j 選項 q 之計分為x ，試題 k 選項jq r 之 計分為x 。 kr 令試題 j與試題k之計分平均分別為x 、_j x ，計分標準差分別為k s 、j s ，則有： k ∑ = = j m q jq j j x m x 1 1 ， = ∑ = k kr k m r k x m x 1 1 ， = ∑

(

−

)

= j j jq j j m q x x x m s 1 2 2 1 ， = ∑ − = k k kr k k m r x x x m s 1 2 2 1 ₍ ₎ 令x 與jq x 之標準化計分分別為kr z 、jq z ，則：kr xj j jq jq s x x z = − ， xk k kr kr s x x z = − 定義非負指示函數如：

[ ]

⎪⎩ ⎪ ⎨ ⎧ = + x x 0 0 0 ≥ < x x ，則「試題 j至試題k」之「關聯順序係數」( Takeya, 1999)，各題均為 m 點計分： ∑ ∑ − − − = ∑ ∑ − − − = − = =+ − = = + 1 1 1 1 1 1 * ₎ ( , ) 1 ( 1 ) , ( ) ( ) 1 ( 1 1 m r m r q jk jk m r m r q jk N r q N m r q r q N r q m N r 此一定義之缺點為各題選項數或計分方式不可以不同。劉湘川( 2003)針對「等級計分資料」及「對稱計分資料」，提出「一階廣義問題關

(20)

聯順序係數」公式，不論選項數相等與否，亦不論是否為等級計分、對稱計分、或其混合型計分資料，均一體適用。劉湘川、楊志良( 2003)提出較靈敏有效不會高估之「改良一級廣義問題關聯順序係數」，劉湘川、簡茂發( 2004)提出具同等功能且訊息量更多之「s 級廣義問題關聯順序係數」。 「試題 j 至試題 k 」之「一階廣義關聯順序係數」（劉湘川&簡茂發，2004）：

[

]

) ( ) , ( 1 1 1 1 − + + = = + − ∑ ∑ − − = z z N r q N z z jk m q m r kr jq jk j k γ 其中：z _j _n _q _m

{ }

zjq j ≤ ≤ ≤ ≤ + =max1 ,1 ，z− =min1≤j≤n,1≤q≤mj

{ }

zjq 特點：各題選項數或計分方式可以不同，使用標準化量尺，降低不同選項數或計分方式造成的影響。 「試題 j 至試題 k 」之「改進一階廣義關聯順序係數」（劉湘川&簡茂發，2004）：

[

]

1 1 1 1 ) , ( 1 U r q N z z jk m q m r jq kr jk j k + = = ⊕ ∑ ∑ − − = γ 其中： max

[

]

( , ) ( ) 1 1 , 1 1 + − + = = ≤ ≤ ⎭⎬≤ − ⎫ ⎩ ⎨ ⎧_{∑ ∑} ₋ = z z N q r N z z U jk m q m r jq kr n k j j k 「試題 j至試題k」之「改進s 階廣義關聯順序係數」（劉湘川&簡茂發，2004）：

(

) (

)

[

]

∑ ∑ − − − − = = − + − − ⊕ mj k q m r s jk s kr s jq jk U r q N z z z z 1 1 1 ) , ( 1 γ ，s=1,2,3 其中：

[

(

) (

)

]

⎭ ⎬ ⎫ ⎩ ⎨ ⎧∑∑ − − − = = = + − − ≤ ≤ − mj k q m r jk s kr s jq n k j s z z z z N qr U 1 1 , 1max ( , ) 當上述各順序係數小於某一閾值（r）時，則定義試題 j 能夠向試題 k 連結，代表兩者之間的關係可以被紀錄成xj→ ，我們說試題 j 與試題 k 之間有順序性。 xk 上述中所列之多點計分試題（問題）關聯係數為適合李克特氏計分之資料，為使之適用於多點計分之試題需將其稍加修改，例如Takeya( 1999)「試題 j 至試題 k 」之 m 點計分「關聯順序係數」，林文質( 2005)將其修改如下：

(21)

∑ ∑ − − = − = = + 1 1 1( ) ( , ) ) 1 ( 1 m q m q r jk jk r q N q r m N λ ，λjk<λ ⇔ Xj→ Xk並可轉換成下列算式： ) , ( ) , ( ) , ( ) 1 ( 1 1 1 1 1 _N w q r p X q X r r q N m q r k j m r q m q r jk m q m q r jk jk ∑ ∑ − = ∑ ∑ = = − = − = = + − = = + λ ，其中 1 r) (q, w_jk − − = m q r 。 ) , (X q X r p j = k = 為發生試題 j 得 q 分且試題 k 得 r 分事件之機率，wjk(q,r)為此事件違反順序的嚴重性加權，違反順序越嚴重，w_jk(q,r)越大。當m=2（二元計分）時，則 * jk jk ε λ = ，即OT 中使用之 * jk ε 為係數λjk之特例。上述λ_jk之缺點與r 相同，僅適用於各題計分點數皆相同之情況，本研究為解決此jk* 一問題，將多點計分試題順序係數重新定義於下，令試題 j 與試題 k 之選項數分別為 j m 、m ，選項得分分別為 q 、 r ，k Νjk( rq, )表試題 j 得 q 分，試題 k 得 r 分之受試人數 且試題 j 選項 q 之計分為x ，試題選項jq r 之計分為x ，假設試題 i 為kr mi +1點計分，即試題i的計分範圍為0,1,2,...,m_i，且 j j j m X Y = 介於0 與 1 之間量尺分數，則令係數ηjk為 ∑ = = = > j k m q m r k k j j jk jk m r Y m q Y p r q w ( , ) ( , ) η 。其中 ∑ − − = > j k m a m b j k j k jk m a m b m q m r r q w ) ( ) , ( ，a=0,1,...,m_j；b=0,1,...,mk ) , ( k k j j m r Y m q Y p = = 相同於發生試題 j 得 q 分且試題k得 r 分事件之機率，wjk( rq, ) 為此事件違反順序的嚴重性加權，違反順序越嚴重，wjk( rq, )越大，當ηjk <η時，則 k j X X → 。

(22)

第四節題組題型

Ebel(1951)提出編寫測驗試題的建議，他認為情境依賴的題組(context-dependent item set)可以測量到較為高階的學習成果。即使發展情境依賴的題組較為困難，但此種題型卻使得客觀式試題也能測量到高階思考的能力(Crehan, Sireci, Haladyna & Henderson, 1993)。Haladyna(1992)也曾針對不同的學科領域，如：閱讀理解、數學問題解決、科學問題解決和統計推理，提出題組(item sets)得以測量到高層次思考的說明；另外，他也認為題組的測驗形式，可以讓測驗發展者獲得更多有關學習者的學習資訊。簡言之，情境依賴的題組，使得受試者得以應用其分析思考和問題解決的知識和能力(Allen & Sudweeks, 2001)。

所謂情境依賴的題組，指的是一組共享一個刺激或共同訊息來源的相關試題 (Haladyna, 1992; Lee, 2000; Allen & Sudweeks, 2001)，因此一個情境依賴的題組必然包含一個刺激(stimulus)或題幹，和一組需以該刺激或題幹作為答題依據的試題。雖然不同學者使用不同名稱來指稱此種題型，如 Ebel(1951) 的解釋性作業 (interpretive exercises)、Cureton(1965)的超級試題(superitems)、Wainer & Kiely(1987)的題組(testlet) 或Yen( 1993)的段落( passages) 等，但無論使用何種名稱，這些學者皆認為情境依賴的題型，提供評量受試者應用分析思考和問題解決能力的方法(Wainer & Lewis, 1990; Allen & Sudweeks, 2001)。

隨著電腦化適性測驗的發展，有學者( Wainer & Kiely, 1987; Wainer & Lewis,1990) 提出以題組的測驗形式來解決電腦化適性測驗所產生的問題。這些學者發現，電腦化適性測驗的試題結構會導致情境效應(context effects)和內容平衡(content balancing)的問題。當某一特定試題的呈現對次一試題的難度有所影響時，就會產生情境效應，此時，若測驗建構的規則未考慮試題的內容，試題間就會產生依賴性(dependency)。內容平衡問題係指電腦化適性測驗在挑選試題時，可能會選擇到相同主題，如水、運動、氣象等，但偏重某一主題對於某些受試者來說，可能是不公平的。為了解決上述電腦化適性測驗所產生的問題，這些學者便提出以題組(testlets)的方式來組織試題。他們認為題組不僅可使測驗發展者重拾測驗結構的控制力，對於受試者來說，試題的內容主

(23)

題也會較為公平。無論題組的測驗形式是為了評量高層次思考，或解決電腦化適性測驗的問題，題組的使用是越來越重要了(Lee, Brennan& Frisbie, 2000)。

由於題組形式可以測量高層次思考，並應用於多種題型上，因此，目前許多大型的標準化成就測驗或國家證照考試，皆採用此種測驗類型來評量學生的成就。例如：美國國家教育進展評量(National Assessment of Educational Progress, NAEP)、國際閱讀素養進展研究(Progress in International Reading Literacy Study, PIRLS)、國際學生評量計畫(Programme for International Student Assessment, PISA)等大型評量；我國的國中基本學力測驗和大學入學考試；托福測驗或英語檢定測驗等，皆使用了題組的測驗形式。

題組的結構發展出來後，不同的學者也給予題組不同的名稱，如：早先的解釋作業(interpretive exercises)(Ebel, 1951; Wesman, 1971)、超級試題(superitems)(Cureton, 1965) 和應用測驗 (application test)(Szeberenyi & Tigyi, 1987)；段落 (passages)(Yen, 1993)；題束(item bundles)(Wilson & Adams, 1995)；或題集(item clusters)(Ferrara, Huynh & Baghi, 1997;Allen & Sudweeks, 2001; Haladyna, 1992)；以及最近的題組(testlets)( Lee, 2000; Lee, 2002; Lee & Frisbie, 1999; Wainer & Kiely, 1987; Wainer & Lewis, 1990)等。依據最近的研究文獻，則歸納出題組(testlets)這一個名詞是目前最廣受學者所接受與使用的。除了名稱之外，題組的定義也隨著不同學者的觀點而有所不同，例如Wainer& Kiely(1987)所提出的題組概念，是為了解決適性測驗所產生的選題問題，因此，他們將題組(testlets)定義為，將一群和單一內容領域有關的試題組合成一個單位，此一單位包含固定數量的預定路徑(predetermined paths)，受試者便可依照此預定的路徑來進行測驗。

Wainer ＆Lewis(1990)更進一步將題組(testlets)定義為小測驗(small tests)，它們小到讓試題編製者得以操控，卻又大到足以涵蓋該題組本身的內容。Lee、Brennan 和 Frisbie(2000)則將題組(testlets)定義為某一測驗題本(test form)中的試題次組合(subset of items)，此種組合在測驗結構(test construction)、實施(administration)和計分(scoring)時被視為測量的單位。無論學者對題組(testlet)所下的定義為何，就試題的結構而言，所

(24)

謂題組(testlet)必然包含一個段落、圖表、或其他刺激(stimulus)材料，並在刺激之後跟隨一些試題。這些試題的應答，都必須依賴相同的刺激(Lee, 2000)。換言之，題組型的試題主要包含兩個部分，一為訊息來源；另外則為一組彼此之間有所關聯的測驗試題(Allen & Sudweeks, 2001; Haladyna, 1992)。和某特定主題或內容領域有關的題組形式，不僅在教育測驗的場合中應用甚多，在國家的證照考試中也是相當普遍，其中最為典型的即為閱讀理解測驗(Gessaroli & Folske, 2002; Haladyna, 1992)。

(25)

第五節系統開發方法本系統的建立是基於希望能夠以最小的資源耗費，達成最大的經濟效益，因此，對於作業系統的選擇，以較安全、穩定的 Linux 系統為平台，其餘相關開發工具也以穩定、免費使用為優先考量。除此之外，本研究的系統乃是建置在網際網路環境之上，因此採用網路三層式主從式架構。下面分別就各相關工具介紹說明。壹、三層式主從架構資料庫技術這個架構主要在用戶端和伺服器端再加上一層中介層，成為三層的主從架構 (client/server)。在這三層的架構下，用戶端使用標準的通訊協定（如：TCP/IP）與中介層溝通；中介層使用標準的資料庫通訊協定或資料庫中介軟體與後端的資料庫溝通。三層式主從架構邏輯層的結構如圖2-1，各層的任務有包含主要為使用者介面的資料展現層(presentation layer)、包含操作資料的處理邏輯層又稱商業邏輯層(functionality/business layer)以及供應資料的存取服務的資料服務層(data layer) （黃朝恭，2000）。

圖2-1 三層式主從架構邏輯圖

由圖2-1得知，處理邏輯層透過PHP(hypertext preprocessor)處理資料庫，並利用結構化查詢語言(Structure Query Language, SQL)來處理資料，也就是說它利用一些簡單的句子構成基本的語法來存取資料庫內容。SQL為非程序性語言 (non-procedural)，它本身並不能單獨存在，需要依照每一行程式順序處理許多的動作來存取資料庫（黃朝恭，2000）。瀏覽器 Apache / PHP 資料庫(MySQL) 資料展現層處理邏輯層資料服務層

(26)

貳、開發工具

PHP(hypertext preprocessor)。這是一種被廣泛使用、多用途的開放原始碼腳本語言(script language)，特別適合於網頁的開發，並可內嵌於HTML 網頁中。除此之外尚可應用在開發應用程式，為相當具有開發彈性的語言。PHP 主要使用於伺服器(server)端的動態網頁的開發，功能與ASP(active serve page)、JSP(java server pages)、Cold Fusion等相似。加上PHP 本身的語法類似C/C++，具有親和易學的特性，所以一般資訊人員或是其曾經接觸過他種程式語言者皆相當容易上手。在實作跨平台系統時是非常好的工具之一，並且支援多種資料庫。參、資料庫系統本研究所使用的資料庫為MySQL，這是一套具有快速、多線性(multithread)、多使用者且穩定的SQL資料庫伺服器，以主從式架構的方式來實現，並且透過一個伺服程式MySQL 及許多不同的用戶端函式庫的組成。加上執行基本SQL 指令效率非常迅速，與坊間常見的微軟SQL( MS-SQL)及甲骨文(Oracle)等商業資料庫來比較是毫不遜色，更重要的是MySQL 在非商業用途上是免費的，並且支援中文大五碼(Big5)，另外針對許多不同的平台也都有對應的支援，在安裝設定上面也是相當容易，因此本研究的後端資料庫決定採用MySQL。肆、網路伺服器

Apache 本身是一套自由軟體，但也是一套高效能的網站伺服器(web server)，目前被廣泛運用在各種作業平台上面，穩定且消耗資源少，在網際網路的伺服器平台上面是遙遙領先其他廠商。而且Apache 網路伺服器本身提供了相當多樣化的模組，系統管理者可以從中挑選適合的部分予以安裝使用，擴充性相當強大，而且具有支援PHP 的模組。

(27)

第三章研究方法與步驟

本研究旨在探討多點計分題組式適性診斷測驗的最佳選題策略，進而建立多點計分題組式適性診斷測驗系統，並實際施測評估其成效。本章主要分為八個部分來說明整個研究架構。分別是：一、研究方法；二、研究流程；三、研究範圍與對象；四、研究工具；五、選題策略實驗設計；六、選題策略成效評估；七、系統分析與設計；八、系統成效評估。第一節研究方法根據研究目的與文獻探討的結果，擬定之研究方法，說明如下：在「探討以結構理論為基礎的多點計分題組式適性診斷測驗的最佳選題策略」方面，結構理論的結構建立方式有好幾種，且選題策略與所建立結構的好壞息息相關，但很少學者針對題組這種題目類型進行選題策略的研究。因此，選擇「怎樣解題」單元，以紙筆測驗進行預試，本研究將評估、比較題組結構二元計分選題策略與題組結構多點計分選題策略之成效，並應用於本研究所要建置「以結構理論為基礎的多點計分題組式適性診斷測驗系統」之中。在「建置以結構理論為基礎的多點計分題組式適性診斷測驗系統」方面，先參考相關文獻探討，再針對系統需求分析，以進行系統實作與修正。除了使用最佳的選題策略外，在學生做完電腦化適性診斷測驗後，進行錯誤類型診斷，並提供一份學習診斷報告書，給學生最立即的回饋。在「以『怎樣解題』單元實作以結構理論為基礎的多點計分題組式適性診斷測驗系統，並評估其成效」方面，本系統建置完成後，實際於國小進行施測，並收集完整的紙筆作答反應，應用預試所估計的題組式多點結構進行選題策略，並評估其成效。第二節研究流程在確定研究主題後，即進行各種相關文獻的收集與探討，分成二個部分同時進行。研究流程圖如圖3-1 所示，分述如下。

(28)

壹、最佳選題策略首先，聘請教學經驗豐富的專業國小教師群，針對「怎樣解題」單元進確定研究主題文獻收集與探討建立學生知識結構分析「怎樣解題」單元以各種適性選題策略進行選題出題、審題、修題、組卷進行預試（紙筆測驗）建立專家知識結構評估各種選題策略成效系統需求分析系統開發實作系統測試、修正正式施測資料收集與分析成效驗正撰寫研究報告圖 3-1 研究流程圖

(29)

行文獻收集與教材分析，並編製該單元知識結構草案，再共同用知識結構檢核表，建立較客觀的專家知識結構。建立專家知識結構後，依據專家知識結構命題，依據電腦化適性診斷測驗之檢核表檢核試題，檢核完畢後進行組卷以利紙筆測驗的進行。組卷之後並進行紙筆測驗，收集學生的作答反應，利用學生的作答反應估計出學生的知識結構，再利用本研究所提出的方式建立題組結構，並依此進行選題，針對紙筆測驗所得到的資料進行選題研究，自行開發程式估計，評估適性選題策略之優劣，將精準度為0.95的多點計分題組結構建置在系統中，作為選題之用。貳、以結構理論為基礎的多點計分題組式適性診斷測驗系統之建置其次，著手對系統的建置做準備，先針對系統需作分析，主要包含帳號管理模組、測驗管理模組、測驗結果管理模組、上傳試題模組，利用物件導向方法與元件化技術進行系統分析、設計。透過需求分析可以了解系統功能性與非功能性上的需求。本研究將利用PHP、HTML等技術來建構以結構理論為基礎的多點計分題組式適性診斷測驗系統，因此在平台方面的自由度比較高。資料庫方面則使用MySQL資料庫做溝通，以本研究目的一所探討的最佳方法作為選題策略。將帳號管理模組、測驗管理模組、測驗結果管理模組、上傳試題模組進行系統整合，使以結構理論為基礎的多點計分題組式適性診斷測驗系統更加完善。參、以「怎樣解題」單元實作將「怎樣解題」單元的試題建置於系統內，實際於國小進行電腦施測，評估以本研究建立之多點計分題組結構所建立之系統的成效，進而撰寫研究報告。第三節研究範圍與對象本研究選定以國小六年級數學領域中 94 年康軒版第十二冊第九單元「怎樣

(30)

解題」進行實作，皆為題組題型，共29 題。研究對象分述如下： 壹、紙筆測驗預試紙筆測驗的預試樣本採立意抽樣，對象為九十四學年度六年級學生，包括台中市國小14個班級，台中縣國小7個班級，有效樣本共計650人，在教完該單元ㄧ周內進行施測。貳、電腦施測電腦施測的施測樣本也採立意抽樣，對象為九十五學年度六年級學生，包括台中市國小10個班級，彰化縣國小20個班級，有效樣本共計1004人，在教完該單元ㄧ周內進行施測。第四節研究工具本研究的研究工具大致可分為三大項，其一為「MATLAB 7.1」，其二為「怎樣解題單元測驗卷」，其三「建置系統所需的平台及軟體」，以下分別敘述之。壹、 MATLAB 7.1 MATLAB是一高階科學運算語言、可分析資料與發展演算法和應用之互動式環境。MATLAB 7中涵蓋了許多新功能，可讓程式撰寫、編碼、繪圖更有效率，同時視覺化、數學運算、資料擷取與效能上都大有提升。因此本研究撰寫MATLAB程式來評估目的一的選題策略之成效，也用來評估目的三系統正式施測之成效。貳、「怎樣解題」單元測驗卷本研究所使用的研究工具包括「94年康軒版第十二冊第九單元怎樣解題測驗卷」，詳如附錄二，這張測驗卷是國立台中教育大學、亞洲大學與階梯數位科技股份有限公司建教合作計畫「以試題結構理論為基礎之國小五、六年級數學領域電腦適性診斷測驗系統與題庫建置」計畫中所發展出來的部分成果，由多位教學經驗豐富的專業國小教師群，針對「怎樣解題」單元進行文獻收集與教材分析，並編製該單元知識結構草案，再共同用知識結構檢核

(31)

表，建立較客觀的專家知識結構，如附錄一所示。建立專家知識結構後，依據專家知識結構命題，依據電腦化適性診斷測驗之檢核表檢核試題，檢核完畢後進行組卷，完整試卷如附錄二所示，分析資料如表3-1、表3-2所示。

(32)

表3-1 古典之試題參數、答題情形以及信度表古典理論模式選答比率(小數點表示) Cronbach's Alpha 0.937 試題鑑別度難度選項 1 選項 2 選項 3 選項 4 未答 IF ITEM DELETED 信度下降 MATH01 0.409 95.2 0.0077 0.0154 0.9523 0.0246 0.0000 0.9363 -0.0007 MATH02 0.518 89.8 0.0215 0.0569 0.8985 0.0231 0.0000 0.9352 -0.0018 MATH03 0.548 91.8 0.0385 0.9185 0.0323 0.0077 0.0031 0.9350 -0.0020 MATH04 0.614 84.5 0.0308 0.8446 0.0631 0.0615 0.0000 0.9341 -0.0029 MATH05 0.621 84.5 0.8446 0.0369 0.0754 0.0431 0.0000 0.9340 -0.0030 MATH06 0.639 86.3 0.8631 0.0523 0.0600 0.0185 0.0062 0.9339 -0.0031 MATH07 0.539 93.4 0.0169 0.9338 0.0231 0.0262 0.0000 0.9352 -0.0018 MATH08 0.518 93.2 0.0200 0.9323 0.0323 0.0138 0.0015 0.9354 -0.0016 MATH09 0.53 93.5 0.0185 0.9354 0.0277 0.0169 0.0015 0.9353 -0.0017 MATH10 0.557 78.3 0.0846 0.0431 0.7831 0.0862 0.0031 0.9348 -0.0022 MATH11 0.561 72.2 0.1200 0.7215 0.0492 0.1000 0.0092 0.9349 -0.0021 MATH12 0.646 78 0.0600 0.0523 0.7800 0.0969 0.0108 0.9337 -0.0033 MATH13 0.419 74.6 0.1554 0.0477 0.7462 0.0385 0.0123 0.9368 -0.0002 MATH14 0.549 90.8 0.0262 0.9077 0.0354 0.0262 0.0046 0.9350 -0.0020 MATH15 0.602 83.8 0.0323 0.0969 0.0277 0.8385 0.0046 0.9342 -0.0028 MATH16 0.551 85.2 0.0292 0.8523 0.0400 0.0738 0.0046 0.9348 -0.0022 MATH17 0.578 80.8 0.0985 0.0492 0.8077 0.0385 0.0062 0.9345 -0.0025 MATH18 0.704 80.5 0.0462 0.8046 0.0569 0.0754 0.0169 0.9330 -0.0040 MATH19 0.68 78.9 0.0477 0.7892 0.0662 0.0785 0.0185 0.9332 -0.0038 MATH20 0.522 75.8 0.1031 0.0662 0.7585 0.0646 0.0077 0.9353 -0.0017 MATH21 0.613 80.9 0.0615 0.0908 0.8092 0.0246 0.0138 0.9341 -0.0029 MATH22 0.62 78.3 0.0585 0.0892 0.7831 0.0538 0.0154 0.9340 -0.0030 MATH23 0.441 70.9 0.0600 0.1185 0.0754 0.7092 0.0369 0.9366 -0.0004 MATH24 0.603 87.1 0.0523 0.0369 0.8708 0.0369 0.0031 0.9343 -0.0027 MATH25 0.627 83.8 0.0677 0.0538 0.8385 0.0277 0.0123 0.9340 -0.0030 MATH26 0.667 84.3 0.0400 0.8431 0.0431 0.0646 0.0092 0.9335 -0.0035 MATH27 0.453 90.9 0.0231 0.0338 0.0262 0.9092 0.0077 0.9358 -0.0012 MATH28 0.644 82.8 0.8277 0.0846 0.0508 0.0231 0.0138 0.9337 -0.0033 MATH29 0.519 88.8 0.0231 0.0323 0.0462 0.8877 0.0108 0.9352 -0.0018 此張試卷經施測後分析作答情形，分析測驗內部一致性的數值， Cronbach α係數值為0.937。其與標準化成就測驗α係數最好在0.9以上，可說是還算相當理想（洪碧霞、吳裕益，1996）；另一方面本測驗所得之信度

(33)

係數值已超過學者Carmines & Zeller(1979)所認為優良教育測驗信度值應達到0.80的標準值之上，所以本份測驗顯示有良好的內在與外在測驗信度，亦即本測驗結果有良好的內部一致性及時間穩定性，如表3-1所示。接著以BILOG-MG3.0分析軟體進行試題參數分析，古典試題理論鑑別度皆大於0.25，具有相當的鑑別度，且難度值適中。表3-2 IRT之ａ、ｂ、ｃ值及_{χ 考驗P-Value表}2 IRT 模式

SLOPE THRESHOLD ASYMPTOTE ITEM 鑑別度(a 值) 難度(b 值) 猜測度(c 值) (PROB) MATH01 1.2191 -2.0904 0.1892 0.0924 MATH02 1.3498 -1.4488 0.1973 0.4838 MATH03 1.5303 -1.5927 0.1664 0.2106 MATH04 1.6147 -1.0664 0.1603 0.0980 MATH05 2.2445 -0.9034 0.2300 0.9016 MATH06 2.7222 -0.9469 0.2527 0.5588 MATH07 1.8951 -1.6554 0.1627 0.0279 MATH08 1.9046 -1.5550 0.2363 0.2198 MATH09 2.0326 -1.6013 0.2052 0.1356 MATH10 1.5648 -0.6945 0.2150 0.6863 MATH11 2.0921 -0.3841 0.2224 0.4224 MATH12 2.2180 -0.6434 0.1976 0.2232 MATH13 0.9722 -0.6035 0.2389 0.0863 MATH14 1.4550 -1.5158 0.1732 0.4302 MATH15 1.4916 -1.0521 0.1652 0.4849 MATH16 1.3052 -1.1770 0.1713 0.6559 MATH17 1.5684 -0.8447 0.1904 0.6522 MATH18 3.2624 -0.7247 0.1807 0.9376 MATH19 2.4368 -0.7169 0.1587 0.8645 MATH20 1.2218 -0.6661 0.1986 0.0109 MATH21 1.8168 -0.7896 0.2117 0.5092 MATH22 1.7212 -0.7321 0.1721 0.3320 MATH23 1.0562 -0.4333 0.2213 0.0014 MATH24 1.7565 -1.1438 0.2030 0.2652 MATH25 2.1083 -0.8921 0.2223 0.1094 MATH26 2.1759 -0.9675 0.1744 0.5854 MATH27 1.1510 -1.5762 0.2408 0.6934 MATH28 1.9519 -0.8800 0.2001 0.9647 MATH29 1.4155 -1.2682 0.2558 0.3564

(34)

再以IRT模式進行分析，表3-2為其分析結果，可看出第8、21、24題的PROB 小於0.05，需要進行題目之修改。在效度方面，本研究從內容效度、建構效度二方面來加以說明：（一）內容效度 1.學者教授審題敦請台中教育大學數學教育系施淑娟、台中教育大學教育測驗統計所郭伯臣兩位教授逐一審查試題是否符合課程綱要和數學領域之教學目標。並就不妥之處作一修訂。 2.專家教師評估商請七位任教國小數學領域五～十年的專家教師評估本份測驗能測出學習成就的有效性。（二）建構效度本測驗之建構效度以內部一致性分析法的方式驗證之（余民寧， 2003）。 1.試題內的一致性依據受試者在測驗答對的題數多寡，將全體受試者均分為高（答對21題以上，共521人）、中（答對11至20題者，共87人）、低（答對10題以下者，共42人）三組，然後比較高、低這兩組受試者在每一道試題上作答的答對率。經以t考驗分析兩組差異，高分組高於低分組的答對率，皆達.05顯著水準。因此，本測驗的試題具有高度的的內部一致性。 2.試題間的一致性將全體受試者在每一道試題的答題情形（答對或者答錯）與其得分（答對的總題數），分別求其積差相關，發現每一道試題與得分的相關考驗，均達.05顯著水準，亦即顯示測驗總分與每一道試題

(35)

的得分皆成正相關。參、建置系統所需的平台及軟體

針對系統需求進行評估之後，採用以下之研究工具，來完成目的二之系統建置：

一、系統主機：IBM Xseries 206 Intel Pentiun4 3.0GHz/800MHz，記憶體 1GB，硬碟160GB，硬碟傳輸界面為SCSI UltraWide II，網路卡傳輸效率100MB/S的伺服器。

二、作業系統：CentOS 4。這款翻版軟體(clone)是由CentOS計畫所推出，全名為「社群企業作業系統」(Community Enterprise Operating System, CEOS)。這個計畫是在2003年紅帽公司決定不再提供免費的技術支援及產品認證之後的部份「紅帽重建者」(Red Hat rebuilders)之一。 CentOS是「Caos Linux」獨立計畫的一個分支， CentOS是以知名的 RedHat平台為基礎，有一定的穩定性與安全性。

三、網站伺服器：Apache 2.2.3。除了主機、作業系統與使用者所製作的網頁外, 我們還需要安裝一套能將網頁放到網路上讓其它人來存取的軟體，也就是所謂的 Web Server。由於我們使用的作業系統平台是CentOS，因此我們使用在 Linux 系統上最受歡迎的 Apache Web Server。四、資料庫：MySQL 5.0.18。MySQL資料庫也是免費的程式，是由MySQL AB公司所開發的資料庫伺服器，可以連結C、C++、Java、Perl、PHP 語言，而且也可在許多平台上運作，如：Linux、Windows、Sun Solaris ... 等，且支援微軟的ODBC規格的資料庫整合。權限的使用也是MySQL 特別的地方，對不同使用者設定權限，在資料庫中必須依權限的設定才能進入資料表，提高了安全性。五、網頁語言：PHP 5.1.6。PHP的全名為 Hypertext Preprocessor ，它是個被廣泛運用在網頁程式撰寫的語言，尤其是它能適用於網頁程式

(36)

的開發及能夠嵌入 HTML 文件之中，它的語法和 C 、 Java 及 Perl 等語法相似，且學習起來更容易上手。PHP的目地是為了能使網站開發者可以快速地撰寫動態網頁。六、網頁編輯軟體：Macromedia Dreamweaver。Dreamweaver是一種「所見即所得」的網頁編輯工具，使網頁編輯類似一般的文書處理，例如：插入圖片、加入表格以及文字。使用者只要在編輯區域中編輯網頁，則可以在瀏覽器中預覽網頁，達到網頁編排上的靈活度與便利性。

(37)

第五節選題策略實驗設計為了探討以結構理論為基礎的多點計分題組式適性診斷測驗的最佳選題策略，分別以「題組結構二元計分選題策略」、「題組結構多點計分選題策略」兩方面，進行實驗設計。壹、題組結構二元計分選題策略在圖3-2的例子中，是利用所收集學生的作答反應，採用OT順序理論技術來估計所得到的學生結構，每一個節點代表一個試題，在上面的節點稱為上位節點，在下面的節點就稱為下位節點，例如：「節點3」是「節點8」、「節點9」、「節點10」的上位節點，「節點8」是「節點1」、「節點3」的下位節點。在上位的節點代表較困難的試題，所以當上位節點答對時，代表其下位節點都會答對，例如：「節點1」是四則運算，「節點2」、「節點3」就可能是加、減、乘、除，會四則運算的學生一定會加、減、乘、除，但是會加、減、乘、除的學生不一定會四則運算。所以上位節點會，下位節點一定會，下位節點會，上位節點不一定會。本研究所提出的二元計分選題策略，是依據OT所分析出的題組結構為基礎進行選題，由於題組的題型有相同的題幹，所以必須將整個題組做完後才題組一題組三題組二 1 3 2 8 10 9 5 7 6 4 圖3-2 題組結構二元選題策略例圖

(38)

換下一個題組，因此，以下就舉圖3-2為例子，詳細說明選題策略如下：首先挑選下位節點數最多的試題為第一題，在本例中會先選「節點1」，若「節點1」答錯。再挑選與第一題相同題組的試題，挑選下位節點數最多的試題繼續進行施測，直到該題組全部做完為止，在本例中題組一剩下「節點2」、「節點3」要進行估計，因「節點3」的下位節點數比「節點2」多，因此，先施測「節點3」再施測「節點2」，若「節點2」與「節點3」皆答錯。當第一個題組施測或估計完時，會在其他的試題中挑選下位節點數最多的試題繼續進行施測，在本例中由於「節點4」的下位節點數最多，因此，從「節點4」繼續施測，若「節點4」答對，則「節點5」、「節點6」、「節點7」會判斷為答對，題組二就算施測完畢，接著繼續選剩下試題中節點數最多的，因此系統施測「節點8」，若「節點8」答對，則判斷「節點5」、「節點6」為答對。當所有節點皆已施測或估計完時，即結束該單元測驗，在本例中紙筆測驗需施測10題，以題組結構二元計分選題策略進行選題可節省5題。貳、題組結構多點計分選題策略多點的選題策略與二元的選題策略不同之處在於，利用林文質(2005)所提出建立能力指標間結構的方法建立題組間的結構，結合二元計分選題策略，應用在題組結構上。

(39)

假設圖3-3為估計出來的題組結構，圖3-3中黑粗的箭頭代表題組間的上下位關係，也就是若題組一通過，題組二也會判斷為通過，這樣可以節省更多的題目，詳細說明選題策略如下：首先必須先設定題組間的通過率，若通過率設定為0.7，就表示需通過該題組內70％以上的試題，才會判斷其下位題組也已經學會，在本例中設定題組間的通過率為0.6。挑選下位節點數最多的試題為第一題，在本例中會先選「節點1」，若「節點1」答錯。再挑選與第一題相同題組的試題，挑選下位節點數最多的試題繼續進行施測，直到該題組全部做完為止，在本例中題組一剩下「節點2」、「節點3」要進行估計，因「節點3」的下位節點數比「節點2」多，因此，先施測「節點3」再施測「節點2」，若「節點2」與「節點3」皆答對。判斷該題組的答對率是否比預先設定題組間的通過率高，若比較高，則將其下位題組皆標示為預測作答正確，若比較低，則繼續在其他的試題中挑選下位節點數最多的試題繼續進行施測，在本例中由於預先設定題組間的通過率為0.6，題組一在此次作答當中答對率為66.6％，較預先設定題組間的通過率高，因此判斷題組一已經學會，並將其下位題組題組二之所有節點判斷題組一題組三題組二 1 3 2 8 10 9 5 7 6 4 圖3-3 題組結構多點計分選題策略例圖

(40)

為答對。當題組施測或估計完時，會在其他的試題中挑選下位節點數最多的試題繼續進行施測，直到所有節點皆已施測或估計完時，即結束該單元測驗，在本例中由於「節點3」已答對，因此，其下位節點「節點8」、「節點9」、「節點10」判斷為答對，即結束測驗。在本例中紙筆測驗需施測10題，以題組結構多點計分選題策略進行選題可節省7題。不論是二元或多點的，每個學生可能因作答反應的不同，有不同的節點要施測，所以每個學生所做的題目不見得相同，藉此達到適性選題，因才施測的目的。

(41)

第六節選題策略成效評估

本研究評估選題策略之成效是使用5-fold cross validation 的方法，將紙筆測驗所有收集的樣本平均切成五等分，將其中四等分做為訓練樣本(training samples)，利用訓練樣本去估計出題組結構，另外一等分做為測試樣本(testing samples)，利用測試樣本來進行模擬適性測驗，一直循環五次計算出精準度，再將五次的精準度平均，即為最後的預測精準度，如圖3-4 所示。第七節系統分析與設計壹、以結構理論為基礎的多點計分題組式適性診斷測驗系統之建置一、需求分析針對以結構理論為基礎的多點計分題組式適性診斷測驗系統，探討系統分析與設計的過程，利用物件導向方法與統一化程序來進行系統分析，並透過元件導向軟體工程的概念，歸納出系統軟體元件。為了建構人性化的執行環境規範，測驗系統必須具備可以上傳試題的功剖面圖訓練 fold (k-1)fold 題組結構測試 fold (k-1)fold 訓練題組結構剖面圖測試精確度圖3-4 評估選題策略之成效圖

(42)

能，以及學生可以透過系統進行適性診斷測驗，並且在測驗的過程中，測驗系統必須提供一個可以紀錄使用者測驗歷程的機制，以清楚紀錄學生在系統上的診斷狀況，系統功能圖如圖3-5 所示。蒐集適性測驗系統之需求分析，了解需要導入哪些功能，在此歸納出上傳試題、參加測驗、帳號管理、查詢學生測驗成果等四個功能。將確認的需求分析，利用物件導向方法與元件化技術進行系統分析、設計與實作，也加入了選題策略，再將實作完成之功能整合成為以結構理論為基礎的多點計分題組式適性診斷測驗系統。系統平台是Cent OS 作業系統，配置方式為系統發展之PHP 技術，負責呈現網頁資訊，後端資料庫部分則採用 MYSQL。二、系統設計透過需求分析可以了解系統功能性、與非功能性上的需求，並針對欲設計之功能加以描述如下，在系統中就是由這些模組與資料庫互相傳遞訊息、溝通、合作所完成的。（一）上傳試題模組上傳試題之功能，主要是將老師欲測驗之內容上傳至伺服器端，提供學生上網施測。此上傳試題模組中，主要完成三件事，最主要的便是上傳題目與配分，因考慮到各瀏覽器的顯示問題，所以所有的題目跟選老師學生帳號管理上傳試題適性測驗成果查詢圖3-5 系統功能圖

(43)

項皆以圖檔上傳；另外，上傳預試所分析出來的試題間的結構與題組間的結構，皆是 Excel 檔，將題組結構以矩陣表示的檔案儲存至伺服端；最後，上傳專家知識結構的線性概念列表，讓欲實施補救教學的學生或老師可以知道學習的路徑，也會有一個試題與專家知識結構的線性列表對應的檔案，負責判斷該概念是否已經通過。（二）帳號管理模組帳號管理的功能，主要是將使用者分為老師與學生，提供老師可以新增該班欲施測學生的帳號與密碼，當新增帳號後，新的帳號就會記錄在資料庫中，當學生要登入系統時，系統會至資料庫做使用者比對，若有該使用者，且帳號密碼正確才允許登入。（三）測驗管理模組測驗管理模組主要功能是紀錄學生考過哪些試題，並依照題組結構做出最佳選題策略，且記錄每一個試題所作答的時間，當學生透過網頁，點選欲選取的答案時，瀏覽器會透過網路將學生代號與課程代號儲存到資料庫，並利用在伺服端題組結構與作答反應兩個表單進行最佳選題策略。測驗管理模組的流程大致為，學生發出參加測驗的需求，系統將學生基本資料及試題資料儲存到資料庫表格中，以紀錄學生參加測驗經過，接著經由查詢測驗結果將測驗資訊與學生代號儲存至資料表，最後，透過SQL 查詢資料表，將此學生下一個試題內容透過網頁的方式呈現，供學生測驗。（四）測驗結果管理模組學生參加完測驗，需給學生應有的回饋，所以測驗結果管理模組會在記錄學生全部作答完成後顯示，有學生的基本資料，及學生每個概念是否通過的概念列表，幫助學生釐清自己的錯誤概念，也可幫助老師迅

題組式適性診斷測驗系統之建置

國立台中教育大學教育測驗統計研究所理學碩士論文

指導教授：郭伯臣 教授