A homophonic DES

Informqtion

f,;;~rw

Information Processing Letters 66 ( 1998) 3 17-320

A homophonic DES

Tsu-Miin Hsieh a,*, Yi-Shiung Yeh ‘3’) Yung-Cheng Hsieh b, Chan-Chi Wang aJ

’

b Department of Industrial Technology, Illinois State linivwsity, Normal, IL 61790-5100, USA Received 3 December 1997: received in revised form 28 January 1998

Communicated by SC. Akl

Abstract

In this paper, we propose a variant of DES called a homophonic DES. The DES algorithm is strengthened by adding some random bits into the plaintext, which are placed in particular positions to maximize diffusion, and to resist differential attack. 0 1998 Elsevier Science B.V. All rights reserved.

Keywords: Cryptography; Block cipher; Differential attack; Random number generator

1. Introduction

DES [9] is one of the most popular block ciphers. It is a cipher encrypting a 64-bit data block with a 56-bit key. The operations in DES are all public and fixed. This feature facilitates cryptanalysis. A well-known attack on DES is the differential cryptanalysis [Z-5] proposed in 1990 by Eli Biham and Adi Shamir.

Differential attack makes use of the exclusive-or difference of plaintext and ciphertext pairs. It esti- mates the probability that certain plaintext difference will result in a certain ciphertext difference, by esti- mating the probability of intermediate difference pat- terns in the DES algorithm. A difference pattern which occurs with high probability can be useful for deduc- tion of some key bits. Right pairs which generate the desired difference pattern will suggest some key val- ues including the correct one, oppositely wrong pairs suggest random values. For a difference pattern which

* Corresponding author. Email: tmhsieh@csie.nctu.edu.tw. ’ Email: ysyeh@csie.nctu.edu.tw.

’ Email: ccwang@csie.nctu.edu.tw.

0020-0190/98/$19.00 0 1998 El. qevier Science R.V. All rights reserved. PII: SOO20-0190(98)00073~8

occurs with high probability, the right key values will be suggested with the highest frequency when enough plaintext pairs have been analyzed.

Differential cryptanalysis requires 247 chosen-plain- texts or 255 known-plaintexts to attack full 16-round DES, with 237 DES operations during analysis [S].

To defend against differential cryptanalysis, we have constructed a DES variant which we name a homophonic DES. In this new scheme, some random bits are added to the plaintext. This increases the complexity of a differential attack. The details of this new scheme are described in the next section.

2. Homophonic DES

A homophonic DES is a variant of DES that maps each plaintext to one of many ciphertexts (for a given key). We propose a homophonic DES that maps a 56-bit plaintext to a 64-bit ciphertext using a 56-bit key. Let P be the set of plaintexts of length 56 bits and C the set of ciphertexts of length 64 bits. The mapping Ek from P to C adds 8 random bits to a

318 2-M. Hsieh et al. /Information Processing Letters 66 (1998) 317-320

56-bit plaintext and encrypts it using DES (k is a 56- bit key). Then there is a partition {Cl,

.

.

.

,

Clpl}

1

PI

P.

lCil=lCjlVi#jandi,j~{l,..., IPl},i.e.,ICiI= 2s = 256.

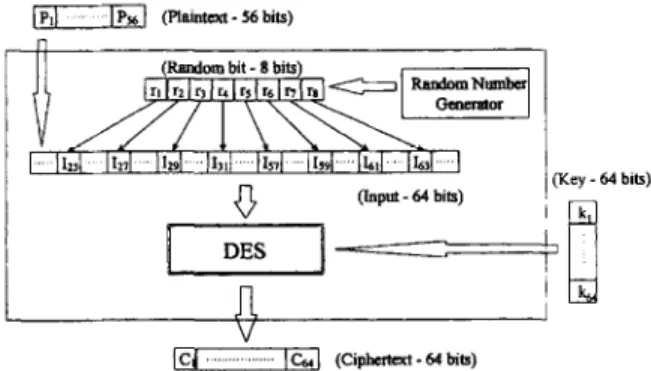
In our scheme, eight random bits are placed in specific positions of the 64-bit input data block to maximize diffusion. The criteria for embedding the random bits are listed below:

(1) After the initial permutation, the eight random bits should all be rearranged to the right half of the data block.

(2) In the first round, all eight random bits should be duplicated by the expansion permutation.

(3) In the first round, each S-box should have 2 input bits that come from two distinct random bits. There are 6 arrangements of random bits which satisfy the above criteria. Specifically, one of the position-sets (1,3,5,7,25,27,29,31), (1,3,5,7,33,35,37,39>, (1,3,5,7,57,59,61,63), (25,27,29,31,33,35,37, 39) (25,27,29,31,57,59,61,63), (33,35,37,39, 57,59,61,63) can be used. We name the algorithms that use the above position-sets HDESl, HDES2, HDES3, HDES4, HDESS, HDES6, respectively.

For example, the random bits in HDESS are the bit- positions 25, 27, 29, 31, 57, 59, 61 and 63. In this algorithm, after the initial permutation and expansion permutation in the first round, these eight random bits will spread to bits 2, 6, 8, 12, 14, 18, 20, 24, 26, 30, 32, 36, 38,42,44,48 of the 48-bit input block to the S-boxes and will affect the output of all the S-boxes. Note that the 48 expanded bits must be exclusive-or’d with some key material before proceeding to the S- boxes, thus two input bits into the S-boxes derived from the same random bit may have different values. This says that the random bits do not regularize the input to the S-boxes, that is, the property of confusion does not reduce while we try to maximize diffusion.

The encryption can be graphically represented as in Fig. 1.

And an input to the S-boxes is shown in the Fig. 2. In DES the 1st and 6th input bits of an S-box decide which one of its four rows is selected and the other four input bits decide the column. In the first round of HDESS, the selection of a row in each S-box is dependent on a distinct random bit, as is the column selection (see Fig. 2). Actually, in addition to HDESS, the three algorithms HDES2, HDES3, and HDES4

&put - 64 bits)

(Key - 64 bits) R

Fig. 1. HDES.5. Pi, q, Ii, Ci, ki denote the ith bit of plaintext, random-bit stream, input block to original DES, ciphertext, and key stream, respectively.

_---

Fig. 2. The random input to the first-round S-boxes in the case of HDESS. r; denotes the ith bit of random-bit stream.

Fig. 3. The random input to the first-round S-boxes in the case of HDES6. ri denotes the ith bit of random-bit stream.

also have the same property. However, HDESl and HDES6 are different: in these two algorithms four S-boxes are independent of the random bits for row selection. The case of HDES6 is shown in the Fig. 3. This property may make HDESl and HDES6 weaker than HDES2, HDES3, HDES4 and HDESS.

The decryption of the homophonic DES is similar to the decryption of DES. The only difference is that eight random bits must be removed to get the original plaintext (56 bits).

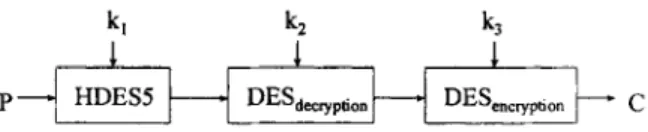
A homophonic DES can easily be transformed into a triple-encryption version by concatenating a DES decryption and a DES encryption after the homophonic DES. Two or three different 56-bit key

7T-h4. Hsieh ef al. /Information Processing Letters 66 (1998) 317-320 319

k,

1

k3

1

Fig. 4. The triple-encryption version of HDESS. P is a 56.bit plaintext, C is the 64-bit ciphertext, kl, k2 and k3 are three 56-bit keys and k 1 may equal kg

strings can be used. For example, the triple-encryption version of HDESS is shown in Fig. 4.

3. Security analysis

In our scheme, the input bits contain eight random bits which are not known to an attacker. This results in the nondetermination of the input difference for a plaintext pair. In other words, when a pair of plaintexts (56 bits) are encrypted, the attacker does not know the exact difference of their corresponding input bits (64 bits). In fact there are 256 possible differences. Thus, choose a pair of plaintexts (56 bits), the probability that they generate the desired difference pattern reduce to about l/256 of the probability in the case that input difference is clear. The differential attack that requires 247 chosen-plaintexts to attack full 16-round original DES now needs about 256 = 28 times that number of chosen-plaintexts to attack HDES, that is, about 255 chosen-plaintexts or (232 x dm) = 260 [5] known-plaintexts are needed. Obviously, the attempt to applying differential attack on HDES is more difficult.

Furthermore, the eight embedded random bits are placed in particular positions to maximize diffusion. Specifically, let m be a plaintext of 56 bits and m' be a plaintext that combines the plaintext m and 8 random bits. Let LoRo = ZP(m’) where ZP is the initial permutation. Lo and Ru are 32-bit strings and Ru contains all the random bits. After the 1st round of DES, we obtain Lt Rt , where Lt = Ro and R1 = Lo ~33 f(Ro, KI) [9]. Lt contains all the random bits and each bit in R1 is affected by the random bits.

4. Random number generator

It is best that the random number generator used in the new cryptosystem does not need any input and

generates nondeterministic output each time. How- ever, it seems very hard to find such a random number generator in the deterministic world of computers [7].

Some mathematical mechanisms with initial vectors such as linear feedback shift registers [8,10,11], which are used to simulate real random bits and called pseudo random number generators, can be applied in our cryptosystem. There is a security issue that has to be noticed: the initial vectors of the generators must be kept secret or the attackers will be able to reproduce the whole random-sequence and break the cipher. Moreover, new values should be placed in the initial vectors each time the encryption program is restarted. This can be achieved by recording the last vectors of the former execution and then using them as the initial vectors of the new execution.

Alternatively, by the use of special hardware, bit sequences that are difficult to reproduce can be con- structed and used as random sequences. For example, a computer’s clock time, charge difference between two capacitors [I], radioactive decay [6], etc., can be uti- lized. We do not explore this issue any further here. In fact, any well-designed random number generator can be incorporated into this cryptosystem.

5. Conclusion

In this paper, we conclude that a homophonic DES provides greater resistance to differential attacks than the original DES. Although there is the side effect of data expansion, in our scheme this is only about 1.14. A similar approach can be applied to other ciphers which are vulnerable to differential attacks. The random bits should be carefully positioned to maximize diffusion. Furthermore, since the adopted random number generator will affect the security of the cryptosystem, it should be chosen carefully.

References

[l] G.B. Agnew, Random sources for cryptographic systems, Advances in Cryptology-EUROCRYPT’ Proceedings, Springer, Berlin, 1988, pp. 77-8 I

[2] E. Biham, A. Shamir, Differential cryptosystems, Advances in Cryptology-CRYPT0’90 Proceedings, Springer, Berlin,

1991, pp. 2-21.

[3] E. Biham, A. Shamir, Differential cryptanalysis of Snefru, Khafre, REDOC-II, LOKI, and Lucifer, Advances in

320 L-M. Hsieh et al. /Information Processing Letters 66 (1998) 317-320

Cryptology-CRYPT0’91 Proceedings, Springer, Berlin, 1992, pp. 156171.

[4] E. Biham, A. Shamir, Differential cryptanalysis of the full 16 Round DES, Advances in Cryptology-CRYPTO’92 Proceed- ings, Springer, Berlin, 1993, pp. 487496.

[5] E. Biham, A. Shamir, Differential Cryptanalysis of the Data Encryption Standard, Springer, New York, 1993.

[6] M. Gude, Concept for a high-performance random number generator based on physical random phenomena, Frequenz 39 (1985) 187-190.

[7] D. Knuth, The Art of Computer Programming, Vol. 2, Seminu- merical Algorithms, 2nd ed.. Addition-Wesley, 1981.

[S] R. Lidl, H. Niederreiter, Introduction to Finite Fields and Their Applications, Cambridge University Press, London, 1986. [9] B. Schneier, Applied Cryptography, 2nd ed., John Wiley &

Sons, 1996.

[IO] ES. Selmer, Linear Recurrence over Finite Field, University of Bergen, Norway, 1966.

[ll] K.C. Zeng, C.H. Yang. D.Y. Wei, T.R.N. Rae, Pseudorandom bit generators in stream-cipher cryptography, IEEE Computer 24 (2) (1991) 8-17.