公共自行車系統靜態配置最佳化

(1)

國立台灣科技大學工業管理系

105 學年度實務專題報告

專題名稱：公共自行車系統靜態配置最佳化專題編號：TR-104-01-101

指導老師：喻奉天教授

研究組員：B10201001 蔡政軒 B10201042 賴郁晴 B10201052 陳姿伃 B10201059 何采維

中華民國 1 0 6 年 1 月 9 日

(2)

1

摘要

近幾年因為環保意識抬頭，在短程的移動時，許多人會選擇騎乘自行車。因此臺北市、新北市、桃園市、新竹市、臺中市、彰化縣與捷安特公司一同經營公共自行車租賃服務，簡稱為「YouBike 微笑單車」，打造環保綠都、帶動自行車風潮，改善空氣品質以及交通環境。但是隨著租賃站數越多，騎乘人口增加，在學校、景點、上班區域等需求量較多的租賃站有缺少自行車及缺少車位的困擾，導致使用者騎乘的數量減少、滿意度下降，此時必須派卡車來搬運微笑單車。因此如何有效率地派遣卡車配送微笑單車是一項非常值得探究的議題。

本研究探討如何在已知各公共自行車租賃站的自行車數及車位數現況下，有效率地利用卡車搬運自行車而將現況轉換成理想狀況。本研究參考車輛途程問題 (Vehicle Routing Problem; VRP)及其相關問題，建立此問題之數學規劃模型，並使用模擬退火法(Simulated Annealing; SA)為基礎建構演算法求解。本研究之模型考量各個租賃站上車數及使用者滿意度並以最小化總運輸成本為目標。本研究以 C++程式語言實作 SA 演算法並以一些標竿問題測試，再將結果與最佳化軟體 AMPL/CPLEX 所得結果比較，以分析研究結果在規劃路線上之效益，並可進一步應用於台北市各個微笑單車租賃站。本研究成果將可做為捷安特公司路線規劃參考。

關鍵字：車輛途程問題；同時收送貨之車輛途程問題；模擬退火法；公共自行車系統；微笑單車

(3)

2

Abstract

Due to the rising of the environmental consciousness in recent years, more and more people choose to ride a bike for short-distance trips. Therefore, the governments of Taipei City, New Taipei City, Taoyuan City, Hsinchu City, Taichung City and Changhua County work with Giant Manufacturing Co. Ltd to setup and operate a public bike renting business “Youbike” to become environment protection cities, promote bike riding population, improve the air quality and traffic condition. But when more and more bike stations are established and population of using the youbike increases, bike and bike post shortages occurred at bike stations in high demand areas such as schools, scenic spots and business districts. This problem causes the decrease of customer satisfaction and the number of users, and thus the company has to send trucks to transport bikes between stations. Therefore, how to effectively dispatch trucks is an important research topic worthy ofdeeper exploration.

This study investigates how to effectively use trucks to transport bikes to convert the current bike distribution into the target distribution assuming that the amount of bikes and the amount of bike posts at each station are known. Based on the Vehicle Routing Problem (VRP) and its related problems, we formulate a mathematic programming model for the problem and develop a heuristic algorithm based on Simulated Annealing (SA) to solve the problem. The objective of the model is minimizing the total cost of transportation, while considering the amount of bikes at each bike station and customer satisfaction. The SA is coded in C++ and tested on some benchmark instances. The results are then compared with those obtained by AMPL/CPLEX to analyze the effect of the outcome of this study on route planning, which can then be applied to each youbike station in Taipei City. The outcome of this research can serve as a reference for Giant Manufacturing Co. Ltd in route planning.

Keywords: Vehicle Routing Problem; Pickup and Delivery Vehicle Routing Problem;

Simulated Annealing; Bike-sharing System; Youbike.

(4)

3

摘要 ... 1

目錄 ... 3

圖目錄 ... 6

表目錄 ... 7

第一章緒論... 8

1.1 研究背景與動機... 8

1.2 研究目的與方法... 8

1.3 研究範圍及內容... 9

1.4 研究架構及流程... 10

第二章文獻回顧... 11

2.1 公共自行車租賃系統... 11

2.2 車輛途程問題... 11

2.3 車輛途程問題延伸... 12

2.4 常用於車輛途程問題之演算法... 13

第三章數學模型規劃... 16

3.1 問題定義與假設... 16

3.2 收送貨車輛途程問題之數學模型... 18

(5)

4

3.3 CPLEX 建構 ... 20

第四章演算法設計... 22

4.1 演算法架構... 22

4.2 路線順序規劃型態... 25

4.2.1 搬運量演算方式... 27

4.2.2 路線選擇範圍演算方式... 33

4.2.3 分析... 36

第五章實作測驗結果與分析... 38

5.1 題組說明... 38

5.2 解的呈現方式... 39

5.3 參數設定分析... 39

5.3.1 績效衡量標準... 40

5.3.2 單因子實驗設計... 40

5.3.3 例題說明... 40

5.3.4 實驗結果... 41

5.4 運算結果分析... 44

第六章結論與建議... 48

6.1 研究結論與貢獻... 48

6.2 建議與未來發展... 49

(6)

5

參考文獻 ... 50

附錄 ... 52

台北市 254 站各站資訊... 52

台北市 255 站各站資訊... 56

(7)

6

圖目錄

圖 1 公共自行車靜態配置路線示意圖 ... 17

圖 2 20160816-20 題組配置結果之行駛路線 ... 21

圖 3 模擬退火演算法示意圖 ... 24

圖 4 交換型態圖示 ... 25

圖 5 插入型態圖示 ... 25

圖 6 反轉型態圖示 ... 26

圖 7 依前站需求量決定此站到缺車或缺位站之機率 ... 26

圖 8 搬運量相關要件說明圖 ... 27

圖 9 有限制之隨機搬運流程圖 ... 29

圖 10 部分隨機不搬運流程規則 ... 32

圖 11 部分不搬運流程圖 ... 33

圖 12 a 站為第 20 站之 b 站選擇範圍 ... 34

圖 13 部分兩區域內選擇流程圖 ... 35

圖 14

T 0

測試結果 ... 41

圖 15

I iteration

測試結果 ... 42

圖 16

T final

測試結果 ... 42

圖 17 α測試結果 ... 43

圖 18

N Non-improving

測試結果 ... 43

圖 19 2016 年 8 月 18 日配置結果路線圖 ... 47

(8)

7

表目錄

表 1 PDVRP 與公共自行車靜態配置比較 ... 16

表 2 CPLEX 求解之題組資訊及最佳解 ... 21

表 3 改良前後之模擬退火法比較 ... 22

表 4 行駛此站時成本 ... 30

表 8 一區(20 站)測試結果 ... 36

表 9 兩區(43 站)測試結果 ... 37

表 10 六區(125 站)測試結果 ... 37

表 11 十二區(255 站)測試結果 ... 37

表 12 題組相關資訊 ... 38

表 13 卡車行駛順序與各站般運量 ... 39

表 14 30 站的行駛狀況 ... 39

表 15 例題大小分佈 ... 40

表 16 模擬退火法各項參數設定 ... 44

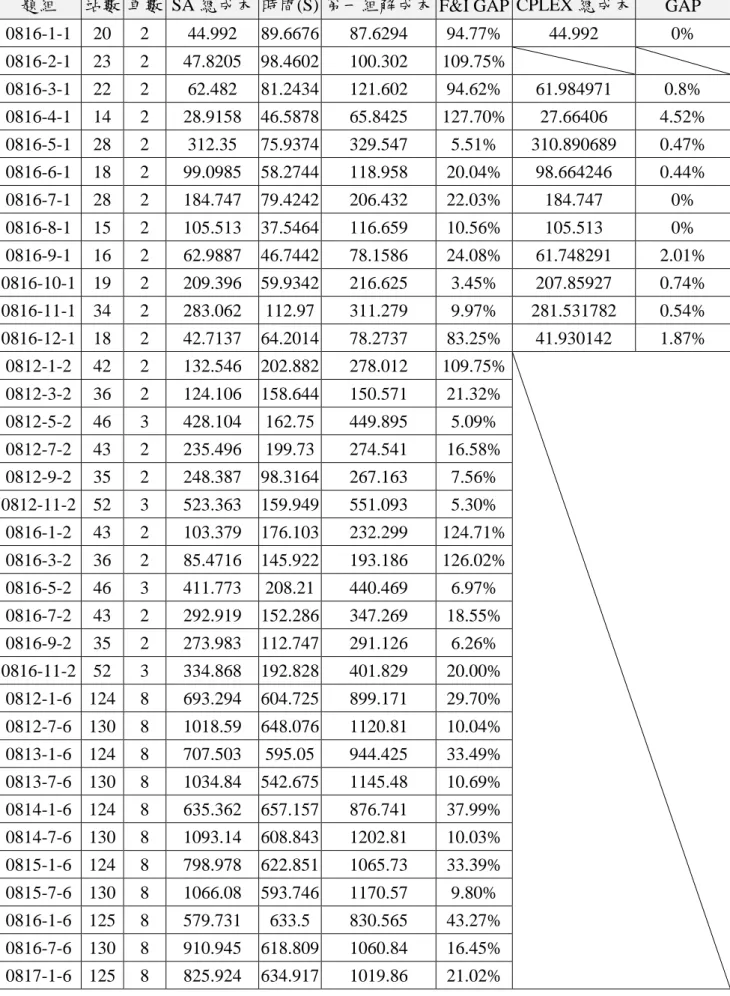
表 17 各題組運算結果與比較 ... 45

表 18 2016 年 8 月 18 日配置結果 ... 46

(9)

8

第一章緒論

隨著科技日新月異，汽、機車與大眾交通運輸在道路上更加頻繁，進步的同時，環保概念也跟著高漲，騎乘公共自行車成為另一種交通方式。對於目前公共自行車租賃站持續增加的情況下，如何有效的降低運輸成本、解決缺車及缺位問題是重要的課題。因此，本研究著重於提升公共自行車系統靜態配置效率，使系統處於較佳的平衡狀態，有效解決使用者的不便，提高使用者滿意度。

1.1 研究背景與動機

環保議題逐漸受到重視，政府推出公共自行車服務系統後，使市民有更便利的交通選擇，完成公共運輸系統的最後一哩路，無論是平日的上下班時段，還是假日的休閒時光，公共自行車已經是一項被廣泛使用的系統。近年來新設許多公共租賃站，熱門景點、捷運出口、學校附近、商業中心…等都可以很方便的騎乘，

讓人與自然更加親近。

儘管此系統提供許多好處，仍有些問題存在，以無人的電子自動化方式管理，

常常造成某一時段自行車數量供不應求，或是目的地站之車位已滿，使得無法停車，這些缺車與缺位的問題層出不窮，造成騎乘人數降低，使用者滿意度下降。

鑒於在多次觀察下，認為配送卡車路線安排有許多改善空間，因此將其做為研究出發點，期望能有效規劃卡車配送路線，同時降低運輸成本，並提升使用者滿意度。

1.2 研究目的與方法

最佳化車輛規劃路徑是最好的方法之一，大多數學者都以車輛途程問題 (Vehicle Routing Problem; VRP)的方法來解決此類問題。最基本的車輛途程問題包含一個已知位置的倉庫、各站點位置及需求量，每個站點只能服務一次且每個

(10)

9

站點的需求量都要被滿足，在這途程中不能超過卡車容量的限制，最主要的目標是派遣最少的卡車數，經路線規劃後，順利達到各點需求量，配送到最佳狀態，

並盡可能降低運輸成本，這就是一般的車輛途程問題。對於公共自行車而言，有收送自行車的動作，並非單方面滿足需求量，故我們用 VRP 作為基礎，建立同時收送貨之車輛途程問題(Pickup and Delivery Vehicle Routing Problem; PDVRP)，

以最低運輸成本之最佳路徑為目標，加強卡車配送自行車路線方面的改善。

VRP 屬於 NP-Hard 問題，而 PDVRP 是從 VRP 延伸型態之一，故 PDVRP 也是屬於 NP-Hard 問題，與 VRP 不同的地方在於有收貨、送貨兩種需求，隨著問題變大而更加複雜，為多項式的結構，因此要使用精密演算法求解此類型問題是相當費時費力，且在現實中，實用程度屈指可數。而啟發式演算法是更常採用的方法，兼顧了速度與品質。因此，本研究同時收送貨之車輛途程問題也將著重在啟發式演算法上，使用模擬退火法找尋最佳解，並藉由 AMPL/CPLEX 建模相互比對兩者之間的差異，相輔相成求得最好的答案。

1.3 研究範圍及內容

本研究進行卡車配送自行車之路徑規劃，並提出以 PDVRP 為基準的方式求得最佳解。卡車從倉庫出發，條件在不得超過卡車容量下，盡可能滿足各租賃站上的需求，若無法滿足則會派遣下一輛卡車繼續配送。

本研究 PDVRP 路線規劃中，配送時間在晚間十一時，此時自行車的流動頻率較低，因此假設此時的公共自行車系統為靜態，並在此狀態下配置，先判斷每個租賃站是屬於拿車或放車的需求情況後，卡車在未載自行車情況下從發車地出發，安排卡車行駛順序，進行各租賃站自行車配送，到達最後一站配送完畢後，

卡車就行駛回發車地。由於實際台北市公共自行車系統模式裡沒有固定的發車地，

所以從發車地出發以及最後返回發車地這兩段路徑是不計算成本，詳細定義與假設將在 3.1 節說明。所採用的實例為臺北市微笑單車 255 個租賃站，在 5.1 節中將逐項說明。

(11)

10

1.4 研究架構及流程

本研究各方法及步驟說明如下：

1. 研究動機與目的

確定目前公共自行車系統的問題後，訂定研究範圍與問題限制。

2. 文獻蒐集與回顧：

藉由網路、書籍、期刊論文等資源找尋有關同時收送貨之車輛途程問題和模擬退火法之應用，整合出適合此問題的求解方式。

3. 建構數學模型：

將 PDVRP 相關概念建立模型，求得同時收送貨之車輛途程問題路徑最佳化。

4. 發展演算法：

針對建構出的模型特性，參考相關文獻，以模擬退火法作為基本架構，再依題目特性發展對 PDVRP 有效的演算法。

5. 撰寫程式、執行與除錯：

根據設計的演算法流程，使用 C++語法設計一套程式系統架構，並使用 AMPL/CPLEX 建模，兩者進行除錯與修改以獲取最佳成果。

6. 實驗分析：

使用現有公共自行車系統數據，套入模型分析結果。

7. 說明成果與貢獻：

提出研究結果及重要貢獻，以及未來可改善部分，做為後續研究方向。

(12)

11

第二章文獻回顧

本章介紹本研究相關之文獻，包括公共自行車租賃系統的發展、車輛途程問題、同時收送貨之車輛途程問題及經常使用於求解車輛途程問題的一些通用啟發式演算法。

2.1 公共自行車租賃系統

公共自行車租賃系統風行於全球，世界上最早的公共自行車系統為法國里昂建置之公共自行車系統 Vélib'，Vélib'是由法文的腳踏車（vélo）和自由（liberté）

兩個字所組成。該系統於 2007 年 7 月 15 日開始運營，其設站密度非常高，幾乎巴黎市內的各車站與各觀光景點皆有自動出租站提供服務。

目前在台灣有臺北市、新北市、桃園市、新竹市、新竹縣、臺中市、彰化縣、

嘉義市、臺南市、高雄市以及屏東縣開辦公共自行車租賃服務。其中臺北市、新北市、桃園市、新竹市、臺中市及彰化縣為知名自行車廠商捷安特所設計研發的微笑自行車系統。台北市的 YouBike 約有 285 個租賃站，民眾可以透過配置於各租賃站的 KIOSK 自動服務機，快速成為會員後，持註冊後的電子票證(悠遊卡) 到停車柱借自行車，其收費方式為前 30 分鐘 5 元；介於半小時到 4 小時內每 30 分鐘 10 元；4 小時～8 小時內每 30 分鐘 20 元；超過 8 小時以上每 30 分鐘 40 元。

2.2 車輛途程問題

車輛途程問題是由 Dantzig and Ramser (1959)首先提出，是指在單一場站為起點，車輛及需求量為已知，且各車輛沒有運輸上的差異，在可載容量限制下，

求得滿足所有顧客需求且總成本最低的路徑。

VRP 屬於 NP-Hard 問題，廣泛應用於交通運輸及工業生產管理領域，一般

(13)

12

的車輛途程問題基本假設為：在單一廠站下，僅考慮純收貨或是純送貨，所有車輛由場站出發，在有限制的車輛數及車容量下，找尋最短路徑並滿足所有顧客，

且每位顧客只能被一台車服務一次，貨車在行駛途中，必須遵守車容量之限制。

而其複雜度會隨需求點數的增加，所費時間呈指數成長，若以求最佳解方式，在問題規模很大時，將難以在短時間內求出，因此多以發展趨近最佳解之啟發式解法，以利於短時間內即可求得不錯的解。VRP 求解方法繁多，Raff (1983)將求解策略分為許多類型：依限制分群再規劃的方式、針對現有路線做連結及合併的方法、交換不同路線中的節點，或是由決策者根據過往經驗及知識作為判斷的準則，

以及利用數學規劃方式直接進行求解。而本研究將採用通用啟發式演算法，常用於 VRP 之通用啟發式演算法將於 2.4 節說明。

2.3 同時收送貨之車輛途程問題

黃信穎 (2005)指出同時收送貨之車輛途程問題可分為：(1)純收貨或純送貨、

(2)去程送貨、回程撿收(先送後收)、及(3)同時收送貨等三種方式，分別說明如下：

1. 純收貨或純送貨

這類問題是屬於傳統車輛途程問題，將收貨的車輛與送貨的車輛分開，所以每一台車輛只負責一種運輸模式，並假設需求點不能同時有收和送的貨物存在，目標為找尋總距離最小的運輸路徑。每一需求點只能由一輛車服務，各路徑的需求點總量不能超過車容量，且每輛車皆以場站為起訖點。此法能降低問題的複雜度，但會降低貨車的載貨率。

2. 去程送貨、回程撿收

此類型的問題先依顧客需求分為收貨與送貨兩部份，因為每個需求點可能同時會有收貨與送貨的要求，但在有車容量的限制下，擔心可能會超載的情形發生，所以貨車在運輸過程中，先將所有須送貨的需求點服務完畢，然後在回場站的途中，進行收貨的動作。每一台車輛在運輸過程中，

必須先將所有送貨服務完成，再開始進行收貨之服務。Golden (1985)提出先送貨之車輛途程，利用節省法一一將各節點插入，再完成回程撿收的路

(14)

13

徑規劃。Potvin (1996)利用基因演算法求解具有時窗限制的回程撿收的問題，在建構初始路線部分作者利用貪婪法(Greedy Method)的方法求得，利用基因演算法的機制分別對途程間與途程內改善路線，以求得較佳的可行解。此法雖然可以克服車容量限制的問題，但若遇到同一需求點有收貨與送貨的要求時，貨車勢必要在同一次的運輸過程中，拜訪同一個需求點兩次，這種情形在實務上是比較不合常理的。

3. 同時收送貨

回程撿收強調貨車先完成送貨部分，然後在回程時再進行收貨的動作，而同時收送貨之車輛途程問題則沒有這項限制，所以此類型問題是較符合現實生活中的情況，但在求解問題的複雜度也相對的比較高。此類型的問題在求解的設計上，一般仍是以車容量為優先考量，所以貨車先對只有送貨項目的需求點進行服務，當貨車空出一定比例的車容量時，才考慮服務同時有收貨和送貨的需求點，並先等送貨服務完成，再進行收貨服務。因此，在尚未完成所有送貨需求以前，盡量不要拜訪僅有收貨的需求點，才能有較多的載貨空間，不僅可提高載貨率，也能避免超載的情形發生，運輸的路線也有較多的選擇。蘇文清 (2005)提出不需騰出一定比例空間，才能進行撿貨服務之限制，只要在車容量允許的情況下，即可前往具有同時收送貨之需求點進行服務，使貨車送貨路徑的安排更具有彈性，結果顯示在成本微幅增加情形下，能有效的提高車輛之使用率，降低運輸車輛回程之空車容量。黃小芬 (2005)除了考量車輛行駛距離成本外，加上途程需求點間空車運行之懲罰成本，並利用禁忌搜尋法求解同時有收送之車輛途程問題，並期望提高車輛使用率及較少的車輛使用數，亦即為較少途程數之路線規劃，結果顯示考慮載貨率之成本模式，並加入懲罰成本後能有效的提高車輛之載貨率，減少車輛使用數。

2.4 常用於車輛途程問題之演算法

禁忌搜尋法(Tabu Search; TS)(Fermín Alfredo Tang Montané, 2006)

禁忌搜索的構想最早由 Fred Glover 提出，它是對局部領域搜索的一種

(15)

14

擴展，是一種全局逐步尋優演算法，是對人類智力過程的一種模擬。TS 演算法通過引入一個靈活的存儲結構和相應的禁忌準則來避免迂迴搜索，並通過藐視準則來赦免一些被禁忌的優良狀態，進而保證多樣化的有效探索以最終實現全局優化。首位用禁忌搜尋法求解車輛途程問題是 Willard (1989)，將已經搜尋過的解紀錄下來，以避免重複或無意義的搜尋，等待將所有鄰近區域搜尋完畢後，選擇一個最佳的方向來進行移步(Move)，當出現有比目前最佳解較好解時則將更新目前最佳解，直到符合終止條件才停止。

賴志豪 (2006)探討宅配方面具時間窗下之車輛途程問題，以最鄰近佳解法作初始可行解的規劃，再藉由禁忌搜尋法作改善階段，分別利用 Swap 交換法及 Or-Opt 交換法擬出四種混合策略作比較測試，找出最佳路線與求取最小化車輛旅行距離與懲罰成本之總和。

基因演算法(Genetic Algorithm; GA)(Goldberg, 1989)

基因演算法的概念是來自於達爾文適者生存的理論，是一種優勝劣汰的遺傳機制，於 1975 年由美國的 John Henry Holland 教授與其學生首先提出。以染色體表示隨機產生的多組起始解，染色體藉由交配(Crossover)或突變(Mutation)的方式產生後代，留下好的解，淘汰差的解，重複產生下一世代，直到達最大世代，結束演化。每條染色體（chromosome，或稱基因型個體 individuals）內的基因都是布林數（由 0 或 1 組成），用以表示分類的法則。

模擬退火法(Simulated Annealing; SA)(Yu & Lin, 2014)

模擬退火法最早由 Nicholas Metropolis (1953)提出，而在 S. Kirkpatrick (1983)的推廣下才更廣為人所知，如今 SA 已經被運用在各種類型的途程和

(16)

15

調度問題，例如：Travelling Salesman Problem(Chang-Sung Jeong, 1991)，

Logistics Resource Planning(Yu & Lin, 2010)，分配問題(Sofianopoulou, 1992)，工作輪轉調度問題(Serap Ulusam Seçkiner, 2007)。模擬退火演算法用於在一個搜尋空間內找尋最佳解。原理來自冶金學的退火，退火是指一種物理過程，將固體加熱至足夠的高溫時，固態轉變成液態，而分子會在液態物質中隨機的自由排列，隨著溫度下降，分子會逐漸到較低能量的結晶重新排列，模擬退火法即是建構在此模型上，當溫度高時，分子的自由移動，產生可行解，溫度下降時，系統的組態在能量表面移動受到限制，

分子逐漸向低能量的區域集中，在每一次的迭代過程中，都是以目前解做為中心，隨機產生新的鄰近解，新的解較佳時即可取代目前解；較差時，

利用機率函數和控制溫度參數來判斷是否接受新解，因此具有能找尋跳脫區域的最佳解。降溫的動作用來控制收斂速度，溫度越下降，接受較差解的機率越小，當溫度降到低點時，僅接受較佳的解，進而達到收斂，獲得最佳解。

(17)

16

第三章數學模型規劃

本章將會定義同時收送貨之車輛途程問題，完整的說明研究目標與基本假設，並運用 PDVRP 數學模型搭配第二章所提及的演算法概念，在第四章使用模擬退火法為基礎來設計，有效解決此類問題且能應用於實例之中。

3.1 問題定義與假設

本研究假設卡車容量、收貨與送貨的地理位置、收貨量及送貨量均為已知，應用數學規劃方法，參考 PDVRP 為基本架構，PDVRP 的部分需求點接受收貨服務，部分需求點接受送貨服務，且車輛具容量限制都與自行車系統配置問題相似。藉由表 1 說明兩者之間的關係，並由圖 1 舉例公共自行車靜態配置中卡車路線配置情況，卡車從發車地出發，分別行駛路線 1-2-3-4 及路線 5-7-9- 10，其中缺位站需將站上的自行車放入卡車，而缺車站需將卡車上的自行車放入站內，以路線 1-2-3-4 為例，卡車由發車地抵達第 1 站取走 10 台自行車，前往第 2 站放入 7 台自行車，再前往第 3 站取走 5 台自行車，最後到第 4 站放入 8 台自行車，此路線成本不包含卡車從發車地出發前往第 1 站及第 4 站回到卡車出發地的成本。

表 1 PDVRP 與公共自行車靜態配置比較

PDVRP 公共自行車靜態配置

收貨站缺車站

送貨站缺位站

轉運中心卡車發車地

路線路線

(18)

17

圖 1 公共自行車靜態配置路線示意圖

定義

卡車於夜間（公共自行車系統的流動量趨近於零的時段）由發車地點出發到各站點取自行車或放置自行車，將各站點的自行車數調整為該站的最佳數量。

基本假設

1. 每台卡車只能到各個站一次。

2. 卡車載的自行車總數不得超過其可載運的數量。

(19)

18

3.2 收送貨車輛途程問題之數學模型

參數

N

車站；i=1,...,|N|。

𝑁

₀

點，包含車站和倉庫(i=0)；i=0,...,|N|。

𝑆

_𝑖 ⁰ i 站在配置前的自行車數量。

𝐶

_𝑖 i 站可放置的自行車數量。

𝑘

_𝑣

卡車可載的自行車數量；v ∈V。

𝑆

_𝑖 ^𝑙 i 站上最佳的自行車數量。

𝑡

_𝑖𝑗

卡車由 i 站到 j 站所花費的時間。

α 卡車行駛的時間成本相對於懲罰成本的權重。

T

每台卡車行駛的限制時間。

。

代表各站未達到最佳數量產生的成本；𝑎𝑖是每相差一台車之成本。

決策變數

𝑥

_𝑖𝑗𝑣

卡車 v 由 i 站到 j 站有行駛等於 1，否則為 0 的二元整數。

𝑦

_𝑖𝑗𝑣

卡車 v 從 i 站到 j 站運輸的自行車數量。

若為零則表示卡車 v 未於 i 站到 j 站間行駛。

𝑦

_𝑖𝑣 ^𝐿

卡車 v 從 i 站取走的自行車數量。

𝑦

_𝑖𝑣 ^𝑈

卡車 v 放入 i 站的自行車數量。

𝑞

_𝑖𝑣

)+ α ∑

_𝑖∈𝑁

₀∑

_𝑗𝜖𝑁

₀∑

_𝑣𝜖𝑉

𝑡

_𝑖𝑗

𝑥

_𝑖𝑗𝑣

(1)

限制式：

𝑆

_𝑖

= 𝑆

_𝑖 ⁰

− ∑

_𝑣∈𝑉

(𝑦

_𝑖𝑣 ^𝐿

− 𝑦

_𝑖𝑣 ^𝑈

) ∀𝑖 ∈ 𝑁

₀

₀

, ∀𝑣 ∈ 𝑉 (3)

𝑦

_𝑖𝑗𝑣

≤ 𝑘

_𝑣

𝑥

_𝑖𝑗𝑣

∀i ∈ 𝑁

₀

, 𝑖 ≠ 𝑗, ∀𝑣 ∈ 𝑉 (4)

∑

_𝑗∈𝑁

₀

_𝑗≠𝑖

𝑥

_𝑖𝑗𝑣

= ∑

∀𝑖 ∈ 𝑁

₀

(7)

∑

_𝑣∈𝑉

𝑦

_𝑖𝑣 ^𝑈

≤𝐶

_𝑖

− 𝑆

_𝑖 ⁰

∀𝑖 ∈ 𝑁

₀

(8)

∑

_𝑖∈𝑁

₀(𝑦

_𝑖𝑣 ^𝐿

− 𝑦

_𝑖𝑣 ^𝑈

) = 0 ∀𝑣 ∈ 𝑉 (9)

∑

_{𝑖𝑗∈𝑁}

₀

_𝑖

≥ 0 ∀𝑖 ∈ 𝑁

₀

(15)

𝑞

_𝑖𝑣

≥ 0 ∀𝑖 ∈ 𝑁

₀

, ∀𝑣 ∈ 𝑉 (16)

(1)表示最小化成本，成本包含懲罰成本及卡車運輸時間。

(2)表示系統配送後的數量等於配送前數量加減運輸數量。

(3)、(4)、(5)、(7)、(8)及(9)表示卡車在各站間運輸的數量要合理，接收數量要在可容量範圍內，而卡車最多只能載走各站上原有自行車數量。

(6)表示每台卡車，最多只能到各站一次。

(10)表示限制每台卡車行駛時間。

(11)表示消除 sub-tour 的式子。

(12)表示站到站是否行駛的變數要為二元整數。

(13)(14)(15)(16)表示各項變數均為正整數。

此模型參考 Tal Raviv (2013)的模型架構，並將其中總配置時間限制改為每台卡車行駛時間限制，懲罰成本計算由原本的函數改為單位成本。

3.3 CPLEX 建構

以 CPLEX 計算 3.2 節數學模型，求解小題組，以驗證數學模型是否正確，

題組資訊與最佳解如表 2，以 20160816-20 題組為例，將配置結果的卡車行駛路線標示於地圖上，如圖 2 所示。

(22)

21

表 2 CPLEX 求解之題組資訊及最佳解

題組總站數卡車數量總需求未滿足數

量總成本

20160812-10 10 1 66 1 16.954421 20160816-20 20 2 157 31 44.992 20160816-28 28 2 205 9 43.8622

圖 2 20160816-20 題組配置結果之行駛路線 -8

+8

-12 -2

+14

-6

+6

-15

+14 -6 -3

+10

-11

(23)

22

第四章演算法設計

本章將說明以模擬退火法為基礎的演算法流程，並額外說明如何產生鄰近解之部分，將提出數種卡車路線選擇範圍及搬運量求得方式，並代入題組運算後相互比較，選擇最適當的演算方式，增加解題效率。

4.1 演算法架構

本研究使用模擬退火法為基礎，並因題目特性再作改良。模擬退火演算法在產生一組鄰近解時，運用的是行駛順序交換，此部分將於 4.2 節說明，而本研究靜態配置最佳化問題為收送貨車輛途程問題，當行駛順序不同時，將連帶影響各站可搬運量，在兩項變數皆會受影響的情況下，若鄰近解為較佳的行駛路線，卻有可能因隨機搬運量的不同而產生不同的成本，因此，本研究將改善鄰近解只能運算其行駛路線中可行的一組搬運數量，增加同一行駛路線下不同搬運量之可行解，使其更為有效的找出最佳解。

本研究所使用演算法流程如圖 3 所示。第一步設定各項參數，所使用的參 數：I 為嘗試次數，其初始值為 0，最大嘗試次數為 I

iteration

(24)

23

生一個在 0 到 1 之間的隨機數 r

2

，判定 r

2

是否小於𝑒

⁽⁻

^𝐾𝑇^∆

⁾

，是則以 Y 取代 X；否 則重新產生新解，由嘗試次數 I=I+1 開始。以 Y 取代 X 後得到新的目標解

Obj(X)，檢查 Obj(X)是否小於目前的最佳解 F best

，是則更新目前的最佳解 F

best

以及將未改善次數 N 歸零，並檢視嘗試次數 I 是否達到最大嘗試次數 I

iteration

； 否則直接檢視嘗試次數 I 是否達到最大嘗試次數 I

iteration

，是則改變溫度；否則 重新產生新解，最後判斷溫度 T 是否小於等於最終溫度 T

final

或未改善次數 N 是 否等於最大未改善次數 N

Non-improving

，是則結束；否則重新產生新解。

為了得知增加同一行駛路線下不同搬運量之可行解，是否能更為有效的找出最佳解，因此比較加入𝑟

₁

<N/N

Non-improving

此步驟前後的差異。表 3 為 2016 年 8 月 16 日題組加入𝑟

₁

<N/N

Non-improving

此步驟前後的差異，經過比較，得出加入這個步驟能有效找出更低成本之解。

表 3 改良前後之模擬退火法比較參數設定值

原始成本改良後成本改良百分比

T 0 T final

α

I iteration N Non-improving

100 0.01 0.965 10000 80 1876.11 1536.68 18.09%

(25)

24

開始

T =T0, I =0, α, Fbest=Obj(X), N=0 隨機產生初始解X；Xbest=X

Δ=Obj(Y)–Obj(X)≦0 Generate of r2

~ U(0,1)

r

2

< e

^(-^Δ^/KT)

X

best=X ; Let X=Y

Obj(X)<F

best Fbest=Obj(X) ; N=0

I=I

iteration

T=αT

T≦T

final or N=NNon-improving

Y

N

結束 Y Y

Y N

N

I=I+1

Y N

N

r

1

<N/N

Non-improving

產生新路線 N

取得Fbest的路徑 Y

Generate of r1

~ U(0,1)

分配卡車和各站拿放數量、計算總成本

N=N+1

圖 3 模擬退火演算法示意圖

(26)

25

4.2 路線順序規劃型態

一個好的路徑可以有效降低成本，因此，有關路線規劃問題中，常見的做法多為在上一組路徑中選出兩站進行交換、插入或反轉得到新路線。以下為交換、插入和反轉的規則說明：

1.

交換(Swap)：

由卡車的配送路線中隨機選出兩站，將這兩站的順序位置互換，得到一條新的路線。如圖 4，若原路線為：1-2-3-4-5-6-7-8-9-10，隨機選出第 4 站與第 9 站，將兩站互換，得到新的路線為：1-2-3-9-5-6-7-8-4-10。

圖 4 交換型態圖示

2.

插入(Insert)：

由卡車的配送路線中隨機選出兩站，將順序較後的站插入順序較前的另一站之前，得到一條新的路線。如圖 5，若原路線為：1-2-3-4-5-6-7-8-9-10，

隨機選出第 5 站和第 7 站後，將第 7 站插入原路線中第 5 站之前，得到新路線為：1-2-3-4-7-5-6-8-9-10。

圖 5 插入型態圖示

3.

反轉(Reverse)：

由卡車的配送路線中隨機選出兩站，將這兩站之間的所有站之順序倒置，

(27)

26

在放置回該路線上的同一位置，得到一條新的路線。如圖 6，若原路線為：

1-2-3-4-5-6-7-8-9-10，隨機選出第 2 站與第 7 站，將兩站之間的所有站(2-3- 4-5-6-7) 順序倒置，得到新路線為：1-7-6-5-4-3-2-8-9-10。

圖 6 反轉型態圖示

為了提高求得最佳路徑的效率，產生初始解時，先將資料內各站點作分區排列，以本研究的例題台北市 YouBike 系統為例，將 255 站以 12 個行政區作區分，再分別從各區內進行排列，每站的安排將會考量前站的需求狀況，所有站點分為從站上拿取自行車到卡車上的缺位站，和從卡車上拿取自行車放入站點的缺車站。若前站需求為拿取 15 輛自行車到卡車上的缺位站，則此站必定會到缺車站；若前站需求為拿 10 到 15 輛自行車到卡車上的缺位站，則此站有較高的機率到缺車站，以此類推，如圖 7 所示，得到初始路線。

圖 7 依前站需求量決定此站到缺車或缺位站之機率

接續 4.1 節所提到，本研究靜態配置最佳化問題為收送貨車輛途程問題，當行駛順序不同時，將連帶影響各站可搬運量，兩項變數皆會受影響，且各租賃站可分為缺車站和缺位站，所以只使用交換、插入和反轉這三種方式所得到的新路

開始

前站的需求量

缺10~14 個位子缺15

個位子

缺5~9 個位子

缺10~14 輛車缺15

輛車

缺5~9 輛車

此站有80%

的機率選擇到缺車站此站有100%

的機率選擇到缺車站

此站有70%

此站有80%

的機率選擇到缺位站此站有100%

的機率選擇到缺位站

此站有70%

結束缺0~4 個位子

此站有50%

缺0~4 輛車

此站有50%

(28)

27

徑，將無法有效的解決問題，因此本研究只保留選擇選取兩站的方法，從路線中選出兩站後，同初始解各區內考慮前站需求情況進行排列的方式，於選出的這兩站之間進行排列。

4.2.1 搬運量演算方式

本節分別說明全部隨機、全部滿足、有限制之隨機、部分隨機不搬運及部

分不搬運五種搬運量演算方式之定義，下列敘述中，「此站」定義為卡車欲前

往搬運的站，其他相關要件如圖 8 所示。

前站 ^此站距離此站 ^下站距離下一站

圖 8 搬運量相關要件說明圖 1. 全部隨機

各站搬運時，若行駛至缺車站，決定此站需求上限為

min (卡車上自行車數量, 此站缺車數量)；

若行駛至缺位站時，需求上限則為

min (卡車可放容量, 此站缺位數量)，

再隨機抽取 0 至需求上限之數量做為此站搬運量。另外，若為該台卡車的最後一站，搬運量則是取能使卡車上自行車為零的搬運數量。

(29)

28

2. 全部滿足

各站搬運時，直接滿足需求上限（同全部隨機方式之計算）之數量做為各站搬運量。另外，若為該台卡車的最後一站，搬運量則是取能使卡車上自行車為零的搬運數量。

3. 有限制之隨機

各站搬運時，先判斷此站與下一將行駛站需求狀況，若兩站需求狀況相同，皆為缺車站或皆為缺位站，且此站需求上限（同全部隨機方式之計算）

大於設定數量，即為目前卡車上自行車數量（或可放容量）有較佳之能力可連續滿足兩站需求，則此站搬運量隨機範圍將因下站需求量多寡按機率減少，

意指若下一站需求量越大，則此站減少能滿足之上限，使需求量較大的下一站更為滿足；反之，若此站需求量大於下一站，則提高此站搬運下限。另外一情況為此站與下一站需求情況相反，一為缺車站一為缺位站時，相加此兩站需求量，加總需求量越高則此站將有越高機率提高搬運下限，使此站完成更多需求量，便能同時讓下站滿足更多所需數量。再於調整後搬運下限至搬運上限隨機抽取做為此站搬運量。其餘不需調整搬運限制狀況時，做法與全部隨機相同。同樣，若為該台卡車的最後一站，搬運量則是取能使卡車上自行車為零的搬運數量。完整流程圖如圖 9 所示。

(30)

29

開始

是否為最後一站?

搬運數量=使卡車上自行車數量為零

^Y

需求下限=0,需求上限=Min(需求量, 卡車可完成數量)

N

此站與下一站需求狀況相同

需求上限>設定數量需求上限>設定數量

Y

依下站需求量多寡決定此站需求上限減少比例

Y

依此站及下站總需求多寡決定此站需求下限提高比例

Y

此站需求>下站需求

此站需求下限提高

此站搬運量=隨機抽取一需求下限至需求上限數量

N

Y

結束

N N

N

圖 9 有限制之隨機搬運流程圖

(31)

30

4. 部分隨機不搬運

各站搬運若遇距離成本大於配置後懲罰成本減少之效益時，將有一定機率不搬運此站，以下將分別舉例呈現此類之兩種狀況：

a. 此站與下站同樣是缺車站或缺位站，且此站需求量乘以單位懲罰成本<

距離成本。以表 4 及表 5 例題作為說明（註：假設懲罰成本每台自行車為 10）。

表 4 行駛此站時成本

目前將行駛站預計下一站將行駛站

需求量需要 3 台自行車需要 8 台自行車

卡車上自行車數量 8 台自行車 8 台自行車

行駛此站的距離成本 40 35

成本計算懲罰成本：30

距離成本：0

懲罰成本：0 距離成本：35

總成本 65

因每站懲罰成本皆為相同，當下一站與此站需求情況相同時，不去懲罰成本降低效益比距離成本低的此站，使下一站需求量更為滿足，會讓總成本更低。

b. 此站與下站的需求狀況相反，且 2 倍需求量乘以單位懲罰成本<距離成本。

當此站與下一站需求情況相反時，即使此站減少的懲罰成本低於距離成本，但因下一站與此站需求相反，在此站卸下或是搬運走的自

需求量需要 3 台自行車需要 8 台自行車

距離成本：40

總成本 105

(32)

31

行車，都會使下一站需求量更多機會被滿足，因此行駛此站所減少的懲罰成本將帶來兩倍的效益，則可以直接取放需求量，反之則隨機決定是否搬運此站。以表 6 及表 7 例題作為說明（註：假設懲罰成本每台自行車為 10）。

需求量需要 2 台自行車需拿走 10 台自行車

距離成本：45

總成本 90

需求量需要 2 台自行車需拿走 10 台自行車

距離成本：0

總成本 85

當遇上述兩項情況時，因為只比較此站及下一站之狀況，之後的變數仍存在，因此以機率決定是否搬運此站，保留更多可能性。除以上情況外，皆與全部滿足做法相同，同樣在該台卡車的最後一站時，

搬運量則是取能使卡車上自行車為零的搬運數量。圖 10 為部分隨機不搬運流程圖。

(33)

32

開始

結束是否為最後一站?

搬運數量=使卡車上自行車數量為零

本站需求狀況與下站相同

需求上限*單位懲罰成本<距離成本

2倍需求上限*單位懲罰成本<距離成本

抽取一0~1之間的隨機數r，r>0.5

搬運數量=0

搬運數量=需求上限

搬運數量=0 抽取一0~1之間的

隨機數r，r>0.5 ^{搬運數量=需求上限} Y

N

Y N

Y

N

Y

N

Y Y

N N

圖 10 部分隨機不搬運流程規則 5. 部分不搬運

做法大致與部分隨機不搬運模式相同，判斷此站與下一站之關係，並計算此站搬運後是否符合效益，不同之處為，當符合上述兩種情況時，判斷若是不去此站，則下一站滿足需求上限時，所減少的懲罰成本是否多於行駛至下一站之距離成本，若下一站無法產生此效益，則此站仍搬運全部需求上限數量；反之，若此站不搬運，下一站能使整體成本降低，則選擇不去此站，

此種做法比隨機不搬運模式多考量下一站將遇情況，進而直接判斷是否搬運此站。圖 11 為此做法之流程圖。

(34)

33

圖 11 部分不搬運流程圖

4.2.2 路線選擇範圍演算方式

分別說明全部區域、部分兩區域內、全部兩區域內及兩行政區內之搬運四種搬運量演算方式定義。

1. 全部區域

從全部站數中隨機抽取不同之兩站，藉由重新排列此兩站之間的路線產生鄰近解行駛順序。

2. 部分兩區域內

根據台北市 Youbike 系統卡車配置方式中，平均每個區域分配一台卡車負責 15 個站點，而各區域的卡車可至鄰近區域協助運送配置，因此，限制抽取的第二個站點（以下簡稱 b 站）的選擇範圍為第一個抽取站點（以下簡

開始

結束是否為最後一站?

搬運數量=使卡車上自行車數量為零

本站需求狀況與下站相同

需求上限*單位懲罰成本<距離成本

2倍需求上限*單位懲罰成本<距離成本計算不去此站後，

下一站需求上限

下一站需求上限*

單位懲罰成本<

下一站距離成本

此站需求上限=0 Y

N

Y N

搬運數量=

此站需求上限

Y Y

N

Y

N N

(35)

34

稱 a 站）周邊的 2 倍平均區域大小，即周邊 30 站的範圍。a 站及 b 站選擇規則，首先判斷 a 站是否為路線中的起始站或終點站，若是，則 b 站由路線中隨機選擇（b 站不等於 a 站），否則判斷 a 站的位置。根據 a 站的位子，b 站有一半的機率從全部站點中隨機選取，另一半的機率是從 a 站往前 30 站或往後 30 站的範圍中選取，例如：隨機取出的 a 站是第 20 站，位於起始站到 30 站之間，所以 b 站有 1/2 的機率由路線中隨機選擇（但 b 站不等於 a 站），有 1/4 的機率從第 21 站到第 50 站之間隨機選取，有 1/4 的機率由第 1 站到第 19 站之間隨機選取，如圖 12 所示。完整流程圖於圖 13 呈現。

圖 12 a 站為第 20 站之 b 站選擇範圍

3. 全部兩區域

與部分兩區域內選擇方式大致相同，不同的是，皆由 a 站的前後 30 站範圍內選取 b 站，藉由重新排列 a、b 兩站之間的路線，產生鄰近解。

4. 兩行政區內

與卡車所負責兩區域內 30 站點選取方式相似，但改為由行政區做為劃分，以台北市為例，行政區共分為 12 區，按相鄰順序分別是北投區、士林區、內湖區、南港區、信義區、松山區、中山區、大同區、萬華區、中正區、

大安區及文山區。作法為隨機抽取其中一區，再選擇此區鄰近一區，從此兩區內抽取 a 站及 b 站，重新排列 a、b 兩站之間的路線，產生鄰近解。

(36)

35

取得目前最佳解的路線順序

a介於2倍區域大小到末站減2倍區域大小之間 a介於起始站到

2倍區域大小之間

a介於末站減2倍區域大小到末站之間從路線中隨機取一

站b且b不等於a

從路線中隨機取一站a

a是起始站或末站

a點的位子 N

r2=1,r2=2 從路線中隨機取一站b且b不等於a

選取b站選取b站選取b站

開始

r2=3 由a點往後2倍區域

大小之間取一站b

r2=4 由a點往前2倍區域

r2=random(1,4) r2=random(1,4) r2=random(1,4)

r2=1,r2=2 從路線中隨機取一站b且b不等於a

r2=3 由a點到末站之間取一站b

r2=4 由a點往前2倍區域

大小之間取一站b r2=1,r2=2

從路線中隨機取一站b且b不等於a

r2=3 由a點往後2倍區域

r2=4 由起點到a點之間取一站b Y

取得a和b

r1=1 交換

產生新路徑

r1=2 插入

r1=3 反轉

得到新路線結束

圖 13 部分兩區域內選擇流程圖

(37)

36

4.2.3 分析

將前兩小節所提到的搬運量及路線範圍演算方式組合搭配，使用 2016 年 8 月 16 日資料，以行政區做分區，分別測試一區(20 站)、兩區(43 站)、六區(125 站)及十二區(255 站)題目，藉以分析各類演算法解題效能。（使用參數：T

0

： 100；T

final

：0.1；α：0.965；I

iteration

：100000；N

Non-improving

：80。）測試結果顯示，搬運方式的部分，「全部滿足」、「部分隨機不搬運」和「部分不搬運」這三種方式求解會得到較好的結果，彼此間差異不大，若測試的區域增加，可以發現「部分不搬運」能得到最好的結果。而在路線選區方式的部分，這四種方式的差異並不明顯，其中十二區(255 站)的測試結果，可以發現「部分不搬運」的搬運方式搭配「全部兩區域內」的路線選取方式所得到的結果最佳，因此本研究將採用「部分不搬運」的搬運方式搭配「全部兩區域內」的路線選取方式解題。

表 8 至表 11 分別為一區(20 站)、兩區(43 站)、六區(125 站)及十二區(255 站)測試結果，其中粗體字表示的結果為該區域測試組合中最低的結果。

表 8 一區(20 站)測試結果搬運方式

路線選取方式

全部隨機全部滿足有限制之隨機

部分隨機不搬運

部分

不搬運平均

全部區域 66.0106 49.0305 55.6754

48.3463 48.3463

53.481732

(38)

37

表 9 兩區(43 站)測試結果搬運方式

路線選取方式

部分

不搬運平均

全部區域/兩行政區 211.972 112.774 170.255 115.411 106.926 143.4676 部分兩區域內 217.114 120.066 169.508 107.814 122.224 147.3452 全部兩區域內 233.812 118.035 161.734 121.982

106.682

148.449

平均 220.966 116.9584 167.1657 115.069 111.944 146.4206

表 10 六區(125 站)測試結果搬運方式

路線選取方式

部分

不搬運平均

全部區域 949.937 617.222 868.583 610.251 638.157 736.83 部分兩區域內 975.138 616.505 883.634 657.202 623.007 751.0972 全部兩區域內 955.68 612.961 882.738 649.536

586.609

737.5048 兩行政區內 960.319 624.141 908.579 646.913 614.426 750.8756 平均 960.2685 617.70725 885.8835 640.9755 615.5498 744.0769

表 11 十二區(255 站)測試結果搬運方式

路線選取方式

部分

不搬運平均

全部區域 2090.81 1550.2 1986.97 1673.49 1563.19 1772.932 部分兩區域內 2105.1 1536.09 2012.96 1756.37 1550.75 1792.254 全部兩區域內 2108.21 1556.19 2015.37 1639.19

1523.16

1768.424 兩行政區內 2112.39 1580.28 2017.57 1666.5 1530.49 1781.446 平均 2104.1275 1555.69 2008.2175 1683.8875 1541.8975 1778.764

公共自行車系統靜態配置最佳化

1

2

Keywords: Vehicle Routing Problem; Pickup and Delivery Vehicle Routing Problem;

3

4

5

6

T 0

I iteration

T final

N Non-improving

7

8

9

10

11

12

13

14

15

16

17

18

N

0

𝑖 0 i 站在配置前的自行車數量。

𝑖 i 站可放置的自行車數量。

𝑣

𝑖 𝑙 i 站上最佳的自行車數量。

𝑖𝑗

T

𝑖

𝑖

𝑖

𝑖

𝑖

𝑖

𝑖 𝑙

2

𝑖𝑗𝑣

𝑖𝑗𝑣

𝑖𝑣 𝐿

𝑖𝑣 𝑈

𝑖𝑣

𝑖

M

19

𝑖∈𝑁

𝑖

𝑖

𝑖∈𝑁

𝑗𝜖𝑁

𝑣𝜖𝑉

𝑖𝑗

𝑖𝑗𝑣

𝑖

𝑖 0

𝑣∈𝑉

𝑖𝑣 𝐿

𝑖𝑣 𝑈

0

𝑖𝑣 𝐿

𝑖𝑣 𝑈

𝑗∈𝑁

≠𝑖

𝑖𝑗𝑣

𝑗∈𝑁

≠𝑖

𝑗𝑖𝑣

0

𝑖𝑗𝑣

𝑣

𝑖𝑗𝑣

0

𝑗∈𝑁

𝑗≠𝑖

𝑖𝑗𝑣

𝑗∈𝑁

𝑗≠𝑖

₀

_𝑖 ⁰ i 站在配置前的自行車數量。

_𝑖 i 站可放置的自行車數量。

_𝑣

_𝑖 ^𝑙 i 站上最佳的自行車數量。

_𝑖𝑗

_𝑖

_𝑖

_𝑖 ^𝑙

²

_𝑖𝑗𝑣

_𝑖𝑗𝑣

_𝑖𝑣 ^𝐿

_𝑖𝑣 ^𝑈

_𝑖𝑣

_𝑖

_𝑖∈𝑁

_𝑖

_𝑖

_𝑖∈𝑁

_𝑗𝜖𝑁

_𝑣𝜖𝑉

_𝑖𝑗

_𝑖𝑗𝑣

_𝑖

_𝑖 ⁰

_𝑣∈𝑉

_𝑖𝑣 ^𝐿

_𝑖𝑣 ^𝑈

₀

_𝑖𝑣 ^𝐿

_𝑖𝑣 ^𝑈

_𝑗∈𝑁

_≠𝑖

_𝑖𝑗𝑣

_𝑗∈𝑁

_≠𝑖

_𝑗𝑖𝑣

₀

_𝑖𝑗𝑣

_𝑣

_𝑖𝑗𝑣

₀

_𝑗∈𝑁

_𝑗≠𝑖

_𝑖𝑗𝑣

_𝑗∈𝑁

_𝑗≠𝑖

_𝑗𝑖𝑣

₀

_𝑗∈𝑁

_𝑗≠𝑖

_𝑖𝑗𝑣

_𝑣∈𝑉

_𝑖𝑣 ^𝐿

_𝑖 ⁰

₀

_𝑣∈𝑉

_𝑖𝑣 ^𝑈

_𝑖

_𝑖 ⁰

₀

_𝑖∈𝑁

_𝑖𝑣 ^𝐿

_𝑖𝑣 ^𝑈

_{𝑖𝑗∈𝑁}

_;𝑖≠𝑗

_𝑖𝑗

_𝑖𝑗𝑣

_𝑗𝑣

_𝑖𝑣

_𝑖𝑗𝑣

₀

_𝑖𝑗𝑣

₀

_𝑖𝑣 ^𝐿

_𝑖𝑣 ^𝑈

₀

_𝑖𝑗𝑣

₀